Discovery of False Identification Using Similarity Difference in GC-MS based Metabolomics

Summary

Compound identification is a critical process in metabolomics. The widely used approach for compound identification in gas chromatography-mass spectrometry (GC-MS) based metabolomics is the spectrum matching, in which the mass spectral similarity between an experimental mass spectrum and each mass spectrum in a reference library is calculated. While various similarity measures have been developed to improve the overall accuracy of compound identification, little attention has been paid to reducing the false discovery rate. We, therefore, develop an approach for controlling false identification rate using the distribution of the difference between the first and the second highest spectral similarity scores. We further propose a model-based approach to achieving a desired true positive rate. The developed method is applied to the NIST mass spectral library and its performance is compared with the conventional approach that uses only the maximum spectral similarity score. The results show that the developed method achieves a significantly higher F1 score and positive predictive value than those of the conventional approach.

1. Introduction

The mass spectrum, as a molecular fingerprint, is widely used for compound identification in gas chromatography-mass spectrometry (GC-MS) by matching to mass spectra recorded in a reference library. The success of the mass spectrum matching-based identification highly depends on the mass spectral similarity measure and the reference library. Most efforts have so far been focused on the development of a better spectral similarity measure to improve the accuracy of compound identification (e.g., Stein and Scott (1994); Kim et al. (2012b); Wagner et al. (2013)).

Stein and Scott (1994) compared among several similarity measures in compound identification and further suggested two modified measures, weighted cosine correlation and composite measure, that served as the stimulus for a series of follow-up works. In the follow-up works, some researchers developed more advanced measures using wavelet and Fourier transformations, optimal weight factors, partial and semi-partial correlations, ratio analysis, and retention indices (Koo et al. (2011); Kim et al. (2012a,b); Gu et al. (2013); Wei et al. (2014)). Using recently developed measures, Koo et al. (2013) performed the comparative analysis with the latest NIST spectral library and showed that the mixture semi-partial correlation outperforms other existing measures, but it is computationally most expensive.

On the other hand, little attention has been paid to how to control the false identification rate after spectral matching. Two decades ago, Stein (1994) proposed a method of obtaining probabilistic indicator of correct identification using a Bayes’ theorem. This method requires the pre-analysis of a reference library with training data to estimate the prior information. In a similar structural hierarchy to Stein (1994), Jeong et al. (2011) later proposed an empirical Bayes model to estimate posterior probabilities for compound identification using competition score. Characterization of the distributions of competition scores and similarity scores are required before applying their method to data. Recently, Matsuda et al. (2013) introduced a method to estimate the statistical significance of compound identification using BLAST. To use this method, mass spectra should be converted into protein-like alphabetical sequences and then the PAM-like score matrix should be estimated using a converted reference library. However, many complicated preprocessing steps, such as analysis of a reference library, high-dimensional parameter estimation, and conversion of mass spectra, are needed to obtain the significance of compound identification when using these existing methods and the result of these methods could be varied by user-defined input parameters, such as rank of similarity, number of mixture components, and range of signal intensity. Therefore, there is a need for a simple user-friendly method that requires no preprocessing with less user-defined parameters.

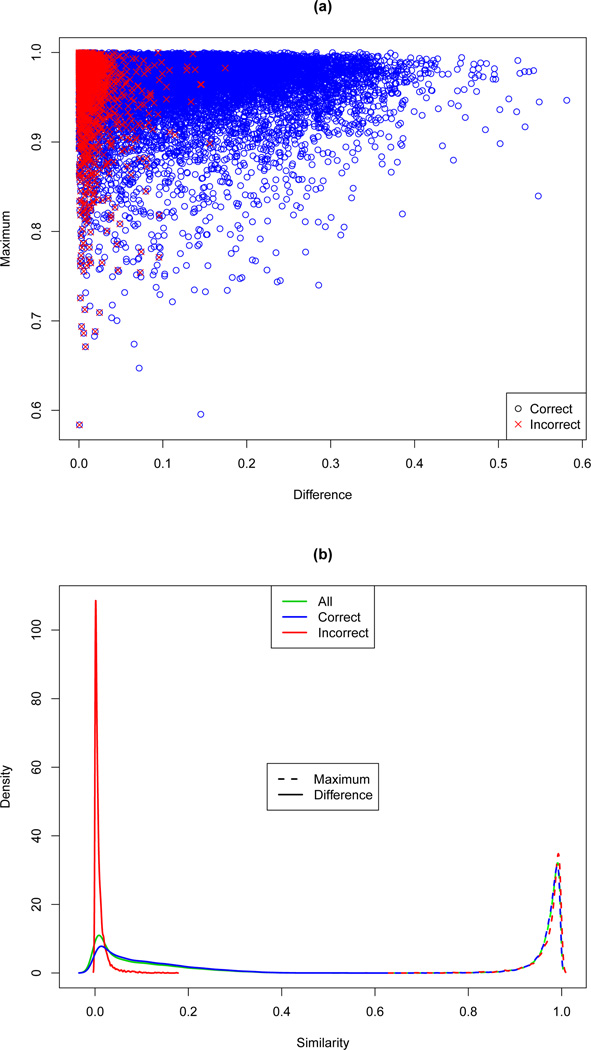
Indeed, due to the complicated tasks required to use, the aforementioned methods have not been widely used. Instead, a maximum spectral similarity score has been commonly used to deal with mismatched compounds. The only task required in this simple approach is for users to empirically set up a threshold of the spectral similarity score (usually, ≥ 0.6 or 0.7). Then the compound identification is considered as a correct identification if the maximum similarity score of a query mass spectrum fulfills this threshold. Otherwise, a match to the query spectrum is considered as a false identification. However, the range of the maximum similarity score of the false identification is generally not distinguished from that of the correct identification (e.g., see the y-axis of Figure 2(a)), which prevents from achieving either a higher true positive identification rate or a lower false identification rate.

Figure 2.

The scatter plot and the empirical distribution of the maximum similarity score and the difference between the first and the second highest similarity scores. The red “x” indicates the incorrect identification and the blue “o” represents the correct identification in (a). The empirical distributions located in the left in (b) are for the similarity difference and these in the right are for the maximum similarity.

The objective of this study is to develop a simple but powerful approach to dealing with false compound identifications. To this end, we use the difference of the first and the second highest spectral similarity scores. Our approach was motivated by the isomers that have very similar mass spectra to each other. In this work, it has been confirmed that isomers are indeed a major bottleneck for achieving a higher accuracy of compound identification, and we have further observed that more than 55% of the false identifications were cases that the true compounds have the second highest rank of spectral similarity, not the first highest rank. Based on these observations, we develop a method for assessing the significance of compound identification using the similarity difference between the first and the second highest scores. Besides, a model-based method of finding the cut-off value is developed using a Beta distribution to achieve a desirable true positive rate.

The rest of the paper is organized as follows. Section 2 describes the effect of isomers on compound identification and compares the maximum similarity scores with the difference of the first and the second highest similarity scores. In particular, it can be seen that the similarity difference has a potential ability to distinguish the distribution of the correct identification with that of the incorrect identification. In Section 3, the two methods, the maximum similarity method and the similarity difference method, are introduced along with the description of the mass spectral library used. In addition, a method of finding the cut-off value to achieve a desirable true positive rate is developed. In Section 4, the two methods are applied to the NIST mass spectral libraries and compared their performance in terms of compound identification. Conclusions are presented in Section 5.

2. Motivation

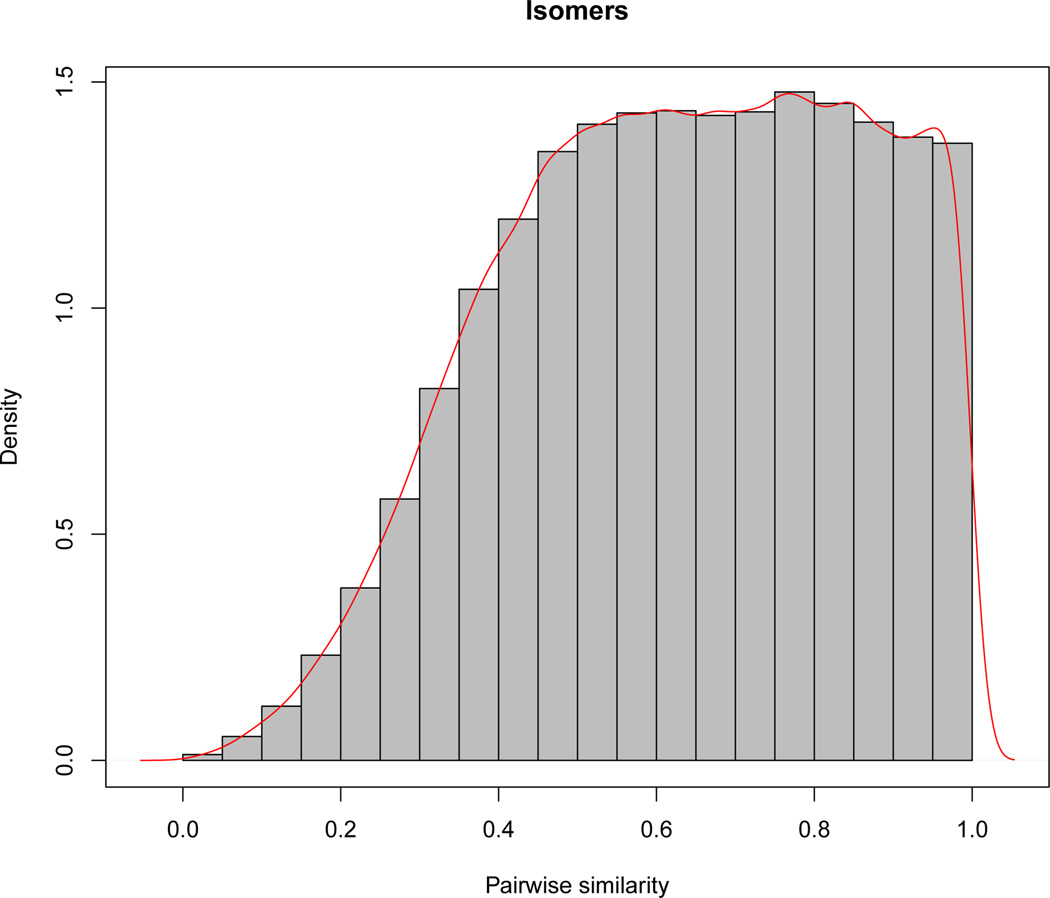
The isomers are compounds with the same molecular weight (and formula) but different chemical structures. Figure 1 depicts the empirical distribution and the histogram of the pairwise similarity scores within a set of isomers estimated using the weighted cosine correlation and the NIST WebBook mass spectral library as described in Kim et al. (2012b). The distribution is left-skewed and more than 17% (= 545/3126) of the isomer sets have the pairwise similarity scores ≥ 0.9, indicating that the mass spectral matching-based compound identification cannot differentiate the isomers from each other.

Figure 1.

The empirical density function and the histogram of the pairwise similarity scores of isomers.

We further investigated the effect of molecular weights (MWs) on compound identification. To do this, we ranked all the reference compounds in descending order of their spectral similarity scores for each query compound, and the MWs of the first and the second ranked reference compounds were further considered. We then recalculated the conditional accuracies (i) when these MWs are identical and (ii) when these MWs are different, respectively. As can be seen in Table 1, the conditional accuracy when these MWs are not equal becomes much higher (95.7%) than the overall accuracy (84.2%). Most of the incorrect matches occur when these MWs are equal. This fact inspired us to consider the difference between the first and the second highest similarity scores for high accuracy compound identification.

Table 1.

Accuracy table of compound identification. Note that “Equal” and “Not Equal” represent when the molecular weights of compounds having the first and the second highest similarity scores are equal and when the molecular weights are not equal, respectively.

	Equal	Not Equal	All
Correct	8071	10034	18105
Incorrect	2957	454	3411
Accuracy	73.19%	95.67%	84.15%

Figure 2 displays the plot of the maximum similarity score and the difference between the first and the second highest similarity scores. Figure 2(a) shows that the range of the incorrect maximum similarity scores is almost the same as that of the correct one, while the range of the incorrect similarity difference is less than or equal to 0.2. This means that the false discovery rate (FDR) can be zero if the similarity difference is used with the cut-off value of 0.2 or larger, while the FDR can never achieve a value of zero in the maximum similarity method. Figure 2(b) shows the empirical distribution of each of the maximum similarity (right-hand side) and the similarity difference (left-hand side). We can see that there is a clear separation between the distributions of the correct (blue solid line) and the incorrect (red solid line) similarity differences, but it is almost indistinguishable for the distributions of the correct (blue dotted line) and the incorrect (red dotted line) maximum similarity scores. Motivated by the information presented in Figures 1 and 2, we developed an approach to controlling the false identification discovery based on the spectral similarity difference between the top ranked compounds, which is described in the next section.

3. Methods

3.1 NIST WebBook mass spectral library and replicate spectral library

We considered the mass spectra extracted from the NIST Chemistry WebBook (NIST library) as a reference library and the repetitive library as query data. The NIST Chemistry WebBook service (http://webbook.nist.gov/chemistry/) provides users with chemical and physical information for chemical compounds including mass spectra generated by electron ionization mass spectrometry. The mass spectra of 23721 compounds were extracted from the NIST Chemistry WebBook as of November 28, 2011. The replicate spectral library was obtained from the NIST 08 Mass Spectral Library (NIST08/2008), which contains 28307 mass spectra for 18569 compounds. The NIST Chemistry WebBook is considered as a reference library and the replicate spectral library is considered as query data. Compounds in the reference library and the query data with the same Chemical Abstracts Service (CAS) registry number are considered as the same compound. Since we assume that the reference library has the mass spectra for all query compounds, compounds that were not present in the reference library were removed from the query data. After the removal, 12850 compounds with 21516 mass spectra were left in the query data. The fragment ion m/z values were ranged from 1 to 892 with a bin size of 1.

3.2 Weighted cosine correlation

The cosine correlation (Stein and Scott (1994)) was used to obtain the mass spectral similarity score between two mass spectra. Suppose $X={(x_i)}_{i=1}^n$ and $Y={(y_i)}_{i=1}^n$ are the mass spectra and then their pairwise mass spectral similarity score is calculated by

$$c_{XY}=\frac{X◦Y}{|X|◦|Y|}$$ (1)

where $X◦Y={\sum }_{i=1}^n{x}_i·y_i$, and $|X|=\sqrt{{\sum }_{i=1}^n{x}_i}$ is the total number of mass-to-charge ratio (m/z).

The fragment ion peaks with large m/z values in a GC-MS spectrum usually have small peak intensities, but carry the most important characteristics for compound identification. To increase the contribution of large fragment ions to compound identification, peak intensity are often weighted as

$${(\text{peak intensity})}^{w_1}·{(\text{mass}(m/z))}^{w_2},$$ (2)

where w₁ and w₂ are weight factors for peak intensity and m/z value, respectively. Then the weighed cosine correlation can be calculated by

$$c_{XY}^w=\frac{X_w◦Y_w}{|X_w|◦|Y_w|},$$ (3)

where $X_w={(x_i^w)}_{i=1}^n,Y_w={(y_i^w)}_{i=1}^n,x_i^w={(x_i)}^{w_1}·{(z_i)}^{w_2}$ and $y_i^w={(y_i)}^{w_1}·{(z_i)}^{w_2}$, where z_i is the m/z value of the ith intensity, i = 1, 2, …, n. In this study, we used w = (w₁, w₂) = (0.53, 1.3) (Kim et al. (2012b)).

3.3 Discovery of false identification

Two methods for discovery of false identification are employed in this study. The first method is the conventional approach based on the maximum similarity score, and the second method is the newly developed approach using the difference between the first and the second highest similarity scores.

Suppose there are m query mass spectra (X₁, X₂, …, X_i, …, X_m) and n reference mass spectra (Y₁, Y₂, …, Y_j, …, Y_n). After matching to the reference mass spectra, each query mass spectrum has the first and the second highest similarity scores, $s^i=\{s_1^i,s_2^i\},i=1,\dots ,m$, where $s_1^i$ and $s_2^i$ are the first and the second highest similarity scores of the ith query mass spectrum X_i, respectively, and $s_1^i\ge s_2^i$. Without loss of generality, we assume that the first t query mass spectra are correctly matched to the reference mass spectra, (X₁, …, X_t), and the rest of the query mass spectra are mismatched, (X_t+1, …, X_m), where t ≤ m. Furthermore, suppose R query mass spectra are declared as discovery using a false identification discovery method and, of these R query mass spectra, V and S query mass spectra are incorrect and correct, respectively, where R = V + S. Then the true positive rate (TPR; also known as (aka) sensitivity or power), the false positive rate (FPR), the positive predictive value (PPV; aka true discovery rate), and the F1 score are defined by

$$TPR=\frac{S}{t};FPR=\frac{V}{m-t};PPV=\frac{S}{R};F1=\frac{2·TPR·PPV}{TPR+PPV}.$$ (4)

In fact, 1 − PPV is the false discovery rate and PPV can be interpreted as accuracy after decision. Table 2 summarized these decisions in a conventional form. Note that we consider TPR, FPR, PPV, and F1 as one when their denominator is equal to zero.

Table 2.

Contingency table of discovery of false identification.

		Decision
		Non-discovery	Discovery
Compound	Incorrect	U	V	m − t
Identification	Correct	Q	S	t
		m − R	R	m

3.3.1 The maximum similarity method

The conventional approach to false identification is simply based on the maximum similarity score. That is, if the highest pairwise mass spectral similarity score is larger than a user-defined cut-off value (ρ), the matched compound is considered as a true identification by

$$R=♯\{X_i|s_1^i\ge \rho ,1\le i\le m\}.$$ (5)

As a general practice, 0.6 or 0.7 is used as a cut-off value.

3.3.2 The similarity difference method

This approach uses the difference of the mass spectral similarity scores between the top two matches. Namely, the total number of discovery after decision is defined by

$$R=♯\{X_i|s_1^i-s_2^i\ge \gamma ,1\le i\le m\},$$ (6)

where γ is a user-defined cut-off value.

3.4 Finding a cut-off value of the similarity difference method to control the true positive rate

In order to achieve an anticipated true positive rate, we further developed a method to find a cut-off value of the proposed similarity difference method. To do this, we infer the distribution of the similarity difference of the true positives (i.e., correctly matched compounds). However, in practice, it is difficult to estimate the true distribution of the true positives and, although it is possible, it cannot guarantee that the data used for estimation represent the true positives only due to the presence of false positives inside. Fortunately, the similarity difference method has an interesting property to estimate the distribution of the similarity difference of the true positives more accurately. Namely, as mentioned in Section 2, we can clearly see that there are only correctly matched compounds when the similarity difference becomes greater than 0.2, representing only the true positives.

Suppose a user-defined cut-off value to find the set of true positives is δ (e.g., δ = 0.2 in this study) and there are m query mass spectra composed of t correctly matched mass spectra, (X₁, …, X_t), and m − t mismatched compounds, (X_t+1, …, X_m), where t ≤ m. Then the desired set of true positives is $D(\delta )=\{d_i|d_i=s_i^1-s_i^2\ge \delta ,1\le i\le m\}$, where d_i is the difference between the first and the second highest similarity scores of the ith query mass spectrum X_i. In fact, for the case of Figure 2(a), the true positive set D(0.2) is equal to {d_i|d_i ≥ 0.2, 1 ≤ i ≤ t}, in which all mass spectra come only from the set of the true positives. To estimate the distribution of the similarity difference of the true positives, we employed a beta distribution based on our estimation using all true positives of the similarity difference since the range of the weighted cosine correlation is the same as a Beta distribution, which is [0, 1].

A left truncated Beta distribution was used to infer the distribution of the similarity difference of the true positives due to that the set of the selected true positives is truncated at δ. We denote the left truncated Beta distribution at δ as

$$t\mathit{\text{Beta}}(\theta =(\alpha ,\beta )|\delta ),$$

where α, β > 0 and 0 < δ < 1. Once the parameter θ of the distribution is estimated, the critical value at ((1 − ε) × 100)% true positive rate (power or sensitivity), q(ε), is calculated using the estimated distribution of the similarity difference, where 0 ≤ ε ≤ 1. The value q(ε) is used as the cut-off value γ for Equation 6 to achieve the true positive rate of 1 − ε. This procedure is summarized as follows:

• Step I. Estimate θ̂ = (α̂, β̂) for the model D ~ tBeta(θ|δ).

• Step II. Calculate the critical value q(ε) with P(q(ε)) = ε using Beta(θ̂) where P(·) is the cumulative density function of Beta(θ̂).

• Step III. Set γ as q(ε).

4. RESULTS

The developed algorithms were applied to the NIST mass spectral data. We compared the performance of the developed algorithms with that of the conventional approach, and evaluated the method of controlling the true positive rate in terms of the accuracy of compound identification.

4.1 Comparison analysis

The developed similarity difference method was compared with the maximum similarity method using the weighted cosine correlation and the NIST mass spectral library. We evaluated their F1 score, PPV, TPR, and FPR for the results of compound identification. A set of 100 cut-off values, between 0 and 0.2 for γ and between 0.6 and 0.99 for ρ, were chosen for comparison based on Figure 2.

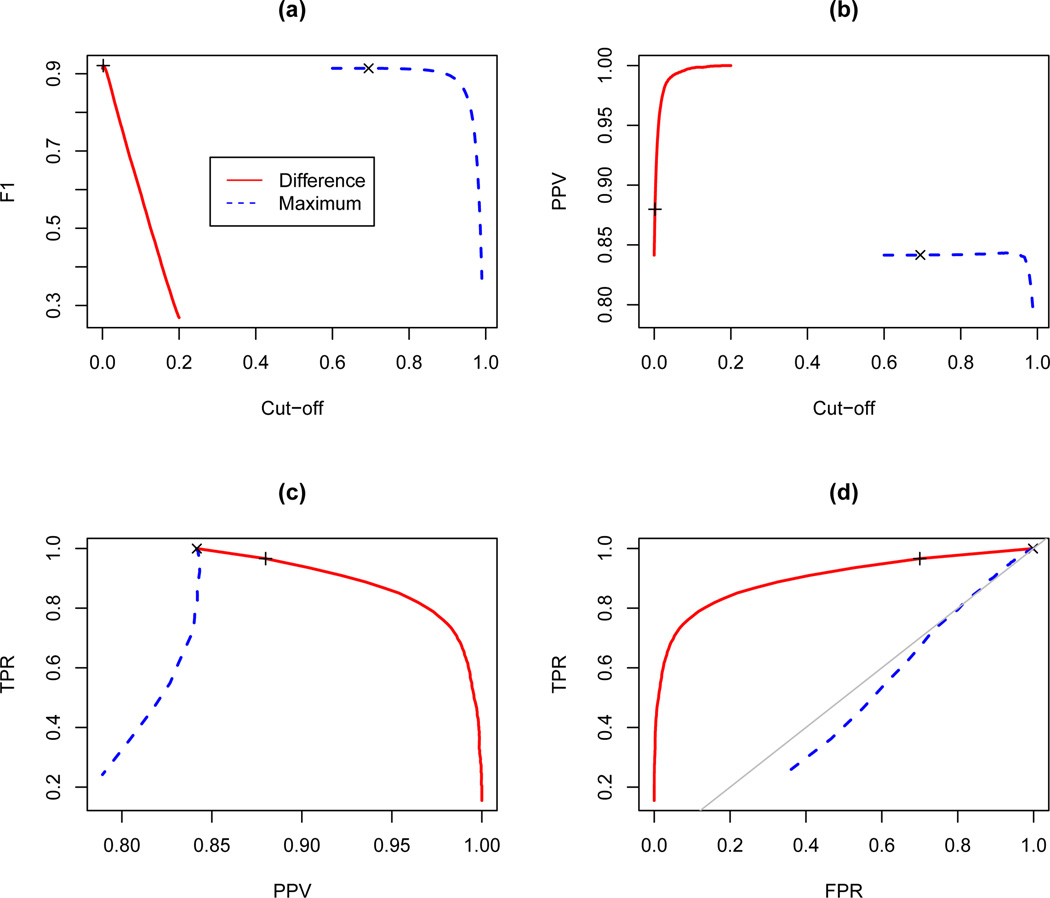
Figure 3(a) shows that the maximum F1 values occur at γ = 0.0020 and ρ = 0.6945 with 92.1% and 91.4% for the similarity difference and the maximum similarity, respectively, indicating that the developed method has a significantly larger F1 score. Namely, 1000 bootstrap replications give us (91.81, 92.36) and (91.12, 91.71) as 95% confidence intervals for the similarity difference and the maximum similarity methods, respectively. However, as expected, the PPV of the similarity difference method is always higher than that of the maximum similarity method in Figure 3(b) and the PPV of the developed algorithm becomes 100% from γ = 0.1756 with the true positive numbers (S) of 3689 in Table 3. The maximum PPV of the conventional approach is 84.3% at ρ = 0.9191, as shown in Table 4.

Figure 3.

Comparison of the maximum similarity and the similarity difference methods. (a) F1 score, (b) PPV, (c) TPR vs. PPV plot, (d) TPR vs. FPR plot (ROC curve). The symbols ‘+’ and ‘x’ indicate the points having the highest F1 score for each method, respectively.

Table 3.

Maximum F1 score. M1 and M2 represent the similarity difference and the maximum similarity methods, respectively.

	M1	M2
γ (ρ)	0.0020	0.6945
F1	92.09%	91.39%
PPV	87.99%	84.16%
TPR	96.60%	99.98%
S	17490	18101
V	2388	3406

Table 4.

Maximum PPV. M1 and M2 represent the similarity difference and the maximum similarity methods, respectively.

	M1	M2
γ (ρ)	0.1758	0.9191
PPV	100%	84.33%
S	3689	16960
V	0	3151

Figures 3(c) and 3(d) depict that the curves of the similarity difference method are closer to the upper right and the upper left than these of the maximum similarity method, respectively, indicating that the overall performance of the developed method is much better than that of the conventional approach.

The NIST replicate spectral library was generated in many different laboratories to represent analytical conditions in practice. Nevertheless, the real query mass spectra could be much noisier than the NIST replicate spectral library, resulting that the true similarity matching scores would be underestimated. This underestimation will cause the false discovery rate to increase so that PPV, TPR, and F1 values will be decreased. Another concern is that the real experimental data could include unknown compounds that are not present in the NIST mass spectral library. These unknown compounds could cause the false identification rate to increase, resulting in higher FPR and lower TPR than those in this study. That is, the ROC curve in Figure 3(d) could be either closer to or down to the diagonal as the number of unknown compounds increase.

4.2 Controlling the true positive rate

To examine the developed method of finding a cut-off value for the similarity difference method to achieve a desired true positive rate (aka power or sensitivity), we compared the result of the set D(δ) with that of the true positives {d_i, 1 ≤ i ≤ t}, which is the entire set of correctly matched mass spectra, as a benchmark. Three different values, 0.1, 0.2, and 0.3, were used for δ to obtain the set of possible true positives D(δ), and then 1000 bootstrap replicates were used to construct the 95% confidence bands. In order to run bootstrap, 1000 sets of query library were first created by resampling the NIST replicate spectral library with replacement. Then the compound identification was performed on each of the resampled sets, resulting in 1000 sets of the similarity differences. Using these similarity differences, the parameters of the Beta distribution were estimated, obtaining the 1000 relationships between the desired true positive rate and the observed true positive rate.

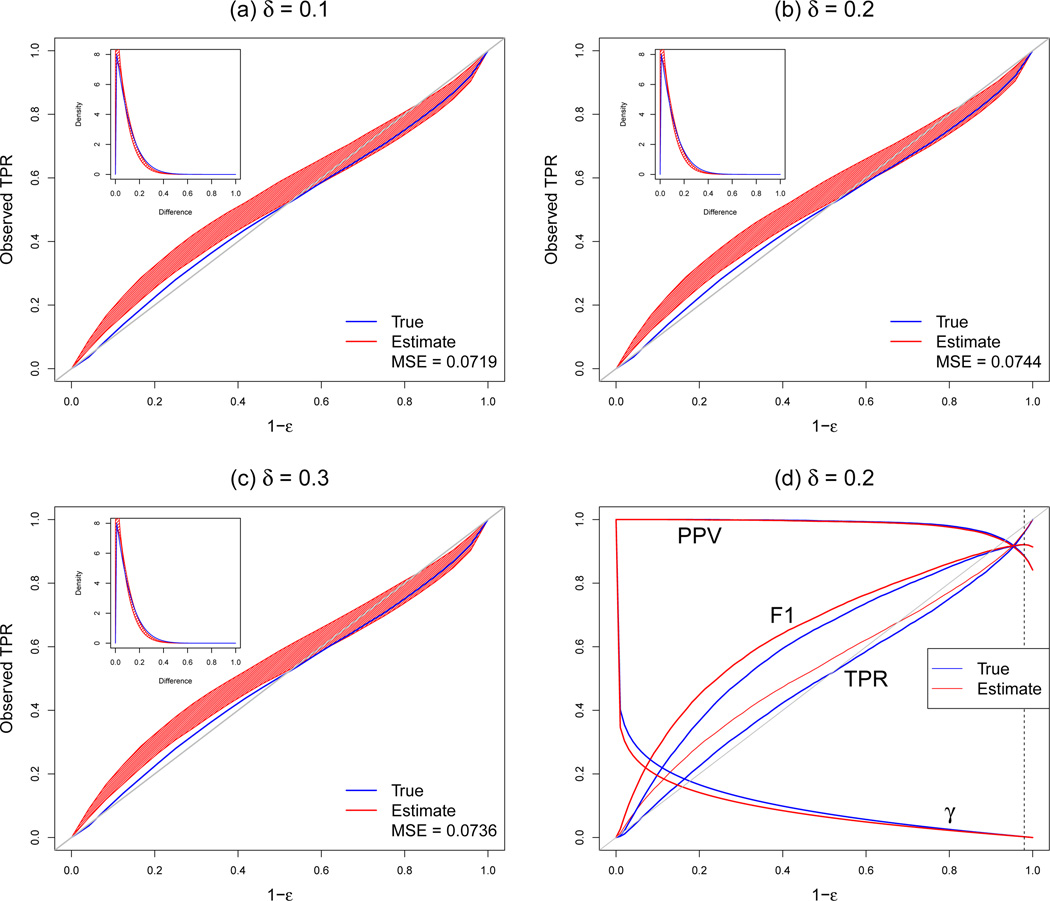
Figure 4 displays the relationship between the desired true positive rate (1 − ε) and the observed true positive rate (TPR) for each of the three δ values along with the 95% confidence bands. The area filled with red indicates the 95% confidence bands of 1000 bootstrap replicates with δ, while the blue line is the result from all correctly matched mass spectra. The inlet represents the estimated Beta distributions of the true similarity difference (blue line) and of the selected subset of the similarity difference (red line). The average of their mean squared errors is also displayed inside the plot. We can see that the observed TPR for both the entire set and the selected subset is underestimated when the desired TPR is greater than 0.5, while that is overestimated when the desired TPR is less than 0.5. Furthermore, the 95% of confidence bands include the true TPR when the desired true positive rate is greater than 0.5. These trends are the same for all three δ values. In terms of the Beta distribution, all three cases have comparable MSE values even though the MSE is the smallest when δ = 0.1. Figure 4(d) shows the relationship among 1−ε, F1 score, PPV, TPR, and the cut-off value (γ) using the entire data of the similarity difference with δ = 0.2. The difference between the true and the estimated lines is small when 1 − ε > 0.9 and is large when 1 − ε ≤ 0.9. The maximum F1 score occurs when ε = 0.0202, which is 92.1% with PPV of 88.4% and TPR of 96.1%.

Figure 4.

The relationship between the desired TPR (1 − ε) and the observed TPR using 1000 bootstrap replicates when (a) δ = 0.1, (b) δ = 0.2, and (c) δ = 0.3. The scatter plots between (1 − ε) and PPV, F1, FPR, and the cut-off value (γ) using the entire data with δ = 0.2 are in (d). In (d), the dotted black line indicates the point when F1 value is the maximum.

5. CONCLUSIONS

A simple but powerful approach for a better true positive identification rate using the difference of the first and the second highest spectral similarity scores was developed for the analysis of GC-MS data for compound identification. A model-based approach to achieve a desired true positive rate was also proposed. Compared to the conventional approach based on the maximum similarity score, the developed algorithms have several advantages. First, it is more powerful in terms of the higher PPV and can further achieve the false discovery rate of zero. Second, it has the ability to infer the distribution of the correctly matched compounds and so to achieve a desirable TPR using a statistical model-based approach.