Abstract
We present a simple framework for classifying mutually exclusive behavioural states within the geospatial lifelines of animals. This method involves use of three sequentially applied statistical procedures: (1) behavioural change point analysis to partition movement trajectories into discrete bouts of same-state behaviours, based on abrupt changes in the spatio-temporal autocorrelation structure of movement parameters; (2) hierarchical multivariate cluster analysis to determine the number of different behavioural states; and (3) k-means clustering to classify inferred bouts of same-state location observations into behavioural modes. We demonstrate application of the method by analysing synthetic trajectories of known ‘artificial behaviours’ comprised of different correlated random walks, as well as real foraging trajectories of little penguins (Eudyptula minor) obtained by global-positioning-system telemetry. Our results show that the modelling procedure correctly classified 92.5% of all individual location observations in the synthetic trajectories, demonstrating reasonable ability to successfully discriminate behavioural modes. Most individual little penguins were found to exhibit three unique behavioural states (resting, commuting/active searching, area-restricted foraging), with variation in the timing and locations of observations apparently related to ambient light, bathymetry, and proximity to coastlines and river mouths. Addition of k-means clustering extends the utility of behavioural change point analysis, by providing a simple means through which the behaviours inferred for the location observations comprising individual movement trajectories can be objectively classified.
Introduction
Characterising patterns of behaviour within the movement trajectories of individuals now is a central theme in animal ecology [1–3]. The geospatial lifelines of animals commonly exhibit multiphasic states of behaviour that can be discriminated by distinct geometric combinations of derived movement attributes such as speed and turning angle [4–7]. Methods to infer patterns of behaviour within animal-tracking data sets include state-space models [6,8,9], first passage time [10], maximum entropy [11], positional entropy [12], phase-state models [13], maximum predictive partitioning [14], local fractal dimension [15], Gaussian mixture models [16], partial sum method [17], exponential-segment mixture models [18], and the multi-scale straightness index [19]. Many of these methods are conceptually complex and computational challenging, however, which limits their accessibility to would-be practitioners [6,20–23].
Developed by Gurarie et al. [23], ‘behavioural change point analysis’ (BCPA) is a likelihood-based means of detecting latent structural changes in the parameters underlying locational time-series data. BCPA is performed on components of persistence- and turning-velocity from a continuous-time, Gaussian (Ornstein-Uhlenbeck) process. The method works by sweeping an analytical window over a geospatial lifeline, identifying elements (‘change points’) in the time series where changes in the autocorrelation structure are abrupt. Change points in trajectories are assumed to correspond to discrete shifts in modes of behaviour; many other methods for modelling patterns of behaviour in animal-tracking data are based on this principle [9,12,13,19]. Advantages of BCPA include its robustness to the missing observations and measurement errors that are common in animal-movement data, its computational efficiency and comparative ease of implementation, and its ability to reveal structure in animal-tracking data without prior assumptions regarding the distributions of movement parameters. The method has been applied to several studies of birds and mammals [24–26]. Unlike most other means for inferring changes in behaviour in movement trajectories, however, BCPA does not classify the individual locations comprising animal-tracking data into one of a pre-determined number of mutually exclusive states [27]. This characteristic limits the biological interpretability of individual bouts of behaviour identified by the procedure, and presents challenges for subsequent analysis of BCPA outcomes using standard statistical methods for categorical data (as in [28]).
The most commonly used means of classifying observations or events into discrete groups or categories is k-means cluster analysis [29,30]. This method encompasses a number of different fitting algorithms that aim to partition n observations into k groups, where individual observations are assigned to respective categories (‘clusters’) in such a manner that the degree of association between two observations is maximal if they belong to the cluster and minimal otherwise. Algorithms for k-means cluster analysis require that the number of clusters (groups) be specified a priori. Comparatively well-known and computationally simple, k-means clustering is a simple and effective procedure for grouping bouts of animal behaviour into homogenous same-state classes. Previously, k-means clustering has been used to group the individual location observations of animal-movement trajectories into different behavioural modes [31–33]; however, applied in this manner the method neglects useful information about temporal autocorrelation structure that realistically represents behavioural processes.
In this study, we extend the utility of BCPA, by combining it with k-means clustering to develop a procedure for classifying the location observations comprising animal-movement trajectories into distinct, mutually exclusive states of behaviour. Our aims are to: (1) evaluate the ability of the method to correctly classify behaviours, using simulated movement trajectories in which the ‘true’ states are known; and (2) demonstrate the operation and utility of the approach, by applying it to high-resolution foraging tracks obtained by GPS telemetry, in a case study of the Little Penguin (Eudyptula minor). Our ultimate intention is to describe a simple yet efficient means of exploring the behavioural patterns of free-ranging animals.
Methods
Study species and site
The little penguin is the smallest of all sphenisciforms; adults weigh ca. 1 kg. The species is widely distributed along the coastlines of southern Australia, as well as the North, South, Stewart, and Chatham Islands of New Zealand. Primarily nocturnal when at their colonies where they nest close to the shore in burrows, little penguins mainly are found within 25 km of land during the breeding season, but are known to travel farther when not breeding [34]. Adults spend most of the year at sea, but during the breeding season they form pair bonds and alternately undertake short foraging trips that range in length from one to seven days [35]. We chose little penguins as our study species because comparatively little is known about their at-sea behaviour [36,37], their non-threatened conservation status, and the ease with which the study colony could be accessed [37,38].
Our study was conducted in November 2012 on birds from a large colony (>200 breeding pairs) located on Matiu/Somes Island (41.26 S, 174.87 E), a 25- ha pest-free wildlife reserve administered by the New Zealand Department of Conservation that is centrally located in highly urbanised Wellington Harbour. Permission for the study was granted by the New Zealand Department of Conservation (Permit number: WE-34306-FAU); all capture and handling protocols were approved by the University of Auckland's Animal Ethics Committee (AEC/001043).
GPS telemetry
We used archival GPS data-loggers (‘i-gotU GT120’, Mobile Action Technology) to track the movements of the study animals. Units were waterproofed by sealing them in a single layer of plastic (polyethylene terephthalate, ‘PET’) heat-shrink wrap (0.5 mm wall thickness; DONGGUAN ANPRY PIPE Co. Ltd.). The loggers were ca. 45mm x 25 mm x 8 mm; total weight including the tape used for attachment ranged between 12.3 g and 15.5 g, comprising 1.1% to 1.8% of the weight of the study birds (900 g to 1250 g). GPS receivers were configured to record location estimates at a nominal sampling interval of 1 fix per min, starting at 03:00 local time (UTC+13h) and running continuously thereafter.
Animal capture and handling
To minimize differences among individuals in body size, reproductive state, and environmental conditions, and to reduce possible deleterious effects on nest attendance, we limited data collection to a 24-h period during the mid-chick-guarding stage. Eight breeding adults were removed from their nest boxes during the afternoon of 6 November 2012, placed in a cloth bag and weighed, then fitted with a GPS data-logger. GPS units were attached dorsally between the flippers with 5–7 strips of 1-cm overlapping waterproof duct tape [39]. After ca. 24 h, individuals were re-captured in their nest boxes and their GPS devices were removed to recover the tracking data.
Data analysis
The workflow of analytical procedures for inferring and classifying behaviours within the tracking data is described in Fig 1. Location observations obtained from the GPS loggers were processed to calculate speeds and relative turning angles (RTAs) between all sequential pairs of position fixes comprising individual movement trajectories. Code available in the R programming language [40] provided by Gurarie et al. [23] was adopted and modified to execute the BCPA. We used a sub-sampling window size of 30 sequential location observations to meet the minimum sample size required for the Bayesian Information Criterion (BIC) to be used for model selection, and to identify changes in behaviour at the smallest temporal scale possible for BCPA. Segments of trajectories between ‘change points’ identified by BCPA hereon are referred to as ‘bouts’. Because the distributions of speed and the RTA values were strongly positively skewed, we calculated medians from the output metrics (rather than using means), and use them to further classify behaviours; such values subsequently were used as inputs in the k-means clustering.
Fig 1. Workflow of analytical methods for inferring and classifying behaviours within animal-movement trajectories using a combination of behavioural-change-point analysis and k-means clustering.
We determined the number of distinct behavioural states for each study animal, through assessment of within-group sums of squares and serial classification of bouts, following the hierarchical cluster method of Kraznowski and Lai [41]. Individual bouts of same-state behaviour were classified into one of three mutually exclusive states based on combinations of median speeds and RTAs, using the k-means clustering algorithm of Hartigan and Wong [42] in the statistical software R (version 3.0.1) with the packages ‘cluster’ and ‘fpc’ [43,44]. Thus, bouts identified by BCPA were assigned to unique behavioural states based on similarities of patterns of movement. Proportions of time spent in each behavioural state by the penguins and the numbers of state changes that occurred per hour were then calculated. To determine which of the two movement metrics best differentiated the three behavioural states, we conducted a linear discriminant function analysis (DFA) for each penguin’s trajectory (in Statistica v. 9 [45]) using speed and RTAs of all observed locations as predictor variables. These values were then transformed to standard ‘z’ scores (i.e., the signed number of standard deviations from means), so that the two movement metrics were weighted equally in subsequent analyses. This analysis is reported in terms of the mean variance explained by the predictor variables and the mean number of observations of each behavioural state that were correctly classified by their movement metrics. Unless otherwise stated, all statistical values are reported as means ± standard errors (SE).
We assessed how accurately the modelling procedure classified behaviour by generating eight synthetic movement trajectories that represented by multiphasic random correlated walks (in NetLogo v 5.0.4 [46]). Each of these tracks contained 1000 observations, and were comprising three known states of behaviour that were parameterised from the means of empirical distributions of the penguins’ inter-fix speeds and RTAs (S1 Text). BCPA and k-means analyses were applied to these trajectories, and the actual states of behaviour at each location were compared to those inferred from the modelling procedure. This approach enabled us to determine the proportions of all observations that were correctly classified.
To visualise spatial variation in patterns of behaviour, we constructed probability-density surfaces of the locations of the state 3 behaviour (foraging) (using the Spatial Analyst extension in ArcMap v. 10.2 [47]), and examined relationships between these surfaces and those of a number of environmental factors (see S2 Text).
Results
Simulated tracks
Application of the modelling procedure to the eight synthetic movement trajectories showed that a mean of 93.2 ± 1.2% of State 1 observations, 92.5 ± 0.8% of State 2 observations, and 90.2 ± 0.2% of State 3 observations were correctly classified (overall accuracy: 92.5 ± 0.8%; see S1 Text), indicating that the method performed reasonably well in discriminating the different behavioural modes. On average, there were 197 ± 12.8 behavioural change points per trajectory identified by BCPA. Following k-means cluster analysis and thus grouping of the bouts, this number fell to 51.5 ± 4.3 behavioural change points per trajectory.
Real penguin tracks
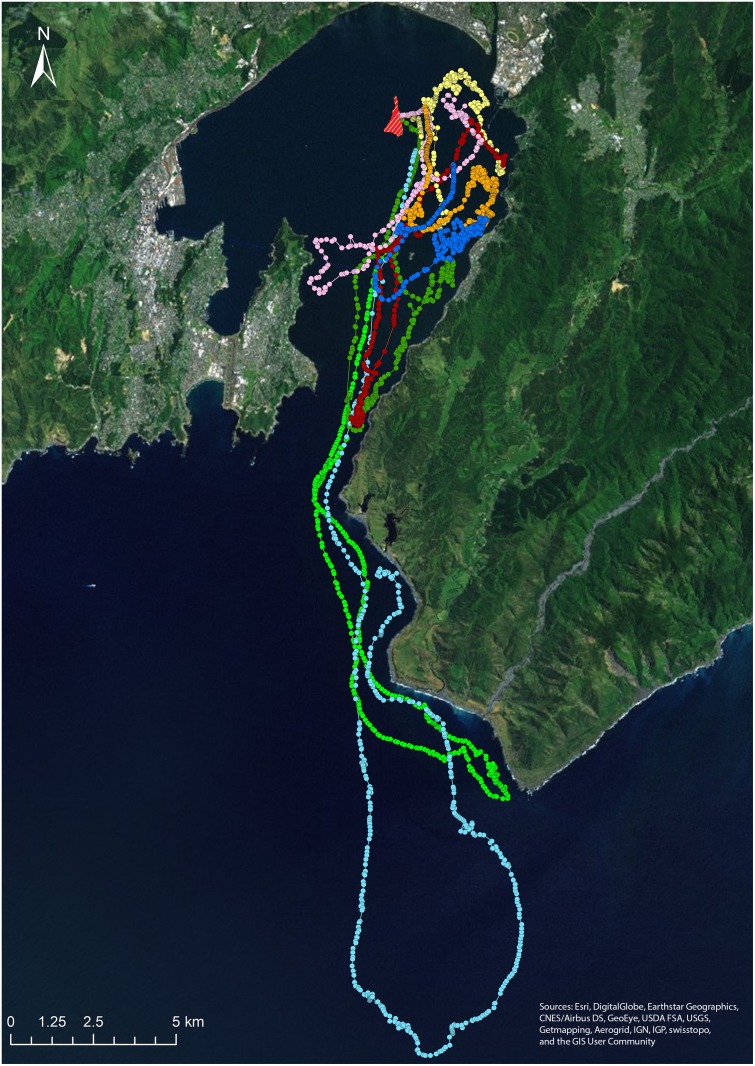
Movement trajectories of the eight penguins are shown in Fig 2, and summary characteristics of these data are reported in S1 Table. All trajectories were incomplete in the sense that no bird had returned to its nest box before the batteries of its GPS logger expired, so that the last fixes of all trajectories were recorded when the penguins were away from the colony. Operational periods of the GPS loggers ranged between 9.9 and 13.3 h (mean = 12.0 ± 0.4 h), the numbers of position fixes recorded during foraging trips ranged between 266 and 506 (mean = 398.3 ± 31.6), and the maximum distance from the nest site observed for each bird ranged between 3.5 and 27.4 km (mean = 9.5 ± 3.0 km).
Fig 2. Foraging trajectories of eight little penguins (Eudyptula minor) as recorded by GPS data-loggers.
The nominal sampling interval of the loggers was 1 fix per min-1. Colours represent tracks of different individuals. The location of the island study colony is indicated by red/yellow hatching. Sources of the background satellite images: Esri, DigitalGlobe, Earthstar Geographics, CNES/Airbus DS, GeoEye, USDA FSA, USGS, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community.
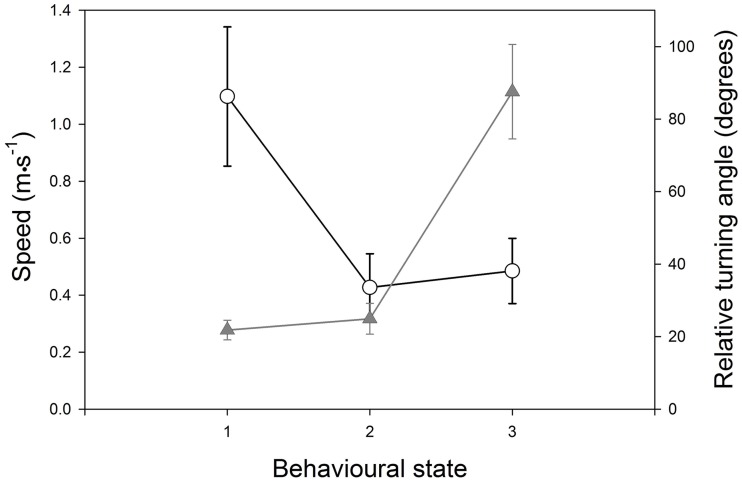
All of the study penguins exhibited three distinct modes of behaviour in their movement trajectories (Fig 3), except M07, which had only two modes. State 1 was characterised by fast (median speed = 1.1 ms-1) and comparatively straight (median RTA = 21.8°) movement trajectories (Fig 4), suggestive of ‘persistent travelling’ or ‘commuting’ behaviour. State 2 was defined by slow swimming speeds (median speed = 0.4 ms-1) and moderately low variation in direction (median RTA = 24.9°). This mode of behaviour typically was observed soon after individuals left the colony or immediately following highly tortuous segments of trajectories. Such behaviour can be interpreted as ‘resting’, and appeared to be due to passive displacement on the ocean surface by wind and/or water currents. State 3 was classified by comparatively slow (median speed 0.5 ms-1) and highly tortuous (median RTA 87.6°) movements, coupled with frequent gaps of missing locations, indicative of diving behaviour during which the GPS data-loggers were unable to operate. In this state, movements of the penguins were highly localised and restricted in area; such behaviour most likely represents active searching or foraging [37].
Fig 3. Statistical definitions of behavioural states inferred for the location observations comprising eight penguin foraging trajectories.
Behaviours were classified through sequential use of behavioural-change-point and k-means cluster analyses, based on combinations of inter-fix speeds (open circles, black lines) and relative turning angles (grey triangles and lines). Circles and triangles represent grand median values of all observations of all penguins, and the vertical bars represent the corresponding inter-quartile ranges.
Fig 4. Examples of individual movement trajectories for which GPS-derived location estimates have been classified into discrete behavioural states, penguins A12 and M02.
Locations assigned as States 1, 2, and 3 are indicated by blue, red, and yellow points, respectively. Plots above the trajectories show observed inter-fix speeds (ms-1; black lines with axis values at the left side of M02 plot) and relative turning angles (degrees; grey lines with axis values at the right side of A12 plot) over time of day. Narrow bars above the plots denote the corresponding inferred states of behaviour.
Within individual penguin tracks, the proportion of time spent in each of the three behavioural states in most cases were roughly evenly distributed. Excluding penguin M07, State 1 behaviours (travelling/commuting) accounted for between 32.0–43.7% of all observations (mean = 38.5 ± 1.6%), State 2 (resting) between 19.7–38.2% (mean = 30.0 ± 2.1%) of all observations, and State 3 behaviours between 25.3–38.3% (mean = 31.4 ± 2.0%) of all observations. On average, there were 1.1 ± 0.1, 1.0 ± 0.1, 0.9 ± 0.1 bouts per hour of State 1, 2 and 3 behaviours, respectively. The grand mean rate of change of all behaviours was 2.9 ± 0.3 events per hour. The DFA results suggest that speed and RTA accounted for, on average, 75.4 ± 5.4% and 24.6 ± 5.4% of the between-group variability of behavioural-state membership, respectively. The DFA correctly classified, on average, 87.6 ± 9.7%, 92.3 ± 4.5%, and 91.4 ± 5.5% of the behavioural bouts of State 1, 2 and 3, respectively. Overall, 90.5 ± 1.4% of all behaviours were correctly classified.
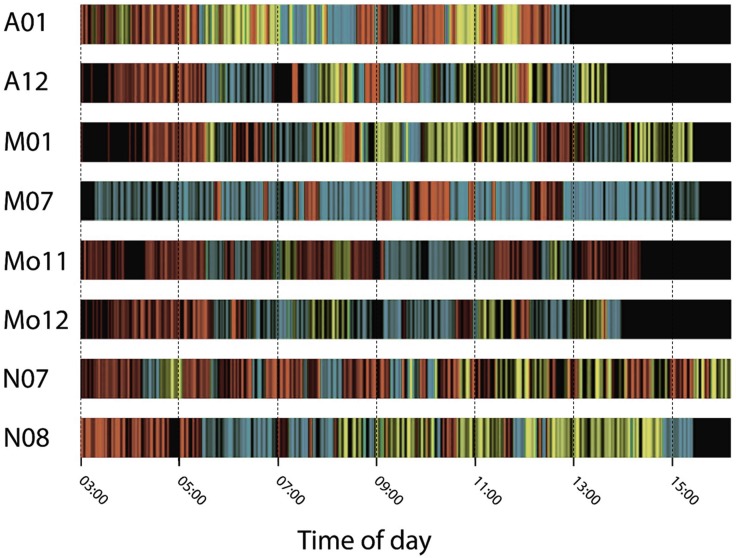
Time series from the combined BCPA/k-means clustering procedure demonstrate how the penguins’ patterns of behaviour differed among individuals (Fig 5). Except for bird A01, which initially undertook a sustained period of mixed State 1 and State 2 behaviours, and bird M07, which began its foraging trip in State 1, initial observations of most study animals were classified as State 2 (‘resting’), beginning at ca. 03:00 when the GPS devices first became operational. After several hours, all birds switched from State 2 to State 1 roughly 30 min before sunrise. Following this period, behaviours varied mostly between bouts of State 1 (rapid travelling) and State 3 (‘slow/area-restricted’), suggesting occurrence of a consistent alternating pattern of searching/commuting and intensive foraging.
Fig 5. Time series of behavioural states inferred during foraging trips.
Colours of vertical bars denote the different states—see Fig 4 for interpretation; black bars denote missing data.
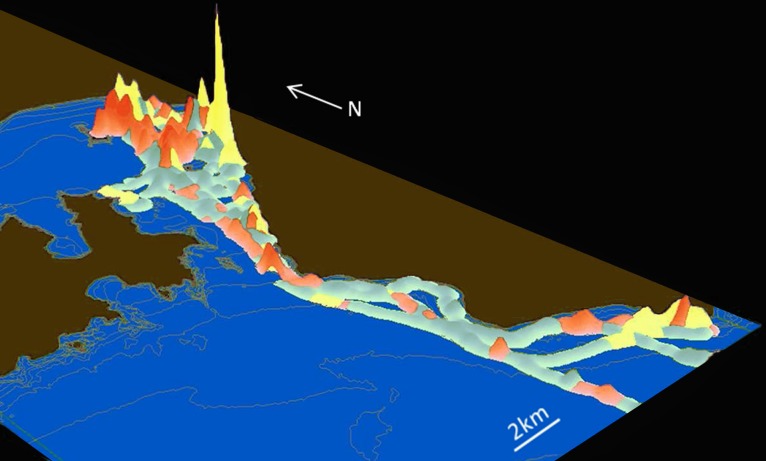
Probability-density surfaces of the locations of inferred states show how patterns of behaviour varied spatially during foraging trips (Fig 6). Compared to State 1 (‘travelling’) and 2 (‘resting’) behaviours, locations classified as State 3 (‘foraging’) were more densely distributed over smaller areas. Locations of State 3 behaviours generally were concentrated in shallow water near the eastern coastline of Wellington Harbour and around river mouths (S5 Fig), suggesting areas where foraging occurred.
Fig 6. Kernel-density surface of inferred behavioural states superimposed on a map of the study area.
Vertical height represents the relative areal density of locations classified as particular behavioural modes. The colours of the behavioural states are the same as those in Figs 3 and 4.
Discussion
Our study demonstrates application of a simple yet effective framework, based on a novel combination of well-known and computationally tractable statistical procedures, for categorising location observations comprising the movement trajectories of animals into discrete modes of behaviour. The method extends the utility of BCPA, by objectively grouping inferred behavioural bouts into standardised classes, thus facilitating interpretation of biological signals. Applied to simulated movement trajectories, the method correctly classified >90% of the ‘true’ modes of behaviour of most individual location observations. Performed on real trajectories of little penguins, the method provided new insights into at-sea behaviour that previously have not been reported.
Evaluation of the method
The combined BCPA/k-means cluster method correctly classified the majority (92.5%) of individual location observations in synthetically generated movement trajectories of known behavioural states (see S1 Text). The few misclassifications of location observations by the BCPA/k-means cluster procedure mostly were located at ‘transitional phases’ of bouts (i.e., where behavioural states changed). Similar misclassifications have been reported for other inferential models, and most likely were due to overlapping distributions of movement parameters between the different behavioural modes [48]. Some incorrect bout classifications also may have resulted simply from the difficulties of discretising continuous movements below the resolution of the observational model [6,8].
Benefits of combining BCPA with k-means clustering to infer states of behaviour within individual movement trajectories include the broad familiarity of the statistical procedures, as well as their comparative conceptual and computational simplicity. K-means cluster analysis is the standard method for grouping objects or events into discrete classes. Open-source code for both analytical procedures is readily available [43,44,49]. Many other inferential models of animal movement require extensive data pre-processing and model training, such as the removal of large outliers, standardisation of intervals between observations, and estimation of the ranges of parameter distributions [28,42]; BCPA is robust to these constraints [23].
Case study: interpretation of the movement patterns of little penguins
Application of the BCPA/k-means clustering procedure provides new insights into the at-sea behaviour of little penguins. The movement patterns of most study birds generally followed a consistent chronological sequence that suggested response to changes in ambient light levels. Before sunrise, most individuals exhibited prolonged bouts of the resting/slow-swimming state, suggestive of a reluctance to move at commuting or active-foraging speeds without being able to visually identify their surroundings, as foraging little penguins rely mostly on visual cues [34,50]. Penguins also use this pre-dawn period for preening and self-maintenance [51]. Finally, the timing of departure from their colony by the penguins may represent evolutionary adaptations to avoid diurnal predators such as skuas (Stercorarius spp.) and giant petrels (Macronectes spp.) [52]. The abrupt increase in proportion of State 1 observations that occurred for most birds ca. 30 min before dawn is indicative of a shift to sustained commuting behaviour associated with travel to preferred foraging areas [53]. Following this period, behaviour varied more among individuals, as the penguins alternated between area-restricted bouts of foraging and commuting/active-searching bouts of movement to foraging areas, similar to what has been reported by others [53,54]. Patterns of the penguins’ behaviour also appeared to be related to the spatial heterogeneity of their environment. State 3 observations representative of bouts of area-restricted foraging regularly occurred in nutrient-rich shallow waters near coastlines and especially in the vicinity of river mouths, consistent with the foraging patterns of other neritic seabird species [53–55].
Conclusion
The BCPA/k-means clustering method we describe shows promise as a simple exploratory procedure for objectively classifying the individual location observations comprising animal-movement trajectories into discrete modes of behaviour. We recommend further evaluation of the procedure, especially comparison of the accuracy of behavioural-state classification with other available approaches, on both real and simulated animal-tracking data sets.
Supporting Information
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Start and end points of the track are indicated by the solid orange circle and open pink square, respectively. The underlying colours of the simulated environment represent ‘resource’ values of the grid that influenced the movement pattern of the model agent. Within the environment, red and blue represent high and low resource values, respectively; in the movement trajectory, colours represent different behavioural states. States 1, 2 and 3 in the trajectory are indicated in blue, orange and yellow, respectively.
(TIF)
(TIF)
Behavioural states in the trajectory (a) are represented by the same colour scale as that of the ‘true’ behavioural states (b,c): states 1, 2, and 3 indicated by blue, orange and yellow, respectively. The two plots on the right show the time series of velocity and turning angles of the synthetic movement trajectory in (a) decomposed into: (b) turning (Vt = V sin ψ); and (c) persistence components (Vp = V cos ψ). Heavy black lines in the centre of the plots represent running mean values (30-element window), while paired red lines represent one standard deviation. Points in the two plots show running means of individual observations in the time series of Vsin(ψ) and Vcos(ψ); colours reflect the magnitude of temporal autocorrelation, with blues and yellows indicating low and high absolute values (i.e., 0 to 1), respectively. Vertical orange lines indicate change points identified by BCPA. Bar charts in the background of (b) and (c) show the ‘true’ behavioural states of the trajectory at each time step, as defined by the NetLogo model, using the same colour scale as that of the synthetic track.
(TIF)
(a) histograms of speed and relative turning angles of the three ‘true’ behavioural states in the synthetic trajectory. (b) from left to the right: ‘true’ behavioural states as defined by the NetLogo movement model; behavioural bouts identified by BCPA, indicated by different colours; behavioural states inferred by the combination of BCPA and k-means cluster analysis; and behavioural states inferred by a switching Markov Chain Monte Carlo model. Start and end points of trajectories and colour scales (except for BCPA output) are the same as indicated in S1 Fig.
(TIF)
Sources of the background satellite image: Esri, DigitalGlobe, Earthstar Geographics, CNES/Airbus DS, GeoEye, USDA FSA, USGS, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community.
(TIF)
(CSV)
Acknowledgments
We thank Jo Greenman from the Department of Conservation for help with accommodation, permits, and fieldwork. We also thank the Ornithological Society of New Zealand and the Penguin Team of Somes/Matiu Island for assistance with fieldwork, especially Ros Batcheler, Mike Rumble, Reg Cotter and Vince Waanders.
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
KO was supported by a Fulbright Senior Scholar Award. JZ received a research grant from the Center for Biodiversity and Biosecurity, the University of Auckland. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Almeida P, Vieira MV, Kajin M, Forero-Medina G, Cerqueira R. Indices of movement behaviour: conceptual background, effects of scale and location errors. Zoologia. 2010;27(5):674–80. [Google Scholar]
- 2. Merrill E, Sand H, Zimmermann B, McPhee H, Webb N, Hebblewhite M, et al. Building a mechanistic understanding of predation with GPS-based movement data. Philosophical Transactions of the Royal Society B-Biological Sciences. 2010;365(1550):2279–88. 10.1098/rstb.2010.0077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Miller LA, Goldman DI, Hedrick TL, Tytell ED, Wang ZJ, Yen J, et al. Using computational and mechanical models to study animal locomotion. Integr Comp Biol. 2012;52(5):553–75. 10.1093/icb/ics115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Jonsen ID, Myers RA, James MC. Identifying leatherback turtle foraging behaviour from satellite telemetry using a switching state-space model. Mar Ecol Prog Ser. 2007;337:255–64. [Google Scholar]
- 5. Breed GA, Jonsen ID, Myers RA, Bowen WD, Leonard ML. Sex-specific, seasonal foraging tactics of adult grey seals (Halichoerus grypus) revealed by state-space analysis. Ecology. 2009;90(11):3209–21. [DOI] [PubMed] [Google Scholar]
- 6. Patterson TA, Thomas L, Wilcox C, Ovaskainen O, Matthiopoulos J. State–space models of individual animal movement. Trends Ecol Evol. 2008;23(2):87–94. 10.1016/j.tree.2007.10.009 [DOI] [PubMed] [Google Scholar]
- 7. Bartumeus F, da Luz MGE, Viswanathan G, Catalan J. Animal search strategies: a quantitative random-walk analysis. Ecology. 2005;86(11):3078–87. [Google Scholar]
- 8. Jonsen ID, Flemming JM, Myers RA. Robust state-space modeling of animal movement data. Ecology. 2005;86(11):2874–80. [Google Scholar]
- 9. Morales JM, Haydon DT, Frair J, Holsinger KE, Fryxell JM. Extracting more out of relocation data: building movement models as mixtures of random walks. Ecology. 2004;85(9):2436–45. [Google Scholar]
- 10. Fauchald P, Tveraa T. Using first-passage time in the analysis of area-restricted search and habitat selection. Ecology. 2003;84(2):282–8. [Google Scholar]
- 11. Edrén S, Wisz MS, Teilmann J, Dietz R, Söderkvist J. Modelling spatial patterns in harbour porpoise satellite telemetry data using maximum entropy. Ecography. 2010;33(4):698–708. [Google Scholar]
- 12. Guilford T, Roberts S, Biro D, Rezek I. Positional entropy during pigeon homing II: navigational interpretation of Bayesian latent state models. J Theor Biol. 2004;227(1):25–38. [DOI] [PubMed] [Google Scholar]
- 13. Ares JO, Bertiller M. Modeling high-frequency position data of large herbivores with a phase-state model. Ecol Model. 2010;221(19):2323–9. [Google Scholar]
- 14. Calenge C. The package “adehabitat” for the R software: a tool for the analysis of space and habitat use by animals. Ecol Model. 2006;197(3):516–9 [Google Scholar]
- 15. Tremblay Y, Roberts AJ, Costa DP. Fractal landscape method: an alternative approach to measuring area-restricted searching behavior. J Exp Biol. 2007;210(6):935–45. [DOI] [PubMed] [Google Scholar]
- 16. Guilford T, Meade J, Freeman R, Biro D, Evans T, Bonadonna F, et al. GPS tracking of the foraging movements of Manx Shearwaters Puffinus puffinus breeding on Skomer Island, Wales. Ibis. 2008;150(3):462–73. [Google Scholar]
- 17. Knell AS, Codling EA. Classifying area-restricted search (ARS) using a partial sum approach. Theoretical Ecology. 2012;5(3):325–39. [Google Scholar]
- 18. Owen-Smith N, Goodall V, Fatti P. Applying mixture models to derive activity states of large herbivores from movement rates obtained using GPS telemetry. Wildl Res. 2012;39(5):452–62. [Google Scholar]
- 19. Postlethwaite CM, Brown P, Dennis TE. A new multi-scale measure for analysing animal movement data. J Theor Biol. 2013;317(0):175–85. [DOI] [PubMed] [Google Scholar]
- 20. Dalziel BD, Morales JM, Fryxell JM. Fitting dynamic models to animal movement data: the importance of probes for model selection, a reply to franz and caillaud. Am Nat. 2010;175(6):762–4. 10.1086/652521 [DOI] [PubMed] [Google Scholar]
- 21. Johnson DS, Thomas DL, Hoef JMV, Christ A. A general framework for the analysis of animal resource selection from telemetry data. Biometrics. 2008;64(3):968–76. [DOI] [PubMed] [Google Scholar]
- 22. McClintock BT, King R, Thomas L, Matthiopoulos J, McConnell BJ, Morales JM. A general discrete-time modeling framework for animal movement using multistate random walks. Ecol Monogr. 2012;82(3):335–49. [Google Scholar]
- 23. Gurarie E, Andrews RD, Laidre KL. A novel method for identifying behavioural changes in animal movement data. Ecol Lett. 2009;12(5):395–408. 10.1111/j.1461-0248.2009.01293.x [DOI] [PubMed] [Google Scholar]
- 24. Kranstauber B, Kays R, LaPoint SD, Wikelski M, Safi K. A dynamic Brownian bridge movement model to estimate utilization distributions for heterogeneous animal movement. J Anim Ecol. 2012;81(4):738–46. 10.1111/j.1365-2656.2012.01955.x [DOI] [PubMed] [Google Scholar]
- 25. Fleming C, Calabrese J, Mueller T, Olson K, Leimgruber P, Fagan WF. Non‐Markovian maximum likelihood estimation of autocorrelated movement processes. Methods in Ecology and Evolution. 2014. 25810896 [Google Scholar]
- 26. Dominoni DM, Carmona‐Wagner EO, Hofmann M, Kranstauber B, Partecke J. Individual‐based measurements of light intensity provide new insights into the effects of artificial light at night on daily rhythms of urban‐dwelling songbirds. J Anim Ecol. 2014;83(3):681–92. [DOI] [PubMed] [Google Scholar]
- 27. Nams VO. Combining animal movements and behavioural data to detect behavioural states. Ecol Lett. 2014;. 10.1111/ele.12328 [DOI] [PubMed] [Google Scholar]
- 28. Dean B, Freeman R, Kirk H, Leonard K, Phillips RA, Perrins CM, et al. Behavioural mapping of a pelagic seabird: combining multiple sensors and a hidden Markov model reveals the distribution of at-sea behaviour. J R Soc Interface. 2012;10 10.1098/rsif.2012.0570(78) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Tryon R. Cluster Analysis (MI: Edwards Brothers, Ann Arbor: ). 1939. [Google Scholar]
- 30. MacQueen J, editor Some methods for classification and analysis of multivariate observations Proceedings of the fifth Berkeley symposium on mathematical statistics and probability; 1967: California, USA. [Google Scholar]
- 31. Schwager M, Anderson DM, Butler Z, Rus D. Robust classification of animal tracking data. Comput Electron Agric. 2007;56(1):46–59. [Google Scholar]
- 32. Van Moorter B, Visscher DR, Jerde CL, Frair JL, Merrill EH. Identifying Movement States From Location Data Using Cluster Analysis. J Wildl Manage. 2010;74(3):588–94. [Google Scholar]
- 33. Hanks EM, Hooten MB, Johnson DS, Sterling JT. Velocity-based movement modeling for individual and population level inference. PLoS ONE. 2011;6(8):e22795 10.1371/journal.pone.0022795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Marchant S, Higgins PJ. Handbook of Australian, New Zealand and Antarctic birds; volume 1. Melbourne: Oxford Univeristy Press; 1990. p. 125 [Google Scholar]
- 35. Kinsky F, Falla RA. A subspecific revision of the Australasian blue penguin (Eudyptula minor) in the New Zealand area National Museum of New Zealand; 1976. [Google Scholar]
- 36. Gales R, Williams C, Ritz D. Foraging behaviour of the little penguin, Eudyptula minor: initial results and assessment of instrument effect. J Zool. 1990;220(1):61–85. [Google Scholar]
- 37. Mattern T. Foraging strategies and breeding success in the Little Penguin, Eudyptula minor: a comparative study between different habitats Otago [dissertation]. the University of Otago; 2001. [Google Scholar]
- 38. Bull L. Fidelity and breeding success of the blue penguin Eudyptula minor on Matiu‐Somes Island, Wellington, New Zealand. N Z J Zool. 2000;27(4):291–8. [Google Scholar]
- 39. Wilson RP, Pütz K, Peters G, Culik B, Scolaro JA, Charrassin J-B, et al. Long-term attachment of transmitting and recording devices to penguins and other seabirds. Wildl Soc Bull. 1997:101–6. [Google Scholar]
- 40. Team RC. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2013. 10.3758/s13428-013-0330-5 [DOI] [Google Scholar]
- 41. Krzanowski WJ, Lai Y. A criterion for determining the number of groups in a data set using sum-of-squares clustering. Biometrics. 1988:23–34. [Google Scholar]
- 42. Hartigan JA, Wong MA. Algorithm AS 136: A k-means clustering algorithm. Applied statistics. 1979:100–8. [Google Scholar]
- 43. Maechler M, Rousseeuw P., Struyf A., Hubert M., Hornik K. cluster: Cluster Analysis Basics and Extensions R package version 1.15.3. 2014. [Google Scholar]
- 44. Hennig C. fpc: Flexible procedures for clustering. R package version. 2010;2:0–3. [Google Scholar]
- 45. StatSoft I. STATISTICA (data analysis software system). Tulsa, USA: 9 ed2009. [Google Scholar]
- 46. Wilensky U. NetLogo Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University; 1999. [Google Scholar]
- 47. ERSI. ArcMap. Redlands, California: ERSI (Environmental Systems Resource Institute); 2013. [Google Scholar]
- 48. Bilmes JA. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. International Computer Science Institute. 1998;4(510):126. [Google Scholar]
- 49. Gurarie E, Gurarie ME, Gurarie RA, Rcpp D, Rcpp L. Package ‘bcpa’. 2013. [Google Scholar]
- 50. Cannell BL, Cullen J. The foraging behaviour of little penguins Eudyptula minor at different light levels. Ibis. 1998;140(3):467–71. [Google Scholar]
- 51. Chiaradia A. Breeding biology and feeding ecology of Little Penguins (Eudyptula minor) at Phillip Island–a basis for a monitoring program [dissertation]. University of Tasmania; 1999. [Google Scholar]
- 52. Klomp N, Meathrel C, Wienecke B, Wooller R. Surface nesting by little penguins on Penguin Island, Western Australia. Emu. 1991;91(3):190–3. [Google Scholar]
- 53. Petersen SL, Ryan PG, Gremillet D. Is food availability limiting African Penguins Spheniscus demersus at Boulders? A comparison of foraging effort at mainland and island colonies. Ibis. 2006;148(1):14–26. [Google Scholar]
- 54. Wilson RP, Wilson M. Foraging ecology of breeding Spheniscus penguins. Penguin biology Academic Press: San Diego; 1990. p. 181–206. [Google Scholar]
- 55. Ropert-Coudert Y, Kato A, Wilson RP, Cannell B. Foraging strategies and prey encounter rate of free-ranging Little Penguins. Mar Biol. 2006;149(2):139–48. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(DOCX)
(DOCX)
(DOCX)
(DOCX)
(DOCX)
Start and end points of the track are indicated by the solid orange circle and open pink square, respectively. The underlying colours of the simulated environment represent ‘resource’ values of the grid that influenced the movement pattern of the model agent. Within the environment, red and blue represent high and low resource values, respectively; in the movement trajectory, colours represent different behavioural states. States 1, 2 and 3 in the trajectory are indicated in blue, orange and yellow, respectively.
(TIF)
(TIF)
Behavioural states in the trajectory (a) are represented by the same colour scale as that of the ‘true’ behavioural states (b,c): states 1, 2, and 3 indicated by blue, orange and yellow, respectively. The two plots on the right show the time series of velocity and turning angles of the synthetic movement trajectory in (a) decomposed into: (b) turning (Vt = V sin ψ); and (c) persistence components (Vp = V cos ψ). Heavy black lines in the centre of the plots represent running mean values (30-element window), while paired red lines represent one standard deviation. Points in the two plots show running means of individual observations in the time series of Vsin(ψ) and Vcos(ψ); colours reflect the magnitude of temporal autocorrelation, with blues and yellows indicating low and high absolute values (i.e., 0 to 1), respectively. Vertical orange lines indicate change points identified by BCPA. Bar charts in the background of (b) and (c) show the ‘true’ behavioural states of the trajectory at each time step, as defined by the NetLogo model, using the same colour scale as that of the synthetic track.
(TIF)
(a) histograms of speed and relative turning angles of the three ‘true’ behavioural states in the synthetic trajectory. (b) from left to the right: ‘true’ behavioural states as defined by the NetLogo movement model; behavioural bouts identified by BCPA, indicated by different colours; behavioural states inferred by the combination of BCPA and k-means cluster analysis; and behavioural states inferred by a switching Markov Chain Monte Carlo model. Start and end points of trajectories and colour scales (except for BCPA output) are the same as indicated in S1 Fig.
(TIF)
Sources of the background satellite image: Esri, DigitalGlobe, Earthstar Geographics, CNES/Airbus DS, GeoEye, USDA FSA, USGS, Getmapping, Aerogrid, IGN, IGP, swisstopo, and the GIS User Community.
(TIF)
(CSV)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.