Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Apr 3;137(15):5163–5169. doi: 10.1021/jacs.5b01687

Visualizing Unresolved Scalar Couplings by Real-Time J-Upscaled NMR

Simon Glanzer 1, Klaus Zangger 1,*
PMCID: PMC4415032  PMID: 25837306

Abstract

graphic file with name ja-2015-016873_0008.jpg

Scalar coupling patterns contain a wealth of structural information. The determination, especially of small scalar coupling constants, is often prevented by merging the splittings with the signal line width. Here we show that real-time J-upscaling enables the visualization of unresolved coupling constants in the acquisition dimension of one-dimensional (1D) or multidimensional NMR spectra. This technique, which works by introducing additional scalar coupling evolution delays within the recording of the FID (free induction decay), not only stretches the recorded coupling patterns but also actually enhances the resolution of multiplets, by reducing signal broadening by magnetic field inhomogeneities during the interrupted data acquisition. Enlarging scalar couplings also enables their determination in situations where the spectral resolution is limited, such as in the acquisition dimension of heteronuclear broadband decoupled HSQC (heteronuclear single quantum correlation) spectra.

Introduction

Structural information in NMR spectra is obtained mainly from resonance frequencies and scalar coupling patterns. The extraction of scalar coupling information is often prevented by signal overlap and, especially for small J-values, by the signal widths. A series of experiments have been described to simplify the extraction of homonuclear coupling constants, especially for overlapped signals and for small couplings. Often two-dimensional (2D) and multidimensional NMR experiments, in particular J-resolved spectra,1 are used. A variety of 2D homonuclear correlation spectra like the small flip angle COSY (correlated spectroscopy),2 E-COSY,3 P.E.COSY,4 or z-COSY5 allow accurate measurements of small J-values, but only those of passive couplings (the ones which are not responsible for the cross peak) in situations when cross peaks are not overlapped. Accurate determination of active coupling constants is possible, e.g., through a comparison of in-phase and antiphase signals, obtained from COSY and TOCSY (total correlation spectroscopy) spectra, respectively.6,7 Information about small coupling constants can also be obtained by monitoring the time evolution of scalar coupling. Typically a 2D experiment is recorded with different scalar J-coupling evolution times and coupling constants obtained by fitting the signal intensity as a function of the J-evolution time.8 Other experiments used for measuring small homonuclear couplings are the HNHA,9 which is used for 3JHNα in 15N labeled proteins or the J-doubling method.10 For easier access to small scalar coupling constants, several techniques for J-upscaling in the indirect dimension of 2D experiments have been reported.11,12 Hosur et al. described J-upscaled 2D COSY spectra, where J-coupling evolution is enhanced compared to chemical-shift evolution in ω1.11,13 This is achieved by an additional period after the evolution time, which only allows scalar coupling but not chemical-shift evolution. J-upscaling of COSY spectra in ω1 not only yields increased resolution for the measurement of coupling constants in the indirect dimension but also has the potential to enhance the sensitivity by reducing signal cancelation of antiphase signals. All these approaches for J-upscaling can only be applied in the indirect dimension of 2D or multidimensional experiments, where the resolution is limited by the acquired number of increments. The resolution achievable by upscaling of homonuclear J-coupling in the indirect dimension of multidimensional NMR spectra depends mainly on the number of increments used. Therefore, high resolution is traded for long measurement times. While homonuclear J-scaling has only been described for the lower resolution indirect dimension of NMR spectra, real-time chemical-shift (δ) scaling was described many years ago.14 It has been used frequently for solid-state NMR15 and occasionally for liquid-state applications.14,16 Downscaling of chemical shifts, which can be achieved by successive refocusing of chemical-shift evolution between the acquisition of individual FID data points, has been used mainly to manipulate the spectra of dynamic systems. It is not possible to upscale chemical shifts or scalar coupling by manipulation between individual data points since their evolution cannot be made faster than it is. Here we present an approach which yields real-time J-upscaled NMR spectra. This is achieved by the insertion of periods of scalar coupling, but not chemical-shift evolution within the data accumulation. The ratio between chemical-shift and scalar coupling evolution can be modulated, by an arbitrary factor λ, during interruption periods of the acquisition.17 The maximum upscaling factor is determined by the transverse relaxation. Real-time J-upscaling not only can be used for (single scan) 1D proton spectra but also can be employed in the direct dimension of any 2D or multidimensional experiment. Since chemical-shift evolution is not affected by the presented scheme, the individual data blocks can simply be concatenated during the acquisition. Therefore, there is no special data processing necessary, and the resulting FID can be processed like any other regular 1D or multidimensional NMR experiment. Real-time J-upscaling not only expands scalar coupled signals but also enhances the resolution of multiplets by lowering the effective transverse relaxation during acquisition interruptions, thereby allowing the direct visualization of small couplings which are hidden in the line shape of a regular spectrum. In addition, it allows enhanced J-evolution during short acquisition times, as needed for heteronuclear decoupled experiments, like HSQCs.18

Theoretical Basis

In order to increase scalar coupling, but leave chemical-shift evolution unchanged, it is necessary to allow for a period of scalar coupling, but not chemical-shift evolution. This is rather easily implemented in the indirect dimension of multidimensional experiments. However, it is not possible to use this approach during a regular data acquisition, i.e., within the dwell time. Therefore, our real-time upscaling approach relies on a combination of FID blocks, which are interrupted by periods of scalar coupling but not chemical-shift evolution. A somewhat related, real-time FID interruption scheme has been employed for homonuclear broadband decoupling (pure-shift) experiments17,19−21 and for long-observation-window band-selective decoupling during acquisition.22 The pulse sequence is shown in Figure 1.

Figure 1.

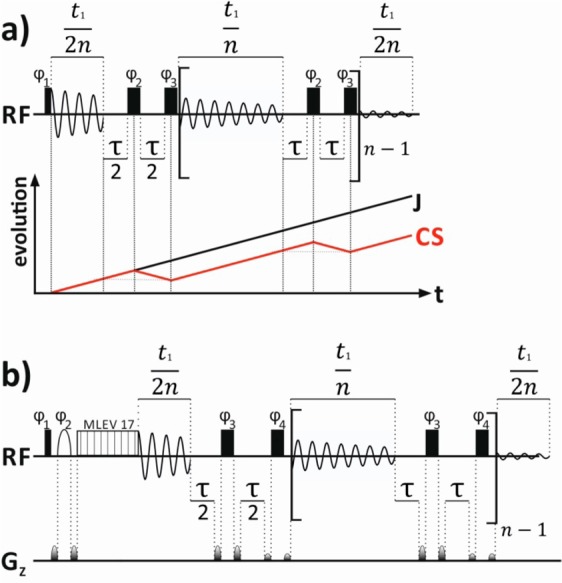
Figure 1

Open in a new tab

Pulse sequences used for real-time J-upscaling of (a) regular 1D spectra and (b) a 1D selective TOCSY. Thin and thick black rectangles are nonselective 90° and 180° pulses, respectively. A selective 180° pulse is indicated by a white half ellipse. The following phase cycles were used: (a) ϕ1 = x, −x, −x, x, y, −y, −y, y; ϕ2 = x, −x; ϕ3 = −x, x; ϕrec = x, −x, −x, x, y, −y, −y, y; (b) ϕ1 = x, −x; ϕ2 = x; ϕ3 = x, x, −x, −x; ϕ4 = −x, −x, x, x; ϕrec = x, −x. The evolution of chemical shift (CS) and scalar coupling (J) is illustrated in part a. During the actual data acquisition both chemical shift and scalar coupling evolve. In the middle of the interruption delay chemical-shift evolution is refocused.

Real-time J-upscaling happens exclusively during the acquisition. The FID is divided into individual blocks. These so-called “data chunks” are approximately 10–20 ms long (t1/n). After each chunk, the acquisition is interrupted for a total duration of 2τ. Evolution of the chemical shift as well as coupling is active during t1/n + τ. A hard 180° pulse then refocuses only the evolution of chemical shift but not scalar coupling. After a second 180° pulse, which turns the evolution of chemical shifts again in the correct direction, the product operators after one complete chunk plus interruption delay, for a weakly coupled 2-spin system, are

graphic file with name ja-2015-016873_m001.jpg
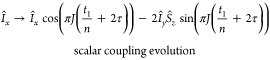graphic file with name ja-2015-016873_m002.jpg

where t1/n is the duration of one acquisition block and 2τ the delay time. Therefore, scalar coupling evolution is active during (t1/n) + 2τ, while chemical shifts evolve only during t1/n. This leads to enhanced scalar coupling evolution, which is scaled by λ according to

graphic file with name ja-2015-016873_m003.jpg
graphic file with name ja-2015-016873_m004.jpg

where λ is the scaling factor of the coupling constant and Jeff the upscaled J-value. It is important that scalar coupling evolution is not substantial during the data chunk in order to prevent the formation of scaling artifacts. Scalar coupling evolves with sin(πJt). A single 5 Hz coupling needs 100 ms to evolve completely into antiphase magnetization. Therefore, chunking times on the order of 10–20 ms are suitable to prevent excessive scalar coupling evolution. We have found that using a shorter first FID block can significantly reduce chunking artifacts. Real-time J-upscaling not only yields stretched multiplets but also increases the resolution of scalar couplings. One might think that by this technique the line width, as well as the coupling, is increased by the same factor resulting in no net advantage with respect to resolution. However, line-broadening by magnetic field inhomogeneities is refocused during 2τ by the central 180° pulse, and thereby reduces the effective transverse relaxation during the interruption to T2, rather than T2*. This leads to increasing coupling resolution by increasing scaling factors. The line width of the resulting spectrum is of course increased. The effective relaxation is T2* + (λ – 1)T2. Therefore, the line width at half height can be approximated by ν1/2 = (1/(π(T2* + (λ – 1)T2))).

The maximum upscaling factor is determined by T2 relaxation and the amount of scalar coupling evolution during 2τ. Significant relaxation losses during the acquisition interruption give rise to steps in the resulting FID, which produce symmetric artifacts in the upscaled spectrum. Similarly, steps in coupling evolution are formed during longer interruptions. Both limitations result in practicable maximum upscaling factors of approximately 10–15. In general, for any given total acquisition time, longer chunking times yield narrower line widths in the upscaled spectra, which result from the smaller number of interruptions and therefore fewer overall relaxation losses. On the other hand, high multiplicities and/or large coupling constants lead to significant J-evolution during the interruption, which also manifests itself, besides in decoupling sidebands, in smaller signal intensity of outer multiplet components. Upscaling sidebands which result from relaxation and coupling evolution during the interruption are found at 1/(t1/n) from the respective signal. Therefore, they can be partially averaged by variation of the chunking length between individual scans. Randomization of t1/n by ∼20% is sufficient for artifact suppression for chunking times between 10 and 20 ms as found empirically. It should be mentioned that, in contrast to pure-shift spectra, which employ real-time data chunking during acquisition,17,19,20 there is no significant sensitivity penalty for real-time J-upscaling. Real-time pure-shift spectra employ spatially selective excitation or a BIRD filter, both of which significantly reduce the sensitivity. The sensitivity of J-upscaled spectra is reduced by the increased line width of the signals as a result of relaxation during the interruptions of the FID. This can also be described as the FID being sampled only at certain time points, depending on the upscaling factor. Therefore, the sensitivity is reduced by approximately √λ. The exact reduction depends on T2 and T2*. Real-time J-upscaling can be used during the acquisition in any kind of 1D, 2D, or multidimensional experiment. It could be combined with fast NMR methods, such as nonuniform sampling,23 covariance processing,24 SOFAST-HMQCs,25 or ASAP-HSQC.26 Since J-upscaling yields broader multiplets and therefore less well-resolved spectra, selective excitation could be used prior to acquisition in order to prevent a detected signal from becoming overlapped upon upscaling. Similarly, e.g., a 1D selective TOCSY experiment can be used to reduce the number of detected signals (Figure 1b). The determination of J-values can be difficult in highly overlapped regions of the proton spectrum. Homonuclear correlated spectra often do not provide the required resolution to separate such signals. On the other hand HSQC spectra do not provide enough resolution in the direct dimension for the determination of scalar coupling constants. This is because the acquisition time is limited to ∼200 ms to prevent extensive heating by proton broadband decoupling during acquisition.27 Here, J-upscaling enables scalar coupling constants to be determined even with the necessarily short acquisition times.

Results and Discussion

As a first example of real-time J-upscaling, its effect on the proton spectrum of n-propanol is shown in Figure 2. A close-up image of the central CH2 group displays an apparent sextet induced by scalar coupling to the neighboring CH2 and CH3 groups, implying similar J-values for both couplings. However, if scalar coupling is increased by J-upscaling, additional splittings appear due to slightly different coupling constants for the CH2 and CH3 groups. In the upscaled spectrum with λ = 7, this difference is 5.5 Hz, which corresponds to a J-value difference of ∼0.8 Hz for the CH2 and CH3 groups. This is in good agreement with the difference obtained for both values using the 1D real-time SERF (selective refocusing) experiment.28 It would be impossible to measure this scalar coupling difference from a regular 1D spectrum, where the spectral line width is on the order of approximately 1 Hz. Upscaling leads to an effectively increased resolution (r) for scalar coupling constant determination. For example, 7-fold J-upscaling yields an increase in line width by a factor of only 2.2 (from 0.8 to 1.8 Hz) and therefore an effective resolution enhancement for J-couplings of 3.1 for this signal.

Figure 2.

Figure 2

Open in a new tab

Regular 1D 1H spectrum of propanol in DMSO-d6 together with a close-up image of the central CH2 group data (1.42 ppm) and the same signal J-upscaled by a factor of 4 and 7. The J-scaling factor λ is indicated for each peak, together with the line width at half height w and the relative resolution enhancement r, which describes λ/w relative to 1/w for the regular proton spectrum. For all spectra, 32k data points were recorded for a spectral width of 8 kHz. For the J-upscaled spectra, 100–200 loops of 10–20 ms were added.

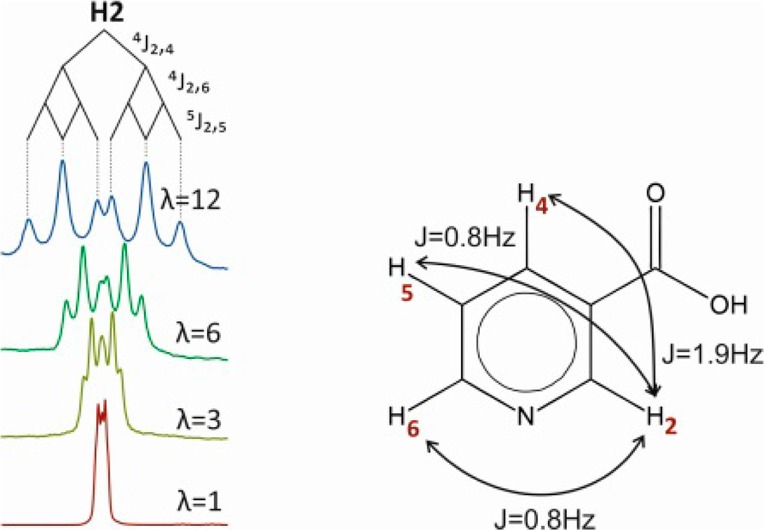
For more elaborate coupled multiplets and/or smaller coupling constants, larger scaling factors might be needed. Up to 12-fold J-upscaling has been used for the determination of all (3-, 4-, and 5-bond) homonuclear coupling constants of nicotinic acid in Figure 3. Most impressively, the signal of H-2, which looks like a distorted triplet in a regular 1H NMR spectrum, is resolved into a double triplet with actual coupling constants of 1.9 (doublet) and 0.8 Hz (triplet). Even splittings of 0.8 Hz are almost baseline separated in the 12-fold upscaled spectrum, and the distance between the two central peaks is 2.4 Hz, corresponding to an actual separation of just 0.2 Hz.

Figure 3.

Figure 3

Open in a new tab

Regular 1D 1H spectrum of nicotinic acid in DMSO-d6 together with close-up views of all peaks with upscaling factors of up to 12-fold. All 3-, 4-, and 5-bond coupling constants could be obtained from the upscaled spectra and are indicated. For the regular 1H spectrum 128k data points were recorded, and 32k for all J-upscaled spectra. The number of loops n was between 60 and 100 for upscaling between λ = 3 and 12, respectively. This corresponds to chunking times t1/n between 11 and 19 ms.

A comparison of the H-2 signal, drawn with the same overall width for direct evaluation of the improvement in resolution, can be found in the Supporting Information. A quantitative demonstration of this resolution enhancement, which results from the removal of magnetic field inhomogeneity broadening during the acquisition interruptions, is given in Figure S3 (Supporting Information) for an extensively shimmed CHCl3 spectrum. This example also shows the signal intensity reduction, which depends on the scaling factor λ as well as T2 and T2*. Upscaling of signals which are in the spectral vicinity of other resonances leads inevitably to a greater chance of multiplets becoming overlapped, which is evident for the signals of H-4 and H-6. In such situations a desired signal can be selectively excited before the start of the acquisition. In the regular proton NMR spectrum of azithromycin in CDCl3 (Figure 4) the H-2′ signal at 3.24 ppm is well-separated from other signals. However, upon J-upscaling nearby peaks would get overlapped. By using selective excitation of H-2′, no interfering signals are retained in the spectrum, and a more accurate measurement of the coupling constants is possible.

Figure 4.

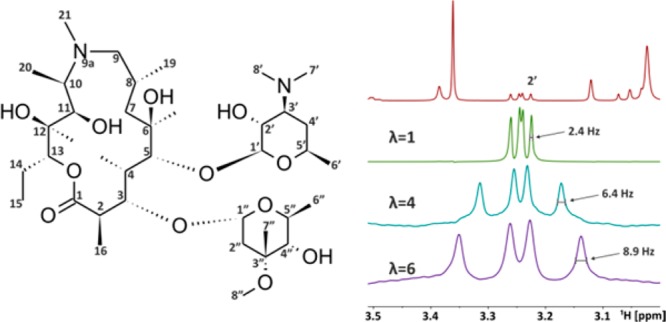
Figure 4

Open in a new tab

Structure of azithromycin with its numbering scheme and the region around H-2′ in a regular 1D 1H NMR spectrum in CDCl3 (red), together with various H-2′ selectively excited, J-upscaled spectra. For the regular spectrum 32k data points, 16 scans, and a spectral width of 8 kHz were used, while 144 scans were accumulated for the upscaled spectra, with otherwise identical acquisition parameters. All spectra were processed with a 0.1 Hz exponential window function. It is possible to measure J without overlapping nearby signals.

When the signal of interest is already hidden in an overcrowded spectral region, one can for example use a 1D selective COSY or TOCSY experiment prior to upscaling. In a selective TOCSY experiment, only the protons within the same spin system of the excited nucleus can be detected. The 1H spectrum (Figure 5, red) of azithromycin in CDCl3 is quite complicated in crowded areas. This approach of a J-upscaled selective 1D TOCSY has been applied to obtain coupling constants of protons close to H-5″ (4.11 ppm). After selective excitation of H-5″ the magnetization gets transferred only to other protons: those at 1.35 (H-6″), 2.16 (H-4″OH), and 3.05 ppm (H-4″). For H-4″ an additional splitting is found. Instead of an apparent triplet, the signal turns out to be a double doublet. In spectra where spectral crowding is not limiting, J-upscaling helps in visualizing scalar coupling constants that are otherwise hidden in the line width. On the other hand, enlarging scalar couplings also enables their determination in situations where the spectral resolution is limited. An example is the 2D 1H,13C HSQC, where carbon broadband decoupling is used during detection in order to remove 1JHC couplings. In order to prevent damage to the NMR probe, acquisition times need to be kept short (∼200 ms), which significantly reduces the resolution in the HSQC spectra and typically allows extraction of only very large couplings. With J-upscaling it is now possible to increase the splittings in the direct dimension and allow the determination of J-values for signals which are heavily overlapped in proton spectra. Additionally, during the interruption delays used for scaling, carbon decoupling can be switched off, leading to a reduction of probe stress and sample heating. As an example, a regular HSQC (Figure 6, blue) of azithromycin is compared with two upscaled HSQCs (red λ = 3 and green λ = 6). Coupling constants are most easily extracted from 1D traces, which are shown in Figure 6.

Figure 5.

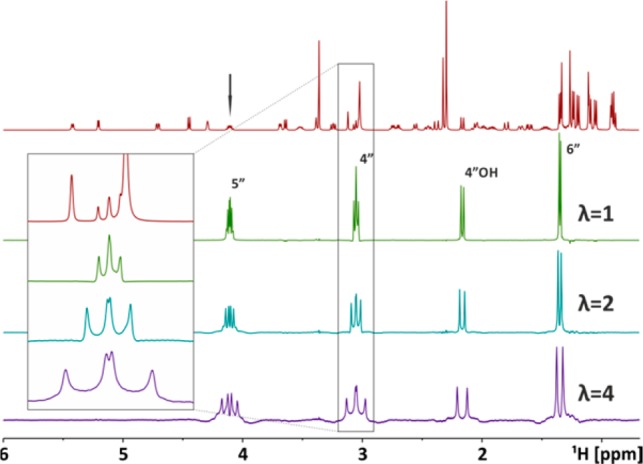
Figure 5

Open in a new tab

Regular 1D spectrum of azithromycin (50 mg/mL) in CDCl3 is drawn in red. J-upscaled selective TOCSY spectra (excitation at 4.11 ppm) of azithromycin are shown in blue (λ = 2) and purple (λ = 4). A TOCSY spin lock (MLEV17) with a duration of 150 ms was used. Additionally, a portion of the region between 2.90 and 3.20 ppm is enlarged to see how a double doublet emerges from an overlapped triplet.

Figure 6.

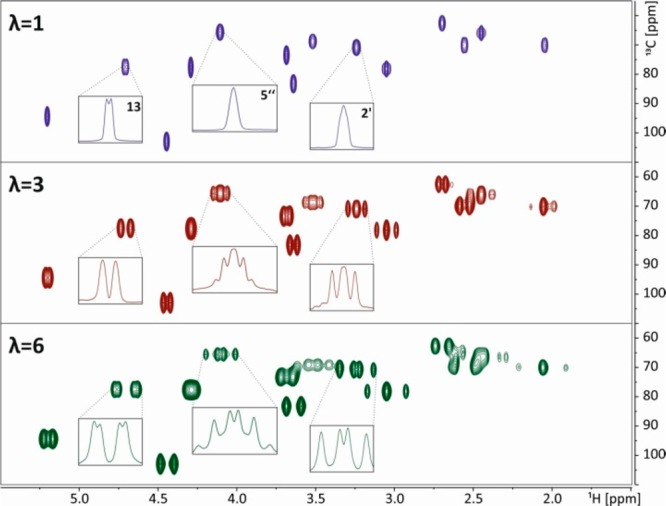
Figure 6

Open in a new tab

Close-up image of the region between 55 and 110 ppm (13C) and between 1.5 and 6 ppm (1H) of a regular HSQC of azithromycin in CDCl3 is shown in blue. The 3-fold J-upscaled HSQC is shown in red and the 6-fold J-upscaled version in green. For all spectra data matrices of 1024 × 64 data points were recorded with 72 scans each. The spectral widths were 4 kHz (1H) × 21 kHz (13C). For λ = 3 the data chunks had a length of around 9 ms, and for λ = 6 the data chunks were ∼5 ms. All HSQCs were processed with sine square 90° window function after 3-fold zero filling along the direct dimension and zero filling to 256 points and the same window function in the indirect dimension. All peaks visible in this figure are multiplet components.

Additional homonuclear splittings are found for every signal in the J-upscaled HSQC. For example the signal of H-5″, which looks like a singlet in the regular HSQC, is visible as a double quartet, with coupling constants of 9.5 and 6.2 Hz in the 6-fold upscaled HSQC. These couplings are to protons 4″ and 6″, respectively.

The usefulness of scalar coupling determination from J-upscaled HSQCs is even more important for molecules with highly overlapped proton spectra. Figure 7a shows a regular 1D spectrum of cholic acid, where only 3 peaks (H-2, H-3, and H-7) are well-resolved. The remaining 27 peaks are all crowded in the area between 0.5 and 2.5 ppm. Homonuclear-correlated 2D spectra would not be sufficient to determine all coupling constants. Carbon-correlated 2D spectra provide the necessary resolution to separate the individual proton signals. A comparison of a regular and a 6-fold J-upscaled HSQC of cholic acid in methanol-d4 is shown in Figure 7. From the J-upscaled HSQC, coupling constants could be obtained for all signals. A few representative traces from the regular and 6- or 9-fold upscaled HSQCs are shown in Figure 7c–e. The signal of H-9 appears to be a triplet in the trace extracted from the regular HSQC, but can be identified as a double triplet in the 9-fold upscaled HSQC. Upscaled homonuclear 1H coupling constants of 78 Hz (triplet) and 103 Hz (doublet) are obtained which correspond to actual J-values of 8.6 and 11.4 Hz, respectively. The larger trans coupling of 11.4 Hz is also found in the upscaled peak of H-8 (see Figure 5e), leaving the triplet with J = 8.6 Hz to the CH2 group at C-11. The remaining couplings of ∼11.4 and 3 Hz for H-8 must then be to H-14 and H-7, respectively. The larger one is again found in the upscaled trace of H-14 (Figure 7d). The missing 3 Hz coupling to H-7 can be confirmed by a regular 1D spectrum since this peak is well-isolated. In these examples we have used rather large scaling factors for an accurate determination of J-values. Sometimes the differentiation between small and large couplings might be needed, and therefore, smaller scaling factors would be sufficient. While upscaling of J-couplings enables their simplified extraction from 1D spectra as well as the direct dimension of 2D or multidimensional experiments, it should also be noted that upscaling of strongly coupled signals could introduce artifacts if the duration between the 180° pulses during the interrupted acquisition is shorter than the difference in signal offsets.29 This would be the case for small scaling factors and relatively strong coupling. On the other hand, J-upscaling of weakly and moderately strongly coupled signals is possible even when the signals become overlapped. During the actual recording of the FID, the coupling is not stronger. An example of such extreme J-upscaling that leads to overlapped doublets is shown in the Supporting Information.

Figure 7.

Figure 7

Open in a new tab

(a) Regular 1D spectrum of cholic acid (10 mg in methanol-d4), recorded with 16 scans, 32 768 data points, and a spectral width of 8000 Hz. (b) A regular HSQC spectrum without J-scaling (λ = 1), 128 increments with 16 scans each, and 512 data points in the direct dimensions. The spectral widths of direct and indirect dimensions are 1500 × 6290 Hz. (f) A J-upscaled HSQC with λ = 6 and the same spectral parameters as in part b but double the number of scans. (c–e) 1D extracts of one particular signal, as indicated in red from a regular spectrum and in blue from a J-upscaled HSQC. The signal indicated by an asterisk is from a λ = 9 HSQC to resolve the splittings completely.

Conclusion

We have presented a method for real-time J-upscaling of NMR spectra by successive interruption of the FID for additional scalar coupling evolution. This approach not only simplifies the extraction of J-values from the acquisition dimension of NMR experiments but also actually visualizes splittings which are hidden within the line width of regular NMR spectra. The improved resolution is a result of removing the effect of magnetic field inhomogeneities during periods of pure scalar coupling evolution. Besides the resolution advantage for determining unresolved couplings, J-upscaling also enables the determination of coupling constants from spectra acquired with limited acquisition time, as are encountered in heteronuclear correlated spectra that employ proton broadband decoupling during acquisition.

Experimental Section

All experiments were carried out on a Bruker Avance III 500 MHz spectrometer using a 5 mm TCI probe with z-axis gradients at 298 K. All chemicals were purchased from Sigma-Aldrich (St. Louis, MO) at >98% purity. No window functions were used for regular (nonscaled) proton spectra, and exponential line-broadening with 0.2 Hz was used for all upscaled spectra. Gradient shimming was used throughout. For the selective TOCSY spectrum, an 80 ms reBURP 180° pulse was used for selective excitation, and the TOCSY mixing time was 150 ms. The number of data chunks n depends on the total acquisition time and the desired chunking time. The pulse sequence for the 1D J-upscaled experiment in Bruker format is available in the Supporting Information and can be obtained from the authors upon request.

Acknowledgments

Financial support by the Austrian Science Foundation (FWF) under Projects P24742 and P27793 to K.Z. as well as the interuniversity program in natural sciences, “NAWI Graz”, is gratefully acknowledged. S.G. thanks the Austrian Academy of Sciences for a DOC fellowship.

Supporting Information Available

Regular and J-upscaled spectra of propenol, a comparison of the actual resolution enhancement in J-upscaled spectra of nicotinic acid, and the pulse sequence for 1D J-upscaled spectra in Bruker format. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

ja5b01687_si_001.pdf (824.8KB, pdf)

References

  1. Aue W. P.; Karhan J.; Ernst R. R. J. Chem. Phys. 1976, 64, 4226. [Google Scholar]
  2. a Aue W. P.; Bartholdi E.; Ernst R. R. J. Chem. Phys. 1976, 64, 2229. [Google Scholar]; b Bax A.; Freeman R. J. Magn. Reson. 1981, 44, 542. [Google Scholar]
  3. a Griesinger C.; Soerensen O. W.; Ernst R. R. J. Am. Chem. Soc. 1985, 107, 6394. [Google Scholar]; b Griesinger C.; Sørensen O.; Ernst R. J. Magn. Reson. 1987, 75, 474. [Google Scholar]
  4. Mueller L. J. Magn. Reson. 1987, 72, 191. [Google Scholar]
  5. Oschkinat H.; Pastore A.; Pfändler P.; Bodenhausen G. J. Magn. Reson. 1986, 69, 559. [Google Scholar]
  6. Titman J. J.; Keeler J. J. Magn. Reson. 1990, 89, 640. [Google Scholar]
  7. Oschkinat H.; Freeman R. J. Magn. Reson. 1984, 60, 164. [Google Scholar]
  8. Neri D.; Otting G.; Wuethrich K. J. Am. Chem. Soc. 1990, 112, 3663. [Google Scholar]
  9. Vuister G. W.; Bax A. J. Am. Chem. Soc. 1993, 115, 7772. [Google Scholar]
  10. a Garza-García A.; Ponzanelli-Velázquez G.; del Río-Portilla F. J. Magn. Reson. 2001, 148, 214. [DOI] [PubMed] [Google Scholar]; b McIntyre L.; Freeman R. J. Magn. Reson. 1992, 96, 425. [Google Scholar]
  11. Hosur R. V. Progr. NMR Spectr. 1990, 22, 1. [Google Scholar]
  12. a Kövér K. E.; Forgó P. J. Magn. Reson. 2004, 166, 47. [DOI] [PubMed] [Google Scholar]; b Kozminski J. Magn. Reson. 1999, 141, 185. [DOI] [PubMed] [Google Scholar]
  13. Hosur R. V.; Chary K.; Kumar M. Chem. Phys. Lett. 1985, 116, 105. [Google Scholar]
  14. Ellett J. D.; Waugh J. S. J. Chem. Phys. 1969, 51, 2851. [Google Scholar]
  15. a DiVerdi J. A.; Opella S. J. J. Chem. Phys. 1981, 75, 5594. [Google Scholar]; b Mehring M.High resolution NMR in solids; Springer: New York, 1983;. [Google Scholar]
  16. a Nuss M.; Olejniczak E. J. Magn. Reson. 1986, 69, 542. [Google Scholar]; b Morris G. A.; Jerome N. P.; Lian L.-Y. Angew. Chem., Int. Ed. 2003, 42, 823. [DOI] [PubMed] [Google Scholar]
  17. Meyer N. H.; Zangger K. Angew. Chem., Int. Ed. 2013, 52, 7143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Davis D. G.; Bax A. J. Am. Chem. Soc. 1985, 107, 2820. [Google Scholar]
  19. Paudel L.; Adams R. W.; Király P.; Aguilar J. A.; Foroozandeh M.; Cliff M. J.; Nilsson M.; Sándor P.; Waltho J. P.; Morris G. A. Angew. Chem., Int. Ed. 2013, 52, 11616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lupulescu A.; Olsen G. L.; Frydman L. J. Magn. Reson. 2012, 218, 141. [DOI] [PubMed] [Google Scholar]
  21. Zangger K. Progr. NMR Spectr. 2015, 86-87, 1–20. [DOI] [PubMed] [Google Scholar]
  22. a Byrne L.; Solà J.; Boddaert T.; Marcelli T.; Adams R. W.; Morris G. A.; Clayden J. Angew. Chem., Int. Ed. 2014, 53, 151. [DOI] [PubMed] [Google Scholar]; b Castañar L.; Nolis P.; Virgili A.; Parella T. Chem.—Eur. J. 2013, 19, 17283. [DOI] [PubMed] [Google Scholar]; c Ying J.; Li F.; Lee J. H.; Bax A. J. Biomol. NMR. 2014, 60, 15. [DOI] [PMC free article] [PubMed] [Google Scholar]; d Ying J.; Roche J.; Bax A. J. Magn. Reson. 2014, 241, 97. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Mobli M.; Hoch J. C. Progr. NMR Spectr. 2014, 83, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. a Foroozandeh M.; Adams R. W.; Nilsson M.; Morris G. A. J. Am. Chem. Soc. 2014, 136, 11867. [DOI] [PubMed] [Google Scholar]; b Zhang F.; Brüschweiler R. J. Am. Chem. Soc. 2004, 126, 13180. [DOI] [PubMed] [Google Scholar]
  25. Schanda P.; Brutscher B. J. Am. Chem. Soc. 2005, 127, 8014. [DOI] [PubMed] [Google Scholar]
  26. Schulze-Sünninghausen D.; Becker J.; Luy B. J. Am. Chem. Soc. 2014, 136, 1242. [DOI] [PubMed] [Google Scholar]
  27. Schleucher J.; Schwendinger M.; Sattler M.; Schmidt P.; Schedletzky O.; Glaser S. J.; Sørensen O. W.; Griesinger C. J. Biomol NMR. 1994, 4, 301. [DOI] [PubMed] [Google Scholar]
  28. Gubensäk N.; Fabian W. M. F.; Zangger K. Chem. Commun. 2014, 50, 12254. [DOI] [PubMed] [Google Scholar]
  29. Gopalakrishnan K.; Aeby N.; Bodenhausen G. ChemPhysChem. 2007, 8, 1791. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja5b01687_si_001.pdf (824.8KB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES