Demonstrating Photoluminescence from Au is Electronic Inelastic Light Scattering of a Plasmonic Metal: The Origin of SERS Backgrounds

Abstract

Temperature-dependent surface-enhanced Raman scattering (SERS) is used to investigate the photoluminescence and background continuum always present in SERS but whose origin remains controversial. Both the Stokes and anti-Stokes background is found to be dominated by inelastic light scattering (ILS) from the electrons in the noble metal nanostructures supporting the plasmon modes. The anti-Stokes background is highly temperature dependent and is shown to be related to the thermal occupation of electronic states within the metal via a simple model. This suggests new routes to enhance SERS sensitivities, as well as providing ubiquitous and calibrated real-time temperature measurements of nanostructures.

The field of surface-enhanced Raman scattering (SERS) has been hindered by the complexity and irreproducibility of spectra produced from differently designed plasmonic nanostructures which support several different enhancement mechanisms. Although SERS reached single molecule sensitivity nearly 20 years ago^1,2 and examples of atomic imaging have started to appear,³ a full understanding of any given SERS spectrum remains an elusive challenge. The complexity arises due to the introduction of metallic nanoantennas and patterned substrates which are used to channel light to molecules of interest and increase the normally extremely weak Raman scattering process into something readily observable. The interaction with metals however, changes the behavior of the Raman effect and the molecular vibrations in various ways. One key change is the appearance of a SERS “background continuum” in the spectra. This background has been thought to arise from several contributions: from photoluminescence of the metal,^4,5 from intraband emission from the metal,⁶ from contaminant molecules on the metal, and from image molecules formed inside the metal which couple to the real molecule.⁹ Even worse than this lack of understanding, the background component is amplified in all plasmonic constructs which enhance the sought-after molecular vibrational lines enough to be seen, and fluctuations in the background dominate the ultimate sensitivity of SERS.

Here, we show that a strong component of this background arises from the inelastic light scattering (ILS) of electrons inside the plasmonic nanostructures. We study its temperature dependence to identify the nature of the scattering and show characteristic differences between the scattering to the higher-energy anti-Stokes side and the lower-energy Stokes side in SERS. The plasmon-enhanced coupling to the ILS together with the required momentum relaxation from nanoscale localized fields explains why electron ILS has not been seen from these bulk coinage metals. Our results critically suggest that new methods may be needed to suppress ILS components to the SERS background in order to provide the full benefit of SERS enhancements in molecular sensing.

One potential origin for the background is from the heavily damped SERS of extrinsic surface contaminants; however, recent experiments have ruled this out using either molecular substitutions⁷ or clean Au.^8,9 Another intrinsic contribution from SERS arising from coupling of molecules to their images inside the Au^7,10 provides only part of the explanation since backgrounds are seen even on clean Au. This suggests that some other mechanism for light emission from the Au must be responsible. While there is a large body of work exploring light emission from plasmonic metals such as Au when excited at photon energies exceeding the onset of the interband (IB) absorption from d–s transitions (around ω_IB ∼ 2.4 eV for Au),^11,12 there is now considerable evidence for light emission when Au nanostructures are excited at much longer wavelengths where vertical transitions in the band diagram are not allowed. Typically, infrared (IR) excitation elicits light emission from bare gold on the Stokes (longer wavelength) side of excitation both for nanoparticles and rough gold surfaces (see refs (6 and 13) and references therein). This light emission has tentatively been suggested to arise from intraband emission from s–s transitions (s–s),⁶ with the required extra momentum provided by the localized field distributions. The emission was found to be prompt, emerging within the 100 fs time resolution available.²⁸ Studies of Stokes emission from copper films annealed at different temperatures led to a suggested scattering model based on a Lorentzian electronic band at the Fermi level with variable line width and dependent on image bands.¹⁴ While it is clear that light emission from plasmonic structures is enhanced at plasmonic resonances,^4,15 this merely accounts for enhancing the coupling of light in and out of the metal, and a proposed mechanism suggesting resonant transfer between excited electron and plasmon is not possible for ω < ω_IB.

To gain an improved understanding, we explore temperature-dependent SERS from 410 to 10 K. We first adsorb a monolayer of benzenethiol onto a gold plasmonic substrate of periodic inverted pyramids (Klarite),¹⁶ with pyramid dimensions tuned to place the plasmon resonance at the Raman excitation wavelength of 785 nm used here.¹⁷ Using this thiol monolayer ensures that the Au surface is well-controlled since all other molecules are displaced.¹⁸ This sample is cooled in a standard liquid helium cryostat with optical access and SERS measurements performed using continuous-wave laser excitation and a Renishaw inVia Raman spectrometer adapted to accommodate the cryostat. A ×5 objective is used to ensure a large area (>50 μm²) of the sample is measured, so that the signal is averaged over many inverted pyramids, removing inconsistencies due to sample drift from any thermal contraction. The laser power is set to 20 mW, giving a power density of approximately 40 kWcm^–2, and the sample is illuminated for 40 s, split over two acquisitions at each temperature point, with no observable difference in intensity observed between the two acquisitions.

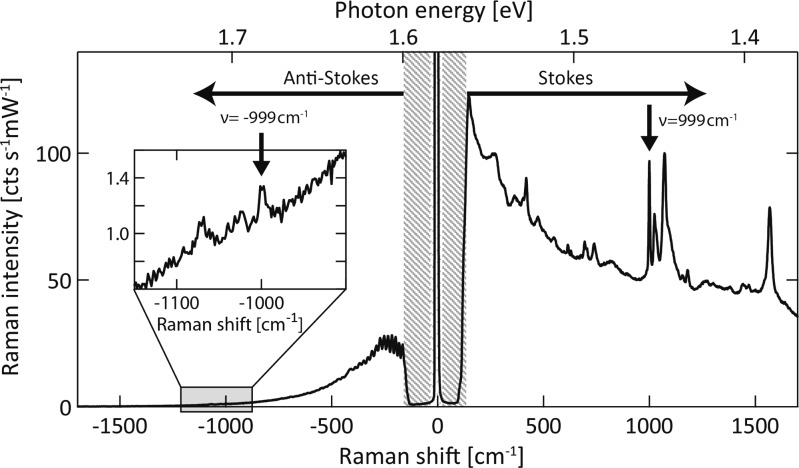
A typical full SERS spectrum of benzenethiol at 285 K (Figure 1) shows strong vibrational peaks on the Stokes side of the spectrum, and a weaker anti-Stokes spectrum which also displays small vibrational peaks around ±1000 cm^–1 corresponding to the benzenethiol aromatic-ring modes. The Stokes peaks are ∼200 times stronger than the anti-Stokes peaks, while fringing around ν = −300 cm^–1 comes from the notch filter removing the laser line.

Figure 1.

Benzenethiol SERS spectra at 285 K showing anti-Stokes (ν < 0) and Stokes (ν > 0) contributions. Inset shows anti-Stokes around the −999 cm^–1 benzenethiol ring-breathing peak (arrow). The shaded region is blocked by the notch filter.

First we focus on one of the strongest SERS peaks at ν = ± 999 cm^–1 which corresponds to an in-plane breathing mode of the benzenethiol phenyl group.¹⁹ Both the peak height and the background at this frequency are extracted at different temperatures for the Stokes and anti-Stokes sides (Figure 2). Since anti-Stokes Raman scattering is produced from molecules which are in excited vibrational states, their occupation and hence peak height increases exponentially with temperature, following:

as indeed found (Figure 2B) with the prediction (dashed line) matching the experimental peak height. Confirmation is also found from the ratio of Stokes to anti-Stokes peak height to extract the temperature and scattering amplitude ratio (not shown), which confirms the molecules are indeed equilibrated with the sample temperature. Above 360 K the intensities of the Stokes peaks drop (with an accompanying relative drop in the anti-Stokes peaks), mostly likely due to desorption of molecules from the surface of the Au. Since the Stokes peaks only depend on the number of molecules in the vibrational ground state, they remain nearly constant below 360 K (with minor changes from increasing Au conductivity and phase changes in the molecular packing^20,21).

Figure 2.

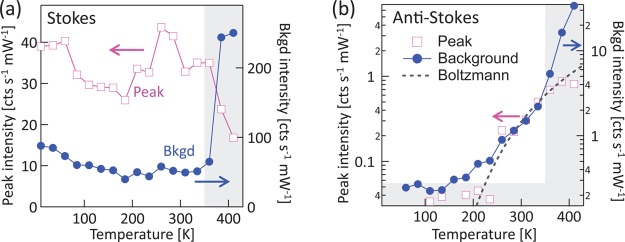
Emission intensities for (a) Stokes peak at 999 cm^–1 and (b) anti-Stokes peak at −999 cm^–1 corresponding to benzenethiol ring breathing mode. Also plotted are SERS background intensities extracted at ±980 cm^–1 respectively. Below 200 K, the anti-Stokes peaks drop below the noise level (shaded). The dashed line in (b) is a Boltzmann fit to occupation at ν = −999 cm^–1. The right shaded area indicates region where temperature affects molecular coverage/surface roughness, and lower shading indicates noise level.

As well as the peaks, continuous backgrounds are observed on both Stokes and anti-Stokes sides (Figure 1). These are linear in laser power and, since the 785 nm excitation is well below the interband energy, cannot be photoluminescence. Due to the very low power densities used and the linear power dependence observed, we rule out two-photon photoluminescence (TPPL) which cannot be efficiently excited with a continuous wave laser. This agrees with comparisons between pulsed and CW excitation of Au at 780 nm which clearly shows TPPL only from the former, although displaying also the backgrounds discussed here in both cases.⁶ Above 360 K these backgrounds increase suddenly (Figure 2a) likely due to molecular desorption roughening the Au and enhancing plasmonic hotspots;¹⁶ hence we focus here on lower temperatures. While the Stokes background (similarly to the SERS peaks) increases slightly with decreasing temperature (Figure2a, below 360 K), the anti-Stokes background strongly decreases at lower temperature (Figures 2b and 3). On a log scale (Figure 3b), it is apparent that the background emission spectrum follows an exponential (apart from within 400 cm^–1 of the laser line where the filter response dominates in etaloning). Fitting to a Boltzmann distribution, ignoring the constant gaussian component from low-level laser leakage through the filter, allows us to extract an effective temperature (Figure 3c) to compare to the sample temperature. Their direct correspondence implies that the full anti-Stokes background is a thermally activated process. Even at the highest temperatures the intensity of this background light emission still increases, although the molecular density (seen in the Raman peaks) decreases, suggesting that it indeed does not originate from the molecules.

Figure 3.

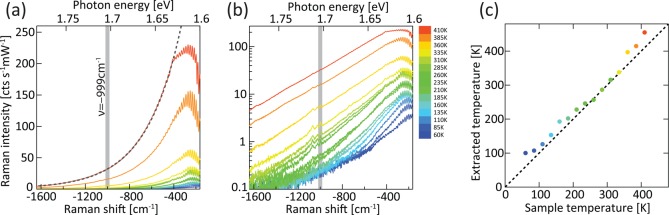
Anti-Stokes SERS spectra from 60 K (blue) to 410 K (red) in 25 K steps displayed on (a) linear scale and (b) log scale, revealing the Raman modes with shaded line highlighting −999 cm^–1 peak. Exponential fit for 410 K shown by dashed lines. (c) Extracted effective temperature from the SERS vs the sample temperature. Colors of points/lines indicate the sample temperature.

This dependence on temperature would not be expected for photoluminescence from the metal and contrasts to semiconductors where typically photoluminescence intensities decrease with increasing temperature. Instead it suggests that only a fraction of electrons excited above the Fermi energy are available to interact with the incoming light. We can explain this if we consider an inelastic light scattering (ILS) process in which electrons in the metal are transiently excited to a virtual state (as in Raman scattering) but then relax to a lower energy on the dispersion (Figure 4a,b). Because only the energy levels just below the Fermi level are empty, this implies the electrons participating in ILS are those initially thermally excited from just above the Fermi level. Only as the temperature increases do final states below the initial electron energy open up, giving the characteristic thermal activation in the anti-Stokes that is observed in the SERS spectra. For the Stokes background, the ILS process does not require thermal activation (the electrons lie below the Fermi energy already), and the slight increase in background at lower temperatures arises from the increased conductivity of gold enhancing plasmonic coupling.

Figure 4.

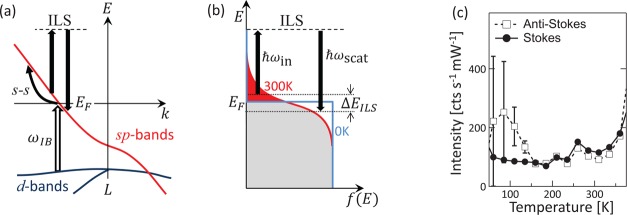
(a) Band diagram of Au around the L point, showing absorption from d to s bands only for ω > ω_IB, intraband scattering (s–s) and inelastic light scattering (ILS). (b) Origin of anti-Stokes scattering background produced by ILS from the thermally excited electrons above the Fermi level (shaded red). Plasmonically coupled light excites these electrons to a virtual state where they relax down to empty states just below the Fermi energy, emitting blue-shifted (anti-Stokes) light. (c) Measured background intensity at ν = ± 0 cm^–1 from fits to Stokes and anti-Stokes data at each temperature.

Compared to intraband processes previously proposed (s–s),⁶ this ILS scattering is not symmetry forbidden and resembles a Raman transition. However, what is required for the electrons to relax back to a different energy on the dispersion is to change their momentum. As previously suggested,^12,14,22 this naturally results from localized plasmonic confinement (of characteristic length Δx), because wavevectors up to Δk ∼ (π/Δx) are then available. For intraband processes, the symmetry-breaking transitions needed require field gradients which are significant on the scale of the bond length (0.1 nm) which is difficult to achieve. In contrast the ILS process introduced here can access energy differences ΔE_ILS = (1/2m*)(ℏπ/Δx)² ∼ 400 meV for 1 nm confinement scales.

The amplitudes of both Stokes and anti-Stokes background processes are found to be equal in the limit ν → 0 (Figure 4c). Here the fits of the anti-Stokes spectra are extrapolated to zero frequency and compared to the extracted background of the Stokes spectra near 0 cm^–1 (error bars increase at low temperatures on anti-Stokes as the signal decreases). This implies that the Stokes background is indeed produced by the exact reverse process that creates the anti-Stokes background. In this case electrons just below the Fermi energy are optically excited to a virtual state, and aided by a momentum shift, they then are driven back onto the band dispersion at energies just above the Fermi energy, inelastically scattering red-shifted light. While electrons anywhere up to the incident photon energy ℏω below the Fermi energy could participate in ILS, the requirement on momentum conservation limits them to a small range from E_F – ΔE_ILS to E_F. This nearly flat background is indeed seen in the experimental spectra, with additional modulation coming not from the inelastic scattering, but from the in/out-coupling efficiencies related to the near-field plasmon spectra.

Plasmons are involved in two ways in this ILS background. Since the optical field excites the electrons in the metal, then the plasmons are important because they provide the strongest optical fields inside the metal, spatially localized to the surface regions around nanogaps. Similarly these plasmons are best at out-coupling the radiation from the electrons relaxing back down from the virtual ILS state. The spectral resonance of the plasmons thus dictates which energy range of electrons contributes to the Stokes background. The second role of the plasmons is to provide the localization needed to provide momentum conservation in the ILS process. Both of these factors are enhanced in tighter confined plasmonic metal nanostructures, and hence the background is predicted to increase in systems with tightly trapped plasmons. Since both ILS and SERS processes depend on the fourth power of field enhancement, |E|⁴, they are both amplified similarly by optical confinement. Similarly the virtual intermediate state that is inherent to ILS guarantees the prompt emission seen in experiments. We note however that quantitative calculation of the absolute strength of ILS requires sophisticated inclusion of many-body interactions between the photoexcited electron and the resulting hole produced around the Fermi level, together with the screening of their Coulomb attraction (responsible for Fermi edge singularities in semiconductors²³), which is beyond the scope of this paper but now of interest.

The identification of ILS as the dominant contribution to the SERS background suggests new strategies are needed for improving the signal-to-noise ratio (SNR) in Raman sensing. Since this background comes from the very electrons collectively supporting the plasmon resonance, it is not straightforward to remove. One possibility is to use semimetals with small bandgaps, or highly doped semiconductors (such as ITO), which prevent ILS by reducing the electron bandwidth while still supporting plasmons. However, no small-bandgap material systems yet have plasma frequencies in the visible or near-infrared region where detection is highest efficiency. Another observation that may be important is that the SERS peak to ILS background ratio depends on the nanostructure geometry, in ways that are not yet understood. For instance this ratio can be varied from 1:1 to 10:1 by modifying the plasmonic nanostructures used from nanovoids^24,25 to nanoparticles. From our model, this SNR ratio depends on the average strengths of the optical field inside the metal (E̅_in), compared to the field just outside the metal (E̅_out) where the molecules are. A suitable figure of merit, 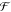_SERS, to evaluate potential structures is thus

and further investigations in highly controlled nanostructures are thus important. In the same way that the outgoing photon in SERS can be stimulated by a second Stokes-tuned laser pulse (in CARS), the ILS process will also be stimulated through coherent anti-Stokes inelastic scattering (which we term CAIS), and such experiments are in progress. Indeed, strong background contributions to CARS arising from this process will control the SNR for biomedical imaging.^26,27

In conclusion, we showed that the anti-Stokes background continuum emitted from plasmonic nanostructures can only be well accounted for using a model based on the inelastic light scattering of electrons within the metal. The temperature dependence observed can be explained in no other way that accounts for the data and suggests that an unavoidable aspect of SERS is the production of this background emission from the free electrons that are also crucial to plasmons. We thus suggest that classification of emission from plasmonic constructs as “photoluminescence” is not correct. Clearing up the understanding of a major part of the SERS continuum background presented should aid both interpretation of spectra, as well as highlight new routes to modify the strength of this background compared to desired vibrational peaks. We also suggest that the precise temperature dependence of this background allows its use to quantify the temperature of samples in real time independent of absolute intensity and thus can be used for temperature sensing concurrently with all SERS measurements. Recent pulsed experiments in Au nanorods show that such signatures can indeed be discerned up to several thousand degrees Kelvin.¹³

Author Present Address

J.T.H.: ICFO-Institut de Ciencies Fotoniques, Mediterranean Technology Park, 08860 Castelldefels (Barcelona), Spain.

The authors declare no competing financial interest.