ElNémo: a normal mode web server for protein movement analysis and the generation of templates for molecular replacement

Abstract

Normal mode analysis (NMA) is a powerful tool for predicting the possible movements of a given macromolecule. It has been shown recently that half of the known protein movements can be modelled by using at most two low-frequency normal modes. Applications of NMA cover wide areas of structural biology, such as the study of protein conformational changes upon ligand binding, membrane channel opening and closure, potential movements of the ribosome, and viral capsid maturation. Another, newly emerging field of NMA is related to protein structure determination by X-ray crystallography, where normal mode perturbed models are used as templates for diffraction data phasing through molecular replacement (MR). Here we present ElNémo, a web interface to the Elastic Network Model that provides a fast and simple tool to compute, visualize and analyse low-frequency normal modes of large macro-molecules and to generate a large number of different starting models for use in MR. Due to the ‘rotation-translation-block’ (RTB) approximation implemented in ElNémo, there is virtually no upper limit to the size of the proteins that can be treated. Upon input of a protein structure in Protein Data Bank (PDB) format, ElNémo computes its 100 lowest-frequency modes and produces a comprehensive set of descriptive parameters and visualizations, such as the degree of collectivity of movement, residue mean square displacements, distance fluctuation maps, and the correlation between observed and normal-mode-derived atomic displacement parameters (B-factors). Any number of normal mode perturbed models for MR can be generated for download. If two conformations of the same (or a homologous) protein are available, ElNémo identifies the normal modes that contribute most to the corresponding protein movement. The web server can be freely accessed at http://igs-server.cnrs-mrs.fr/elnemo/index.html.

INTRODUCTION

One of the best suited theoretical methods for studying collective motions in macromolecules is normal mode analysis (NMA), which leads to the expression of protein dynamics in terms of a superposition of collective variables, namely, the normal mode coordinates [see (1) for a review]. Though the first normal mode studies were performed as early as 20 years ago (2,3), they remained restricted to small-size proteins until more recently, when methodological advances (4–8), simplified protein descriptions (9–11), and ever faster computer systems allowed them to address increasingly large macromolecular systems, up to entire protein complexes, including the entire ribosome (12–14).

Noteworthy is that by analysing more than 3800 known protein motions, Krebs et al. (15) have shown that more than half of them can be approximated by applying a perturbation in the direction of at most two low-frequency normal modes of the considered protein. Moreover, when the collective character of the protein motion is obvious, a single low-frequency normal mode often proves to be enough, and it is usually one of the three lowest-frequency ones (12,13). Such results strongly suggest that protein movements between open and closed forms (e.g. with and without ligand) may actually be under selective pressure, so as to follow mainly one, or a few, low-frequency normal modes of the protein. In other words, amino-acid sequences may have evolved so that low-energy barriers are found when the protein is displaced along the few corresponding normal mode coordinates.

One major application of normal modes is the identification of potential conformational changes, e.g. of enzymes upon ligand binding (7,12,13). The method has also been used recently in the study of membrane channel opening (16), the analysis of structural movements of the ribosome (14), viral capsid maturation (17), transconformations of the SERCA1 Ca-ATPase (8,18), tertiary and quaternary conformational changes in aspartate transcarbamylase (19) and the analysis of domain motions in large proteins in general (11,20). NMA is most often used in order to try to guess what kind of conformational change a protein undergoes in order to fulfil its function, by analysing its lowest-frequency modes one after the other. It can also be used to check if a conformational change proposed on the basis of non-structural experimental data is likely to occur or not, as recently done in the case of membrane channel opening (16). As a tool able to predict large-amplitude motions, it has been suggested that it has the potential to improve the resolution of the final reconstructions of single particles from electron cryomicroscopy (21). Moreover, the fact that 50% of the observed protein movements can be accurately described by only one or two low-frequency normal modes prompts for an application of NMA in X-ray crystallography data phasing, i.e., to use normal mode perturbed models as templates in molecular replacement. We have shown that this approach allows to break difficult phasing problems where the original unperturbed template fails to yield a usable solution (22). NMA thus represents a powerful tool for a wide range of applications in structural biology and X-ray crystallography. We designed ElNémo as a comprehensive, but still easy-to-use interface for NMA. Particular emphasis was put on its ability to handle large protein systems with 500–1000 or more residues in an all-atom level of description, having in mind the generation of a great number of normal mode perturbed models as templates for MR.

METHODS

The details of NMA have been described elsewhere (7,16). Here we summarize the basic principles of the computations that are performed by ElNémo.

Normal mode calculation is based on the harmonic approximation of the potential energy function around a minimum energy conformation. This approximation allows the analytic solution of the equations of motion by diagonalizing the Hessian matrix (the mass-weighted second derivatives of the potential energy matrix). The eigenvectors of this matrix are the normal modes, and the eigenvalues are the squares of the associated frequencies. The protein movement can be represented as a superposition of normal modes, fluctuating around a minimum energy conformation. For proteins, the normal modes responsible for most of the amplitude of the atomic displacement are associated to the lowest frequencies. In order to avoid time-consuming energy minimizations, as well as the corresponding drift of the studied structure, a single-parameter Hookean potential is used, which was shown to yield low-frequency normal modes as accurate as those obtained with more detailed, empirical, force fields (9):

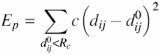
where d_ij is the distance between two atoms i and j, is the distance between the atoms in the three-dimensional structure, c is the spring constant of the Hookean potential (assumed to be the same for all interacting pairs) and R_c is an arbitrary cut-off, beyond which interactions are not taken into account (the ElNémo default cut-off is 8 Å, but the user is free to change this setting; values of 10–13 Å are often used when only C-alpha atoms are taken into account). This approximation implies that the reference structure represents the minimum energy conformation. Moreover, all atom masses are set to the same fixed value in the kinetic energy term, as this approximation was shown to have little influence on the low-frequency modes. Therefore, only normalized frequencies are reported, the lowest non-trivial frequency being set to one. Note that there are always six zero frequencies (corresponding to the three overall rotations and three overall translations of the system), but more than six can be obtained if a group of atoms is at a distance larger than R_c from the others.

The building block approximation, also named RTB (for ‘rotation-translation-block’), groups several residues into a single super-residue, the rigid-body rotations and translations of the super-residues being used as a set of new coordinates instead of the Cartesian ones (5). Tama et al. (7) have shown that this approximation has very little influence on the low-frequency modes. Due to this approximation it becomes possible to treat very large proteins in an all-atom level of description in reasonable computing time (ElNémo automatically determines the number of residues to be grouped together based on the number of residues in the protein, but the user may override this setting; for small proteins, each block contains a single residue). Note that for larger and larger proteins, the size of the domains involved in functional motions is expected to grow. Thus, when the system is large, the grouping of several residues into a single block is expected to have little impact on the lowest-frequency modes, which depend mainly on the overall shape of the system. Indeed, they can be captured at extremely high levels of coarse-graining (23) or by using low-resolution structural data (21).

Normal mode perturbed models are structural models in PDB (Protein Data Bank) format that correspond to the original reference structure, with a perturbation proportional to the corresponding normal mode applied to every atom. As normal modes define only the direction, but not the amplitude, of the conformational change of a protein, the user can specify a range of amplitudes (in arbitrary units) that will be used in the computation. Note that, due to the approximation of the atom–atom interactions by a harmonic potential, application of too large amplitudes may yield distorted structures and result in sterical clashes. However, it is necessary to specify amplitudes larger than those allowing for a fair comparison with B-factors, because the latter reflect atomic motions at room temperature, while in the present context the purpose of normal mode perturbation is to capture much larger amplitude motions.

Distance fluctuation maps highlight residue pairs i and j with the strongest variation in the distance between their C-alpha atoms in a given mode. In ElNémo, the top ranking (10%) distance fluctuations are coloured in blue (increase) and red (decrease). Flexible and rigid blocks, as well as their relative movements can be easily identified in such maps.

The degree of collectivity indicates the fraction of residues that are significantly affected by a given mode. For maximal collective movements the degree of collectivity tends to be a value of one, whereas for localized motions, where the normal mode movement only involves few atoms, the degree of collectivity approaches zero. While low-frequency normal modes are expected to have collective characters, especially those related to functional conformational changes of proteins (12), computed ones sometimes happen to be localized. In such cases, they correspond to motions of some extended parts of the system, as often observed in crystallographic protein structures for N- or C-termini. These motions are usually meaningless and can be ignored, though it is common practice, and probably safer, to remove such extended parts prior to the normal mode computation.

The overlap measures the degree of similarity between the direction of a chosen conformational change and the direction of a given normal mode. A conformational change is here defined by the difference vector between the reference structure and a second conformation of the same protein or that of a close homologue. ElNémo reports cumulative values for the square of the overlap, starting with the lowest-frequency non-trivial normal mode. Note that, because the normal modes form a basis, this cumulative sum reaches a value of one when it is computed over all modes. If the considered conformational change has a collective character, the cumulative sum usually reaches a value of 0.7–0.8 already within the 20–50 lowest-frequency modes (13,24). What makes NMA useful for predicting protein movements is the fact that in a large number of cases, one or two low-frequency normal modes, i.e. those with the highest overlap are enough for providing a fair description of the conformational change (1,12).

B-factors are computed from the mean square displacement 〈R²〉 of the first 100 lowest-frequency normal modes using the relationship B = (8π²/3)〈R²〉 and linear scaling to the observed B-factors in the reference structure as described in (7). Correlations between NMA and crystallographic B-factors are usually found to be >0.5–0.6 (13), while values >0.8 have been reported (1). Adjusting R_c can slightly improve such correlations. This probably reflects the fact that modifying R_c affects low-frequency densities (9). The comparison between computed and observed crystallographic B-factors provides a measure of how well the protein's flexibility in its crystal environment is described by the normal modes.

Root mean square distances (RMSD) between the normal mode perturbed models and a second (not necessarily sequence-identical) structure are computed by a rigid body superposition using the lsqman software (25). Reported are the RMSD between all C-alpha atoms of the two protein conformations, the number of C-alpha atoms that are closer than 3 Å in the rigid body superposition and the RMSD between those atoms only. These numbers can be used as a proxy for the overlap in the case of not 100% sequence-identical proteins.

USING THE WEB INTERFACE

The principal input to ElNémo is a protein model in PDB format (26). A numerical FORTRAN code, which is the heart of ElNémo, determines the corresponding interaction matrix for the elastic network model and computes its 100 largest eigenvalues and their eigenvectors (the normal modes). For each mode, its degree of collectivity of movement and the mean square displacement of all residues is output. The user may select the number of low-frequency modes for which normal mode perturbed models will be computed, specifying an amplitude range and increment (DQMIN, DQMAX, DQSTEP). The automatic generation of three-dimensional animated views of these modes from three different viewpoints (using Molscript; 27) can be requested. Distance fluctuation maps are also made available for all normal mode perturbed models. B-factors are derived from the mean square displacements of all atoms in the 100 lowest-frequency modes. When a second conformation of the same protein is submitted, ElNémo computes the degree of collectivity of motion for all normal modes and reports the contribution of each of the 100 lowest-frequency modes to the conformational change (amplitude). This option requires that both models have the same number of atoms and that the residues are numbered identically. If only a homologue of the reference protein (<100% sequence identity) is available in a different conformation, ElNémo computes the RMSD between the normal mode perturbed models and the homologous structure in order to identify the normal mode perturbations that best describe the associated protein movement (Figure 1).

Figure 1.

An example of a typical ElNémo output that is available for every run through the result page (top left). The normal mode analysis page (top right) displays the different properties of the first 100 lowest-frequency modes, i.e. their frequency, degree of collectivity of movement, mean square displacement 〈R²〉, overlap (if two conformations are available) and its corresponding amplitude. Three-dimensional animations from three orthogonal viewpoints are available in large and small sizes. Comparison of a normal mode perturbed structure and a second conformation in terms of RMSD and number of residues that are closer than 3 Å can be done (bottom right). Analysis of distance fluctuations between all CA atoms is presented in the form of a cross-plot, where red and blue dots indicate those residues for which the pairwise distance changes most significantly in the movement defined by a given mode. The result page also allows submission of normal mode calculations for new modes with varying amplitude ranges. The resulting normal mode perturbed models in PDB format can be downloaded for further processing (e.g. using VMD (28) to visualize the protein movements as presented on the ElNémo example page) or as templates for MR.

Although ElNémo will probably produce useful results when using original (unprocessed) PDB files, some modifications of the input data are advisable. Note that ElNémo only reads the ‘ATOM’ record from the PDB file, and that water residues are ignored. Therefore, molecules that are coded as ‘HETATM’ need to be changed to ‘ATOM’ if they are to be accounted for in the normal mode calculation. Examples are seleno-methionine residues, haeme groups, nucleic acids and calcium ions. However, this conversion is not done automatically by ElNémo to avoid inclusion of crystallogenic agents, such as 2-methyl-2,4-pentanediol (MPD) and Tris, that are unrelated to the protein in its real environment. To prevent lumping of residues that are part of separate molecules into one RTB super-residue, different chain identifiers should be used. Alternate conformations and hydrogen atoms should be erased, as their presence will have only a minor influence on the results. More specific hints on how to best prepare an ElNémo job can be found on the help page.

The computation of the normal modes for small- to medium-size proteins (100–400 residues) in an all-atom level of description takes between 10 and 30 min when using default settings. Even very large proteins, such as the capsid-like protein lumazine synthase complex and the entire ribosome take no longer than some hours to complete (both molecules are constituted of more than 9000 residues). Preparation of additional normal mode perturbed models and animated views takes between 3 and 10 min per mode to complete for small- to medium-size proteins. However, this part of the computation becomes the most time-consuming part of an ElNémo run for larger proteins. Therefore, the user is advised to limit the number of normal mode perturbed models and visualizations in these cases to the first three to five modes at this stage and to request additional models and animations once the initial job is completed based on an analysis of the degree of collectivity of movement of the different modes. At that time, models that are perturbed using two normal modes at the same time can also be requested (i.e. for use as MR templates). ElNémo jobs are processed in a linear batch queue on a first-come first-served basis. Notification of the user by email about the job status is available. A second, independent queue is used for the computation of additional modes. As walk-through examples, some of our recent applications of NMA to conformational changes of membrane channel proteins and to molecular replacement are presented in the example section of the ElNémo web server. The corresponding input and output is available under the job id EXAMPLE-n on the job-status page, so that the interested user can analyse and re-run the corresponding jobs.

FINAL REMARKS

NMA is a powerful tool for the study of protein movements and conformational changes, proven by the ever-growing range of applications in different structural biology domains and more recently in X-ray crystallography as a source of templates for molecular replacement. Methodological and technical advances, i.e. the elastic network model and the RTB approximations, make NMA of whole viruses and of the entire ribosome possible. The ElNémo web server reflects the long-standing experience in this domain of the second author (Y.H.S.) and his co-workers. It makes the respective tools available to a wide community of potential NMA users, without exposing them to the need to gain in-depth understanding of the technique and its implementations. The availability of a comprehensive and easy-to-use dedicated NMA web server like ElNémo will therefore facilitate an even more widespread application of this interesting technique.