Abstract
Analysis of vibrational motions and thermal fluctuational dynamics is a widely used approach for studying structural, dynamic and functional properties of proteins and nucleic acids. Development of a freely accessible web server for computation of vibrational and thermal fluctuational dynamics of biomolecules is thus useful for facilitating the relevant studies. We have developed a computer program for computing vibrational normal modes and thermal fluctuational properties of proteins and nucleic acids and applied it in several studies. In our program, vibrational normal modes are computed by using modified AMBER molecular mechanics force fields, and thermal fluctuational properties are computed by means of a self-consistent harmonic approximation method. A web version of our program, MoViES (Molecular Vibrations Evaluation Server), was set up to facilitate the use of our program to study vibrational dynamics of proteins and nucleic acids. This software was tested on selected proteins, which show that the computed normal modes and thermal fluctuational bond disruption probabilities are consistent with experimental findings and other normal mode computations. MoViES can be accessed at http://ang.cz3.nus.edu.sg/cgi-bin/prog/norm.pl.
INTRODUCTION
Analysis of biomolecular vibrational and thermal fluctuational dynamics provides clues to the structural, dynamic and functional properties of proteins, nucleic acids and other biomolecules (1–3). It has been extensively applied for probing biomolecular association (4–9), conformation changes (3,10–13), domain motions and collective motions (14–17), structural fluctuations (18–21), pressure effect (22,23), entropic effect (24), energy transfer (25) and proton transfer (26). A useful computational method for studying vibrational and thermal fluctuational dynamics of biomolecules is normal mode analysis (1,27–30), which has been used in a variety of studies (2,14,31–43). To the best of our knowledge, no freely accessible web-based software is available for computing the vibrational and thermal fluctuational dynamics of biomolecules. It is thus desirable to develop such a tool.
We have developed a program for computing vibrational normal modes (14,44) and thermal fluctuational dynamics of proteins and nucleic acids (19,21). The computed vibrational modes (14,44), thermal fluctuational hydrogen-bond disruption probabilities (19–21) and molecular binding affinities (9) are broadly consistent with experimentally estimated values. The normal modes of a biomolecule are computed by using the harmonic component of the atomic level molecular mechanics energy functions and modified AMBER force fields that include bond stretch, bond angle bending, bond torsion, hydrogen bonding and contributions from intermolecular non-bonded van der Waals and electrostatic interactions (14,44). The thermal fluctuational dynamics of a biomolecule is derived from a self-consistent harmonic approach using the full atomic level molecular mechanics energy functions and modified AMBER force fields (19–21). To facilitate the study of the properties of proteins and nucleic acids, a web version of our program, MoViES (Molecular Vibrations Evaluation Server), was set up for computation of vibrational normal modes and thermal fluctuational properties of proteins and nucleic acids. This software was tested on several proteins to compare the computed normal modes, thermal fluctuational bond disruption probabilities, and free energy changes with experimental findings and the results from other normal mode studies.
SOFTWARE ACCESS
The MoViES webpage is at http://ang.cz3.nus.edu.sg/cgi-bin/prog/norm.pl, which is shown in Figure 1. The three-dimensional structural file of a biomolecule, in PDB format, can be uploaded via the explorer window provided. The average CPU time ranges from minutes for a protein of a few hundred non-hydrogen atoms to hours for one of 1000 atoms, and up to seven days for one of 4000 atoms on an HP J6750 workstation. Because of the long CPU time needed for performing a computation request, the computed results are returned via email and currently the computation is limited to a protein or nucleic acid of 4000 non-hydrogen atoms.
Figure 1.
Interface of MoViES.
Five files are returned. One file, out_modes, gives the computed normal mode frequencies and mode assignments provided in terms of potential energy distribution (PED) function and kinetic energy distribution (KED) function. The physical meaning and algorithm of PED and KED are discussed in the next section. PED describes the distribution local interaction. Because modes below 30 cm−1 are increasingly non-local in nature, no PED functions below 30 cm−1 are provided in this file. Another file, out_hbnds, provides the computed thermal fluctuational bond disruption probability for all of the hydrogen bonds. The third file, out_therm, gives the computed vibrational thermodynamic quantities, including the vibrational free energy, entropy and specific heat of the studied biomolecule. Moreover, the static energies and their components, computed by using AMBER-based molecular mechanics force fields, are also provided in this file. The fourth file, out_distr, provides the distribution of computed normal modes with respect to frequencies. The last file, out_eigen, is a compressed file that gives the eigenvectors for the lower-frequency modes. Because of the size limit of mailboxes in the majority of mail servers, the size of the file out_eigen is tentatively restricted to approximately 100000 lines. Thus for a biomolecule of 100, 1000, and 4000 atoms, only the eigenvectors in the frequency range of 0–1000 cm−1, 0–100 cm−1 and 0–25 cm−1, respectively are provided in the out_eigen file.
COMPUTATIONAL METHODS
Potential functions and parameters
Internal motion of a protein can be modelled by the following Hamiltonian, described in the literature (45–47):
where i and j are indexes for atoms, l and m are indexes for bonds (including covalent, disulfide and hydrogen bonds). Bond stretch, angle bending and torsion terms are for bond vibration, motions that change the angle between two neighbouring bonds and rotation around respective rotatable bonds, respectively. S-bond and H-bond terms are for disulfide bond and hydrogen bond interactions, respectively. Pi and mi are momentum and mass of the i-th atom. rl is the distance between the two end atoms of a bond (covalent, H-bond or S-bond). 
and 〈rl〉 are force constant and equilibrium bond length for the l-th covalent bond (other than disulfide bond); θlm, 
and 〈θlm〉 are bond angle, angle bending force constant and equilibrium bond angle between the l-th and m-th bonds φl, Vl, nl and γl are torsion angle, potential depth, periodicity and the phase angle for bond rotation (torsion) for the l-th rotatable bond. These parameters are from AMBER (45). 
, 
, al and 
in an S-bond and H-bond are the potential depth, width and minimum potential position for the l-th S-bond or H-bond. rij is the distance between the i-th and j-th atoms; Aij and Bij are non-bonded van der Waals potential parameters between the i-th and j-th atoms; qi and qj are the partial charges of the i-th and j-th atoms; ɛij is the dielectric constant between the i-th and j-th atoms. These H-bond and S-bond parameters can be found from earlier publications (45–47).
Normal mode computation
Under harmonic approximation, internal motions of a bimolecular can be modelled by the following Hamiltonian:
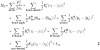
The first term is the kinetic energy term. Vst is the static part of the Hamiltonian, i.e. the potential energy terms at equilibrium positions. 
and Kij are torsion, S-bond, H-bond and non-bonded force constant, respectively; 〈φl〉, 〈rl〉 and 〈rij〉 are equilibrium torsion angle, bond length (for H-bond or S-bond) and distance between non-bonded atom pairs, respectively. The rest of the parameters are the same as in Equation 1.
The equation of motions associated with the Hamiltonian in Equation 2 is solved in the mass weighted Cartesian coordinate system to derive the vibrational frequency ωσ and eigenvector qi for each normal mode (14). The assignment of the underlying motions of a normal mode can be made by analysis of the distribution of potential energy of individual internal motions in that mode (48). This distribution is described by the PED function 
(48)
in which φjk is the force constant and 
is the internal coordinate given by 
where bjk is the element of the B matrix corresponding to a particular connection in a particular motion. M is a matrix whose element is 
, qσ is the matrix of eigenvectors corresponding to a particular frequency ωσ. The kinetic energy distribution function is
Thermal fluctuational hydrogen-bond disruption probability
Thermal fluctuational H-bond disruption probability is computed based on the Bogoliubov variational theorem, which states that the free energy G of a system described by a Hamiltonian H can be approximated by the solutions of an effective Hamiltonian H0. From Bogoliubov inequality,
one can self-consistently adjust the parameters of a trial effective Hamiltonian H0 so as to minimize the right-hand-side terms so that the trial system H0 can best approach the original system H. Here G0 is the free energy of the trial system.
For small displacement thermal fluctuational motions involved in protein H-bond disruption, the hydrophobic forces are relatively unchanged and the changes in torsion and non-bonded van der Waals and Coulomb interactions are small. Hence one can use the harmonic Hamiltonian H0 in Equation 2 as the dynamic component. The H-bond force constant 
is determined by minimization of free energy expansion in Equation 5 which gives
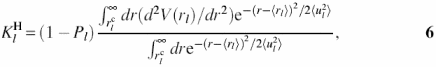
where 
is H-bond potential, 
is the inner-bound cut-off determined from 
. The scaling factor (1 − Pl) is introduced to take into consideration disrupted H-bonds in the statistical ensemble and Pl is the disruption probability of the l-th H-bond. 
is the mean square vibrational amplitude of the l-th H-bond given in terms of vibrational normal modes:
where ωn and n are the frequency and index of n-th normal mode, sln is the mass weighted eigenvector of the n-th normal mode for the l-th H-bond, T is the temperature, kB Boltzmann's constant and ħ Planck's constant divided by 2π.
The average length 〈rl〉 of an H-bond was computed by setting
where 
is the full width at half maximum of the Gaussian distribution function 
given in Equation 6.
The probability of finding an H-bond fluctuating beyond a certain break-away point, i.e. the disruption probability of law individual H-bond, is given by
where 
is the maximum stretch length (break-down point) of the H-bonds. It is given as the smaller of the maximum allowed bond length 3.5 Å and the potential inflection point (where V″ = 0, which gives 
) (9). Based on the Boltzmann relationship, Pl ∼ eRTΔG, −RTlnPl can be considered as a quantity approximately associated with H-bond disruption free energy.
RESULTS AND DISCUSSION
Table 1 gives the computed lowest normal mode frequencies (below 20 cm−1) of Crambin (PDB id: 1CNR) along with those of the same protein entry computed by Teeter and Case using both normal mode and quasi-harmonic analysis (49). Teeter and Case have used eight potential functions for normal mode computation. Table 1 gives only the modes computed by using DISCOVER functions, which are closest to those obtained from the quasi-harmonic analysis in the same study. The reported quasi-harmonic frequencies in that study were computed by using the simulation data at several time scales. Only the frequencies from the results of the longest simulation scale, 100 ps, are listed in Table 1. Table 1 shows that our computed frequencies are in fair agreement with those of quasi-harmonic analysis, and these frequencies are also in qualitative agreement with those of normal mode analysis obtained by Teeter and Case.
Table 1. Comparison of the computed lowest normal mode frequencies of Crambin (PDB id: 1CNR) with those derived from a normal mode study and quasi-harmonic analysis by Teeter and Case (49).
| Our method | Normal mode analysis by Teeter and Case (DISCOVER potential functions) | Quasi-harmonic analysis by Teeter and Case (100 ps simulation time) |
|---|---|---|
| 4.3 | 4.7 | 2.6 |
| 5.4 | 5.8 | 7.7 |
| 5.6 | 6.3 | 8.3 |
| 7.2 | 9.3 | 9.0 |
| 7.6 | 9.9 | 9.9 |
| 9.1 | 10.6 | 10.3 |
| 9.3 | 12.6 | 11.6 |
| 10.2 | 13.3 | 12.0 |
| 11.2 | 15.8 | 12.4 |
| 11.4 | 16.1 | 13.8 |
| 12.2 | 16.4 | 14.2 |
| 13.0 | 16.9 | 15.8 |
| 13.8 | 18.1 | 16.2 |
| 13.9 | 18.1 | 17.0 |
| 15.0 | 19.4 | 17.7 |
| 15.8 | 20.7 | 17.9 |
| 18.0 | 21.2 | 18.2 |
| 18.3 | 21.8 | 18.9 |
| 19.1 | 22.8 | 19.3 |
| 19.8 | 23.2 | 20.3 |
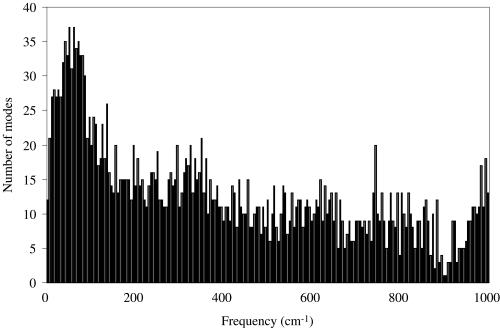
Figure 2 shows the distribution of the computed normal modes for the wild-type alpha-lytic protease (PDB id: 1GBK). The distribution of the normal modes of this protein has also been computed by Miller and Agard (39). The shape of the distribution of our computed normal modes is very similar to that of Miller and Agard, and it is also similar to those reported for other proteins (29,50–52).
Figure 2.
The distribution of normal modes for wild-type alpha-lytic protease (PDB id: 1GBK). The histograms show the mode density versus frequency for all normal modes less than 1000 cm−1. The bin width is 5 cm−1.
Table 2 gives the computed frequencies and mode assignments, in terms of PED, for the normal modes of hen lysozyme (PDB id: 1LSE) in the frequency range between 755 and 1665 cm−1 that have available experimental data. For comparison, the observed vibrational spectra described in the literature (53) are also given in the table. As in our previous studies (14,44), the computed frequencies are consistent with observed frequencies. Table 3 shows the computed individual H-bond disruption probability, in terms of -RTlnPl, at 293 K, and the derived theoretical H-bond free energy change, in terms of 
, for a selected set of H-bonds in two proteins, T4 lysozyme (PDB id: 3LZM) and ribonuclease T1 (PDB id: 9RNT). These H-bonds were selected because each of them is connected to an amino acid subjected to substitution in site directed mutagenesis experiments (57,58). For rough comparison, the estimated free energy ΔGexpt from these experiments for the deletion of the corresponding H-bonds is included in the table.
Table 2. Comparison between the observed (Raman) frequencies ωexpt of hen egg-white lysozyme (53) and the calculated normal mode frequencies ωtheor for hen lysozyme (PDB code 1LSE).
| Raman | Calculation | ||
|---|---|---|---|
| ωexpt (cm−1) | ωtheor (cm−1) | Assignment (PED%) | Residue |
| 759 | 760.5 | CB-CG-CD2 (3); CB-CG-CD1 (3); CG-CD2-CE3 (3); | TRP111, TRP108, TRP123, TRP62 |
| 838 | 831.9 | CA-C-O (5); O-C-N (5); C-N-CA (4); | TYR20, TYR23, ARG21, CYS127, ARG45 |
| 857 | 858.8 | CA-CB-CG (3); C-CA-CB(2.); CG-CD1-NE1 (2) | TRP 62, TRP28, TRP63, HIS15, NET105 |
| 878 | 874.8 | CA-CB-CG (2); C-N-CA (2); C-CA-CB (2) | TRP 63, MET105 |
| 901 | 902.5 | CG-CD1 (14); CG-CD2 (8); CB-CG (4) | LEU 83, LEU129, LEU17, LEU56, LEU25, LEU8, ILE98 |
| 933 | 932.2 | CB-CG2 (12); CB-CG1 (7); CA-CB (2) | VAL 99, VAL2, ARG21, ARG73, ARG68, TYR23, LEU25, LEU8 |
| 1004 | 1003.5 | CG1-CD1 (7); CB-CG (3); CA –CB (2) | ILE 78, ILE98, ILE88,.ILE124, ARG 73, ARG5, CYS 76 |
| 1012 | 1013.2 | CA-CB (7); NE1-CE2(2); | TRP 62, TRP63, TRP123, LEU183, TYR20, ARG14, ALA31 |
| 1033 | 1033.9 | CG-CD (10); CA-CB (9); | ARG 61, ARG114,ARG14, PRO70, TRP 62, ALA110 |
| 1077 | 1078.2 | CG-CD2 (21); CG-CD1 (11) | LEU 8, LEU17, LEU84, LEU75, ARG68 |
| 1106 | 1104.6 | N-CA(12); CB-CG(5); CA-CB (3) | GLY 26, LEU 25, GLY4 |
| 1130 | 1130.4 | CA-CB (5); CB-OG(5); N-CA(5) | TYR 53, SER 50, GLY54, SER100, SER86, ALA107, ARG68, ASN103 |
| 1197 | 1197.4 | CA-CB (15); CB-CG (5); N-CA (2) | GLU 35, SER36, LYS13, LEU8, ASN27, ASN113, PHE3, GLN121 |
| 1211 | 1211.8 | CA-CB (23); N-CA (3) | ILE 78, PRO 79, ARG5, ARG112, LYS97, LEU83, LEU17, VAL120 |
| 1237 | 1237.1 | N-CA (15); CA-CB(5) | TYR 23,SER 24,GLY26,ARG128, GLY117, GLY71 |
| 1249 | 1249.4 | N-CA (12); CA-CB (6); | GLY126, GLY22, GLY104, ILE124, ALA10 |
| 1273 | 1274.7 | N-CA (14); CA-CB (4) | ASP 18, LEU 17, PHE34, SER86, ALA95, TYR23, ALA122 |
| 1336 | 1336.4 | CD1-CE1(11); CD2-CE2 (10); CE1-CZ (5) | PHE 34, PHE3, PHE38 |
| 1362 | 1358.0 | CD1-NE1(14); CE2-CZ2 (6); CE3-CZ3 (4) | TRP 28, TRP123, TRP108, TRP111, TRP63 |
| 1448 | 1442.6 | CE1-NE2 (17); CG-ND1 (5); ND1-CE1 (4) | HIS 15 |
| 1460 | 1461.4 | CB-CG (11); CD2-CE2 (7); CD1-CE1 (7) | PHE 38, PHE3 |
| 1555 | 1561.2 | CA-C (14); C-N(5) | TRP63, CYS64, TRP 62, ALA11, ARG128, HIS15, GLY67 |
| 1581 | 1581.3 | CZ3-CH2(10); CE3-CZ3(8); CZ2-CH2 (4) | TRP123, TRP111, TRP63, TRP62, TRP128 |
| 1621 | 1624.6 | NE-CZ (20); CZ-NH2(10) | ARG 21, ARG125, ARG5, ARG21 |
| 1659 | 1661.8 | C-O (18); C-N (13); | ASN65, ASP66, TYR53, ALA10, TRP111, ILE98, CYS80 |
The assignments of the modes are from the analysis of PED. Only those modes that appear in the Raman spectrum are given. The frequencies and PED of the corresponding modes in other residues are relatively close to those given in this Table. These corresponding modes are indicated by in the residue column.
Table 3. Computed H-bond disruption probability −RTlnP and free energy change ΔHtheor at 293 K along with observed H-bond free energy change ΔGexpt from protein engineering in T4 lysozyme (PDB id: 3LZM) and ribonuclease T1 (PDB id: 9RNT).
| Protein | H-bonded atom | H-bonded partner | H-bond type | Partner % burieda | 〈rl〉 Å | −RTlnPl kcal/mol | ΔHtheor kcal/mol | ΔGexpt kcal/mol |
|---|---|---|---|---|---|---|---|---|
| T4 lysozymeb | OG1 THR157 | OD1 ASP159 | Normal | 0 | 2.95 | 2.08 | 0 | 1.6 |
| Ribonuclease T1b | ND2 ASN9 | OD2 ASP76 | Normal | 57 | 2.97 | 1.80 | 1.0 | 1.6 |
| OH TYR11 | OD2 ASP76 | 3-centre | 97 | 2.89 | 3.82 | 5.49 | 3.2 | |
| O ILE61 | 97 | 2.97 | 1.84 | |||||
| OG SER12 | OD2 ASP15 | Normal | 55 | 2.95 | 2.17 | 1.19 | 1.4 | |
| OD1 ASN36 | OG SER35 | Normal | 30 | 2.93 | 2.53 | 0.76 | 0.6 | |
| ND2 ASN44 | O PHE48 | Normal | 76 | 3.26 | 0.54 | 0.41 | 2.5 | |
| OD1 ASN44 | N PHE48 | 3-centre | 88 | 2.96 | 1.99 | 4.21 | ||
| OH TYR42 | 97 | 2.93 | 2.54 | |||||
| OH TYR56 | O VAL 52 | Normal | 73 | 2.91 | 2.91 | 2.12 | 1.8 | |
| OH TYR 57 | OE1 GLU82 | Normal | 70 | 2.86 | 5.21 | 3.64 | 1.4 | |
| OG SER 64 | OD2 ASP66 | Normal | 0 | 2.97 | 1.79 | 0 | 1.7 | |
| OH TYR68 | O GLY71 | Normal | 31 | 2.88 | 4.18 | 1.30 | 2.5 | |
| ND2 ASN81 | O SER53 | Normal | 24 | 3.05 | 1.18 | 0.28 | 3.5 | |
| OD1 ASN81 | N ASN83 | 3-centre | 16 | 2.98 | 1.72 | 1.02 | ||
| N GLN 85 | 47 | 2.99 | 1.57 |
The observed value for T4 lysozyme is from Alber et al. (54) and those for ribonuclease T1 are from Shirley et al. (55). H-bond partners at the experimental mutation sites are included. Calculated mean bond length 〈rl〉 is also listed.
bIn the T4 lysozyme, Thr→Val; in ribonuclease T1, all Tyr→Phe, Ser→Ala, Asn→Ala, (see text).
An H-bonded atom may have more than one potential H-bonding partner, including both protein atoms and water molecules found in the crystal structure. Only intra-protein hydrogen bonds are included in Table 3 so that their possible correlation with protein engineering experiments may be fully explored. There are a number of three-centre (bifurcated) H-bonds found in Table 3. A three-centre H-bond involves a hydrogen atom shared by two acceptor atoms and one donor atom, which differs from a normal H-bond in that a hydrogen atom interacts with two acceptor atoms instead of one. The free energy of the disruption of such a bond can be estimated by using the solvent-accessibility weighted sum of the logarithm of the probability for these two interactions, as discussed below (21).
Therefore the computed H-bond free energy change 
for normal H-bonds and three-centre H-bonds is given by
where σi is solvent accessibility (percentage buried) for the i-th H-bond partners in l-th H-bond. As shown in Table 3, there are two hydrogen bonds with zero σ0. Although the computed 
of zero differs from experiments, it is due to the neglecting of water-mediated H-bonds. Our earlier study (21) showed that inclusion of water-mediated H-bonds at the surface of a protein improves the agreement between computed results and experimentally estimated values.
Substantial difference was found between our computed and experimental results for hydrogen bonds from the majority of Tyr and Asn. One possible reason for this is the difficulty in estimating the contribution from conformational entropy to ΔG in a site-mutagenesis experiment. Conformational entropy of Tyr→Phe and Asn→Ala mutants in these proteins was found to make a larger contribution to ΔG, while there is presently no reliable way to make corrections (55).
The difference between ΔGexpt and 
is expected for several reasons. First, although efforts were made to separate from ΔGexpt factors such as small changes in configurational entropy, hydrophobic burying, Coulomb and van der Waals interactions, a clear-cut separation is not always possible (55,56). These factors introduce small deviations in experimentally estimated H-bond free energies. Second, as shown in Table 3, some sites might involve three-centre H-bonds and the measured free energy is associated with this kind of H-bond rather than a single H-bond. The pairwise potential commonly used to describe a single H-bond may not be accurate enough for bifurcated H-bonds. Third, the unpaired partners in a mutant protein might be able to form H-bonds to alternative partners. It is highly possible when the protein is surrounded by a large number of water molecules in a real thermal fluctuational situation. Moreover, neglect of the effect of structured water (such as water-mediated H-bonds) may also result in the discrepancy between computed and experimental results.
CONCLUSION
A web-based software program MoViES for computing vibrational properties of proteins and nucleic acids is presented. Molecular-mechanics-based force fields and self-consistent methods are used for the computation. The computed results on selected proteins are consistent with experimental results. Efforts are being made to expand the range of MoViES to include small molecules and structured waters (such as water-mediated hydrogen bonds). These, along with further improvement in the molecular force fields, will enable the development of MoViES into a useful tool for facilitating the study of the fluctuational dynamics of biomolecules.
REFERENCES
- 1.Nishikawa T. and Go,N. (1987) Normal modes of vibration in bovine pancreatic trypsin inhibitor and its mechanical property. Proteins, 2, 308–329. [DOI] [PubMed] [Google Scholar]
- 2.Roux B. and Karplus,M. (1988) The normal modes of the gramicidin-A dimer channel. Biophys. J., 53, 297–309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jaaskelainen S., Verma,C.S., Hubbard,R.E., Linko,P. and Caves,L.S. (1998) Conformational change in the activation of lipase: an analysis in terms of low-frequency normal modes. Protein Sci., 7, 1359–1367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tsubaki M., Yoshikawa,S., Ichikawa,Y. and Yu,N.T. (1992) Effects of cholesterol side-chain groups and adrenodoxin binding on the vibrational modes of carbon monoxide bound to cytochrome P-450scc: implications of the productive and nonproductive substrate bindings. Biochemistry, 31, 8991–8999. [DOI] [PubMed] [Google Scholar]
- 5.Breton J., Boullais,C., Berger,G., Mioskowski,C. and Nabedryk,E. (1995) Binding sites of quinones in photosynthetic bacterial reaction centers investigated by light-induced FTIR difference spectroscopy: symmetry of the carbonyl interactions and close equivalence of the QB vibrations in Rhodobacter sphaeroides and Rhodopseudomonas viridis probed by isotope labeling. Biochemistry, 34, 11606–11616. [DOI] [PubMed] [Google Scholar]
- 6.Cheng H., Sukal,S., Deng,H., Leyh,T.S. and Callender,R. (2001) Vibrational structure of GDP and GTP bound to RAS: an isotope-edited FTIR study. Biochemistry, 40, 4035–4043. [DOI] [PubMed] [Google Scholar]
- 7.Rai B.K., Durbin,S.M., Prohofsky,E.W., Timothy Sage,J., Ellison,M.K., Robert Scheidt,W., Sturhahn,W. and Ercan Alp,E. (2002) Iron normal mode dynamics in a porphyrin-imidazole model for deoxyheme proteins. Phys. Rev. E Stat. Nonlin. Soft Matter Phys., 66, 051904. [DOI] [PubMed] [Google Scholar]
- 8.Yu Y.B., Privalov,P.L. and Hodges,R.S. (2001) Contribution of translational and rotational motions to molecular association in aqueous solution. Biophys. J., 81, 1632–1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen Y.Z. and Prohofsky,E.W. (1994) Premelting base pair opening probability and drug binding constant of a daunomycin-poly d(GCAT)·poly d(ATGC) complex. Biophys. J., 66, 820–826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hamm P., Lim,M., DeGrado,W.F. and Hochstrasser,R.M. (1999) The two-dimensional IR nonlinear spectroscopy of a cyclic penta-peptide in relation to its three-dimensional structure. Proc. Natl Acad. Sci. USA, 96, 2036–2041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Alvarez R.M., Della Vedova,C.O., Mack,H.G., Farias,R.N. and Hildebrandt,P. (2002) Raman spectroscopic study of the conformational changes of thyroxine induced by interactions with phospholipid. Eur. Biophys. J., 31, 448–453. [DOI] [PubMed] [Google Scholar]
- 12.Dian B.C., Longarte,A. and Zwier,T.S. (2002) Conformational dynamics in a dipeptide after single-mode vibrational excitation. Science, 296, 2369–2373. [DOI] [PubMed] [Google Scholar]
- 13.Cheng H., Sukal,S., Callender,R. and Leyh,T.S. (2001) Gamma-phosphate protonation and pH-dependent unfolding of the Ras·GTP·Mg2+ complex: a vibrational spectroscopy study. J. Biol. Chem., 276, 9931–9935. [DOI] [PubMed] [Google Scholar]
- 14.Cao Z.W., Chen,X. and Chen,Y.Z. (2003) Correlation between normal modes in the 20–200 cm−1 frequency range and localized torsionmotions related to certain collective motions in proteins. J. Mol. Graph. Model., 21, 309–319. [DOI] [PubMed] [Google Scholar]
- 15.Verma C.S., Caves,L.S., Hubbard,R.E. and Roberts,G.C. (1997) Domain motions in dihydrofolate reductase: a molecular dynamics study. J. Mol. Biol., 266, 776–796. [DOI] [PubMed] [Google Scholar]
- 16.Cusack S. and Doster,W. (1990) Temperature dependence of the low frequency dynamics of myoglobin. Measurement of the vibrational frequency distribution by inelastic neutron scattering. Biophys. J., 58, 243–251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Walther M., Plochocka,P., Fischer,B., Helm,H. and Uhd Jepsen,P. (2002) Collective vibrational modes in biological molecules investigated by terahertz time-domain spectroscopy. Biopolymers, 67, 310–313. [DOI] [PubMed] [Google Scholar]
- 18.Melchers B., Knapp,E.W., Parak,F., Cordone,L., Cupane,A. and Leone,M. (1996) Structural fluctuations of myoglobin from normal-modes, Mossbauer, Raman, and absorption spectroscopy. Biophys. J., 70, 2092–2099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen Y.Z. and Prohofsky,E.W. (1992) The role of a minor groove spine of hydration in stabilizing poly(dA)·poly(dT) against fluctuational interbase H-bond disruption in the premelting temperature regime. Nucleic Acids Res., 20, 415–419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Chen Y.Z. (1999) Modified self-consistent harmonic approach to thermal fluctuational disruption of disulfide bonds in proteins. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics, 60, 5938–5942. [DOI] [PubMed] [Google Scholar]
- 21.Cao Z.W. and Chen,Y.Z. (2001) Hydrogen-bond disruption probability in proteins by a modified self-consistent harmonic approach. Biopolymers, 58, 319–328. [DOI] [PubMed] [Google Scholar]
- 22.Galkin O., Buchter,S., Tabirian,A. and Schulte,A. (1997) Pressure effects on the proximal heme pocket in myoglobin probed by Raman and near-infrared absorption spectroscopy. Biophys. J., 73, 2752–2763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen Y.Z. and Prohofsky,E.W. (1993) Theory of presure-dependent melting of the DNA double helix: role of strained hydrogen bonds. Phys. Rev., E47, 2100. [DOI] [PubMed] [Google Scholar]
- 24.Tidor B. and Karplus,M. (1993) The contribution of cross-links to protein stability: a normal mode analysis of the configurational entropy of the native state. Proteins, 15, 71–79. [DOI] [PubMed] [Google Scholar]
- 25.Moritsugu K., Miyashita,O. and Kidera,A. (2000) Vibrational energy transfer in a protein molecule. Phys. Rev. Lett., 85, 3970–3973. [DOI] [PubMed] [Google Scholar]
- 26.Zscherp C., Schlesinger,R. and Heberle,J. (2001) Time-resolved FT-IR spectroscopic investigation of the pH-dependent proton transfer reactions in the E194Q mutant of bacteriorhodopsin. Biochem. Biophys. Res. Commun., 283, 57–63. [DOI] [PubMed] [Google Scholar]
- 27.Bandekar J. and Krimm,S. (1985) Vibrational analysis of peptides, polypeptides, and proteins. XXX. Normal mode analyses of gamma-turns. Int. J. Pept. Protein Res., 26, 407–415. [DOI] [PubMed] [Google Scholar]
- 28.Brooks B. and Karplus,M. (1985) Normal modes for specific motions of macromolecules: application to the hinge-bending mode of lysozyme. Proc. Natl Acad. Sci. USA, 82, 4995–4999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Levitt M., Sander,C. and Stern,P.S. (1985) Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol., 181, 423–447. [DOI] [PubMed] [Google Scholar]
- 30.Naik V.M., Krimm,S., Denton,J.B., Nemethy,G. and Scheraga,H.A. (1984) Vibrational analysis of peptides, polypeptides and proteins. XXVII. Structure of gramicidin S from normal mode analyses of low-energy conformations. Int. J. Pept. Protein Res., 24, 613–626. [PubMed] [Google Scholar]
- 31.Hao M.H. and Harvey,S.C. (1992) Analyzing the normal mode dynamics of macromolecules by the component synthesis method. Biopolymers, 32, 1393–1405. [DOI] [PubMed] [Google Scholar]
- 32.Kidera A. and Go,N. (1990) Refinement of protein dynamic structure: normal mode refinement. Proc. Natl Acad. Sci. USA, 87, 3718–3722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Thomas A., Field,M.J., Mouawad,L. and Perahia,D. (1996) Analysis of the low frequency normal modes of the T-state of aspartate transcarbamylase. J. Mol. Biol., 257, 1070–1087. [DOI] [PubMed] [Google Scholar]
- 34.Chen Y.Z. and Prohofsky,E.W. (1995) Normal mode calculation of a netropsin-DNA complex: effect of structural deformation on vibrational spectrum. Biopolymers, 35, 657–666. [DOI] [PubMed] [Google Scholar]
- 35.Ma J. and Karplus,M. (1997) Ligand-induced conformational changes in ras p21: a normal mode and energy minimization analysis. J. Mol. Biol., 274, 114–131. [DOI] [PubMed] [Google Scholar]
- 36.Mouawad L. and Perahia,D. (1996) Motions in hemoglobin studied by normal mode analysis and energy minimization: evidence for the existence of tertiary T-like, quaternary R-like intermediate structures. J. Mol. Biol., 258, 393–410. [DOI] [PubMed] [Google Scholar]
- 37.Delarue M. and Sanejouand,Y.H. (2002) Simplified normal mode analysis of conformational transitions in DNA-dependent polymerases: the elastic network model. J. Mol. Biol., 320, 1011–1024. [DOI] [PubMed] [Google Scholar]
- 38.Rai B.K., Durbin,S.M., Prohofsky,E.W., Sage,J.T., Wyllie,G.R., Scheidt,W.R., Sturhahn,W. and Alp,E.E. (2002) Iron normal mode dynamics in (nitrosyl)iron(II)tetraphenylporphyrin from X-ray nuclear resonance data. Biophys. J., 82, 2951–2963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Miller D.W. and Agard,D.A. (1999) Enzyme specificity under dynamic control: a normal mode analysis of alpha-lytic protease. J. Mol. Biol., 286, 267–278. [DOI] [PubMed] [Google Scholar]
- 40.Krebs W.G., Alexandrov,V., Wilson,C.A., Echols,N., Yu,H. and Gerstein,M. (2002) Normal mode analysis of macromolecular motions in a database framework: developing mode concentration as a useful classifying statistic. Proteins, 48, 682–695. [DOI] [PubMed] [Google Scholar]
- 41.Schuyler A.D. and Chirikjian,G.S. (2004) Normal mode analysis of proteins: a comparison of rigid cluster modes with C(alpha) coarse graining. J. Mol. Graph. Model., 22, 183–193. [DOI] [PubMed] [Google Scholar]
- 42.Reuter N., Hinsen,K. and Lacapere,J.J. (2003) Transconformations of the SERCA1 Ca-ATPase: a normal mode study. Biophys. J., 85, 2186–2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bu L. and Straub,J.E. (2003) Vibrational frequency shifts and relaxation rates for a selected vibrational mode in cytochrome C. Biophys. J., 85, 1429–1439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen Y.Z., Powell,J.W. and Prohofsky,E.W. (1997) Vibrational normal modes and dynamical stability of DNA triplex poly(dA). 2poly(dT): S-type structure is more stable and in better agreement with observations in solution. Biophys. J., 72, 1327–1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cornell W.D., Cieplak,P., Bayly,C.I., Gould,I.R., Merz,K.M.J., Ferguson,D.M., Spellmeyer,D.C., Fox,T., Caldwell,J.W. and Kollman,P.A. (1995) A second generation force field for the simulation of proteins and nucleic acids. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- 46.Gelin B.R. and Karplus,M. (1979) Side-chain torsional potentials: effect of dipeptide, protein, and solvent environment. Biochemistry, 18, 1256–1268. [DOI] [PubMed] [Google Scholar]
- 47.Baird N.C. (1974) Simulation of hydrogen bonding in biological systems: Ab initio calculations for NH3-NH3 and NH3-NH4+. Int. J. Quantum Chem. Symp., 1, 49–53. [Google Scholar]
- 48.Bwivedi A.M. and Frimm,S. (1984) Vibrational analysis of peptides, polypeptides, and proteins. 19. Force fields for alpha-helix and beta-sheet structures in a side-chain point-mass approximation. J. Phys. Chem., 88, 620–627. [Google Scholar]
- 49.Teeter M.M. and Case,D.A. (1990) Harmonic and quasiharmonic descriptions of Crambin. J. Phys. Chem., 94, 8091–8097. [Google Scholar]
- 50.Brooks B. and Karplus,M. (1983) Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc. Natl Acad. Sci. USA, 80, 6571–6575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Gibrat J.F. and Go,N. (1990) Normal mode analysis of human lysozyme: study of the relative motion of the two domains and characterization of the harmonic motion. Proteins, 8, 258–279. [DOI] [PubMed] [Google Scholar]
- 52.Tirion M.M. and ben-Avraham,D. (1993) Normal mode analysis of G-actin. J. Mol. Biol., 230, 186–195. [DOI] [PubMed] [Google Scholar]
- 53.Jacob J., Krafft,C., Welfle,K., Welfle,H. and Saenger,W. (1998) Melting points of lysozyme and ribonuclease A crystals correlated with protein unfolding: a Raman spectroscopic study. Acta Crystallogr. D Biol. Crystallogr., 54, 74–80. [DOI] [PubMed] [Google Scholar]
- 54.Alber T., Sun,D.P., Wilson,K., Wozniak,J.A., Cook,S.P. and Matthews,B.W. (1987) Contributions of hydrogen bonds of Thr 157 to the thermodynamic stability of phage T4 lysozyme. Nature, 330, 41–46. [DOI] [PubMed] [Google Scholar]
- 55.Shirley B.A., Stanssens,P., Hahn,U. and Pace,C.N. (1992) Contribution of hydrogen bonding to the conformational stability of ribonuclease T1. Biochemistry, 31, 725–732. [DOI] [PubMed] [Google Scholar]
- 56.Dill K.A. (1990) Dominant forces in protein folding. Biochemistry, 29, 7133–7155. [DOI] [PubMed] [Google Scholar]
- 57.Rose G.D. and Wolfenden,R. (1993) Hydrogen bonding, hydrophobicity, packing, and protein folding. Annu. Rev. Biophys. Biomol. Struct., 22, 381–415. [DOI] [PubMed] [Google Scholar]
- 58.Rauh J.J., Holyoke,C.W., Kleier,D.A., Presnail,J.K., Benner,E.A., Cordova,D., Howard,M.H., Hosie,A.M., Buckingham,S.D., Baylis,H.A. et al. (1997) Polycyclic dinitriles: a novel class of potent GABAergic insecticides provides a new radioligand, [3H]BIDN. Invert Neurosci, 3, 261–268. [DOI] [PubMed] [Google Scholar]