Abstract
In the era of big data, we can easily access information from multiple views which may be obtained from different sources or feature subsets. Generally, different views provide complementary information for learning tasks. Thus, multi-view learning can facilitate the learning process and is prevalent in a wide range of application domains. For example, in medical science, measurements from a series of medical examinations are documented for each subject, including clinical, imaging, immunologic, serologic and cognitive measures which are obtained from multiple sources. Specifically, for brain diagnosis, we can have different quantitative analysis which can be seen as different feature subsets of a subject. It is desirable to combine all these features in an effective way for disease diagnosis. However, some measurements from less relevant medical examinations can introduce irrelevant information which can even be exaggerated after view combinations. Feature selection should therefore be incorporated in the process of multi-view learning. In this paper, we explore tensor product to bring different views together in a joint space, and present a dual method of tensor-based multi-view feature selection (dual-Tmfs) based on the idea of support vector machine recursive feature elimination. Experiments conducted on datasets derived from neurological disorder demonstrate the features selected by our proposed method yield better classification performance and are relevant to disease diagnosis.
Index Terms: tensor, brain diseases, multi-view learning, feature selection
I. Introduction
Many neurological disorders are characterized by ongoing injury that is clinically silent for prolonged periods and irreversible by the time symptoms first present. New approaches for detection of early changes in subclinical periods would afford powerful tools for aiding clinical diagnosis, clarifying underlying mechanisms and informing neuroprotective interventions to slow or reverse neural injury for a broad spectrum of brain disorders, including HIV infection on brain [10], [12], Alzheimer’s disease [30], Parkinson’s Disease, Schizophrenia, Depression, etc. Early diagnosis has the potential to greatly alleviate the burden of brain disorders and the ever increasing costs to families and society. For example, total healthcare costs for those 65 and older, are more that three times higher in those with Alzheimer’s and other dementias [15].
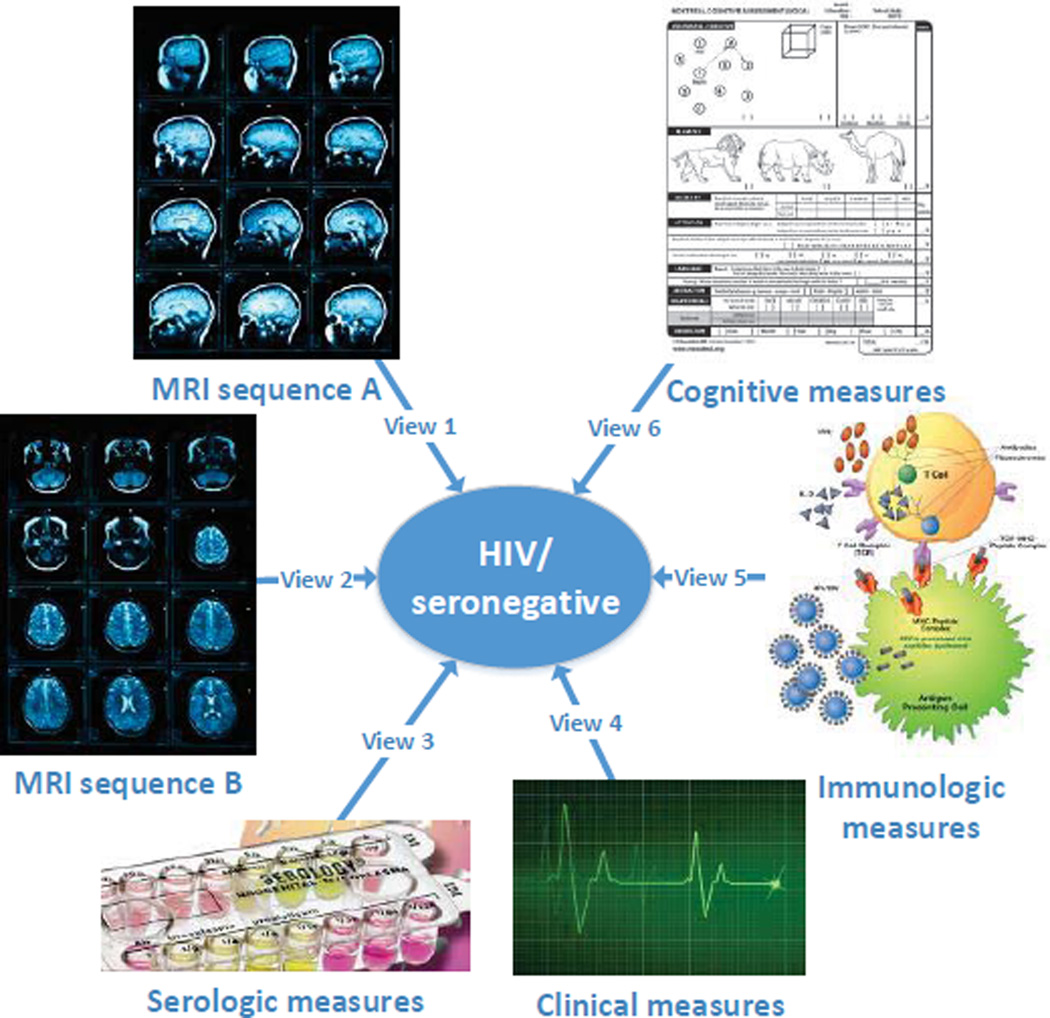
As diagnosis of neurological disorder is extremely challenging, many different diagnosis tools and methods have been developed to obtain a large number of measurements from various examinations and laboratory tests. Information may be available for each subject for clinical, imaging, immunologic, serologic, cognitive and other parameters, as shown in Figure 1. In Magnetic Resonance Imaging (MRI) examination, for example, multiple strategies are used to interrogate the brain. Volumetric measurements of brain parenchymal and ventricular structures, and of major tissue classes (e.g. white matter, gray matter and CSF) can be derived. Volumetric measurements can also be quantified for a large number of individual brain regions and landmarks. While a single MRI examination can yield a vast amount of information concerning brain status at different levels of analysis, it is difficult to consider all available measures simultaneously, since they have different physical meanings and statistic properties. Capability for simultaneous consideration of measures coming from multiple groups is potentially transformative for investigating disease mechanisms and for informing therapeutic interventions.
Fig. 1.
An example of multi-view learning in medical studies.
As mentioned above, medical science witnesses everyday measurements from a series of medical examinations documented for each subject, including clinical, imaging, immunologic, serologic and cognitive measures. Each group of measures characterize the health state of a subject from different aspects. Conventionally this type of data is named as multi-view data, and each group of measures form a distinct view characterizing subjects in one specific feature space. An intuitive idea is to combine them to improve the learning performance, while simply concatenating features from all views and transforming a multi-view data into a single-view data would fail to leverage the underlying correlations between different views. We observe that tensors are higher order arrays that naturally generalize the notions of vectors and matrices to multiple dimensions.
In this paper, we propose to use a tensor-based approach to model features (views) and their correlations hidden in the original multi-view data. Taking the tensor product of their respective feature spaces corresponds to the interaction of multiple views. In the multi-view setting for neurological disorder, or for medical studies in general, however, a critical problem is that there may be limited subjects available yet introducing a large number of measurements. Within the multi-view data, not all features in different views are relevant to the learning task, and some irrelevant features may introduce unexpected noise. The irrelevant information can even be exaggerated after view combinations thereby degrading performance. Therefore, it is necessary to take care of feature selection in the learning process. Feature selection results can also be used by researchers to find biomarkers for brain diseases. Such biomarkers are clinically imperative for detecting injury to the brain in the earliest stage before it is irreversible. Valid biomarkers can be used to aid diagnosis, monitor disease progression and evaluate effects of intervention [13].
Considering feature selection, most of the existing studies can be categorized as filter models [17], [20] and embedded models based on sparsity regularization [7], [6], [26], [27]. While in this paper, we focus on wrapper models for feature selection. We propose a dual method of tensor-based multi-view feature selection (dual-Tmfs), taking care of both the input space and the reconstructed tensor product space and exploiting their underlying correlations. In addition, our proposed method can naturally extend to many views and nonlinear kernels. Empirical studies on datasets collected from the Chicago Early HIV Infection Study [19] demonstrate that the proposed method can obtain better accuracy for classification tasks on multi-view feature selection than compared approaches. While the empirical studies are based on medical data from a clinical application in HIV infection on brain, the dual-Tmfs technique developed for detecting brain anomalies have considerable promise for early diagnosis for other neurological disorders.
For the rest of the paper, we first state the problem of multi-view feature selection for classification and introduce related notations in section II. Then we introduce our dual-Tmfs algorithm in section III. Experimental results are discussed in section IV. In section VI, we conclude the paper.
II. Problem Definition
In this section, we state the problem of multi-view feature selection for classification and introduce the notation. Table I lists some basic symbols that will be used throughout the paper. Note that although we use the same symbol to represent a set of data instances and the space that contains them, it is always clear from the context what we mean.
TABLE I.
List of symbols
| Symbol | Definition and Description |
|---|---|
| s | each lowercase letter represents a scale |
| v | each boldface lowercase letter represents a vector |
| M | each boldface capital letter represents a matrix |
| 𝒯 | each calligraphic letter represents a tensor, set or space |
| ⊗ | denotes tensor product |
| 〈․, ․〉 | denotes inner product |
| |․| | denotes absolute value |
| ‖․‖F | denotes (Frobenius) norm of vector, matrix or tensor |
Suppose we have a multi-view classification task with n labeled instances represented from m different views: , i ∈ {1, ⋯, n}, υ ∈ {1, ⋯, m}, where Iυ is the dimensionality of the υ-th view, and yi ∈ {− 1, 1} is the class label of the i-th instance. We denote , 𝒴 = {y1, ⋯, yn}, and 𝒟 = {(𝒳1, y1), ⋯, (𝒳n, yn)}, respectively. The task of multi-view classification is to find a classifier function f : ℝI1 × ⋯ × ℝIm → {−1, 1} that correctly predicts the label of an unseen instance 𝒳 = {x(1), ⋯, x(m)}.
One of the major challenges of multi-view classification comes from the fact that the combination of multiple views can potentially incur redundant and even conflicting information which is unfavorable for classifier learning. In order to tackle this problem, feature selection has been the focus of interest for quite some time and much work has been done in a supervised setting. A straightforward solution is to handle each view separately and conduct feature selection independently. This paradigm is based on the assumption that each view is sufficient on its own to learn the target concept [29]. However, individual views can often provide complementary information to each other leading to improved performance in real-world applications.
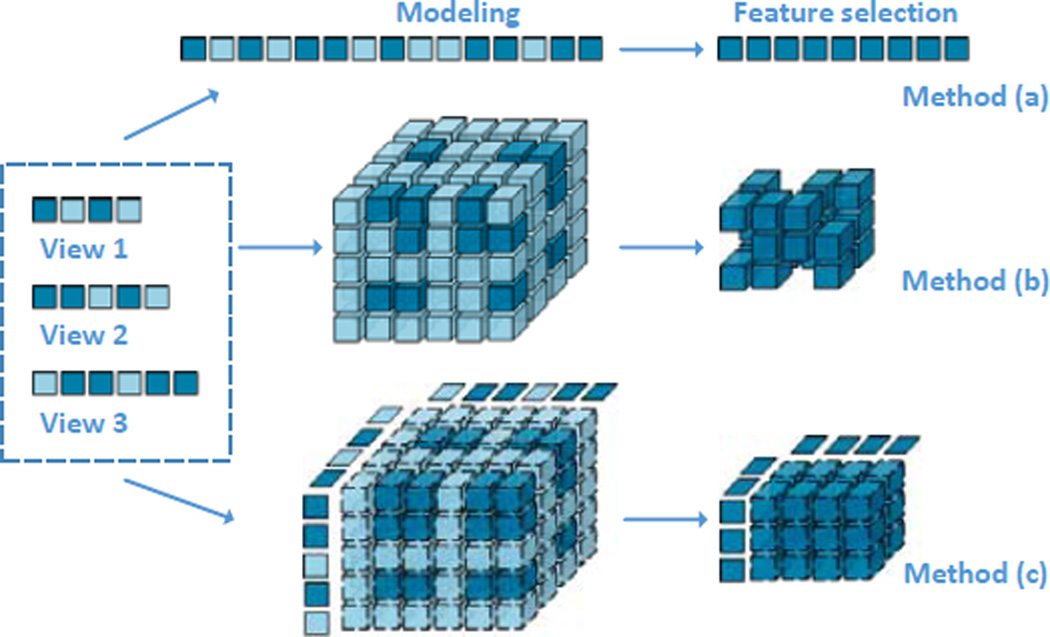
More generally, learning that involves conceptual multi-view is not just providing tools to analyze the data in multiple ways, which is more about managing the correlations among different views. Most previous feature selection approaches focus on exploiting multi-view features simultaneously to facilitate the learning process, which usually use the reconstructed data to represent the original multi-view information and perform analysis, such as the method (a) and method (b) shown in Figure 2. However, intrinsic properties of raw multi-view features and hidden relationships between the original data and its reconstruction are totally ignored in these methods.
Fig. 2.
Schematic view of the key differences among three strategies of multi-view feature selection. Method (a) concatenates features from all views in the input space. Method (b) converts multiple views into a tensor and directly performs feature selection in the tensor product space. Our method (c) efficiently conducts feature selection in the input space while effectively leveraging relationships between the original data and its reconstruction in the tensor product space.
Taking into account the latent interactions among views and the redundancy triggered by multiple views, in this paper, we aim at combining multiple features in a principled manner and performing feature selection to obtain a consensus and discriminative low-dimensional feature representation. In particular, we will leverage the relationship between the original multi-view features and reconstructed data to facilitate the implementation of feature selection.
III. Proposed Method
As noted in the introduction, one of the key issues for multi-view classification is to choose an appropriate tool to model features (views) and their correlations hidden in the original multi-view features, since this directly determines how information will be used. The concept of tensor serves as a backbone for incorporating multi-view features into a consensus representation by means of tensor product, where the complex multiple relationships among views are embedded within the tensor structures. By mining structural information contained in the tensor, knowledge of multi-view features can be extracted and used to establish a predictive model. In this paper, we propose a dual method of tensor-based multi-view feature selection (dual-Tmfs) in the tensor product space inspired by the idea of support vector machine recursive feature elimination (SVM-RFE) [9]. Our goal is to select useful features in conjunction with the classifier and simultaneously exploit the correlations among multiple views.
A. Tensor Propagation for Multiple Views
We start by introducing some related concepts and notation about tensors, and conceptually analyzing our motivation of utilizing tensor to organize all the multi-view information.
Tensors are higher order arrays that generalize the notions of vectors (first-order tensors) and matrices (second-order tensors), whose elements are indexed by more than two indices. Each index expresses a mode of variation of the data and corresponds to a coordinate direction. The number of variables in each mode indicates the dimensionality of a mode. The order of a tensor is determined by the number of its modes. The use of this data structure has been advocated in virtue of certain favorable properties. A key to this work is to borrow the tensor structure to fuse all possible dependence relationships among different views. We first recall the definition of tensor product (i.e., outer product) of two vectors and then give a formal mathematical definition of the tensor, which provides an intuitive understanding of the algebraic structure of the tensor.
Definition 1 (Tensor product)
The tensor product of two vectors x ∈ ℝI1 and y ∈ ℝI2, denoted by x ⊗ y, represents a matrix with the elements (x ⊗ y)i1,i2 = xi1 yi2.
Definition 2 (Tensor)
A tensor is an element of the tensor product of vector spaces, each of which has its own coordinate system.
The tensor product of vector spaces forms an elegant algebraic structure for the theory of tensors. Such structure endows the tensor with the inherent advantage in representing real-world data, which naturally results from the interaction of multiple factors. Each mode of the tensor corresponds to one factor. For this reason, we conclude that the use of tensorial representation is a reasonable choice for adequately capturing the possible relationships among multiple views of data. Another advantage in representing all the multi-view information in the tensor data structure is that we can flexibly explore those useful knowledge in the tensor product space by virtue of tensor-based techniques.
Based on the definition of tensor product of two vectors, we can then express x ⊗ y ⊗ z as a third-order tensor in ℝI1 ⊗ ℝI2 ⊗ ℝI3, of which the elements are defined by (x ⊗ y ⊗ z)i1, i2, i3 = xi1yi2zi3 for all values of the indices. Proceeding in the same way, 𝒳 = (xi1,…,im) is used to denote an mth-order tensor 𝒳 ∈ ℝI1×⋯×Im and its elements. For υ ∈ {1, ⋯, m}, Iυ is the dimensionality of 𝒳 along the υ-th mode. To indicate the object resulting by fixing the υ-th mode index of 𝒳 to be iυ, we introduce the generic subscript : and denote by 𝒳:,…,:,iυ,:,…,:.
In addition, we define the inner product and norm associated with tensor, which will be used in the following.
Definition 3 (Inner product)
The inner product of two same-sized tensors 𝒳, 𝒵 ∈ ℝI1×⋯×Im is defined as the sum of the products of their elements:
| (1) |
Most importantly, note that for tensors 𝒳 = x(1)⊗⋯⊗x(m) and 𝒵 = z(1) ⊗⋯⊗z(m), it holds that
| (2) |
For the sake of brevity, in the following we will use the notation and to denote x(1) ⊗ ⋯ ⊗ x(m) and 〈x(1), z(1)〉 ⋯ 〈x(m), z(m)〉, respectively.
Definition 4 (Tensor norm)
The norm of a tensor 𝒳 ∈ ℝI1 ×⋯×Im is defined to be the square root of the sum of all elements of the tensor squared, i.e.,
| (3) |
As can be seen, the norm of a tensor is a straightforward generalization of the usual Frobenius norm for matrices and of the Euclidean or l2 norm for vectors.
B. Multi-view SVM in the Tensor Setting
Following the introduction above to the concepts of tensors, we describe how multi-view classification can be consistently formulated and implemented in the framework of the standard SVM in the tensor setting.
By the reasoning given in section III-A, we use tensor product operation to bring m-view feature vectors of each instance together, leading to a tensorial representation for common structure across multiple views, and allowing us to adequately diffuse relationships and encode information among multi-view features. In this manner, we have essentially transformed the multi-view classification task from an independent domain of each view {(𝒳(1), ⋯, 𝒳(m)), 𝒴} to a consensus domain {𝒳(1) × ⋯ × 𝒳(m), 𝒴} as a tensor classification problem.
For the sake of simplicity, we are slightly abusing notation by using 𝒳i to denote . Then the dataset of labeled multi-view instances can be represented as 𝒟 = {(𝒳1, y1), ⋯, (𝒳n, yn)}. Note that each multi-view instance 𝒳i is an mth-order tensor that lies in the tensor product space ℝI1 ×⋯×Im, but one must keep in mind that each element of 𝒳i is the tensor product of multi-view features in the input space, which we denote by xi(i1,…,im). Now, based on the definitions of inner product and tensor norm, we can formulate multi-view classification as a global convex optimization problem in the framework of the standard SVM as follows:
| (4) |
| (5) |
| (6) |
where 𝒲 can be regarded as the weight tensor of the separating hyperplane in the tensor product space ℝI1 ×⋯×Im, b is the bias, ξi is the error of the i-th training sample, and C is the trade-off between the margin and empirical loss. As such it can be solved with the use of optimization techniques developed for SVM, and the weight tensor of 𝒲 can be obtained from
| (7) |
where αi is the dual variable corresponding to each instance. The resulting decision function is
| (8) |
where 𝒳 denotes a test multi-view instance given by the tensor product of its multi-view features x(υ) for all υ ∈ {1, ⋯, m}. We simply call the model as multi-view SVM.
Despite this property, there are two major drawbacks incurred by the combination of multiple views. First, the dimensionality of the resulting tensor in a multi-view dataset can be extremely large, which grows at an exponential rate with respect to the number of views. Direct application of the multi-view SVM will suffer from the curse of dimensionality. Second, such tensors may contain much redundant and irrelevant information due to the intrinsic multi-view property, which will negatively influence the performance of the learning process.
Therefore, in order to implement multi-view classification using multi-view SVM, it is necessary to perform dimensionality reduction by feature extraction or selection to concentrate multi-view information and improve tensorial representation. Many tensor-based algorithms have been proposed as dimensionality reduction for classification problems. However, to the best of our knowledge, all of them discard the original multi-view features after constructing tensors. In the following, we investigate their relationship to each other and proceed to develop a wrapper feature selection approach dual-Tmfs.
C. Dual Feature Selection in the Tensor Product Space
Based on the multi-view SVM classifier in the tensor setting, in this subsection, we approach the problem of identifying and concentrating multi-view knowledge via tensors by proposing the linear dual-Tmfs method. We will extend it to the nonlinear case in the next subsection.
Inspired by SVM-RFE [9], we can see from Eq. (8) that the inner product of weight tensor 𝒲 = (wi1,…,im) and input tensor 𝒳 = (xi1,…,im) determines the value of f (𝒳). Intuitively, the input features that are weighted by the largest absolute values influence most on the classification decision, and correspond to the most informative features. Therefore, the absolute weights |wi1,…,im| or the square of the weights (wi1,…,im)2 can be used as feature ranking criterion to select the most discriminative feature subset. Based on this observation, we can conduct feature selection on multi-view SVM.
Let us denote the ranking score of each feature xi1,…,im as ri1,…,im. Our target is to perform feature elimination in the tensor product feature space by
| (9) |
SVM-RFE performs SVM-based feature selection in the vector space, as the method (a) shown in Figure 2. A straightforward approach, which can be seen as a natural tensorial extension of SVM-RFE, is to directly perform feature elimination in the tensor product space using the following feature ranking criterion:
| (10) |
As the method (b) shown in Figure 2, however, the number of variables wi1,…,im is equivalent to the dimensionality of the resulting tensors in tensor product space. Obviously, it is computationally intractable to enumerate all values of wi1,…,im in such a high-dimensional tensor product space. On the other hand, the original multi-view features usually contain much redundant and irrelevant features. It can be further exaggerated over the manipulation of tensor product, thereby degrading the generalization performance. In order to overcome these problems, it would be desirable to remove irrelevant features before manipulating the tensor product.
Considering that each view has specific statistical properties and its intrinsic physical meanings, we conduct multi-view feature selection in the input space and maintain independent rankings of features in each view. We leverage the weight coefficients 𝒲 in the tensor product space to facilitate the implementation of feature selection in the input space. That is, for the υ-th view, supposing , the ranking score of the feature , iυ ∈ {1, ⋯, Iυ} in the input space is , which means is a function of wi1,…,im.
Now we can formulate the problem in terms of the process, for which we need to minimize the following function in each view υ ∈ {1, ⋯, m}:
| (11) |
An alternative approach is to evaluate the value of from wi1,…,im by virtue of the relationship between the input space and the tensor product space. Based on the definition of the tensor product, we can see that the feature in the input space will diffuse to 𝒳:,…,:,iυ,:,…,: in the tensor product space, thus to 𝒲:,…,:,iυ,:,…,:. Intuitively, it means that the contribution of determining the value of decision function f (𝒳) transfers to 𝒳:,…,:,iυ,:,…,:. For this reason, the ranking score of can be estimated from the elements of 𝒲:,…,:,iυ,:,…,:. To realize such purpose, we set equal to the sum of the square of all elements in 𝒲:,…,:,iυ,:,…,:, which is given as follows:
| (12) |
By substituting the exact solution given in Eq. (7) into the right-hand side of this equality, we find that
| (13) |
In this way, compared with performing feature selection in the tensor product space, the computational complexity is largely reduced, since irrelevant and redundant features can be detected by the classifier constructed in the tensor product space, but removed in the input space, which concentrates the multi-view information within tensor operations. Conducting feature selection in the input space is superior in terms of better readability and interpretability, because it maintains the physical meanings of the original features without any manipulation. This property has its significance in many real-world applications such as finding clinical markers to a specific disease.
Nevertheless, although this is expected to improve tensorial representation of multi-view data and perform feature selection for multi-view classification, it can result in potential over-fitting, since the number of variables wi1,…,im grows at an exponential rate as m (i.e., the number of views) increases. Especially in medical studies, there may be limited subjects available yet introducing a large number of measurements in many views. Therefore, the problem reduces to improving the generalization capability of multi-view SVM in the tensor setting, for which we need a more sophisticated approach to reduce the number of variable wi1,…,im (i.e., the number of elements of 𝒲 that need to be estimated) and facilitate feature selection without incurring extensive computation.
In the context of supervised tensor learning, tensor decompositions are usually used to reduce the number of unknown tensors (i.e., the dimensionality of tensor), and meanwhile avoid overfitting. Following assumptions in the supervised tensor learning framework [24], here we assume that 𝒲 can be decomposed as , where . By applying Eqs. (2) and (3), we can then represent the optimization problem in Eqs. (4)–(6) as:
| (14) |
| (15) |
| (16) |
thus the optimal decision function is:
| (17) |
Clearly, in this manner, the number of variables with respect to 𝒲 is greatly reduced from to . Moreover, from Eq. (17), we can see that the influence of input feature on the value of decision function f (𝒳) constructed in the tensor product space is determined only by its corresponding weight coefficient , i.e., the feature ranking criterion defined in Eq. (12) can be simplified as:
| (18) |
Theorem 1
The ranking criterion Eq. (18) is equivalent to Eq. (12) for each view.
Proof
Based on the definition of tensor product, we have . Substituting this into Eq. (12), it can be written as:
| (19) |
where . For the υ-th mode, the multiplier P(− υ) is constant and non-negative, thus has no effect on ranking orders. The proof is complete.
Now we illustrate how to solve the optimization problem in Eqs. (14)–(16). In an iterative manner, we can update the variables associated with a single mode at each iteration. That is, for the υ-th mode, we need to fix variables in other modes and solve the following optimization problem:
| (20) |
| (21) |
| (22) |
where P(−υ) and are constants that denote and .
Let and , then the optimization problem in Eqs. (20)–(22) is equivalent to the following problem:
| (23) |
| (24) |
| (25) |
which reduces to the standard linear SVM, and thus can be efficiently solved by available algorithms, obtaining w(υ) as follows:
| (26) |
where is the dual variable corresponding to each instance in the υ-th mode, obtained in Eqs. (23)–(25).
It is illustrated in Figure 2 that, the method (c) leveraging the ranking criterion Eq. (18) jointly considers the input space and the tensor product space, and effectively exploits their underlying relationship. We summarize our proposed dual method of multi-view feature selection (dual-Tmfs) in Figure 3.
Fig. 3.
The DUAL-TMFS algorithm
D. Extension to Nonlinear Kernels
As discussed above, tensor is an effective approach of capturing correlations across multiple views. However, correlations between features within the same view are not considered by taking the tensor product of features in different views. In such case, we can replace the linear kernel with a nonlinear kernel. Through implicitly projecting features into a high dimensional space within each view, a nonlinear kernel can work together with the tensor tools to exploit correlations across different views as well as those within each view.
In the case of nonlinear SVMs, we first represent optimization problem in Eqs. (23)–(25) in the dual form as:
| (27) |
| (28) |
| (29) |
where H is the matrix with elements .
To compute the change in cost function caused by removing input component iυ in the υ-th mode, one leaves the α’s unchanged and one re-computes matrix H. This corresponds to computing , yielding matrix H(−iυ), where the notation (−iυ) means that component iυ has been removed in the υ-th mode. Thus, the feature ranking criterion for nonlinear SVMs is:
| (30) |
The input corresponding to the smallest difference shall be removed. In the linear case, and . Therefore , which is equivalent to the one we proposed in the previous section for linear SVMs.
IV. Experiments
In this section, we conduct experiments on datasets collected from HIV infected brain disease, to evaluate our proposed method in different aspects. In section IV-C, we have seven methods compared on the classification tasks composing of two views. Experiments extend to more than two views in section IV-D. In nonlinear cases, our method can still be effectively applied, as shown in section IV-E.
A. Data Collections
In order to evaluate the performance of multi-view feature selection for classification, we compare methods on datasets collected from the Chicago Early HIV Infection Study [19], which have 56 HIV and 21 seronegative control subjects enrolled. For each subject, hundreds of clinical, imaging, immunologic, serologic and cognitive measures were documented. This illustrates the curse of dimensionality because there are far more variables of interest than available subjects. Thus, it is important to incorporate feature selection in the learning process for disease diagnosis.
There are seven groups of measurements investigated in our datasets, including neuropsychological tests, flow cytometry, plasma luminex, freesurfer, overall brain microstructure, localized brain microstructure, brain volumetry. Each group can be regarded as a distinct view that partially reflects subject status, and measurements from different medical examinations can provide complementary information. Simultaneous consideration of all the data, exploiting correlations among multiple measurements can be transformative for investigating disease mechanisms and for informing therapeutic interventions. Different views are sampled to form multiple combinations. The datasets used for our experiments are summarized in Table II. Additionally, features are normalized within [0, 1].
TABLE II.
Summary of datasets. “■” indicates the view is selected in the dataset, while “□” indicates not selected. Each number in braces indicates the number of features in each view.
| Name | D2.1 | D2.2 | D3.1 | D3.2 | D4.1 | D4.2 | D5.1 | D5.2 | D6.1 | D6.2 |
|---|---|---|---|---|---|---|---|---|---|---|
| #Views | 2 | 2 | 3 | 3 | 4 | 4 | 5 | 5 | 6 | 6 |
| neuropsychological tests (36) | □ | □ | ■ | □ | □ | □ | ■ | □ | ■ | ■ |
| flow cytometry (65) | □ | □ | □ | □ | ■ | ■ | ■ | ■ | ■ | ■ |
| plasma luminex (45) | ■ | □ | ■ | ■ | ■ | □ | □ | ■ | ■ | ■ |
| freesurfer (28) | □ | ■ | ■ | □ | □ | ■ | □ | ■ | □ | ■ |
| overall brain microstructure (21) | ■ | ■ | □ | □ | ■ | ■ | ■ | □ | ■ | ■ |
| localized brain microstructure (54) | □ | □ | □ | ■ | □ | ■ | ■ | ■ | ■ | ■ |
| brain volumetry (12) | □ | □ | □ | ■ | ■ | □ | ■ | ■ | ■ | □ |
B. Compared Methods
In order to demonstrate the effectiveness of our multi-kernel learning approach, we compare the following methods:
Cf refers to single-kernel SVM applying on concatenated features.
Tpf refers to single-kernel SVM applying on the tensor product feature space [11]. By taking the tensor product of features from different views, adequate correlations among different views are exploited.
Linear-mkl is a conventional multi-kernel method [5]. Different kernels can naturally correspond to different views. Through an optimization framework, weights can be learned that reflect the relative importance of different views. It implements a linear combination of multiple kernels.
rfe-Cf denotes the method that directly applies SVMR-FE on the concatenation of all the features [9].
rfe-Tpf denotes the method that SVM-RFE is applied on the tensor product feature space [21].
miqp-Tpfs refers to the method of iterative tensor product feature selection with mixed-integer quadratic programming [21]. It explicitly considers the cross-domain interactions between two views in the tensor product feature space. The bipartite feature selection problem is formulated as an integer quadratic programming problem. A subset of features is selected that maximizes the sum over the submatrix of the original weight matrix.
dual-Tmfs is the proposed dual method of tensor-based multi-view feature selection in the tensor product feature space. It effectively exploits the correlations among different views in the tensor product feature space, and also efficiently completes feature selection in the input space at the same time.
A detailed comparison between these methods is summarized in Table III, against four dimensions on whether the schemes can conduct feature selection, discriminate against different views, be applicable to many views and compatible with nonlinear kernels. Note that sparsity regularization models [8], [27] are not considered as we focus on wrapper models in this paper, without looking into embedded models.
TABLE III.
Summary of compared methods.
| Property | Cf | Tpf[11] | Linear-mkl[5] | rfe-cf[9] | rfe-Tpf[21] | miqp-Tpfs[21] | dual-Tmfs |
|---|---|---|---|---|---|---|---|
| conducting feature selection | ✕ | ✕ | ✕ | ✓ | ✓ | ✓ | ✓ |
| discriminating different views | ✕ | ✓ | ✓ | ✕ | ✓ | ✓ | ✓ |
| applicability to many views | ✓ | ✓ | ✓ | ✓ | ✕ | ✕ | ✓ |
| compatibility with nonlinear kernels | ✓ | ✕ | ✕ | ✓ | ✕ | ✕ | ✓ |
For a fair comparison, we use LibSVM [3] with linear kernel as the base classifier for all the compared methods. In the experiments, 3-fold cross validations are performed on balanced datasets. The soft margin parameter C is selected through a validation set. For all the methods with feature selection, the number of features selected is explicitly set to 50%.
C. Two Views
We first study the effectiveness of our proposed method on the task of learning from two views. Results on D2.1 and D2.2 are shown in Table IV, where the average performances of the compared methods with standard deviations are reported with respect to four evaluation metrics: accuracy, precision, recall and F1-measure.
TABLE IV.
Classification performance “average score  ” in the linear case. For each dataset, the top-3 methods are without feature selection.
” in the linear case. For each dataset, the top-3 methods are without feature selection.
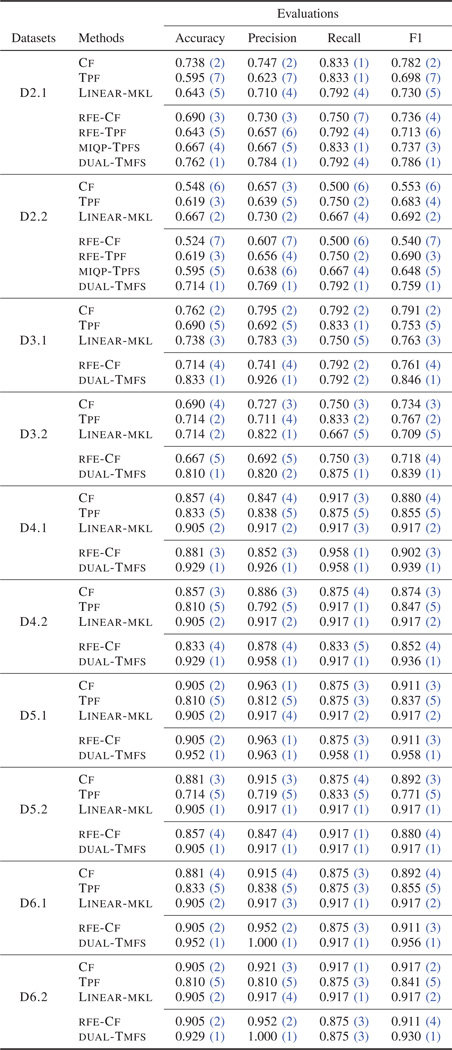 |
In comparison of the top three methods not conducting feature selection, there is no clear advantage for any of the methods. Performance can vary depending on datasets, if the redundancy coming from different views is not taken care of. Thus, it is necessary to select discriminative features and eliminate redundant ones when multiple views are combined.
While considering feature selection, dual-Tmfs significantly improves the accuracy over other methods by effectively pruning redundant and irrelevant features. On the other hand, simply applying SVM-RFE method on either the input space (i.e., rfe-Cf) or the tensor product feature space (i.e., rfe-Tpf) cannot achieve better performance. For rfe-Cf, correlations between multiple views are not exploited when selecting features; while for rfe-Tpf, features are directly selected in the tensor product space, leaving the potential of overfitting. miqp-Tpfs can take advantage of feature selection by maximizing the sum over the weight submatrix in the tensor product feature space.
D. Many Views
In real-world applications, there are usually more than two views. It is desirable to leverage all of them simultaneously. However, rfe-Tpf and miqp-Tpfs need to explicitly compute the tensor product feature space, resulting in complexity and space complexity exponential to the number of views. They are therefore no longer feasible in the case of many views, due to high dimensionality of the tensor product feature space. Although dual-Tmfs also exploits the correlations among different views in the tensor product feature space, it can efficiently complete feature selection in the input space. Thus, our proposed method have time complexity and space complexity linear with respect to the number of views and can naturally extend to more than two views. The experimental results are summarized at D3.1-D6.2 in Table IV.
As can be seen, neither Cf nor rfe-Cf performs well. This shows that simply concatenating all features across multiple views does not work well. We next consider schemes that discriminate different views. Tpf performs badly as it computes the tensor product feature space, introducing some potentially irrelevant features coming from the correlations among multiple views. In general, Linear-mkl performs well in most cases by linearly weighting multiple kernels. However, by further performing feature selection, dual-Tmfs achieves a significant improvement over other methods and always ranks first on F1 and accuracy, indicating that compared with approaches not distinguishing different views or not conducting feature selection, a better subset of discriminative features can be selected for classification by considering the correlations across multiple views based on tensor.
E. Nonlinear Kernels
As discussed above, tensor is an effective approach of capturing correlations across multiple views. However, correlations between features within the same view are not considered by taking the tensor product of features in different views. In such case, we can replace a linear kernel with a nonlinear kernel. Through implicitly projecting features into a high dimensional space within each view, a nonlinear kernel can work together with the tensor tools to exploit correlations across different views as well as that within each view.
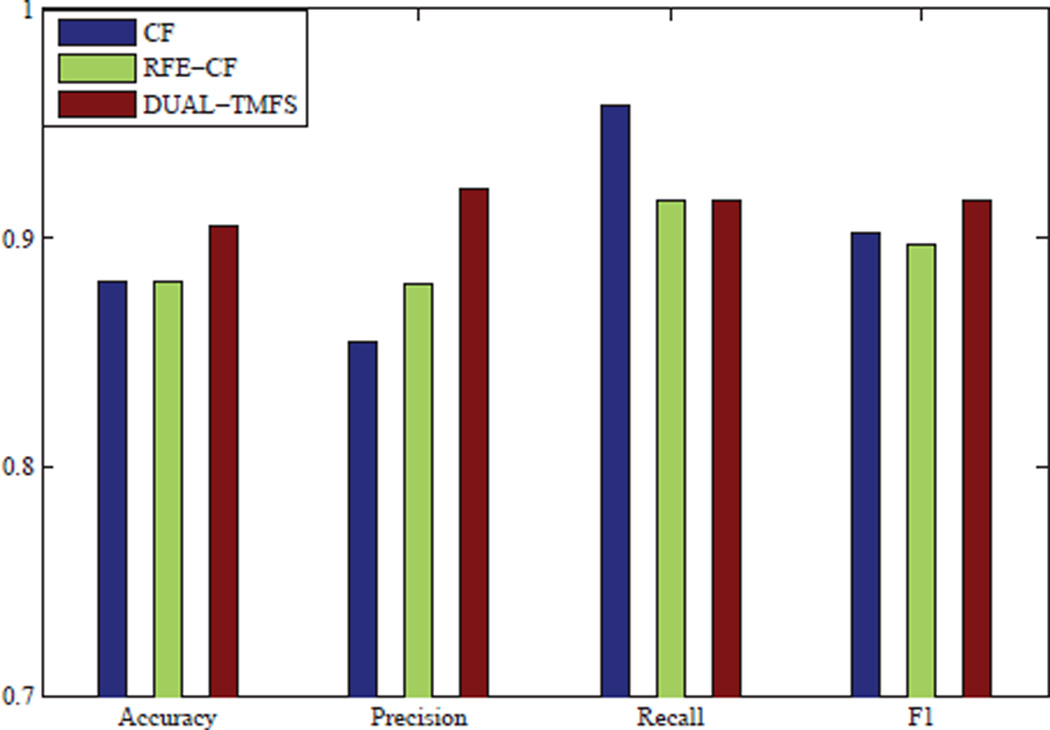
Here we replace the linear kernel with the RBF kernel for all the compared methods, and show experimental results in Figure 4. Linear-mkl is not applicable in the nonlinear case. Neither do Tpf, rfe-Tpf and miqp-Tpfs, because they need to explicitly compute the high dimensional feature space which is intractable when we apply a nonlinear kernel. It illustrates that dual-Tmfs still outperforms other methods in the nonlinear case, in the sense of accuracy and F1-measure.
Fig. 4.
Classification performance in the nonlinear case.
F. Feature Evaluation
Table V lists the most discriminative measures selected by dual-Tmfs. Our results are validated by literature on brain diseases. The Karnofsky Performance Status is the most widely used health status measure in HIV medicine and research [16]. [2] observes CD4+ T cell depletion during all stages of HIV disease. Mycoplasma membrane protein (MMP) is identified as a possible cofactor responsible for the progression of AIDS. The fronto-orbital cortex, one of the cerebral cortical areas, is mainly damaged in AIDS brains [28]. Whole brain MTR is reduced in HIV-1-infected patients [18]. [1] concludes HIV dementia is associated with specific gray matter volume reduction, as well as with generalized volume reduction of white matter.
TABLE V.
Top-3 measures selected in each view.
| neuropsychological tests : Karnofsky Performance Scale, NART FSIQ, Rey Trial |
| flow cytometry : Tcells 4+8-, 3+56-16+NKT Cells 4+8-, Lymphocytes |
| plasma luminex : MMP-2, GRO, TGFa |
| freesurfer : Cerebral Cortex, Thalamus Proper, CC Mid Posterior |
| overall brain microstructure : MTR-CC, MTR-Hippocampus, MD-Cerebral-White-Matter |
| localized brain microstructure : MTR-CC Mid Anterior, FA-CC Anterior, MTRCC_Central |
| brain volumetry : Norm Peripheral Gray Volume, BPV, Norm Brain Volume |
V. Related Work
Currently, representative methods for multi-view learning can be categorized into three groups [29]: co-training, multiple kernel learning, and subspace learning. Generally, the co-training style algorithm is a classic approach for semi-supervised learning, which trains alternatively to maximize the mutual agreement on different views. Multiple kernel learning algorithms combine kernels that naturally correspond to different views, either linearly [14] or nonlinearly [25], [4] to improve learning performance. Subspace learning algorithms learn a latent subspace, from which multiple views are generated. Multiple kernel learning and subspace learning are generalized as co-regularization style algorithms [22], where the disagreement between the functions of different views is taken as one part of the objective function to be minimized. Overall, by exploring the consistency and complementary properties of different views, multi-view learning is more effective than single-view learning.
One of the key challenges of multi-view classification comes from the fact that the incorporation of multiple views will bring much redundant and even conflicting information which is unfavorable for classifier learning. In order to tackle this problem, feature selection has been the focus of interest and much work has been done. Most of the existing studies can be categorized as filter models [17], [20] and embedded models based on sparsity regularization [7], [6], [26], [27]. While in this paper, we focus on wrapper models for feature selection. The problem of feature selection in the tensor product space is formulated as an integer quadratic programming problem in [21]. However, this method is limited to the interaction between two views and hard to extend to many views, since it directly selects features in the tensor product space resulting in the curse of dimensionality. [23] studies multi-view feature selection in the unsupervised setting.
We notice that support vector machine recursive feature elimination (SVM-RFE) can intelligently select discriminative features using the weight vector produced by support vector machine [9], but it can only be applied on a single-view data. In this paper, we use tensor product to organize multi-view features and study the problem of multi-view feature selection based on SVM-RFE and tensor techniques. Different from existing approaches, we leverage the correlations between the original data and the reconstructed tensors and develop a wrapper feature selection approach.
VI. Conclusion
In this paper, we studied the problem of multi-view feature selection. We explored tensor product to bring different views together in a joint space, and presented a dual method of tensor-based multi-view feature selection (dual-Tmfs). Empirical studies in brain disease demonstrate the features selected by our proposed method yield better classification performance and are relevant to disease diagnosis.
Our proposed method has broad applicability for biomedical applications. Capabilities for simultaneous analysis of multiple feature subsets has transformative potential for yielding new insights concerning risk and protective relationships, for clarifying disease mechanisms, for aiding diagnostics and clinical monitoring, for biomarker discovery, for identification of new treatment targets and for evaluating effects of intervention.
Acknowledgements
This work is supported in part by NSF through grants CNS-1115234, OISE-1129076, US Department of Army through grant W911NF-12-1-0066, NIH through grant R01-MH080636, and National Science Foundation of China (61472089).
Contributor Information
Bokai Cao, Email: caobokai@uic.edu.
Lifang He, Email: lifanghescut@gmail.com.
Xiangnan Kong, Email: xkong@wpi.edu.
Philip S. Yu, Email: psyu@cs.uic.edu.
Zhifeng Hao, Email: zfhao@gdut.edu.cn.
Ann B. Ragin, Email: ann-ragin@northwestern.edu.
References
- 1.Aylward Elizabeth H, Brettschneider Paul D, McArthur Justin C, Harris Gordon J, Schlaepfer Thomas E, Henderer Jeffrey D, Barta Patrick E, Tien Allen Y, Pearlson Godfrey D. Magnetic resonance imaging measurement of gray matter volume reductions in HIV dementia. The American journal of psychiatry. 1995;152(7):987–994. doi: 10.1176/ajp.152.7.987. [DOI] [PubMed] [Google Scholar]
- 2.Brenchley Jason M, Schacker Timothy W, Ruff Laura E, Price David A, Taylor Jodie H, Beilman Gregory J, Nguyen Phuong L, Khoruts Alexander, Larson Matthew, Haase Ashley T, et al. CD4+ T cell depletion during all stages of HIV disease occurs predominantly in the gastrointestinal tract. The Journal of experimental medicine. 2004;200(6):749–759. doi: 10.1084/jem.20040874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chang Chih-Chung, Lin Chih-Jen. LIBSVM: a. library for support vector machines. 2001 Software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm. [Google Scholar]
- 4.Cortes Corinna, Mohri Mehryar, Rostamizadeh Afshin. Learning non-linear combinations of kernels. NIPS. 2009:396–404. [Google Scholar]
- 5.Fan Rong-En, Chang Kai-Wei, Hsieh Cho-Jui, Wang Xiang-Rui, Lin Chih-Jen. Liblinear: A library for large linear classification. The Journal of Machine Learning Research. 2008;9:1871–1874. [Google Scholar]
- 6.Fang Zheng, Zhang Zhongfei Mark. Discriminative feature selection for multi-view cross-domain learning. CIKM. 2013:1321–1330. ACM. [Google Scholar]
- 7.Feng Yinfu, Xiao Jun, Zhuang Yueting, Liu Xiaoming. Adaptive unsupervised multi-view feature selection for visual concept recognition. ACCV. 2012:343–357. [Google Scholar]
- 8.Friedman Jerome, Hastie Trevor, Tibshirani Robert. A note on the group lasso and a sparse group lasso. arXiv. 2010 [Google Scholar]
- 9.Guyon Isabelle, Weston Jason, Barnhill Stephen, Vapnik Vladimir. Gene selection for cancer classification using support vector machines. Machine learning. 2002;46(1–3):389–422. [Google Scholar]
- 10.He Lifang, Kong Xiangnan, Yu Philip S, Ragin Ann B, Hao Zhifeng, Yang Xiaowei. DuSK: A dual structure-preserving kernel for supervised tensor learning with applications to neuroimages. SDM. 2014 doi: 10.1137/1.9781611973440.15. SIAM. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kolda Tamara G, Bader Brett W. Tensor decompositions and applications. SIAM review. 2009;51(3):455–500. [Google Scholar]
- 12.Kong Xiangnan, Yu Philip S. Brain network analysis: a data mining perspective. SIGKDD Explorations Newsletter. 2014;15(2):30–38. [Google Scholar]
- 13.Kong Xiangnan, Yu Philip S, Wang Xue, Ragin Ann B. Discriminative feature selection for uncertain graph classification. SDM. 2013 doi: 10.1137/1.9781611972832.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lanckriet Gert RG, Cristianini Nello, Bartlett Peter, Ghaoui Laurent El, Jordan Michael I. Learning the kernel matrix with semidefinite programming. The Journal of Machine Learning Research. 2004;5:27–72. [Google Scholar]
- 15.Mebane-Sims Irma. 2009 alzheimer’s disease facts and figures. Alzheimer’s & Dementia. 2009 doi: 10.1016/j.jalz.2009.03.001. [DOI] [PubMed] [Google Scholar]
- 16.O’Dell Michael W, Lubeck Deborah P, O’Driscoll Peter, Matsuno Suzie. Validity of the karnofsky performance status in an HIV-infected sample. Journal of Acquired Immune Deficiency Syndromes. 1995;10(3):350–357. [PubMed] [Google Scholar]
- 17.Peng Hanchuan, Long Fulmi, Ding Chris. Feature selection based on mutual information criteria of max-dependency, max-relevance, and minredundancy. Pattern Analysis and Machine Intelligence. 2005;27(8):1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 18.Price RW, Epstein LG, Becker JT, Cinque P, Gisslén Magnus, Pulliam L, McArthur JC. Biomarkers of HIV-1 CNS infection and injury. Neurology. 2007;69(18):1781–1788. doi: 10.1212/01.wnl.0000278457.55877.eb. [DOI] [PubMed] [Google Scholar]
- 19.Ragin Ann B, Du Hongyan, Ochs Renee, Wu Ying, Sammet Christina L, Shoukry Alfred, Epstein Leon G. Structural brain alterations can be detected early in HIV infection. Neurology. 2012;79(24):2328–2334. doi: 10.1212/WNL.0b013e318278b5b4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Robnik-Šikonja Marko, Kononenko Igor. Theoretical and empirical analysis of relieff and rrelieff. Machine learning. 2003;53(1–2):23–69. [Google Scholar]
- 21.Smalter Aaron, Huan Jun, Lushington Gerald. Feature selection in the tensor product feature space. ICDM. 2009:1004–1009. doi: 10.1109/ICDM.2009.101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Sun Shiliang. A survey of multi-view machine learning. Neural Computing and Applications. 2013;23(7–8):2031–2038. [Google Scholar]
- 23.Tang Jiliang, Hu Xia, Gao Huiji, Liu Huan. Unsupervised feature selection for multi-view data in social media. SDM. 2013 [Google Scholar]
- 24.Tao Dacheng, Li Xuelong, Wu Xindong, Hu Weiming, Maybank Stephen J. Supervised tensor learning. Knowledge and Information Systems. 2007;13(1):1–42. [Google Scholar]
- 25.Varma Manik, Babu Bodla Rakesh. More generality in efficient multiple kernel learning. ICML. 2009:1065–1072. [Google Scholar]
- 26.Wang Hua, Nie Feiping, Huang Heng. Multi-view clustering and feature learning via structured sparsity. ICML. 2013:352–360. [Google Scholar]
- 27.Wang Hua, Nie Feiping, Huang Heng, Ding Chris. Heterogeneous visual features fusion via sparse multimodal machine. CVPR. 2013:3097–3102. [Google Scholar]
- 28.Weis S, Haug H, Budka H. Neuronal damage in the cerebral cortex of AIDS brains: a morphometric study. Acta neuropathologica. 1993;85(2):185–189. doi: 10.1007/BF00227766. [DOI] [PubMed] [Google Scholar]
- 29.Xu Chang, Tao Dacheng, Xu Chao. A survey on multi-view learning. arXiv. 2013 [Google Scholar]
- 30.Ye Jieping, Chen Kewei, Wu Teresa, Li Jing, Zhao Zheng, Patel Rinkal, Bae Min, Janardan Ravi, Liu Huan, Alexander Gene, Reiman Eric. Heterogeneous data fusion for Alzheimer’s disease study. KDD. 2008:1025–1033. ACM. [Google Scholar]