Abstract
Two-dimensional semiconductors such as MoS2 are an emerging material family with wide-ranging potential applications in electronics, optoelectronics, and energy harvesting. Large-area growth methods are needed to open the way to applications. Control over lattice orientation during growth remains a challenge. This is needed to minimize or even avoid the formation of grain boundaries, detrimental to electrical, optical, and mechanical properties of MoS2 and other 2D semiconductors. Here, we report on the growth of high-quality monolayer MoS2 with control over lattice orientation. We show that the monolayer film is composed of coalescing single islands with limited numbers of lattice orientation due to an epitaxial growth mechanism. Optical absorbance spectra acquired over large areas show significant absorbance in the high-energy part of the spectrum, indicating that MoS2 could also be interesting for harvesting this region of the solar spectrum and fabrication of UV-sensitive photodetectors. Even though the interaction between the growth substrate and MoS2 is strong enough to induce lattice alignment via van der Waals interaction, we can easily transfer the grown material and fabricate devices. Local potential mapping along channels in field-effect transistors shows that the single-crystal MoS2 grains in our film are well connected, with interfaces that do not degrade the electrical conductivity. This is also confirmed by the relatively large and length-independent mobility in devices with a channel length reaching 80 μm.
Keywords: two-dimensional materials, MoS2, epitaxial growth, electronic transport, grain boundaries, Kelvin probe force microscopy
The most investigated member of the transition metal dichalcogenide (TMD) family, molybdenum disulfide (MoS2), has attracted widespread attention for a variety of next-generation electrical and optoelectronic device applications because of its unique properties. In the bulk, this material has a crystalline structure consisting of covalently bonded layers weakly coupled to each other by weak van der Waals (vdW) forces. Owing to the weak coupling, two-dimensional (2D) monolayer MoS2 can be easily obtained by exfoliation using Scotch tape1 or liquid-phase exfoliation.2,3 Whereas bulk MoS2 is a semiconductor with an indirect band gap of 1.2 eV,4 monolayer MoS2 is a direct gap semiconductor with a band gap of at least 1.8 eV5−8 due to the 2D confinement.8 It also has Raman-active modes that are very sensitive to the thickness, which provides a convenient method for determining the number of layers with a reliable precision9 in addition to atomic force microscopy and optical detection techniques.10 The dramatic difference in the electronic structure of monolayer MoS2 in comparison with its bulk counterpart offers many opportunities for diverse applications. Using 2D crystals of MoS2 mechanically exfoliated from bulk geological samples, versatile devices including field-effect transistors with high on/off current ratio,10 memory cells,11 ultrasensitive photodetectors,12,13 and nanopores14 have been reported. Because MoS2 has a high mechanical flexibility and breaking strength,15 all these devices can in principle be implemented on flexible substrates.16
However, exfoliation of geological material and samples grown using chemical vapor transport17 lacks the systematic control of the thickness, size, and uniformity of the 2D film and is not scalable for large-scale device fabrication. Because of this, several methods, such as decomposition of thiomolybdates18 and sulfurization of Mo metal19 or molybdenum oxide,20−22 have been exploited to synthesize MoS2 on diverse substrates. Among them, chemical vapor deposition (CVD) is the most promising method to synthesize monolayer MoS2 triangular islands tens of micrometers in size.20−22 In most of these reports, SiO2 was used as the growth substrate, resulting in the random orientation of MoS2 domains because of the amorphous nature of the substrate and its relatively high surface roughness. This inevitably results in a large concentration of grain boundaries that can be detrimental to the electrical23,24 and mechanical properties of the grown films over length scales exceeding several micrometers. In order to avoid this, it is necessary to control the crystallographic orientation of MoS2 islands during growth so that they can coalesce into a uniform layer with a reduced density of grain boundaries.
Such control could in practice be achieved using a suitable atomically smooth crystalline substrate. In the case of classical three-dimensional materials this is normally achieved using epitaxial growth. Recently, van der Waals epitaxy has shown its potential for circumventing the need for a lattice-matched substrate and still keeping an ordered relation with the substrate.25,26 Van der Waals interaction between the substrate surface and the grown material governs the formation of the initial nuclei (islands), which constitute the precursors of the layers. Only energetically stable nuclei are able to grow by lateral spreading through the lateral facets. This leads to an overall preferential orientation of the grown layers. The relatively low strength of the van der Waals interaction and the relaxed requirement for lattice matching for substrates and overlayers without dangling bonds make it difficult in practice to control the lattice orientation of the deposited films. This was the case in previously reported deposition of centimeter-scale monolayer MoS2 films that have been deposited on other layered materials such as mica27 or graphene,28−30 where MoS2 grains showed a wide distribution of orientations with respect to each other and the substrate lattice.
Results and Discussion
Here, we use highly polished, EPI-ready grade sapphire substrates to achieve control over lattice orientation during CVD growth of monolayer MoS2. Such crystals are commonly used as growth substrates for GaN growth in LED manufacturing and for the growth of III–V high electron mobility transistors.31 Even though MoS2 and sapphire interact only via the relatively weak van der Waals interaction, commensurability of the sapphire lattice with MoS2 allows the van der Waals interaction to control the lattice orientation of MoS2 in a similar way to the lattice matching requirement in covalent semiconducting materials. While growth of MoS232 and TMDs33 on sapphire substrates has been reported before, this is the first time control over lattice orientation with centimeter-scale uniformity has been achieved during the growth of a monolayer 2D semiconductor, and it opens the way to large-area growth of high-quality MoS2. Key to achieving such lattice orientation is in the preparation of atomically smooth sapphire terraces on the surface of sapphire by annealing it in air for 1 h at a temperature of 1000 °C just prior to the growth process (Supporting Figure S1).34 An AFM-based analysis shows that the sapphire surface is characterized by atomically flat terraces ∼50–70 nm wide with a step height of 0.22 nm due to a small miscut angle estimated to be ∼0.2°. The terrace edges follow the [112̅0] direction on average.35 Annealed samples are transferred to the CVD system, and growth occurs. The growth process is based on the gas-phase reaction between MoO3 and sulfur evaporated from solid sources21,22 using ultra-high-purity argon as the carrier gas.
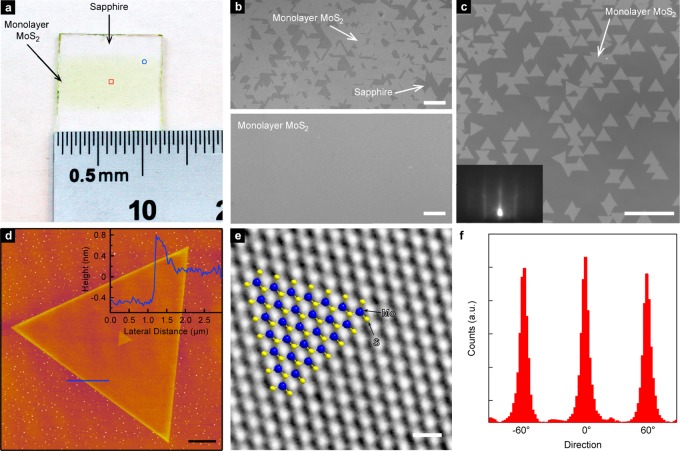
The growth procedure results in characteristic single-crystal domains in the shape of well-defined equilateral triangles that merge into a continuous monolayer film covering a typical area of 6 mm × 1 cm in the middle portion of the growth substrate, Figure 1a. Figure 1b presents optical images of regions showing partial (top image) and almost full (bottom) coverage. A careful examination of a region with incomplete coverage, Figure 1c, reveals that most of the single-crystal domain edges are oriented along dominant directions. A reflection high-energy electron diffraction (RHEED) pattern is shown in the inset of Figure 1c. The appearance of streaks typical of 2D materials and the MoS2 (1×1) pattern indicate the growth of a homogeneous and well-structured film over a large area. The majority (91.5% of islands shown in Figure 1c) of single-crystal domains are well aligned with the relative orientation of edges that can be expressed as multiples of 60°. This is confirmed by the orientation histogram presented in Figure 1f for the same area as in Figure 1c, showing that the dominant edge orientations are 0° and ±60°. A small fraction of domains (6% of islands in Figure 1c) show edges with a relative angle of ±30°, while the rest (2.5%) show other orientations.
Figure 1.
Monolayer MoS2 growth with controlled lattice orientation. (a) Photograph of centimeter-scale monolayer MoS2 grown on sapphire. (b) Optical microscopy images from different regions of the sample showing incomplete coverage close to the edges (upper image, position marked by the circle in a) and full coverage close to the center of the growth substrate (lower image, position marked by the rectangle in a). Scale bar length is 20 μm on the top image and 10 μm for the bottom image. Original optical images were converted to grayscale, and the contrast was enhanced. (c) Optical microscopy image of monolayer MoS2 grains grown on atomically smooth sapphire. Scale bar length is 50 μm. Inset: RHEED pattern acquired on the CVD-grown sample showing a film with long-range structural order. (d) Atomic force microscope image of a monolayer MoS2 grain. Scale bar is 2 μm long. Inset: Line scan showing the thickness profile along the blue line in the AFM image. (e) High-resolution TEM image of a suspended MoS2 film showing the crystallinity of the sample. View of the structural model is overlaid. Scale bar is 0.5 nm long. (f) Orientation histogram based on the area shown in part c confirms that the majority of MoS2 grain edges are oriented along 0° and ±60° angles.
Figure 1d shows an AFM image of a single crystal of monolayer MoS2. According to previous STM studies, these MoS2 edges are expected to be (101̅0) Mo zigzag edges likely terminated with sulfur.36 The sapphire terrace step height of 0.22 nm is sufficiently low to ensure the growth of continuous MoS2 single crystals, as confirmed by TEM imaging and electrical transport measurements. Figure 1e shows a high-resolution TEM image of a freestanding membrane37 of monolayer MoS2 showing its regular atomic structure with a clearly discernible hexagonal symmetry. White spots correspond to holes in the atomic structure, while dark spots correspond to sulfur and molybdenum atoms.
We first check the quality of our large-area monolayer MoS2 films by performing optical characterization. Figure 2a shows typical Raman spectra of the CVD material compared to monolayer MoS2 exfoliated onto sapphire. The spectra show two characteristic peaks in this spectral range: the out-of-plane vibration of S atoms (A1′) with a Raman shift of ∼405 cm–1 and the in-plane vibration of Mo and S atoms (E′) at ∼385 cm–1.9 The observed frequency difference confirms that the deposited material is monolayer MoS2. The ratio between the A1 and E′ mode intensities can be used as an indicator of doping levels,38 and it indicates that the CVD material is less doped than the exfoliated counterpart. Another indication of a smaller structural disorder39 in the CVD material is the smaller width of the A1′ mode.
Figure 2.
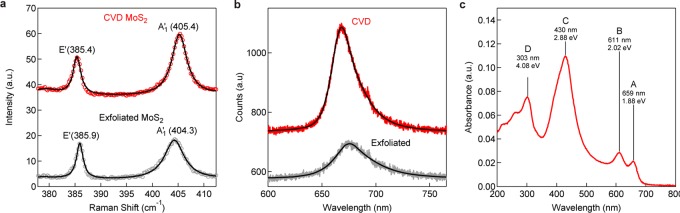
Optical properties of large-area monolayer MoS2. (a) Raman spectra of as-grown monolayer MoS2 on sapphire and monolayer MoS2 exfoliated from bulk crystals and transferred onto sapphire. (b) Photoluminescence spectra of as-grown monolayer MoS2 on sapphire and monolayer MoS2 exfoliated from bulk crystals onto sapphire. Black lines in parts a and b correspond to fits. (c) UV–vis optical absorbance spectra acquired from large-area monolayer MoS2 showing the A and B absorption peaks due to band-edge excitons as well as C and D peaks associated with van Hove singularities of MoS2.
Figure 2b shows a photoluminescence spectrum acquired at room temperature on CVD-grown and adhesive tape exfoliated monolayer MoS2. We can clearly resolve the intense A excitonic peak at 659 nm (1.88 eV), while the B exciton is not expected to be visible at low excitation intensities due to state-filling effects.40 Typical peak widths are ∼26 nm (∼72 meV) and are smaller than in exfoliated MoS2 samples (∼40 nm or ∼111 eV), indicating that our CVD MoS2 has superior optical qualities to the exfoliated material. Relative photoluminescence (PL) intensities also indicate a reduced doping level in the CVD material. Detailed photoluminescence mapping of single domains did not resolve any internal structure, indicating the absence of internal grain boundaries.
Thanks to the optical transparency of the sapphire substrate and the large area of the sample covered by monolayer MoS2, we can perform UV–visible absorption characterization using a simple benchtop spectrophotometer. The resulting spectrum shown in Figure 2c represents broadband absorbance measurements on MoS2. The spectrum shows the well-known A and B excitonic absorption bands at 695 nm (1.78 eV) and 611 nm (2.02 eV).6,7 This demonstrates the high optical quality and uniformity of our monolayer MoS2 over a large area. In addition, we can also clearly observe the recently reported C peak at 430 nm (2.88 eV)41 as well as the D peak at 303 nm (4.08 eV). Whereas the A and B peaks are associated with optical absorption by band-edge excitons, peaks C and D are associated with van Hove singularities42 of monolayer MoS2. The fact that MoS2 shows enhanced absorbance in the 200–500 nm range along with the relatively high mobility of the material could play an important role in designing solar cells and UV-sensitive photodetectors.
We proceed to analyze the large-scale crystal structure and its relative orientation using bright-field TEM imaging and selected-area electron diffraction. The asymmetry of the Mo and S sublattices allows us to determine the orientation of the MoS2 lattice with respect to the island edges (Supporting Section 3)22,37 and to confirm that the observed single-crystal domains share the same lattice orientation within the grains. This allows us to identify the lattice orientation based on the orientation of the triangular single crystals.
Figure 3a shows a low-magnification image of the group of aligned MoS2 triangular islands. We closely examine a small region involving two neighboring islands by positioning the select-area aperture at the red circle containing two islands with their edges forming a 60° angle and acquiring the diffraction pattern shown in the inset of Figure 3a. Even though this diffraction pattern has been acquired from both triangles, we can observe only one set of diffraction spots with 6-fold symmetry, showing the precise alignment of lattices in both of the islands. Figure 3b shows another example of a much less frequently occurring situation with two islands merging under a 90° angle. In this case, we can clearly distinguish two sets of [1̅100] diffraction spots, rotated by 30°.
Figure 3.
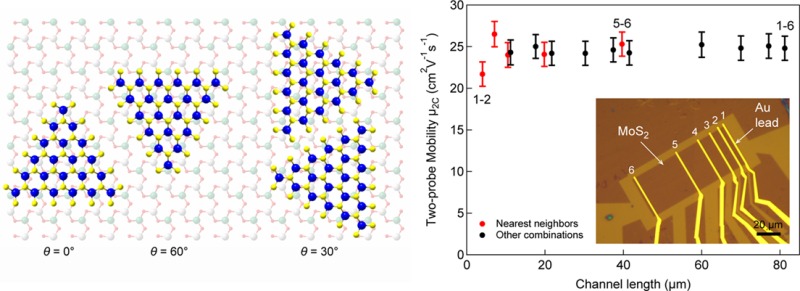
Diffraction patterns from different island orientations. (a) Low-magnification TEM image of several neighboring MoS2 islands. The diffraction pattern acquired from the area denoted with the red circle is shown in the inset and corresponds to the most common arrangement between neighboring islands. Only one set of diffraction spots can be detected from such islands, indicating that their crystalline lattices are aligned. The MoS2 structure drawing indicates the lattice orientation within the single-crystal island and is not to scale. (b) Low-magnification TEM image and the corresponding diffraction patterns from two merging islands with their edges forming a 90° angle. Two sets of diffraction spots, rotated by 30°, can be observed, indicating a 30° lattice misorientation angle. (c) Schematic drawing showing the top view of relative lattice orientations between monolayer MoS2 and c-plane sapphire. In the case of the arrangement of the left-hand side, corresponding to lattice rotation angles θ = 0° and θ = 60°, the two lattices are commensurate. Two minority orientations can be observed in our sample, corresponding to a lattice rotation angle θ = 30° and θ = 90° (right-hand side).
Figure 3c schematically illustrates the most likely relative orientations for monolayer MoS2 growing epitaxially on the atomically smooth surface of sapphire, corresponding to ∼97% of the observed grain orientations. The 0° and 60° orientations correspond to the 3-on-2 superstructure of MoS2 (lattice constant 3.212 Å) and sapphire (lattice constant 4.814 Å).
In order to explain the presence of privileged growth orientations for MoS2 islands on sapphire, we have first performed first-principles, van der Waals corrected density functional theory (DFT) simulations of MoS2-covered sapphire. These calculations confirm that the interactions between MoS2 and the sapphire surface are of vdW nature and magnitude (see Supporting Section 4). DFT calculations need to be performed in the coincident-site lattice of common supercells in which the MoS2 monolayers are in registry with the substrate. Since these cells exhibit a limited size, some amount of artificial strain needs to be introduced in order to limit the size of the supercells used. In reality, the MoS2 overlayers are not expected to show much strain26 because of their weak vdW interactions with the substrate. The strain energy turns out to be of similar magnitude to the vdW interaction energy with the substrate. As a consequence, it becomes difficult to ascertain the stability of one orientation with respect to another from DFT calculations alone. On the other hand, these results also clearly point to a vdW nature for the interactions. This prompted us to construct a simple model of adsorption accounting only for pairwise atom–atom interactions of a −C6/r6 nature. To our surprise, this model shows an extremely rich adsorption phenomenology that is in agreement with the experimental findings, notably, pointing out that only MoS2 configurations at either 0° or 60° equivalent orientations (see Figure 3c) provide a structured potential energy surface that is sensitive to arbitrary in-plane translations of the MoS2 plane, and with well-defined maxima and minima in the adsorption energies (Figure 4). All other orientations yield instead a flat energy surface where the adsorption energy is completely independent of translations and rotations of MoS2 with respect to the surface. From this, we can conclude that the MoS2 layer would be free to rotate and slide along the surface of sapphire until it would find the orientation and positions of strongest adsorption. The oriented growth of MoS2 would proceed as follows: using low supersaturation conditions very few MoS2 nuclei are formed and grow laterally on the substrate. Weak (vdW) interactions with the substrate guarantee a certain degree of rotation/translation with respect to the surface in the initial phase. When the nucleus reaches a certain size, not only is it stable against decomposition but it gets pinned down in the most stable orientation with the substrate. Growth proceeds then forming a continuous and oriented layer. We cannot help but see the analogy of this pinning process with the process of attaching a Lego brick onto another larger Lego brick surface, in an analogy introduced by A. Geim in ref (43). Last, the presence of surface defects could be at the origin of less frequently observed lattice orientations.
Figure 4.
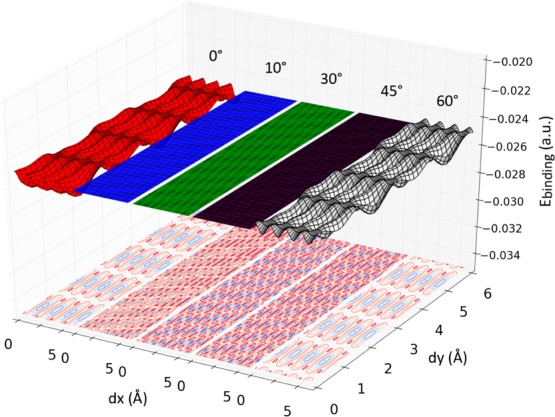
Binding energies for MoS2 and sapphire. Data are shown as a 3D surface and contour plot of relative binding energies for MoS2 on sapphire, for different relative lattice orientations and as a function of relative shift in x- and y-directions, corresponding to the lateral motion of the MoS2 monolayer on the surface of atomically smooth sapphire. Only the 0° and 60° orientations result in significant corrugation and substantial stable minima. The distance between MoS2 and sapphire is 3.24 Å, as obtained from DFT calculations.
We characterize the electrical quality of constituent grains by performing electrical transport measurements on single grains (Supporting Section 5). Results show that the mobility reaches a value of 43 cm2/(V s), comparable to results from previous two-terminal measurements on CVD MoS2 (ref (44)) and slightly higher than in devices based on exfoliated MoS2 prepared in the same way.45,46 Good stitching of such high-quality single crystals into continuous films is necessary in order to realize large-area MoS2 with the same quality as that of the single crystal. We first study the influence of grain boundaries on the electrical properties of MoS2, by measuring local electrical potentials using scanning Kelvin probe microscopy47 (SKPM), on back-gated MoS2 field-effect transistors (FETs) incorporating two grains possibly separated by a grain boundary. The advantage of this method over conventional techniques such as FET device characterization using the transfer length method is that it allows direct imaging of the impact of nanoscale features such as grain boundaries in laterally inhomogeneous materials. With this AFM-based method, we can record the local variation of the local potential of the surface, relative to the metallic probe. Grain boundaries that contribute additional electrical resistance and degrade device mobility readily show up on such scans (Supporting Section 6). Figure 5 shows local potential maps (upper panels) and potential line scans (lower panels) across the three types of conjoined single-crystal MoS2 grains that account for pairs formed by orientations shown in Figure 3c. All other possible combinations involving pairs composed of any of the MoS2 lattice and triangle orientations shown in Figure 3c can be reduced to these three misorientation angles. Figure 5a shows measurements acquired across two grains sharing the same crystalline orientation. In this case, the two grains can join without the appearance of a grain boundary, while in the case of merged single crystals shown in Figure 5b and c with relative lattice orientations characterized by the misorientation angles θrel = 60° and θrel = 30°, a grain boundary is expected to be present at their interface. Potential line scans, acquired along the red lines overlaid on the potential maps for all three configurations, show a clear monotonic drop of the voltage between the contacts, revealing the absence of an additional voltage drop (resistance) due to the presence of a grain boundary. This shows that for misorientation angles θrel = 60° and θrel = 30° occurring in our samples, the single crystals are joined by twin grain boundaries, previously shown not to degrade the electrical properties of polycrystalline MoS2.22,23 This proves that the epitaxial growth of MoS2 on sapphire, providing these predominant domain orientations, can dramatically suppress the formation of tilted grain boundaries, which are detrimental for the electrical properties of the polycrystalline material, and that epitaxial growth of MoS2 is crucial for the formation of nonresistive grain boundaries in a polycrystalline film. We now turn to polycrystalline films and examine their electrical properties by performing measurements on a section of a continuous film with a length L = 81.2 μm and width W = 36.6 μm, contacted by multiple electrodes (Supporting Section 7). The effective field-effect mobility as a function of channel length, extracted from two contact measurements in various lead configurations, is shown in Figure 6. We observe no degradation in mobility with increasing length from 4 μm to ∼80 μm, within the measurement error. We compare our findings with recent results23 on polycrystalline continuous CVD MoS2 films, where the material was grown on SiO2 with random relative orientation of grains as well as bilayer formation on grain boundaries influencing electrical transport properties. In our case these sources of scattering are eliminated and mobility stays constant in the devices built on multiple merged grains. We estimate that there are ∼16 junctions between single crystals along the length of the 82 μm channel (Supporting Section 7). This shows that the superior electrical properties of the single crystals are preserved over length scales larger than those corresponding to single grains.
Figure 5.
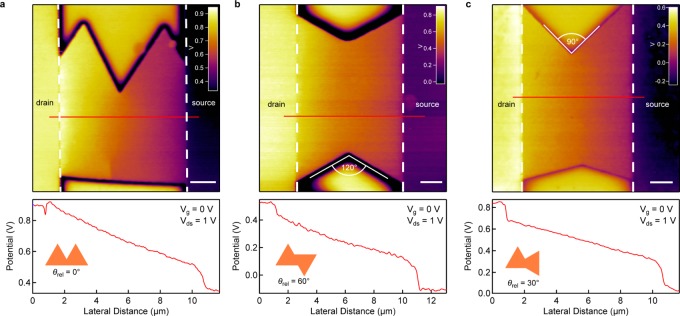
Mapping the local electrical properties across grain boundaries in large-area monolayer MoS2. (a) Local potential map (upper panel) and line scan across the red line (lower panel) showing the potential drop over the conductive channel of a biased field-effect transistor based on two merged MoS2 single crystals with the same lattice orientation. In this case, no grain boundary is expected. The smooth potential drop indicates the absence of abrupt changes of potential that would indicate the presence of an electrically resistive grain boundary. (b) Local potential map and line scan over two merged triangles with a 60° misorientation angle. This configuration is expected to result in a twin grain boundary. Its presence does not introduce an extra potential drop, indicating that it does not degrade the electrical conductivity of the material. (c) Local potential map and line scan over two merged triangles with a 30° misorientation angle. The presence of the grain boundary does not introduce an extra potential drop in the channel. Insets in line scan plots indicate relative orientations of MoS2 single crystals. Scale bars are 2 μm long.
Figure 6.
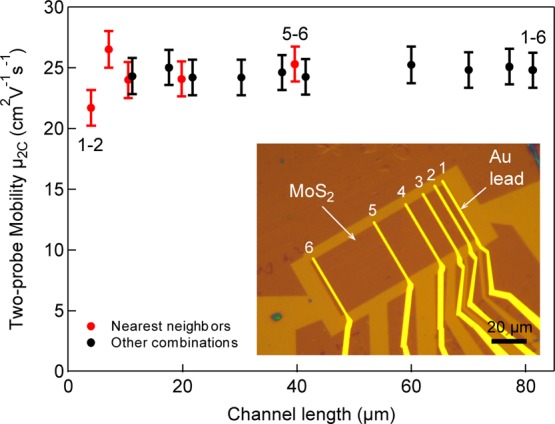
Electrical properties of large-area devices. Field-effect mobility as a function of channel length. Values are extracted from two-contact measurements performed on the device based on the continuous film shown in the inset with Au leads labeled 1–6. Red symbols correspond to values obtained using two nearest neighbor electrodes as source and drain terminals with the longest segment between electrodes 5 and 6 having a length of 39.7 μm. Black symbols denote values extracted by using other combinations of electrodes with the longest segment between terminals 1 and 6 having a length of 81.2 μm.
Conclusions
In conclusion, we have achieved epitaxial chemical vapor deposition growth of monolayer MoS2 with a high degree of control over lattice orientation by using atomically smooth surfaces of sapphire as the growth substrate. The large-area MoS2 film is formed from merging single-crystalline domains, with the majority of the domains having lattice orientations being restricted to high-symmetry cases. This shows that even the relatively weak van der Waals interaction can control the crystalline orientation of the overlayer in a similar way to chemical bonds in covalently bonded semiconductors such as GaAs or Si. Here, the preferred MoS2 orientation corresponds to the one with the highest commensuration.
While DFT calculations had difficulty explaining the existence of a preferred orientation due to complications related to applying periodic boundary conditions to an incommensurate structure, a remarkably simple model based on pairwise interactions results in predictions in good agreement with the experiment. We believe that this result is general for all vdW heterostructures, and hence we suggest this method as an excellent tool for prediction of such structures.
Local electrical measurements across grain boundaries reveal good stitching between the single crystals in our film with the absence of electrical resistance at most common types of grain boundaries in our sample. The use of sapphire substrates can therefore suppress the formation of tilted grain boundaries, which are detrimental for the electrical properties of the polycrystalline CVD-grown MoS2.23 The high quality of our sample is further demonstrated by optical and electrical measurements showing properties superior to exfoliated samples. The high degree of uniformity of our film also allowed optical absorbance measurements to be performed in a broad wavelength range, showing the presence of high-energy absorbance peaks that indicate the suitability of MoS2 for harvesting the green and blue regions of the solar spectrum and for the fabrication of photodetectors operating in this wavelength range. The proposed growth strategy involving the use of atomically smooth sapphire substrates could pave the way for large-area growth of MoS2 with high optical and electrical quality retained over large length scales, allowing its use in future electronic and optoelectronic devices.
Methods
Growth Procedure
Monolayer MoS2 has been grown by chemical vapor deposition on c-plane sapphire. After consecutive cleaning by acetone/2-propanol/DI-water and piranha solution, the substrates were annealed for 1 h at 1000 °C in air. After that, they were placed face-down above a crucible containing ∼5 mg of MoO3 (≥99.998% Alfa Aesar) and loaded into a split-tube three-zone CVD furnace with a 32 mm outer diameter quartz tube. CVD growth was performed at atmospheric pressure using ultra-high-purity argon as the carrier gas. A second crucible containing 350 mg of sulfur (≥99.99% purity, Sigma-Aldrich) was located upstream from the growth substrates. The growth recipe is as follows: set the temperature of 300 °C with 200 sccm for 10 min, ramp to 700 °C with a rate of 50 °C min–1 and 10 sccm of carrier gas flow, set the temperature to 700 °C for 10 min, cool to 570 °C with 10 sccm gas flow, increase the gas flow to 200 sccm, and open the furnace for rapid cooling. For more details, please refer to Supporting Sections 1 and 2.
TEM and AFM Imaging
CVD MoS2 was transferred from sapphire using the wet transfer KOH method. Samples were first spin coated at 1500 rpm with PMMA A2, resulting in a ∼100 nm thick polymer film. These were detached in a 30% KOH solution, washed several times in DI water, and transferred onto TEM grids. TEM grids were annealed in the flow of Ar and H2 for 8 h at 400 °C in order to remove the polymer film. For low-resolution imaging and diffraction studies, 10 nm thick Si3N4 windows were used, while for high-resolution TEM (HR-TEM) we used PELCO holey silicon nitride support film with 2.5 um holes in a 200 nm thick Si3N4 support. Transmission electron microscopy was performed using a JEOL 2200 FS operated in the 120–200 keV energy range. HR-TEM images were recorded at a magnification of 1 M×. A series of 10–30 images was recorded and stacked with drift correction and averaging using the Stackreg plugin in Fiji (ImageJ). Island orientations in optical images were analyzed using the directionality plugin in Fiji (ImageJ). Samples were also imaged using an atomic force microscope (Asylum Research Cypher) operating in ac mode.
Density Functional Theory Modeling
All ab initio simulations have been performed within density functional theory, using Quantum-ESPRESSO as implemented in PWscf code of the Quantum-ESPRESSO distribution48 and VASP.49,50 For calculations using Quantum-ESPRESSO, in order to account for dispersion interactions, we used a revised version51 of the nonlocal density functional by Vydrov and Van Voorhis52 (rVV10). Ion–electron interactions were taken into account by means of ultrasoft pseudopotentials,53,54 with energy cutoffs of 60 Ry for wave functions and 600 Ry for density. Pseudopotentials have been generated using parameters taken from the PSlibrary repository (v.0.3.0) of the QEforge distribution and setting rPW8654,55 as exchange functional and PBE53 as semilocal contribution to the correlation functional, in agreement with the rVV10 parametrization.52 Surface calculations were performed by considering Al2O3 slabs with six oxygen O3 layers and 10 (12) aluminum layers in the case of OH (Al) termination. In order to minimize the interaction between periodic replicas, supercells were built including 20 Å of vacuum. Brillouin-zone integration for different supercells was carried out using appropriately converged Monkhorst–Pack grids, corresponding approximately to a gamma-centered 6 × 6 × 1 grid for the sapphire surface and 9 × 9 × 1 for MoS2. The Broyden–Fletcher–Goldfarb–Shanno method was adopted to relax the structures until forces acting on atoms were below 0.025 eV/Å. For calculations using VASP, we have used the density functional theory calculations as implemented in the VASP code49,50 using the PAW approach.56,57 The used functional was the self-consistently implemented vdW-DF58−60 with the optB88 exchange following the results of Mittendorfer etal.61 for graphene adsorption on Ni, where that combination produced results in agreement with RPA calculations and experimental findings. A sufficient number of k-points was used (gamma-centered Monkhorst–Pack grid of 3 × 3 × 1 for the R0 supercell). An energy cutoff of 500 eV was used along with a 15 Å vacuum spacing between the periodic images in the z-direction, and the dipole correction was applied.62 The atomic relaxation was performed until the forces dropped below 0.1 meV/Å. The sapphire surface was simulated with the five-layer-thick slab, of which three top layer were allowed to relax. The top surface was Al terminated.
Kelvin Probe Imaging
For the KPFM measurement an atomic force microscopy system (Asylum Research Cypher) was utilized, allowing the simultaneous measurement of topography and Kelvin voltage with a spatial resolution of about 20 nm and a potential resolution of a few millivolts. We used silicon KPFM probes (Olymups, OMCL-AC240TM) with a nominal radius of ∼30 nm, which were covered with a conductive Ti/Pt (5/20 nm) layer and had a resonance frequency of ∼70 kHz. An ac modulation voltage (VAC) of 3 V was applied to the probe for the Kelvin probe measurements. An external bias between the two contacts’ (source and drain) Vds of 1 V was applied, and the gate voltage Vg was typically kept at 0 V. All measurements were performed under ambient conditions.
Optical Characterization
Raman measurements were performed on a commercial system (Jobin-Yvon Horiba LabRam) using a 532 nm laser for excitation. Photoluminescence measurements were performed using a 488 nm laser and a spectrometer (Princeton Instruments SP-2500i) with a liquid nitrogen cooled camera (PiXIS/Pylon/Spec-10:256). Broadband absorbance measurements were performed using a Varian Cary 50 Bio UV–vis spectrophotometer.
Electrical Characterization
CVD-grown single domains of MoS2 were transferred using PMMA A2 as a support film and etching in 30% KOH onto a degenerately doped Si substrate covered with 270 nm thick SiO2. The PMMA film is dissolved in acetone, and residues are removed by annealing in Ar atmosphere at 350 °C for 5 h. PMMA A4 was used as the etching mask during oxygen plasma etching. The devices were annealed at 200 °C in Ar atmosphere to eliminate resist residues and reduce contact resistance.
Acknowledgments
Thanks go to D. Walters and J. Cleland from Asylum Research for suggestions related to sapphire surface preparation. We thank R. Gaal for technical assistance with the Raman setup, T. Heine for useful discussions, M. G. Friedl for technical assistance, and A. Allain for help with electrical transport measurements. Device fabrication was carried out in the EPFL Center for Micro/Nanotechnology (CMI). We thank Z. Benes (CMI) for technical support with e-beam lithography and D. Alexander (CIME) for support with electron microscopy. P.L. thanks I. Žutić and the Center for Computational Research, University at Buffalo. M.G. and N.M. acknowledge the Swiss National Supercomputing Centre (CSCS) for simulation time under project ID s337. This work was financially supported by Swiss SNF Sinergia Grant No. 147607, funding from the European Union’s Seventh Framework Programme FP7/2007-2013 under Grant Agreement No. 318804 (SNM), Marie Curie ITN network “MoWSeS” (Grant No. 317451), ERC Grant No. 240076, and SNF Grant 135046. We acknowledge funding by the EC under the Graphene Flagship (grant agreement no. 604391). D.D. and D.K. worked on CVD growth. D.D. performed AFM, Raman, and broadband optical characterization. D.O. performed TEM acquisition, data analysis, and long-channel FET fabrication and characterization. D.O. and K.M. worked on Kelvin probe measurements. K.M. fabricated and characterized single-crystal FET devices. P.L. performed DFT calculations using VASP and modeling based on pairwise interactions. M.G. performed DFT calculations using Quantum ESPRESSO. O.L.S. performed PL measurements. M.W.C. performed RHEED acquisition and analysis. Y.C.K. developed and applied the transfer method used for realizing large-area devices. S.B. prepared exfoliated samples for Raman measurements. P.G. supervised Raman measurements, A.F.i.M. supervised PL measurements, A.R. supervised broadband optical measurements, and N.M. supervised DFT calculations performed by M.G. A.K. coordinated and initiated the work. A.F.i.M. contributed to the discussion on the growth mechanisms. All authors performed work on manuscript preparation.
Supporting Information Available
Substrate preparation, growth setup, SAED analysis, sapphire-MoS2 van der Waals interaction, electrical transport measurements on a single crystal, scanning Kelvin probe microscopy, and electrical transport measurements on large-area films. This material is available free of charge via the Internet at http://pubs.acs.org.
Author Contributions
# D. Dumcenco, D. Ovchinnikov, and K. Marinov contributed equally.
The authors declare no competing financial interest.
Supplementary Material
References
- Novoselov K. S.; Jiang D.; Schedin F.; Booth T. J.; Khotkevich V. V.; Morozov S. V.; Geim A. K. Two-Dimensional Atomic Crystals. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 10451–10453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coleman J. N.; Lotya M.; O’Neill A.; Bergin S. D.; King P. J.; Khan U.; Young K.; Gaucher A.; De S.; Smith R. J.; etal. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [DOI] [PubMed] [Google Scholar]
- Smith R. J.; King P. J.; Lotya M.; Wirtz C.; Khan U.; De S.; O’Neill A.; Duesberg G. S.; Grunlan J. C.; Moriarty G.; etal. Large-Scale Exfoliation of Inorganic Layered Compounds in Aqueous Surfactant Solutions. Adv. Mater. (Weinheim, Ger.) 2011, 23, 3944–3948. [DOI] [PubMed] [Google Scholar]
- Kam K. K.; Parkinson B. A. Detailed Photocurrent Spectroscopy of the Semiconducting Group Vib Transition Metal Dichalcogenides. J. Phys. Chem. 1982, 86, 463–467. [Google Scholar]
- Lebegue S.; Eriksson O. Electronic Structure of Two-Dimensional Crystals from ab Initio Theory. Phys. Rev. B 2009, 79, 115409. [Google Scholar]
- Splendiani A.; Sun L.; Zhang Y.; Li T.; Kim J.; Chim C.-Y.; Galli G.; Wang F. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [DOI] [PubMed] [Google Scholar]
- Mak K. F.; Lee C.; Hone J.; Shan J.; Heinz T. F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [DOI] [PubMed] [Google Scholar]
- Kuc A.; Zibouche N.; Heine T. Influence of Quantum Confinement on the Electronic Structure of the Transition Metal Sulfide TS2. Phys. Rev. B 2011, 83, 245213. [Google Scholar]
- Lee C.; Yan H.; Brus L. E.; Heinz T. F.; Hone J.; Ryu S. Anomalous Lattice Vibrations of Single- and Few-Layer MoS2. ACS Nano 2010, 4, 2695–2700. [DOI] [PubMed] [Google Scholar]
- Benameur M. M.; Radisavljevic B.; Heron J. S.; Sahoo S.; Berger H.; Kis A. Visibility of Dichalcogenide Nanolayers. Nanotechnology 2011, 22, 125706. [DOI] [PubMed] [Google Scholar]
- Bertolazzi S.; Krasnozhon D.; Kis A. Nonvolatile Memory Cells Based on MoS2/Graphene Heterostructures. ACS Nano 2013, 7, 3246–3252. [DOI] [PubMed] [Google Scholar]
- Lopez-Sanchez O.; Lembke D.; Kayci M.; Radenovic A.; Kis A. Ultrasensitive Photodetectors Based on Monolayer MoS2. Nat. Nanotechnol. 2013, 8, 497–501. [DOI] [PubMed] [Google Scholar]
- Yin Z.; Li H.; Li H.; Jiang L.; Shi Y.; Sun Y.; Lu G.; Zhang Q.; Chen X.; Zhang H. Single-Layer MoS2 Phototransistors. ACS Nano 2012, 6, 74–80. [DOI] [PubMed] [Google Scholar]
- Liu K.; Feng J. D.; Kis A.; Radenovic A. Atomically Thin Molybdenum Disulfide Nanopores with High Sensitivity for DNA Trans Location. ACS Nano 2014, 8, 2504–2511. [DOI] [PubMed] [Google Scholar]
- Bertolazzi S.; Brivio J.; Kis A. Stretching and Breaking of Ultrathin MoS2. ACS Nano 2011, 5, 9703–9709. [DOI] [PubMed] [Google Scholar]
- Chang H.-Y.; Yang S.; Lee J.; Tao L.; Hwang W.-S.; Jena D.; Lu N.; Akinwande D. High-Performance, Highly Bendable MoS2 Transistors with High-K Dielectrics for Flexible Low-Power Systems. ACS Nano 2013, 7, 5446–5452. [DOI] [PubMed] [Google Scholar]
- Schäfer H.Chemical Transport Reactions; Academic Press: New York, 1964. [Google Scholar]
- Liu K.-K.; Zhang W.; Lee Y.-H.; Lin Y.-C.; Chang M.-T.; Su C.-Y.; Chang C.-S.; Li H.; Shi Y.; Zhang H.; etal. Growth of Large-Area and Highly Crystalline MoS2 Thin Layers on Insulating Substrates. Nano Lett. 2012, 12, 1538–1544. [DOI] [PubMed] [Google Scholar]
- Zhan Y.; Liu Z.; Najmaei S.; Ajayan P. M.; Lou J. Large-Area Vapor-Phase Growth and Characterization of MoS2 Atomic Layers on a SiO2 Substrate. Small 2012, 8, 966–971. [DOI] [PubMed] [Google Scholar]
- Lee Y.-H.; Zhang X.-Q.; Zhang W.; Chang M.-T.; Lin C.-T.; Chang K.-D.; Yu Y.-C.; Wang J. T.-W.; Chang C.-S.; Li L.-J.; etal. Synthesis of Large-Area MoS2 Atomic Layers with Chemical Vapor Deposition. Adv. Mater. (Weinheim, Ger.) 2012, 24, 2320–2325. [DOI] [PubMed] [Google Scholar]
- Najmaei S.; Liu Z.; Zhou W.; Zou X.; Shi G.; Lei S.; Yakobson B. I.; Idrobo J.-C.; Ajayan P. M.; Lou J. Vapour Phase Growth and Grain Boundary Structure of Molybdenum Disulphide Atomic Layers. Nat. Mater. 2013, 12, 754–759. [DOI] [PubMed] [Google Scholar]
- van der Zande A. M.; Huang P. Y.; Chenet D. A.; Berkelbach T. C.; You Y.; Lee G.-H.; Heinz T. F.; Reichman D. R.; Muller D. A.; Hone J. C. Grains and Grain Boundaries in Highly Crystalline Monolayer Molybdenum Disulphide. Nat. Mater. 2013, 12, 554–561. [DOI] [PubMed] [Google Scholar]
- Najmaei S.; Amani M.; Chin M. L.; Liu Z.; Birdwell A. G.; O’Regan T. P.; Ajayan P. M.; Dubey M.; Lou J. Electrical Transport Properties of Polycrystalline Monolayer Molybdenum Disulfide. ACS Nano 2014, 8, 7930–7937. [DOI] [PubMed] [Google Scholar]
- Yazyev O. V.; Chen Y. P. Polycrystalline Graphene and Other Two-Dimensional Materials. Nat. Nanotechnol. 2014, 9, 755–767. [DOI] [PubMed] [Google Scholar]
- Koma A. Van Der Waals Epitaxy for Highly Lattice-Mismatched Systems. J. Cryst. Growth 1999, 201, 236–241. [Google Scholar]
- Bakti Utama M. I.; Zhang Q.; Zhang J.; Yuan Y.; Belarre F. J.; Arbiol J.; Xiong Q. Recent Developments and Future Directions in the Growth of Nanostructures by Van Der Waals Epitaxy. Nanoscale 2013, 5, 3570–3588. [DOI] [PubMed] [Google Scholar]
- Ji Q.; Zhang Y.; Gao T.; Zhang Y.; Ma D.; Liu M.; Chen Y.; Qiao X.; Tan P.-H.; Kan M.; etal. Epitaxial Monolayer MoS2 on Mica with Novel Photoluminescence. Nano Lett. 2013, 13, 3870–3877. [DOI] [PubMed] [Google Scholar]
- Shi Y.; Zhou W.; Lu A.-Y.; Fang W.; Lee Y.-H.; Hsu A. L.; Kim S. M.; Kim K. K.; Yang H. Y.; Li L.-J.; et al. Van Der Waals Epitaxy of MoS2 Layers Using Graphene as Growth Templates. Nano Lett. 2012, 12, 2784–2791. [DOI] [PubMed] [Google Scholar]
- Ago H.; Endo H.; Solís-Fernández P.; Takizawa R.; Ohta Y.; Fujita Y.; Yamamoto K.; Tsuji M. Controlled Van Der Waals Epitaxy of Monolayer MoS2 Triangular Domains on Graphene. ACS Appl. Mater. Interfaces 2015, 7, 5265–5273. [DOI] [PubMed] [Google Scholar]
- Lin Y.-C.; Lu N.; Perea-Lopez N.; Li J.; Lin Z.; Peng X.; Lee C. H.; Sun C.; Calderin L.; Browning P. N.; et al. Direct Synthesis of Van Der Waals Solids. ACS Nano 2014, 8, 3715–3723. [DOI] [PubMed] [Google Scholar]
- Gonschorek M.; Carlin J.-F.; Feltin E.; Py M. A.; Grandjean N.. High Electron Mobility Lattice-Matched Alinn/Gan Field-Effect Transistor Heterostructures. Appl. Phys. Lett. 2006, 89, -. [Google Scholar]
- Yu Y.; Li C.; Liu Y.; Su L.; Zhang Y.; Cao L.. Controlled Scalable Synthesis of Uniform, High-Quality Monolayer and Few-Layer MoS2 Films. Sci. Rep. 2013, 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Zhang Y.; Ji Q.; Ju J.; Yuan H.; Shi J.; Gao T.; Ma D.; Liu M.; Chen Y.; et al. Controlled Growth of High-Quality Monolayer WS2 Layers on Sapphire and Imaging Its Grain Boundary. ACS Nano 2013, 7, 8963–8971. [DOI] [PubMed] [Google Scholar]
- Yoshimoto M.; Maeda T.; Ohnishi T.; Koinuma H.; Ishiyama O.; Shinohara M.; Kubo M.; Miura R.; Miyamoto A. Atomic-Scale Formation of Ultrasmooth Surfaces on Sapphire Substrates for High-Quality Thin-Film Fabrication. Appl. Phys. Lett. 1995, 67, 2615–2617. [Google Scholar]
- Curiotto S.; Chatain D. Surface Morphology and Composition of C-, a- and M-Sapphire Surfaces in O2 and H2 Environments. Surf. Sci. 2009, 603, 2688–2697. [Google Scholar]
- Lauritsen J. V.; Kibsgaard J.; Helveg S.; Topsoe H.; Clausen B. S.; Laegsgaard E.; Besenbacher F. Size-Dependent Structure of MoS2 Nanocrystals. Nat. Nanotechnol. 2007, 2, 53–58. [DOI] [PubMed] [Google Scholar]
- Brivio J.; Alexander D. T. L.; Kis A. Ripples and Layers in Ultrathin MoS2 Membranes. Nano Lett. 2011, 11, 5148–5153. [DOI] [PubMed] [Google Scholar]
- Chakraborty B.; Bera A.; Muthu D. V. S.; Bhowmick S.; Waghmare U. V.; Sood A. K. Symmetry-Dependent Phonon Renormalization in Monolayer MoS2 Transistor. Phys. Rev. B 2012, 85, 161403. [Google Scholar]
- Islam M. R.; Kang N.; Bhanu U.; Paudel H. P.; Erementchouk M.; Tetard L.; Leuenberger M. N.; Khondaker S. I. Tuning the Electrical Property via Defect Engineering of Single Layer MoS2 by Oxygen Plasma. Nanoscale 2014, 6, 10033–10039. [DOI] [PubMed] [Google Scholar]
- Plechinger G.; Mann J.; Preciado E.; Barroso D.; Nguyen A.; Eroms J.; Schüller C.; Bartels L.; Korn T. A Direct Comparison of CVD-Grown and Exfoliated MoS2 Using Optical Spectroscopy. Semicond. Sci. Technol. 2014, 29, 064008. [Google Scholar]
- Klots A. R.; Newaz A. K. M.; Wang B.; Prasai D.; Krzyzanowska H.; Caudel D.; Ghimire N. J.; Yan J.; Ivanov B. L.; Velizhanin K. A.; et al. Probing Excitonic States in Ultraclean Suspended Two-Dimensional Semiconductors by Photocurrent Spectroscopy. [DOI] [PMC free article] [PubMed]; arXiv:1403.6455.
- Britnell L.; Ribeiro R. M.; Eckmann A.; Jalil R.; Belle B. D.; Mishchenko A.; Kim Y.-J.; Gorbachev R. V.; Georgiou T.; Morozov S. V.; et al. Strong Light-Matter Interactions in Heterostructures of Atomically Thin Films. Science 2013, 340, 1311–1314. [DOI] [PubMed] [Google Scholar]
- Geim A. K.; Grigorieva I. V. Van Der Waals Heterostructures. Nature 2013, 499, 419–425. [DOI] [PubMed] [Google Scholar]
- Schmidt H.; Wang S.; Chu L.; Toh M.; Kumar R.; Zhao W.; Castro Neto A. H.; Martin J.; Adam S.; Özyilmaz B.; et al. Transport Properties of Monolayer MoS2 Grown by Chemical Vapor Deposition. Nano Lett. 2014, 14, 1909–1913. [DOI] [PubMed] [Google Scholar]
- Radisavljevic B.; Kis A. Mobility Engineering and a Metal-Insulator Transition in Monolayer MoS2. Nat. Mater. 2013, 12, 815–820. [DOI] [PubMed] [Google Scholar]
- Baugher B.; Churchill H. O. H.; Yang Y.; Jarillo-Herrero P. Intrinsic Electronic Transport Properties of High Quality Monolayer and Bilayer MoS2. Nano Lett. 2013, 13, 4212–4216. [DOI] [PubMed] [Google Scholar]
- Nonnenmacher M.; Oboyle M. P.; Wickramasinghe H. K. Kelvin Probe Force Microscopy. Appl. Phys. Lett. 1991, 58, 2921–2923. [Google Scholar]
- Paolo G.; Stefano B.; Nicola B.; Matteo C.; Roberto C.; Carlo C.; Davide C.; Guido L. C.; Matteo C.; Ismaila D.; etal. Quantum Espresso: A Modular and Open-Source Software Project for Quantum Simulations of Materials. J. Phys.: Condens. Matter 2009, 21, 395502. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Sabatini R.; Gorni T.; de Gironcoli S. Nonlocal Van Der Waals Density Functional Made Simple and Efficient. Phys. Rev. B 2013, 87, 041108. [Google Scholar]
- Vydrov O. A.; Van Voorhis T. Nonlocal Van Der Waals Density Functional: The Simpler the Better. J. Chem. Phys. 2010, 133, 244103. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [DOI] [PubMed] [Google Scholar]
- Murray É. D.; Lee K.; Langreth D. C. Investigation of Exchange Energy Density Functional Accuracy for Interacting Molecules. J. Chem. Theory Comput. 2009, 5, 2754–2762. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Yue W. Accurate and Simple Density Functional for the Electronic Exchange Energy: Generalized Gradient Approximation. Phys. Rev. B 1986, 33, 8800–8802. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [DOI] [PubMed] [Google Scholar]
- Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [DOI] [PubMed] [Google Scholar]
- Dion M.; Rydberg H.; Schröder E.; Langreth D. C.; Lundqvist B. I. Van Der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [DOI] [PubMed] [Google Scholar]
- Klimeš J.; Bowler D. R.; Michaelides A. Chemical Accuracy for the Van Der Waals Density Functional. J. Phys.: Condens. Matter 2010, 22, 022201. [DOI] [PubMed] [Google Scholar]
- Klimeš J.; Bowler D. R.; Michaelides A. Van Der Waals Density Functionals Applied to Solids. Phys. Rev. B 2011, 83, 195131. [Google Scholar]
- Mittendorfer F.; Garhofer A.; Redinger J.; Klimeš J.; Harl J.; Kresse G. Graphene on Ni(111): Strong Interaction and Weak Adsorption. Phys. Rev. B 2011, 84, 201401. [Google Scholar]
- Neugebauer J.; Scheffler M. Adsorbate-Substrate and Adsorbate-Adsorbate Interactions of Na and K Adlayers on Al(111). Phys. Rev. B 1992, 46, 16067–16080. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.