Are There Long-Run Effects of the Minimum Wage?

Abstract

An empirical consensus suggests that there are small employment effects of minimum wage increases. This paper argues that these are short-run elasticities. Long-run elasticities, which may differ from short-run elasticities, are policy relevant. This paper develops a dynamic industry equilibrium model of labor demand. The model makes two points. First, long-run regressions have been misinterpreted because even if the short- and long-run employment elasticities differ, standard methods would not detect a difference using US variation. Second, the model offers a reconciliation of the small estimated short-run employment effects with the commonly found pass-through of minimum wage increases to product prices.

Inflation and rising real wages make most minimum wage increases temporary.¹ As such, the empirical minimum wage literature has made substantial progress estimating the short-run employment effects of minimum wage increases. This effect appears to be small.² Despite apparent consensus, the profession remains divided about the employment effects of minimum wage increases.³

A reasonable reading of this divide is that there are some questions about the effects of minimum wage increases for which the empirical consensus provides the answer. For other questions, however, economists extrapolate differently depending on whether they think that the relevant short- and long-run employment elasticities differ.⁴ To the question: “what is the employment effect of a temporary nominal minimum wage increase likely to be?”, the empirical consensus suggests that there are unlikely to be significant employment effects because similar increases have not resulted in significant employment effects. To the question: “what is the employment effect—after a few years—of a permanent minimum wage increase?,” the empirical consensus suggests an answer only if the short- and long-run elasticities of minimum wage increases are the same. In the United States, this latter question is of immediate policy relevance: President Obama’s 2013 State of the Union address contained a proposal to index the Federal minimum wage to inflation, which would be a more permanent increase.

To contribute to this important debate, this paper studies the empirical implications of a model that has a distinction between the short- and long-run employment elasticities. The model is based on the putty-clay nature of capital. It was first informally discussed in the minimum wage context by Card & Krueger (1995, pg. 366–8) and I build on the Gourio (2011) version.⁵ In the model, when firms pay the entry cost of building a machine, they can freely substitute between capital and labor. Once capital is installed, a firm cannot change its labor demand. The key features of the model are that the labor demand choice of an entering firm is a forward-looking, dynamic, decision that depends on the (expected) stochastic process for minimum wages. And because only some firms adjust each period, the industry-level labor demand response to a minimum wage increase is slow, and also depends on the stochastic process for minimum wages.

The model has two main empirical implications. The first empirical implication is that the reduced-form long-run effects estimated in the literature are essentially uninformative about the true long-run elasticity. I simulate employment data from the model to replicate the dataset used in Dube et al. (2010).⁶ They find very small short-run employment effects and, using a common reduced-form long-run regression, no distinction between the short- and long-run employment effects of minimum wages in the United States. They interpret these results as evidence against the view that short- and long-run elasticities differ.⁷ On the simulated data, however, the reduced-form regression recovers a long-run employment effect that is barely different than the short-run employment effect.⁸

The second empirical implication is that the putty-clay model is consistent with the pass-through of minimum wage increases to product prices commonly found in the literature, even though minimum wage increases are relatively temporary. Card & Krueger (1994, pg. 792) emphasize that their finding of product price rises in response to minimum wage increases are inconsistent “with models in which employers face supply constraints (e.g., monopsony or equilibrium search models).” Despite this, the minimum wage literature has focused on models of search frictions to rationalize the small employment effects, without focusing on the price results.⁹

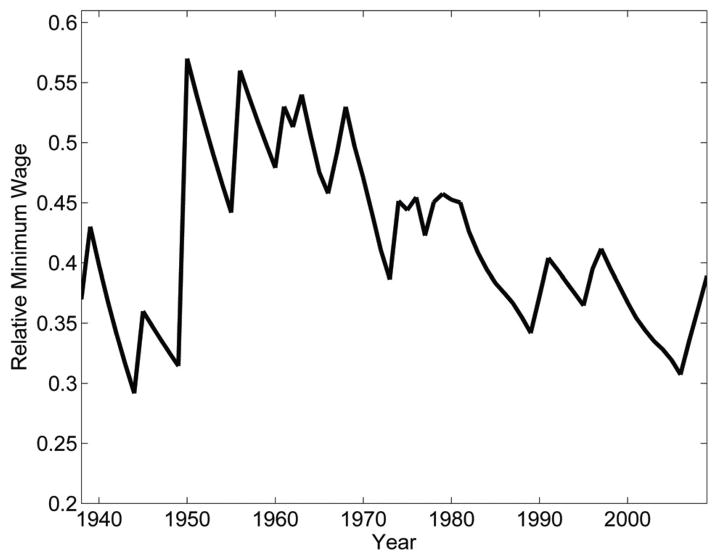
Figure 1 suggests why the stochastic process apparently generating US Federal minimum wage variation is unpromising for finding long-run effects: the variation in the real value of the Federal minimum wage follows a “sawtooth” pattern of regular nominal increases that are temporary because they are eroded by inflation and rising real wages. Meer & West (2013, pg. 10) provide evidence that state-level variation is similar.¹⁰ As such, other countries might present promising opportunities for finding long-run effects. Unfortunately, the literature suggests that such opportunities are few and far between (or difficult to exploit). For example, in Dolado et al. (1996)’s comprehensive survey of minimum wages in Europe, they do not distinguish between short- and long-run responses. Pereira (2003) studies an interesting coverage change in Portugal, and finds slightly larger effects at a two year horizon than a one year horizon, but does not study longer-run effects. And Lemos (2007) emphasizes that in Brazil minimum wage increases are similarly temporary due to high inflation. The main exception—also emphasized by Neumark & Wascher (2008)—is Baker et al. (1999). They find larger long-run effects of minimum wage increases in Canada than in the US and suggest that this is due to the variation in the US being less permanent than that in Canada.¹¹ Their long-run elasticity is around −0.6, which is similar to the long-run elasticity in my model.

Figure 1.

Federal minimum wage relative to average hourly earnings in the private sector

Source: Brown (1999) table 1 updated with the Bureau of Labor Statistics for the nominal federal minimum wage (http://www.dol.gov/whd/minwage/chart.htm), and then deflated using the Current Employment Statistics for average hourly wage in the private sector among production and non-supervisory employees (historical hours and earnings, table B-2). This figure uses annual data and plots the largest minimum wage in each year.

My paper complements the work in Baker et al. (1999) by developing an economic model which formalizes when the nature of the variation might matter, develops conditions under which the common reduced-form approach to estimating long-run effects is valid, and shows via simulation how quantitatively important the temporariness of the variation might be in masking the long-run effect of minimum wage increases.¹²

This paper proceeds as follows. Section 1 discusses evidence on adjustment costs, and other mechanisms in the model. Section 2 develops the putty-clay model of labor demand. Section 3 analyzes the implications of the model for the interpretation of empirical work. Section 4 discusses the calibration and Section 5 develops stylized simulations of the model. Section 6 shows that given US variation in minimum wages, the estimated short- and long-run employment effects on data simulated from the model do not differ. Section 7 concludes.

1. Model assumptions

1.1. Adjustment costs on labor

There is a difference between the short- and long-run elasticities if there are adjustment costs for labor. There is a tradition in the minimum wage literature of arguing that high turnover among workers in minimum wage industries means that adjustment costs are likely small.¹³ High turnover, however, is evidence against adjustment costs for changing the identity of workers rather than for changing the number of jobs.¹⁴

There is substantial evidence that establishments incur significant and lumpy costs to adjust the number of jobs. Hamermesh (1989) documents that establishments adjust their number of jobs infrequently, while Hamermesh et al. (1996) documents that even without adjusting the number of jobs the identity of workers changes. These findings have been confirmed and amplified in other data.¹⁵ Under the assumption that the underlying shock process is relatively smooth, the infrequency of adjustment of the number of jobs points to the importance of lumpy or fixed adjustment costs at the level of the job. Similarly, empirical models of establishment level employment dynamics study lumpy adjustment costs on the number of jobs (e.g. Cooper & Willis (2009)). Finally, companies think about labor demand in terms of jobs. Lazear (1995, pg. 77) (quoted in Campbell & Fisher (2000)) writes: “Human resource managers think in terms of slots or jobs, and think of these slots or jobs as being fundamental to the organization of the firm.”

1.2. Entry and exit

The price dynamics in the model derive from the empirical feature of the product market that there is always entry and exit of firms. Aggregate statistics suggest that there is always entry and exit. For example, 9% of fast food restaurants that existed in March 2009 exited by March 2010.¹⁶ And there is evidence, for example Campbell & Lapham (2004), that entry and exit among restaurants is responsive to economic shocks.

1.3. Capital heterogeneity

The model formalizes the following idea. If adopting new machines is the way that firms substitute between capital and labor, then such substitution is unlikely to be caused by minimum wage increases when these increases are (perceived as) sufficiently temporary. Sufficiently temporary increases have little impact on the relative price of capital and labor over the life of the capital. On the other hand, if the change in labor costs is permanent, or the differences in labor costs across locations is permanent, then these technologies will be adopted, or adopted more quickly.

A few examples highlight the idea that labor demand is embodied in the firm’s choice of capital.¹⁷ McDonald’s in Europe plans on replacing many of its cashiers and their registers with touchscreen terminals so that customers do not interact with cashiers.¹⁸ To do so it needs to purchase new registers that embody the labor-saving capital. Similarly, in the grocery store industry, self-checkout scanners represent a labor-saving technology that requires a new capital stock. And self-service gas stations required new gas pumps.

A similar kind of evidence comes from Seltzer (1997). He studies the seamless hosiery—sock—industry in the US in the 1930s, which was hit by the implementation of Federal minimum wages. The fundamental technological choice facing the seamless hosiery industry was whether to use machines where the top of the stocking was knit on a different machine than the stocking itself, or machines where the top was knit on the same machine as the stocking. The most labor-intensive process used the hand-transfer machine, where the top of the stocking was knit on a separate machine and then carried by hand to the knitting machine. What is striking in Seltzer (1997)’s data is that while the lower-wage plants adjusted their capital stock towards the labor-saving technology, the speed of adjustment was relatively slow: two years after the change in relative labor costs, the use of the most labor-intensive machines declined by less than a quarter. Similarly, Lewis (2011) shows how an influx of low-skilled immigrants slowed the adoption of more technologically intensive (labor-saving) capital stocks.

These examples are in line with the model because two choices of $\frac{K}{L}$ require different machines, rather than being able to vary $\frac{K}{L}$ while using the same machines. Over the long-term, these new kinds of capital are adopted because their price relative to labor falls. Minimum wages also affect the relative price of capital and labor. In the examples, the change in the relative price of capital and labor is permanent and so the substitution occurs. The idea of the model is that the change in the relative price of capital and labor induced by a minimum wage increase is temporary and so the substitution is unlikely to occur.

2. The putty-clay model

This section develops a dynamic labor demand model in industry equilibrium (e.g. Hopenhayn (1992)). The model has three features that make it well-suited to study minimum wages. First, it models industry-level variables such as prices. Industry equilibrium means that employment is industry-wide employment as in Dube et al. (2010), rather than employment within a continuing set of firms as in Card & Krueger (1994). Second, it explicitly parameterizes the transition path between the short- and long-run elasticities. Third, the model is sufficiently tractable that it is possible to derive analytic results both about steady state to steady state comparative statics, as well as about the response of the model to temporary shocks. Because minimum wage increases are mostly temporary, the data are dominated by temporary shocks, so understanding these is essential.

The model is based on the putty-clay model in Gourio (2011), which he uses to study asset pricing. Putty-clay technology is putty and flexible when firms make their investment decisions. After installation, the capital hardens to clay and firms can no longer adjust the labor needs of the capital. Only a small share of firms have their capital stock expire each period, so market-level labor demand takes time to adjust to a wage increase.

The model has an alternate interpretation as a time-dependent adjustment cost model. The Poisson machine expiration process is a stand-in for the endogenous decision of firms to pay an adjustment cost to change their labor demand. Section 2.1.2 discusses why this is not a (particularly) restrictive assumption.

2.1. The model

Since this paper is concerned with minimum wages, wages are set exogenous to the industry. Firms in the industry face a sequence of expected wages given by $E_t[{(w_{t+j})}_{j=0}^{\infty }]$, where time is discrete. Minimum wages are always binding. The uncertainty in the wage path reflects only uncertainty about minimum wage policy. The labor market is frictionless and there is an infinite supply of labor at each minimum wage.

The model is closed with a downward-sloping product demand curve and an entry condition. The entry condition is that the expected profits of newly entering firms (or machines) are always zero, though of course firms have to pay an entry fee by building machines. Firm entry and exit drives the product price responses.

2.1.1. Production technology

The continuum of firms produce from a Cobb-Douglas production function, y = k^αl^1−α, where k is the amount of capital in the machine, and l is the amount of labor. Ex-post, production is Leontief so that k and l are chosen when the machine is built, and are then fixed for the life of the machine.¹⁹ Because of constant returns to scale, normalize to one worker per machine. Setting l = 1, y = k^α, where k is the size of the machine (the capital intensity of production). Machines fail with probability δ ∈ (0, 1) each time period.

2.1.2. Firm maximization

A firm’s entry cost is the cost of building a machine. When a firm builds a machine at time t, it chooses the capital intensity of a machine and then is stuck with that choice for the life of the machine. The capital choice takes into account the present discounted value of product prices and wage, where the discount rate is the combination of failure probability of the machine and the market discount rate, β. The price of a unit of capital is normalized to 1.

Let

$$q_t\equiv E_t\sum _{j=0}^{\infty }{\beta }^j{(1-\delta )}^j{P}_{t+j}$$ (1)

be the expected effective present discounted value of product prices (P_t) and let

$$q_{w,t}\equiv E_t\sum _{j=0}^{\infty }{\beta }^j{(1-\delta )}^j{w}_{t+j}$$ (2)

be the expected effective present discounted value of wages. These quantities are referred to as present discounted values of product prices and wages. The relative prices that the firm faces reflect time-varying prices and wages, but capital intensity is fixed and the capital cost is paid once.

A firm chooses k_t to maximize

$${\mathrm{\Pi }}_t=q_t{k}_t^{\alpha }-q_{w,t}-k_t.$$ (3)

k_t is the capital choice of firms that enter in time t, while k is all active capital in the industry. Writing the maximization problem in terms of present discounted values of product prices and wages reflects a no-shutdown assumption. Once capital is in place, a firm’s shutdown decision treats capital costs as sunk. A firm that invested in period t′ operates in period t > t′ if $P_t{k}_{t^{\prime }}^{\alpha }-w_t\ge 0$. Following Gourio (2011) a machine, once installed, is always operated. This no-shutdown assumption never binds in the simulations below, which means that the Poisson adjustment is not too restrictive.²⁰

There is good economic reason for the no-shutdown assumption to never bind. In the model, the only shock facing firms is a minimum wage increase. Following a minimum wage increase, incumbent firms see their flow profits change for two reasons: wages rise and the product price rises. For local changes from steady state these two effects exactly cancel, which limits how quantitatively important endogenous exit would be in speeding up adjustment.²¹ For larger changes these effects do not exactly cancel and incumbents see their flow profits fall. That incumbents are (partially) protected by equilibrium responses is the “insulation effect” of Caballero & Hammour (1994).

2.1.3. Product price determination

Two features of the model together pin down the product price: a free entry condition and a product demand curve. The free entry condition does not mean that entry is free: firms need to construct their capital stock when they enter.

Denote gross entry (investment) by h_t, the number of machines built at time t. Free entry implies that

$$h_t{\mathrm{\Pi }}_t=0$$ (4)

for all t. If there is gross entry, then there are zero expected profits—net of the cost of constructing the capital stock—from entering. Following Gourio (2011), there is positive gross entry for all time t so that there are zero expected profits from entering (Π_t = 0∀t). As with the no-shutdown assumption, this assumption is never binding in the simulations.²²

The industry faces an isoelastic product demand curve

$$Q_t=\theta P_t^{-\gamma },$$ (5)

where Q is market quantity and P is the product price. This demand curve is consistent with the industry making up a small portion of the economy, and the exogenous product demand and factor prices are standard in models of industry equilibrium (e.g. Hopenhayn (1992)). It does rule out general equilibrium explanations for small employment effects of minimum wages such as the argument caricatured by Kennan (1995, pg. 1961) as “teenagers like cheeseburgers.”

2.1.4. Aggregation and laws of motion

Employment evolves as machines expire with probability δ each time period and the new investment is implemented. The law of motion for machines (and employment) is

$$N_t=(1-\delta )N_{t-1}+h_t.$$ (6)

Aggregate output is given by integrating over the distribution of the capital stock of all ages at time t, G_t (recall that k_t is the capital chosen by entering firms at time t and k represents all active capital in the industry):

$$Q_t={\int }_0^{\infty }{k}^{\alpha }{dG}_t(k).$$

Identical to employment, output evolves as machines expire and new investment is implemented:

$$Q_t=(1-\delta )Q_{t-1}+h_t{k}_t^{\alpha }.$$ (7)

2.1.5. Equilibrium

An equilibrium in the model is a sequence of endogenous variables ${\{k_t,h_t,P_t,Q_t,N_t\}}_{t=-\infty }^{+\infty }$ that takes the sequence of realized ${\{w_t\}}_{t=-\infty }^{+\infty }$ and expected, ${\{E_t[{(w_{t+j})}_{j=0}^{\infty }]\}}_{t=-\infty }^{+\infty }$, minimum wages as given such that in every time period:

• Firm’s choose k_t to maximize profits subject to their production technology (equation (3));

• The entry condition is satisfied (equation 4));

• The product market clears (equation (5)); and

• The laws of motion for employment and output hold (equations (6) and (7)).

A steady state equilibrium is an equilibrium in which the the sequence of realized and expected minimum wages are constant. The resulting endogenous variables are all constant as well.

2.1.6. Equilibrium computation

Equilibrium computation is straightforward when there is entry in every period and the no-shutdown assumption holds. The core of the model can be reduced to three equations in three unknowns:

• The firm’s first order condition of equation (3) implies one equation in three unknowns (q_w,t, k_t, q_t).

• The sequence of expectations of minimum wages provides a second equation through the sequences of present discounted value of minimum wages: q_w,t, q_w,t+1···

• The entry condition with entry (4) implies that the firm’s profit in equation (3) is equal to zero, providing the third equation.

The resulting capital intensity is:

$$k_t=\frac{\alpha }{1-\alpha }{q}_{w,t}.$$ (8)

A firm considers the present discounted value of future relative prices when making its investment decision, unlike in a static model where a firm only considers time t relative prices.

Solving for the expectation of next time period’s present discounted value of product prices is straightforward. The sequence of equilibrium present discounted value of product prices can be rewritten as the current product price:

$$P_t=q_t-\beta (1-\delta )E_t[q_{t+1}].$$ (9)

A minor complication arises in computing the equilibrium when there is uncertainty in the wage path because the present discounted value of prices, q_t, is a non-linear function of the present discounted value of wages, q_w,t.

2.2. Comparison to long-run elasticities

The putty-clay model is a dynamic version of the textbook static labor demand elasticities. In particular, the long-run (steady state) elasticities in the model match the long-run textbook results exactly.²³

Appendix A.1 derives expressions for the number of workers and the product price in steady state in the putty-clay model. Differentiating these expressions with respect to the present discounted value of wages gives the long-run elasticities for employment

$$\frac{\partial N}{\partial q_w}\frac{q_w}{N}=-\underset{\text{scale}}{\underbrace{\gamma (1-\alpha )}}-\underset{\text{substitution}}{\underbrace{\alpha }}$$ (10)

and for prices

$$\frac{\partial P}{\partial q_w}\frac{q_w}{P}=1-\alpha .$$ (11)

These elasticities are identical to the long-run textbook elasticities with respect to the wage and imply complete pass-through of the minimum wage increase to product prices. The employment effect operates through two channels. The scale effect measures the reduction in employment because of the contraction in the size of the product market from the product price increase. The substitution effect measures the reduction in employment because of substitution between capital and labor.

The difference between the putty-clay model and the textbook framework emerges in the short-run and in the transition to the long-run. In the textbook model, the capital-labor ratio can adjust for all firms in the short-run, while in the putty-clay model only some firms adjust the capital-labor ratio. In the textbook model, no firms can acquire capital in the short-run, while in the putty-clay model all firms have the option of doing so. Unlike the textbook model, the putty-clay model explicitly parameterizes the transition from the short- to long-run. As the rate of capital expiration, δ, increases the long-run arrives more quickly.

3. Interpreting empirical work in light of the model

This section analytically shows how employment and product prices move in response to temporary and permanent minimum wage increases. Surprisingly, product prices move even in response to temporary minimum wage increases.

In this section, a temporary minimum wage increase is an increase that lasts for a single time period. This is a stylized way of capturing what happens if the minimum wage is increased in nominal terms and then eroded by inflation. Section 5 numerically studies environments where temporary minimum wage increases are more persistent than one period and where real minimum wages follow a sawtooth pattern. The perfect foresight assumption implicit in this section is relaxed in section 6.

3.1. Short-run employment response to temporary increase is through the change in output

The minimum wage literature has focused on estimating short-run employment response to minimum wage increases. Card & Krueger (1994) look at a 9 month window around a minimum wage increase, while in the panel data literature, e.g. Neumark & Wascher (1992) and Dube et al. (2010) the focus is on the response within a quarter. These estimates are interpreted as testing “[t]he prediction from conventional economic theory” (Card & Krueger (1994, pg. 772)) about the employment effects of minimum wage increases. In the model, these very short-run employment responses capture the part of the employment response that operates through the change in output (the scale effect), and very little of the substitution of labor for capital (the substitution effect). This second effect is quantitatively much larger in my simulations.

The following result shows how these two effects are reflected in the contemporaneous employment response to a temporary minimum wage increase. The proof of this and all other results are in Appendix A.3.

Result 1

The elasticity of contemporaneous employment with respect to a temporary minimum wage hike from steady state is:

$$\frac{\partial N_t}{\partial w_t}\frac{w_t}{N_t}=-\underset{\mathit{scale}}{\underbrace{\gamma (1-\alpha )}}-\underset{\mathit{substitution}}{\underbrace{\alpha \delta (1-\beta (1-\beta ))}}.$$

The first term shows that the full scale effect occurs contemporaneously, which follows from the result in a subsequent subsection that prices move with wages. Unlike the scale effect, the substitution effect is dramatically attenuated relative to the long-run benchmark of α displayed in Equation (10). The attenuation occurs because each period only δ share of firms adjust and because the capital decision is forward-looking and the increase is temporary, the firms that adjust engage in very little capital-labor substitution. This second form of attenuation is captured by the 1 − β(1 − δ) term, which can be very small.

3.2. Long-run observed employment response depends on how permanent the increase is

While the literature has focused on the short-run employment response, as a robustness exercise some papers include lags of the minimum wage to capture any potential long-run effects (e.g. Neumark & Wascher (1992, Table 5), Baker et al. (1999, Table 7) and Dube et al. (2010, Equation 7)). That the coefficients on these lags are often quite small is interpreted as evidence that the long-run employment effects of a minimum wage increase are the same as the short-run employment effects (Dube, Lester & Reich (2010, pg. 956)).²⁴

Table 5.

Distributed lag specification: varying δ

δ	Contemporaneous	Long-run
0.08	−0.051	−0.094
0.16	−0.050	−0.089
0.33	−0.062	−0.159
0.50	−0.084	−0.238

Note: This table reports the contemporaneous (quarter 0) and long-run elasticities (24 quarters) of using the preferred Dube et al. (2010) specification to estimate the employment effects of minimum wages. I estimate equation (15) having simulated the model as described in section 6.3.

Formally, the standard robustness exercise builds on the following distributed lag form:

$$ln{N}_{i,t}={\alpha }_i+{\alpha }_t+{\beta }_{0}ln{w}_{i,t}+\sum _{j=1}^J{\beta }_{j}ln{w}_{i,t-1}+{\epsilon }_{i,t},$$ (12)

where N is employment in location i at time t, w_i,t is the measure of minimum wages at location i at time t and w_i,t−j is lags of the minimum wage. The model provides a “structural” interpretation of this robustness exercise. Equation (A19) shows that employment in time t is a function of past, current and expected minimum wages and parameters of the model. A first-order expansion of equation (A19) with respect to a minimum wage increase in a given time period provides a justification for estimating equation (12) since it contains employment on the left hand side and functions of the minimum wage and parameters of the model on the right hand side.

When is the structural interpretation warranted? When there is a distinction between the short- and long-run elasticities (δ ≠ 1), two conditions jointly imply that the coefficients of the regression in equation (12) are structural parameters and do not depend on the nature of minimum wage variation. First, the minimum wage increase is one-time and permanent and is perceived as permanent. Second, employment was initially in steady state. The following result provides the explicit time-path that such a regression would return.

Result 2

If q_w,j = E_j[q_w,j+1] = q_w ∀j ≤ t and the change in wages at time t is unexpected and permanent (and perceived as such), then

$${\beta }_0=\frac{\partial N_t}{\partial q_{w,t}}\frac{q_{w,t}}{N_t}=-\gamma (1-\alpha )-\delta \alpha$$ (13)

$${\beta }_j=\frac{\partial N_{t+j}}{\partial q_{w,t}}\frac{q_{w,t}}{N_{t+j}}=-{(1-\delta )}^j\delta \alpha ,\forall j>0.$$ (14)

Moreover, ${\sum }_{j=0}^{\infty }\frac{\partial N_{t+j}}{\partial q_{w,t}}\frac{q_{w,t}}{N_{t+j}}=-\gamma (1-\alpha )-\alpha$, which is the elasticity given in (10).²⁵

The temporary nature of the mininum wage hike mutes the observed long-run effects of the minimum wage hike for two reasons. First, the contemporaneous response is smaller when firms expect the hike to be temporary because the extent of firms’ adjustment depends on the increase in the expected present discounted value of wages. Formally, $\frac{\partial q_{w,t}}{\partial w_t}\frac{w_t}{q_{w,t}}<1$. Second, the subsequent adjustments are made to smaller and smaller minimum wage increases. Formally, $\frac{\partial q_{w,t+j}}{\partial q_{w,t}}\frac{q_{w,t}}{q_{w,t+j}}<1$. Hence, if the short- and long-run elasticities to permanent minimum wage hikes differ, then both the short- and long-run reduced-form estimates would be biased down relative to the structure for temporary minimum wage hikes.

Being out of steady state can also induce bias. The bias is ambiguous in sign. If the capital stock was on average installed when the minimum wage was expected to be higher than it is after the increase, then employment can actually rise following a minimum wage increase. Conversely, the employment decline can be larger if the capital stock was installed when the minimum wage was expected to be lower than it is after the increase.

3.3. Short- and long-run observed price response: Product prices move with the wage

While much of the minimum wage literature since Card & Krueger (1994) has focused on their employment results, they also document some evidence of an increase in the product price following minimum wage increases. Subsequent work by Aaronson (2001) and Aaronson et al. (2008) has extended and confirmed this finding. Card & Krueger (1994), Aaronson & French (2007) and Aaronson et al. (2008) emphasize that these price increases are consistent with full pass-through of the minimum wage increase to product prices and inconsistent with employment increases. In most models, if prices go up then output falls so inputs, including labor, have fallen.

The putty-clay model is consistent with full pass-through of the minimum wage increase to product prices in the short-run because there is always entry (and exit). With entry, the market price is set by the marginal entrant and so it is responsive to changes in market conditions. Consider an increase in minimum wages that is known to last only one quarter. To see what has to happen to prices in the quarter of the increase, let us examine what happens after the minimum wage has fallen again. In quarters after the minimum wage has fallen, new entrants face the same expected costs as before the increase. So free entry implies that the product price immediately returns to its pre-increase level. Now let us return to the quarter of the increase. Potential entrants in the quarter of the minimum wage increase face higher costs that quarter, but know that prices will fall immediately. To compensate entrants in the quarter of the minimum wage increase, there must be complete pass-through of the minimum wage increase to the product price. There is an additional channel that generates more than complete pass-through. If entrants adjust their input mix so that it is suboptimal in later periods, then to compensate firms for this distortion the contemporaneous product price response is larger following a temporary minimum wage increase than a permanent increase.

The following result shows that the contemporaneous price response to a temporary minimum wage increase is very similar to the response to a permanent increase documented in Equation (11). When firms are “myopic” and assume that the current wage lasts forever, they do not need to be compensated for having a suboptimal input mix in later periods. In this case, the contemporaneous response is the same to temporary and permanent increases.

Result 3

Under perfect foresight, the elasticity of the product price with respect to the contemporaneous wage is:

$$\frac{\partial P_t}{\partial w_t}\frac{w_t}{P_t}=\underset{\mathit{long}-\mathit{run}}{\underbrace{(1-\alpha )}}\underset{\mathit{adjustment}\mathit{term}}{\underbrace{\frac{w_t}{{\stackrel{\sim }{w}}_t}\frac{1-\beta (1-\delta )}{1-\beta (1-\delta ){\left(\frac{{\stackrel{\sim }{\omega }}_{t+1}}{{\stackrel{\sim }{\omega }}_t}\right)}^{1-\alpha }}}}$$

where w̃_t = (1 − β(1 − δ))q_w,t is the flow equivalent of period t’s present discounted value of wages and w̃_t+1 = (1 − β(1 − δ))q_w,t+1 is the flow equivalent of period t + 1’s present discounted value of wage.

Under myopic expectations (β = 0):

$$\frac{\partial P_t}{\partial w_t}\frac{w_t}{P_t}=1-\alpha .$$

The additional increase in the product price from a temporary increase due to a suboptimal input mix can be seen by considering the two components of the adjustment term separately. Consider first the $\frac{w_t}{{\stackrel{\sim }{w}}_t}$ term. This term is the ratio of the contemporaneous wage to the flow equivalent of wages. If wages fall over time, then the contemporaneous wage is bigger than the flow equivalent. Consider second the $\frac{1-\beta (1-\delta )}{1-\beta (1-\delta ){\left(\frac{{\stackrel{\sim }{w}}_{t+1}}{{\stackrel{\sim }{w}}_t}\right)}^{1-\alpha }}$ term. Its magnitude relative to one depends on whether $\frac{{\stackrel{\sim }{w}}_{t+1}}{{\stackrel{\sim }{w}}_t}$ is bigger or less than one. If wages do not fall too rapidly, then this term will be close to one. Hence, the $\frac{w_t}{{\stackrel{\sim }{w}}_t}$ term will dominate and the adjustment term can be greater than one.

4. Parameter values

Much empirical work in the minimum wage literature, including Dube et al. (2010), has focused on the restaurant industry. Hence, I calibrate the model to the restaurant industry. Table 1 displays the parameter values.

Table 4.

Employment response to minimum wage increases: varying δ

	δ = 0.08	δ = 0.16	δ = 0.33	δ = 0.5
Year	A. Permanent increase
0	−0.062	−0.073	−0.099	−0.130
1	−0.100	−0.148	−0.246	−0.338
2	−0.136	−0.212	−0.345	−0.442
3	−0.169	−0.265	−0.411	−0.494
4	−0.199	−0.310	−0.456	−0.520
5	−0.227	−0.348	−0.485	−0.533
6	−0.252	−0.379	−0.505	−0.539
∞	−0.546	−0.546	−0.546	−0.546
	B. Temporary increase
0	−0.059	−0.065	−0.087	−0.117
1	−0.063	−0.090	−0.168	−0.256
2	−0.061	−0.100	−0.197	−0.284
3	−0.057	−0.099	−0.191	−0.257
4	−0.049	−0.089	−0.164	−0.203
5	−0.040	−0.075	−0.125	−0.139
6	−0.029	−0.057	−0.084	−0.077
	C. Sawtooth increase
0	−0.056	−0.057	−0.066	−0.081
1	−0.049	−0.055	−0.082	−0.125
2	−0.040	−0.046	−0.071	−0.107
3	−0.030	−0.033	−0.044	−0.061
4	−0.020	−0.019	−0.013	−0.007
5	−0.010	−0.006	+0.012	+0.037
6	−0.002	+0.002	+0.018	+0.044
Policy elast.	−0.584	−0.584	−0.583	−0.580

Note: see footnotes to table 2.

A key parameter is the share of minimum wage workers in firms’ expenses, which is set to 0.1. This number is arrived at as follows. Aaronson & French (2007) report that the labor share is 0.3 and the minimum wage worker share in the wage bill is 0.17. They report that about one-third of workers are minimum wage workers, but about two-thirds of workers are low-skill. They attribute the fact that not all low-skill workers are paid the minimum wage to wage dispersion across labor markets, rather than to skill dispersion among low-skill labor workers (pg. 181). Since in the model the minimum wage is binding in all labor markets (and Dube et al. (2010) treat all labor markets identically), I assume that all low-skill workers earn the minimum wage. Hence, low-skill workers account for 0.3 × 0.17 × 2 ≈ 0.1 share of firms’ expenses.

The choice of capital pins down materials use as well as high and low-skill labor use. As a result, materials and high-skill labor adjusts with the capital stock and so they can be combined. This assumption means the short-run substitutability between minimum wage labor and intermediate inputs and high-skill labor is zero, which is the same as that between minimum wage labor and capital.²⁶ Aaronson & French (2007) report a land, structure and machines share of 0.3, material share of 0.4 and my calculations above leave high-skill workers with a share of 0.2. Hence, α, the non-minimum-wage-worker share of inputs, is 0.9. The long-run price elasticity in the model is thus 1 − α = 0.1, and Aaronson (2001) finds a price elasticity of 0.07. Setting α = 0.9 represents a low estimate of the importance of the non-minimum wage worker inputs.

I report elasticities of the combination of high-skill and low-skill employment, not just employment of workers subject to the minimum wage. This choice aligns with Dube et al. (2010) who use total employment in the restaurant industry as their measure of employment. It is also similar to other studies of minimum wages where researchers have not been able to directly identify minimum wage workers (see for example the discussion of studies of teenagers in Brown (1999, pg. 2114)). Letting a bar over a variable represent steady state, define employment in time t, $E_t=N_t+n_h\frac{\overline{N}}{\overline{K}}{K}_t$, where K_t is the aggregate capital stock and n_h is a constant. The quantity $n_h\frac{\overline{N}}{\overline{K}}{K}_t$ represents high-skill employment, which moves with the capital stock. Set $n_h=\frac{1}{2}$ so that in steady state low-skill employment, N_t, is two-thirds of total employment. Set the price elasticity of demand for output to γ = 0.6, which is within the range reported by Aaronson & French. Set the market discount rate, β, to ${(0.95)}^{\frac{1}{4}}\approx 0.987$ on a quarterly basis, which is standard.

The final parameter is the machine expiration rate, δ. Unfortunately, there is not detailed evidence as to the value of δ in the restaurant industry, though the main result turns out not to be particularly sensitive to δ. Since I build on his model, I use the value in Gourio (2011), 0.08 on an annual basis (0.0206 on a quarterly basis), which he chooses as a high estimate of capital depreciation rates. Two alternative approaches yield similar values of δ. First, δ could be thought of as the exit probability of a fast food restaurant. In 2009–2010, this rate was 0.09.²⁷ Second, δ could be thought of as the rate at which existing fast food restaurants are remodeled. Some anecdotal evidence on this point comes from McDonald’s. As of 2003, many McDonald’s restaurants looked “as they did during the Reagan administration.” And a plan launched in 2003 to renovate all McDonald’s had resulted in only half being renovated by 2010.²⁸ The first anecdote suggests that McDonald’s are updated less frequently than once every 15 years (or δ smaller than 0.08), while the second suggests a half-life of 6 years (or δ of about 0.08). In section 6.7 I show that the main result of this paper is quite robust to varying δ, even to using δ = 0.33 as suggested in Card & Krueger (1995).

5. Quantitative implications of the model with stylized minimum wage variation

To illustrate the quantitative implications of the calibrated version of model, I perform three minimum wage experiments. The first experiment considers a one-time and permanent increase. This experiment corresponds to the ceteris paribus condition implicit in interpreting reduced-form long-run regression coefficients as long-run elasticities. The second experiment considers a one-time increase that is eroded by inflation. This experiment shows how the observed long-run response differs dramatically depending on the nature of the variation. The third experiment considers a stylized version of the sawtooth pattern that characterizes US data of repeated temporary increases. This experiment shows how sawtooth variation is expected to affect estimates.

This section and the next section reports reduced-form elasticities of employment with respect to the magnitude of the minimum wage hike. This practice is in keeping with the convention in the empirical literature. One point that this paper makes is that these elasticities are not structural objects, and in fact depend on the nature of the policy change.

To starkly display the quantitative implications of the model, in this section firms have perfect foresight about the minimum wage process. In section 6, firms expect that minimum wages follow a stochastic process

5.1. One-time changes

I report results of a one-time and permanent 15% increase in the minimum wage from steady state that is permanent, and such an increase that is eroded by 2.2% annual inflation and so is temporary. Consistent with the industry being small relative to the economy, the product price does not feed back into the inflation rate. Appendix B describes the simulation algorithm.

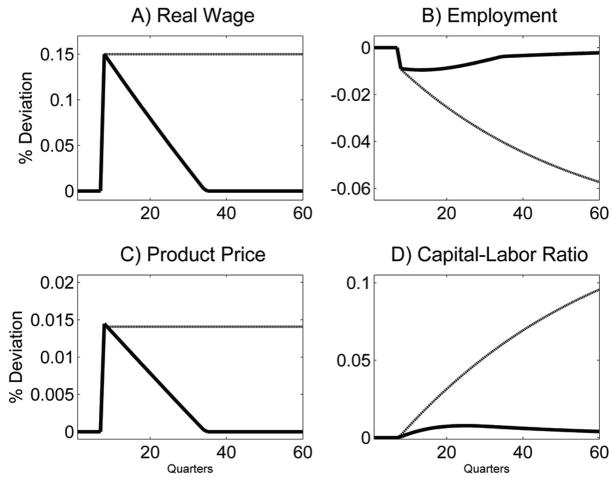
Figure 2 displays the response of employment, product prices and the aggregate capital-labor ratio to the permanent and temporary minimum wage increase. The product price moves with the minimum wage, while the capital-labor ratio and employment are slower moving variables.

Figure 2.

Impulse responses to temporary and permanent minimum wage increases

Note: based on simulations of the putty-clay model using the parameterization in Table 1. The thick line shows the impulse response to a temporary increase: one-time unanticipated increase of 15% that is eroded by annual inflation of 2.2% a year. The thin line shows the impulse-response to a permanent increase of 15%.

Table 2 displays the arc elasticities of employment, defined as the percent change in employment divided by the percent change in wages. Column (1) shows that the long-run elasticities of a permanent minimum wage increase are substantial. The contemporaneous elasticity is about −0.06, which is within the range of elasticities discussed by, for example, Brown (1999) and Dube et al. (2010). After six years the employment elasticity with respect to the initial minimum wage increase is −0.25. Once all adjustment is complete, the elasticity is −0.55, which is larger than elasticities discussed in Brown (1999). Column (2) shows that when the increase is temporary the contemporaneous employment effect is similar, but over time the employment effect fades as the minimum wage erodes.

Table 1.

Annual parameter values

Parameter	Value	Description
	0.3	Land, structures and machines
	0.4	Materials share
	0.2	High skill labor share
α	0.9	Non-minimum wage-labor share
δ	0.08	Expiration chance
γ	0.6	Price elasticity of demand
β	0.95	Discount rate
nh	0.5	$\frac{\text{high}-\text{skill}\text{labor}}{\text{low}-\text{skill}\text{labor}}$ in steady state

Source: See the discussion in Section 4.

Table 3 displays the arc elasticities of prices. Column (1) shows that all of the price response occurs immediately. Column (2) shows that even when the minimum wage hike is temporary, the contemporaneous price response is not muted. In fact, the price response is slightly larger because the firms that enter have to be compensated for the fact that their capital-labor ratio will be suboptimal in all periods. The price response fades as the minimum wage erodes.

Table 2.

Employment response to minimum wage increases

Year	Permanent (1)	Temporary (2)	Sawtooth (3)
0	−0.062	−0.059	−0.056
1	−0.100	−0.063	−0.049
2	−0.136	−0.061	−0.040
3	−0.169	−0.057	−0.030
4	−0.199	−0.049	−0.020
5	−0.227	−0.040	−0.010
6	−0.252	−0.029	−0.002
∞	−0.546	0	NA Policy Elasticity
			−0.584

Note: An elasticity is defined as the percent change in employment divided by the percent change in wages. The permanent columns shows the total employment elasticity after X years from a one-time and permanent 15% minimum wage increase. The temporary column reports the total employment elasticity after X years from a one-time 15% minimum wage increase that is eroded at 2.2% per year. The sawtooth equilibrium is minimum wages increasing by 15% every seven years and then inflating away at 2.2% per year. The sawtooth column shows the total employment elasticity after X years following the minimum wage increase in the sawtooth equilibrium. The policy elasticity is defined using the average level of employment in the sawtooth equilibrium relative to never having a minimum wage and the wage is the average wage in the sawtooth equilibrium relative to having wages always at the lowest level.

5.2. Repeated temporary increases: a sawtooth equilibrium

A message of Figure 1 is that all minimum wage increases are not permanent and in fact follow a sawtooth pattern of regular temporary increases that are eroded. I simulate the model in a sawtooth equilibrium. The shape of the sawtooth is chosen as an approximation to Federal minimum wages, where the minimum wage has been raised once every 7 years on average.²⁹ In the sawtooth equilibrium, minimum wages increase every seven years by 15% and the inflation rate of 2.2% annually is chosen so that the minimum wage does not have a trend.³⁰

Results

Column (3) of Table 3 shows that the contemporaneous price response in the sawtooth equilibrium is basically identical to that from even the permanent minimum wage increase. The contemporaneous price response is insensitive to the nature of the variation: it is similar across permanent, temporary and repeated and predictable temporary minimum wage increases.

Column (3) of Table 2 displays the cumulative time path of the employment response to a minimum wage increase in the sawtooth equilibrium and makes two points. The first message of the table is that repeated temporary increases are not well-suited to to finding large employment effects of minimum wage increases even in a model that embodies large long-run elasticities. The contemporaneous employment effect is −0.06 and there are no observed long-run effects.

A second message of Table 2 is that long-run elasticities explain the employment consequences of a policy of repeated temporary minimum wage increases. On average, employment is about 3% lower than if wages were always at their lowest level in the simulation, and real minimum wages are about 6% above the lowest level. The implied “policy elasticity” of the average employment level with respect to the average minimum wage is −0.58, which is identical to the long-run elasticity of −0.55. Why is this? Firms choose a capital-intensity well-suited to the long-run average level of the minimum wage. Employment fluctuates around this lower steady state level, but these fluctuations are small relative to the lower steady state. These level difference in employment would not be easy to measure in empirical work. In standard empirical approaches, such level differences would be absorbed in the location fixed effects. The location fixed effects contain many other differences across places that are probably not solely due to the average level of minimum wages.

6. Quantitative implications of the model with actual minimum wage variation

So far I have studied a dynamic model embodying an important distinction between short- and long-run elasticities. If minimum wage increases are sufficiently temporary, I have shown that there would be little difference in the observed short- and long-run employment responses.

The model emphasizes two channels through which temporariness matters. First, temporariness matters because of how many firms adjust to the realized minimum wage increase: if in realization the minimum wage increase is temporary, then few firms adjust and the long-run effects are small. Second, temporariness matters because of firms’ expectations: if firms expect minimum wage increases to be temporary, then the firms that adjust do so by less and the long-run effects are small.

To address whether minimum wages used in empirical work are sufficiently temporary to make inference from standard empirical approaches misleading, I simulate the model to replicate the dataset used by Dube et al. (2010). In the simulation, expectations are pinned down by estimating a stochastic process for minimum wages in-sample.

Replicating a dataset that contains actual minimum wages directly addresses the first channel through which temporariness matters: the simulation uses realized variation, which might contain a mix of temporary and permanent changes. Estimating a stochastic process on the data partially addresses the second channel: in the model, the extent to which firms expect increases to be temporary is tied to the data. Of course, the estimated stochastic process may be misspecified.

Simulating the model using realized minimum wages directly addresses another concern: the use of counties also subject to inflation as the control group renders the main mechanism for temporariness moot. In the simulations, the control counties are also subject to inflation.

6.1. Data description

Dube et al. (2010) use county-level variation in the minimum wage in the US from 1990–2006. Their research design generalizes the Card & Krueger (1994) case study approach by pairing bordering counties with different minimum wages to control for local economic shocks. They study employment in the restaurant industry using data from the Quarterly Census of Employment and Wages.

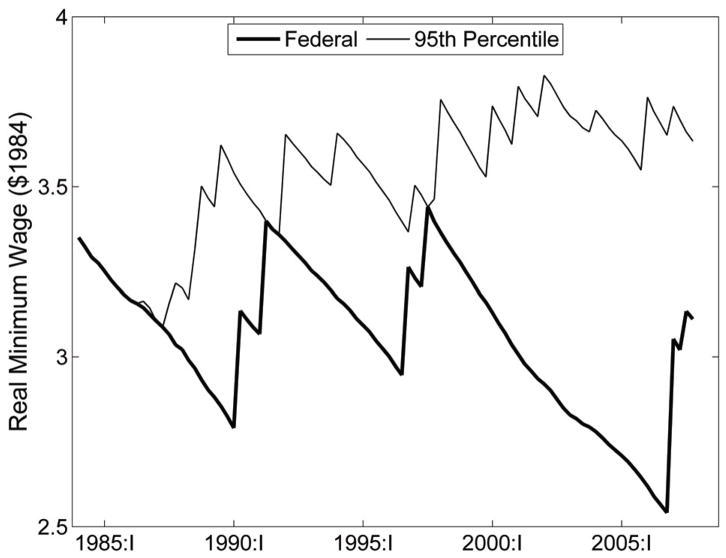
Figure 3 shows both the real value of the Federal minimum wage and the 95th percentile of the effective county-level minimum for the sample used by Dube et al. (2010). The 95th percentile of the effective minimum wage is often above the Federal minimum wage because many states set a minimum wage above the Federal minimum.³¹

Figure 3.

County-level variation in minimum wages in the US: 1984–2006

Note: Units are minimum wages deflated by average private sector hourly wage to 1984:I. The figure plots the minimum wages in the contiguous border county sample in Dube, Lester & Reich (2010).

6.2. Expectations: the stochastic process of wages

An important input to the simulation is firms’ expectations about the path of minimum wages. A minimum wage process with two features attempts to capture the sawtooth pattern. First, a minimum wage increase is more likely the lower is the minimum wage relative to its long-run average. Second, conditional on an increase occurring, there is still some uncertainty about the size.

Formally, the minimum wage evolves according to the following process:

$$w_{i,t+1}\mid w_{i,t}=\{\begin{array}{l}(1-\mathit{inf})w_{i,t}\text{with}\text{probability}(1-h(w_{i,t}-{\overline{w}}_i))\hfill \\ w_{i,t}(1+g)\text{with}\text{probability}h(w_{i,t}-{\overline{w}}_i),\hfill \end{array}$$

where I now define notation. The location-time invariant inflation rate is inf. The long-run location-specific average minimum wage is w̄_i. The current minimum wage is w_i,t. The realization of the size of a minimum wage increase is g, which is drawn from a location-time invariant distribution G. Finally, h: ℝ → [0, 1] is the function that captures the idea that minimum wage increases are more likely the lower is the minimum wage relative to its long-run average. In particular, this is true when h′ < 0.

I estimate all parameters of this process, except for inf, in-sample on the pooled contiguous border county sample of Dube et al. (2010). The inf parameter is chosen so that the estimated stochastic process does not have a trend. Appendix B.2 provides details. Figure 4a shows that the estimated quarterly probabilities of a minimum wage hike are consistent with sawtooth dynamics. The probability of an increase becomes very small (below 5%) when the current minimum wage is above the long-run average and rises rapidly when the current minimum wage falls below the long-run average—when the current minimum wage is 30% below the long-run average the per period probability of an increase exceeds 50%. Figure 4b shows that the empirical distribution of minimum wage hikes places the most mass between 15% and 25% hikes.

Figure 4.

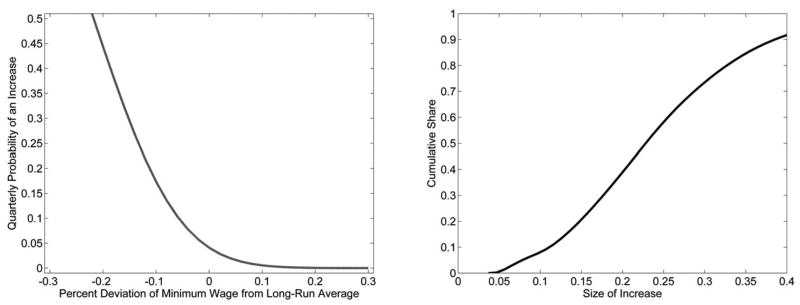
The stochastic process for minimum wages

Note: The left panel plots implied probabilities of minimum wage hikes at different values relative to the long-run average of the minimum wage estimated on the contiguous border county sample (dropping duplicate counties) from 1984:I–2007:IV. The regression coefficients are in Table A1. The right panel plots the distribution of minimum wage increases in the contiguous border county sample (dropping duplicate counties) from 1984:I–2007:IV.

An important assumption in estimating the stochastic process that governs firms’ expectations on the pooled sample is that the process—which reflects a particular form of temporariness of minimum wage increases—is common across locations. To explore the validity of this assumption, Appendix B.2.1 specifies an auxilliary statistical model of the persistence of minimum wages and shows that the dispersion across locations in the data is similar to that in data simulated from the stochastic process. Using only in-sample information, firms would be unlikely to reject the null that observed minimum wages are consistent with the estimated stochastic process, rather than there being place specific minimum wage processes. Because I do not horserace the fit of auxilliary statistical models with and without permanent shocks, this exercise does not shed light on whether or not there are permanent shocks in the minimum wage process.

6.3. Simulated data

Appendix B describes both the simulation algorithm and construction of the minimum wage series in detail. Firms’ expectations about the minimum wage are given by the stochastic process described in subsection 6.2. The county-level employment series is generated using the realized minimum wage histories at the county-level. I use 9 runs through the realized minimum wage histories as a burn-in period and store the 10th run. Visual inspection reveals that 9 runs are more than adequate to ensure convergence. The resulting dataset is exactly the same size as the Dube et al. (2010) dataset and includes the measures of employment and population from the Dube et al. (2010) dataset.

6.4. Specification

I estimate a distributed lag specification on the actual dataset and the simulated dataset. Following Dube et al. (2010) I use logs and their preferred specification (equation (7)).³² The unit of observation is county-level restaurant employment (restemp) in county i, border-pair p, and at time t. A county enters the dataset if it has a bordering county with a different minimum wage at any point between 1990:I-2006:II. A county can be in the dataset multiple times if it borders multiple counties with different minimum wages. There are two additional data series total employment (totemp) and population (pop). To control for local economic shocks the regression includes a border-pair time period specific fixed effect, τ_pt.³³

The estimating equation is:

$$ln{(\text{restemp})}_{\mathit{ipt}}=a_1+\sum _{j=0}^{23}{\eta }_{-j}\mathrm{\Delta }ln({MW}_{i,t-j})+{\eta }_{-24}ln({MW}_{i,t-24})+a_2\text{ln}{(\text{totemp})}_{it}+a_3\text{ln}{(\text{pop})}_{it}+{\varphi }_i+{\tau }_{pt}+{\epsilon }_{\mathit{ipt}}$$ (15)

where ϕ_i is a county fixed effect and ε_ipt is an error term. Equation 15 follows Baker et al. (1999) and examines six year (24 quarters) of lagged responses, rather than two years of leads and four years of lags as in Dube et al. (2010). This choice allows comparison to other Baker et al. (1999) specifications discussed in Section 6.6.

Equation 15 uses differenced minimum wages, which means that η_−j is the average employment effect of the j^th lag of minimum wages. The η’s are identified based on periods when within a given county-border pair the two counties have different minimum wages; in periods when the county-border pair have the same minimum wages the fixed effect absorbs the common component of restaurant employment. Following Dube et al. I report Cameron et al. (2011) standard errors clustered at the state and border segment separately, and corrected for certain forms of heteroskedasticity.³⁴

6.5. Employment results

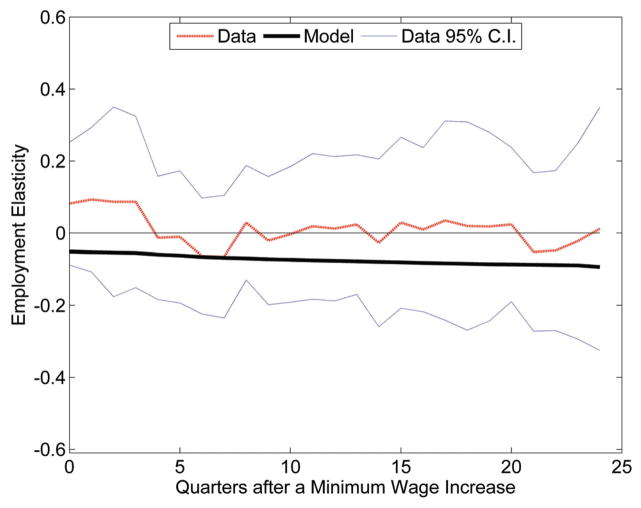
Figure 5 shows that because minimum wage increases are temporary there are not large estimated employment effects of minimum wage changes. The figure plots the elasticities estimated on the actual data and the simulated data.³⁵ The estimates on simulated data are very small negative elasiticities in the first quarters—about −0.05—and in subsequent periods the employment response barely grows, reaching −0.09 after 24 quarters. At all horizons the simulated data lies within the confidence bands of the actual data, though these bands are very wide.

Figure 5.

Distributed lag specification

Note: This figure plots the coefficients from the distributed lag specification. The regressions also include a border pair times period interaction term. The outcome is total employment in the restaurant industry. The regressions use the contiguous border sample. The thin line shows the pointwise 95% confidence interval from the data, where the standard errors are clustered at the state and border segment separately. The data plot shows estimates based on actual data. The model line plots coefficients based on data simulated from the putty-clay model. The coefficients are in table A2.

6.6. Additional specifications

Appendix C reports the results of the two additional long-run specifications used by Baker et al. (1999). These results are consistent with small employment effects of minimum wage changes. Neither of these specifications yield an elasticity after six years that exceeds −0.07 on the simulated data.

6.7. Robustness

It might seem like the results should be very sensitive to the rate at which firms adjust, δ. To provide intuition as to why this is not the case, Table 4 reproduces the calculations of employment elasticities with respect to permanent, temporary and sawtooth minimum wage increases presented in Table 2 and discussed in Section 5 for many of values of δ. For sawtooth increases, the interaction of the erosion of the minimum wage and the expectation of future increases limits the sensitivity to δ. Indeed, as in the more complex simulations described immediately below, the elasticities with δ = 0.08 and δ = 0.16 are basically the same. On the other hand, the Table shows that the response to permanent increases is very sensitive to δ.³⁶ Consistent with the main themes of this paper, results for permanent increases provide a misleading guide to increases in a sawtooth environment.

Table 3.

Price response to minimum wage increases

Year	Permanent (1)	Temporary (2)	Sawtooth (3)
0	+0.094	+0.096	+0.093
1	+0.094	+0.081	+0.078
2	+0.094	+0.066	+0.063
3	+0.094	+0.051	+0.049
4	+0.094	+0.036	+0.034
5	+0.094	+0.021	+0.020
6	+0.094	+0.006	+0.007
∞	+0.094	0	NA Policy Elasticity
			+0.097

Note: An elasticity is defined as the percent change in price divided by the percent change in wages. The permanent columns shows the total price elasticity after X years from a one-time and permanent 15% minimum wage increase. The temporary column reports the total employment elasticity after X years from a one-time 15% minimum wage increase that is eroded at 2.2% per year. The sawtooth equilibrium is minimum wages increasing by 15% every seven years and then inflating away at 2.2% per year. The sawtooth column shows the total price elasticity after X years following the minimum wage increase in the sawtooth equilibrium. The policy elasticity is defined using the average level of prices in the sawtooth equilibrium relative to never having a minimum wage and the wage is the average wage in the sawtooth equilibrium relative to having wages always at the lowest level.

For the robustness exercise, I replicate the Dube et al. (2010) data using δ ∈ {0.16, 0.33, 0.5}. Table 5 reports the point estimates from the distributed lag specification for the contemporaneous elasticity and the “long-run” (at 24 quarters) elasticity. The contemporaneous and long-run elasticities are basically identical for 0.08 and 0.16. This indicates that raising δ in this range increases the extent of attenuation, since Table 4 shows the employment effect of a permanent increase at 24 quarters is 50% larger with the higher value of δ. With δ = 0.33, the long-run elasticity grows to −0.16. Similar to δ = 0.08, this estimate is about one-third of the long-run elasticity implied by the model, because the response to a permanent increase grows with δ.³⁷ With δ = 0.5, the contemporaneous elasticity is −0.08 and the long-run elasticity is −0.24. Again, this exhibits substantial attenuation relative to a permanent minimum wage increase (in Table 4 it is −0.54).

7. Conclusion

If there were differences between short- and long-run employment elasticities would it be possible to tell? This paper has suggested that because of the nature of variation in minimum wages the answer is no. In particular, because minimum wage increases are mostly temporary, the ceteris paribus condition implied in the long-run elasticities—that of a permanent minimum wage increase—is unlikely to obtain. Even without such a ceteris paribus condition, it might be the case that standard regressions could overcome this challenge. In the presence of a distinction between the short- and long-run elasticities, standard regressions in the literature do not overcome this challenge and so have potentially been misinterpreted.

As such, the paper suggests that it would be a mistake to infer from existing empirical work on the employment effects of minimum wage increases that the President’s 2013 proposal to index minimum wages to inflation would have minimal effects on employment. Taking the model at face value shows how misleading such an inference might be: the results in Table 2 show that a contemporaneous elasticity of −0.002 in response to a temporary increase is consistent with an elasticity after 6 years of −0.252 for a permanent increase.

The putty-clay model also offers a rationalization of two divergent strands of empirical work on effects of minimum wage increases. On the one hand, the evidence of small short-run employment effects is inconsistent with standard static models of labor demand; on the other hand, product price increases are inconsistent with models of “supply side constraints” (e.g. search models). The putty-clay model is consistent with both. In the model, observed long-run effects of temporary minimum wage increases are also small, though the long-run effect on employment of a permanent change in the real value of the minimum wage is large and equilibrium employment is below what it would have been were it not for the minimum wage.

This paper suggests several avenues for future research. The putty-clay model could be extended along a couple dimensions. First, the labor market is assumed to be perfectly competitive, which omits potentially important mechanisms that models of search emphasize. Second, the firm’s problem is simplified by using an exogenous adjustment probability, rather than an endogenous adjustment process. More broadly, it would be interesting to bring detailed evidence to bear on several mechanisms that are emphasized by the putty-clay model: the speed with which employers of low-skill labor adjust labor demand in response to shocks, how firms form expectations about minimum wages, and how these expectations affect decisionmaking.

Appendix A. Omitted calculations

This appendix derives the steady state relationships in the model, demonstrates that firms never want to shutdown, that there is entry in every period, details the insulation effect, and provides complete proofs of all results stated in the text.

Appendix A.1. Steady state values

Given a constant wage,

$$q_w=\sum _{j=0}^{\infty }{\beta }^j{(1-\delta )}^{j}w=\frac{w}{1-\beta (1-\delta )}.$$ (A1)

From (8),

$$k=q_w\frac{\alpha }{1-\alpha }.$$ (A2)

Combining the optimal size of a machine, equation (A2), with the zero profit condition, equation (3) set to zero in steady state, gives

$$q={\alpha }^{-\alpha }{\left(\frac{q_w}{1-\alpha }\right)}^{1-\alpha }.$$ (A3)

From (9) with a constant q,

$$P=(1-\beta (1-\delta ))\frac{q_w^{1-\alpha }}{{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }}.$$ (A4)

From (5),

$$Q=\theta P^{-\gamma }=\theta \left[\frac{{\alpha }^{\gamma \alpha }{(1-\alpha )}^{\gamma (1-\alpha )}}{{(1-\beta (1-\delta ))}^{\gamma }{q}_w^{\gamma (1-\alpha )}}\right].$$ (A5)

The number of workers in steady state is

$$N=\frac{Q}{k^{\alpha }}=\theta \left[\frac{{\alpha }^{\alpha (\gamma -1)}{(1-\alpha )}^{\gamma (1-\alpha )+\alpha }}{{(1-\beta (1-\delta ))}^{\gamma }{q}_w^{\gamma (1-\alpha )+\alpha }}\right].$$ (A6)

Appendix A.2. No shutdown, entry in every period and the insulation effect

No shutdown

A machine built at time t has capital $k_t=\frac{\alpha }{1-\alpha }{q}_{w,t}$. Assume that after time t′ > t the wage will be constant and equal to w_t′. Considering permanent movements allow me to derive results in closed-form. The price in period t′ is $P_{t^{\prime }}=(1-\beta (1-\delta ))\frac{q_{w,t^{\prime }}^{1-\alpha }}{{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }}$. If in period t′ > t a firm wants to shut down a machine that was installed in period t this implies that $P_{t^{\prime }}{k}_t^{\alpha }-w_{t^{\prime }}<0$ or using the expressions for k_t and $P_{t^{\prime }}\frac{q_{w,t}}{q_{w,t^{\prime }}}<{(1-\alpha )}^{\frac{1}{\alpha }}$. Then shutdown requires (using α = 0.9) $q_{w,t}<q_{w,t^{\prime }}{(1-\alpha )}^{\frac{1}{\alpha }}=q_{w,t^{\prime }}0.077$. Shutdown requires that the present discounted value of wages to rise by more than a factor of 10 from when the investment was made. In the dataset the real value of wages varies by less than a factor of two, and the present discounted value of wages is less volatile than the wage. So firms never want to shutdown.

Entry in every period

Entry in every period requires: $h_t>0\iff Q_t-(1-\delta )(Q_{t-1})>0\iff P_t^{-\gamma }-(1-\delta )P_{t-1}^{-\gamma }>0\iff {\left(\frac{1}{1-\delta }\right)}^{\frac{1}{\gamma }}>\frac{P_t}{P_{t-1}}$. Using the baseline calibration, having no entry in a period requires one quarter increases in the present discounted value of wages of more than 40%, while in the simulation the largest one quarter increase in the minimum wage is 34% (and the present discounted value of wages moves by even less). So there is always entry.

Insulation effect

This section demonstrates the insulation effect. The comparative static is an incumbent firm’s revenue from steady state with respect to the wage, where the wage and the price is allowed to respond, but the capital stock is not.

$$R={Pk}^{\alpha }-w$$ (A7)

$$\frac{\partial R}{\partial w}\frac{w}{P}=\frac{\partial P}{\partial w}\frac{w}{P}{k}^{\alpha }-\frac{w}{P}.$$ (A8)

Combining equations (A1) and (A4), in steady state

$$\frac{w}{P}=q_w^{\alpha }{\alpha }^{\alpha }{(1-\alpha )}^{1-\alpha }.$$ (A9)

Result 3 has as a special case with perfect foresight from steady state that

$$\frac{\partial P}{\partial w}\frac{w}{P}=1-\alpha .$$ (A10)

Combining the previous expressions with equation (A2) gives

$$\frac{\partial R}{\partial w}\frac{w}{P}={(1-\alpha )}^{1-\alpha }{\alpha }^{\alpha }{q}_w^{\alpha }-{(1-\alpha )}^{1-\alpha }{\alpha }^{\alpha }{q}_w^{\alpha }$$ (A11)

$$=0.$$ (A12)

Appendix A.3. Proofs

First write labor demand in terms of model parameters and the q_w,t.

Writing labor demand in terms of model parameters

Iterating equation (6) gives

$$N_t=\sum _{j=0}^{\infty }{(1-\delta )}^j{h}_{t-j}.$$ (A13)

The goal is to write equation (A13) in terms of q_w,t−j. Rearrange equation (7):

$$h_t=\frac{Q_t-(1-\delta )Q_{t-1}}{k_t^{\alpha }}.$$ (A14)

Combine equations (3) set to zero, (5), and (9):

$$Q_t=\theta P_t^{-\gamma }$$ (A15)

$$=\theta {[q_t-(\beta (1-\delta ))E_t[q_{t+1}]]}^{-\gamma }$$ (A16)

$$=\theta {\left(\frac{{\alpha }^{-\alpha }}{{(1-\alpha )}^{1-\alpha }}\right)}^{-\gamma }{[q_{w,t}^{1-\alpha }-(\beta (1-\delta ))E_t[q_{w,t+1}^{1-\alpha }]]}^{-\gamma }.$$ (A17)

Combine equations (8), (A14) and (A17):

$$h_t=\frac{\theta \left\{{[q_{w,t}^{1-\alpha }-(\beta (1-\delta ))E_t[q_{w,t+1}^{1-\alpha }]]}^{-\gamma }-(1-\delta ){[q_{w,t-1}^{1-\alpha }-(\beta (1-\delta ))E_{t-1}[q_{w,t}^{1-\alpha }]]}^{-\gamma }\right\}}{\frac{{\alpha }^{1-\alpha \gamma }}{{(1-\alpha )}^{1+\gamma (1-\alpha )}}{q}_{w,t}}.$$ (A18)

Substitute suitably modified versions of equation (A18) into (A13):

$$N_t=\sum _{j=0}^{\infty }{(1-\delta )}^j\frac{\theta \left\{{[q_{w,t-j}^{1-\alpha }-(\beta (1-\delta ))E_{t-j}[q_{w,t+1-j}^{1-\alpha }]]}^{-\gamma }-(1-\delta ){[q_{w,t-1}^{1-\alpha }-(\beta (1-\delta ))E_{t-1-j}[q_{w,t-j}^{1-\alpha }]]}^{-\gamma }\right\}}{\frac{{\alpha }^{\alpha -\alpha \gamma }}{{(1-\alpha )}^{\alpha -\gamma (1-\alpha )}}{q}_{w,t-j}^{\alpha }}.$$ (A19)

Proof of result 1

Proof

Equation (6) gives

$$N_t=h_t+(1-\delta )N_{t-1}.$$ (A20)

Using equation (A20) and converting to an elasticity at the end,

$$\frac{\partial N_t}{\partial w_t}=\frac{\partial h_t}{\partial w_t}$$ (A21)

$$=\frac{\partial \left\{\frac{Q_t-(1-\delta )Q_{t-1}}{k_t^{\alpha }}\right\}}{\partial w_t}$$ (A22)

$$=\frac{\partial Q_t}{\partial w_t}\frac{1}{k_t^{\alpha }}-\alpha \frac{\partial k_t}{\partial w_t}\frac{1}{k_t}\frac{Q_t-(1-\delta )Q_{t-1}}{k_t^{\alpha }}$$ (A23)

$$=\frac{\partial Q_t}{\partial w_t}\frac{1}{k_t^{\alpha }}-\alpha \frac{\partial k_t}{\partial w_t}\frac{h_t}{k_t}$$ (A24)

$$\frac{\partial N_t}{\partial w_t}\frac{w_t}{N_t}=\frac{\partial Q_t}{\partial w_t}\frac{1}{k_t^{\alpha }}\frac{w_t}{N_t}-\alpha \frac{\partial k_t}{\partial w_t}\frac{w_t}{k_t}\frac{h_t}{N_t}.$$ (A25)

Solve for the RHS of (A25) in pieces. I am interested in an increase of w_t from steady state.

First, collect some useful facts about steady state. Start with equation (2)

$$q_{w,t}=w_t+\beta (1-\delta ){\mathbb{E}}_t[q_{w,+1}]$$ (A26)

$$\frac{\partial q_{w,t}}{\partial w_t}=1$$ (A27)

$$\frac{\partial q_{w,t}}{\partial w_t}\frac{w_t}{q_{w,t}}=\frac{w_t}{q_{w,t}}.$$ (A28)

In steady state (equation (A1)):

$$\frac{w}{q_w}=1-\beta (1-\delta ).$$ (A29)

Rewrite equation (A13) in steady state.

$$N=\sum _{j=0}^{\infty }{(1-\delta )}^{j}h=\frac{h}{\delta }\iff \delta =\frac{h}{N}.$$ (A30)

Rewrite equation (A14) in steady state.

$$h=\frac{Q-(1-\delta )Q}{k^{\alpha }}=\frac{\delta Q}{k^{\alpha }}.$$ (A31)

Combine (A30) and (A31):

$$\delta N=\frac{\delta Q}{k^{\alpha }}\iff Q=N{k}^{\alpha }.$$ (A32)

This completes the preliminary facts.

Now solve for terms on the RHS of equation (A25). Substitute equation (A32) into the first term on the RHS of equation (A25) and expand:

$$\frac{\partial Q_t}{\partial w_t}\frac{w_t}{Q_t}=\frac{\partial Q_t}{\partial P_t}\frac{\partial P_t}{\partial w_t}\frac{w_t}{Q_t}\frac{P_t}{P_t}$$ (A33)

$$=\frac{\partial Q_t}{\partial P_t}\frac{P_t}{Q_t}\frac{\partial w_t}{\partial P_t}\frac{P_t}{w_t}$$ (A34)

$$=-\gamma (1-\alpha ),$$ (A35)

where the last step computes an elasticity from equation (5) and uses the special case of Result 3 from steady state.

Now consider part of the second term on the RHS of equation (A25) combined with equation (A30).

$$\frac{\partial k_t}{\partial w_t}\frac{w_t}{k_t}=\frac{\partial k_t}{\partial q_{w,t}}\frac{\partial q_{w,t}}{\partial w_t}\frac{w_t}{k_t}\frac{q_{w,t}}{q_{w,t}}$$ (A36)

$$=\frac{\partial k_t}{\partial q_{w,t}}\frac{q_{w,t}}{k_t}\frac{\partial q_{w,t}}{\partial w_t}\frac{w_t}{q_{w,t}}$$ (A37)

$$=\frac{w_t}{q_{w,t}}$$ (A38)

$$=1-\beta (1-\delta ),$$ (A39)

where the elasticities are computed from (8) and (A28) and equation (A39) uses (A29).

Finally, substituting equation (A39), (A35), and (A30) into the RHS of (A25) in steady state gives the result:

$$\frac{\partial N_t}{\partial w_t}\frac{w_t}{N_t}=\frac{\partial Q_t}{\partial w_t}\frac{1}{k_t^{\alpha }}\frac{w_t}{N_t}-\alpha \frac{\partial k_t}{\partial w_t}\frac{w_t}{k_t}\frac{h_t}{N_t}$$ (A40)

$$=-\gamma (1-\alpha )-\alpha \delta (1-\beta (1-\delta )).$$ (A41)

Proof of result 2

Proof

I first compute the contemporaneous elasticity. I then compute the lagged effects. Throughout, I make use of steady state facts derived in result 1.

Equation (6) gives

$$N_t=h_t+(1-\delta )N_{t-1}.$$ (A42)

I am interested in the effect of a change in q_w,t on N_t (contemporaneous effect of a permanent minimum wage increase on employment). Taking the relevant derivative of (A42)

$$\frac{\partial N_t}{\partial q_{w,t}}=\frac{\partial h_t}{\partial q_{w,t}},$$ (A43)

since N_t−1 is predetermined. Substitute in (A14):

$$\frac{\partial N_t}{\partial q_{w,t}}=\frac{\partial \left[\frac{Q_t-(1-\delta )Q_{t-1}}{k_t^{\alpha }}\right]}{\partial q_{w,t}},$$ (A44)

$$\frac{\partial Q_t}{\partial q_{w,t}}\frac{1}{k_t^{\alpha }}-\alpha \frac{\partial k_t}{\partial q_{w,t}}\frac{h_t}{k_t}.$$ (A45)

Convert to an elasticity:

$$\frac{\partial N_t}{\partial q_{w,t}}\frac{q_{w,t}}{N_t}=\frac{\partial Q_t}{\partial q_{w,t}}\frac{1}{k_t^{\alpha }}\frac{q_{w,t}}{N_t}-\alpha \frac{\partial k_t}{\partial q_{w,t}}\frac{h_t}{k_t}\frac{q_{w,t}}{N_t}$$ (A46)

$$=\frac{\partial Q_t}{\partial q_{w,t}}\frac{q_{w,t}}{Q_t}-\alpha \delta \frac{\partial k_t}{\partial q_{w,t}}\frac{q_{w,t}}{k_t},$$ (A47)

where this last equation makes use of (A32) and (A30). From equation (8),

$$\frac{\partial k_t}{\partial q_{w,t}}\frac{q_{w,t}}{k_t}=1.$$ (A48)

The last term to solve for is $\frac{\partial Q_t}{\partial q_{w,t}}\frac{q_{w,t}}{Q_t}$. The assumption of permanence—and expectations thereof—is that $E_t[q_{w,t+1}^{1-\alpha }]=q_{w,t}^{1-\alpha }$ and $\frac{\partial E_t[q_{w,t+1}^{1-\alpha }]}{\partial q_{w,t}}=(1-\alpha )q_{w,t}^{-\alpha }$. Using equation (A17) and then substituting in for the expectations:

$$\frac{\partial Q_t}{\partial q_{w,t}}\frac{q_{w,t}}{Q_t}=-\gamma \frac{(1-\alpha )q_{w,t}^{1-\alpha }-\beta (1-\beta )\frac{\partial E_t[q_{w,t+1}^{1-\alpha }]}{\partial q_{w,t}}{q}_{w,t}}{[q_{w,t}^{1-\alpha }-(\beta (1-\delta ))E_t[q_{w,t+1}^{1-\alpha }]]}$$ (A49)

$$=-\gamma \frac{(1-\alpha )q_{w,t}^{1-\alpha }-\beta (1-\delta )(1-\alpha )q_{w,t}^{1-\alpha }}{[q_{w,t}^{1-\alpha }-(\beta (1-\delta ))q_{w,t}^{1-\alpha }]}$$ (A50)

$$=-\gamma (1-\alpha ).$$ (A51)

Substituting (A48) and (A51) into (A47) gives the result for the contemporaneous elasticity:

$$\frac{\partial N_t}{\partial q_{w,t}}\frac{q_{w,t}}{N_t}=-\gamma (1-\alpha )-\alpha \delta .$$ (A52)

Now consider the lagged response. I am interested in the effect of a change in q_w,t on N_t+n (the lagged effects of a permanent minimum wage increase on employment). From equation (A19), q_w,t appears in two terms making up N_t+n (since we want partial and not total derivatives). Using the representation in equation (A13) gives

$$N_{t+n}=h_{t+n}+\dots +{(1-\delta )}^{n-1}{h}_{t+1}+{(1-\delta )}^n{h}_t+\dots$$ (A53)

Hence the direct effect of a change in q_w,t on N_t+n is (substituting in (A14)):

$$\frac{\partial N_{t+n}}{\partial q_{w,t}}={(1-\delta )}^{n-1}\frac{\partial h_{t+1}}{\partial q_{w,t}}+{(1-\delta )}^n\frac{\partial h_t}{\partial q_{w,t}}$$ (A54)

$$={(1-\delta )}^{n-1}\frac{\partial \left[\frac{Q_{t+1}-(1-\delta )Q_t}{k_{t+1}^{\alpha }}\right]}{\partial q_{w,t}}+{(1-\delta )}^n\frac{\partial \left[\frac{Q_t-(1-\delta )Q_{t-1}}{k_t^{\alpha }}\right]}{\partial q_{w,t}}$$ (A55)

$$=-{(1-\delta )}^n\frac{1}{k_{t+1}^{\alpha }}\frac{\partial Q_t}{\partial q_{w,t}}+{(1-\delta )}^n\left[\frac{\partial Q_t}{\partial q_{w,t}}\frac{1}{k_t^{\alpha }}-\alpha \frac{\partial k_t}{\partial q_{w,t}}\frac{h_t}{k_t}\right].$$ (A56)

Since the increase is permanent, q_w,t = q_w,t+1 so that (using equation (8)) $k_{t+1}^{\alpha }=k_t^{\alpha }$. Simplifying, converting to elasticities, applying equation (A48), using the fact that the change is local so that N_t = N_t+n, and finally that the economy starts in steady state so that equation (A30) holds gives the result:

$$\frac{\partial N_{t+n}}{\partial q_{w,t}}=-\alpha {(1-\delta )}^n\frac{\partial k_t}{\partial q_{w,t}}\frac{h_t}{k_t}$$ (A57)

$$\frac{\partial N_{t+n}}{\partial q_{w,t}}\frac{q_{w,t}}{N_{t+n}}=-\alpha {(1-\delta )}^n\frac{\partial k_t}{\partial q_{w,t}}\frac{h_t}{k_t}\frac{q_{w,t}}{N_{t+n}}.$$ (A58)

$$=-\alpha {(1-\delta )}^n\frac{h_t}{N_{t+n}}$$ (A59)

$$=-\alpha \delta {(1-\delta )}^n.$$ (A60)

Proof of result 3

Proof

Start with equation (9) and substitute in the combination of equation (8) and the zero profit condition, equation (3), set to zero. Then expand q_w,t using equation (2):

$$P_t=q_t-\beta (1-\delta )E_t[q_{t+1}]$$ (A61)

$$={\alpha }^{-\alpha }{\left[\frac{q_{w,t}}{1-\alpha }\right]}^{1-\alpha }-\beta (1-\delta ){\alpha }^{-\alpha }{E}_t\left\{{\left[\frac{q_{w,t+1}}{1-\alpha }\right]}^{-1\alpha }\right\}$$ (A62)

$$={\alpha }^{-\alpha }{\left[\frac{w_t+\beta (1-\delta )E_t[q_{w,t+1}]}{1-\alpha }\right]}^{1-\alpha }-\beta (1-\delta ){\alpha }^{-\alpha }{E}_t\left\{{\left[\frac{q_{w,t+1}}{1-\alpha }\right]}^{1-\alpha }\right\}.$$ (A63)

Imposing perfect foresight provides a convenient alternative representation of P_t:

$$P_t={\alpha }^{-\alpha }{\left[\frac{q_{w,t}}{1-\alpha }\right]}^{1-\alpha }-\beta (1-\delta ){\alpha }^{-\alpha }\left\{{\left[\frac{q_{w,t+1}}{1-\alpha }\right]}^{1-\alpha }\right\}$$ (A64)

$$={\alpha }^{-\alpha }{\left[\frac{q_{w,t}}{1-\alpha }\right]}^{1-\alpha }\left[1-\beta (1-\delta )\left\{{\left[\frac{q_{w,t+1}}{q_{w,t}}\right]}^{1-\alpha }\right\}\right].$$ (A65)

Take a derivative of equation (A63) with respect to w_t, convert to elasticity form and substitute in for P_t while imposing perfect foresight (equation (A65)):

$$\frac{\partial P_t}{\partial w_t}={\alpha }^{-\alpha }{\left[\frac{w_t+\beta (1-\delta )E_t[q_{w,t+1}]}{1-\alpha }\right]}^{-\alpha }$$ (A66)

$$\frac{\partial P_t}{\partial w_t}\frac{w_t}{P_t}={\alpha }^{-\alpha }{\left[\frac{w_t+\beta (1-\delta )E_t[q_{w,t+1}]}{1-\alpha }\right]}^{-\alpha }\frac{w_t}{P_t}$$ (A67)

$$={\alpha }^{-\alpha }{\left[\frac{q_{w,t}}{1-\alpha }\right]}^{-\alpha }\frac{w_t}{{\alpha }^{-\alpha }{\left[\frac{q_{w,t}}{1-\alpha }\right]}^{1-\alpha }\left[1-\beta (1-\delta ){\left(\frac{q_{w,t+1}}{q_{w,t}}\right)}^{1-\alpha }\right]}$$ (A68)

$$=(1-\alpha )\frac{1}{q_{w,t}}\frac{w_t}{\left[1-\beta (1-\delta ){\left(\frac{q_{w,t+1}}{q_{w,t}}\right)}^{1-\alpha }\right]}.$$ (A69)

Let w̃_t = (1 − β(1 − δ))q_w,t and w̃_t+1 = (1 − β(1 − δ))q_w,t+1. Then:

$$\frac{\partial P_t}{\partial w_t}\frac{w_t}{P_t}=(1-\alpha )\frac{w_t}{{\stackrel{\sim }{w}}_t}\frac{1-\beta (1-\delta )}{1-\beta (1-\delta ){\left(\frac{{\stackrel{\sim }{w}}_{t+1}}{{\stackrel{\sim }{w}}_t}\right)}^{1-\alpha }}.$$ (A70)

For local changes from steady state, w_t = w̃_t and w̃_t+1 = w̃_t so that

$$\frac{\partial P}{\partial w_t}\frac{w_t}{P_t}=(1-\alpha ).$$ (A71)

Appendix B. Simulation details

Appendix B.1. Simulation algorithm for perfect foresight

This appendix describes how to simulate the model in section 5. The model is solved under perfect foresight. There are two steps: first, initializing the model, and second, solving the dynamics given a varying minimum wage.

Initializing the model to steady state

Suppose that the economy is in the steady state defined by w. Then the steady state values are computed in the following order using the formulas in Appendix A.1:

$$\begin{array}{l}{q}_w=\frac{w}{(1-\beta (1-\delta ))},\\ k=q_{w,t}\frac{\alpha }{1-\alpha },\\ q={\alpha }^{(-\alpha )}{\left(\frac{q_w}{1-\alpha }\right)}^{(1-\alpha )},\\ P=q_t(1-\beta (1-\delta )),\\ Q=\theta P^{-\gamma },\\ N=\frac{Q}{k^{\alpha }},\\ K=Nk,\end{array}$$

where K_t is the aggregate capital stock. The employment numbers include the high-skill workers:

$$E=(1+n_h)N.$$

Dynamics to changing minimum wages

Suppose that after time t the wage will vary. At the beginning of time t + 1 firms know ${\{w_{t+1+j}\}}_{j=0}^{\infty }$. Define

$$q_{w,t+1+j}=\sum _{i=0}^{\infty }{(\beta (1-\delta ))}^i{w}_{t+1+j+i}\forall j\ge 0.$$

Given the sequence of q_w,t+j, the following loop shows how to simulate the model starting from the time t steady state.

For j = 1, 2, 3 …:

$$\begin{array}{l}{q}_{t+j}={\alpha }^{(-\alpha )}{\left(\frac{q_{w,t+j}}{1-\alpha }\right)}^{(1-\alpha )}\\ q_{t+j+1}={\alpha }^{(-\alpha )}{\left(\frac{q_{w,t+j+1}}{1-\alpha }\right)}^{(1-\alpha )}\\ P_{t+j}=q_{t+j}-\beta (1-\delta )q_{t+j+1}\\ Q_{t+j}=\theta P_{t+j}^{-\gamma }\\ k_{t+j}=q_{w,t+j}\frac{\alpha }{1-\alpha }\\ h_{t+j}=\frac{Q_{t+j}-Q_{t+j-1}(1-\delta )}{k_{t+j}^{\alpha }}\\ N_{t+j}=N_{t+j-1}(1-\delta )+h_{t+j}\\ K_{t+j}=K_{t+j-1}(1-\delta )+h_{t+j}{k}_{t+j}\\ E_{t+j}=N_{t+j}+n_h\frac{N_t}{K_t}{K}_{t+j}.\end{array}$$

Appendix B.2. The stochastic process for wages

Estimating the stochastic process requires estimating the following objects: w̄_i, inf, h(w_i,t − w̄_i), and G (the distribution of increases). I proceed in the following steps:

• Recover w̄_i as the location-specific fixed effect by running a regression on 1984:I – 2007:IV data:

  $$ln{\mathit{rmw}}_{it}={\overline{w}}_i+{\epsilon }_{it},$$

  where rmw_it is the real minimum wage in location i in period t. Store the residuals, ε̂_it, which are the deviations from long-run averages.

• Assume that the h function takes a probit form. Let Increase_it be an indicator for a minimum wage hike in period i in location t. To account for the fact that there are staggered increases, only count the first increase in a five quarter window as an increase, and to not count changes due to indexation an increase has to be least 5%. To measure the size, sum together the two increases. Estimate h based on the following regression:

  $$Pr({\mathit{Increase}}_{it}=1\mid {\widehat{\epsilon }}_{it})=\mathrm{\Phi }({\alpha }_0+{\alpha }_1{\widehat{\epsilon }}_{it}),$$

  where Φ is the normal CDF.

• Estimate the distribution of increases, G, nonparametrically by taking the distribution of increases observed in the data.

• Compute the inflation parameter, inf, so that in expectation minimum wages do not have a trend. In practice, I use simulation to calibrate the inflation parameter by picking the inflation parameter such that after 100, 000 runs of the series the average wage is zero. This yields an annual inflation rate of 3.3%.

Appendix B.2.1. Does the minimum wage process vary across locations?

Operationalize persistence as the AR(1) coefficient of a basic time series regression on a single location i:

$${\widehat{\epsilon }}_{it}={\alpha }_i+{\rho }_i{\widehat{\epsilon }}_{it-1},$$

Does persistence, the estimated ρ_i, vary across locations? It does. The appropriate null hypothesis, however, is that the dispersion in ρ_i is equal to that from the estimated stochastic process. To construct this null distribution, simulate 50,000 minimum wage series of length 96 (the same length as in the data) based on the estimated stochastic process and estimate the same AR(1) regression.

Figure A1 plots the PDFs of the two distributions of ρ_i, where both distributions are centered at their respective medians (the median from regressions on data simulated from the stochastic process is 0.8895, and on the data is 0.9105.). Visual inspection of the Figure suggests that the dispersion in the estimated ρ_i in the data is very similar to what the estimated stochastic process would imply.

Appendix B.3. Simulation algorithm for uncertainty

This appendix describes how to simulate the model in section 6. This simulation takes into account the uncertainty in the wage path. Firms expect the minimum wage process to be that described in section 6.2. This modifies the algorithm described in the previous subsection in that the the present discounted values of prices and wages are computed via simulation.

The following describes how to simulate the present discounted value of wages and prices, and the product price, in a period given the log deviation.

• Given ε̂_i,t, simulate T periods of log deviations of real minimum wages using the stochastic process in appendix Appendix B.2: ${\left\{{\widehat{\epsilon }}_{i,t+j}\right\}}_{j=1}^T$.

• Convert to real levels using the long-run average in the real value of the minimum wage: w_i,t+j = w̄_i(1 + ε̂_i,t+j), where w_i,t is the real minimum wage and w̄_i is the long-run average of the real value of the minimum wage.

• Compute and store $q_{w,t}^s={\sum }_{x=1}^T{(\beta (1-\delta ))}^{x-1}{w}_{i,t+x}$.

• Repeat the previous three steps S times.

• For the present discounted value of wages: $q_{w,t}=\frac{1}{S}{\sum }_{s=1}^S{q}_{w,t}^s$.

• For the contemporaneous present discounted value of prices: $q_t={\alpha }^{(-\alpha )}{\left(\frac{q_{w,t}}{1-\alpha }\right)}^{(1-\alpha )}$.

• For next period’s expected present discounted value of prices: $E_t[q_{t+1}]=\frac{1}{S}{\sum }_{s=1}^S\left\{{\alpha }^{(-\alpha )}{\left(\frac{q_{w,t+1}^s}{1-\alpha }\right)}^{(1-\alpha )}\right\}$, where the $q_{w,t+1}^s$ are based on simulations using the period t wage.

• Compute the price: P_t = q_t − β(1 − δ)E_t[q_t+1].

Set T = 960 and S = 100.

The remaining aspects of the simulation are identical to the simulation with perfect foresight.

Appendix B.4. Dube, Lester & Reich (2010) dataset

Construct a county-level series of real quarterly minimum wages. Take the quarterly nominal minimum wages at the county-level from the Dube et al. (2010) dataset from 1984:I - 2007:IV (96 entries). Use as a measure of inflation the average hourly wage of production and non-supervisory workers from the Bureau of Labor Statistics (series code CES0500000008). This series is monthly. Convert it to quarterly using the geometric average of the three months. Create an index with 1984:I as the base period and equal to 1. Use this index to convert the nominal minimum wages to real minimum wages.³⁸

Then simulate a county-level employment series using realized variation in minimum wages. For each county, start with the real minimum wage series from 1984:I – 2007:IV. In particular, the regression in appendix Appendix B.2 implies for each county-period a real minimum log deviation pair: (rmw_it, ε̂_it). Feed through the sequence of ε̂_it to the algorithm described in the previous subsection. Start with employment in the steady state defined by average minimum wages from 1984:I–2007:IV. Use this steady state to define the adjustment ratio for high-skill labor.

To deal with initial conditions, copy this minimum wage series and expectations 10 times. This means that the first 96 entries are 1984:I–2007:IV, and the 97th entry is 1984:I. Run the resulting 960 periods through the algorithm and store the final 96 observations.

Appendix C. Additional specifications

Baker et al. (1999) present three long-run specifications. Two specifications filter the minimum wage series into their high and low frequency components. The last specification is the distributed lag specification already presented in the text.

First, the “informal” filter splits minimum wage movements into low and high-frequency components, where these components are defined as the two-period moving average and the first difference of minimum wages. Baker et al. use annual data and so to be consistent compute the moving average four periods apart and use fourth differences. This specification is:

$$ln{(\text{restemp})}_{\mathit{ipt}}=a_1+{\eta }_1\frac{{\mathrm{\Delta }}_4\text{ln}{(MW)}_{it}}{2}+{\eta }_2\frac{(\text{ln}{MW}_{it}+ln{(MW)}_{i-t-4})}{2}+a_2\text{ln}{(\text{totemp})}_{\mathit{ipt}}+a_3\text{ln}{(\text{pop})}_{it}+{\varphi }_i+{\tau }_t+{\tau }_{pt},$$

where η₁ is the elasticity with respect to high-frequency movements and η₂ is the elasticity with respect to low frequency movements. Table A3 shows that the low-frequency filter returns an elasticity on data simulated from the model of −0.07.

Second, the formal filter is based on a formal frequency decomposition of the natural log of the real minimum wage series. See Baker et al. (1999, pg. 334) for details, or Hamilton (1994, pg. 159) for a statement of the relevant theorem. Baker et al. decompose the real minimum wage series directly, I decompose the natural log. Doing the analysis in levels yields smaller coefficients on the simulated data. Following Baker et al. enter the nine lowest frequencies as five sums, where adjacent frequencies are summed starting from the lowest, except for the highest frequency. They report that they enter five frequencies, which are each the sum of two frequencies. The 10th frequency is a constant. The results are identical if the frequencies are entered separately. Table A4 shows that the lowest frequency movements in the minimum wage estimated on data simulated from the model yield elasticities of −0.07.

Table A1.

Probit model of the probability of a minimum wage increase

	Increase
Deviation	−6.673 (0.182)
Constant	−1.991 (0.016)
N	36480

Note: The outcome variable is an indicator for a minimum wage increase. The deviation is defined as the residual from a regression of log minimum wages on county fixed effects using 1984:I–2007:IV data. The sample is a modified form of the contiguous border county sample from Dube, Lester & Reich (2010), where duplicate counties are dropped.

Table A2.

Distributed lag specification

	Data	Model
ΔlnMW_(t)	0.082 (0.087)	−0.051 (0.001)
ΔlnMW_(t + 1)	0.093 (0.102)	−0.053 (0.001)
ΔlnMW_(t + 2)	0.087 (0.134)	−0.054 (0.001)
ΔlnMW_(t + 3)	0.087 (0.121)	−0.055 (0.001)
ΔlnMW_(t + 4)	−0.013 (0.087)	−0.060 (0.001)
ΔlnMW_(t + 5)	−0.010 (0.093)	−0.062 (0.001)
ΔlnMW_(t + 6)	−0.063 (0.082)	−0.066 (0.001)
ΔlnMW_(t + 7)	−0.065 (0.087)	−0.068 (0.001)
ΔlnMW_(t + 8)	0.029 (0.081)	−0.070 (0.001)
ΔlnMW_(t + 9)	−0.021 (0.091)	−0.072 (0.001)
ΔlnMW_(t + 10)	−0.003 (0.096)	−0.074 (0.001)
ΔlnMW_(t + 11)	0.019 (0.103)	−0.075 (0.001)
ΔlnMW_(t + 12)	0.012 (0.102)	−0.076 (0.001)
ΔlnMW_(t + 13)	0.024 (0.099)	−0.078 (0.001)
ΔlnMW_(t + 14)	−0.027 (0.119)	−0.079 (0.001)
ΔlnMW_(t + 15)	0.029 (0.121)	−0.081 (0.001)
ΔlnMW_(t + 16)	0.010 (0.116)	−0.082 (0.001)
ΔlnMW_(t + 17)	0.035 (0.141)	−0.084 (0.001)
ΔlnMW_(t + 18)	0.020 (0.147)	−0.085 (0.001)
ΔlnMW_(t + 19)	0.018 (0.134)	−0.086 (0.001)
ΔlnMW_(t + 20)	0.024 (0.109)	−0.087 (0.001)
ΔlnMW_(t + 21)	−0.052 (0.112)	−0.087 (0.001)
ΔlnMW_(t + 22)	−0.048 (0.113)	−0.088 (0.001)
ΔlnMW_(t + 23)	−0.022 (0.138)	−0.089 (0.001)
ΔlnMW_(t + 24)	0.012 (0.172)	−0.094 (0.002)
N	41448	41448

Note: The regressions also include a border pair times period interaction term, a measure of total employment and a measure of population. The outcome is total employment in the restaurant industry. The regressions use the contiguous border sample. The standard errors are clustered at the state and border segment separately. The data column reports estimates based on the data. The model column reports estimates based on data simulated from the putty-clay model.

Table A3.

“Lag operator” filtered effects of minimum wages.

	Data	Model
High Frequency Minimum Wage	0.166 (0.158)	−0.029 (0.004)
Low Frequency Minimum Wage	−0.008 (0.076)	−0.072 (0.002)
N	41448	41448

Note: The high frequency minimum wage is an annual log difference. The low frequency minimum wage is an annual log moving average. The other variables are in logs. The regressions also include a border pair times period interaction term, a measure of total employment and a measure of population. The outcome is total employment in the restaurant industry. The regressions use the contiguous border sample. The standard errors are clustered at the state and border segment separately. The data column reports estimates based on actual data. The model column reports estimates based on data simulated from the putty-clay model.

Table A4.

Frequency decomposition-based dynamic lagged specification.

	Data	Model
Lowest Frequency	−0.001 (0.122)	−0.067 (0.002)
Lower Frequency	0.017 (0.122)	−0.064 (0.003)
Medium Frequency	0.183 (0.135)	−0.064 (0.003)
Higher Frequency	0.116 (0.203)	−0.059 (0.006)
Highest Frequency	−0.015 (0.206)	−0.051 (0.008)
N	41448	41448

Note: The frequency decomposition is based on the logged real minimum wage series deflated using average hourly wage of private sector production and non-supervisory workers from 1987:2–2006:2. Lowest frequency are movements at a frequency at 19.2 year and 9.6 years; lower frequency are movements at 6.4 years and 4.8 years; medium frequency are movements at 3.85 and 3.2 years; higher is at 2.75 and 2.4; and highest is at 2.1 years. The regressions also include a border pair times period interaction term, a measure of total employment and a measure of population. The outcome is total employment in the restaurant industry. The regressions use the contiguous border sample. The standard errors are clustered at the state and border segment separately. The data column reports estimates based on actual data. The model column reports estimates based on data simulated from the putty-clay model.

Figure A1.

Persistence in the data and the estimated stochastic process

Note: This figure plots the PDF of the persistence coefficients of an AR(1) regression of minimum wages on lags of itself within location, with their median removed. The median from regressions on data simulated from the stochastic process is 0.8895, and on the data is 0.9105. The minimum wage is defined as the residual from a regression of log minimum wages on county fixed effects using 1984:I–2007:IV data. The sample is a modified form of the contiguous border county sample from Dube, Lester & Reich (2010), where duplicate counties are dropped. The procedure to generate the distribution from the stochastic process is given in Appendix B.2.1.