A population model of early rheumatoid arthritis disease activity during treatment with methotrexate, sulfasalazine and hydroxychloroquine

Abstract

Aims

To develop a population model describing the disease activity (DAS28) time course in patients with early rheumatoid arthritis (RA) treated with triple disease-modifying anti-rheumatic drug (DMARD) therapy (methotrexate, sulfasalazine and hydroxychloroquine).

Methods

DAS28 was obtained in 263 patients with early RA from initiation of therapy until 60 weeks. Using nonmem®, base models (DAS28 vs. time) and covariate influences were investigated for the population.

Results

The best model was an exponential model of DAS28 vs. time that was additive to baseline DAS28, with covariance between parameters, and a combined residual error model. Age and patient smoking history were covariates significantly affecting response to therapy. Population estimates were baseline DAS28 (5.7), extent of change in DAS28 (−2.8) and the half-life of disease activity (6.2 weeks; time to steady disease state achieved within approximately 30 weeks). Older individuals exhibited more severe baseline DAS28, described by a power function centred around 57 years (baseline DAS28 for 40- and 70-year-old patients were 5.4 vs. 5.8, respectively) and current smokers took longer to achieve a steady disease state (approximately 50 weeks). There was considerable within-patient random variability in DAS28 over time (empirical 90% CI for DAS28 in a population typical patient at 60 weeks: 1.8, 4.2 with median value of 2.8).

Conclusions

This is the first report of a disease activity model for early RA treated with triple DMARD therapy. Smoking and age were identified as covariates.

What is Already Known about this Subject

• A combination of methotrexate, sulfasalazine and hydroxychloroquine (triple disease modifying anti-rheumatic drug (DMARD) therapy) applied in a ‘treat-to-target’ approach is effective in reducing disease activity in rheumatoid arthritis.

• Less than half of patients with early rheumatoid arthritis treated with ‘triple DMARD therapy’ achieve remission, and many patients continue to have active disease and require alternative management strategies.

• An understanding of the differences in the rate and extent of change in disease activity during triple DMARD therapy could lead to individualized treatment strategies that minimize joint destruction and disease progression.

What this Study Adds

• The 28-joint disease activity score (DAS28) changes in response to triple DMARD therapy can be described using a population-based model where the typical patient has an exponential change in DAS28 from baseline to a new treated value, although between subject variability in response is relatively high.

• Population modelling of treatment outcomes for triple DMARD therapy may provide a tool to facilitate the early identification of individual patients with a poor disease trajectory.

• The residual unexplained variability in DAS28 was high, with potential implications for the interpretation of DAS28 in relation to disease trajectory.

Introduction

Rheumatoid arthritis (RA) is a systemic inflammatory autoimmune disease that affects approximately 1% of the population. It is characterized by pain and swelling in multiple joints and, in the long term, can lead to joint destruction and reduced quality of life 1,2. The cornerstone of medical management is the disease modifying anti-rheumatic drugs (DMARDs) which, when initiated soon after disease onset, reduce synovitis, joint swelling, pain and systemic inflammation, thus limiting progressive joint damage 2. Early treatment employing combinations of DMARDs, with frequent assessments and dosage adjustments until a pre-defined low disease activity state has been achieved (the treat-to-target approach) increases the proportion of patients whose RA enters remission and has the potential to minimize the proportion of patients progressing to expensive biological DMARDs 3. One such strategy is the use of triple DMARD therapy, a combination of methotrexate, sulfasalazine and hydroxychloroquine, which is very effective in reducing short and long term disease activity 4,5. Despite these contemporary treatment strategies, less than half the patients with early RA who commence pharmacotherapy soon after disease onset achieve remission, and consequently have ongoing active disease and develop joint damage 2,3.

Currently, dose adjustments using a treat-to-target strategy are based on disease activity, which is commonly measured by the 28-joint disease activity score (DAS28), a composite measure that encompasses the 28-swollen joint count, the 28-tender joint count, the erythrocyte sedimentation rate (ESR) and the patient global assessment (of disease activity; measured on a 100 mm visual analogue scale) 6. DAS28 is a continuous variable, but can be used to categorize RA disease activity as remission (DAS28 < 2.6), low (DAS28 2.6–3.2), moderate (DAS28 3.2–5.1) or high (DAS28 > 5.1) disease activity 7. Reducing DAS28 in the short term has been shown to improve long term outcomes by minimizing joint damage and maintaining physical function 8.

A number of key factors that affect an individual's response to DMARD therapy have been identified 9, but these have tended to be associated with a change in the empirical assessment of disease activity at discrete time points. The relationship between these factors and disease activity over the time period in which the altered response occurred is more difficult to study. Hence, there is limited understanding of how disease (e.g. anti-cyclic citrullinated peptide (anti-CCP) antibodies and rheumatoid factor [RF]) and patient-related (genetic e.g. shared epitope [SE], smoking status, body composition and age) factors systematically alter a patient's response to DMARD therapy and their subsequent extent or rate of change of disease activity.

One approach to integrating the relationships between triple DMARD therapy, intrinsic patient and disease-related factors and RA disease activity is to utilize pharmacometric analyses 10,11. Holford et al. have previously described the time course of RA disease activity when treated with a single DMARD that achieved phase II of development, and demonstrated how population analyses can improve clinical understanding of a drug and its impact on disease activity 12.

Given the relatively low remission rate with current treatment strategies, it is possible that other triggers for dose adjustment of DMARDs may result in improved short and long term outcomes for RA patients. Development of a population model that describes RA disease trajectory (including the effect of covariates) is an important first step in determining if utilizing these models via Bayes forecasting may be valuable in facilitating informed decisions to optimize pharmacotherapy earlier in RA. Using data collected over 14 years from an inception cohort of patients with early RA treated with treat-to-target triple therapy, the aims of this study were to:

1. develop a population model to describe the time course and between subject variability of RA disease activity (as measured by DAS28) following initiation of DMARD therapy,

2. identify patient factors affecting change in DAS28 in response to this regimen and

3. quantify the influence of random variability on the measurement of disease activity using DAS28.

Using this approach we hypothesized that a structural model for DAS28 following initiation of triple DMARD therapy, between-subject variability (BSV) in the DAS28 response and the magnitude of residual unexplained variability (RUV; comprised of intra-individual variability, model misspecification, measurement error (of DAS28 components such as 28-tender and swollen joint counts), etc.) in DAS28 could be constructed.

Methods

Data were obtained from 263 patients who attended the Early Arthritis Clinic (EAC) at the Royal Adelaide Hospital (RAH) for a total of 2080 visits between September 1998 and March 2012. Inclusion criteria required an age older than 18 years, a diagnosis of RA according to the 1987 Revised ACR Criteria 13 and no prior use of DMARDs. The baseline characteristics of the patient population are summarized in Table 1.

Table 1.

Baseline summary of the patient population

Characteristic		Value*	Missing data (%)
DAS28		5.6 (1.8–8.5)	0
Follow-up		52 (0–60)	0
Age (years)		57 (18–86)	0
Weight (kg)		72.5 (40.4–143.5)	22
BMI (kg m−2)		27.4 (16.1–60.5)	22
Gender	Female	187 (71%)	0
Smoking status	Never	123 (47%)	5
	Current	48 (18%)
	Past	79 (30%)
Corticosteroid†	Administration	125 (48%)	0
anti-CCP	Positive	143 (55%)	2
Rheumatoid factor	Positive	155 (59%)	0
Shared epitope	Positive	159 (64%)	6

^*Continuous variables are represented as median (minimum–maximum) and categorical variables are represented as the proportion of individuals with that characteristic when excluding missing data. BMI = body mass index; anti-CCP = anti-cyclic-citrullinated-peptide antibodies at diagnosis.

^†‘Corticosteroid administration’ consists of those individuals who received any dose of i.a., i.m. or oral corticosteroids throughout the 60 week period. Doses administered were converted to oral prednisolone equivalent doses with a mean of 0.93 mg day⁻¹.

Subjects were treated according to a standardized DMARD regimen consisting of methotrexate (10 mg week⁻¹ with folic acid 0.5 mg day⁻¹), sulfasalazine (500 mg day⁻¹ increased by 500 mg day⁻¹ week⁻¹ to 1000 mg twice daily) and hydroxychloroquine (200 mg twice daily) as described in Proudman et al. 3. Intra-articular (i.a.; 40 to 80 mg methylprednisolone acetate) and intramuscular (i.m.) corticosteroid injections (80 to 120 mg methylprednisolone acetate) were administered at the physician's discretion. Oral corticosteroids and non-steroidal anti-inflammatory drugs (NSAIDs) were actively discouraged, but were used if deemed necessary by the treating physician. DMARD doses were increased to a maximum of 25 mg week⁻¹ for methotrexate and 3000 mg day⁻¹ for sulfasalazine in response to active disease in accordance with predefined disease activity criteria 3. Approval was obtained from the RAH Human Research and Ethics Committee (RAH Protocol Number: 120618) and all patients gave informed consent.

Patient data

At the initiation of triple therapy (regarded as ‘baseline’ in this study), patient age, gender, height, weight, smoking status, co-morbidities, full blood count, liver function, serum creatinine, SE status, anti-CCP and RF titre were recorded. Disease activity was assessed at baseline and at each follow-up visit until 60 weeks after the initiation of therapy by assessment of 28-tender joint count, 28-swollen joint count, ESR and patient global assessment, from which DAS28 was calculated 14. All corticosteroid and NSAID use, and the DMARDs administered (and their doses) were recorded at each clinic visit. Patients were also questioned about side effects to DMARDs, and full blood count and liver function were recorded at each visit. Visits typically occurred every 3 to 6 weeks until disease was stable, in which case visits occurred every 3 months. Before the population modelling commenced, missing values for continuous covariates were imputed with the median and those for categorical covariates were imputed with the mode of the available data using the R® Software (Version 2.15.2, 2012). The maximum amount of missing data was 22% for weight and BMI, with many covariates having no missing data (Table 1).

Base model development

Population modelling was of the dependent variable, DAS28, against the independent variable time since initiation of DMARD therapy, and used nonmem® Version VII Level 2.0 (ICON Dev. Soln., Ellicott City, MD) 15 with the Wings for nonmem (Version 720) interface (http://wfn.sourceforge.net/) and the G95 Fortran complier. Population parameter estimation used the first order conditional estimation with interaction (FOCE-I) method and individual parameter estimates were obtained using the Bayesian POSTHOC functionality of nonmem®. The disease activity model was based on DAS28 collected from the initiation of triple DMARD therapy until 60 weeks of treatment. A logit transform was employed to constrain the predicted DAS28 values within a plausible range of 0 and 9.2 (corresponding to 28 swollen and tender joint counts, 100 mm on the visual analogue scale for patient global assessment and 120 mm h⁻¹ ESR).

Structural models

To describe RA disease activity, structural models of linear, quadratic, E_max, sigmoidal E_max, exponential or Weibull functions of transformed DAS28 (DAS28_t) vs. time (t), either additive or proportionally additive to baseline DAS28 (BASE), were tested (model equations presented in Supplementary Material).

Random effect models

Population parameter variability (PPV) was added to structural model parameters to account for different time courses of DAS28 between subjects and was represented using either a log normal (equation 1) or a normal (equation 2) distribution as appropriate:

1

2

where P_j was the individual value for the parameter in the j^th individual, θ_S was the population mean and η_j was an independent random variable describing the variability in θ_S among individuals with a mean of 0 and variance, ω². Equation 1 was used in candidate models where it was not biologically or structurally plausible for the parameter to be less than 0. Models with and without covariance for random effects were also investigated using a variance-covariance matrix and the OMEGA BLOCK functionality of nonmem®.

A combined (proportional and additive) residual error model, as described in equation 3, was tested. Proportional and additive residual error models alone were also considered.

3

where LGT3 was the observed DAS28 at time, t, in the j^th individual in the logit domain, DAS28_tj was the model predicted DAS28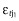, and and 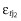were normally distributed error terms with means of 0 and variances of σ₁² and σ₂² for proportional and additive error terms, respectively.

Model selection

Model selection was based on a composite of goodness-of-fit criteria including numeric and graphical tests. The Akaike Information Criterion (AIC) was used to compare non-nested models and candidate models with lower AIC values were ranked higher for base model selection. Candidate base models were considered for further analysis if standard errors of θs were less than 30% and ηs were less than 50%. The validity of inferring individual parameter estimates was assessed by η-shrinkages, as provided by nonmem®, for each of the population parameters. Diagnostic plots used to assess model performance included the distribution density of observed vs. individual predicted (IPRE) DAS28 at 0, 26, and 52 weeks, observed vs. population predicted (PRED) or IPRE, conditional weighted residuals (CWRES) vs. weeks or PRED, distribution density of residuals and quantile−quantile (QQ) plot of residuals.

Covariate analyses

Covariates that were highly correlated with weight (e.g. BSA and BMI), serum creatinine (as a marker of renal function, e.g. creatinine clearance) or constituents of the DAS28 (e.g. tender and swollen joint counts, ESR and patient assessment of disease activity), were judged as surrogate markers, and therefore were excluded from covariate analyses. There was also a very low frequency of ethnicities other than Caucasian (91%). Therefore with a low power to detect covariate effects, ethnicity was not tested. Resultant patient characteristics to be investigated included DMARD doses, use of corticosteroids (i.e. time points where patients received i.a. or i.m. corticosteroids, patients who received no, local or systemic corticosteroids), use of alternative management (i.e. time points where patients received leflunomide or gold salts), gender, presence of RF and anti-CCP antibodies at diagnosis, and carriage of the SE, smoking status, weight, height and age.

The effect of a categorical covariate on a parameter was represented as a binary relationship. For example, the effect of gender on baseline disease severity (BASE) was described as:

4

where SEXCOV had a value of 0 for males and 1 for females. Therefore, BASE_j had the value of BASE_POP for males and BASE_POP·(1 + θ_SEX) for females, θ_SEX was the estimable parameter for the effect of female gender on BASE and BASE was normally distributed across the population.

The effect of a continuous covariate on a parameter was represented as a power function referenced to the median of the observed data. For example, the effect of weight (WT) on maximum change in disease severity (WE1) was described as:

5

where WE1_tj was the estimate for the change in disease severity for the j^th individual at time t, WE1_POP was the population mean, WT_tj was the weight calculated for the j^th individual at time t, WTS was the median weight value for the observed data, θ_WT was the estimable parameter for the effect of weight on WE1 and WE1 was normally distributed across the population.

The effects of drug doses on a parameter were represented as a linear function:

6

where WE1_tj was the estimate for the change in disease severity for the j^th individual at time t, WE1_POP was the population mean, MTX_tj was the methotrexate dose for the j^th individual at time t, θ_MTX was the estimable parameter for the effect of methotrexate dose on WE1 and WE1 was normally distributed across the population.

All covariates were empirically tested on all parameters. The effect of incorporating an additional covariate parameter compared with the base model was assessed by the likelihood ratio test (LRT). The covariate model was considered to be significantly better than the base model if the P value of the LRT was less than 0.01. Candidate covariates also needed to satisfy additional criteria; precision error of the estimable parameter for the covariate less than 51.2%, the addition of the covariate on the parameter reduced the PPV of the parameter, and improved simulation performance of the model as judged by a visual predictive check (VPC) of 1000 simulations facetted for covariate values/categories. All covariates shown to be significant from univariate analyses were then arranged into all possible combinations to be tested in multivariate analyses. The total number of covariate combinations was limited if significant covariates had a similar influence on the model. For example, if corticosteroid use represented as the clinic visit where i.m. corticosteroids were administered and corticosteroid use represented as at least one dose of systemic corticosteroids (i.m. or oral) within the 60 week period were both found to affect the BASE parameter significantly, the combination of these two covariates was not tested. Of the possible tested combinations and previous univariate models, the model with the lowest P value (as well as fulfilling the above described selection criteria) compared with the base model was the final model.

Model evaluation

The simulation performance of key models was evaluated by prediction-corrected VPCs using the final parameter estimates to simulate 1000 datasets based on the patient data in the index dataset. An assessment of autocorrelation of residuals was also performed in order to examine whether there were systematic changes in DAS28 not captured by the model, for example a non-random cyclical fluctuation of symptoms.

Simulations

The final model was used to demonstrate the impact of RUV in the DAS28. A simulation was performed for the population typical patient to compare the range of possible DAS28 calculated at a given clinic visit (as nominated by DV in nonmem®) with the underlying disease state as predicted by the model (PRED). To remove the impact of BSV, PPV terms in the final model were fixed to zero. This simulation model was then used to simulate the time course of DAS28 for 2000 population typical patients once a week for 60 weeks. The population predicted DAS28 (PRED) and empirical 90% CIs of simulated DV DAS28 were then determined.

Results

Characteristics of the study population

The study population consisted of 263 subjects (Table 1). The median baseline DAS28 was 5.6, indicating severe disease activity. On average, the study population experienced a decrease in DAS28 of approximately 2 and steady disease state was typically achieved after approximately 25 weeks of triple DMARD therapy (Figure 1). The median number of DAS28 observations collected from each individual was 8, ranging from 1 observation at the initiation of triple therapy to 15 across the 60 week period. The median age at the initiation of triple therapy was 57 years and the age range was 18 to 86 years.

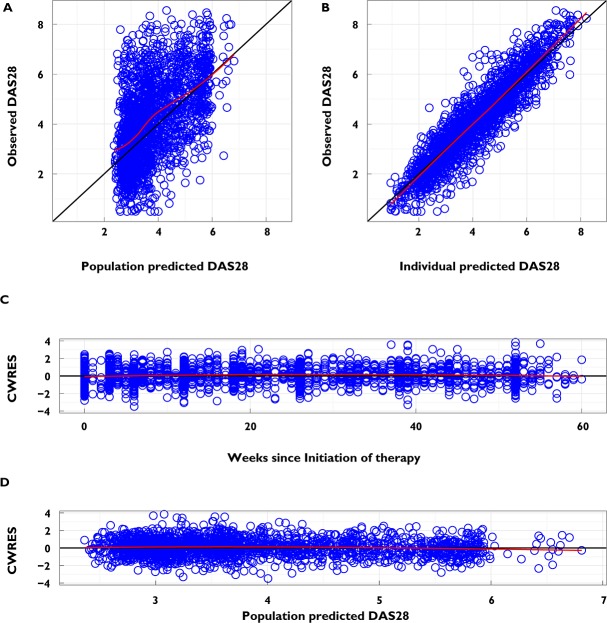
Figure 1.

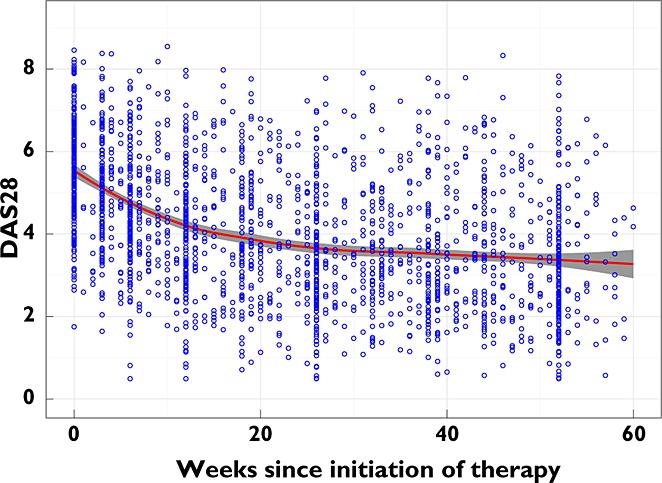
Observed data. Blue circles represent the DAS28 observed in the study population, the red line is a loess-smoothed line and the grey ribbon shows the 95% confidence intervals of the smoothed line

Model development

The best structural model obtained the lowest AIC value of 1951 and was an exponential function additive to baseline DAS28 (equation 7), with covariance between all random parameters (PPV for BASE, EX1 and EX2) and a combined residual error model.

7

where DAS28_t represents the DAS28 at time, t, BASE is baseline DAS28, EX1 is the maximum change in DAS28 and EX2, is the first order rate constant for change in DAS28.

PPV in BASE and EX1 parameters was normally distributed, whereas PPV for EX2 was log normally distributed. In all models tested, the change in DAS28 was best described as additive to baseline DAS28. The best linear and quadratic structural models provided inferior fits to the data than the best exponential model and demonstrated increases in the AIC by 434 and 162 units, respectively. E_max and sigmoidal E_max models were an improvement on linear and quadratic models. However they still exhibited a poorer fit compared with the best exponential model (12 < ΔAIC < 26). Weibull models were superior to linear, quadratic, E_max and sigmoidal E_max models, but collapsed to an exponential model as WE3 tended to less than or equal to 1. While Weibull models were able to incorporate a delay in DMARD effect at the initiation of triple therapy, models with this structure estimated the WE3 parameter poorly (precision error of 79%).

For the covariate search, all univariate models were an improvement over the base model as indicated by lower minimum objective function values. However, only 18 proved to be significant improvements at the P < 0.01 level, and of those, only seven fulfilled the additional model selection criteria.

The univariate analyses revealed that the effect of age and administration of i.m. corticosteroids on the BASE parameter significantly improved the fit of the model (P < 0.0001). The addition of systemic corticosteroid use (patients who received either i.m. or oral corticosteroids at any time throughout the 60 week period) to the EX1 parameter also showed a significant improvement of the model to the observed data (P = 0.003). It also showed that smoking status had a substantial effect on two of the population parameters of the model (BASE represented as never, current or past smoker [P = 0.009] and EX2 as never/past versus current smoker [P = 0.002]).

The final model (equation 9, Table 2) included age and i.m. corticosteroid administration on BASE, any systemic corticosteroid use throughout the 60 week period affecting the maximum change in DAS28 (EX1), and smoking status affecting the rate (EX2) of this change (ΔAIC by −53).

8

where CSIM = 1 and BASE = 0.820 at times where the patient received i.m. corticosteroids and CSIM = 0 and BASE = 0.472 if not (for age 57 years), where CSSYS = 1 and EX1 = – 0.977 if the patient received systemic (i.m./oral) corticosteroids at any time point throughout the 60 week period and CSSYS = 0 and EX1 = −1.28 for if they did not, where SMOKING = 1 and EX2 = 0.067 for current smokers and SMOKING = 0 and EX2 = 0.111 for never/past smokers.

Table 2.

Parameter values for the final model

Parameter		Description	Estimate (95% CI)	Shrinkage (%)
Population parameter
BASE	θ1	Baseline DAS28	0.472 (0.392, 0.552)
	θ4	Effect of age	0.672 (0.406, 0.938)
	θ5	Effect of i.m. corticosteroid administration on BASE	0.737 (0.379, 1.095)
EX1	θ2	ΔDAS28	−1.28 (−1.17, −1.39)
	θ6	Effect of systemic corticosteroids on EX1 (during 60 week period)	−0.237 (−0.079, −0.394)
EX2	θ3	Rate constant, week−1	0.111 (0.093, 0.129)
	θ7	Effect of currently smoking on EX2	−0.398 (−0.145, −0.651)
Population parameter variability
BASE (η1)	ω1	SD	0.492 (0.348, 0.636)	13.3
EX1 (η2)	ω2	SD	0.740 (0.536, 0.945)	14.4
EX2 (η3)	ω3	% CV	86.1 (42.1, 130)	30.9
Covariance
θ1, θ2	ω1,2	Covariance between BASE and EX1	−0.376
θ1, θ3	ω1,3	Covariance between BASE and EX2	−0.137
θ2, θ3	ω2,3	Covariance between EX1 and EX2	0.651
Combined residual error
Proportional error	σ1	% CV	18.4 (0, 37.5)
Additive error	σ2	DAS28 units (SD)	0.327 (0.249, 0.405)

Description of the final model

The mean population estimates of structural parameters were a baseline DAS28 of 5.7, extent of response to DMARD therapy was a decrease in DAS28 of 2.8 from the initiation of therapy up until 60 weeks after, and the first order rate constant for decline in disease activity was 0.111 week⁻¹. The final model demonstrated an acceptable description of the data, as assessed by key diagnostic plots (Figure 2). The final parameter values for the model are given in Table 2 and were estimated with acceptable precision. In summary, DAS28 was found to decline exponentially over time with a typical population half-life of 6.2 weeks (10.4 weeks for current smokers). DAS28 was found to be correlated with higher disease activity at observations where i.m. corticosteroids were administered, such that in a population typical patient (age 57 years, never smoked) who received i.m. corticosteroids at baseline, DAS28 was 6.4 compared with 5.7 in a population typical patient who did not receive i.m. corticosteroids at baseline. Systemic corticosteroid use was associated with a higher final DAS28 compared with not using systemic corticosteroids (ΔDAS28 −2.2 vs. −2.8, respectively). There was high BSV in all model parameters and RUV was also very high (Table 2).

Figure 2.

Diagnostic plots for the final model. (A) Observed DAS28 vs. population predicted DAS28. Data should be evenly distributed about the line of identity, indicating no major bias in the population component of the model. (B) Observed DAS28 vs. individual predicted DAS28. Data should be evenly distributed about the line of identity, indicating an appropriate covariate model could be found for each individual. (C) Conditional weighted residuals vs. weeks since initiation of therapy. Data should be evenly distributed about 0, indicating no major bias in the structural model. (D) Conditional weighted residuals vs. the population predicted DAS28. Data should be evenly distributed about 0, indicating no major bias in the residual error model. The black line is a line with slope of 1 or 0, and the red line is a loess-smoothed line for the data

Model evaluation

The model showed acceptable predictive performance when assessed by prediction-corrected visual predictive checks (Figure 3).

Figure 3.

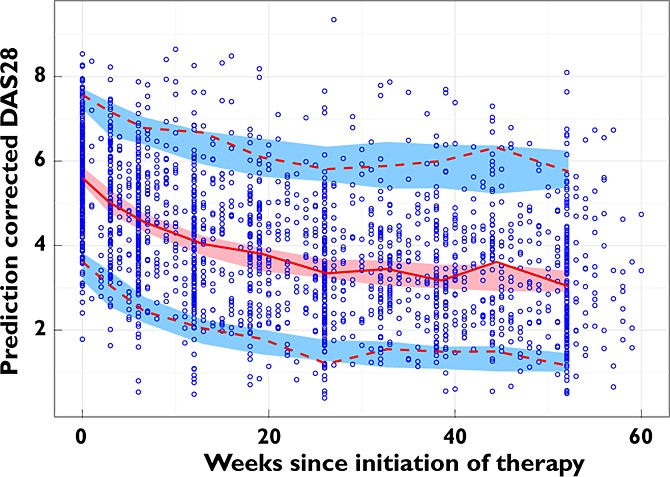
Prediction-corrected visual predictive check of the final model. The prediction-corrected observed data are represented by blue circles, a red solid line (median), and the red dashed lines (5^th and 95^th percentiles). The prediction-corrected simulated DAS28 are represented by the red shaded area (empirical 95% confidence interval of median) and the blue shaded areas (empirical 95% confidence intervals of 5^th and 95^th percentiles). Statistical data were binned into 10 groups to calculate the median and 5^th and 95^th percentiles without the lines being influenced by areas of sparse data. The model predictions overlay the observed data with good agreement, and show the progressive drop in DAS28 from the baseline value to a new treated level

Impact of residual unexplained variability in measured DAS28

The residuals for the final model showed no evidence of autocorrelation (Figure 4), suggesting that RUV in DAS28 was not due to a failure of the model to capture a non-random cyclical fluctuation of disease. The impact of RUV alone on DAS28 for the population typical patient's disease time course is shown in Figure 5. It is most notable that at any time the empirical 90% CIs of DAS28 typically span 2 units, allowing for conclusions of ‘remission’ or ‘severe’ disease activity despite the true underlying time course of improvement in disease status.

Figure 4.

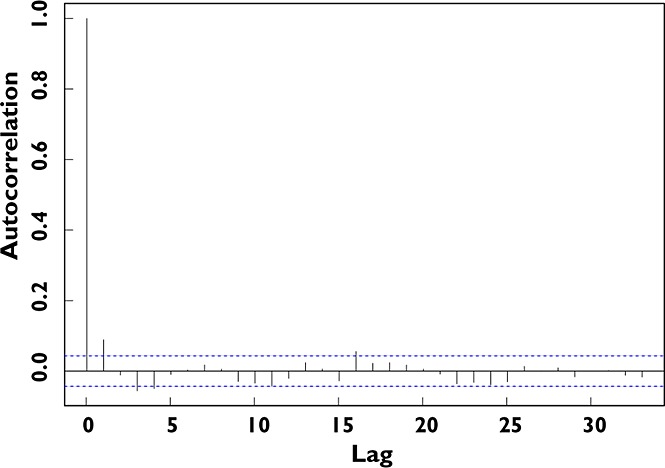
Autocorrelation of residuals. An autocorrelation plot of the conditional weighted residuals (CWRES) for the final model, where the residuals are treated as a discrete time series (i.e. consecutive observations). The plot shows the similarity between CWRES observations as a function of the time lag between them. The horizontal axis represents the lag between two observed CWRES values (e.g. a lag of 5 indicates the comparison of two residuals 5 observations apart in time). The vertical axis is the autocorrelation for all residuals with a given lag, with 1 and −1 indicating perfect correlation (a high chance of a repeating pattern) and 0 indicating no repeating pattern. The autocorrelation was minor for all non-zero lags (0 lag indicating correlation of an observation with itself)

Figure 5.

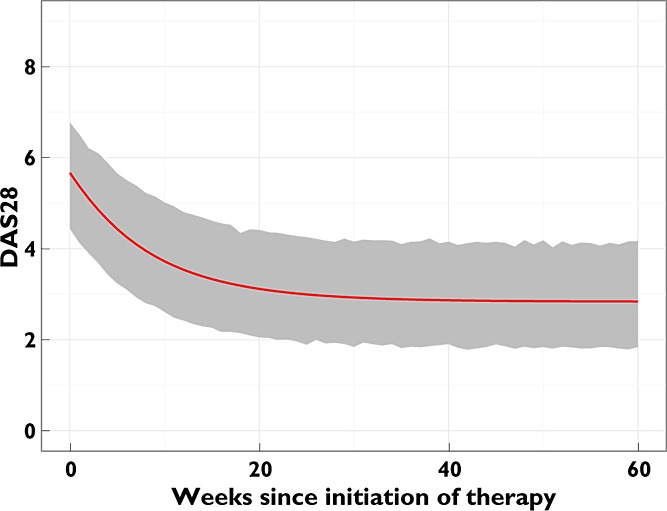
Impact of RUV on measured DAS28. Simulation of the time course of DAS28 for 2000 population typical patients (57 years old, non-smoker, and did not receive any i.m. or oral corticosteroids during the 60 week period) for 60 weeks. The PRED DAS28 time course is represented by the red line and empirical 90% confidence intervals of simulated DAS28 by the grey shaded area

Discussion

For the first time, a model has been developed that accurately describes the time course of RA disease activity over the first 12 months in a population of patients treated with triple DMARD therapy. It was found that the DAS28 in a typical patient declined in an exponential manner to a new final treated value, but that BSV in baseline disease activity and the extent and rate of response to triple therapy was high. Variability in the DAS28 time course was, to some extent, explained by age, smoking status and corticosteroid therapy. Development of the model revealed several important properties of the disease's response to triple DMARD therapy.

Relationship of rate of response to baseline DAS28

It has been proposed that increased RA severity at baseline results in reduced ability to achieve low disease activity after 12 months of DMARD therapy 16. This analysis indicated that models that incorporated baseline DAS28 to affect the rate and extent of disease activity (so called ‘proportionally additive’) failed to describe adequately baseline DAS28 when compared with models that did not consider baseline DAS28 as an influence of disease activity (‘additive’ models). As such, the extent and rate of change in disease activity appeared to be independent of baseline disease severity. Due to the greater decrease required to achieve low disease activity after 12 months of triple DMARD therapy, individuals with higher baseline DAS28 were less likely to achieve such a goal.

Influence of covariates

Covariate analyses revealed that age, corticosteroid use and smoking status were factors that significantly improved the fit of the model to the observed data. Older age has previously been shown to be a significant predictor of failing to achieve remission at 6 months 17. The effect of age revealed that individuals older than 57 years (population median age) had more severe disease activity at baseline rather than a difference in the rate of change in disease activity. The effect of receiving i.m. corticosteroids on BASE was the most significant factor that improved the fit of the model to the observed data. I.m. corticosteroids, when added to the BASE parameter, allowed for a vertical shift in disease activity at times they were administered, i.e. bouts of higher disease activity, such as flare-ups, in the disease trajectory. In addition to effects on BASE, administration of systemic (i.e. i.m. or oral) corticosteroids on the EX1 parameter further improved the fit of the model and allowed for the model to describe the time course of those who obtained an insufficient response that required concomitant systemic corticosteroid therapy. Alternatively, corticosteroids are associated with improved responses in RA 18 and therefore it is possible that individuals who received them obtained a different response to triple DMARD therapy compared with those who did not. However, within our cohort, single dose i.m. corticosteroids and low dose oral corticosteroids were usually given to individuals with high disease activity, so the improved ability of the model to describe disease activity may simply be reflecting this practice.

The covariate analyses also showed that current smokers had an impaired rate of response to triple DMARD therapy when compared with non- and past-smokers. The effects of smoking upon response is consistent with prior findings, showing that current smokers achieve diminished responses or are less likely to achieve remission when compared with current non-smokers 19,20. The model identified that current smokers achieved 60% of the rate of change in DAS28 of non- and past-smokers (effect of current smoking on EX2 −0.398).

Whilst age and smoking status were identified as covariates and were consistent with previous findings, other documented factors were not identified through this modelling analysis. The presence of the SE, anti-CCP antibodies, RF and female gender are documented as predictors of poorer response 17,21,22. However, when added on their own, none was considered to be a significant contributor to improving the fit of the model. These differences could be attributable to differences in the conservative modelling approach used compared with a traditional statistical approach, or the distribution of characteristics within the population and different treatment regimen used. In addition, many of these markers, such as SE, smoking status and anti-CCP antibodies are highly related 23.

The treatment regimen utilized a treat-to-target protocol where drug doses were increased in response to poor disease control. As expected, drug doses were not identified as covariates and their exclusion does not imply that increasing drug doses is ineffective at reducing disease activity. Titrating drug doses based on disease severity could explain why gender and RF and/or anti-CCP positive disease did not significantly affect disease activity, as their effects were accounted for by higher doses. In addition, despite a treat-to-target protocol, it could be considered that the impact of smoking and age could not be overcome by dose titration.

Potential clinical implications

Pharmaceutical benefits scheme and progression to biological agents

The potential clinical implications of the model developed here are illustrated by the current regimen for public funding of DMARD therapy in Australia. Given the expense associated with biological DMARDs, the Australian Pharmaceutical Benefits Scheme (PBS) has strict criteria that must be fulfilled prior to approving a financial subsidy to patients using these agents. For example, the patient must complete an adequate trial of conventional agents, which is defined as the use of conventional DMARDs for at least 6 months, where at least 3 months must be combination therapy with methotrexate (at a weekly dose of at least 20 mg) and one of either hydroxychloroquine, sulfasalazine or leflunomide 24. Currently there is no mechanism to estimate whether an individual has achieved their maximum response to conventional DMARD therapy and therefore no longer receiving additional benefit to warrant regimen adjustment at 6 months. In individuals achieving a steady disease state (where no further benefits of therapy are gained) prior to 6 months, but are experiencing active RA, there is a risk of under suppression of inflammation and joint erosion whilst waiting to meet the requirements for the PBS subsidy of biological agents. Conversely, those who achieve maximum response later than 6 months may fulfil the PBS requirements at this time, but since they have not experienced the full benefit from the conventional agents, the expense of biological agents may be unnecessary. Therefore the question arises, is 6 months an adequate guideline with regards to adding expensive biological DMARDs to a patient's regimen?

Residual unexplained variability of DAS28

Although a relatively high degree of RUV in DAS28 was observed (Table 2, Figure 5), this is likely to be characteristic of actual fluctuations in RA disease activity and the DAS28 itself, as it includes subjective measurements and non-RA-specific assessments which can be influenced by different clinicians and intercurrent illnesses at discrete time points 25. It is important to note that the large residual variability is not likely to be due to the model failing to capture non-random cyclical fluctuations of disease activity, as demonstrated by a lack of autocorrelation of the residuals (Figure 4). The model developed here, however, may provide the basis of a tool with which these issues can be more formally investigated. Long term outcomes in RA have been significantly improved by regular measurement of disease activity scores such as the DAS28, and intensification of therapy if pre-defined treatment targets are not met 26. As shown in Figure 5, DAS28 decreases between clinic visits in the population typical patient, but due to the high residual variability, differences in measured DAS28 between visits can range from remission to significant worsening, despite only minor changes in the underlying disease trajectory. These results suggest that, in the context of this high residual variability, the true underlying time course of disease activity (and hence any decision to modify treatment) may be better inferred from multiple observations of DAS28 rather than a single current DAS28 observation. Whilst a clinician can map the trend of a patient's disease status, this requires a degree of clinical judgement, and the residual variability demonstrated in this study is sufficiently large to suggest that there is a potential risk of basing decisions on the ‘noise’ in DAS28 rather than the true changes in disease status. Quantifying the magnitude of this variability may have important implications for the interpretation of DAS28 in the clinic, and it is possible that the use of multiple DAS28 measurements as the basis upon which to make changes to treatment could result in additional benefits over and above those already achieved by the use of disease activity scores.

Limitations and future directions

Pharmacometric models and Bayesian forecasting may potentially provide a method for supporting the decision making process regarding dose adjustment and combination treatment strategies. This process takes into account prior information from a model and individual observed assessments of disease activity to guide new estimates of the time course of disease activity for the patient and accounts for the inherent RUV 27. However, a limitation of the application of the disease activity model is its generalizability to other early RA patient populations. This includes the treatment strategy employed, as the use of triple DMARD therapy is relatively intense compared with other regimens such as single agent methotrexate, and the strict treat-to-target protocol used. The model was not validated by an external dataset, and this will be required to determine whether it is representative of a different early RA patient population or treatment with a different DMARD protocol.

Furthermore, the model in its present form is not be suitable for forecasting disease activity. The reasons are predominantly due to the representation of corticosteroids not being predictive of response (rather explanatory) to triple DMARD therapy and the displayed high RUV would add noise to a forecast. Rather, the model provides a good description of the time course of DAS28 in a cohort of early RA patients treated with triple DMARD therapy using a treat-to-target strategy.

Understanding the model's limitations with respect to direct clinical application has opened investigation to identifying RA disease activity measures that are associated with less noise and developing a RA disease activity model with improved predictive capabilities that can ultimately be used to conduct simulation studies and forecast disease activity in a clinical setting via Bayesian methods.

In conclusion the population modelling process has identified patient factors (age and smoking status) correlated with differences in observed response that are consistent with previous literature, whilst other known ones (such as SE, anti-CCP antibodies and RF) were not. It is anticipated that informed decisions using a model-based analysis might eventually allow clinicians to optimize pharmacotherapy at more appropriate times, which will subsequently reduce the risk of joint erosions and increase the quality of life for RA patients.

Competing Interests

All authors have completed the Unified Competing Interest form at http://www.icmje.org/coi_disclosure.pdf (available on request from the corresponding author) and declare no support from any organization for the submitted work, no financial relationships with any organizations that might have an interest in the submitted work in the previous 3 years and no other relationships or activities that could appear to have influenced the submitted work.

The authors acknowledge that the Australian Centre for Pharmacometrics is an initiative of the Australian Government as part of the National Collaborative Research Infrastructure Strategy.

Supporting Information

Additional Supporting Information may be found in the online version of this article at the publisher's web-site: