Skip to main content
PMC home page
Nucleic Acids Research logoLink to Nucleic Acids Research
. 2004 Jul 1;32(Web Server issue):W64–W68. doi: 10.1093/nar/gkh451

CRASP: a program for analysis of coordinated substitutions in multiple alignments of protein sequences

Dmitry A Afonnikov 1,2,*, Nikolay A Kolchanov 1
PMCID: PMC441589  PMID: 15215352

Abstract

Recent results suggest that during evolution certain substitutions at protein sites may occur in a coordinated manner due to interactions between amino acid residues. Information on these coordinated substitutions may be useful for analysis of protein structure and function. CRASP is an Internet-available software tool for the detection and analysis of coordinated substitutions in multiple alignments of protein sequences. The approach is based on estimation of the correlation coefficient between the values of a physicochemical parameter at a pair of positions of sequence alignment. The program enables the user to detect and analyze pairwise relationships between amino acid substitutions at protein sequence positions, estimate the contribution of the coordinated substitutions to the evolutionary invariance or variability in integral protein physicochemical characteristics such as the net charge of protein residues and hydrophobic core volume. The CRASP program is available at http://wwwmgs.bionet.nsc.ru/mgs/programs/crasp/.

INTRODUCTION

Multiple sequence alignment can provide information for comparative analyses of proteins. Analysis of the variations in amino acids at different alignment positions allows inferences to be made about the structural–functional role of residues at these positions and to predict protein structure (1–3).

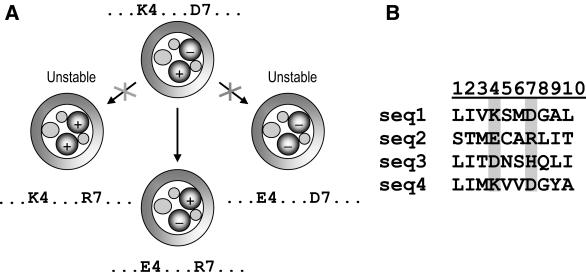
Useful information can also be obtained by covariation analysis of amino acid substitutions at protein sequence positions (4). The analysis proceeds on the assumption that substitutions between functionally interacting residues may be mutually constrained; in other words, the effect of substitutions in these residues, in terms of energy, is non-additive (5–7). There is experimental evidence indicating that proteins contain pairs of amino acids that appear to covary (8–10). In sequence alignments of homologous proteins, these interactions can be manifested in correlations between substitutions at pairs of alignment positions (11–13). A pair of salt-bridge-forming residues that vary interdependently is given as an example in Figure 1.

Figure 1.

Figure 1

Open in a new tab

(A) A schematic representation of coordinated substitutions in a pair of amino acid residues forming a salt-bridge in a putative protein. (B) Proteins that contain residues of the same charge at positions 4 and 7 are unstable and are eliminated during evolution; in contrast, those containing residues of different charges are stable and can occur in multiple sequence alignments.

A range of methods for the detection of coordinated substitutions are now being used in analyses of the sequences of protein families, e.g. fold recognition (14), predictions of the spatial structure of proteins (15), protein–protein interactions (16) and inter-residue contacts (17,18).

An important feature of coordinated substitutions is their additional contribution to the invariance of the integral physicochemical characteristics of a protein, such as the total volume and net charge; their invariance may result from the pressure of selection either on the entire protein or on its functionally or structurally significant parts (19,20). Information on these characteristics would facilitate predictions of the functional motifs in proteins (21).

Therefore, multifunction computer programs are needed for the analysis of functionally linked covarying substitutions in sequence alignments. We have developed the CRASP program package for this purpose. CRASP allows statistical evaluation of pairwise correlations between physicochemical property values at protein positions and of the significance of the contribution of coordinated substitutions to the invariance or variability of the integral physicochemical characteristics of a protein. The algorithm has been described in detail elsewhere (22).

METHODS

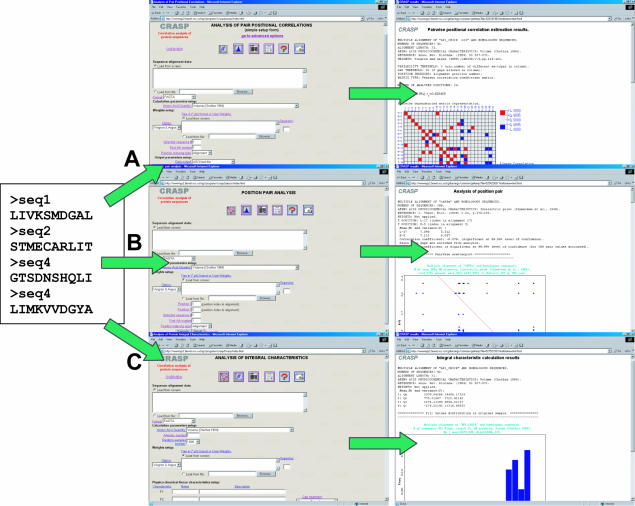
The program package CRASP consists of three modules. Two modules are designed for the detection of dependent amino acid substitutions at a pair of a positions of a protein sequence alignment and the third serves to estimate the statistical significance of the contribution of coordinated substitutions to the variability of the integral physicochemical characteristics of a protein. Figure 2 shows schematically how the program package CRASP works.

Figure 2.

Figure 2

Open in a new tab

The program package CRASP. The three main modules for analysis of coordinated substitutions accept multiple sequence alignments and enable the estimation of (A) pairwise covariation between the physicochemical property values at protein positions, (B) analysis of dependencies at specific position pairs and (C) the contribution of covarying substitutions to the invariance or variability in integral physicochemical characteristics.

Relationships between amino acid substitutions at a pair of positions in multiple sequence alignments

Analysis is based on the assumption that functionally significant coordinated substitutions of residues in proteins result from physicochemical interactions (electrostatic, steric, hydrophobic, among others). The interactions are dependent on the physicochemical property values of the residues (23). For this reason, correlations between the values at a pair of covarying positions of a protein may be evidence not only of coordinated amino acid substitutions at these positions, but also of the specificity of the interaction between two residues in a protein. When the correlation coefficient is negative, an increase in the value of a property at position i will make more likely a substitution at position j that will result in a decrease in the value of the property. In such a case, one is dealing with a net value compensatory substitution of the property at positions i and j. For example, for the pair of residues in Figure 1 the correlation for the charge property value is negative. When the correlation coefficient is positive, it may be assumed that substitutions are compensatory for the difference between the property values of two residues.

For a given physicochemical characteristic, the CRASP program is able to estimate correlation coefficients of two types, Pearson's and the paired conditional (partial) (22). The latter estimates the mutual relationship between a pair of positions of a protein provided that the property values at the other positions of the protein remain unaltered (24). This eliminates the effect of mediated correlations arising when interrelated substitutions at residue pair i, j may result from their interaction with a third residue at position k (25). Our previous analysis of a numerical model of evolving proteins with interacting residues has demonstrated that conditional correlation coefficients enable one to decrease considerably the proportion of correlation coefficients resulting from indirect interactions (26).

In estimating the significance of the correlation coefficients, it is important to remember that homologous sequences are not statistically independent of one another because they share common evolutionary ancestry. As a consequence, the variation in the correlation coefficient estimates increases (27). Therefore, the occurrence probability for large absolute values of the correlation coefficients is high, even for position pairs in which substitutions are independent of one another (25,28). Weighting is an approach that allows the removal of the effect of phylogeny. CRASP provides three weighting schemes for the user to choose from. They are based on the pairwise similarities between amino acid sequences (29), the occurrence frequencies of amino acids at each position in a sequence alignment (30) and the phylogenetic tree (27). Weights may also be defined by the user. As is known, mutually dependent substitutions can occur not only in pairs, but also in groups of protein positions (13,31–33). The CRASP program allows the detection of groups of interdependent positions using hierarchical cluster analysis: the larger the absolute correlation coefficient value, the closer the positions cluster on the plot (34). The results of analysis of correlations in clusters of dependent positions may be helpful in making inferences about the possible invariant and variable integral characteristics of proteins.

Contribution of coordinated amino acid substitutions to the invariance of an integral characteristic of a protein

An important feature of groups of dependent positions is that the mutual correlations can provide invariance of the integral physicochemical characteristics of a protein, i.e. values are dependent on several protein positions (19,20). The decrease in variation may be a consequence of selection pressure and evidence of the functional–structural importance of interactions between protein residues (20,35). Here, an integral characteristic F of a protein is described as the sum of the values of a physicochemical property at protein positions with coefficients ci:

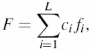
graphic file with name gkh451equ1.gif

where L is sequence length, fi is the value of the physicochemical property f for the residue at position i and the ci value denotes the contribution of the residue at position i to the value of the integral characteristic F. For a characteristic such as net protein charge, f represents a residue charge, and coefficients ci = 1 at all positions. The ci can be real numbers. For example, for a value such as the projection of the hydrophobic moment of the alpha-helix, they are defined by the orientation of the side chain about the helix axis (36).

A measure of the variability of the integral characteristic is its sample variance D(F). The variance of an integral characteristic F is defined as the sum of two components,

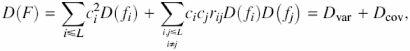
graphic file with name gkh451equ2.gif

where D(fi) is the variation in property f at position i, and rij is the correlation coefficient for the property for the position pair i,j. It is easy to see that Dvar is dependent on the variability in protein positions and Dcov is dependent on the coordinated substitutions. Note, Dvar is always ≥0, whereas Dcov can be positive, negative or zero. The latter can be used as the null hypothesis for testing the significance of the contribution of coordinated substitutions to D(F). In this case (for all rij = 0), the expected variance of the physicochemical characteristic is graphic file with name gkh451equ3.gif. Coordinated substitutions contribute to the stability of the integral characteristic F if D(F) < Dexp (F).

To test this inequality for significance the variance ratio λ = Dexp(F)/D(F) is used; thus, λ serves as a characteristic of the contribution of coordinated substitutions to the variation in the integral characteristic F. At λ > 1, the contribution narrows the variation range (increases conservation); at λ < 1 it widens the variation range (increases variability). At λ ≈ 1, the contribution of coordinated substitutions is insignificant. It is known that λ obeys Fisher's F distribution with L(N−1) and N−1 degrees of freedom, where N is the number of sequences (37). Therefore, percentile points of the F distribution can be used for estimating the significance of the deviation of λ from 1. Additionally, a Monte Carlo simulation is applied to test for the significance of the observed deviation of the variance D from Dexp(F). M random samples are generated. There are no pairwise dependencies of the physicochemical characteristic values of the residues (rij = 0). Every sample consists of N sets of Gaussian distributed independent numbers with means and variances equal to the estimates at each analyzed position. Then, the variation Drand(F) for such random samples is calculated and the number m of the samples with Drand > D is counted. The ratio m/M is an estimate of the significance of the deviation of D(F) from Dexp(F). In the course of the Monte Carlo simulation, the λrand = Dexp(F)/Drand(F) value is calculated for every random sample, using the D(fi) value in a random sample to estimate Dexp(F). The proportion of random samples with λ > λrand is also the estimate of the significant contribution of the coordinated substitution to the constancy of the F characteristic. CRASP also allows us to estimate the parameters of the linear functional relationship between a pair of integral characteristics.

INPUT AND OUTPUT

The calculation of pairwise correlations

For the calculation of pairwise correlations, CRASP accepts sequence alignments of a protein family, a phylogenetic tree for weight calculation or user-defined weights for each sequence. The user can choose a physicochemical characteristic of amino acids from the AAIndex database (38) or from a menu. A number of input parameters enable the user to filter the positions that are too conserved or those containing an unacceptably large number of deletions. For the sake of convenience, one of the sequences can be taken as reference and the reference sequence positions can be appropriately numbered. Extended data input and a simplified input routine with certain parameters given by default are available.

The main result of the module is a correlation matrix. CRASP offers three formats to display the matrix, a textual alternative, a hypertext display and graphical. The diagram of the hierarchical position clustering is displayed as a separate graph. The statistics for the frequencies of occurrence of amino acids at the alignment positions and the data on the distribution of the physicochemical characteristics at each alignment position can be displayed visually as text files.

The analysis of the physicochemical characteristic in a position pair

This module allows estimation of the Pearson's correlation coefficient and the linear functional regression equation (23) for the physicochemical value in a position pair. The results are displayed in a textual format, and a scatter plot of the property values at a pair of alignment positions is also displayed.

The analysis of the integral characteristics

Multiple sequence alignment, weighting parameters and physicochemical property of the residues are defined as in the analysis of pairwise correlations. Integral characteristics are calculated using the numerical coefficients corresponding to the alignment positions. The user can define up to four characteristics in one run.

The output data are the estimates of the statistical significance of the contribution of the coordinated substitutions to the variation in the integral characteristics D, and the D/Dvar values in the random samples. The distributions can be displayed in either textual or graphical format upon output.

The CRASP website provides examples of analysis for a number of protein families, help on using input parameters and also tutorial pages.

Acknowledgments

ACKNOWLEDGEMENTS

The authors are grateful to D. A. Grigorovich for programming assistance, I. V. Lokhova for technical assistance and A. N. Fadeeva for translating the manuscript. This work was partly supported by grants from the Russian Foundation for Basic Research (03-07-96833-p2003, 03-07-96833), the Siberian Branch of the Russian Academy of Sciences (project No. 148, 119), the Russian Ministry of Industry, Sciences and Technologies (No. 43.073.1.1.1501, subcontract 28/2003), MCB RAS (No. 10.4), the CRDF and the Ministry of Education of the Russian Federation within the Basic Research and Higher Education Program (Y1-B-08-20, NO-008-X1).

REFERENCES

  • 1.Benner S.A., Badcoe,I., Cohen,M.A. and Gerloff,D.L. (1994) Bona fide prediction of aspects of protein conformation. Assigning interior and surface residues from patterns of variation and conservation in homologous protein sequences. J. Mol. Biol., 235, 926–958. [DOI] [PubMed] [Google Scholar]
  • 2.Livingstone C.D. and Barton,G.J. (1996) Identification of functional residues and secondary structure from protein multiple sequence alignment. Meth. Enzymol., 266, 497–512. [DOI] [PubMed] [Google Scholar]
  • 3.Lichtarge O., Bourne,H.R. and Cohen,F.E. (1996) An evolutionary trace method defines binding surfaces common to protein families. J. Mol. Biol., 257, 342–358. [DOI] [PubMed] [Google Scholar]
  • 4.Benner S.A. and Gerloff,D. (1991) Patterns of divergence in homologous proteins as indicators of secondary and tertiary structures: the catalytic domain of protein kinases. Advan. Enzyme Regulat., 31, 121–181. [DOI] [PubMed] [Google Scholar]
  • 5.Kimura M. (1991) Recent development of the neutral theory viewed from the Wrightian tradition of theoretical population genetics. Proc. Natl Acad. Sci. USA, 88, 5969–5973. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Pritchard L. and Dufton,M.J. (2000) Do proteins learn to evolve? The Hopfield network as a basis for the understanding of protein evolution. J. Theor. Biol., 202, 77–86. [DOI] [PubMed] [Google Scholar]
  • 7.Kondrashov A.S., Sunyaev,S. and Kondrashov,F.A. (2002) Dobzhansky–Muller incompatibilities in protein evolution. Proc. Natl Acad. Sci. USA, 99, 14878–14883. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Vernet T., Tessier,D.C., Khouri,H.E. and Altschuh,D. (1992) Correlation of co-ordinated amino acid changes at the two-domain interface of cysteine proteases with protein stability. J. Mol. Biol., 224, 501–509. [DOI] [PubMed] [Google Scholar]
  • 9.Mateu M.G. and Fersht,A.R. (1999) Mutually compensatory mutations during evolution of the tetramerization domain of tumor supressor p53 lead to impaired hetero-oligomerization. Proc. Natl Acad. Sci. USA, 96, 3595–3599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Jespers L., Lijnen,H.R., Vanwetswinkel,S., Van Hoef,B., Brepoels,K., Collen,D. and De Maeyer,M. (1999) Guiding a docking mode by phage display: selection of correlated mutations at the staphylokinase–plasmin interface. J. Mol. Biol., 290, 471–479. [DOI] [PubMed] [Google Scholar]
  • 11.Göbel U., Sander,C., Schneider,R. and Valencia,A. (1994) Correlated mutations and residue contacts in proteins. Prot. Struct. Funct. Genet., 18, 309–317. [DOI] [PubMed] [Google Scholar]
  • 12.Shindyalov I.N., Kolchanov,N.A. and Sander,C. (1994) Can three-dimensional contacts in protein structures be predicted by analysis of correlated mutations? Prot. Eng., 7, 349–358. [DOI] [PubMed] [Google Scholar]
  • 13.Lockless S.W. and Ranganathan,R. (1999) Evolutionary conserved pathways of energetic connectivity in protein families. Science, 286, 295–299. [DOI] [PubMed] [Google Scholar]
  • 14.Olmea O., Rost,B. and Valencia,A. (1999) Effective use of sequence correlation and conservation in fold recognition. J. Mol. Biol., 293, 1221–1239. [DOI] [PubMed] [Google Scholar]
  • 15.Ortiz A.R., Kolinski,A. and Skolnick,J. (1998) Fold assembly of small proteins using Monte Carlo simulations driven by restraints derived from multiple sequence alignment. J. Mol. Biol., 277, 419–448. [DOI] [PubMed] [Google Scholar]
  • 16.Pazos F., Helmer-Citterich,M., Ausiello,G. and Valencia,A. (1997) Correlated mutations contain information about protein–protein interaction. J. Mol. Biol., 271, 511–523. [DOI] [PubMed] [Google Scholar]
  • 17.Fariselli P. and Casadio,R. (1999) A neural network based predictor of residue contacts in proteins. Protein Eng., 12, 15–21. [DOI] [PubMed] [Google Scholar]
  • 18.Larson S.M., Di Nardo,A.A. and Davidson,A.R. (2000) Analysis of covariation in an SH3 domain sequence alignment: applications in tertiary contact prediction and the design of compensating hydrophobic core substitutions. J. Mol. Biol., 303, 433–446. [DOI] [PubMed] [Google Scholar]
  • 19.Lim V.I. and Ptitsyn,O.B. (1970) On the constancy of the hydrophobic nucleus volume in molecules of myoglobins and hemoglobins. Mol. Biol. (USSR), 4, 372–382. [Google Scholar]
  • 20.Gerstein M., Sonnhammer,E.L. and Chothia,C. (1994) Volume changes in protein evolution. J. Mol. Biol., 236, 1076–1078. [DOI] [PubMed] [Google Scholar]
  • 21.Eisenhaber B., Bork,P. and Eisenhaber,F. (1999) Prediction of potential GPI-modification sites in proprotein sequences. J. Mol. Biol., 292, 741–758. [DOI] [PubMed] [Google Scholar]
  • 22.Afonnikov D.A., Oshchepkov,D.Y. and Kolchanov,N.A. (2001) Detection of conserved physico-chemical characteristics of proteins by analyzing clusters of positions with co-ordinated substitutions. Bioinformatics, 17, 1035–1046. [DOI] [PubMed] [Google Scholar]
  • 23.Tomii K. and Kanehisa,M. (1996) Analysis of amino acid indices and mutation matrices for sequence comparison and structure prediction of proteins. Protein Eng., 9, 27–36. [DOI] [PubMed] [Google Scholar]
  • 24.Kendall M.G. and Stuart,A. (1967) The Advanced Theory of Statistics. Vol. 2. Inference and Relationship, 2nd edn. Charles Griffin & Co. Ltd., London. [Google Scholar]
  • 25.Lapedes A.S., Giraud,B.G., Liu,L.C. and Stormo,G.D. (1997) Correlated mutations in protein sequences: phylogenetic and structural effects. In Proceedings of the AMS/SIAM Conference on Statistics in Molecular Biology, Vol. 33, Monograph Series of the Institute for Mathematical Statistics, Hayward, CA, pp. 236–256. [Google Scholar]
  • 26.Afonnikov D.A. (2000) Stability of the partial correlation coefficient estimates for residue characteristics at different positions of amino acid sequences. The Second International Conference on Bioinformatics of Genome Regulation and Structure (BGRS'2000), Novosibirsk, Russia, August 7–11, 2000, Vol. 2, Institute of Cytology and Genetics, Novosibirsk, pp. 207–210. [Google Scholar]
  • 27.Felsenstein J. (1985) Phylogenies and the comparative method. Am. Nat., 125, 1–15. [Google Scholar]
  • 28.Pollock D.D. and Taylor,W.R. (1997) Effectiveness of correlation analysis in identifying protein residues undergoing correlated evolution. Protein Eng., 10, 647–657. [DOI] [PubMed] [Google Scholar]
  • 29.Vingron M. and Argos,P. (1989) A fast and sensitive multiple sequence alignment algorithm. CABIOS, 5, 115–121. [DOI] [PubMed] [Google Scholar]
  • 30.Henikoff S. and Henikoff,J.G. (1994) Position-based sequence weights. J. Mol. Biol., 243, 574–578. [DOI] [PubMed] [Google Scholar]
  • 31.Clarke N.D. (1995) Covariation of residues in homeodomain sequence family. Prot. Sci., 4, 2269–2278. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Nagl S.B. (2001) Can correlated mutations in protein domain families be used for protein design? Brief Bioinform., 2, 279–288. [DOI] [PubMed] [Google Scholar]
  • 33.Atchley W.R., Wollenberg,K.R., Fitch,W.M., Terhalle,W. and Dress,A.W. (2000) Correlations among amino acid sites in bHLH protein domains: an information theoretic analysis. Mol. Biol. Evol., 17, 164–178. [DOI] [PubMed] [Google Scholar]
  • 34.Sneath P.H.A. and Sokal,R.R. (1973) Numerical Taxonomy. The Principles and Practice of Numerical Classification. W.H. Freeman and Co., San Francisco, CA. [Google Scholar]
  • 35.Afonnikov D.A. (2004) Contribution of coordinated substitutions to the constancy of physicochemical properties of ATP-binding loop in protein kinases. In Kolchanov,N. and Hofestaedt,R. (eds), Bioinformatics of Genome Regulation and Structure. Kluwer Academic Publishers, Boston/Dordrecht/London, pp. 223–230. [Google Scholar]
  • 36.Eisenberg D., Weiss,R.M. and Terwilliger,T.C. (1982) The helical hydrophobic moment: a measure of the amphiphilicity of a helix. Nature, 299, 371–374. [DOI] [PubMed] [Google Scholar]
  • 37.Selvin S. (1998) F distribution. In Armitage,P. and Colton,T. (eds), Encyclopedia of Biostatistics. John Wiley & Sons, Chichester, vol. 2, pp. 1469–1472. [Google Scholar]
  • 38.Kawashima S. and Kanehisa,M. (2000) AAindex: amino acid index database. Nucleic Acids Res., 28, 374. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Nucleic Acids Research are provided here courtesy of Oxford University Press

RESOURCES