Abstract
The search for DNA regions with low complexity is one of the pivotal tasks of modern structural analysis of complete genomes. The low complexity may be preconditioned by strong inequality in nucleotide content (biased composition), by tandem or dispersed repeats or by palindrome-hairpin structures, as well as by a combination of all these factors. Several numerical measures of textual complexity, including combinatorial and linguistic ones, together with complexity estimation using a modified Lempel–Ziv algorithm, have been implemented in a software tool called ‘Complexity’ (http://wwwmgs.bionet.nsc.ru/mgs/programs/low_complexity/). The software enables a user to search for low-complexity regions in long sequences, e.g. complete bacterial genomes or eukaryotic chromosomes. In addition, it estimates the complexity of groups of aligned sequences.
INTRODUCTION
Analysis of genomic sequences raises the challenge of searching for regions with low textual complexity which could be functionally important (1–4). Low-complexity regions are often defined as regions of biased composition containing simple sequence repeats (1). A sequence enriched with imperfect direct and inverted repeats may also be considered as a sequence with low complexity (5).
Intuitively, the complexity of a symbolic sequence reflects an ability to represent a sequence in a compact form based on some structural features of this sequence. To evaluate textual complexity, several groups of methods have been developed: entropy measures (6), with the simplest of them using only alphabetical symbol frequencies (7); the method of clusterization of cryptically simple sequences (8); evaluation of the alphabet-capacity l-gram (combinatorial complexity and linguistic complexity) (9–12); modifications of the complexity measure by Lempel and Ziv (13–15); stochastic complexity (16), http:www.bioinfo.de/isb/2002/02/0022/); and grammatical complexity (17).
The general approach to estimating the complexity of symbolic sequences (texts) was suggested by A. N. Kolmogorov (18). He proved that there exists an optimal algorithm or program for the text generation. Kolmogorov complexity is the length of the shortest code generating a given sequence. Kolmogorov complexity is not a recursive function (i.e. it is not incorporated in a computational scheme). However, for a sequence of finite length, various constructive realizations of non-optimal coding have been developed (19), including applications for DNA analysis (13–15).
As the method for complexity evaluation, we have chosen a scheme of text representation in terms of repeats, which uses the concept of the complexity of a finite symbolic sequence introduced by Lempel and Ziv (19). The approach of Lempel and Ziv is oriented to the development of an efficient algorithm for data compression. While studying complexity, we are interested not in a mere compression of genetic texts, but rather in searching for regularities underlying them. The Lempel–Ziv complexity measure is based on text segmentation; we have termed it a ‘complexity decomposition’. It may be interpreted as the representation of a text in terms of repeats. Initially, this approach was implemented for analyzing DNA by Gusev and coauthors (13,14). Based on this approach, we present here the Internet-available tools LZcomposer (http://wwwmgs.bionet.nsc.ru/mgs/programs/lzcomposer/) and Complexity (http://wwwmgs.bionet.nsc.ru/mgs/programs/low_complexity/ and http://emj-pc.ics.uci.edu:8080/low_complexity/).
We have incorporated into this software several known estimates of complexity in order to compare different approaches. A user may choose a method of interest or construct several complexity profiles simultaneously. In particular, we have incorporated the following evaluations of textual complexity: (i) by frequency of nucleotide content (7); (ii) by entropy of the given order of words (oligonucelotides); (iii) by linguistic complexity (10,12). In the third approach, linguistic complexity refers to combinatorial complexity denoted as the power of the l-gram dictionary under fixed l. By summing up the values of combinatorial complexity over all values of l, 1 ≤ l ≤ N, where N is the sequence length, and dividing by maximal dictionary size, we obtain the value of linguistic complexity. This measure was applied for studying the patterns composing nucleosomes and promoters (11,12).
By applying l-gram trees for the sequence representation in our software, we have resolved the computational problems stemming from the considerable length of the sequences processed. Our package is designed for analysis of an arbitrary symbolic sequence, including DNA and amino acid sequences.
The software is designed to search effecitvely for the regions with low complexity in extended DNA sequences. The search is provided by different methods and its operation time is linearly dependent upon the sequence length. The program software is able to calculate an average complexity profile for sets of sequences given in FASTA format. By using the Complexity system, we have demonstrated that the complexity of exons is, on average, higher, whereas that of introns is lower (20). Also, we have found an alteration in the local textual complexity for splicing sites.
METHODS AND ALGORITHMS
Complexity estimation by Lempel and Ziv scheme
Lempel and Ziv proposed measuring the complexity of a sequence by the number of steps in the generating process (19). The permitted operations here are generation of a new symbol (this operation is necessary at least to synthesize the alphabet symbols) and direct copying of a fragment from the already generated part of the text. Copying implies the search for a prototype (i.e. repeat in a common sense) in the text and extension of the text by attaching the ‘prepared’ block.
We use direct and inverted repeats as standard prototypes. The other repeats, i.e. symmetric (the repeated sequence is oppositely oriented on the same DNA strand), and direct complementary (a direct repeat on the complementary DNA strand), may effect hairpin loop formation with subsequent microdeletions and microinsertions (4). Thus four types of repeat differing by orientation and localization in direct or complementary chains are considered: direct, symmetric, inverted and direct complementary. A user may choose any type of copying operation.
The scheme for generating the sequence S may be represented as a concatenation H of the fragments:
![]()
where S [ik−1+1 : ik] is a fragment (component) generated at the k-th step (a sequence of elements ranging from positions ik−1 + 1 to ik), N is the length of a sequence and m = mH(S) is the number of steps generating the process. The scheme with minimal number of steps m should be selected. This scheme determines the complexity of the sequence S:
![]()
The minimal number of components in Equation 1 is provided by selection at each step of the longest prototype in the previous history. The complexity decomposition of a sequence is performed from left to the right. If there exist some alternative variants of copying, the program applies the prototype which is the nearest to the component synthesized. The algorithm implementation for DNA research was described in detail in (13,14).
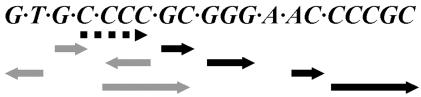
In Figure 1, there is an example of complexity decomposition of a nucleotide sequence containing the AP2 transcription factor binding site, GTGCCCCGCGGGAACCCCGC. The components of complexity decomposition are separated by dots. Black and gray arrows mark the copied fragments and their prototypes. A tandem repeat characterized by partial overlapping of the prototype on the copied fragment is marked by a dotted line. In this decomposition, the first one-lettered components, G and T, are produced by an operation generating a novel symbol. The complexity of this 20-lettered sequence = 10 [the number of components in H(S)].
Figure 1.
Example of the complexity decomposition of the nucleotide sequence GTGCCCCGCGGGAACCCCGC using the modified Lempel–Ziv method with direct and inverted repeats. Decomposition components are separated by dots. Components and prototypes are indicated by black and gray arrows, respectively. Gray arrow orientation indicates direct or inverted repeat type. The striped arrow marks a poly (C) tract.
We construct the complexity profile in a sliding window of length N; the evaluation of complexity is calculated as the whole number CLZ(S) of components of complexity decomposition in the window N, or as the number of components CLZ(S)/N.
The program for complexity evaluation by the Lempel–Ziv method, with supplementary options aimed at analysis of components of the decomposition, is available at http://wwwmgs.bionet.nsc.ru/mgs/programs/lzcomposer/.
Other estimates of text complexity
In the software presented, we have included the algorithm evaluating word complexity in accordance with nucleotide frequency (7). This algorithm is used as BLAST search preprocessing for masking the low complexity regions.
The evaluation of complexity in a text region CWF by Wootton and Federhen (7) is given by the formula
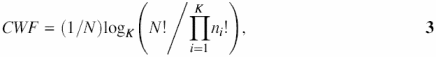
where N is the window size, ni is the number of symbols in a window, i = 1,…,K and K is the alphabet size (for DNA, K = 4).
Another method included for estimating complexity is evaluation of the entropy CE of symbols:
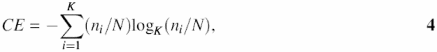
where N is the window size, ni is the number of symbols in a window and K is the alphabet size.
As is known, by increasing the length of the region analyzed, the complexity CWF tends to the value of CE. However, with small window size N, the values of equations (3) and (4) differ, which is why both these variants are incorporated into the program. As the logarithm is taken by the basis K, the complexity values fall within the interval [0; 1].
The complexity may be estimated using the entropy measures, including the entropy of the high-order Markov model given as:
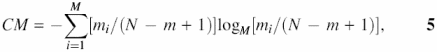
where mi is the number of i-th word in a window, i = 1,…,M, M = Km is the total number of words with length m and K is the alphabet size. By ‘word’ (substring), we mean any short word (oligonucleotide) in a given sequence.
The complexity of a sequence can be defined as the richness of its vocabulary: how many different words of length i appear in the sequence (10). This linguistic complexity CT introduced by Trifonov (10) is computable by multiplying the ratios of words of all possible lengths in the window to the total number of different words that could possibly be found:

where Vi is the number of different words of length i, 1 ≤ i ≤ N, and N, is the length of the sequence (window). Vmaxi is the maximum possible number of words of the length i. For a window of size N, and alphabet size K, this number is calculated according to the formula:
![]()
For example, in a window of 20 bp, it is possible to displace all 4 nucleotides, all 16 dinucleotides, 18 trinucleotides (of 64 trinucleotides, only 18 may be input into a sequence 20 bp long), etc. including two words of 19 bp and one word of 20 bp. All in all, we arrive at ![]() . Linguistic complexity can also be defined as the ratio of the sum of numbers of words occurring in a sequence analyzed to the maximum possible number of such words (12):
. Linguistic complexity can also be defined as the ratio of the sum of numbers of words occurring in a sequence analyzed to the maximum possible number of such words (12):
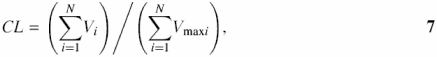
Both CL and CT vary in the range 0–1. We calculate both complexity estimates using multiplication (10) and summation (12), respectively. To limit the usage of long words in a calculation, which is especially important to large windows with N varying from 10 kb to 100 kb, calculation may be limited by the parameter m, m ≤ N. Thus, we suggest a more convenient variant of linguistic complexity estimation with vocabulary restricted to words of the size m, m ≤ N:
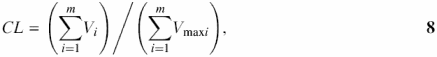
As an example, let us consider calculation of linguistic complexity for the same sequence GTGCCCCGCGGGAACCCCGC with N = 20 (Figure 1):
In total, 173 words were found, whereas 191 words could potentially have been found. Using Equation 7, linguistic complexity CL is 0.906 (=173/191).
Linguistic complexity gives evidence about the variability of words, but it is not suitable for searching for particular repeats and determining their localization.
For the example sequence, the complexity estimates are:
Comparison of methods and analysis of sequence sets
By applying the software, it is possible to analyze a sequence by all the methods simultaneously and to obtain several complexity profiles in an output. Also, a complexity profile may be constructed for a group of sequences by means of any desirable method. We can analyze both aligned sequences and phased sequences that are not homologous. By definition, phased sequences are equal in length, e.g. promoter sequences between positions −200 and 50 relative to the transcription start. For each position of a phased sequence, one may calculate a complexity value in a sliding window. In accordance with a user-defined method, the mean, minimum and maximum values are calculated and displayed as the program output.
Estimation of complexity values for a set of phased sequences is provided through Internet-available software for the first time, since the other software programs known produce a complexity profile only for a single sequence (8,12).
IMPLEMENTATION AND RESULTS
Calculation mode in a sliding window
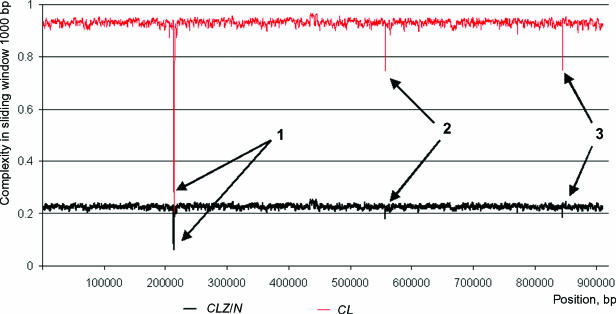
A user may choose a program mode aimed at analysis by different methods of (i) a single extended sequence or (ii) a group of relatively short sequences up to 1 kb in length. A table of complexity values is constructed for a window, of ordered size N, sliding along the sequence. The sequence complexity is assigned to the window center. The calculation mode in a sliding window (complexity profile) is demonstrated here using the example of the Borrelia burgdorferi genome. In Figure 2, complexity profiles for a window sliding along the sequence are illustrated.
Figure 2.
Complexity profiles in sliding windows of length 1000 bp for genomic sequences of the Lyme disease spirochete, B.burgdorferi: x-axis, sequence positions; y-axis, complexity value in the window. The arrows indicate three regions with minimal linguistic and Lempel–Ziv complexity.
The minimum values for Lempel–Ziv complexity and linguistic complexity coincide (Figure 2). All the windows displaying complexity value fall into regions with pronounced periodicity (regions marked by arrows 1, 2 and 3 in Figure 2). The largest peak corresponds to periodicity localized within the gene BB0210 (positions 212 061–215 420) coding the cell surface-located membrane protein lmp1 (arrow 1). This gene contains a direct tandem repeat, 162 bp in length, repeated seven times. The second and third peaks of the complexity profile mark the genes BB0546 (positions 556 563–557 423, arrow 2) and BB0801 (positions 844 454–847 102, arrow 3), respectively. These regions also house imperfect direct tandem repeats, of 60 and 33 bp length, respectively.
Note that for revealing structures with extended imperfect repeats, the Lempel–Ziv complexity and linguistic complexity estimates are the most suitable. The entropy and complexity values of Wootton and Federhen are strongly correlated, with the correlation coefficient equaling 0.95–0.99 for the genome sequences analyzed. However, the Lempel–Ziv complexity values and linguistic complexity values are less correlated with entropy estimates.
Treatment of a group of sequences
The program is designed to analyze groups of sequences, or to calculate the mean value of a complexity profile at each position. This analysis evaluates the alteration of text complexity for functional groups.
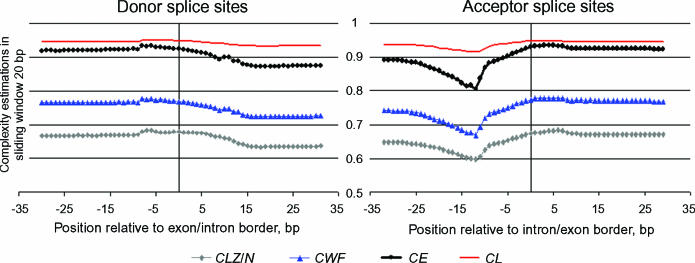
To illustrate the operational mode with a group of phased sequences, we have analyzed the set of acceptor and donor splice sites extracted from the database SpliceDB (21). An attempt was made to find regularities that are common to the splicing sites. The sequences were of length 82 nucleotides with canonical dinucleotides GT and AG marking the border between exon and intron in the center. We have calculated complexity within a sliding window of length 20 bp. The profile was constructed by averaging the complexity values along all sequences of the set in a window. The step size for the sliding window is one position. Mean values of the profiles for the sets of donor and acceptor splicing sites are overlaid and illustrated in Figure 3. On the abscissa, the window positioning relative to the canonical dinucleotide is given.
Figure 3.
The averaged complexity profiles in a sliding window of 20 bp for the sets of (a) donor and (b) acceptor splicing sites in mammals. The profile of linguistic complexity (CL), entropy (CE), complexity estimation by Wootton–Federhen (CWF) and Lempel–Ziv complexity (CLZ) are shown. On the abscissa is shown the position of the window center relative to the border between exon and intron (for donor sites) and from intron to exon (for acceptor sites). The sequence length equals 82 bp.
As can be seen, the average complexity of acceptor splicing site sequences in the sliding window increases from intron towards exon. In contrast, for the donor splicing sites, the sequence complexity drops. Hence, the complexity of coding regions of a genome is higher than that of non-coding regions. The decrease in complexity for acceptor splicing sites within the region [−20; −10] relative to the border between exon and intron points to the fact that this sequence structure is conserved. The results of complexity analysis of the phased sites of splicing, exons, introns and promoters are available at http://wwwmgs.bionet.nsc.ru/mgs/programs/lzcomposer/ResPromoters.htm.
CONCLUSION
The study of complexity reveals regularities related to the structure of repeats, types of repeats and their rate of occurrence in the regions of genome. Comparison of several methods evaluating textual complexity is presented for the first time (http://wwwmgs.bionet.nsc.ru/mgs/programs/low_complexity/). The operation time for the program is linear to sequence length. One can construct complexity profiles for sequences ranging from 2 bp up to 20 Mb in length with sliding window size varying from 2 bp to 100 kb.
An Internet-accessible software tool LZcomposer (http://wwwmgs.bionet.nsc.ru/programs/lzcomposer/) based on Lempel–Ziv complexity detects structural regularities and the longest exact repeats in complete genomes. The maximal sequence length for estimating complete complexity decomposition using the Lempel–Ziv method is 12 Mb. This tool was implemented for analysis of complexity decompositions of complete bacterial genomes and fragments of eukaryotic chromosomes (http://wwwtest.bionet.nsc.ru/mgs/programs/lzcomposer/ResBacterial.htm) (20). Applying the tool, maximal perfect repeats and the regions with low complexity were detected for 140 complete genomes.
By comparing sequence complexity in functional regions, we have demonstrated that the complexity of sequences containing introns and regulatory regions is less than that of coding regions. Our results support the data obtained previously for bacterial genomes (12): linguistic complexity calculated for the coding and non-coding gene regions is different. We have proved that this observation is also valid in eukaryotes by estimating complexity of gene regions using several other complexity measures.
The Internet-available tool designed by us for analysis of complexity is applicable to the study of nucleotide sequences, amino acid sequences, extended genome regions and complete genomes.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
| Length of a word | No. of possible words in a window | No. of words found in the example sequence |
|---|---|---|
| 1 | 4 | 4 |
| 2 | 16 | 9 |
| 3 | 18 | 13 |
| 4 | 17 | 14 |
| 5 | 16 | 14 |
| 6 | 15 | 14 |
| 7 | 14 | 14 |
| … | … | … |
| 19 | 2 | 2 |
| 20 | 1 | 1 |
| Complexity estimation | Complexity value |
|---|---|
| CLZ | 10 |
| CLZ/N | 0.5 |
| CE | 0.789 |
| CM | 0.706 |
| CWF | 0.650 |
| CL | 0.906 |
| CT | 0.273 |
Acknowledgments
ACKNOWLEDGEMENTS
The authors are grateful to N. A. Kolchanov, V. D. Gusev, L. A. Miroshnichenko and A. S. Poplavsky for valuable discussions. This work was supported in part by the RFBR (02-07-90355, 03-07-96833, 03-04-48506), the Russian Ministry of Education (E 02-6.0-250), Ministry of Industry, Science and Technology (43.073.1.1.1S01), NATO (LST.CLG 979815) MCB RAS (No. 10.4) and SB RAS (Integration project no. 119).
REFERENCES
- 1.Hancock J.M. (2002) Genome size and the accumulation of simple sequence repeats: implications of new data from genome sequencing projects. Genetica, 115, 93–103. [DOI] [PubMed] [Google Scholar]
- 2.Wan H., Li,L., Federhen,S. and Wootton,J.C. (2003) Discovering simple regions in biological sequences associated with scoring schemes. J. Comput. Biol., 10, 171–185. [DOI] [PubMed] [Google Scholar]
- 3.Stern L., Allison,L., Coppel,R.L. and Dix,T.I. (2001) Discovering patterns in Plasmodium falciparum genomic DNA. Mol. Biochem. Parasitol., 118, 175–186. [DOI] [PubMed] [Google Scholar]
- 4.Chuzhanova N.A., Anassis,E.J., Ball,E., Krawczak,M. and Cooper,D.N. (2003) Meta-analysis of indels causing human genetic disease: mechanisms of mutagenesis and the role of local DNA sequence complexity. Hum. Mutation, 21, 28–44. [DOI] [PubMed] [Google Scholar]
- 5.Cox R. and Mirkin,S.M. (1997) Characteristic enrichment of DNA repeats in different genomes. Proc. Natl Acad. Sci. USA, 94, 5237–5242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shannon C.E. (1948) A mathematical theory of communication. Bell Syst. Tech. J., 27, pt I, 379–423; pt II, 623–656. [Google Scholar]
- 7.Wootton J.C. and Federhen,S. (1996) Analysis of compositionally biased regions in sequence databases. Methods Enzymol., 266, 554–571. [DOI] [PubMed] [Google Scholar]
- 8.Alba M.M., Laskowski,R.A. and Hancock,J.M. (2002) Detecting cryptically simple protein sequences using the SIMPLE algorithm. Bioinformatics, 18, 672–678. [DOI] [PubMed] [Google Scholar]
- 9.Kisliuk O.S., Borovina,T.A. and Nazipova,N.N. (1999) Evaluation of genetic test redundancy using a high-frequency component of the l-gram graph. Biofizika (Mosk.), 44, 639–648 (in Russian). [PubMed] [Google Scholar]
- 10.Trifonov E.N. (1990) Making sense of the human genome. In Sarma,R.H. and Sarma,M.H. (Eds), Structure & Methods Adenine Press, Albany, Vol. 1, pp. 69–77. [Google Scholar]
- 11.Gabrielian A. and Bolshoy,A. (1999) Sequence complexity and DNA curvature. Comput. Chem., 23, 263–274. [DOI] [PubMed] [Google Scholar]
- 12.Troyanskaya O.G., Arbell,O., Koren,Y., Landau,G.M. and Bolshoy,A. (2002) Sequence complexity profiles of prokaryotic genomic sequences: a fast algorithm for calculating linguistic complexity. Bioinformatics, 18, 679–688. [DOI] [PubMed] [Google Scholar]
- 13.Gusev V.D., Kulichkov,V.A. and Chupakhina,O.M. (1991) Complexity analysis of genomes. I. Complexity and classification methods of detected structural regularities. Mol. Biol. (Mosk). 25, 825–834. [PubMed] [Google Scholar]
- 14.Gusev V.D., Nemytikova,L.A. and Chuzhanova,N.A. (1999) On the complexity measures of genetic sequences. Bioinformatics, 15, 994–999. [DOI] [PubMed] [Google Scholar]
- 15.Chen X., Kwong,S. and Li,M.A. (1999) Compression algorithm for DNA sequences and its applications in genome comparison. Genome Inform. Ser. Workshop Genome Inform., 10, 51–61. [PubMed] [Google Scholar]
- 16.Orlov Y.L., Filippov,V.P., Potapov,V.N. and Kolchanov,N.A. (2002) Construction of stochastic context trees for genetic texts. In Silico Biol., 2, 233–247. [PubMed] [Google Scholar]
- 17.Jimenez-Montano M.A., Ebeling,W., Pohl,T. and Rapp,P.E. (2002) Entropy and complexity of finite sequences as fluctuating quantities. Biosystems, 64, 23–32. [DOI] [PubMed] [Google Scholar]
- 18.Kolmogorov A.N. (1965) Three approaches to definition of information quantity. Probl. Peredachi Inf. 1, 3–11 (in Russian). [Google Scholar]
- 19.Lempel A. and Ziv,J. (1976) On the complexity of finite sequences. IEEE Trans. Inf. Theory, IT-22, 75–81. [Google Scholar]
- 20.Orlov Y.L., Gusev,V.D. and Miroshnichenko,L.A. (2004) LZcomposer: decomposition of genomic sequences by repeat fragments. Biofizika (Mosk.) in press. [Google Scholar]
- 21.Burset M., Seledtsov,I.A. and Solovyev,V.V. (2001) SpliceDB: database of canonical and non-canonical mammalian splice sites. Nucleic Acids Res., 29, 255–259. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.