SA-Search: a web tool for protein structure mining based on a Structural Alphabet

Abstract

SA-Search is a web tool that can be used to mine for protein structures and extract structural similarities. It is based on a hidden Markov model derived Structural Alphabet (SA) that allows the compression of three-dimensional (3D) protein conformations into a one-dimensional (1D) representation using a limited number of prototype conformations. Using such a representation, classical methods developed for amino acid sequences can be employed. Currently, SA-Search permits the performance of fast 3D similarity searches such as the extraction of exact words using a suffix tree approach, and the search for fuzzy words viewed as a simple 1D sequence alignment problem. SA-Search is available at http://bioserv.rpbs.jussieu.fr/cgi-bin/SA-Search.

INTRODUCTION

The detection and analysis of structural similarities among proteins can provide important insights into their functional mechanisms or their functional relationships and offer the basis for classifications of protein folds. The detection of structural similarities in proteins is complex, and several approaches have been proposed based on the direct consideration of protein alpha-carbon coordinates (1–8). As our knowledge of protein structure increases, it is becoming more and more obvious that recurrent structural motifs occur in protein structures at all levels of their organization. Tools developed to search for similarities at the level of complete proteins are confronted with the large number of comparisons to perform, for example, at the super-secondary structure level.

To search for similarities, we transpose the three-dimensional (3D) structure of proteins into a one-dimensional (1D) sequence of letters marking up a Structural Alphabet (SA). The identification of the letters and the encoding of the structures within the SA space can be achieved using hidden Markov model (HMM) techniques (9). A facility coming with the use of hidden markov models is that it is possible to quantify, during the SA encoding of proteins of known structure, the probability of substituting one letter for another. This allows us to quantify the similarity of protein fragments encoded as different series of letters. Moreover, this offers the possibility of being able to work with a 1D representation of 3D structures using the classical 1D amino acid alignment methods.

SA-Search is a fast and simple method to search within the 1D SA space for structural similarities of a protein to a bank of non-redundant protein chains.

ENCODING OF STRUCTURES IN THE 1D STRUCTURAL ALPHABET SPACE

Hidden Markov model approach

We describe protein structures as series of overlapping fragments of four-residue length. Only the alpha-carbons are used. A hidden Markov model was used to identify a set of letters representative of all protein structures, called the Structural Alphabet. The Markovian approach learns simultaneously the geometry of the letters and the local rules that govern their assembly process (9). Currently, we use an alphabet size of 27, which provides the most accurate description of protein structures, with no overfitting of the model parameters (10). From such an SA space, the structural approximation induced by the discretization of structures remains minimal. Protein structures can be reconstructed with a reasonable accuracy of <1.1 Å RMSD.

Encoding of structures

Given HMM parameters, and given the alpha-carbon coordinates of a protein, the Viterbi algorithm (11) can determine the optimal series of letters among all the possible paths usign a dynamic programming algorithm that takes into account the Markovian dependence between consecutive letters. This results in the compression of protein 3D coordinates into a 1D SA sequence. Encoding can be performed only for fragments that have no missing alpha-carbon coordinates.

APPLICATION TO MINING FOR PROTEIN STRUCTURES

To search for structural similarities, we use well-known algorithms for string comparison (suffix trees and alignment methods).

Exact matches

A suffix tree is a very efficient structure for finding all the matches between two or more strings (12). It can be constructed in linear time, using a linear space that is proportional to the sum of the lengths of the strings. We use this data structure to find all exact maximal matches between two proteins or between a protein and a bank of proteins. The deviation between structures described by identical series of letters is low, even for matches of length >15 in non-helical regions. This can be checked using SA-Search to run, for example, a query for 1l0q against a non-redundant collection of proteins of <30% sequence identity, which leads to 10 matches of length >15, with an RMSD <1Å.

Structural alignment

Dynamic programming algorithms (13) with linear gaps, and a faster version of such algorithms where gaps are not allowed, have been considered to search for fuzzy matches. Such methods require that one quantify the equivalence between letters of the SA. The scoring matrix defining the similarity between the letters was extracted during the encoding of 1429 proteins. The probabilities of observing each letter but the optimal letter at each position were built up. These probabilities are totally different from those of the transition matrix of the Markovian process. Their significances are directly related to the probability, derived from the model, of substituting one letter for another. Substitution scores are based on a log-odds ratio obtained by computing the probabilities of the different letters observed in a bank of encoded structures.

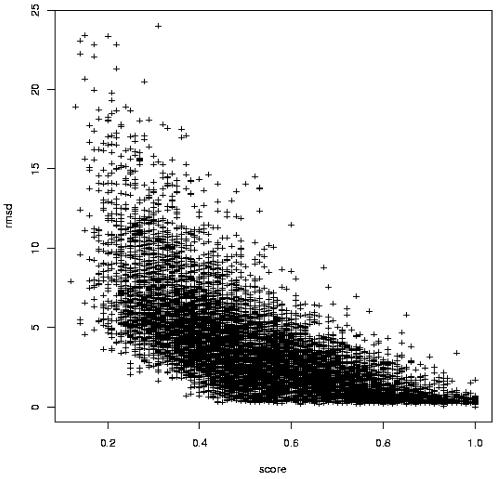
During the alignment of the SA sequences, we use these scores to guide the algorithm. Having identified the alignments, we normalize the scores by dividing the value by the score obtained for identical series of letters. This score is used as a parameter of SA-Search. As shown in Figure 1, obtained on a set of >14 000 matches, there is a significant correlation (p < 0.0001) between the normalized score of the alignment and the RMSD for the matching fragments. Large scores (>0.6) correspond to matches having RMSD <5 Å. Scores <0.3 correspond to matches having RMSD >4 Å. One difficulty of this approach occurs for the medium score values, which can be associated with both good and poor structural similarity. This leads to a search for structural similarities using a two-step procedure. First, use the alignment as a means of mining for candidate matches, and then perform the three-dimensional best-fit superposition to assess the quality of the match. In such a procedure, the minimum score becomes a means of adjusting the depth of the search.

Figure 1.

RMSD of the matches as a function of the normalized alignment score. Over 14 000 comparisons are plotted.

IMPLEMENTATION

The web server can currently be used to perform a comparison using one of the three approaches: search for exact matches, search for fuzzy matches with or without gap. The search can be performed for a protein against a single protein or against a collection of proteins. Different sets of proteins have been defined using an approach similar to that of the culled PDB (Protein Data Bank) (14). These sets of structures are pre-encoded into the Structural Alphabet.

Query proteins can be specified as PDB identifiers or as PDB-format files to be uploaded. The search criteria are

1. a minimum match length expressed as a fraction of the query length;

2. a minimum score value expressed as a value between 0 and 1, 1 corresponding to the ratio of the maximum possible score to the actual alignment score;

3. an RMSD threshold (RMSD between aligned fragments must be less than the specified threshold);

4. the maximum number of matches accepted;

5. finally, since we use algorithms designed for protein amino acid sequence similarity searches, we also suggest running the search using the amino acid sequence instead of the SA sequence. Hence, the user can mine the data using both types of information.

Other parameters describe the formatting of the results.

OUTPUT

The program returns information characterizing the candidate fragments (Table 1) and sends it back in NBRF/PIR format (for subsequent analysis) or in a row/column format. The information returned by the program for each of the selected fragments is the PDB identifier, the matching positions, the normalized score, the RMSD and the two matching fragments aligned in terms of the the amino acid or Structural Alphabet sequence.

Table 1. Comparison of amino acid similarity search (AA) with Structural Alphabet similarity search (SA) using the Smith and Waterman algorithm based on precision–recall with a minimum alignment length of 20 and maximum RMSD of 5 Å.

PDB Id	SCOP fold	SA recall	SA prec.	AA recall	AA prec.
1dlwA	a.1	0.72	0.04	0.33	0.09
1kr7A	a.1	0.69	0.04	0.56	0.17
1bwwA	b.1	0.95	0.58	0.73	1.00
1m1sA	b.1	0.66	0.47	0.06	0.22
1timA	c.1	0.83	0.1	0.20	0.19
1ej7L	c.1	0.66	0.09	0.10	0.11
1a2pA	d.1	0.78	0.04	0.44	0.08
153l	d.2	0.75	0.01	0.25	0.03

Recall is the ratio of matches identified in the query fold class to the total number of similar protein structures in the data bank; precision (prec.) is the ratio of matches belonging to the query fold class to the total number of matches.

DISCUSSION AND FUTURE WORK

The performance of SA-Search suggests that it is an efficient approach to mining for protein structures in large collections of protein structures. The inherent limitation in the impossibility of searching for similarities for proteins with residues missing can be partially overcome by successive searches for each fragment. This is implemented in the current version of SA-Search. It remains the case that some protein structures of poor quality cannot be encoded properly into the SA space.

An important requirement for any structure comparison method is its ability to detect weak structural similarities. The different algorithms implemented in SA-Search meet this requirement. Overall, our results show that SA-Search is able to identify matches for proteins having various folds.

Compared with DALI (2), we observe that, overall, the average size of the matches obtained using SA-Search is shorter. For some of the difficult examples proposed in the literature (7) the difference can be even larger. For example, for 1tie versus 4fgf, SA-Search identifies a match of only 46 amino acids versus >100 using DALI. Similarly, the match of 1ubq against 1fxiA results in a match of length 26 versus close to 55 for DALI. Finally, in the particularly difficult case of 1d7c versus 1i8a, with two proteins sharing a common core of strands but having very different loop conformations, SA-Search will only identify similarities at the strand level. This can be related to a theoretical limit inherent in SA-Search due to the fact that the SA describes the protein conformation locally, which poses the problem of the significance of gaps. In this respect, the performance of the Smith and Waterman algorithm, which is able to detect significant structural alignments including gaps, can certainly be improved (Figure 2). Once proteins have been encoded, any sequence comparison methods can be used on them. Thus, we expect to increase the average size of matches by implementing techniques such as successive match assembly and BLAST search.

Figure 2.

Example of a structural match detected using the Smith and Waterman algorithm with gaps. Light: 1aam; Dark: 1c7nA. The two proteins have 10.2% SA sequence identity. The alignment length is 280 residues.

In Table 1 we compare our results with amino acid similarity searches using the Smith and Waterman algorithm. In order to obtain some representativity in the comparison, we present results for a series of proteins with different folds, as described by the SCOP (version 1.65) structural classification (15). Users can easily check the results on other proteins since SA-Search offers the option of both 3D searches and amino acid searches. Compared with searches based on amino acid sequence, we observe that the performances of SA-Search are much better. Using the Smith and Waterman local alignment with the SA-sequence, we obtain a sensitivity (the ratio of matches identified in the query fold class to the total number of similar protein structures in the data bank) more than twice that obtained using the amino acid sequence. In addition, the precision of the search (the ratio of matches belonging to the query fold class to the total number of matches) is lower, which means that SA-Search is better able to identify matches in proteins belonging to unrelated fold classes. This is promising from the perspective of applying this approach to SA sequences predicted from the amino acid sequence to perform structural prediction.

One strong point of SA-Search is that it allows the fast mining of protein structures, a typical run being on the order of a few seconds. Future directions are to make available bank-against-bank searches, and to offer the possibility of searching against a user bank of proteins.