Consequences of biomechanically constrained tasks in the design and interpretation of synergy analyses

Abstract

Matrix factorization algorithms are commonly used to analyze muscle activity and provide insight into neuromuscular control. These algorithms identify low-dimensional subspaces, commonly referred to as synergies, which can describe variation in muscle activity during a task. Synergies are often interpreted as reflecting underlying neural control; however, it is unclear how these analyses are influenced by biomechanical and task constraints, which can also lead to low-dimensional patterns of muscle activation. The aim of this study was to evaluate whether commonly used algorithms and experimental methods can accurately identify synergy-based control strategies. This was accomplished by evaluating synergies from five common matrix factorization algorithms using muscle activations calculated from 1) a biomechanically constrained task using a musculoskeletal model and 2) without task constraints using random synergy activations. Algorithm performance was assessed by calculating the similarity between estimated synergies and those imposed during the simulations; similarities ranged from 0 (random chance) to 1 (perfect similarity). Although some of the algorithms could accurately estimate specified synergies without biomechanical or task constraints (similarity >0.7), with these constraints the similarity of estimated synergies decreased significantly (0.3–0.4). The ability of these algorithms to accurately identify synergies was negatively impacted by correlation of synergy activations, which are increased when substantial biomechanical or task constraints are present. Increased variability in synergy activations, which can be captured using robust experimental paradigms that include natural variability in motor activation patterns, improved identification accuracy but did not completely overcome effects of biomechanical and task constraints. These results demonstrate that a biomechanically constrained task can reduce the accuracy of estimated synergies and highlight the importance of using experimental protocols with physiological variability to improve synergy analyses.

the neuromuscular and musculoskeletal systems provide unparalleled complexity, which enable movements of daily life. These systems are highly redundant, with many more actuators (i.e., muscles) than mechanical degrees of freedom (i.e., joints). This redundancy provides flexibility and versatility but also creates a challenging system to control. There are many ways that muscles can be recruited to execute a given task, but it is unclear how we select from these many options to control this complex system. One hypothesis is that muscles are recruited in weighted groups, commonly referred to as synergies or modes (Ivanenko et al. 2005; Krishnamoorthy et al. 2003; Ting and Macpherson 2005; Tresch et al. 1999). Controlling via synergies could provide a simplified, lower-dimensional control space compared with controlling each muscle individually. Analyses of electromyographic (EMG) signals from a variety of tasks in humans and animals have demonstrated that muscle activity can be described by lower-dimensional spaces, commonly estimated using matrix factorization algorithms. These behavioral studies have shown that synergies can describe the variance in muscle activity across a broad array of movements such as walking, reaching, and postural control (d'Avella and Bizzi 2005; Ivanenko et al. 2007; Ting and Macpherson 2005). Furthermore, synergies have been shown to change after brain injury, such as after stroke, and may provide a useful framework for guiding rehabilitation (Cheung et al. 2012; Clark et al. 2010).

A challenge in synergy analyses is determining the relationship between synergy structure and the underlying organization of the neuromotor system (Tresch and Jarc 2009). In addition to neural constraints, the low dimensionality of EMG signals may reflect other factors such as biomechanical and task constraints, reflex control, or experimental protocols (Kutch and Valero-Cuevas 2012). For example, biomechanical constraints including muscle moment arms and skeletal geometry reduce the set of feasible muscle activations that can be recruited to execute a specific task. Thus the lower-dimensional subspace identified with matrix factorization algorithms may be influenced by these biomechanically enforced task constraints. These constraints require that certain groups of muscles be consistently activated together. If there is a synergistic organization within the neuromotor system, biomechanically enforced task constraints could result in correlated activations of synergies. However, matrix factorization algorithms assume some degree of independence between the activation of synergies, and accurate synergy identification may be negatively impacted by consistent coactivation. One recent study using musculoskeletal modeling demonstrated that physical constraints can negatively impact the ability of nonnegative matrix factorization (NNMF), one common matrix factorization algorithm, to correctly identify specified synergies (Burkholder and van Antwerp 2013). There are also some tasks, such as applying force with the index finger, in which synergies cannot accurately describe muscle activity (Valero-Cuevas et al. 2009).

Experimental choices may also influence the ability to accurately estimate neurally mediated muscle synergies. Some protocols use averaged muscle activity or muscle activity at specific time points to calculate synergies (Roh et al. 2012; Torres-Oviedo et al. 2006), whereas others use muscle activity throughout a dynamic task, such as walking or reaching (Cheung et al. 2009; Clark et al. 2010). Prior research has suggested that filtering or averaging muscle activity, rather than using data with physiological variability, either across instants of time or across repetitions of a task, may negatively impact the ability to accurately identify synergies (Hart and Giszter 2004). Understanding the generalizability of these findings is important for informing the design and interpretation of future synergy analyses.

The aim of this project was to determine how matrix factorization algorithms are influenced by the impact of biomechanical and task constraints on the suitable patterns of muscle activation and on the experimental choices influencing how those activations are recorded. We tested the ability of matrix factorization algorithms to accurately identify synergies using a musculoskeletal model to simulate an experimental paradigm similar to prior studies that analyzed synergies (Kutch and Valero-Cuevas 2012; Roh et al. 2012; Torres-Oviedo et al. 2006; Tresch et al. 2006). An advantage of using a musculoskeletal model is that we can specify and manipulate the underlying control strategy, as well as the simulated task and experimental conditions. We specified arbitrary sets of synergies as the underlying control strategy, simulated the task to determine muscle activations constrained to the specified synergies, and then estimated synergies from the simulated data using several common matrix factorization algorithms. Using this paradigm, we could also evaluate the impact of correlation between synergy activations during a task and analyze the impact of signal processing, such as using averaged muscle activity or multiple measurements with physiological variability. For each algorithm, the estimated and specified synergies were compared to determine whether the algorithm could accurately identify the underlying control strategy. Our results highlight some of the challenges associated with estimating synergies from experimental data and provide guidance to at least partially address these issues in experimental design and data analysis. In particular, it was found that many common matrix factorization algorithms cannot accurately identify existing motor synergies if the selected experimental tasks and biomechanical constraints lead to synergy activations that are substantially correlated. Importantly, this limitation can be at least partly resolved by employing experimental protocols and data collection techniques that capture the natural variability in motor command signals.

METHODS

Musculoskeletal model.

A previously developed musculoskeletal model of the upper extremity (Holzbaur et al. 2005) was adapted to evaluate whether matrix factorization algorithms can accurately identify synergies (Fig. 1). Skeletal geometry and inertial properties of a previously developed dynamic model of the arm were used for the humerus, ulna, radius, and hand (Hamner et al. 2010). The model was simplified to include 30 muscles (Table 1) and 4 degrees of freedom, including a ball-and-socket joint at the shoulder and a pin joint for flexion/extension at the elbow. Muscles were modeled using a standard equilibrium muscle model based on the Hill model (Thelen 2003) with muscle paths and properties (i.e., optimal fiber length, maximum isometric force, tendon slack length, and pennation angle) based on the model by Holzbaur and colleagues (2005). Because of simplifications in the degrees of freedom of the model, especially at the shoulder, muscle moment arms were modified compared with the original model with an average difference across all muscles and postures included in this analysis of <0.5 cm.

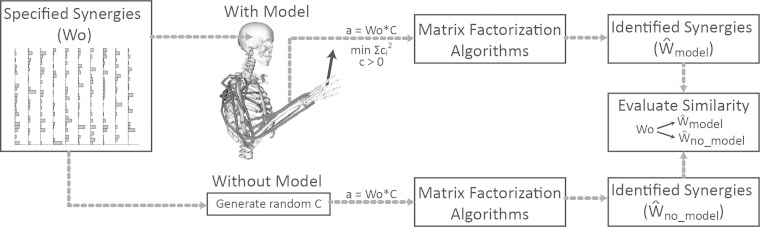
Fig. 1.

Random synergies were generated from an exponential distribution (Wo) and used to calculate muscle activations with and without biomechanical and task constraints. With biomechanical and task constraints, muscle activations (a) were calculated using a musculoskeletal model to execute an isometric force task and were constrained to the specified synergies. Without biomechanical or task constraints, a random matrix of synergy activations, C, was generated from an exponential distribution, and activations were solved for as a = Wo × C. In both cases, matrix factorization algorithms were used to calculate the estimated synergies from the muscle activations. The synergies estimated by the matrix factorization algorithms were then compared with Wo, the specified synergies.

Table 1.

Muscles included in model

	Muscle
DELT1	Anterior deltoid
DELT2	Medial deltoid
DELT3	Posterior deltoid
SUPSP	Supraspinatus
INFSP	Infraspinatus
SUBSC	Subscapularis
TMIN	Teres minor
TMAJ	Teres major
PT	Pronator teres
PECM1	Pectoralis major clavicular
PECM2	Pectoralis major medial
PECM3	Pectoralis major inferior
LAT1	Latissimus dorsi superior
LAT2	Latissimus dorsi medial
LAT3	Latissimus dorsi inferior
CORB	Coracobrachialis
TRIlong	Triceps long head
TRIlat	Triceps lateral head
TRImed	Triceps medial head
ANC	Anconeus
SUP	Supinator
BIClong	Biceps long head
BICshort	Biceps short head
BRA	Brachialis
BRD	Brachioradialis
ECRL	Extensor carpi radialis longus
ECRB	Extensor carpi radialis brevis
ECU	Extensor carpi ulnaris
FCR	Flexor carpi radialis
FCU	Flexor carpi ulnaris

We positioned the model in five different postures and simulated an isometric force task similar to previous physical experiments designed to evaluate synergies (Roh et al. 2012, 2013). The first posture mimicked the experimental protocol, with the hand of the model positioned at half an arm's length in front of the shoulder and the wrist degrees of freedom restrained to simulate the cast used in the experimental protocols. The other four postures were selected to cover a wide range of shoulder and elbow positions. Using these postures, we were able to evaluate synergies estimated from the muscle activations required to execute the task in each posture or over multiple postures. For each posture, we recreated the experimental protocol for generating isometric forces at the hand. The original experimental protocol had the subjects generate constant magnitude isometric forces in 54 or 210 uniformly distributed directions around the hand. Because our simulations were not limited by subject time or comfort, for each posture we included 1,000 randomly selected directions distributed around the hand; each simulated end point force had a magnitude of 10 N.

Synergy optimization.

The control strategy for the musculoskeletal model was specified using a new synergy optimization algorithm in OpenSim, an open-source musculoskeletal modeling and simulation platform (Delp et al. 2007). In this algorithm, the user specifies a set of synergies that can be used by the model to execute the task. Thus we were able to specify and “know” the underlying control strategy of the model. Each synergy is a vector of weights for all the muscles in the model. For this analysis, we generated sets of 10 synergies. Prior experimental results using EMG from eight muscles have demonstrated that an average of four synergies can describe over 95% of muscle activity for this task (Roh et al. 2012). However, the number of synergies is dependent on the number of muscles included in the analysis (Steele et al. 2013), and, because the model used in this analysis had 30 muscles, we increased the number of synergies to 10 to ensure the model could execute the task in all force directions with random synergies. Similar to the prior study by Tresch et al. (2006), the synergies were generated from an exponential distribution with a mean of 0.1. To create synergies more similar to prior experimental results, we created sparse synergies by setting a random number of muscles in each synergy to a weight of zero. Each synergy was then normalized to unit length. Not all sets of random synergies could execute the task to generate force in all 1,000 directions. Sets of synergies that could not execute the task were discarded, and the process was repeated until 100 sets of synergies that could successfully execute the task were identified.

Each set of specified synergies was used to calculate the muscle activations required to execute the isometric force task. The Synergy Optimization algorithm solves for a set of synergy activations that satisfies the task constraints (i.e., generates the target end-point force) and minimizes the sum of squared synergy activations. Thus, if muscle activations, a = W × C, where W is an m × n matrix of n muscle synergies for m muscles and C is an n × t matrix of synergy activation coefficients for t force directions, we minimized the sum of c squared (where c is 1 column of C) for each force direction. The output of the Synergy Optimization algorithm is a set of muscle activations for each force direction that satisfies the biomechanical and task constraints and use the specified set of muscle synergies. This analysis was repeated for all 100 sets of specified synergies and each posture. For many sets of synergies, only a subset of the 10 specified synergies was used to generate force in the majority of the 1,000 force directions. Any synergies that had an activation, c, <0.001 for over 99% of the force directions (i.e., 990 of the 1,000 force directions) were excluded from further analyses.

Our primary simulation considered only a single synergy activation vector for each force direction. This is analogous to a physical experiment that makes a single estimate of steady-state muscle activity for each force direction or averages the results of many isotonic measurements to obtain a single value (Roh et al. 2012; Torres-Oviedo et al. 2006). However, prior research has suggested that making multiple independent measurements or recording for extended periods of time is needed to capture the inherent variability of motor command signals and that this variability is important for estimating synergy structure (Hart and Giszter 2004). Note that such variability is distinct from simple measurement error and reflects potential interactions between intrinsic noise processes in the central nervous system (Harris and Wolpert 1998) and neural control strategies (Latash et al. 2002; Scholz and Schöner 1999). In an effort to replicate the motor variability that might be observed when making multiple independent measurements or recording for extended periods of time, we also simulated repeated measurements with perturbations added to the synergy activations. Ten repeated measurements were simulated for each force direction. For each simulation, normally distributed random noise was added to the original synergy activation vector described above, with synergy activations constrained to be >0 and muscle activations constrained to be between 0 and 1. Signal-to-noise ratios (SNRs) from −20 to 20 dB were simulated. When perturbations were added to the synergy activations, the resulting end-point force changed because of changes in the resulting muscle activations. To ensure task performance was maintained after perturbing synergy activations, a second optimization was performed, finding the minimum change in synergy activations (relative to the new, perturbed activations) needed to produce the correct end-point force. This second optimization is similar to the corrections that might be produced in a “minimum-intervention” control strategy (Valero-Cuevas et al. 2009) and, in general, will not result in synergy activations identical to those produced before the perturbations.

Analysis without musculoskeletal model.

To separate the influence of the biomechanical and task constraints from the performance of the algorithms, we also generated muscle activations that were not impacted by these constraints. The same 100 sets of random specified synergies (W) were used in an analysis that did not involve task performance. In the case with the model, we solved an optimization for C (i.e., where muscle activations = W × C as described above), which determined muscle activations that satisfied the biomechanical and task constraints. Without a musculoskeletal model, we randomly generated C from an exponential distribution with a mean of 0.7 (Tresch et al. 2006). The mean was chosen to achieve a C matrix with similar magnitude as the C matrix from synergy optimization with the musculoskeletal model. For each set of specified synergies (W), only the synergies that had an activation >0.001 for 99% of the force directions with the musculoskeletal model were included. Thus random sets of muscle activations were calculated for each set of specified synergies that were based on the same synergies, W, as the analysis with the musculoskeletal model and had synergy activations, C, of similar magnitude. In the case with the model, C was dictated by the biomechanical and task constraints, whereas, without the model, there were no biomechanical or task constraints, and C was randomly generated from a distribution with equal variances for each row and no correlation between rows.

Matrix factorization algorithms.

The muscle activations calculated both with and without the musculoskeletal model were used to estimate synergies with several matrix factorization algorithms that have previously been used to analyze muscle synergies including NNMF, principal component analysis (PCA), fast independent component analysis (fICA), a combination of PCA and fICA (PCAICA), and probabilistic ICA (pICA). Each of these algorithms estimates synergies as muscle activations = W × C + error; however, the algorithms make different assumptions about the elements in this model (Attias 1999; Hyvarinen and Oja 2000; Lee and Seung 1999; Roweis and Ghahramani 1999; Tresch et al. 2006). NNMF was implemented using the NNMF function in MatLab and incorporated an iterative optimization that tested random initial estimates of W and C and selected the combination of W and C with the minimum sum of squared error between the estimated and original muscle activations. The princomp function in MatLab was used to execute PCA, which uses the data covariance to identify components. For fICA, the fastica function was used in MatLab (http://research.ics.aalto.fi/ica/fastica/), which implements a fixed-point iteration that determines a set of non-Gaussian random variables that are as independent as possible (Hyvarinen and Oja 2000). PCAICA used a combination of the PCA and fICA algorithms in which the dimension of the muscle activations was first reduced to the specified number of synergies using PCA and then run through fICA. The final algorithm, pICA, is an extension of ICA that allows estimates of noise for each data dimension and nonnegativity constraints on W and C to be incorporated (Hojen-Sorensen et al. 2002). For all algorithms, the number of synergies was specified as the number of synergies used to execute the task.

Similarity to specified synergies.

The similarity of the synergies estimated from the muscle activations with the matrix factorization algorithms to the original, specified synergies was calculated as the average correlation coefficient. For each set of synergies, the average correlation coefficient was determined by matching pairs of synergies from the specified and estimated synergies that had the greatest similarity and averaging the correlation coefficients across pairs. The correlation coefficient was normalized from 0 to 1, where 0 is the similarity expected by chance and 1 is perfect similarity (Tresch et al. 2006). The similarity expected by chance was calculated as the average correlation coefficient comparing each set of synergies to 25 randomly generated sets of synergies of the same size (i.e., same number of muscles). We also evaluated the similarity of the subspaces spanned by the specified and identified synergies. We calculated the average principle angle between the subspaces of the specified and identified synergies (Golub and Van Loan 1983; Tresch et al. 2006). Similar to the correlation coefficient, we normalized the subspace similarity from 0 to 1, with 0 equal to the average angle between subspaces attributable to chance and 1 equal to perfect similarity between subspaces. This process was repeated for the synergies with and without the musculoskeletal model. PCA identifies a unique solution of synergies, but the other algorithms included in this analysis can identify slightly different synergies in each iteration. We evaluated the variability in the normalized similarity across iterations of each algorithm and found that the average standard deviation in normalized similarity was 0.05 for NNMF, 0.03 for fICA, 0.03 for PCAICA, and 0.06 for pICA.

To compare the similarity of the specified and estimated synergies with and without the musculoskeletal model, we calculated the difference in similarity between these two simulation sets. With simulation, we can adjust the number of total trials. Therefore, we did not use standard Student's t-tests or ANOVA to compare results because these tests are dependent on the number of trials and can produce significant results if a sufficiently high number of trials is used. Instead, we directly compared the distributions of the simulation results to determine whether changes in similarity estimated with and without the musculoskeletal model were significantly different from 0. For example, to determine whether the similarity of estimated and specified synergies was significantly different with and without the model, we calculated the difference in similarity for each of the 100 sets of synergies. We then calculated the percentage of cases that were either >0 or <0. Similar comparisons of distributions were used to determine whether posture and correlation of synergy activations impacted the similarity of estimated and specified synergies.

Impact of synergy activation correlation.

Because the same synergies, W, were used in the analysis both with and without the musculoskeletal model, any difference in the ability of matrix factorization algorithms to accurately identify synergies in this protocol is tied to the differences in synergy activations, C. This protocol allowed us to quantify the impact of the biomechanical and task constraints on the accuracy of matrix factorization algorithms and critically evaluate how biomechanically constrained tasks impact the identification of synergies. One of the primary differences in C, with and without the musculoskeletal model, was the correlation between the rows of C. Each row of C corresponds to the activation of a synergy across all force directions. With the musculoskeletal model, several synergies were sometimes recruited in similar force directions leading to high covariance, whereas, without the musculoskeletal model, the randomly generated synergy activations had no covariance. To test the impact of correlation of synergy activations independently from the biomechanical model, we systematically added covariance from 0.1 to 0.9 to the randomly generated C without the musculoskeletal model. To create a C matrix with set levels of covariance, we created a set of random vectors from a multivariate normal distribution with the same mean vector as the C matrices used in the original analysis without a musculoskeletal model and a symmetric positive semidefinite covariance matrix with values ranging from 0.1 to 0.9. This resulted in a C matrix where all rows had a covariance with one another at the specified level (i.e., 0.1 to 0.9). We compared the similarity of the synergies with each level of covariance to the similarity of the original synergies estimated without a musculoskeletal model, which had no covariance.

RESULTS

Influence of biomechanical and task constraints.

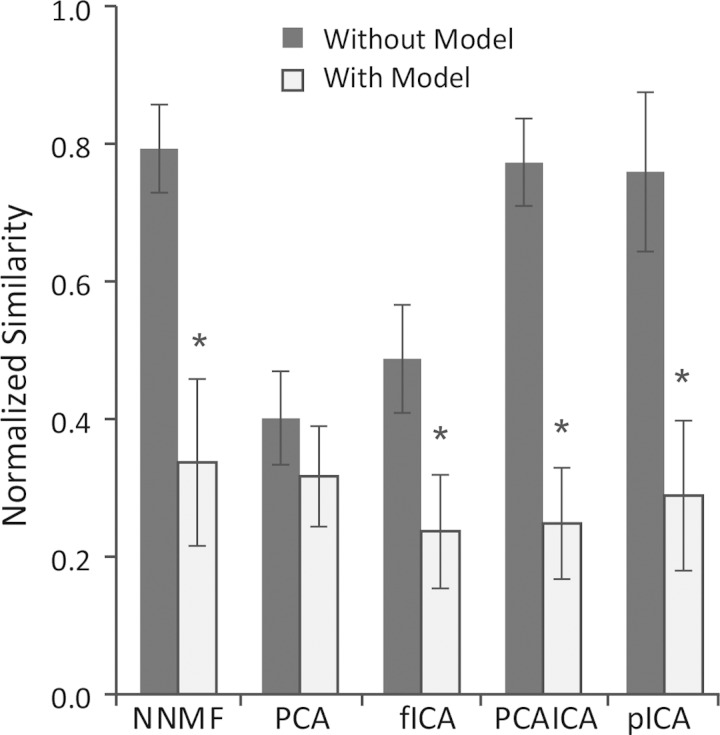
The ability of matrix factorization algorithms to accurately identify synergies decreased when biomechanical and task constraints were included in the analysis using a musculoskeletal model (Fig. 2). Without biomechanical and task constraints, the normalized similarity of estimated synergies and the original, specified synergies ranged from 0.79 ± 0.06 for NNMF to 0.40 ± 0.06 for PCA (means ± SD). These results are similar to those reported by Tresch et al. (2006) but slightly reduced because more muscles and more synergies were included in this analysis (Steele et al. 2013). NNMF, PCAICA, and pICA consistently estimated the synergies more accurately than PCA or fICA without a model. When a musculoskeletal model was included in the analysis, the normalized similarity decreased for all factorization algorithms. NNMF, PCAICA, and pICA, the best performing algorithms without biomechanical and task constraints, all had substantial and statistically significant decreases in normalized similarity. The normalized similarity of the specified and estimated synergies was reduced to 0.34 ± 0.12 for NNMF, 0.25 ± 0.08 for PCAICA, and 0.29 ± 0.11 for pICA. The maximum normalized similarity across the 100 trials was 0.66 for NNMF, 0.50 for PCA, 0.44 for fICA, 0.44 for PCAICA, and 0.54 for pICA.

Fig. 2.

Similarity of estimated and specified synergies with and without biomechanical and task constraints normalized to similarity expected by chance (0 equals similarity expected by chance, 1 equals perfect similarity). *Algorithms that had a significant decrease in normalized similarity with biomechanical and task constraints at a significance level of 0.05. Error bars indicate means ± SD. NNMF, nonnegative matrix factorization; PCA, principal component analysis; fICA, fast independent component analysis; PCAICA, a combination of PCA and fICA; pICA, probabilistic ICA.

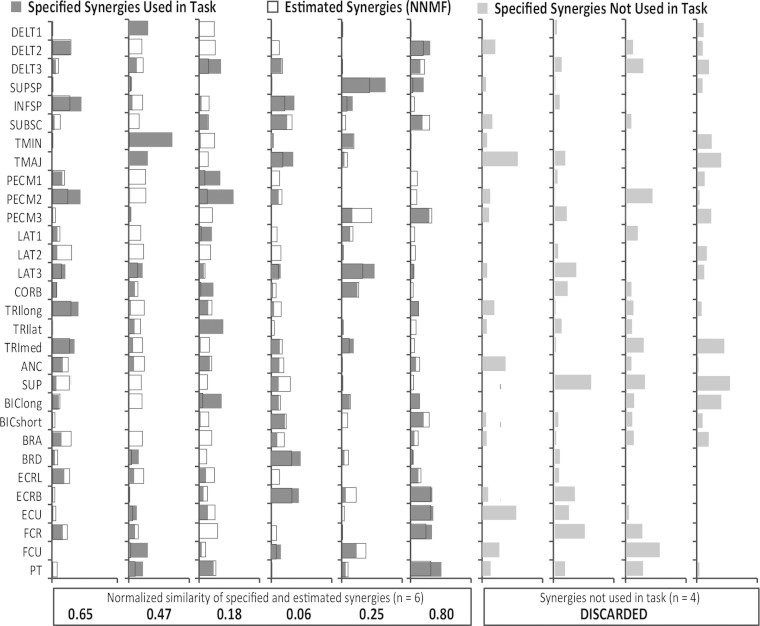
To illustrate how these results were obtained, we have included an example for one set of random synergies (Fig. 3). For this analysis, 10 random synergies were specified, which included weights for all 30 muscles in the model. These synergies were used to generate forces in 1,000 directions around the hand; however, 4 of the 10 synergies had an activation, c, <0.001 for 99% of the force directions and were discarded from further analysis. The remaining six synergies had an activation >0.001 for between 378 and 1,000 of the force directions. The muscle activations were used to solve for six synergies using each of the matrix factorization algorithms (estimated synergies from NNMF shown as an example, Fig. 3, open bars). To analyze synergies estimated without a musculoskeletal model, we specified random activations (C) of the six synergies used to execute the task, which kept the number of synergies consistent with the results from the musculoskeletal model. We then estimated synergies from the muscle activations (muscle activations = W × C) using each matrix factorization algorithm. The similarity of the six synergies estimated with and without the biomechanical and task constraints to the six specified synergies was calculated as the average correlation coefficient and normalized to similarity expected by chance. For this example, the similarity without biomechanical or task constraints was 0.85 for NNMF, PCAICA, and pICA but decreased to 0.40, 0.43, and 0.45 for each algorithm, respectively, when biomechanical and task constraints were incorporated using a musculoskeletal model. This same process was completed for all 100 sets of random synergies.

Fig. 3.

Example of analysis and results for 1 set of synergies. 10 synergies were specified, and 6 of these synergies were used by the simulation to execute the isometric force task (dark gray bars). The 4 synergies with an activation <0.001 for over 99% of the force directions (light gray bars) were discarded from further analysis. Synergies estimated from each matrix factorization algorithm were paired by greatest correlation coefficient with the specified synergies. In this example, the synergies estimated from NNMF (open bars) had an average normalized similarity of 0.40. The normalized similarity of the NNMF estimated synergies, and specified synergies are shown at the bottom. Muscle abbreviations are defined in Table 1.

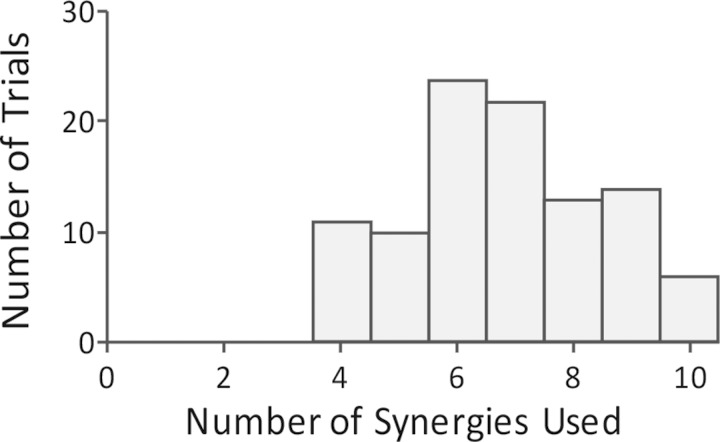
In the example shown in Fig. 3, six synergies were used to execute the task; however, the number of synergies with an activation >0.001 for 99% of the force directions varied between 4 and 10 synergies across all 100 sets of randomly generated synergies (Fig. 4). The relationship between number of synergies used to execute the task and resulting similarity was weak across all algorithms (r² < 0.05 for all algorithms). The synergies estimated with all algorithms explained >90% of the total variance in muscle activity across the 30 muscles in the model. The average total variance accounted for by each algorithm was: 96 ± 11% for NNMF, 100 ± 0% for PCA, 99 ± 1% for fICA, 100 ± 0% for PCAICA, and 93 ± 12% for pICA. There was no significant correlation between total variance accounted for and similarity of specified and estimated synergies. The high total variance accounted for suggests that all algorithms were able to describe the data and identify a relevant low-dimensional subspace. However, the ability of algorithms to identify the correct subspace spanned by the original synergies was decreased by inclusion of biomechanical and task constraints. Without biomechanical and task constraints, the average angle between subspaces was 22.1 ± 4.84° for NNMF, 22.2 ± 4.8° for PCA, 30.6 ± 4.0° for fICA, 22.2 ± 4.8° for PCAICA, and 24.1 ± 6.5° for pICA, resulting in an average normalized subspace similarity of 0.63 ± 0.07 for NNMF, 0.63 ± 0.07 for PCA, 0.49 ± 0.06 for fICA, 0.63 ± 0.07 for PCAICA, and 0.59 ± 0.12 for pICA. However, when a musculoskeletal model was used in the analysis, the average angle between subspaces increased to 34.5 ± 7.9 for NNMF, 36.9 ± 6.8 for PCA, 33.0 ± 6.4 for fICA, 33.0 ± 6.4 for PCAICA, and 42.3 ± 9.2 for pICA, resulting in a decrease in average normalized subspace similarity to 0.42 ± 0.13 for NNMF, 0.39 ± 0.09 for PCA, 0.45 ± 0.09 for fICA, 0.45 ± 0.09 for PCAICA, and 0.29 ± 0.16 for pICA.

Fig. 4.

Histogram of the number of specified synergies used to execute the isometric force task. Across all sets of random synergies, between 4 and 10 of the specified synergies were used.

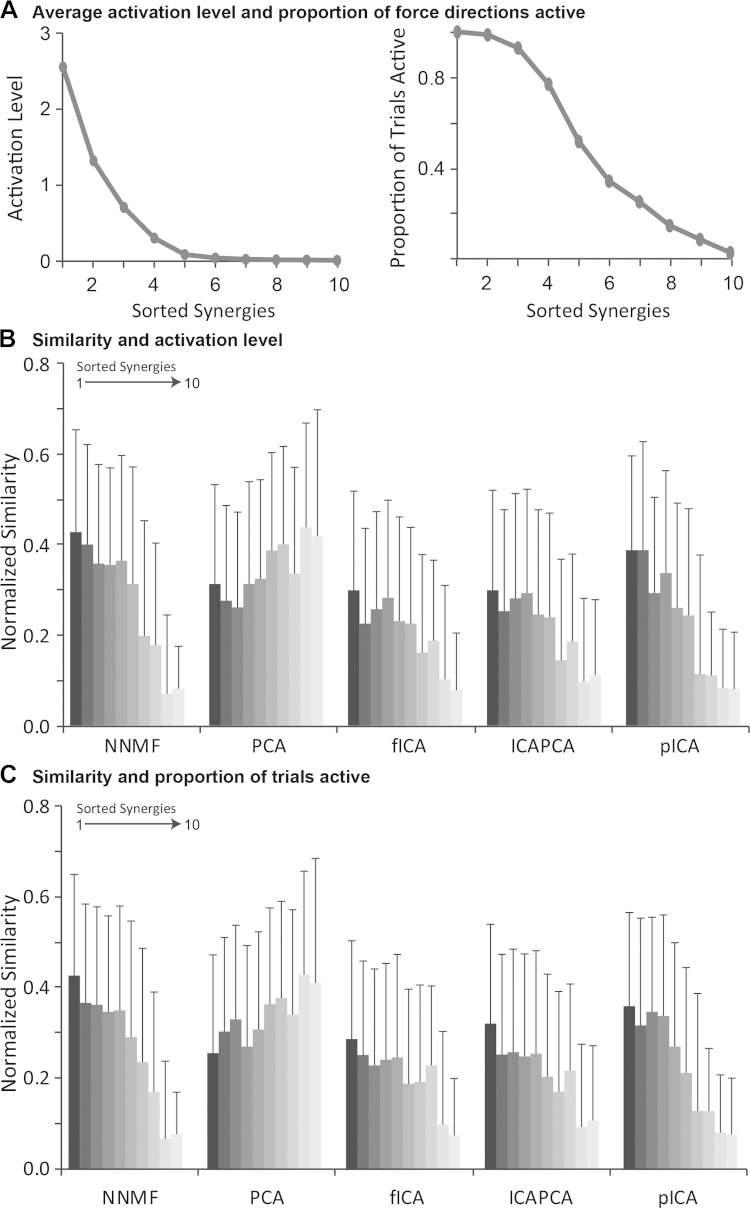
When the synergies were sorted by average activation level or proportion of force directions a synergy was active, the first two to three synergies tended to have much larger activation levels than the other synergies (Fig. 5A). The similarity of the specified and estimated synergies was greatest for synergies that were more active (Fig. 5B) or used for a greater proportion of the force directions (Fig. 5C) for all algorithms except PCA. However, the average normalized similarity was still below 0.6 for even the most active synergies, significantly less than the normalized similarity without the biomechanical and task constraints.

Fig. 5.

A: synergies were sorted by activation level (from the C matrix) and proportion of force directions active. Normalized similarity was greatest for synergies that were more active (B) or that were active for a greater proportion of force directions (C) for NNMF, fICA, PCAICA, and pICA. Error bars indicate means ± SD.

Because synergy matrices were identical in the analyses with and without biomechanical and task constraints, the difference in the ability of the matrix factorization algorithms to identify the specified synergies had to be influenced by the structure of the synergy activations (i.e., C matrix). Without a model, C was randomly selected from an exponential distribution, similar to Tresch et al. (2006). With the model, C was determined through an optimization procedure that minimized the sum of c² and constrained solutions to activations that successfully executed the isometric force task. One of the primary differences in C with and without the biomechanical and task constraints was the relative correlation of the synergy activations. Without the biomechanical and task constraints, there was no correlation between the activation of synergies because all values were randomly chosen. However, with biomechanical and task constraints, the average correlation of the synergy activations was 0.27 ± 0.24. To successfully complete the simulated task, some synergies were consistently activated with other synergies.

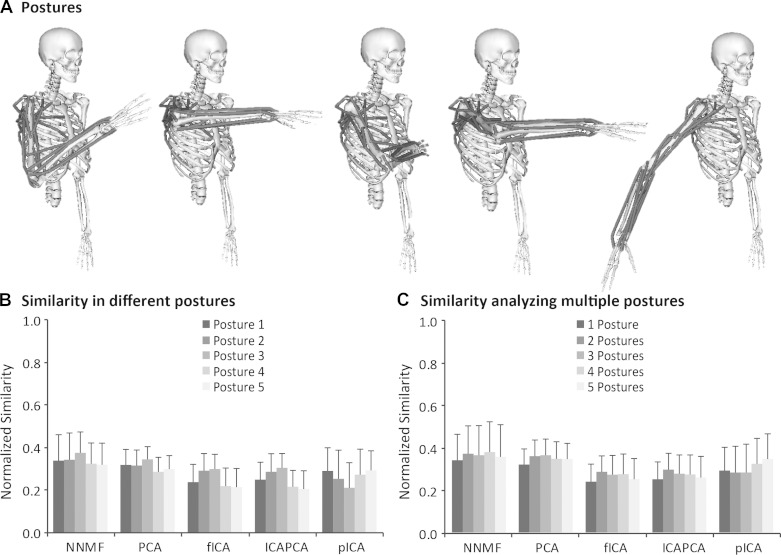
Biomechanical and task constraints may change with different postures and may impact the ability of matrix factorization algorithms to accurately identify synergies. We tested the posture used in the original experimental protocol and four additional postures over a range of shoulder and elbow positions (Fig. 6A). Across all algorithms, the normalized similarity was not significantly different between postures (Fig. 6B). Furthermore, the normalized similarity did not change when muscle activations from all five postures were used to estimate synergies (Fig. 6C). Although there was no significant change in normalized similarity with posture, the correlation between synergy activations differed between postures, and there was a significant correlation between average correlation of synergy activations and normalized similarity for all algorithms except pICA. For example, although the average normalized similarity of synergies estimated from NNMF only varied between 0.32 in posture 5 to 0.37 in posture 2, the average correlation also varied from 0.38 in posture 5 to 0.12 in posture 2, with an r² between average normalized similarity and correlation of 0.71 across the five postures (r² = 0.52 for PCA, r² = 0.92 for fICA, and r² = 0.92 for PCAICA). Thus, as correlation of synergy activations increased, the ability to accurately identify synergies in a given posture decreased.

Fig. 6.

A: 5 postures were tested to evaluate the impact of choice and number of postures included in the analysis. Normalized similarity was not significantly different between postures (B) or when multiple postures (C) were used in the analysis. Error bars indicate means ± SD.

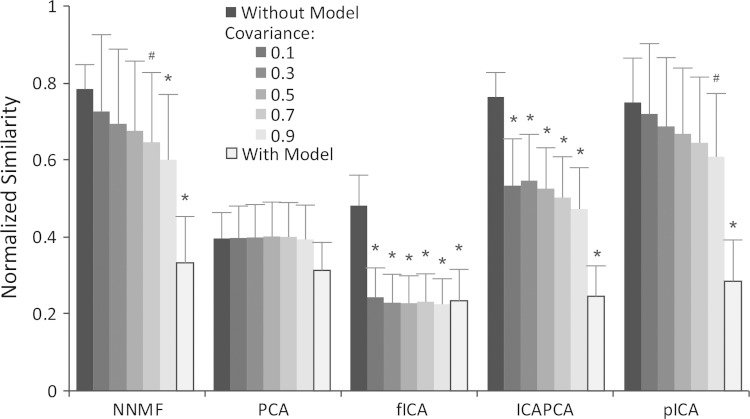
We tested the impact of increasing the correlation of synergy activations without the model (Fig. 7). Increasing covariance between the synergy activations decreased the similarity for all algorithms, except PCA. The similarity of the synergies estimated with fICA and PCAICA decreased significantly with even a small amount of covariance, whereas the similarity decreased with increasing similarity for NNMF and pICA. PCA requires the synergies to be orthogonal, which results in a low initial similarity that is not impacted by increasing covariance between the synergy activations. Although the normalized similarity did not drop to the level with the model, correlation of synergy activations was a contributing factor to the decreased ability of matrix factorization algorithms to correctly identify synergies.

Fig. 7.

Impact of covariance of synergy activations on normalized similarity. *#Algorithms that had a significant decrease in normalized similarity compared with similarity without biomechanical and task constraints and no covariance in the C matrix at significance levels of 0.05 and 0.10, respectively. Error bars indicate means ± SD.

Influence of motor variability.

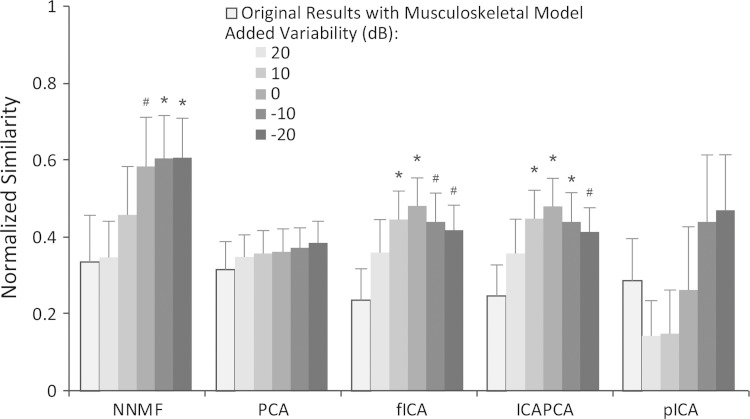
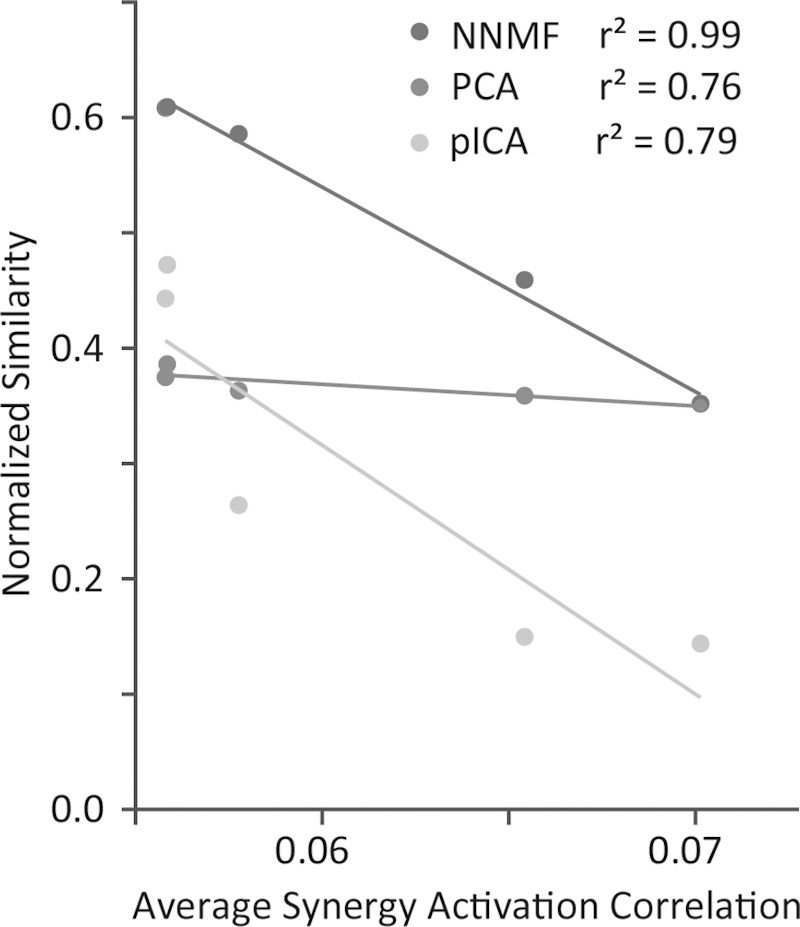
Adding variability to synergy activations and including multiple data points analyzed for each force direction also significantly improved the ability of NNMF, fICA, and PCAICA to accurately identify the specified synergies (Fig. 8). With an SNR of 0 dB, the average normalized similarity improved to 0.58 ± 0.13, 0.48 ± 0.07, and 0.48 ± 0.07 for NNMF, fICA, and PCAICA, respectively. For further reductions in the SNR beyond 0 dB, the improvements in the average normalized similarity plateaued for NNMF and decreased back to levels without added variability for fICA and PCAICA. There was no significant change in the normalized similarity for PCA or pICA with a peak normalized similarity with variability of 0.39 ± 0.06 and 0.47 ± 0.15, respectively. With added variability, the average normalized similarity of the most active synergies increased to 0.73 ± 0.13 for NNMF. However, for all algorithms, the normalized similarity still remained significantly less than without a model, suggesting that the correlation between synergy activations still negatively impacted synergy identification. Similar to the analysis of different postures, the average correlation between synergy activations decreased with added variability. With an SNR of −20 dB, the average correlation was reduced to 0.05. For all algorithms, there was a significant correlation between average normalized similarity and average correlation of synergy activations with r² equal to 0.99, 0.76, 0.39, 0.37, and 0.79 for NNMF, PCA, fICA, PCAICA, and pICA, respectively (Fig. 9).

Fig. 8.

Average normalized similarity of estimated synergies from each algorithm with a model and no variability (outlined bars) and with increasing variability. Variability was added to the synergy activations for 10 trials in each force direction with a magnitude specified by the signal-to-noise ratio scaled to the synergy activations. Similarity was normalized to similarity expected by chance (0 equals similarity expected by chance, 1 equals perfect similarity). *#Significant change in normalized similarity compared with the original analysis with biomechanical and mechanical task constraints and no variability at significant levels of 0.05 and 0.10, respectively. Error bars indicate means ± SD.

Fig. 9.

Correlation between average normalized similarity and average synergy activation correlation when synergy activation variability was included in the analysis (signal-to-noise ratio of −20 dB, −10 dB, 0 dB, 10 dB, and 20 dB). Results are shown for the three algorithms with the strongest correlation: NNMF, PCA, and pICA. As synergy activation variability increased, average synergy activation decreased. NNMF and pICA had significant increases in normalized similarity with increasing variability, but other algorithms, such as PCA, had smaller changes in normalized similarity.

DISCUSSION

The aim of this study was to evaluate the impact of different experimental protocols as well as biomechanical and task constraints on the ability of matrix factorization algorithms to accurately identify a synergy-based neuromuscular control strategy. We determined that the accuracy of synergies estimated with matrix factorization algorithms was sensitive to constraints on the suitable patterns of muscle activation and the chosen experimental and analysis protocols. In simulations mimicking experiments or analyses that minimize physiological variability, all algorithms performed poorly at identifying the synergies used to generate the simulated data. Without biomechanical or task constraints, some of the algorithms including NNMF, PCAICA, and pICA were able to identify synergies with a high normalized similarity, but, when a biomechanically constrained task was incorporated into the analysis using a musculoskeletal model, the ability of all of these algorithms to accurately identify synergies decreased significantly. The average normalized similarity of the estimated and specified synergies was significantly greater than chance, but even the most active synergies still had a normalized similarity <0.5 on average. Matrix factorization algorithms assume some level of independence between synergy activations, and the influence of this assumption was evident in our results. Simulations that increased the correlation between synergy activations resulted in a decreased similarity between the synergies specified in the simulations and those estimated by the various matrix factorization algorithms.

Incorporating motor variability in synergy activations significantly improved the accuracy of synergies estimated by NNMF, fICA, and PCAICA. Variability is endemic in physiological systems and can improve neural signal processing, as demonstrated by these results. Data that include physiological variability provide a richer dataset compared with averaged EMG or single time points. For example, Hart and Giszter (2004) previously demonstrated the importance and impact of filtering on synergy identification from EMG. Similarly, in this study, we found that due to increasing variability or different postures, correlation of synergy activations could be reduced and covariance was correlated with resulting similarity of the estimated and specified synergies. These results demonstrate that caution needs to be exercised in designing both experimental protocols and data processing techniques for estimating synergies from EMG. Protocols that use averaged data or single time points may be missing the critical variability in muscle activity needed to accurately estimate synergies. Hence, the sensitivity of estimated synergies to filtering and data processing should be examined. Protocols that incorporate time-series data, dynamic tasks, or a variety of tasks may similarly further improve the ability of these algorithms to accurately identify synergies. Note, however, that these considerations introduce further complexity to synergy identification analyses, as it is unclear a priori how to process EMG data to eliminate measurement noise while preserving any potential latent variability in synergy activations.

Impact of biomechanical and task constraints.

Previous studies have also suggested that biomechanical constraints can negatively impact the results of synergy analyses. In the original evaluation of the accuracy of synergies estimated with matrix factorization algorithms by Tresch et al. (2006), which did not use a musculoskeletal model and randomly generated muscle activations, the authors noted that the similarity of estimated synergies decreased if the activation of two synergies was coupled. Our results demonstrate that the activation of synergies can be coupled because of biomechanical and task constraints, as illustrated by the increased correlation of synergy activations with a musculoskeletal model in this study. Our analysis of covariance also supports the results of Burkholder and van Antwerp (2013), who reported that synergies are dependent on the volume of the control space included in an analysis. They found that restricting the sampling of the control space does not impact the ability of NNMF to identify the correct number of synergies but does impact the ability of NNMF to accurately identify synergy structure. Similarly, we determined that covariance increased and the size of the control space decreased in the face of biomechanical and task constraints and that this negatively impacted the ability of NNMF and other matrix factorization algorithms to accurately identify synergies.

Many other hypotheses for how humans control the musculoskeletal system beyond muscle synergies have also been proposed (Ivanenko et al. 2009; Thelen and Anderson 2006; Todorov and Jordan 2002; Valero-Cuevas et al. 2009; Winter 1990). Kutch et al. (2012) demonstrated that alternative control strategies such as optimal control that minimize metabolic energy can also result in muscle activation patterns that can be described by a low-dimensional subspace with matrix factorization algorithms. Thus the presence of a low-dimensional subspace describing muscle activations is not sufficient for concluding that muscle synergies are the building blocks for an underlying control strategy. Our results do not shed light on the debate regarding the existence of synergies but rather demonstrate that, if a synergy-based control system does exist, it could be challenging to identify uniquely from EMGs.

Performance of matrix factorization algorithms.

Our results also highlight some of the relative advantages and disadvantages of different matrix factorization algorithms. NNMF and pICA restrict synergy weights to be all nonnegative, which mirrored the underlying constraints with the musculoskeletal model, improving the accuracy of these algorithms to identify synergies and reflecting the fact that the net activation of muscles measured by EMG must be positive. PCA was consistently the worst-performing algorithm both with and without the musculoskeletal model, reflecting the negative impacts of requiring orthogonal components. When combined with fICA in PCAICA, accuracy improved, and PCAICA was one of the most computationally efficient algorithms (Tresch et al. 2006). However, fICA and PCAICA had dramatic drops in similarity when even small amounts of correlation were present because activation covariance violates one of the basic assumptions of the ICA algorithm. It is important to note that only two variants of ICA were tested in this study but that there are many variants of the ICA algorithm, and our results may not extend to other implementations (Bell and Sejnowski 1995).

Generalizability and applications of synergies.

Matrix factorization algorithms have been widely used as a tool to calculate and compare low-dimensional representations of muscle activity. These results highlight some of the limitations of matrix factorization algorithms; however, evidence for synergies and low-dimensional neuromuscular control extends beyond these algorithms. Prior experiments have provided physiological evidence of synergy-based control (Kargo and Giszter 2000; Overduin et al. 2012). For example, with the use of simultaneous spinal and muscle recordings in the frog, prior research has demonstrated that some neurons from the spinal cord project to lower-dimensional motor pools identified with a variant of ICA (Hart and Giszter 2010; Kargo and Giszter 2008), and these synergies can be summed or perturbed in amplitude or phase (Kargo and Giszter 2008). Recent research has suggested that these results extend beyond frogs, including the identification of “motor synergy encoders” or neurons in the mouse spinal cord that receive direct input from the motor cortex and project to motor groups (Levine et al. 2014). Beyond matrix factorization algorithms, there are also a multitude of other algorithms used to cluster muscle activity based on features not available in this analysis, such as by muscle onsets (Krouchev et al. 2006), which may provide insight into low-dimensional representations of neuromuscular control.

Recently, synergy analyses have been applied to clinical populations such as individuals after stroke (Cheung et al. 2012; Clark et al. 2010; Roh et al. 2013). These studies document a reduction in the number of synergies used during tasks and changes in the structure of synergies after stroke. On the basis of our results, synergies may be useful for identifying changes in dimensionality, but caution should be exercised in evaluating the relative weights of muscles in each synergy. When designing protocols to evaluate synergies in these populations, one should include physiological variability and multiple tasks to decrease correlation of synergy activations, which may improve the accuracy and reliability of these analyses. Understanding the link between changes in muscle synergies with changes in control strategy after brain injury may provide insight into both the application of muscle synergies and implications for motor recovery (Bowden et al. 2013).

The methods and results of this study provide further evidence that complex musculoskeletal systems can be controlled in a low-dimensional space (Ivanenko et al. 2006; Kargo and Giszter 2008; Ting and Chvatal 2010; Todorov et al. 2005; Tresch and Jarc 2009). In this study, a musculoskeletal model with 30 muscles could execute a task to generate end-point forces at the hand in 1,000 directions with as few as 4 synergies. However, our results highlight the need for caution in the design of experiments and interpretation of results from matrix factorization algorithms. Matrix factorization algorithms made it difficult to accurately identify synergy-based control strategies in the presence of biomechanical and task constraints. Synergies estimated from protocols that use averaged or single trials of muscle activity should be used with caution to make muscle-specific conclusions regarding synergy weights. Synergies and matrix factorization algorithms may still be useful in these circumstances to examine the complexity or dimensionality of muscle activity. For example, after stroke, the reduced dimensionality of synergies may still provide a powerful tool for guiding rehabilitation programs and evaluating changes in the complexity of control after treatment. As the use of matrix factorization algorithms and synergies move from the research laboratory to the clinic, understanding and testing the generalizability and sensitivity of these methods will be important to support interpretation and clinical decision making. Musculoskeletal modeling and simulation can provide a unique test bed to specify underlying neuromuscular control strategies and evaluate different algorithms, experimental protocols, and interpretations of synergy analyses.

GRANTS

This work was funded by NIH K12HD073945, 5R24HD050821-09, and R01 NS053813.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: K.M.S., M.C.T., and E.J.P. conception and design of research; K.M.S. performed experiments; K.M.S. analyzed data; K.M.S., M.C.T., and E.J.P. interpreted results of experiments; K.M.S. prepared figures; K.M.S. drafted manuscript; K.M.S., M.C.T., and E.J.P. edited and revised manuscript; K.M.S., M.C.T., and E.J.P. approved final version of manuscript.