Temporal evolution of both premotor and motor cortical tuning properties reflect changes in limb biomechanics

Abstract

A prevailing theory in the cortical control of limb movement posits that premotor cortex initiates a high-level motor plan that is transformed by the primary motor cortex (MI) into a low-level motor command to be executed. This theory implies that the premotor cortex is shielded from the motor periphery, and therefore, its activity should not represent the low-level features of movement. Contrary to this theory, we show that both dorsal (PMd) and ventral premotor (PMv) cortexes exhibit population-level tuning properties that reflect the biomechanical properties of the periphery similar to those observed in M1. We recorded single-unit activity from M1, PMd, and PMv and characterized their tuning properties while six rhesus macaques performed a reaching task in the horizontal plane. Each area exhibited a bimodal distribution of preferred directions during execution consistent with the known biomechanical anisotropies of the muscles and limb segments. Moreover, these distributions varied in orientation or shape from planning to execution. A network model shows that such population dynamics are linked to a change in biomechanics of the limb as the monkey begins to move, specifically to the state-dependent properties of muscles. We suggest that, like M1, neural populations in PMd and PMv are more directly linked with the motor periphery than previously thought.

according to one view of the cortical control of voluntary movement, movement plans are generated by the premotor cortexes (Weinrich and Wise 1982) and are thought to be represented in a high-level, extrinsic coordinate system such as a Cartesian frame of reference associated with the visual system (Batista et al. 2007; Boussaoud et al. 1998; Graziano et al. 1994; Hoshi and Tanji 2006, 2007; Kakei et al. 2001; Kurata and Hoshi 2002; Pesaran et al. 2006; Schwartz et al. 2004; Shen and Alexander 1997; Wu and Hatsopoulos 2007; Xiao et al. 2006). These high-level plans are then transmitted to the primary motor cortex (M1), where they are transformed into low-level, intrinsic motor commands that are executed by the motor periphery via the corticospinal tract (Scott et al. 1997). Following this hierarchical view, the physiological properties of M1 neurons should reflect the biomechanical features of the musculoskeletal system, and, in fact, previous work has demonstrated that population-level responses in the M1 arm area do just this. In particular, the distribution of preferred directions (PDs) is bimodal, having a strong correlation with the intrinsic, mechanical anisotropies prominent in both planar (Kurtzer et al. 2006; Lillicrap and Scott 2013; Scott et al. 2001; Scott and Kalaska 1997) and unconstrained, three-dimensional (Mitsuda and Onorati 2002) reaching movements. For example, when the limb moves in the horizontal plane, the distribution of muscle PDs exhibited two modes away and towards the body, which is similar to the observed bimodal distribution of M1 PDs (Kurtzer et al. 2006). More importantly, recent modeling work suggests that a bimodal distribution of MI PDs emerges naturally from a model that directly and optimally controls a musculoskeletal system. The key observation from this modeling study is that the empirically observed distribution of PDs occurs only when realistic limb geometry, intersegmental dynamics, and muscle biomechanical properties are included in the model, suggesting that bimodality reflects properties of the periphery (Lillicrap and Scott 2013). This contrasts with the uniform (i.e., isotropic) distribution that would be expected from an area performing computations in an extrinsic reference frame (Georgopoulos et al. 1982, 1986; Li et al. 2001; Moran and Schwartz 1999). Such expectations are derived from the intuition that populations of neurons performing computations in an extrinsic coordinate system should represent each part of space equally. It remains unclear, however, whether neural populations in the dorsal premotor cortex (PMd) and ventral premotor cortex (PMv) reflect limb biomechanics or are buffered from them by M1.

Here, we examine simultaneously recorded ensembles of neurons in PMd, PMv, and M1 while monkeys performed an instructed delay, center-out reaching task. Our data demonstrate two important conceptual advances. First, in apparent contradiction to the traditional hierarchical view of the cortical control of movement, we show that the distributions of PDs in PMd and PMv exhibit anisotropies during voluntary movement similar to those observed in M1. In particular, the PD distribution in PMd is bimodal during both planning and execution, while the PD distribution in PMv exhibits a change in shape from uniform during planning to bimodal during execution perhaps reflecting a fundamental shift in the type of computation performed by this region. Second, we demonstrate that the orientations of the population-level distributions in M1, PMd, and PMv evolve smoothly in time beginning at the transition from movement planning to execution. We developed an optimal control model to address this second finding. The model commands muscle activity, and it reveals that the temporal evolution in the population-level properties during the perimovement period emerges as a direct result of the state-dependent, mechanical properties of muscles.

MATERIALS AND METHODS

Six rhesus macaques (4 males and 2 females) were trained to move a cursor to hit visual targets using a two-link robotic exoskeleton (BKIN Technologies, Kingston, ON). The monkeys sat in a primate chair and placed one arm in the exoskeleton. Their arm was abducted by 90° at the shoulder and was supported by the exoskeleton so that all movements were restricted to the horizontal plane. Real-time movement feedback was provided on a horizontal screen via a visual cursor that was aligned to the robot's handle and served as a proxy for the location of the monkey's hand. Motion of the head was restricted, requiring the monkeys to observe visual feedback using eye movements alone. We did not monitor eye position. Each monkey performed an instructed-delay, center out reaching task making point-to-point, reaching movements (∼6 cm) from a central target to eight peripheral targets uniformly distributed around the center. The monkeys held the cursor within the center target for either a fixed (1,000 ms, monkey B) or randomly selected (1,000-1,500 ms; uniform distribution) instruction period after the appearance of the peripheral target. After receiving the “Go” cue (flashing peripheral target), they were required to acquire and hold within the peripheral target for 500 ms to complete the task and receive a reward. Each dataset contained at least 10 successful reaches to each of the 8 targets. All of the surgical and behavioral procedures were approved by the University of Chicago's Institutional Animal Care and Use Committee and conform to the principles outlined in the Guide for the Care and Use of Laboratory Animals.

Electrophysiology.

Monkeys were chronically implanted with 100-electrode microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT) in contralateral arm areas of primary motor cortex (M1), caudal dorsal premotor cortex (PMd), and ventral premotor cortex (PMv). All arrays were arranged in a 10 × 10 matrix with 400-μm interelectrode separation. The length of each electrode was either 1.0 or 1.5 mm, and their tips were coated with either platinum or iridium oxide. Array placement for each monkey is shown in Fig. 1. During a recording session, signals from up to 96 electrodes were amplified (gain of 5,000), band-pass filtered between 0.3 and 7.5 kHz, and recorded digitally (14-bit) at 30 kHz per channel using a Cerebus acquisition system (Blackrock Microsystems). Only waveforms (1.6 ms in duration; 48 sample time points per waveform) that crossed a user-defined threshold were stored and spike-sorted using Offline Sorter (Plexon, Dallas, TX). In some cases more than one unit was sorted from the neural activity on a single electrode. Signal-to-noise ratios were defined as the difference in mean peak-to-trough voltage divided by twice the mean standard deviation. The mean standard deviation was computed by measuring the standard deviation of the spike waveform over all acquired spikes at each of the 48 sample time points of the waveform and then averaging. All isolated single units used in this study possessed a signal-to-noise ratio of three or higher.

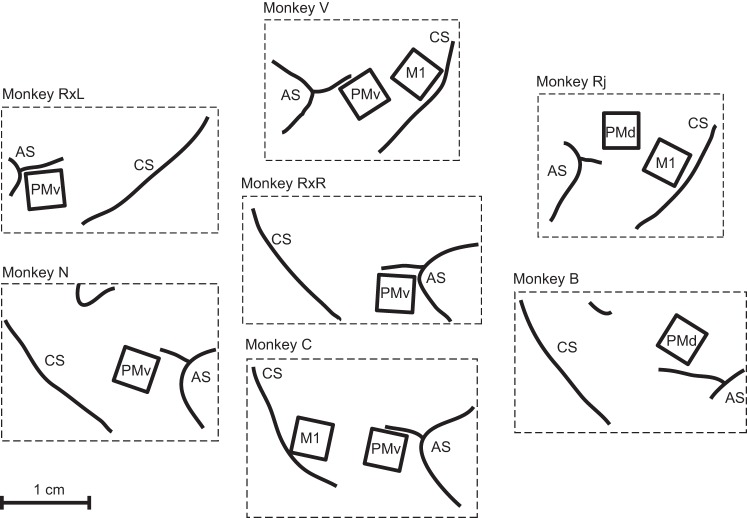
Fig. 1.

Anatomy and placement of arrays for each monkey-hemisphere. Recordings of neural activity during center-out reaching were collected from a total of 10 arrays implanted in 6 monkeys: 3 in primary motor cortex (MI), 2 in dorsal premotor (PMd), and 5 in ventral premotor (PMv). In 3 monkeys, recordings were taken from each of 2 areas, and in 1 monkey (RX) recordings were taken from the same area (PMv) in both hemispheres. Placement is shown relative to the central sulcus (CS) and arcuate sulcus (AS).

Data from 22 separate experimental sessions were analyzed in this study with a data set being defined as the simultaneously recorded neural activity during a single session containing at least 10 successful reaches in each of the 8 directions. A total of 858, 375, and 926 “neuron samples” were recorded from M1, PMd, and PMv, respectively. We use the term “neuron samples” when aggregating units over multiple datasets to make clear that these represent independent samples but may or may not represent different neurons given that previous work has demonstrated that up to 39% of neurons are preserved over a 15-day recording period (Dickey et al. 2009).

Kinematic analysis.

Hand position was binned in 50-ms bins and smoothed using a 150-ms sliding rectangular window. Hand velocity was estimated by computing the forward difference of the X and Y position time series and subsequently smoothed using a 150-ms sliding rectangular window. Velocity estimates were converted to hand speed by computing the magnitude of the component velocities. Joint angles for the shoulder and elbow were computed from the binned position time series using the inverse kinematic equations of the two-joint robotic arm. Joint angular velocities and accelerations were estimated by computing the forward difference of the shoulder and elbow angle time series. Joint torque for the shoulder and elbow was computed using the inverse dynamics equations for the KINARM and the monkey's arm. This methodology has been described previously (Fagg et al. 2009).

Neural analysis.

To determine the preferred direction of movement for each cell, we fit the reach direction-dependent discharge rate to a sinusoidal firing rate model using linear regression. The regression model took the form,

$$y=b_0+b_1\hspace{0.17em}\cos \theta \hspace{0.17em}+\hspace{0.17em}{b}_2\hspace{0.17em}\sin \theta ,$$

where y is the firing rate of a single cell, b₀ is the baseline firing rate, b₁ and b₂ are the components of the firing rate modulated by movement direction, and θ is the cued reach direction (Georgopoulos et al. 1982). Individual cells were considered to be significantly tuned to movement direction if the P value of the full model F-statistic was less than the α = 0.05 significance level. Neurons that were not tuned to movement direction in any epoch were discarded. A neuron's PD was estimated by computing the arctangent of the ratio b₂/b₁, while its modulation depth (MD) for each neuron was defined as the vector magnitude of the coefficients b₂ and b₁. We used a circular permutation technique (Stark and Abeles 2005) to test for significant rotations in a neuron's PD between the instructed delay and movement periods. To estimate the accuracy of the preferred direction measurement, we estimated its standard deviation for each neuron using a bootstrap (1,000 draws of movement direction/firing rate pairs with replacement).

The PDs of significantly tuned neurons were pooled and circular frequency distributions were created as a measure of population level activity. Using a Rayleigh test (Batschelet 1981), we evaluated whether the distribution of PDs (for each area and time window) was uniform compared with unimodal and bimodal alternatives. To satisfy the assumptions of the Rayleigh test for bimodal variants, all angles were doubled before testing for uniformity. In cases where the null hypothesis (uniform distributions) could be rejected in favor of both the unimodal and bimodal alternatives, we report the results from the test having the lowest P value.

Network model.

We optimized a neural network control law to move a physical model of a two-joint revolute arm via six lumped muscle actuators. We then examined the activity of the constituent neuron-like units and performed analyses equivalent to those applied to the monkey data described in this article. Simulations were similar to those described in Lillicrap and Scott (2013): important differences are discussed below. The network was taught to make center-out reaches (16 directions evenly spaced around a circle with radius of 6 cm) in a similar workspace position and with reach kinematics and dynamics similar to those in the empirical experiments described in this article; average movement time of ≈700 ms, with roughly bell-shaped velocity profiles. The networks were trained on a cost function that penalizes the distance to the target at the final time, i.e., at t = T, balanced against keeping the neural activity z_t, muscle activity u_t, and synaptic weights w, small.

The control law used in this study was a continuous time recurrent neural network (CTRNN) composed of two layers of tanh(·) units, which we will here refer to as y_t and z_t. The input layer, y_t, received feedback from the plant, x_t, and context information specifying the goal state, x*. In the simulations presented here y_t contained 100 units, and z_t contained 500 units. Each layer had recurrent connections internal to itself. z_t Receives connections from y_t but not vice versa. The weighted output of this network was used as input to six lumped muscle actuators, u_t, which in turn moved a two-joint revolute arm.

In the following we have used the convention that matrices are given by bolded upper case and vectors by bolded lower case; unbolded symbols are scalars unless otherwise specified. Vector functions are also given in bolded lower case. We use [·]_↓ to denote the flattening of a matrix into a vector and with analogy to the Matlab usage, we use semicolon to denote vector concatenation, e.g., [·;·]. We use ⊙ for element-wise multiplication.

The following equations govern the deterministic time evolution of the controller:

$${\mathbf{y}}_{\mathit{t}}=\left(1-{\tau }_h\right)\cdot y_{t-1}+{\tau }_h\cdot \text{tanh}\left(W_{xy}[x_{t-1};x*]+W_{yy}{y}_{t-1}+b_y\right)$$ (1)

$${\mathbf{z}}_t=\left(1-{\tau }_h\right)\cdot z_{t-1}+{\tau }_h\cdot \text{tanh}\left(W_{yz}{y}_{t-1}+W_{zz}{z}_{t-1}+b_z\right)$$ (2)

$${\mathbf{u}}_t=\left(1-{\tau }_u\right)\cdot u_{t-1}+{\tau }_u\cdot {\sigma }_u\left(W_{zu}{z}_{t-1}+b_u\right)$$ (3)

Signal-dependent noise was applied to the neural activity, so that at each time step: y_t = y_t + ξ_y ⊙ (y_t ⊙ y_t); z_t = z_t + ξ_z ⊙ (z_t ⊙ z_t) with the elements of ξ_y, ξ_z drawn i.i.d. at each time step from N (μ = 0, σ = 0.01). In the above, the goal state is given by x* = ${\theta *}_i$ The muscle activation function, σ_u(·), was the standard sigmoid function with a simple offset term; i.e., the vector version of σ(x) = $\frac{1}{1-\exp \left(x-5\right)}$. τ_h = 0.5 And τ_u = 0.2 are time constants governing the integration of the network and muscle activity, respectively. Initial states for the network activities (i.e., z₀) were fixed to vectors drawn from the uniform distribution over the range [−0.05, 0.05]; muscle initial activation states were fixed to u₀ = 0.

For a reach to joint position ${\theta }_i^{*}$ (i.e., the limb configuration at the terminis of a reach to the ith target), the cost function was thus given by,

$$J_{{\theta }_{\mathit{i}}^{\ast }}=\frac{1}{2}{\Vert {\theta }_i^{\ast }-{\theta }_T\Vert }^2+{\displaystyle \sum _{t=0}^T\left({\alpha }_z{\Vert z_t\Vert }^2\hspace{0.17em}+\hspace{0.17em}{\alpha }_u{\Vert u_t\Vert }^2\right)+}{\alpha }_w{\Vert w\Vert }^2$$ (4)

where θ_T is the vector of joint positions at t = T, and α_z, α_u, α_w are the respective regularization constants for the neural activity, muscle activity, and network weights. Thus we sought the parameter vector, w = [[W_xy]_↓, [W_yy]_↓, [W_yz]_↓, [W_zz]_↓, b_y, b_z, b_u], which minimizes $J=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{J}_{{\theta }_i^{\ast }}}$. This optimization was impractical via straightforward gradient descent, and we found that to find good solutions it was necessary to use apply a technique that takes advantage of second-order curvature information. In practice these optimizations were accomplished via the limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm (LBFGS).

In our simulations plant dynamics were governed by:

$$x_t=x_{t-1}\hspace{0.17em}+\hspace{0.17em}f\left(x_{t-1},u_t,\Delta t\right)$$ (5)

where f(·,·,·) gives the change in the plant from one time step to the next based on the current state of the system and inputs u_t from the control law. Integration of the plant dynamics was accomplished via the Euler method with a fixed Δt = 0.01 s.

The equations governing the f(·,·,·) plant dynamics were identical to those described in Lillicrap and Scott (2013) with the exception of those for the two-joint revolute arm. In the present work we have used a different set of equations for the intersegmental dynamics from those described in Lillicrap and Scott (2013). The derivation of the equations used here is based on that developed in Spong et al. (2006). The current set of equations assumes that the mass of each link is distributed evenly over the link, rather than located at a single point. This assumption prevents the inertia matrix from becoming singular in certain parts of the state space, leading to intractable explosions in acceleration.

As in Lillicrap and Scott (2013), the matrix of connections from the controller to lumped muscles, W_zu, was drawn element-wise from N(μ = 0, σ = 0.05) and was fixed at these values. This assumption is unphysiological in several regards but is straightforward and is common in the literature (Todorov 2000; Trainin et al. 2007). We collected the remaining synaptic connections and biases into a single free parameter vector, w. The most computationally expensive aspect of these simulations lies in the computation of the gradient $\frac{\partial \mathit{J}}{\partial w}$. In Lillicrap and Scott (2013) this was accomplished via by-hand differentiation of each piece of the network and plant forward dynamics and corresponding custom-built C/Mex code. Here, we approached this problem via a more flexible approach. We developed the forward dynamics in a Python based library called Theano (Bergstra et al. 2010), which allows fast automatic differentiation of symbolic expressions.

In Lillicrap and Scott (2013), the Matlab-based minFunc library (Schmidt 2005–2009) was used for optimization. Here we used a custom-built python optimization routine based on the minFunc implementation of the LBFGS algorithm. This routine estimates second order curvature information from successive evaluations of the gradient, $\frac{\partial \mathit{J}}{\partial w}$, and uses a customized learning rate schedule to find good optima. A notable difference between the present simulations and those in Lillicrap and Scott (2013) is that here a penalty encouraging straightness was not included in the cost function. Optimization only focused on attaining the end point, and so reaches tended to be more curved than in this previous work.

We optimized eight random instantiations (synaptic weights and biases drawn from normal distributions) of the control law for each of the two plant model variants described above (i.e., the simple linear muscles, and the muscle model with included force-length/velocity properties). The networks were trained in a minibatch mode where all N = 16 reaches were included, each iteration with a different random instantiation of the neural noise applied for each batch. In this fashion the learned control laws were robust to internal noise and could also generalize to reaches nearby to those learned. Learning was terminated when the loss plateaued and no appreciable gains were observed for 500 updates. The regularization constants penalizing neural and muscle activities and synaptic weight size were set as, α_z = 1 × 10⁻⁶, α_u = 1 × 10⁻², and α_w = 1 × 10⁻⁶, respectively.

Statistical inference.

Due to the directional nature of the tuning data we applied circular statistical measures using implementations of each statistical test from CircStat: A Circular Statistics Toolbox for Matlab (Berens 2009). All other statistical tests were carried out using functions available in the Matlab Statistics Toolbox (Mathworks, Natick, MA). Effects were considered significant at the α = 0.05 level of significance.

RESULTS

Rhesus macaques were trained to perform an instructed-delay, center-out reaching task while we recorded the activity of neural ensembles in M1, PMd, and PMv. Using standard cosine tuning methods, we characterized the relationship between the discharge of individual neurons and behavior during the instructed delay period (INS; a 400-ms interval beginning 200 ms after the appearance of the peripheral target), the reaction time period (RT; the 400 ms before the start of movement), and movement execution (MOVE; the 500 ms following the start of movement). Because the activities of neurons in these areas are often broadly tuned to many movement parameters, we view cosine directional tuning as a statistical assay of the task-related discharge of individual neurons rather than a characterization of their causal role in generating movements. Movements to each of the targets were generally straight and on average contained the invariant features typically associated with point-to-point reaching movements (Fig. 2, A–D, shown for a representative animal). Reaction and movement times for each animal are shown in Table 1. Similarly, the estimates of torque and velocity at the shoulder and elbow joints computed from the Cartesian hand position data were consistent with empirical measurements from others [cf. Figs. 1 and 4. (Kurtzer et al. 2006)]. In agreement with previous reports involving planar reaching movements (Scott et al. 2001), we found that hand speed was quite isotropic (Fig. 2E). In contrast, joint based parameters varied greatly with movement direction reflecting the complex mechanics of the upper limb (Fig. 2, F and G).

Fig. 2.

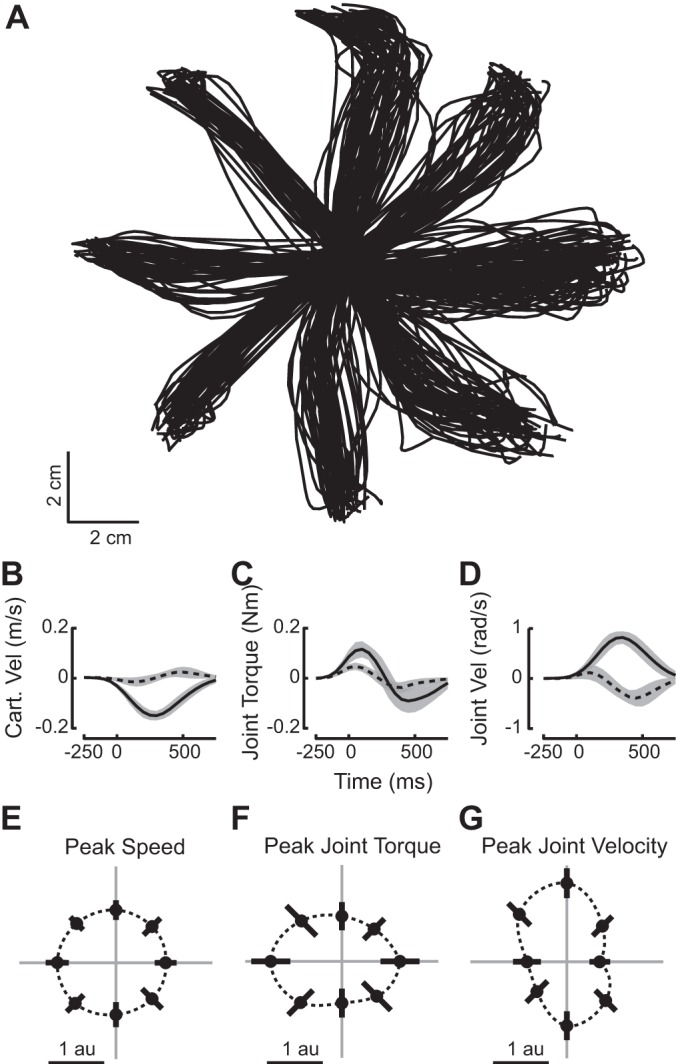
Kinematic features of reaching movement. A: hand trajectories from center to peripheral targets for all reaches during one recording session. B–D: averaged time courses for three features of reaching movements in the leftward direction (180°) during the same recording session. B: Cartesian velocity in the X (solid line) and Y (dotted line) dimensions. C: shoulder (solid) and elbow (dotted) torque. D: shoulder and elbow angular velocity. Traces are averaged over all reaches to the left (180°), and shading represents 1 SD on either side of the mean. Time 0 corresponds to the start of movement (SOM). E–G: polar plots of peak speed, peak joint torque, and peak joint velocity during reaches to 8 targets. The mean quantity and the corresponding SD derived from data normalized and pooled over all recording sessions are shown as dots and bars, respectively. Peak hand speed, joint angular velocity, and joint torque were compared across the 8 directions in the task. The total joint velocity refers to the sum of rectified shoulder and elbow angular velocities. Similarly, the total joint torque refers to the sum of rectified torques in the shoulder and elbow. For each dataset, the peak values of each feature were found for every reach and normalized by the mean across all trials in all directions. The normalized peak values for each direction were pooled across all datasets (for monkeys using the left hand, directional data were reflected about the y-axis to allow for pooling with right-handed data).

Table 1.

Reaction time, movement time, and directional tuning data for each individual

	Behavior		Directionally Tuned Neuron Samples
			M1		PMd		PMv
Monkey	RT, s	MT, s	Number	Proportion	Number	Proportion	Number	Proportion
B	0.249	0.474	—	—	152	98.1	—	—
C	0.433	0.410	16	88.9	—	—	165	98.2
N	0.260	0.525	—	—	—	—	58	93.6
RJ	0.458	0.815	442	97.2	211	95.9	—	—
RXl	0.355	0.462	—	—	—	—	45	84.9
RXr	0.342	0.509	—	—	—	—	159	56.4
V	0.520	1.062	377	97.9	—	—	343	95

RT, reaction time; MT, movement time; M1, primary motor cortex; PMd, dorsal motor cortex; PMv, ventral premotor cortex.

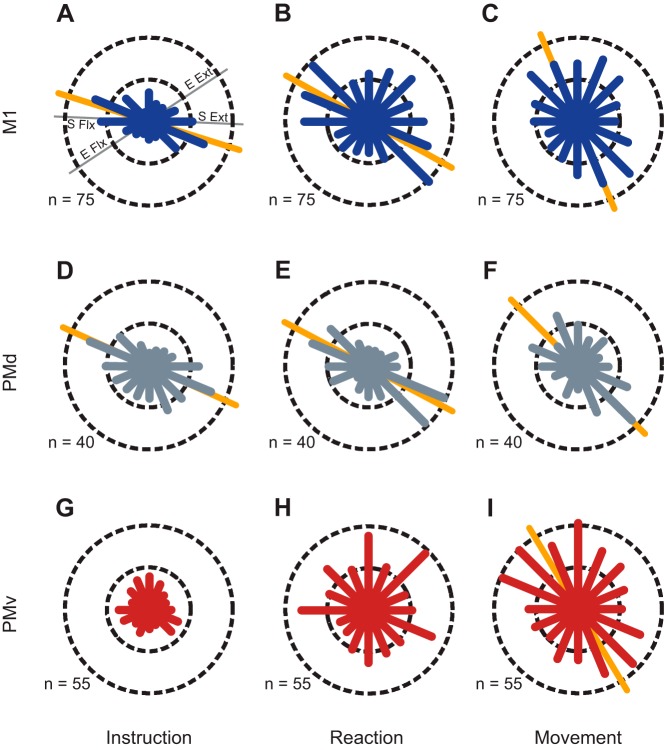
Fig. 4.

Pooled distributions of preferred directions during the instruction (A, D, G), reaction time (B, E, H), and movement (C, F, I) epochs where the preferred direction (PD) of individual neurons was computed with respect to the target direction. Circular frequency histograms for M1 (blue), PMd (gray), and PMv (red) show the numbers of cells with PDs that fall into each of 16 bins. Where applicable, the primary axes of bimodal distributions are shown as orange lines behind the histogram. The dashed circles show the scale of each histogram in number of cells per bin. The thin gray lines in A show representative axes for shoulder flexion/extension (S Flx/Ext) and elbow flexion/extension (E Flx/Ext).

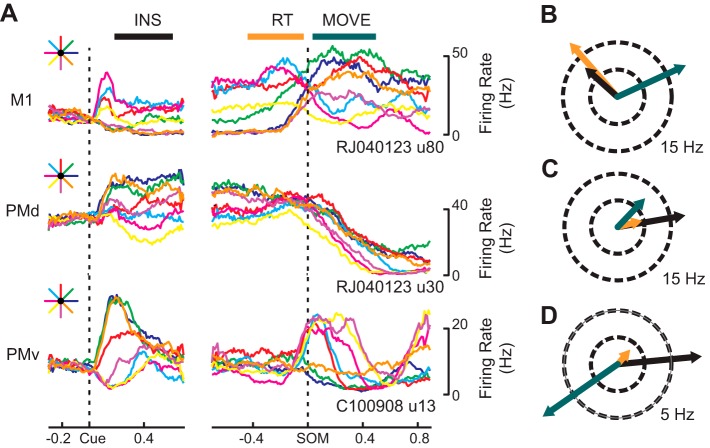
Consistent with the reports of others (Churchland and Shenoy 2007; Hatsopoulos et al. 2007; Johnson et al. 1999; Sergio and Kalaska 1998), we found that the tuning properties (i.e., preferred direction and modulation depth) of many neurons evolved over time, often changing markedly between the INS and MOVE periods (Fig. 3A). Take, for example, a neuron located in M1 (Fig. 3A, top) whose firing rate increased both at the presentation of a visual target (Cue) and just before the start of a movement (SOM) and was tuned to movement direction during the INS, RT, and MOVE periods. This neuron became more deeply modulated as the task progressed and exhibited a large difference in preferred direction between the INS (black arrow) and RT (orange arrow) periods and the MOVE (green arrow) period, rotating clockwise by ∼113° (Fig. 3B). In contrast, Fig. 3C shows an example of a neuron in PMd whose PD remained relatively consistent while modulation depth varied across trial epochs. Unlike the M1 neuron described above, this PMd neuron was more deeply modulated in the INS epoch compared with the RT and MOVE epochs. A final example shows a neuron whose tuning properties change abruptly as the movement time approaches. This PMv neuron was directionally tuned during each task period preferring rightward instructed targets during INS and leftward movements toward the body during MOVE and an intermediary direction during RT (Fig. 3D), but its modulation depth was greatly reduced (almost to zero) during RT. Thus it appears that this neuron performs very different functions in the INS and MOVE periods.

Fig. 3.

Examples of single cell activity and directional tuning. A: perievent average firing rates from example cells in M1, PMd, and PMv for reaches made in each direction. Left: firing surrounding the instruction cue. Right: firing surrounding the start of movement. B: Preferred direction for an M1 cell during the instruction (INS, black), reaction (RT, orange), and movement (MOVE, green) epochs plotted on a circle, where ray length is determined by the depth of cosine modulation in spikes per second. Preferred directions in each epoch for a cell from PMd and PMv are shown in C and D, respectively.

State-dependent changes in PD distributions.

Significant directional tuning in each area during at least one experimental epoch was apparent in 97.3% of neurons (835/858) in M1, 96.8% (363/375) in PMd, and 83.2% in PMv (770/926) and is shown for individual animals in Table 1. Tuning directions were quite stable within experimental epochs having an estimated, average standard deviation of 10.0, 9.6, and 11.4 for M1, PMd, and PMv, respectively. We pooled the PDs of neurons across animals and examined the statistics of the distributions using a Rayleigh test (Batschelet 1981). Distributions from monkeys that used their left arm to move the exoskeleton were mirrored across the y-axis before pooling, making all animals appear to be right handed. In M1, we observed bimodal distributions of PDs during the INS (P < 10⁻¹⁰), RT (P = 1.5 × 10⁻⁸), and MOVE (P = 6.1 × 10⁻⁶) periods (Fig. 4, A–C, respectively). In all three time windows, the distributions were oriented with their long axis aligned to movements requiring shoulder flexion (extension) and elbow extension (flexion). The distributions of PDs in PMd were also bimodal, having orientations similar to those observed in M1 (Fig. 4, D–F; P = 1.0 × 10⁻⁸, P < 10⁻¹⁰, and P = 5.8 × 10⁻⁷ for the INS, RT, and MOVE periods, respectively). In contrast to M1 and PMd, the distribution of tuning directions in PMv during INS was not different from uniform (Fig. 4G; P = 0.38 and P = 0.57 for the unimodal and bimodal variants of the Rayleigh test, respectively) and we observed a tendency toward a unimodal distribution during the RT period (Fig. 4H; P = 0.02). However, the distribution changed dramatically during MOVE, exhibiting a bimodal distribution (P = 9.2 × 10⁻⁵) with an orientation similar to M1 and PMd (Fig. 4I). We found no difference in the median orientation of the distributions when comparing the instruction and reaction time periods in M1 (P = 0.18), PMd (P = 0.87), or PMv (P = 0.63). Thus all subsequent analyses focused only on the INS and MOVE epochs.

To ensure that the statistical significance of our results concerning these distributions did not depend on cell stability in these shared arrays, we recreated the distributions using only one dataset from each array (3 in M1, 2 in PMd, and 5 in PMv). For each array, the dataset with the greatest number of cells tuned in INS and MOVE was chosen for pooling. We found that pooling with this alternate method did not affect our findings. In M1, distributions remained bimodal during INS and MOVE (P = 1.7 × 10⁻⁵ and P = 2.1 × 10⁻³, respectively). PMd exhibited similar bimodal distributions in both INS (P = 2.9 × 10⁻⁴) and MOVE (P = 0.021), although bimodality during MOVE was not as strong as that observed when all the data were pooled. In PMv, as before, we found a uniform distribution in INS (P = 0.36 and P = 0.38 for the unimodal and bimodal variants of the Rayleigh test, respectively) giving way to a bimodal distribution during movement (P = 9.5 × 10⁻³). The primary axis of all distributions in this analysis was also similar to those observed when all data were pooled. This eliminates the possibility that the shape of the tuning distributions was an artifact due to stability in the chronic neural recordings (Dickey et al. 2009).

When viewed at this coarse resolution, we observed a significant shift in the orientation of the tuning distributions of M1 and PMd coinciding with the change from movement preparation to execution (i.e., INS to MOVE). In M1, the orientation of the bimodal distribution rotated clockwise over the course of the trial from 160° during INS to 115° during MOVE (orange lines in Fig. 4, A and C). The orientation of the tuning distribution was similar in PMd having an orientation of 155° during INS and 133° during MOVE (orange lines in Fig. 4, D and F). In each case, a two-sample nonparametric circular test (circ_cmtest) found that the median orientation of the INS and MOVE distributions was significantly different (P = 2.8 × 10⁻¹⁰ and P = 0.005 for M1 and PMd, respectively). In PMv, the orientation of the preferred direction distribution in MOVE was 121°; however, the lack of discernable PD distribution orientation during INS precluded comparison of these distributions and some subsequent analyses.

We also considered the tuning properties of each neuron with respect to the initial movement direction (i.e., the vector between start position and the position at peak velocity) observed during the reach instead of the target direction. In examining the pooled PD distributions for each area during each time period, we found that the relationships described in Fig. 4 were largely preserved (data not shown) suggesting that the shape of the PD distributions and population temporal dynamics are not simply due to a change in the encoding properties of the neural population. The lone difference was the PD distributions measured from the population of PMv neurons based on initial movement direction; we found that these distributions during the INS and RT periods were bimodal although not highly significant (P = 0.03 and 0.02, respectively).

To understand the temporal evolution of the ensemble, we first examined variations in preferred direction among single neurons that were significantly tuned during both the INS and MOVE epochs. We limited our analysis to neurons whose PD rotated significantly (by bootstrap analysis) between the INS and MOVE epochs. The median difference in PD for this population of neurons was significantly different from zero in both M1 and PMd (circ_medtest; P = 0.029 and P = 0.007, respectively) having a median angle of −27.3° in M1 neurons and −48.9° in PMd neurons (Fig. 5, A and B, top). These changes in tuning directions are consistent with the clockwise rotation observed in the pooled distributions shown in Fig. 4. The median PD difference among neurons in PMv was not significantly different from zero (Fig. 5C, top; circ_medtest; P = 0.71). Similar population statistics were observed when tuned neurons with nonsignificant PD rotations were included in the analysis. Next, we investigated the relationship between tuning direction during the INS epoch and the magnitude and direction of PD rotation observed in the MOVE epoch. Examination of the resulting two-dimensional histograms reveals that M1 and PMd neurons having PDs located in the primary modes of the bimodal distributions during the INS epoch tended to have PDs in the MOVE epoch that are rotated by ∼45° clockwise (Fig. 5, A and B, bottom). Unlike M1 and PMd, PMv neurons whose PD changed significantly between INS and MOVE possessed PDs that were more uniformly distributed during INS (Fig. 5C, bottom). Thus we observe temporal dynamics in the PDs of neurons that lie within one of the primary modes during INS that preserves their membership in the rotated primary mode we observed during the MOVE epoch.

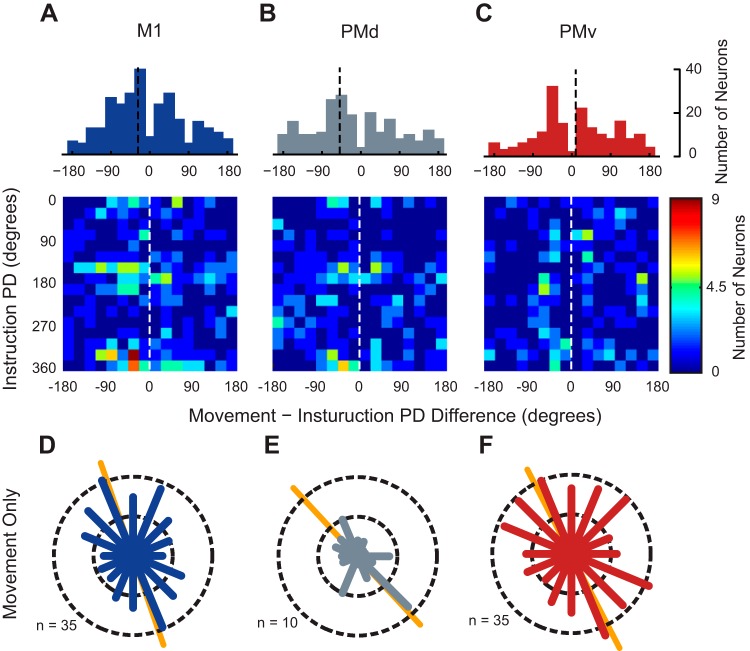
Fig. 5.

Changes in orientation of PD distributions are due to two populations of neurons. A–C, top: 1-dimensional histograms showing the difference between PDs calculated during INS and MOVE. Black dashed lines indicate the median PD of the population. A–C, bottom: 2-dimensional histograms showing the differences between the PDs calculated during the INS and MOVE epochs with respect to their PD in the INS period. Dashed white lines indicate a PD change of 0°. For a cell to be included in these analyses it had to be significantly tuned in both epochs. D–F: pooled distributions of preferred directions for neurons tuned only in the movement epoch. Conventions are the same as Fig. 4.

The PD changes of single neurons, however, do not fully capture the behavior of the neural ensemble as only 43.4, 71.2, and 25.2% of neurons (M1, PMd, and PMv, respectively) were tuned in both epochs, neglecting a large number of neurons tuned only during MOVE. We wondered if the neurons tuned only during MOVE possessed bimodal PD distributions with orientations rotated clockwise compared with the distribution of tuned cells in INS. Indeed, the PD distributions of neurons tuned only during MOVE were bimodal in each area (Fig. 5, D–F; Rayleigh test; P = 4.1 × 10⁻⁷, P = 0.039, and P = 1.2 × 10⁻³ for M1, PMd, and PMv, respectively) and had orientations of 108, 133, and 117°, which were rotated compared with INS (see Fig. 4, A, D, and G). Thus it appears that two distinct mechanisms contribute to the temporal dynamics we observe: first, tuning dynamics of neurons that remain tuned throughout the task, and second, recruitment of an additional population of neurons that exhibit directionally tuned activity only during MOVE.

To capture the precise timing of these tuning changes at the ensemble level, we computed the tuning properties of each cell in 200-ms sliding windows (100-ms increments) beginning at the instruction cue and ending approximately at target acquisition and pooled the PDs of significantly tuned neurons across monkeys within each cortical area. Figure 6A shows an example of these high temporal resolution PD distributions for M1. Notice how the primary orientation of the bimodal distribution (orange line) rotated clockwise from the middle of the instruction period (Ins + 400) to the SOM until it was almost vertical toward the end of the reach (SOM + 400).

Fig. 6.

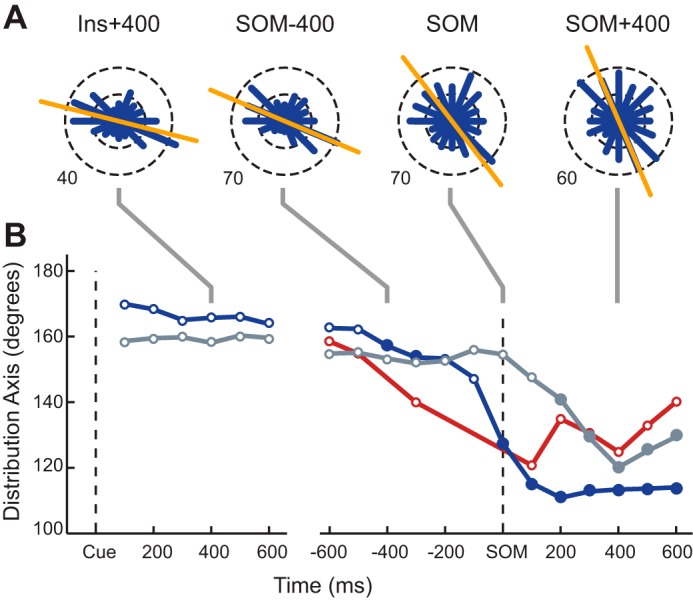
Temporal evolution of the primary axis of the distribution of preferred directions. Preferred directions for M1 (blue), PMd (gray), and PMv (red) were computed using firing rates binned in 200-ms sliding windows with an increment of 100 ms. A: circular frequency histograms of the preferred directions of M1 cells pooled across all datasets. Each panel shows the distribution at a different point in the trial. The orange line shows the primary axis of the distribution. B: summary of the temporal evolution of the PD distribution axis orientation in each area over the course of a trial. Time axes are referenced to the appearance of the instruction cue (Cue) and to SOM. Circular markers represent times where PD distributions were found to be significantly bimodal compared with a uniform alternative. Filled circles indicate times where the orientation of primary axis of the distribution was found to be significantly different than the average orientation measured during the instruction period in the same area.

Changes in the primary axis of the distribution across time are summarized for M1, PMd, and PMv in Fig. 6B. Data points were plotted only when a Rayleigh test rejected the null hypothesis of a uniform distribution of PDs in favor of a bimodal distribution (i.e., when the distributions had a significant directional bias). In M1 and PMd, a bimodal distribution emerged 100 ms after the presentation of the instruction cue and was maintained throughout the trial. In the perimovement period we saw signs of bimodality emerging in PMv as early as 600 ms before the start of movement with a stable bimodal distribution appearing as the arm began to move (Fig. 6B, SOM). The PD distributions of both M1 and PMd had remarkably stable orientations during INS (166.3 ± 3.2 and 158.8 ± 1.3°, respectively), and in all three cortical areas we saw a clear change in the distributions during the perimovement period. A circular equivalent of the one-sample t-test (circ_mtest) was used to determine if the orientation of the PD distribution for each time window changed compared with the mean orientation of the distributions during INS (Fig. 6B, significant change in orientation denoted by filled symbols). The earliest rotation in the PD distribution was observed in M1, at 400 ms before movement onset. The rotation progressed further at movement onset and reached a floor 200 ms after movement onset, at an orientation of 112°. This phenomenon was similar in PMd but differed in that the change in orientation began at movement onset with the first significant difference occurring 200 ms after the start of movement. The total rotation from INS to MOVE was ∼38.6°. In PMv, the primary axis of the distribution appeared to change early in the perimovement period much like M1 reaching a minimum 100 ms after movement onset and then reversing direction, similar to PMd.

Temporal variability and limb biomechanics.

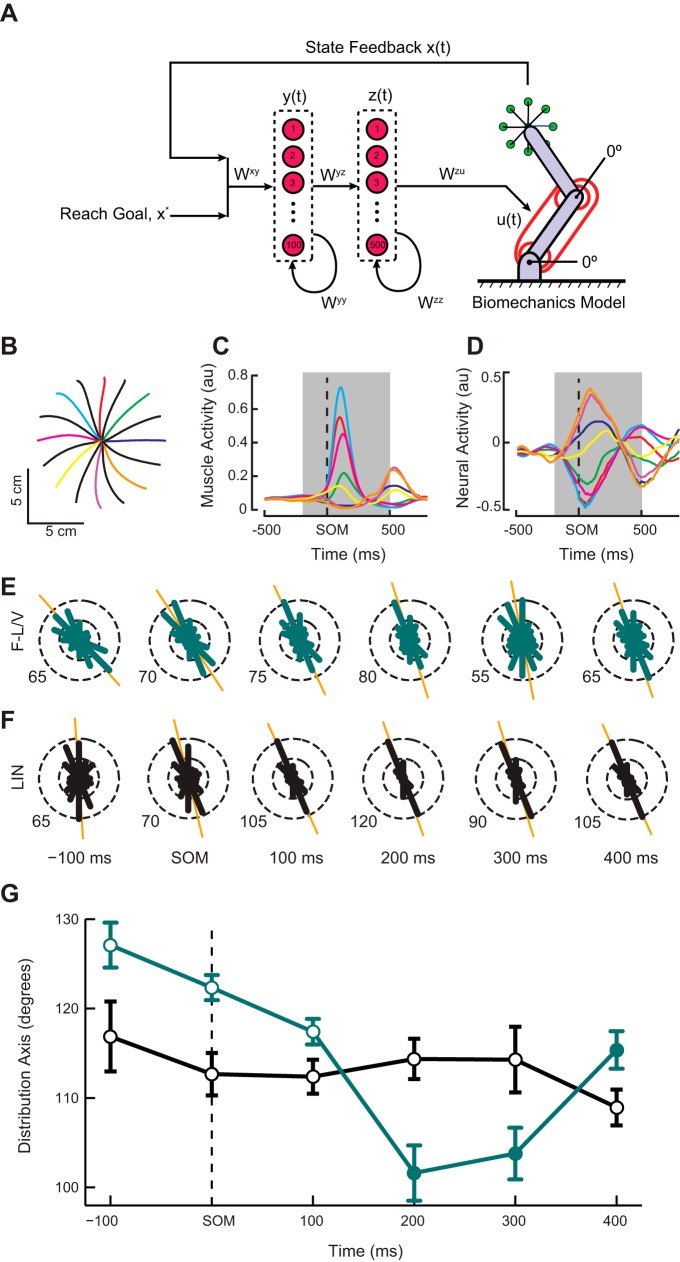
Previous work has shown that bimodal PD distributions observed in M1 can be explained by a simple model in which neurons are directly involved in commanding muscle activity (Lillicrap and Scott 2013). To examine whether the temporal evolution of these bimodal distributions could be explained as the outcome of an optimization process, we trained a two-layer, recurrent neural network control law to move a physical model of a two-joint revolute arm via six lumped muscle actuators (Fig. 7A). The input layer (100 neurons) receives feedback from the plant and context information specifying the goal of the reach. It projects to the output layer (500 neurons) whose weighted activity is used to drive the lumped muscle actuators. In previous work with a variant of the model, Lillicrap and Scott (2013) showed that the essential bimodal distributions observed in output layer neurons could be explained by the presence of a limb with specific geometry and intersegmental dynamics. In contrast, the current work examines a higher order feature of the neural population, namely the temporal dynamics of the bimodal distributions and the properties of the motor periphery that lead to their emergence. To this end, we utilized two distinct physical models that differed in their muscle properties. The first contained actuators that simulated the state-dependent mechanical properties (i.e., the force-length and force-velocity relationships) of muscle (F-L/V) while these nonlinear state-dependent properties were excluded in the second model (LIN). We trained eight networks with different random initializations under each variant of the plant equations.

Fig. 7.

Schematic representation, behavioral performance and neural activities of the network models with state-dependent (F-L/V) and linear (LIN) muscle-like actuators performing a center-out reaching task. A: schematic diagram of neural network and physical model (see materials and methods for definitions). B: representative hand trajectories made by a network whose muscles included the force-length and force velocity properties. C: reach-related activity from the lumped shoulder flexor muscle. D: activity from a single neuron-like unit in the network model demonstrating robust movement related tuning. In our network models neural activity is a signed quantity and should be interpreted as a change in activity from a baseline. The colored traces in B–D correspond to different movement directions. Black lines in B are not shown in C and D. Subsequent analyses are focused on neural activity during the shaded regions in C and D. E and F: circular frequency histograms of the preferred directions for representative single optimizations are plotted for the F-L/V (green) and LIN (black) network models. Preferred directions for the neuron-like units were computed using firing rates binned in 200-ms sliding windows with an increment of 100 ms. G: temporal evolution of the PD distribution orientation for the F-L/V and LIN networks over the course of a trial averaged across the 8 simulations of each model. Time axes are referenced to the SOM. Circular markers represent times where PD distributions were found to be significantly bimodal compared with a uniform alternative (P < 0.05, Rayleigh test). Filled markers indicate points in time where the orientation of primary axis of the distribution was found to be significantly different than its orientation 100 ms before the start of movement (P < 0.05, post hoc t-test).

Following optimization, the network performed an instructed-delay, center-out reaching task similar to our monkeys, and we recorded the activity of the network units. Examination of the simulated movements revealed that the network produced smooth, mostly straight movements (Fig. 7B) with associated patterns of muscle activity (Fig. 7C) and neural activity (Fig. 7D). Much like the data from our monkeys, the output layer PD distributions from the F-L/V and LIN network models were strongly anisotropic having bimodal distributions with orientations lying along an axis requiring shoulder flexion (extension) and elbow extension (flexion) movements (Fig. 7, E and F; P < 0.005, Rayleigh test). To summarize these findings we computed the average orientation of the PD distribution for each set of network models and used separate one-way ANOVAs to test if the orientation changed as a function of time. Importantly, we found a dramatic difference in the temporal evolution of the PD distributions between the two sets of simulations. In the F-L/V case (Fig. 7G, green), the ensemble behaved similarly to our empirical data with the preferred orientation of the PD distribution rotating clockwise beginning around the time of movement onset (F_5,42 = 18.76; P = 9.2 × 10⁻¹⁰). In contrast, no rotation of the PD distribution was observed in the network optimized to control the model in the LIN simulation (Fig. 7G, black; F_5,42 = 0.88; P = 0.5). The ensemble of input layer neurons also showed similar bimodal distributions for both physical model variants, although no temporal dynamics were observed (data not shown).

DISCUSSION

We have demonstrated that, similar to M1, ensemble activity in PMd and PMv exhibits pronounced bimodal PD distributions, suggesting that these areas are subject to the biomechanical properties of the limb. This motivates a different view of these premotor areas. Rather than a strict hierarchy in which premotor cortex specifies high-level information to the M1 in an extrinsic space, it implies that PMd and PMv may both compute precursors to muscle activity, which are then refined by computations performed downstream in M1 and spinal cord. Although these results are unexpected for premotor cortex given previous physiological data (Kakei et al. 2001; Schwartz et al. 2004; Shen and Alexander 1997), anatomical studies have shown that the premotor cortexes in addition to the primary motor cortex do contribute substantially to the cortico-spinal tract (Dum and Strick 1991; He et al. 1993). Furthermore, we found that the responses of the populations in each area varied in time. This variation at the ensemble level was manifest as a clockwise rotation in the orientation of the preferred direction distribution from the preparatory to the movement period (see Fig. 4, orange lines). Examination of the PD distributions at a higher temporal resolution revealed their orientation remained constant throughout the instruction and reaction time periods and experienced a rapid transition around the time the movement started likely corresponding to a transition into the neural state necessary for execution (Kaufman et al. 2014). Based on our network model the adjustment in the neural state (i.e., rotation of PD distributions) of M1, PMd, and PMv in the perimovement period likely emerges as a result of the state-dependent, biomechanical properties of the limb that coincide with the onset of movement.

Specifically, our network model suggests that neural populations in motor cortexes likely compute a quantity related to a muscle activation signal rather than the explicit kinematics or kinetics of movements themselves. This is revealed by the fact that the anisotropy and temporal dynamics observed in our empirical data are captured by the network model containing a plant including the state-dependent mechanical properties of muscles (F-L/V) but not the model (LIN) mapping neural activity linearly onto the torque output of the muscle. Recently, Oby et al. (2013) showed that single neurons in M1 were better able to predict the electromyogram across a range of postures compared with end-point force. Similarly, some have demonstrated the ability to decode patterns of muscle activity from populations of neurons in the primary motor cortex (Carmena et al. 2003; Pohlmeyer et al. 2007). These results along with our data and simulations reinforce the idea that cortical areas involved in the control of movement should be concerned with the details of the motor periphery.

In a previous modeling study, Lillicrap and Scott (2013) examined how the specific orientation of PDs was related to limb mechanics. They considered a series of alterations of the limb biomechanics and showed that the PD distribution modes adjusted predictably as a function of the modifications of the limb physics. Specifically, work suggested that PD distributions tend to be oriented toward those directions of movement (or applied torque) that required the largest muscle activation recruitment. A similar explanation may apply to the clockwise rotations of the PD distributions observed in the data described in this report. That is, if the reaches that require the largest muscle recruitment change as a function of time, this could lead to a rotation of the PD distribution over time. This idea agrees, at least in broad strokes, with previous empirical work that examined shoulder and elbow joint power (which is thought to be a good proxy for muscle force) as a function of time through the course of center-out reaching (Graham et al. 2003). Figure 8 of Graham et al. (2003) shows that, as reaching progresses through time, the joint power of the shoulder is larger at the beginning of the reach and maintains roughly the same orientation throughout (∼135°). The joint power of the elbow develops later in the reach and has an orientation that sits closer to 90°. Thus the clockwise rotation may be explained by this straightforward fact of the biomechanics. That is, as the reach progresses, proportionately more muscle activity is required in the fore/aft directions of movement than at the beginning of the movement.

In PMv, we found a uniform distribution of PDs during the preparatory period consistent with its role in representing peripersonal space in an extrinsic reference frame (Hoshi and Tanji 2006, 2007). In MOVE, however, we saw a marked change in the distribution to one that is strongly bimodal indicating an intrinsic representation (see Fig. 4i). The change in distributions from extrinsic-like to intrinsic-like during preparation and execution, respectively, is supported by the finding that neurons in PMv encode information in multiple coordinate frames (Wu and Hatsopoulos 2007) and likely perform a coordinate transformation from a visual to motor space (Kurata and Hoshi 2002; Xiao et al. 2006). Our finding of an intrinsic-like reference frame in PMv during movement execution contrasts with multiple reports (Kakei et al. 2001; Xiao et al. 2006). For example, Kakei, et al. (2001) showed that single neurons in PMv have a strong bias toward an extrinsic, movement-related representation during motor execution using a paradigm that dissociated wrist muscle activity and movement directionn. However, they did not compare the population level distribution of PDs in the preparatory and movement periods and the shape of the distributions is unclear given the data presented (cf. Fig. 5A in Kakei et al. 2001). The discrepancy between the results of these studies and ours is likely related to our experimental design involving planar flexion and extension movements of the shoulder and elbow, which is known to increase the mechanical anisotropies of the limb and by proxy the neural activity.

Similar to the responses observed in PMv during movement execution, the population-level distributions of PDs in M1 and PMd reflect the anisotropic biomechanics of our reaching task. Our data demonstrated that the distribution of PDs in each area was nonuniform during both movement preparation and execution consistent with a low-level, intrinsic reference frame. This interpretation is supported by the observation that the movement preparation and execution distributions mirror the joint based kinematic/kinetic measures more closely than the Cartesian velocity (see Fig. 2, E–G). Further evidence is found in the observation that both neurons and arm muscles exhibit similar bimodal distributions of preferred movement directions (Kurtzer et al. 2006) and that the discharge of single neurons in both areas during motor execution is known to vary significantly depending on the configuration of the limb (Ajemian et al. 2008; Caminiti et al. 1990, 1991; Scott and Kalaska 1997; Scott et al. 1997).

While historically there has been a tendency to ask what the motor cortexes encode, our present work and that of others (Kaufman et al. 2014; Pruszynski et al. 2011) show that there is an intimate relationship between limb biomechanics and the dynamics of motor cortical activity and, therefore, suggest that motor cortex may not explicitly encode any single quantity (Wu and Hatsopoulos 2006). Given that upper limb biomechanics vary between behavioral states (Darainy et al. 2007; Gomi and Osu 1998), are influenced by the environment (Burdet et al. 2001), and are considered when deciding between candidate movements (Cos et al. 2011), the present study suggests that motor cortical activity emerges from the interactions between the intrinsic, neural dynamics of motor cortex (Churchland et al. 2012) and the biomechanical dynamics of the periphery necessary to perform a particular motor behavior (Hatsopoulos 1996).

GRANTS

This work was supported by National Institute of Neurological Disorders and Stroke Grants R01-NS-045853 and R01-NS-048845.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: A.J.S. conception and design of research; A.J.S., P.M., and T.P.L. analyzed data; A.J.S., P.M., T.P.L., and N.G.H. interpreted results of experiments; A.J.S., P.M., and T.P.L. prepared figures; A.J.S., P.M., T.P.L., and N.G.H. drafted manuscript; A.J.S., T.P.L., and N.G.H. edited and revised manuscript; A.J.S., P.M., T.P.L., and N.G.H. approved final version of manuscript.