Abstract
Dynamic mechanical analysis (DMA) is a common way to measure the mechanical properties of materials as functions of frequency. Traditionally, a viscoelastic mechanical model is applied and current DMA techniques fit an analytical approximation to measured dynamic motion data by neglecting inertial forces and adding empirical correction factors to account for transverse boundary displacements. Here, a finite element (FE) approach to processing DMA data was developed to estimate poroelastic material properties. Frequency-dependent inertial forces, which are significant in soft media and often neglected in DMA, were included in the FE model. The technique applies a constitutive relation to the DMA measurements and exploits a non-linear inversion to estimate the material properties in the model that best fit the model response to the DMA data. A viscoelastic version of this approach was developed to validate the approach by comparing complex modulus estimates to the direct DMA results. Both analytical and FE poroelastic models were also developed to explore their behavior in the DMA testing environment. All of the models were applied to tofu as a representative soft poroelastic material that is a common phantom in elastography imaging studies. Five samples of three different stiffnesses were tested from 1 – 14 Hz with rough platens placed on the top and bottom surfaces of the material specimen under test to restrict transverse displacements and promote fluid-solid interaction. The viscoelastic models were identical in the static case, and nearly the same at frequency with inertial forces accounting for some of the discrepancy. The poroelastic analytical method was not sufficient when the relevant physical boundary constraints were applied, whereas the poroelastic FE approach produced high quality estimates of shear modulus and hydraulic conductivity. These results illustrated appropriate shear modulus contrast between tofu samples and yielded a consistent contrast in hydraulic conductivity as well.
Index Terms: Poroelasticity, Dynamic Mechanical Analysis, Soft Tissue, Finite Element Method
I. Introduction
Dynamic mechanical analysis (DMA) is a powerful technique that characterizes materials, primarily polymers, as a function of time, temperature, or frequency. A sample of material is placed in one of a series of clamps (e.g. 3 - point bending, compression, shear) and a periodic stress is applied, eliciting a periodic strain response. Mechanical energy loss in materials with non-negligible damping results in a strain response which is out of phase with the applied stress. The amplitude and phase lag of the strain response is sufficient to calculate complex moduli, such as bulk, elastic, or shear, and damping properties of materials. The stress wave can also be applied over a range of frequencies or temperatures, even in a single experiment, to alter the mechanical response of the material of interest.
While DMA is important for characterizing material properties, it is commonly limited to viscoelastic material assumptions where the physical interactions are represented by a network of springs and dashpots [1], although a number of different viscoelastic models exist (e.g. Maxwell, Kelvin-Voigt). These assumptions are sufficient for many materials, including polymers, but they do not account for mechanical behaviors associated with hyperelasticity, poroelasticity, or anisotropy. In the latter materials, viscoelastic assumptions create model-DMA-data mismatch, which can cause significant differences, for example, in stiffness estimates of porous media between the DMA-based viscoelastic material model and a magnetic resonance poroelastography estimate [2].
Biological tissues like brain parenchyma are mechanically complex, in part because they are composed of solid and fluid phases, where the latter can account for up to 75% of the volume [3]. Studies have demonstrated that brain tissue responds most like a poroelastic material when probed [4]; yet, viscoelasticity is still more common in brain modeling [5]–[7]. Poroelastic theory, developed initially by Biot for soil consolidation [8], assumes materials like brain to be biphasic, where a porous elastic matrix is penetrated by a viscous fluid. Here, the physical mechanisms of mechanical energy loss result from interactions between the solid and liquid phases when a force is applied.
Poroelastic models have been widely applied in the quasistatic case, where a slow increase in applied pressure develops fluid flow through the elastic matrix obeying the principles of Darcy’s Law [9]–[11]. Cheng et al. [12] developed the dynamic equivalent and modeled the transient response under specific conditions. Studies have applied dynamic poroelastic models in the assessment of seismic waves and soil settlement [13]–[15]. For biological applications, poroelasticity has been used to study the deformation effects on articular cartilage [16], [17] and bone [18]. In many of these cases, an analytic evaluation was considered to simplify the algorithms involved [12], [19], [20], but the solutions were constrained to one dimension. Studies typically investigate the deformation effects of the porous material where property parameters are assigned values based on results reported in the literature or from empirical tests [21]. Errors in the property assumptions can cause large changes in the deformation estimate, so accurate material property representation is important. Also, if measured correctly, these properties would provide more information on the material and its response to applied stress.
Ex vivo studies of biological tissue like brain could help differentiate normal and diseased states. Tumors, hydrocephalus, and Alzheimer’s disease are all known to change the mechanical characteristics of brain tissue [3], [22], [23], and a poroelastic model would represent both solid matrix and fluid related changes due to disease. Similarly, understanding the porous properties of brain could create a more accurate model for estimating tissue displacement during surgery [24], [25]. Food science is another application, where studying the consistency of matrix and fluid properties of consumables like tofu would be advantageous for quality control [26]. Lastly, frequency dependent poroelastic properties of soils estimated using this technique could assist in modeling the propagation of seismic waves during an earthquake [13].
Here, a 3-D finite element (FE) inversion approach was applied to estimate the frequency-dependent poroelastic material properties of porous media using a DMA platform (DMA Q800, TA Instruments, New Castle, DE). Analytical solutions were derived to test the limits of viscoelastic (visco-analytic) and poroelastic (poro-analytic) models in 1-D. A viscoelastic FE (visco-FE) method was also considered to compare the accuracy of a numerical approach relative to the analytical estimates. Sensitivity analyses were performed with different poroelastic boundary conditions (BCs) to determine the feasibility of estimating poroelastic material properties accurately. Using the DMA-acquired displacement and force data, the poroelastic FE (poro-FE) scheme generated high quality estimates of shear modulus and hydraulic conductivity of porous samples of tofu of different compositions over frequency.
II. Methods
A. Governing equations
1) Viscoelasticity
Deformation of an isotropic, viscoelastic medium is described by the partial differential equation (PDE) [27], [28]
| (1) |
where μ is the shear modulus, λ is the first Lamé’s constant, u is the 3-D displacement vector, ξ is the viscosity of the compressional wave, η is the shear viscosity, and ρ is the material density. For time harmonic motions, u(x, t)=ū(x)eiwt (where ω is the actuation frequency), the equation simplifies to
| (2) |
where Lamé’s constants become complex-valued, μ* = μ + iωη and λ* = λ + iωξ and the overbar (−) represents the complex-valued amplitude of the variable. At the frequencies used in this paper, the attenuation of the compressional wave can be neglected by setting ξ = 0.
2) Poroelasticity
The governing equations to model time-harmonic poroelastic deformation are based on the work on quasistatic deformation by Biot [8]. Dynamic poroelasticity equations were later developed by Cheng et al. [12]. More recent papers present analytical variations explored by Schanz et al. [20] and a 3-D finite element equivalent outlined by Perríñez et al. [29] in which the generalized Cheng equations were simplified through assumptions of isotropic behavior, a fully saturated material, and incompressible constituents. The resulting coupled set of equations include a stress equation similar to Eqn. 2 with an additional fluid interaction term and corresponding pressure equation
| (3a) |
| (3b) |
and
| (4) |
where μp and λp represent the poroelastic shear modulus and first Lamé’s constant, P̄ is the fluid pressure and β includes a compilation of the poroelastic material properties, including hydraulic conductivity, κ (the ease with which fluid penetrates the pores), porosity, ϕ (volume fraction of pore space), fluid density, ρf, and apparent mass density, ρa. For more detailed descriptions of dynamic poroelasticity and these parameters, see Cheng et al. [12] and Perríñez et al. [29].
B. Visco-analytic solution
The DMA technique for the Q800 applies a user-specified periodic displacement or force amplitude to the material, and measures the amplitude and phase lag of the other (induced) parameter. The material properties are typically estimated through an analytical approximation based on the sample geometry and the actuation parameters [30]. Specifically, for parallel plate compression, the relation is given as
| (5) |
where E is the complex elastic modulus, F is the force, L is the sample thickness, A is the sample cross-sectional area, and x is the displacement. An empirical correction factor, C, is incorporated based on sample geometry and the material’s Poisson’s ratio. The correction factor is used because transverse displacements are assumed to be small in the model equation, but are not necessarily negligible in practice.
C. Poro-analytic solution
An analytic solution has been reported in poroelasticity [20], [31], but is limited to a 1-D column with certain boundary condition (BC) constraints. Poroelastic analytical solutions in higher dimensions have been described [32], but their forms are lengthy and implementation is cumbersome. Here, a 1-D analytic solution was created and applied to (1) explore the feasibility of using a 1-D approach to estimate poroelastic properties using DMA data and (2) verify the poro-FE method. While previous work applied a stress BC on the top surface of the column, to represent the DMA appropriately, the corresponding equations need to be developed with a displacement BC applied on the top surface. With q representing fluid flow calculated from Darcy’s Law and following similar analysis from Schanz et al. [20] and Perríñez et al. [31], Eqn. 3 can be reduced to a 1-D ordinary differential equation with four known BCs (Uz(z = 0) = 0, Uz(z = L) = −Uo, Pz(z = L) = 0, qz(z = 0) = 0) which leads to closed form solutions for displacement (U) and pressure (P) expressed as a function of depth, z, along a column with length L given as
| (6a) |
| (6b) |
where λ3 is a complex root of the eigenvalue problem expressed as
| (7) |
and ES is written as
| (8) |
The force on the top face, Fporo, was computed by summing the elastic matrix forces, Fσ, and fluid pressures, FP, expressed as
| (9) |
Zero pressure BCs are applied to the top surface and the elastic force is given by , where A is the area of the top face, resulting in an analytic expression for Fporo,
| (10) |
D. Non-linear inversion
In-house 3-D viscoelastic (visco-FE) and poroelastic (poro-FE) finite element solvers were developed using linear tetrahedral finite elements implemented in Fortran and solved on the Discovery Cluster available on the Dartmouth College campus. Material properties for each model were estimated from the DMA-acquired data through iterative minimization of the objective function
| (11) |
where Fc is the force amplitude on the top face computed by the FE code with the current estimate of the material property values, θ, and Fm is the force amplitude measured by the DMA.
Eqn. 11 requires the force on the top surface to be computed from the FE models for comparison with the DMA force measurement, which is the amplitude of the oscillating vertical force on the top face as indicated in Fig. 1. For visco-FE, the appropriate force is computed by summing the terms on the right hand side of the FE matrix-vector system for all elements which have a face on the top surface [33]. The force from the elastic matrix for poro-FE can be computed in the same way; however, the additional stress from the fluid pressure must also be included,
Fig. 1.
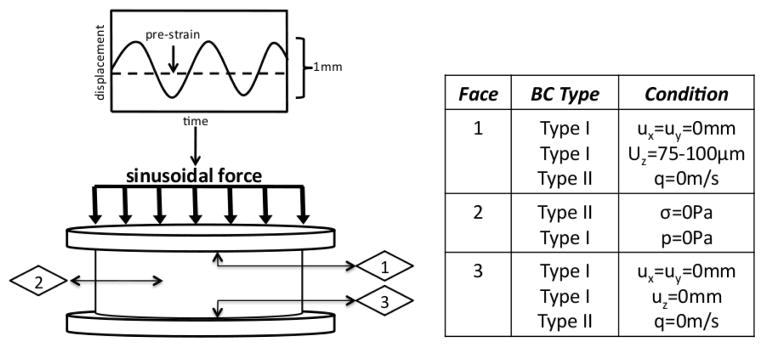
An example of a tofu sample placed between the two DMA platens (left) with a depicted sinusoidal force (top left) applied to the top surface. Corresponding boundary conditions are listed (right) for the three faces of interest (1 = top; 2 = cylindrical sides; 3 = bottom).
| (12) |
The amplitude and phase of the strain response are measured by the DMA; therefore, two unique parameters can be estimated in the FE model. The visco-analytic and visco-FE techniques estimate a complex-valued shear modulus, whereas a real shear modulus and hydraulic conductivity were found in the poro-FE method. Shear modulus is the common property determined through DMA techniques but κ has been shown to have a significant effect on the dynamic response of porous media and is a critical factor as well [2].
In this approach, each iteration finds an update to the material properties that reduces the squared difference expressed in Eqn. 11. A series of Steepest Gradient Descent and Gauss-Newton steps achieved the best match between Fc and Fm.
III. Experiments
A. Experiment 1: Comparison of visco-analytic and visco-FE methods
The visco-analytic solution in Eqn. 5 produces a complex modulus based on the force-displacement interaction of the material sample at frequency. To validate the visco-FE method, the estimated complex moduli should be close to their analytic values. A sample was examined over a frequency range (further explanation in Experiment 3) and the two results were compared.
B. Experiment 2: Comparison of poro-analytic and poro-FE methods
The poro-analytic solution given in Eqn. 10 would provide a simple way to estimate the shear modulus of a porous material sample, but the 1-D problem assumptions could prove to be inappropriate in the DMA testing environment. Force estimates were calculated from Eqn. 10 over a frequency range of 10−3–102 Hz and compared with the forces estimated by the poro-FE solution with (1) the 1-D BCs used to derive Eqn. 6 and (2) the BC constraints shown in Fig. 1 that emulate the DMA testing environment more closely. A cylindrical FE mesh was created to represent a standard DMA sample size (d = 25 mm, h = 10 mm).
C. Experiment 3: Dynamic testing of porous materials
Tofu is considered to be a poroelastic material and was used for this experiment [9], [11], [29]. Silken (Mori-nu) tofu is available in three different consistencies, denoted ‘soft’, ‘firm’, and ‘extra firm’, and these products were used to demonstrate the validity of the poro-DMA technique. Five samples were extracted from the larger tofu block and cut into small cylinders that were 28.5 mm in diameter and 7.5 –10 mm in thickness. Displacement BCs on the top surface were selected to limit the strain to about 1%, resulting in displacements between 75 – 100 μm depending on the sample thickness. A 0.1 N preload was applied to keep the platens attached to the tofu surface throughout the duration of the DMA data acquisition. To emulate the BCs in Fig. 1 as closely as possible, a rough surface was applied to the top and bottom platens on the DMA sample holder to eliminate transverse slippage which counteracts the fluid-solid interactions, and therefore, the poroelastic effects within the sample [34]. The samples were tested over a frequency range of 1 – 14 Hz, and the resultant normal force on the top platen was acquired. The Poisson’s ratio was assumed to be 0.45.
IV. Results
A. Experiment 1: Comparison of visco-analytic and visco-FE methods
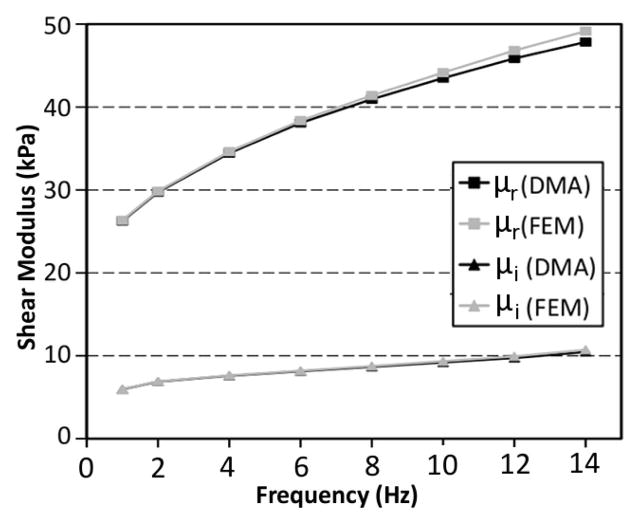
Excellent agreement was found between the dynamic shear modulus estimates from the visco-analytic (the traditional DMA approach) and visco-FE methods (Fig. 2). Relative errors in the storage modulus were 1.12% on average with a maximum error of 2.59% at 14 Hz. The smallest differences occurred at the lower frequencies.
Fig. 2.
Storage modulus (μr) and loss modulus (μi) estimates obtained from the visco-analytic (DMA) algorithm compared to the visco-FE method over a frequency range of 1 – 14 Hz.
The increasing error observed with frequency prompted an investigation to see if the frequency-dependent inertial forces (ρω2, which are neglected in the visco-analytic model) were a contributing factor. These forces were removed from the visco-FE model and the storage modulus results were recalculated for multiple tofu samples. The difference between the visco-analytic and visco-FE results decreased with removal of inertial terms in all cases. Fig. 3 illustrates an example where the average relative difference between the two models was decreased from 1.17% to 0.72%. The remaining difference is attributed to FE discretization error which decreases with mesh refinement. The mesh size used in the experiments was chosen to produce acceptable discretization error with reasonable processing time.
Fig. 3.
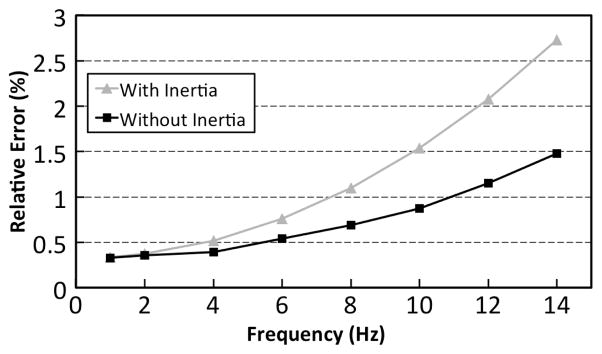
Illustration of the change in error between the visco-analytic and visco-FE results when the inertial terms (ρω2) are removed from the visco-FE model. The results show an average decrease in relative error of 38.5%.
B. Experiment 2: Comparison of poro-analytic and poro-FE methods
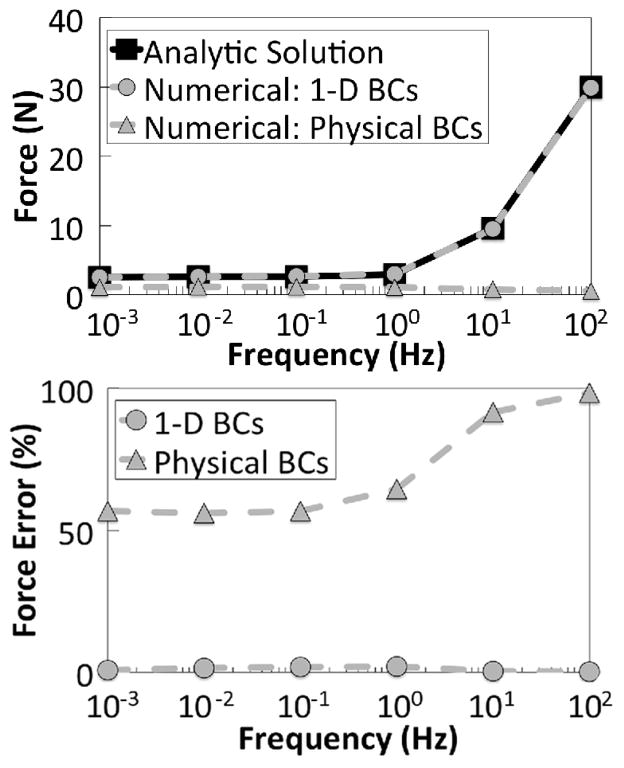
The poro-analytic and poro-FE methods produced very similar force estimates in the 1-D case up to 100 Hz, indicating that the poro-FE force calculation is correct. When the physical BCs (that allow lateral distension of the sample) were applied to the poro-FE method, the difference in the two solutions was substantial, as shown in Fig. 4. In the frequency range of interest, 60% error in the estimated force was found at 1 Hz with nearly 90% error occuring at 10 Hz. These results suggest that a 1-D analytic solution (i.e. confined compression) is not sufficient for mechanical analysis of poroelastic materials even at very low frequencies.
Fig. 4.
Force estimation as a function of frequency (top) for the analytic solution, the poro-FE method with 1-D BCs, and the poro-FE method with BCs representing the physical DMA conditions. Relative error (bottom) between the analytic solution and the poro-FE method with 1-D BCs and physical BCs. The FE mesh resembled the geometry of a typical sample found in DMA experiments.
C. Experiment 3: Dynamic testing of porous materials
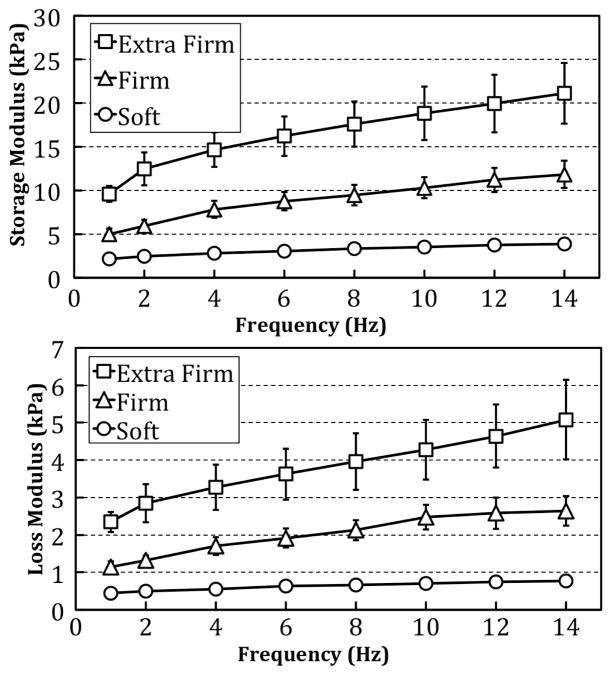
For the tofu samples, the visco-FE results in Fig. 5 demonstrate the expected contrast in storage modulus for the three compositions (soft, firm, extra firm). The loss modulus properties have similar contrast with the stiffer materials having larger imaginary shear modulus values. Damping ratios ( ) were found to be similar between the three types of tofu and had values ranging from 0.10 to 0.12. Values at 14 Hz are listed in Table I.
Fig. 5.
Viscoelastic parameter estimates obtained from the DMA data of shear storage modulus (top) and loss modulus (bottom) for five ‘extra firm’, ‘firm’, and ‘soft’ tofu samples measured from 1 – 14 Hz.
TABLE I.
Results for the visco-FE and poro-FE methods at 14 Hz. The columns represent the three tofu types, denoted ‘Soft’, ‘Firm’, and ‘Extra Firm’. μr corresponds to the real component of the complex shear modulus, DR is the damping ratio (given as ), μp is the poroelastic shear modulus, and κ is hydraulic conductivity.
| Soft | Firm | Extra Firm | ||
|---|---|---|---|---|
| Visco-FE | ||||
| μr (kPa) | 3.88 ± 0.636 | 11.8 ± 1.56 | 21.1 ± 3.49 | |
| DR | 0.100 ± 0.124 | 0.112 ± 0.126 | 0.120 ± 0.152 | |
|
| ||||
| Poro-FE | ||||
| μp (kPa) | 2.96 ± 0.402 | 8.10 ± 1.16 | 14.7 ± 2.42 | |
|
|
2.97 ± 0.617 | 0.229 ± 0.0686 | 0.0909 ± 0.0269 | |
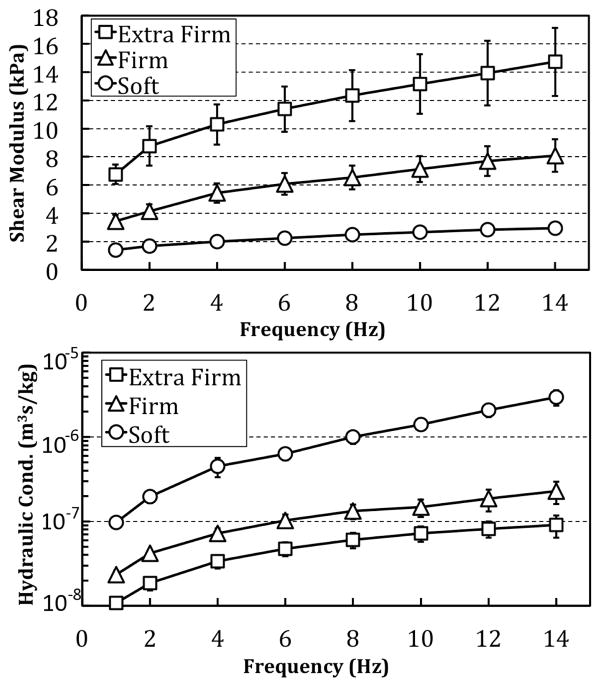
The poro-FE method was applied to the same data, and the results appear in Fig. 6. Shear modulus values illustrate contrast with the extra firm tofu being stiffest (14.7 kPa at 14 Hz), firm tofu being significantly softer (8.10 kPa at 14 Hz) and soft tofu being the least stiff (2.96 kPa at 14 Hz). These values represent similar contrast between tofu types as the visco-FE results, but are found to be much softer in absolute terms by comparison. Furthermore, the κ values exhibit the opposite contrast. κ is largest (fluid flows freely) in the soft tofu, whereas it is smallest (fluid flow is difficult) in the extra firm tofu. The κ contrast between the three types of tofu was consistent over the frequency range and the shear modulus and κ values were repeatable across samples of the same tofu composition. The values at 14 Hz are listed in Table I.
Fig. 6.
Poroelastic parameter estimates obtained from the DMA data of shear modulus (top) and hydraulic conductivity (bottom) for five ‘extra firm’, ‘firm’, and ‘soft’ tofu samples measured from 1 – 14 Hz.
V. Discussion
Dynamic tests on the three grades of tofu stiffness were performed using dynamic mechanical analysis. The visco-FE method applied to DMA data on material samples agreed very closely with the traditional visco-analytic approach which verified that an FE model would produce accurate material property estimates. The visco-FE results in Fig. 2 demonstrate that the mechanical property estimates are accurate and suggest that similar FE techniques could be applied to other material models to measure specimen properties accurately. For the quasistatic response (0 Hz, not shown), the storage and loss modulus results were identical (here, the frequency was set as 10−5 Hz) to the analytic model shown in Eqn. 5. As the frequency was increased from 1 – 14 Hz, the material property estimates in Fig. 2 remain very similar. The relative error between the visco-analytic and visco-FE methods increased nominally as the frequency increased (1.12% to 2.59%).
The increasing error with frequency between the two methods is partially due to FE discretization error. However, the visco-analytic approach does not consider inertial forces (ρω2), whereas the visco-FE method incorporates these effects. Also, these forces are larger at higher frequency and are proportionally large, especially in soft materials. Fig. 3 illustrates a decrease in the error between the two models, once the inertial forces were removed in the visco-FE method, revealing that these forces are important in dynamic testing. Thus, the FE models presented here may better characterize the true response of a material under dynamic loading than the current standard DMA approach that discards the inertial effect.
The dynamic test results are revealing. The visco-FE data (in Fig. 5) show that the tofu samples yield an expected contrast between the three stiffness grades. The damping ratios (DR) of the different tofu types, however, do not exhibit much contrast (all values fell between DR = 0.10 and DR = 0.12). The poro-FE results (in Fig. 6) demonstrate similar trends to the visco-FE findings. The shear modulus values present the correct trends and the contrast ratios between the three types of tofu are similar to the viscoelastic case. An increase in shear modulus from 1 – 14 Hz is observed, which is also similar to viscoelastic theory where material stiffness increases with frequency. However, the increase may be a result of limitations of the poroelastic model, which does not directly include any viscous damping effects associated with the solid matrix or other frequency-dependent variables like the effective porosity. As shown in Table I, the poroelastic shear modulus values are much lower than their viscoelastic counterparts because of the addition of the fluid pressure in the governing poroelastic equations. The lower shear modulus values also agree with reports by Perríñez et al. [2] where poroelastic magnetic resonance elastography estimates were lower than the DMA-acquired storage modulus.
More interesting, however, are the κ results because these data represent the first time that κ has been measured over a range of frequencies. The trend is opposite from the shear modulus: κ is higher for the soft tofu, and lower for the firm and extra firm compositions. High κ values indicate that fluid can move more easily through the porous matrix relative to materials with lower values. κ increases (the fluid moves more easily) with higher frequency, as well, and the values reported here fall within the range of those found in the literature for tissues and other porous media [25], [35]–[37].
Comparison can be drawn between the damping characteristics of the two models because κ represents the damping characteristics in a poroelastic material similarly to the energy loss found in the viscoelastic equivalent. Lower values of κ signify more difficult fluid transport whereas higher values represent easy fluid flow. At the upper and lower limits of κ, damping loss is near zero, with the maximum damping properties occurring at some intermediate value dependent on the pore structure and stiffness of the material. In both models, extra firm tofu is found to exhibit the most highly damped environment (highest DR, lowest κ).
Several drawbacks are associated with the technique presented here. An obvious disadvantage is the small frequency range over which mechanical properties can be estimated. Values were only recovered from 1 – 14 Hz because of DMA limitations like machine resonance when testing very soft materials. As frequency increased above 14 Hz, the DMA sample-holder platen would detach from the sample and yield unusable data. One option to extend the frequency range is to employ Time-Temperature Superposition, which relates changes in temperature with frequency to generate high frequency estimates from low temperature and low frequency data [38]. Other options would include linear extrapolation of the curve to higher frequencies or fitting a log curve to the data. A power-law fit is a popular alternative [39], [40], but is commonly related to viscoelasticity, and may not be appropriate for a poroelastic material.
Another shortcoming with the poro-FE technique is the assumption of Poisson’s ratio. The visco-analytic solution also requires a Poisson’s ratio assumption for compression tests; hence, accurate comparisons can be made. Here, Poisson’s ratios of tofu and brain are not well known, leading to an added source of uncertainty in the final estimates of shear modulus. Introducing a shear clamp or attempting to estimate a Poisson’s ratio would reduce this source of variation. Acquiring more independent force measurements for each material and frequency would enable accurate estimation of additional material properties by amending Eqn. 11 to include multiple force measurements.
The visco-FE method presented here demonstrates that viscoelastic parameters can be estimated accurately from data recorded with a DMA and they match the visco-analytic results very closely. Also, the FE model accounts for inertial forces inherent in viscoelastic materials, possibly providing better property estimates for soft materials at frequency. While viscoelastic estimates are sufficient in many applications, model-data mismatch can be lowered through a poroelastic FE method when considering fluid-saturated materials like tofu (or, more importantly, brain tissue). The poroelastic properties of shear modulus and κ reported here demonstrate consistency and contrast with respect to the three different grades of tofu that were evaluated.
VI. Conclusion
The ability to estimate both solid- and fluid-related material properties may produce greater understanding of disease processes. For instance, malignant tissue properties vary based on tumor location, disease type, and stage. In benign cysts, the stiffness of the abnormality may be the defining difference relative to the surrounding normal tissue. In other cases, a tortuous vasculature may have more edema and fluid flow; thus, the defining characteristic could be κ. Knowledge of the material structure would help with quality control in food science, where accuracy of the food stiffness and the ease of fluid flow through the solid matrix would create more consistent products [9], [41]. Higher order characterization of poroelastic mechanical properties through stiffness and hydraulic conductivity in materials like brain tissue is of great interest and could increase the understanding of complex pathological processes such as Alzheimer’s disease [23] and hydrocephalus [3].
Acknowledgments
This work was supported by a grant from the National Institutes of Health (R01EB018230).
Contributor Information
Adam J Pattison, Email: adam.j.pattison.TH@dartmouth.edu, Thayer School of Engineering, Dartmouth College, Hanover, NH, 03755, USA.
Matthew McGarry, Thayer School of Engineering, Dartmouth College, Hanover, NH, 03755, USA.
John B Weaver, Thayer School of Engineering, Dartmouth College, Hanover, NH, 03755, USA. Dartmouth-Hitchcock Medical Center, Lebanon, NH, 03756, USA.
Keith D Paulsen, Thayer School of Engineering, Dartmouth College, Hanover, NH, 03755, USA. Dartmouth-Hitchcock Medical Center, Lebanon, NH, 03756, USA.
References
- 1.Menard KP. Dynamic Mechanical Analysis: A Practical Introduction. CRC Press LCC; 1999. [Google Scholar]
- 2.Perriñez PR, Pattison AJ, Kennedy FE, Weaver JB, Paulsen KD. Contrast detection in fluid-saturated media with magnetic resonance poroelastography. Journal of Medical Physics. 2010;37(7):3518–3526. doi: 10.1118/1.3443563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Penn RD, Linninger A. The physics of hydrocephalus. Pediatric neurosurgery. 2009 Jan;45:161–174. doi: 10.1159/000218198. [DOI] [PubMed] [Google Scholar]
- 4.Franceschini G, Bigoni D, Regitnig P, Holzapfel GA. Brain tissue deforms similarly to filled elastomers and follows consolidation theory. Journal of the Mechanics and Physics of Solids. 2006 Dec;54:2592–2620. [Google Scholar]
- 5.Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR, Ehman RL. Magnetic resonance elastography of the brain. NeuroImage. 2008;39:231–237. doi: 10.1016/j.neuroimage.2007.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hrapko M, Van Dommelen JAW, Peters GWM, Wismans JSHM. Characterisation of the mechanical behaviour of brain tissue in compression and shear. Biorheology. 2008;45:663–676. [PubMed] [Google Scholar]
- 7.Christ AF, Franze K, Gautier H, Moshayedi P, Fawcett J, Franklin RJM, Karadottir RT, Guck J. Mechanical difference between white and gray matter in the rat cerebellum measured by scanning force microscopy. Journal of biomechanics. 2010 Nov;43(15):2986–92. doi: 10.1016/j.jbiomech.2010.07.002. [DOI] [PubMed] [Google Scholar]
- 8.Biot MA. General Theory of Three-Dimensional Consolidation. Journal of Applied Physics. 1941;12(2):155–164. [Google Scholar]
- 9.Berry GP, Bamber JC, Miller NR, Barbone PE, Bush NL, Armstrong CG. Towards an acoustic model-based poroelastic imaging method: II. experimental investigation. Ultrasound in medicine & biology. 2006 Dec;32(12):1869–85. doi: 10.1016/j.ultrasmedbio.2006.07.013. [DOI] [PubMed] [Google Scholar]
- 10.Konofagou EE, Harrigan T, Ophir J, Krouskop TA. Poroelastography: Imaging the poroelasic properties of tissues. Ultrasound in Medicine and Biology. 2001;27(10):1387–1397. doi: 10.1016/s0301-5629(01)00433-1. [DOI] [PubMed] [Google Scholar]
- 11.Righetti R, Righetti M, Ophir J, Krouskop TA. The feasibility of estimating and imaging the mechanical behavior of poroelastic materials using axial strain elastography. Physics in Medicine and Biology. 2007 Jun;52:3241–3259. doi: 10.1088/0031-9155/52/11/020. [DOI] [PubMed] [Google Scholar]
- 12.Cheng AH-D, Badmus T, Beskos DE. Integral Equation for Dynamic Poroelasticity in Frequency Domain with BEM Solution. Journal of Engineering Mechanics. 1991;117(5):1136–1157. [Google Scholar]
- 13.Dineva P, Datcheva M, Manolis G, Schanz T. Seismic wave propagation in laterally inhomogeneous poroelastic media via BIEM. International Journal for Numerical and Analytical Methods in Geomechanics. 2012;36:111–127. [Google Scholar]
- 14.Dvorkin J, Nur A. Dynamic poroelasticity: A unified model with the squirt and the Biot mechanisms. Geophysics. 1993 Apr;58(4):524–533. [Google Scholar]
- 15.Burridge R, Vargas CA. The fundamental solution in dynamic poroelasticity. Geophys J R astr Soc. 1979;58:61–90. [Google Scholar]
- 16.Mow V, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression: Theory and experiments. Journal of Biomechanical Engineering. 1980 Feb;102(1):73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 17.Nia HT, Han L, Li Y, Ortiz C, Grodzinsky A. Poroelasticity of cartilage at the nanoscale. Biophysical journal. 2011 Nov;101(9):2304–13. doi: 10.1016/j.bpj.2011.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cowin SC. Bone poroelasticity. Journal of biomechanics. 1999 Mar;32(3):217–38. doi: 10.1016/s0021-9290(98)00161-4. [DOI] [PubMed] [Google Scholar]
- 19.Schanz M, Cheng AH-D. Transient wave propagation in a one-dimensional poroelastic column. Acta Mechanica. 2000 Mar;145(1):1–18. [Google Scholar]
- 20.Schanz M, Diebels S. A comparative study of Biot’s theory and the linear Theory of Porous Media for wave propagation problems. Acta Mechanica. 2003;161:213–235. [Google Scholar]
- 21.Ivanchenko O, Sindhwani N, Linninger AA. Experimental techniques for studying poroelasticity in brain phantom gels under high flow microinfusion. Journal of Biomechanical Engineering. 2010 Mar;132(5):051008. doi: 10.1115/1.4001164. [DOI] [PubMed] [Google Scholar]
- 22.Yu H, Mouw JK, Weaver VM. Forcing form and function: biomechanical regulation of tumor evolution. Trends in cell biology. 2010 Sep;21(1):47–56. doi: 10.1016/j.tcb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Paparcone R, Keten S, Buehler MJ. Atomistic simulation of nanomechanical properties of Alzheimer’s Abeta(1-40) amyloid fibrils under compressive and tensile loading. Journal of biomechanics. 2010 Apr;43(6):1196–201. doi: 10.1016/j.jbiomech.2009.11.026. [DOI] [PubMed] [Google Scholar]
- 24.Paulsen KD, Miga MI, Kennedy FE, Hoopes PJ, Hartov A, Roberts DW. A computational model for tracking subsurface tissue deformation during stereotactic neurosurgery. IEEE Transactions on Biomedical Engineering. 1999 Feb;46(2):213–25. doi: 10.1109/10.740884. [DOI] [PubMed] [Google Scholar]
- 25.Miga MI, Paulsen KD, Hoopes PJ, Kennedy FE, Hartov A, Roberts DW. In vivo modeling of interstitial pressure in the brain under surgical load using finite elements. Journal of Biomechanical Engineering. 2000 Aug;122(4):354–63. doi: 10.1115/1.1288207. [DOI] [PubMed] [Google Scholar]
- 26.Carpenter RP, Lyon DH, Hasdell TA. Guidelines for sensory analysis in food product development and quality control. 2. Gaithersburg, Maryland: Aspen Publishing; 2000. [Google Scholar]
- 27.Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography. Magnetic Resonance in Medicine. 2005 Feb;53:372–387. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- 28.Landau L, Lifschitz E. Theory of Elasticity. New York: Pergamon Press; 1986. [Google Scholar]
- 29.Perriñez PR, Kennedy FE, Van Houten EEW, Weaver JB, Paulsen KD. Magnetic resonance poroelastography: an algorithm for estimating the mechanical properties of fluid-saturated soft tissues. IEEE Transactions on Medical Imaging. 2010 Mar;29(3):746–755. doi: 10.1109/TMI.2009.2035309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Instruments T. DMA Modulus Equations. New Castle, DE: 2010. pp. 1–9. [Google Scholar]
- 31.Perriñez PR, Marra SP, Kennedy FE, Paulsen KD. 3D Finite Element Solution to the Dynamic Poroelasticity Problem for Use in MR Elastography. In: Manduca A, Hu XP, editors. SPIE. Vol. 6511. Mar, 2007. pp. 65 111B–65 111B-11. [Google Scholar]
- 32.Li P, Lu D. An Analytical Solution of Two-Dimensional Flow and Deformation Coupling Due to a Point Source Within a Finite Poroelastic Media. Journal of Applied Mechanics. 2011;78(6):061020. [Google Scholar]
- 33.Zienkiewicz OC, Taylor RL. The Finite Element Method, Solid Mechanics. 2. New York, NY: Wiley; 2000. [Google Scholar]
- 34.Miller K. Modelling Soft Tissue Using Biphashic Theory - A Word of Caution. Computer Methods in Biomechanics and Biomedical Engineering. 1998;1(3):261–263. doi: 10.1080/01495739808936706. [DOI] [PubMed] [Google Scholar]
- 35.Basser PJ. Interstitial pressure, volume, and flow during infusion into brain tissue. Microvascular research. 1992 Sep;44(2):143–65. doi: 10.1016/0026-2862(92)90077-3. [DOI] [PubMed] [Google Scholar]
- 36.Nagashima T, Shirakuni T, Rapoport SI. A two-dimensional, finite element analysis of vasogenic brain edema. Neurol Med Chir. 1990 Jan;30(1):1–9. doi: 10.2176/nmc.30.1. [DOI] [PubMed] [Google Scholar]
- 37.Kalyanasundaram S, Calhoun VD, Leong KW. A finite element model for predicting the distribution of drugs delivered intracranially to the brain. Am J Physiol Regul Integr Comp Physiol. 1997;273:R1810–R1821. doi: 10.1152/ajpregu.1997.273.5.R1810. [DOI] [PubMed] [Google Scholar]
- 38.Peters GWM, Meulman JH, Sauren AAHJ. The Applicability of the Time/Temperature Superposition Principle to Brain Tissue. Biorheology. 1997;34(2):127–138. doi: 10.1016/S0006-355X(97)00009-7. [DOI] [PubMed] [Google Scholar]
- 39.Guo J, Posnansky O, Hirsch S, Scheel M, Taupitz M, Braun J, Sack I. Fractal network dimension and viscoelastic powerlaw behavior: II. An experimental study of structure-mimicking phantoms by magnetic resonance elastography. Physics in medicine and biology. 2012 Jun;57(12):4041–53. doi: 10.1088/0031-9155/57/12/4041. [DOI] [PubMed] [Google Scholar]
- 40.Clayton EH, Garbow JR, Bayly PV. Frequency-dependent viscoelastic parameters of mouse brain tissue estimated by MR elastography. Physics in medicine and biology. 2011 Mar;56(8):2391–2406. doi: 10.1088/0031-9155/56/8/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Cheng Y, Shimizu N, Kimura T. The viscoelastic properties of soybean curd (tofu) as affected by soymilk concentration and type of coagulant. International Journal of Food Science and Technology. 2005 Apr;40(4):385–390. [Google Scholar]