Impulse response method for characterization of echogenic liposomes

Abstract

An optical characterization method is presented based on the use of the impulse response to characterize the damping imparted by the shell of an air-filled ultrasound contrast agent (UCA). The interfacial shell viscosity was estimated based on the unforced decaying response of individual echogenic liposomes (ELIP) exposed to a broadband acoustic impulse excitation. Radius versus time response was measured optically based on recordings acquired using an ultra-high-speed camera. The method provided an efficient approach that enabled statistical measurements on 106 individual ELIP. A decrease in shell viscosity, from 2.1 × 10⁻⁸ to 2.5 × 10⁻⁹ kg/s, was observed with increasing dilatation rate, from 0.5 × 10⁶ to 1 × 10⁷ s⁻¹. This nonlinear behavior has been reported in other studies of lipid-shelled UCAs and is consistent with rheological shear-thinning. The measured shell viscosity for the ELIP formulation used in this study [κ_s = (2.1 ± 1.0) × 10⁻⁸ kg/s] was in quantitative agreement with previously reported values on a population of ELIP and is consistent with other lipid-shelled UCAs. The acoustic response of ELIP therefore is similar to other lipid-shelled UCAs despite loading with air instead of perfluorocarbon gas. The methods described here can provide an accurate estimate of the shell viscosity and damping for individual UCA microbubbles.

I. INTRODUCTION

Physical models for encapsulated ultrasound contrast agent (UCA) microbubbles have been developed and improved over the past two decades. The models give accurate predictions of the nonlinear radial dynamics of individual UCA microbubbles, particularly under forced, or acoustically driven, conditions.¹ Such models are largely based on Rayleigh–Plesset-type equations, which describe the dynamics of a gas bubble in response to pressure variations. The effects of the shell encapsulation on the microbubble motion are incorporated by adding additional terms that describe the viscoelastic behavior of the shell.² The presence of the shell increases the resonance frequency from that of a free bubble and damps the oscillations in response to the acoustic forcing.³ The shell also affects the nonlinear response of microbubbles, a key property of UCAs that is often exploited in diagnostic imaging modes for enhanced discrimination between the contrast agent and surrounding tissue.⁴

In addition to traditional diagnostic ultrasound imaging, there has been recent interest in advancing the applications of microbubbles for molecular imaging and therapeutic applications. These applications exploit the nonlinear response for selective detection of microbubbles in a given volume for diagnosis and specific targeting of disease. Molecular imaging techniques with targeted UCAs are being used increasingly for noninvasive diagnosis of inflammation, thrombus, and neovascularization.⁵ Targeted microbubble agents are also being developed for controlled drug-delivery applications.⁶ Clinical application of these UCAs necessitates accurate prediction of the frequency-dependent response of single isolated microbubbles. A better understanding of the shell properties that can be expected for individual UCA microbubbles within a population is also critical. The acoustic response of microbubbles can depend on the morphology and viscoelastic properties of the encapsulating shell,⁷ particularly if lipids are not homogeneously distributed throughout the shell.⁸ Therefore single microbubble characterization techniques and physical models that accurately describe the dynamics of an encapsulated microbubble are increasingly important.

The introduction of optical methods to resolve microbubble oscillations has provided new insights into the dynamic response of single microbubbles. Optical methods based on direct measurement of the bubble radius versus time can be used due to availability of ultra-high-speed imaging systems^9,10 such as the Brandaris 128 fast-framing (0.5–25 Mfps) camera.¹¹ This system enables optical characterization studies by imaging single microbubble dynamical phenomena occurring at multiple time scales.¹² Acoustic measurements of the scattered echo from an isolated microbubble have been simultaneously recorded and compared to the optically measured radial dynamics to verify the effectiveness of this approach.¹³

Optical studies of the radial dynamics of UCAs typically rely on measuring the steady-state forced response of a microbubble to a narrow-band burst excitation. For example, the amplitude response of a microbubble exposed to multiple-cycle, low amplitude ultrasound bursts at various frequencies can be analyzed to build up a resonance curve and fit to a linearized model to derive the viscoelastic shell parameters.¹⁴ This microbubble spectroscopy technique^14–17 requires multiple recordings to characterize the frequency-dependent response of an individual microbubble. In addition, the shell morphology can be altered or destroyed due to multiple burst excitations.¹⁸ A method using a single excitation would improve the efficiency of UCA characterization techniques and would minimize the effect of alterations to the microbubble shell under successive excitations.

In this study, we investigated the use of the impulse response to characterize the damping imparted by the encapsulation of microbubbles stabilized by a lipid shell, echogenic liposomes (ELIP).¹⁹ The shell viscosity is the dominant mechanism affecting the damping of microbubble response to acoustic excitation and most directly influences the onset of nonlinear oscillations. An understanding of this physical property of the shell encapsulation can be exploited for optimization of contrast-enhanced imaging and therapeutic applications. Through this technique, we aim to acquire a better understanding of the transient dynamics of ELIP in response to short-pulse excitations for both diagnostic and therapeutic applications. This method is also of particular interest to improve the efficiency of UCA characterization techniques in general as it requires only a single acoustic excitation when the impulse response is recorded using an ultra-high-speed camera.

ELIP are under development as theragnostic ultrasound contrast agents and differ from other commercially available UCAs primarily in shell material and gas content.⁴ ELIP formulations include a small amount of cholesterol to increase membrane rigidity and are echogenic due to the presence of air, which is entrapped and stabilized by the lipid during the rehydration process.¹⁹ The exact location of the entrapped air pockets, morphology of the encapsulation, and amount of air in each carrier has not been fully ascertained.^19–21 The objective of the present study was to measure the damping due to the encapsulation and to estimate the shell viscosity based on the unforced response of individual ELIP exposed to a broadband acoustic impulse excitation.

An ultra-high-speed camera was used to capture the radius versus time response. During each recording, an isolated ELIP was excited using two ultrasound pulses with a phase difference of 180°. Following each pulse, the bubble oscillated at its natural frequency with diminishing amplitude determined by the damping, and eventually returned to its resting radius. A generic model was developed to estimate the shell viscosity based on the amplitude decay time constant, which was determined from the experimentally measured radius versus time curve for an individual ELIP. Gas diffusion was neglected in our model, and this approach was verified experimentally by comparing the resting radius before and after the impulse excitation. The shell viscosity of individual ELIP obtained using the optical method presented here is compared to our previously reported value obtained for a population of ELIP using a broadband acoustic attenuation spectroscopy technique.²¹

II. MATERIALS AND METHODS

A. Experimental setup

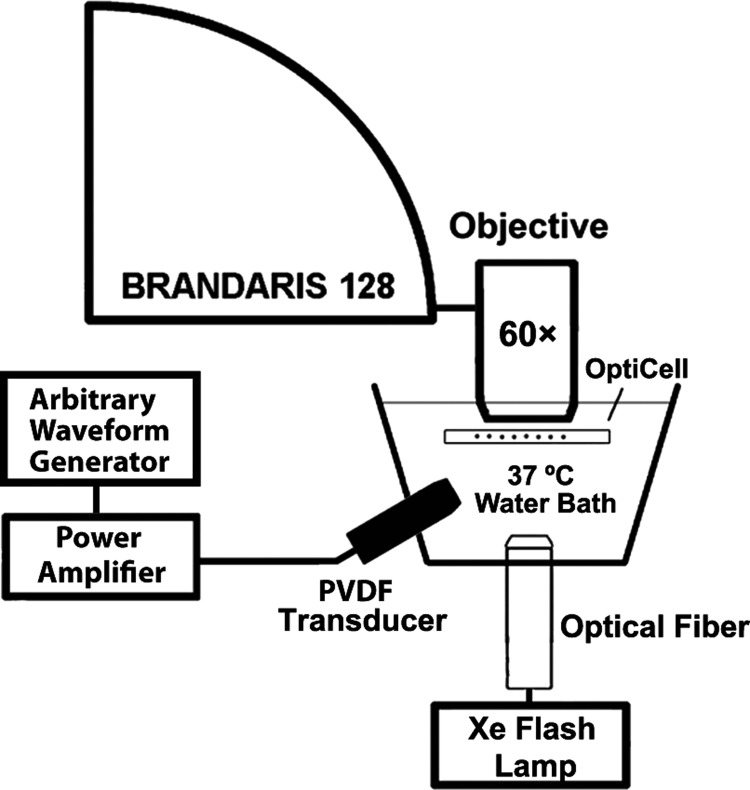
Freeze-dried ELIP dispersions consisting of L-α-phosphatidylcholine,1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC),1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine (DPPE),1,2-dipalmitoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (DPPG),cholesterol (27:42:8:8:15, mol. %) [all lipids were purchased from Avanti Polar Lipids (Alabaster, AL)] were prepared as previously described.²² ELIP suspensions were prepared by reconstituting 10 mg/ml lyophilized lipid powder using air-saturated, filtered (type I) water at room temperature as described by Huang.¹⁹ The suspension was diluted (∼100×) into air-saturated phosphate-buffered saline (PBS) mixed with 0.5% (wt./vol.) bovine serum albumin (BSA) solution (Sigma Chemical Co., St. Louis, MO), loaded into an OptiCell^® (Nunc/Thermo Scientific, Wiesbaden, Germany), and placed on an optical stage in a 37 °C water bath. A microscope with a 60× water-immersion objective and 2× magnifier was used to image the bubble dynamics at approximately 17 Mfps using the Brandaris 128 fast-framing camera.^11,12 A diagram of the ultra-high-speed optical imaging setup is presented in Fig. 1.

FIG. 1.

Schematic of the setup used to optically record the microbubble oscillation.

Figure 2(a) shows an optical image of a dilute suspension of ELIP suspended in an OptiCell^® using a 40× objective to obtain a larger field of view. A single frame from a Brandaris 128 recording using the 60× objective and 2× magnifier is shown in Fig. 2(b). Figures 2(c) and 2(d) show super-resolution fluorescence microscope images of fluorescently labeled ELIP obtained using the methods outlined by Kooiman et al.²³ Briefly, a 4Pi confocal laser-scanning microscope (Leica TCS 4Pi) with two opposing objective lenses (100×, HCX PL APO, 1.35 NA) was used to generate super-resolution three-dimensional image stacks. For this supporting study, 2 mol. % fluorescently labeled 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (rhodamine-DPPE) (Avanti Polar Lipids) was substituted into the ELIP formulation and the reconstituted liposomes were suspended in 87% (vol./vol.) glycerol between quartz cover slips at room temperature. The images show the distribution of the lipid molecules in the shell encapsulation of the ELIP. The size distribution of the microbubbles deduced from optical images presented in Figs. 2(a) and 2(c) is consistent with Coulter counter measurements of the particle size distribution for this ELIP formulation, which indicated a volume-weighted mean diameter of 2 μm.²¹ Previously published transmission electron microscopy images have shown liposomes on the order of 2 μm diameter²⁴ as well as vesicles in the nanometer size range that could not be resolved using the optical methods described here.^25,26 Atomic force microscopy²⁰ and fluorescence microscopy studies²⁶ also indicate a broad size distribution, with particle sizes ranging over three orders of magnitude from tens of nanometers to microns.

FIG. 2.

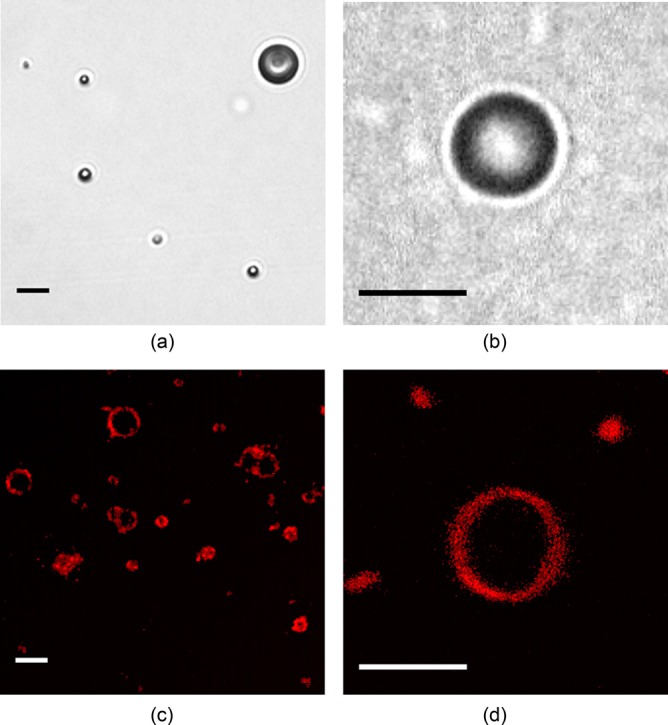
(Color online) (a) Optical image of a dilute suspension of ELIP suspended in an OptiCell^® (40× magnification). (b) Single frame of a Brandaris 128 recording (120× magnification), (c) and (d) Super-resolution confocal microscope images of fluorescently labeled (2 mol. % rhodamine-DPPE) ELIP in glycerol (Leica TCS 4Pi, 100× magnification). Scale bars represent 5 μm in all images.

B. Acoustic excitation pulse

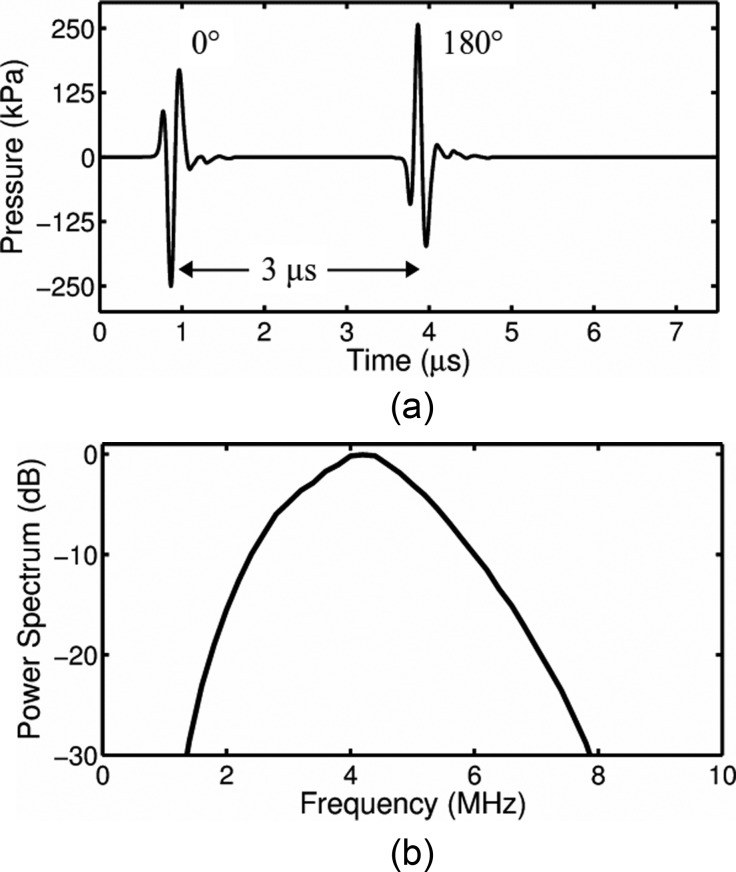
A focused, broadband PVDF transducer (23 mm diameter, 25 mm focal distance, PA275; Precision Acoustics, Dorchester, UK) was positioned in the water bath at a 45° angle below the sample and the acoustic focus (0.5 mm full-width at half-maximum pressure) aligned with the optical field of view. To detect potential nonlinear bubble dynamics, a pulse inversion pair was utilized to excite individual ELIP. For each optical recording, a sequence of two phase-inverted acoustic pulses, temporally separated by 3 μs, was used to excite each ELIP impulsively. The pulses had a phase difference of 180° but were otherwise identical with center frequency of 4 MHz and pulse duration of ∼0.33 μs (1.5 cycles). Pulse excitations with peak pressure amplitude of 125, 250, or 500 kPa (210, 420, or 840 kPa peak-to-peak acoustic pressure, respectively) were generated by a programmable arbitrary waveform generator (8026, Tabor Electronics Ltd., Tel Hanan, Israel) and amplified using a wideband RF amplifier (0.3–35 MHz, A-500; Electronic Navigation Industries, Rochester, NY). During calibration, a 0.2 -μm needle-type hydrophone (Precision Acoustics) was positioned approximately 2 mm from the sample holder membrane (a modified OptiCell^® with one membrane removed), such that the hydrophone location corresponded to the location of the ELIP during the optical measurement. The transmitted acoustic pressure amplitude in situ was attenuated by a factor of 3 dB relative to the free-field pressure due to the presence of the membrane and the 45° angle of incidence of the acoustic wave. The in situ pressure waveform and power spectrum for a 250 kPa peak pressure amplitude excitation pulse are shown in Fig. 3.

FIG. 3.

(a) Measured pressure waveform and (b) corresponding spectrum of the acoustic excitation pulses.

C. Estimation of the shell viscosity

Linearization of a Rayleigh–Plesset-type bubble dynamics equation yields the equation of motion for a damped harmonic oscillator. In the absence of forcing this equation can be written,¹

$$\ddot{x}+{\omega }_0\delta \dot{x}+{\omega }_0^{2}x=0.$$ (1)

The eigenfrequency, ω₀, is given by the Minnaert relation for a free gas bubble,¹⁷ and for an encapsulated bubble, this expression can be modified to include an additional term that depends on the elasticity of the shell.²⁷ The damped natural frequency for unforced oscillations, ω_d, is related to the eigenfrequency of the system by the damping coefficient, ${\omega }_d={\omega }_0\sqrt{(1-{\delta }^2/4)}$, where δ represents the total damping of the system.^28,29 If the system is modeled as a linearized, single degree-of-freedom system which is underdamped (δ < 2), the solution can be written in terms of an oscillatory signal with a decaying exponential envelope characterized by the time constant, $\tau =2/(\delta {\omega }_0)$.

Analysis of the experimental data consists of calculating the envelope signal, A(t), from the measured radius versus time curves for each individual pulse excitation using the Hilbert transform. The time constant can be readily determined by fitting a line to the natural logarithm of the envelope signal,³⁰ with a slope given by

$$\frac{d\left(\ln \left|A\left(t\right)\right|\right)}{\mathit{d}\mathit{t}}=\frac{\delta {\omega }_0}{2}=\frac{1}{\tau }.$$ (2)

In general, the total damping consists of contributions from all of the dissipative loss mechanisms, including: Acoustic radiation (δ_rad), thermal diffusion and conduction (δ_th), viscosity of the surrounding liquid (δ_vis), and viscosity of the shell (δ_sh), such that δ = δ_rad + δ_th + δ_vis + δ_sh.²⁸ For an encapsulated bubble, the last term represents the damping imparted by the shell,³ and for an unencapsulated bubble, δ_sh = 0. Assuming a Newtonian rheology, the expression for δ_sh in terms of the total non-dimensional damping coefficient can be written,³¹

$${\delta }_{\mathit{s}\mathit{h}}=\delta -{\delta }_0=\frac{4{\kappa }_s}{\rho {\omega }_0{R}_0^3},$$ (3)

where δ₀ = δ_rad + δ_th + δ_vis represents the total damping coefficient evaluated at resonance for an unencapsulated gas bubble with the same radius and eigenfrequency as the encapsulated bubble. The shell viscosity in dimensional units, κ_s, can be estimated as a function of the time constants, τ and τ₀,

$${\kappa }_s=\frac{\rho R_0^3}{2}\left(\frac{1}{\tau }-\frac{1}{{\tau }_0}\right),$$ (4)

where τ and τ₀ are the time constants for an encapsulated bubble (measured) and unencapsulated bubble with the same initial radius (calculated), respectively.

The expression given in Eq. (2) for the interfacial shell viscosity is consistent with the Rayleigh–Plesset-type model for phospholipid-encapsulated bubbles developed by Marmottant et al.³² In this model, the effective surface tension is described by three regimes of shell behavior: Buckled, elastic, or ruptured. In the elastic regime, the shell contributes an additional restoring force, characterized by the elasticity χ, which shifts the resonance for small amplitude oscillations of an encapsulated bubble to higher frequencies. Oscillations in the purely elastic regime occur only at exceedingly low vibrational amplitudes [e.g., R/R₀ < 1.01 for χ = 2.5 N/m (Ref. 17)]. Above a threshold radius, the shell is in the ruptured regime and the interfacial dynamics are also controlled by the free air-water surface tension. We estimate the rupture radius for ELIP to be R/R₀ = 1.02 based on the elasticity determined previously [χ = 1.55 N/m (Ref. 21)]. Overvelde et al.¹⁷ demonstrated that for oscillations exceeding this amplitude, the bubble is no longer oscillating in the purely elastic regime and the natural frequency for a encapsulated bubble approaches a value that is only slightly greater (∼10%) than would be predicted for an unencapsulated bubble. For simplicity, we consider ω₀ to be the same for both encapsulated and unencapsulated bubbles and use the eigenfrequency of an unencapsulated bubble [e.g., Eq. (5) in Ref. 26] to calculate τ₀ in Eq. (4).

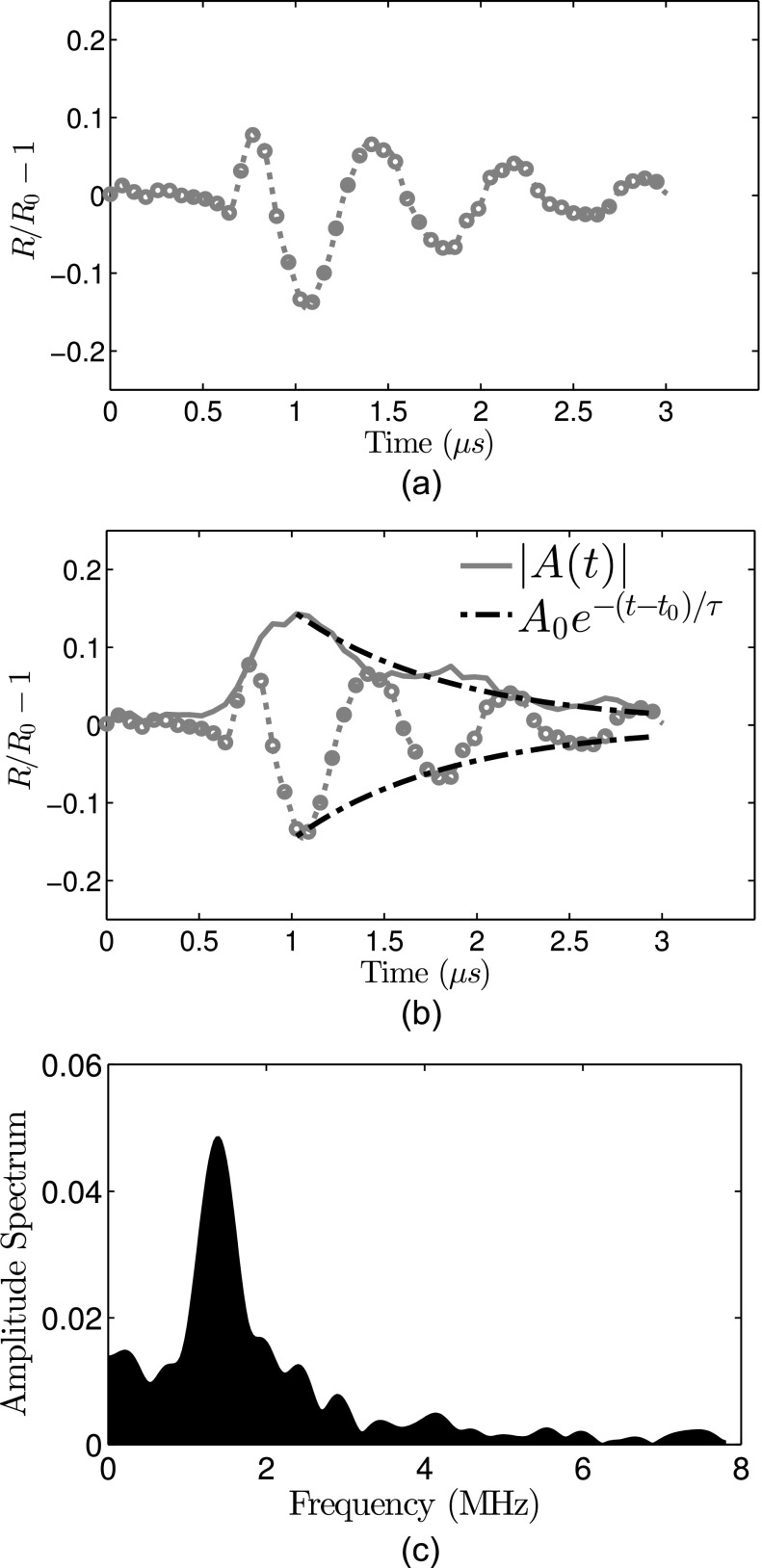
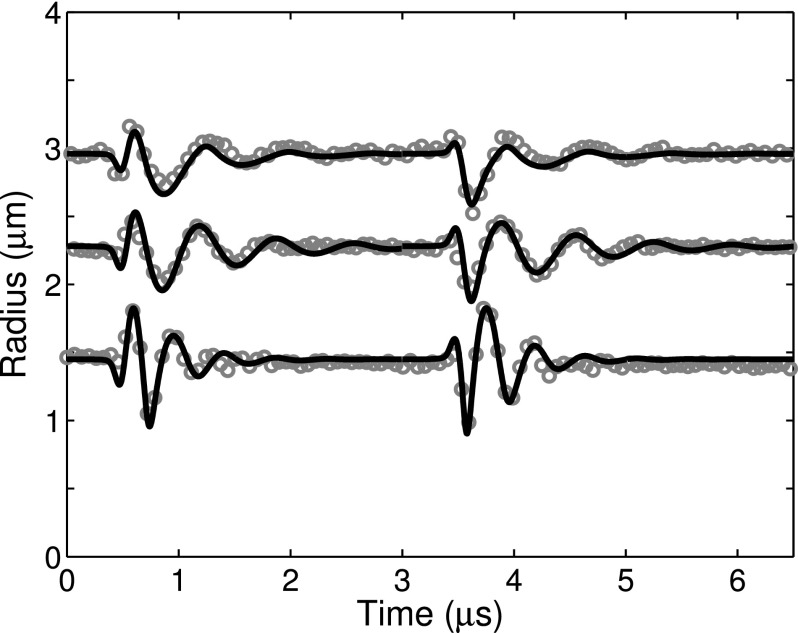
Each ELIP was excited by both peak-negative and peak-positive pulses, which were analyzed separately. A subset of ELIP were excited several times using 125, 250, or 500 kPa peak pressure amplitude pulses. An example of the damping analysis for an individual 0° pulse excitation is shown in Figs. 4(a) and 4(b). The natural frequency of unforced oscillation was estimated from the Fourier spectrum of the radius versus time response, shown in Fig. 4(c).

FIG. 4.

Schematic of the damping analysis. (a) Radius versus time curve measured in response to 0° impulse excitation (the response due to 180° excitation is truncated for clarity). (b) The amplitude decay envelope (solid line) is calculated using the discrete Hilbert transform. The time constant is obtained by fitting an exponential decay (dashed-dotted line) to the envelope using Eq. (1). For this example, R₀ = 2.5 μm, τ = 0.85 μs, κ_s = 5.6 × 10⁻⁹ kg/s. (c) Amplitude spectrum of the radius versus time curve.

D. Simulations

To evaluate the validity of the shell viscosity estimates obtained for individual ELIP, radius versus time curves were simulated using the dynamical model for lipid-encapsulated microbubbles developed by Marmottant et al.³² The measured acoustic pressure waveforms (see Fig. 3) were used as the forcing function for the bubble dynamics simulations that were compared with the experimental data. The values of the physical parameters used for the simulations were: Ambient pressure P₀ = 100 kPa, density of the liquid, ρ = 1007 kg/m³, viscosity of the liquid (at 37 °C), μ = 0.76 × 10^–3 kg/(m s), surface tension of the free air-water interface, σ_water = 0.072 N/m, and speed of sound, c = 1536 m/s. These parameters correspond to air-filled microbubbles suspended in PBS with 0.5% BSA solution at 37 °C.²¹ The effective polytropic exponent was calculated from the ratio of specific heats using the expression given by Hoff et al.³³ following other researchers who have used similar expressions.³⁴ The parameters used in the Marmottant model for describing the interfacial rheological properties of the shell are the elasticity, χ = 0.1–1.55 N/m, and the shell surface viscosity, κ_s, which was estimated based on experimental measurements as described in Sec. II C. Marmottant et al.³² and others¹⁷ have demonstrated that a phospholipid shell stabilizes a quiescent gas bubble by counteracting the Laplace pressure, therefore most microbubbles have an initial surface tension much lower than the surface tension of the free air-water interface, σ_water.³⁵ In this study, we assume the shell encapsulation is initially in the pre-buckled state (i.e., the transition between the elastic and buckled regions) and consequently the initial surface tension was taken as σ₀ = 0 for all numerical simulations.

E. Excitation of ELIP with a tone burst

A subset of ELIP was also excited using a 3 MHz tone burst to record the radius versus time response to acoustic forcing. Burst excitations were generated using the same arbitrary waveform generator and transducer but consisted of a 10-cycle, 3-MHz sinusoidal wave with a 2-cycle Gaussian ramp and taper. The in situ acoustic pressure amplitude for the tone burst excitation was 180 kPa, calibrated using the same methods as described in the preceding text. An impulse response excitation was recorded prior to the tone burst excitation to obtain an estimate of the shell viscosity using the methods described in the preceding text. This data acquisition scheme enabled a post hoc comparison of the measured forced response to simulations using the estimated value of shell viscosity for a particular liposome.

III. RESULTS

A total of 476 radius versus time curves for 106 individual ELIP were analyzed. The equilibrium radii of the individual ELIP ranged between 0.9 and 3.4 μm. Only trials for which the microbubble did not show any dissolution were analyzed in this study (|Δr| < 0.1 μm, where Δr is the difference between the bubble resting radius before and after the acoustic excitation). A small number of recordings (12 in total, <3%) with |Δr| > 0.1 were therefore not included in the analysis.

Figure 5 shows the estimated natural frequency obtained from the Fourier spectrum of the individual radius versus time responses. The median value of the measured resonance frequency was 16% higher than the eigenfrequency of an unencapsulated bubble, given by 2πω₀.

FIG. 5.

Estimates of the natural frequency obtained using the Fourier transform of the radius versus time curves. The eigenfrequency for an unencapsulated bubble, 2πω₀, which was used in the calculation of τ₀ is shown for reference (solid line). A fit using the median of the measured values is also shown (dashed line).

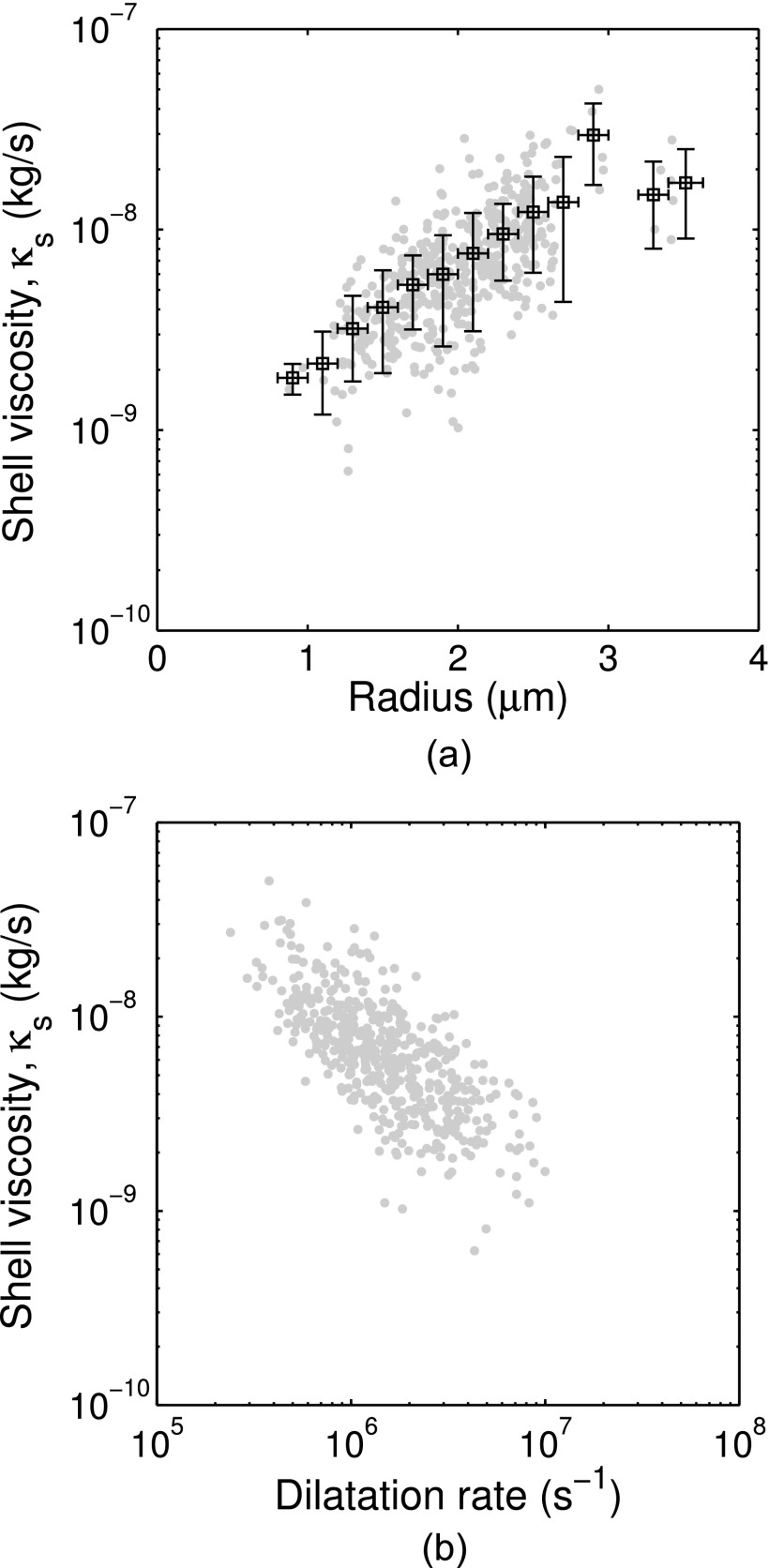
Results of the measured shell viscosity as function of size are shown in Fig. 6(a). Due to the large number of individual data points, the mean value and standard deviation of the points within radius bins spaced by 0.2 μm are also shown for clarity. There is a considerable spread of the shell viscosity estimates among microbubbles of the same size range (indicated by vertical error bars). However, the estimated shell viscosity increases with increasing bubble size, as has been shown in other investigations of lipid-shelled agents.^14,36,37 The shell viscosity estimates range from 2.1 × 10^–9 kg/s for microbubbles of 0.9–1.4 μm radius to 2.3 × 10^–8 kg/s for microbubbles of 2.5–3.4 μm radius. These values are the same order of magnitude as values obtained in other studies based on population estimates of commercially available lipid-shelled microbubbles such as SonoVue^® (κ_s = 5.4 × 10^–9 kg/s),³⁸ Sonazoid^® (κ_s = 1.2 × 10^–8 kg/s),³⁹ and Definity^® (κ_s = 3 × 10^–9 kg/s).⁴⁰

FIG. 6.

Shell viscosity versus (a) radius and (b) dilatation rate. Horizontal bars represent the bin width and vertical error bars represent one standard deviation of the points within each radius bin.

The dependence of the shell viscosity on the maximum dilatation rate is shown in Fig. 6(b). The maximum dilatation rate ($\dot{R}/R$)_max was determined directly from the experimentally measured radius versus time curves by calculating the derivative with respect to time. Despite the dispersion in the individual shell viscosity estimates, this plot demonstrates a decrease of the shell viscosity with increasing dilatation rate. By fitting the data to a power law relation of the form,⁴¹ ${\kappa }_s=k{(\dot{R}/R)}^{n-1}$, the 95% confidence interval for the power-law index n is between 0.1 and 0.25. A power-law index less than one is consistent with rheological shear-thinning behavior and has been reported earlier for lipid-shelled bubbles.¹⁴ For low dilatation rates (<0.50 × 10⁶ s^–1), the mean value and standard deviation of the shell viscosity estimates in this study was κ_s = (2.1 ± 1.0) × 10^–8 kg/s (n = 23).

Figure 7 shows three examples of numerically simulated and experimentally measured radius versus time curves for individual ELIP with equilibrium radii of 1.5, 2.3, and 3.0 μm. The excitation peak pressure amplitude for all cases was 250 kPa. Simulations were carried out using the experimentally derived shell viscosity (κ_s) for each individual ELIP (i.e., the average of the estimates derived from both 0° and 180° impulses). The shell elasticity (χ) was varied over one order of magnitude with the upper limit corresponding to the value previously determined for ELIP in the linear regime, χ = 0.1–1.55 N/m.²¹ The numerical simulations show good agreement with the experimentally measured transient impulse response dynamics for each case.

FIG. 7.

Example of simulated and experimentally measured radius versus time curves for ELIP with equilibrium radii of 1.5, 2.3, and 3.0 μm. The excitation peak pressure amplitude for all cases was 250 kPa. Estimates of the shell viscosity were derived from the experimental measurements for each case and used as inputs for the numerical simulation, yielding κ_s = 3.3 ± 0.4 × 10⁻⁹, 6.0 ± 0.3 × 10⁻⁹, and 2.15 ± 0.2 × 10⁻⁸ kg/s, respectively. Other simulation parameters were R₀ = 1.5, 2.3, and 3.0 μm and χ = 0.1, 0.2, and 1.55 N/m, respectively.

Figure 8 shows an example of simulated and experimentally measured radius versus time curves for a single ELIP exposed to three different peak pressure amplitude pulses: 125, 250, and 500 kPa. As expected, the shell viscosity values obtained from each independent excitation are similar. The estimates of κ_s for each pressure are 5.7, 5.6, and 5.6 × 10^–9 kg/s, respectively.

FIG. 8.

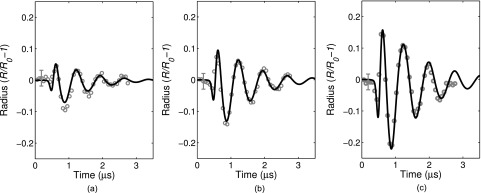
Example of experimental and simulated radius versus time curves for a single ELIP (R₀ = 2.5 μm, χ = 0.25 N/m) excited by (a) 125 kPa, (b) 250 kPa, and (c) 500 kPa peak pressure amplitude pulses (0° pulse). Vertical bars represent the relative error of the radius tracking algorithm, which was determined by the difference between the maximum and minimum radius measured from a recording of the same ELIP without ultrasound exposure.

IV. DISCUSSION

The goal of this study was to improve the understanding of the transient oscillation dynamics and shell properties of ELIP. We estimated the damping and shell viscosity from the unforced response of individual ELIP excited by a broadband acoustic impulse excitation measured using ultra-high-speed imaging. This technique can achieve the measurement of individual ELIP in a single run using the Brandaris 128 ultra-high-speed framing camera and provides an efficient alternative approach to the microbubble spectroscopy technique as reported previously.^14–16 The results derived from estimates for individual ELIP were in good agreement with our previously obtained values based on bulk acoustic attenuation measurements. Overall the shell viscosity estimates for ELIP in this study are consistent with values reported for commercially available lipid-shelled UCAs. Furthermore, we found that the Marmottant model accurately describes the transient dynamics of an individual ELIP when compared with radius versus time measurements obtained from ultra-high-speed recordings. Thus despite the encapsulation of air instead of perfluorocarbon gas, the viscoelastic shell properties of ELIP are similar to other lipid-shelled agents such as SonoVue^® and Definity^®.

A. Natural frequency of unforced oscillations

The eigenfrequency of an unencapsulated bubble is used to calculate the time constant, τ₀, in Eq. (4). To evaluate the validity of the assumption that the surface tension dominates the bubble dynamics, we obtained estimates of the natural frequency from the Fourier transform of the radius versus time curves (Fig. 5). The median natural frequency measured was 16% higher than the eigenfrequency for an unencapsulated bubble, given by 2πω₀. A 16% error in the natural frequency translates to a ∼4% change in τ₀ (and therefore in our estimates of κ_s) for the size range of bubbles studied.

B. Contributions to damping effects

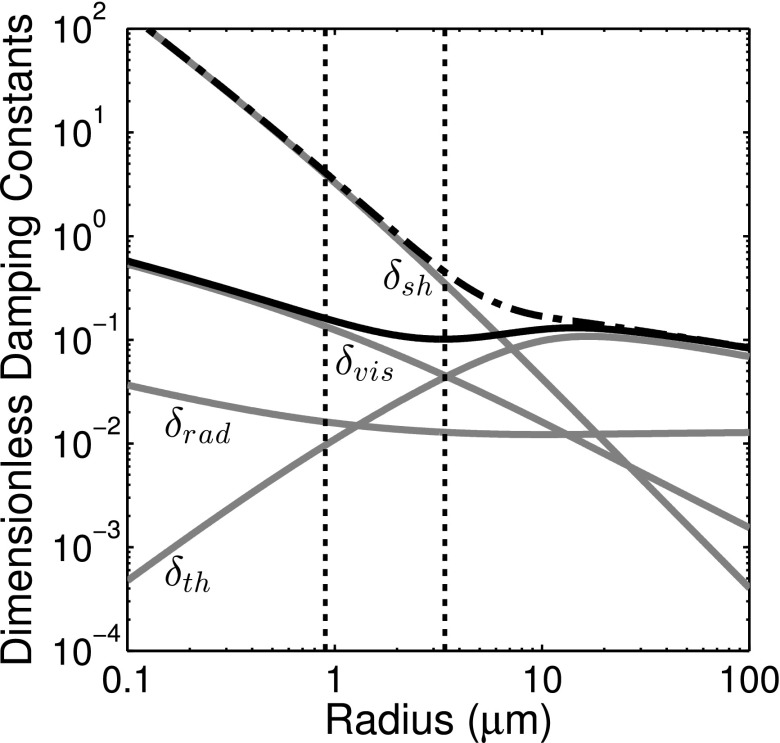
The total damping coefficient is the summation of the shell damping (δ_sh) and three other damping terms: The radiation damping (δ_rad), the thermal damping (δ_th), and the viscous damping due to the surrounding liquid (δ_vis). Theoretical expressions for predicting the damping factors of a spherically oscillating gas bubble are well-established,²⁸ and the latter three terms can be readily calculated based on the known equilibrium size and eigenfrequency of the microbubble. Figure 9 shows the resonance damping coefficients versus radius for an air bubble under the experimental conditions used in this study. Viscous damping (δ_vis or δ_sh) dominates, and the radiation damping is approximately an order of magnitude smaller for bubbles in the size range considered in this study. However, thermal damping can be appreciable and is included in our model for air-filled microbubbles at resonance.

FIG. 9.

The variation of dimensionless damping coefficients (δ_rad, δ_vis, δ_th, δ_sh) versus microbubble size at resonance. The total damping coefficients for a free bubble (solid line) and an encapsulated bubble with a shell viscosity of κ_s = 2 × 10⁻⁸ kg/s (dashed-dotted line) are also shown. The vertical dotted lines represent the size range of ELIP considered in this study.

Thermal damping is not accounted for explicitly in the Rayleigh–Plesset formulation and is often neglected in linearized models of UCAs as well.¹ However, thermal damping can be significant for resonant bubbles larger than about 1 μm and is dominant for resonant bubbles larger than ∼10 μm.³ Figure 9 shows that for a 1.3 μm radius bubble, δ_th is approximately equal to δ_rad and only amounts to 15% of the viscous term δ_vis. For a bubble of about 3.5 μm radius, δ_th is approximately equal to the viscous damping coefficient. In this study, we estimated the thermal damping and polytropic exponent based on the resting radius of the microbubble using the expressions given by Hoff et al.³³ It should be noted that the values of δ_th shown in Fig. 9 were calculated for an unencapsulated air bubble at resonance and include the effects of surface tension on the equilibrium gas pressure. However, δ_th may be less significant for an encapsulated bubble due to a lower equilibrium gas pressure resulting from the reduced initial surface tension for a bubble with a stabilizing shell (for example, σ₀ = 0 for a pre-buckled bubble as was assumed in this study).⁴² Therefore we may have a slight underestimation of the shell damping effect.

C. Shell viscosity

Overall our estimates of the shell viscosity of individual ELIP based on the optical method developed in this study are consistent with our previous measurements obtained using a broadband attenuation spectroscopy technique.^21,25 For low dilatation rates (< 0.5 × 10^–6 s^–1), the average value of the shell viscosity in this study [κ_s = (2.1 ± 1.0)× 10^–8 kg/s, n = 23] is in agreement with our previously reported bulk acoustic measurements in the linear regime [κ_s = (2.0 ± 0.14) × 10^–8 kg/s].²¹ Moreover the shell viscosity estimates derived from damping measurements on 106 individual ELIP in this study indicate an apparent increase of the shell viscosity with increasing radius and a decrease with increasing dilatation rate, indicative of shear-thinning behavior. This observation is consistent with previous measurements on commercially available lipid-shelled microbubbles such as SonoVue^® (Ref. 14) and Definity^® (Ref. 37) but is not explained by existing shell models where the viscosity is assumed to be constant over all radii. However, there have recently been attempts to account for this behavior using ad-hoc rheological models.^43,44

The shell viscosity estimates based on the optical approach also showed considerable variations among ELIP of the same size range (see Fig. 6). Variations in shell properties and acoustic response have also been reported in previous studies on lipid-shelled microbubbles. Kwan and Borden³⁵ and Kooiman et al.²³ present convincing microscopic images of heterogeneous lipid domains and ascribe this phenomenon to phase separation of the different lipid species on the bubble surface. Similar variations in the local lipid concentration on the shell have been found to affect the nonlinear behavior of DSPC microbubbles at high frequencies,⁴⁵ although no clear relation between the nonlinear response and shell microstructure was evident. Hosny et al.⁷ quantified the spatial distribution of viscosity in the microbubble shell using a fluorescence lifetime imaging technique and also found a large variation in viscosity that was correlated to differences in the ultrasound response of microbubbles of similar size. Based on the chemical composition and preparation method of ELIP, we expect similar inhomogeneities in local lipid concentration as well as variation between individual ELIP particles within a population. Moreover, lipid diffusion and the phase transition influenced by the surrounding temperature can be other key factors affecting the heterogeneity of the ELIP shell.^8,22

Nanostructural surface morphology that could not be resolved using the optical techniques in this study (e.g., Fig. 2) may nevertheless play a large role in the dynamic behavior of ELIP. For lipid-encapsulated bubbles, the shell is usually assumed to be a monolayer due to thermodynamic considerations.³⁵ However, the shell thickness has not been directly measured for microscopic encapsulated gas bubbles and estimates based on the dynamic response of the microbubble only give information about the interfacial rheological properties of the microbubble (i.e., zero-thickness interface model).²⁰ Therefore the large variation in viscosity estimates could be due to the number of lipid layers surrounding the encapsulated microbubbles.⁷ The resolution of the fluorescence images presented in Fig. 2 is limited by the focal spot size, which is about 220 nm in the lateral dimension. Thus we are unable to conclude whether the shell is a lipid monolayer or if it is multilamellar. Multilamellar vesicles, in which the lipid monolayer immediately adjacent to the gas bubble is surrounded by one or more bilayers, have been observed in transmission electron microscopy images of ELIP.²⁵ The spread of the shell viscosity estimates for ELIP of similar size may indicate the presence of multilamellar vesicles, where the apparent viscosity depends on the number of lamallae.

Another factor affecting the interpretation of the variation in the shell viscosity estimates is the uncertainty, which can be approximated as the random error associated with separate measurements on the same ELIP. We calculated the random error by considering the relative difference between the values obtained from separate analysis of the two phase-inverted excitation pulses (0° and 180°), i.e., the absolute difference between the two shell viscosity estimates normalized by the average of the two estimates. The median random error was 40% which is approximately the same as the standard deviation shown in Figs. 6(a) and 6(b).

D. Impulse response measurements and analysis

Evaluation of the damping coefficient based on the impulse response is a new and efficient approach applied to characterization of lipid-shelled ELIP in this study. A broadband pulse was applied to acquire the radius versus time impulse response of an individual ELIP, requiring only a single exposure of a few microseconds using an ultra-high-speed camera. Using the Brandaris 128, we were able to record the unforced, exponentially decaying amplitude response from two acoustic impulse excitations, a pulse inversion pair, during each high speed recording (128 frames). This method provides an efficient approach that enabled statistical measurements on a large number of individual ELIP. Additionally, data analysis was straightforward, and the simulated transient response of the lipid-encapsulated microbubble accurately tracked the measured radius versus time curves (Figs. 7 and 8).

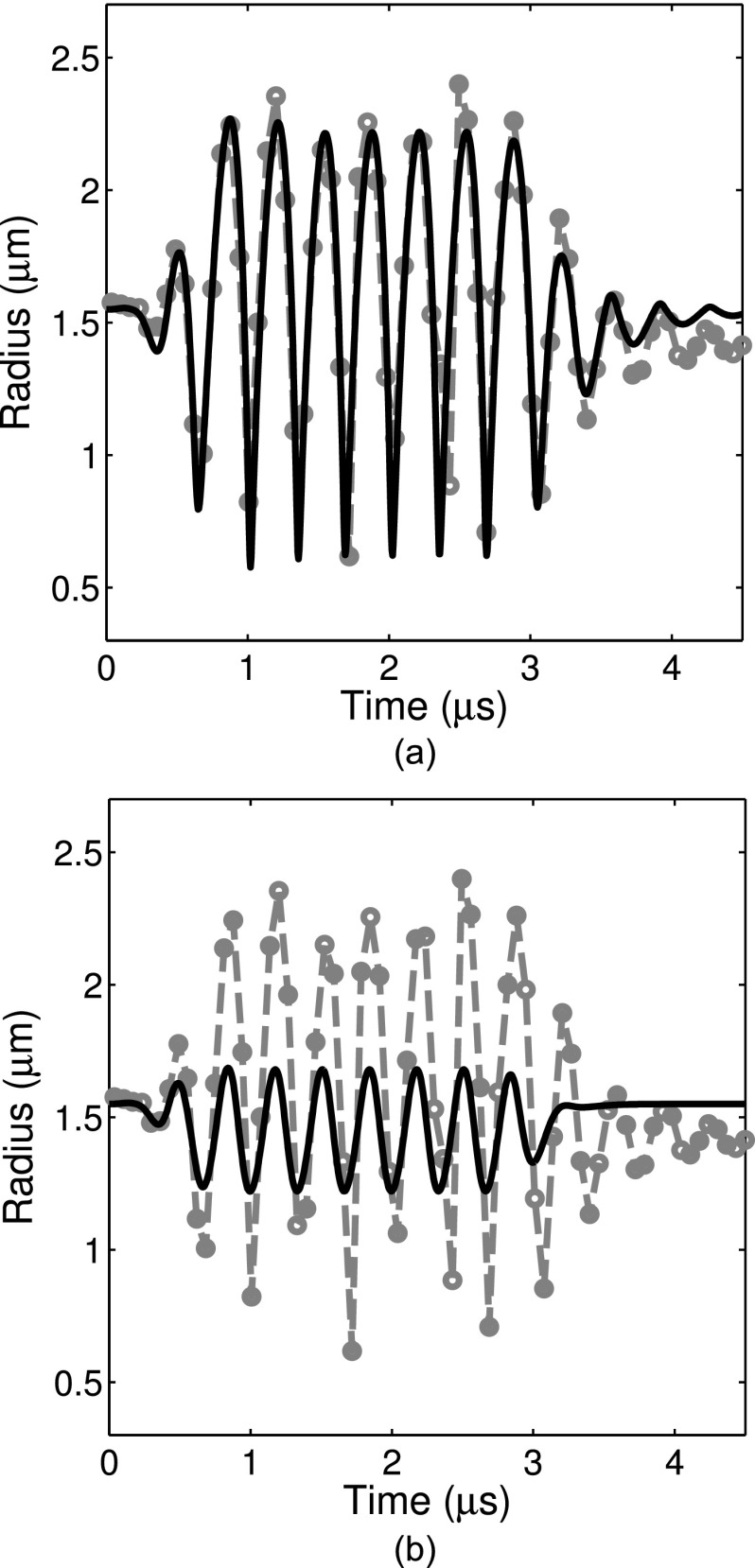
We also assessed the validity of this technique by comparing the forced response measured using a 10-cycle narrow-band burst excitation with numerical simulations. An example is shown in Fig. 10 in which simulations using two different shell viscosity values (derived from the optical method described here or the bulk acoustic method reported in Raymond et al.,²¹ respectively) are compared with experimental measurements. Excellent agreement was found between the simulated and measured radius versus time curves when the effect of the shell was taken into account using the viscosity estimate obtained in this study. For the example shown in Fig. 10(a), the shell viscosity estimate (κ_s = 3.0 × 10^–9 kg/s) was obtained during a previous impulse response exposure of the same particular liposome. Alternatively, using the population-averaged shell viscosity obtained in Raymond et al.²¹ (κ_s = 2.0 × 10^–8 kg/s) results in an under-prediction of the amplitude of the response to narrow-band forcing [Fig. 10(b)]. Use of the estimated value obtained for a specific ELIP in this study allows one to obtain much more precise agreement between the experimental theoretical data using the Marmottant model.

FIG. 10.

Experimentally measured radius versus time curve for a bubble in response to narrow-band forcing (f = 3 MHz, dashed lines). Theoretical radius versus time curves for two different values of the damping coefficient are shown. The solid line represents the simulated damping using (a) the method described in this paper (κ_s = 3.0 × 10⁻⁹ kg/s) and (b) the shell damping estimated from bulk acoustic measurements (κ_s = 2 × 10⁻⁸ kg/s). The shell elasticity parameter was taken to be χ = 1.55 N/m as reported in Ref. 20.

E. Implications for contrast-enhanced imaging

The size range of ELIP is known to be polydisperse with particle sizes ranging from tens of nanometers to several microns.^21,24,25 Differences in the characteristics of nanoscale versus microscale ELIP vesicles may play a role in the scattering properties of individual ELIP. This study found that smaller ELIP are characterized by a substantially lower shell viscosity, which may contribute to increased nonlinear scattering, especially at higher frequencies. Such nonlinear behavior of the smaller populations of ELIP could be exploited for diagnostic ultrasound applications that utilize higher frequencies, such as intravascular ultrasound. For example, the nonlinear acoustic signatures of ELIP could be utilized for improved imaging of pathology in the vasa vasorum, the proliferative small vessels that play a role in atheroma progression in the cardiovascular system.

Goertz et al.⁴⁶ demonstrated that sub-populations of the lipid-shelled clinical UCA Definity^® exhibited different frequency-dependent scattering properties as a function of size. These authors hypothesized that differences in the encapsulation microstructure for small and large bubbles may be a key factor influencing the nonlinear scattering at high frequencies. A subsequent study by Helfield et al.⁴⁷ demonstrated that smaller sub-populations of lipid-shelled microbubbles were not only resonant at higher frequencies but were also characterized by a substantially lower shell viscosity, suggesting a possible frequency dependence of the lipid shell properties. It is still not clear whether this effect is due solely to the size or if frequency-dependent considerations need to be taken into account in the dynamical models. Doinikov et al.⁴⁴ point out that existing shell models may not capture the observed radius or frequency dependence of the shell material properties and that full description of the rheological properties of the shell may require the use of more complex models in order to describe the shear-thinning behavior. A more detailed exploration of alternative rheological models could be explored in future studies.

F. Limitations

Inherent limitations of the optical system resolution result in a bias of the size range of ELIP selected for analysis in this study. The optical resolution of the ultra-high-speed imaging system was 0.4 μm (Ref. 11), and the smallest individual ELIP that was measured in this study was several times larger than the optical resolution limit. The size range of ELIP considered here focused on measurable particles larger than 0.9 μm in radius only and smaller ELIP were not considered for investigation.

The proximity of the microbubble to the OptiCell^TM membrane may affect the measured response of ELIP to acoustic excitation. Previous studies have found that the presence of a membrane near an oscillating microbubble can affect the resonance frequency and oscillation amplitude in response to acoustic forcing.^48,49 Functionalized UCAs such as ELIP are being developed for targeted imaging and drug-delivery applications, and therefore similar effects are expected to play a role in vivo. The acoustic response of adherent targeted bubbles may be influenced by the ligand distribution and bubble-wall interaction.²³ Therefore future work to investigate the damping for adherent targeted agents using this approach is recommended.

The simulations presented in Figs. 7, 8, and 10 are not unique solutions because there is more than one free parameter in the Marmottant model, namely the shell elasticity, χ, and initial surface tension, σ₀. We have chosen to assume the phospholipid shell stabilizes a gas bubble by counteracting the Laplace pressure, so that σ₀ = 0, throughout this paper. Using empirical fits, the values for the data presented in Fig. 7 are: χ = 0.1, 0.2, and 1.55 N/m for R₀ = 1.5, 2.3, and 3.0 μm, respectively. A radius-dependent shell elasticity parameter has also been observed and modeled by Chetty et al.⁹ and Doinikov et al.⁴⁴ The measured oscillation amplitudes were not always in the “elastic” regime range of the Marmottant model (R/R₀ < 1.02). However, the 3.0 μm bubble did behave near this regime (R/R₀ ∼ 1.07) and the shell elasticity determined from the optical measurements agreed with previous measurements.²¹

V. CONCLUSIONS

In this study, a model based on time domain analysis was developed to estimate the shell viscosity for individual ELIP using optically measured radius versus time curves. The decay time constant was measured from the unforced response of the ELIP following excitation by a short acoustic pulse. At low dilatation rates, the shell viscosity is in quantitative agreement with our previously determined values for ELIP. The viscoelastic shell of ELIP was found to behave similarly to other lipid-shelled agents. We demonstrated that qualitative agreement between the measured and simulated radius versus time curves under transient and steady-state acoustic forcing is highly dependent on the shell viscosity. The methods described here can provide accurate estimates of the shell viscosity and damping for individual UCA microbubbles. In contrast to acoustic measurements of a microbubble population with a relatively wide size distribution, this method provides some insight on the variation of properties among single particles within a population. This method also enables efficient measurements on a large number or individual UCA microbubbles because it is based on the response to a single acoustic impulse excitation.