Acoustical transmission-line model of the middle-ear cavities and mastoid air cells

Abstract

An acoustical transmission line model of the middle-ear cavities and mastoid air cell system (MACS) was constructed for the adult human middle ear with normal function. The air-filled cavities comprised the tympanic cavity, aditus, antrum, and MACS. A binary symmetrical airway branching model of the MACS was constructed using an optimization procedure to match the average total volume and surface area of human temporal bones. The acoustical input impedance of the MACS was calculated using a recursive procedure, and used to predict the input impedance of the middle-ear cavities at the location of the tympanic membrane. The model also calculated the ratio of the acoustical pressure in the antrum to the pressure in the middle-ear cavities at the location of the tympanic membrane. The predicted responses were sensitive to the magnitude of the viscothermal losses within the MACS. These predicted input impedance and pressure ratio functions explained the presence of multiple resonances reported in published data, which were not explained by existing MACS models.

I. INTRODUCTION

Sound energy within the human ear canal moves the tympanic membrane, and this tympanic-membrane motion generates a motion in the ossicular chain of the middle ear to generate a forward traveling wave within the cochlea. The motion of the tympanic membrane also creates an acoustic field within the middle-ear cavities and mastoid air cells; this interaction must be included in a description of sound transmission through the middle ear. The middle-ear cleft refers to the set of inter-connected cavities within the temporal bone that comprise the Eustachian tube, tympanic cavity, aditus, antrum, and mastoid air cells; all of these cavities are air-filled in a normal-functioning middle ear (Ars, 2008). The Eustachian tube between the nasopharynx and tympanic cavity in the normal middle ear is closed except when yawning or swallowing, and no acoustical disturbance is present in the Eustachian tube in its closed state. Assuming a one-dimensional theory of sound transmission, the acoustical effect of the middle-ear cavities and mastoid air cells on the tympanic membrane motion is described in terms of an acoustical impedance $Z_{\text{cav}}$, which acts at the location of the tympanic membrane (Zwislocki, 1962).

The mastoid air cells are small air pockets within a porous bone structure called the mastoid process of the temporal bone, such that the sound field with the tympanic cavity is coupled to the sound field within the mastoid air cell system (MACS). The entryway from the tympanic cavity to the mastoid air cells is via a narrow aditus, which expands into the antrum from which the mastoid air cells develop (Zollikofer and Weissmann, 2008). The goal of the present study is to model $Z_{\text{cav}}$ for a middle-ear cleft with closed Eustachian tube that includes the acoustical effects of the branching system of mastoid air cells. The model is used to predict the input impedance $Z_{\text{MACS}}$ of the MACS, and the ratio of the pressure in the antrum ($P_{\text{an}}$) to the pressure in the tympanic cavity ($P_{\text{tc}}$).

Previous modeling studies for the human middle ear have used a variety of approaches to represent the acoustical responses in the tympanic cavities and MACS. Onchi (1961) modeled the tympanic cavity by a shunt compliance, and the antrum and the MACS by a one-dimensional cascade of circuits, such that each circuit was composed of a shunt compliance and a series inertance and resistance. Effectively, $Z_{\text{cav}}$ was the parallel combination of the compliant impedance of the tympanic cavity and the input impedance of the cascade of circuits representing the aditus, antrum, and MACS. Each series resistance in the circuit represented viscous losses along the length of the airways at the airway walls, whereas the absence of a shunt conductance meant that no effects of thermal losses were represented. The antrum was represented by a single circuit. The MACS was generally represented by one or more cascaded circuits although detailed calculations were performed using only a single circuit. The airway branching of each air cell into multiple air cells would not be described in this representation, even if the function of the MACS were represented using a cascade of two or more circuits.

In the middle-ear model of Zwislocki (1962), $Z_{\text{cav}}$ was the parallel combination of three impedances: a compliance for the volume of the tympanic cavity, a resistance for the (thermal) loss in the tympanic cavity, and an impedance of the aditus, antrum, and MACS that comprised an inertance, resistance, and compliance in series. Zwislocki interpreted the inertance and latter resistance as describing the effect of the aditus with its narrow passage (leading to high flow-related or viscous-dominated losses), and the latter compliance as representing the volume compliance of the antrum and MACS. Zwislocki stated that this compliance “can be considered an adequate analog only at low frequencies.” The Onchi and Zwislocki models were similar except that Zwislocki represented damping in the tympanic cavity, while Onchi had a more complex circuit structure to model the antrum and MACS responses.

Later lumped-element circuit models of the middle ear were variations of these two models. For example, the Kringlebotn (1988) model of the middle-ear cavities and MACS was the same as Zwislocki (1962), except that Kringlebotn omitted the lossy component of the tympanic-cavity impedance. The Goode et al. (1994) model of the middle-ear cavities was the same as in Zwislocki (1962), although with different impedance parameter values.

The acoustics of the middle-ear cleft has also been represented in finite element models of middle-ear responses. The finite element model of Koike et al. (2002) included effects of the tympanic cavity, aditus, and antrum, but omitted a description of the MACS. The finite element model of Gan et al. (2006) represented the tympanic cavity using an acoustic element, but did not represent the MACS. The effects of the acoustical field within the tympanic cavities and the mastoid air cells were included in a finite element model (Lee et al., 2010), although the mastoid air cells were assumed to act only as an equivalent mastoid cavity with a volume in the range of measured MAC volumes.

The present acoustic model of the middle-ear cleft includes acoustic standing waves within the tympanic cavity, aditus, and antrum, and is terminated by the impedance of a branching airway model of the MACS. This model addresses a gap in previous studies by taking account of the branching airway structure between the air cells of the MACS. The model is assumed to be linear and does not include bone-conduction effects. Model predictions of $Z_{\text{cav}}$, $Z_{\text{MACS}}$, and $P_{\text{an}}/P_{\text{tc}}$ are compared in the results section to measured responses in adult human temporal bones (Stepp and Voss, 2005).

II. MODEL FORMULATION

A. Acoustical transmission-line theory with excess viscothermal losses

The acoustical model is based on a one-dimensional transmission or transfer-function matrix approach (Lampton, 1978). All variables (except where otherwise stated) are functions of frequency $f$ or radian frequency $\omega =2\pi f$ with time dependence ${e^j}^{\omega t}$ using $j=\sqrt{-1}$. The transfer matrix is a $2\times 2$ complex matrix that describes the frequency response of a linear system. It has a unit determinant due to reciprocity.

Some useful properties are summarized. Given a transfer matrix $\mathbf{T}=(\begin{array}{cc}A\hfill & B\hfill \\ C\hfill & D\hfill \end{array})$ with complex elements A, B, C, D that are arbitrary subject to $AD-BC=1$, its inverse transfer matrix is ${\mathbf{T}}^{-1}=(\begin{array}{cc}\hfill D\hfill & \hfill -B\hfill \\ \hfill -C\hfill & \hfill A\hfill \end{array})$. The cascade of a pair of sections of the transmission line is represented by matrix multiplication of the transfer matrices. The inverse of the product of any transfer matrices ${\mathbf{T}}_1{\mathbf{T}}_2$ is the reversed product of the inverses, i.e., ${({\mathbf{T}}_1{\mathbf{T}}_2)}^{-1}={\mathbf{T}}_2^{-1}{\mathbf{T}}_1^{-1}$.

The transfer function $\mathbf{T}$ for an acoustical transmission line of length L relates transmission between the entry pressure and volume velocity ($P_0$ and $U_0$) and the exit pressure and volume velocity ($P_1$ and $U_1$), and is a function of the propagation wave number $\Gamma$ and characteristic impedance $Z_c$ as follows:

$$\begin{array}{c}(\begin{array}{c}{P}_0\\ U_0\end{array})=\mathbf{T}(\begin{array}{c}{P}_1\\ U_1\end{array}),\\ \mathbf{T}=(\begin{array}{cc}\cosh \hspace{0.17em}\Gamma L& Z_c\hspace{0.17em}\sinh \hspace{0.17em}\Gamma L\\ Z_c^{-1}\hspace{0.17em}\sinh \hspace{0.17em}\Gamma L& \cosh \hspace{0.17em}\Gamma L\end{array}).\end{array}$$ (1)

For an acoustical wave in a cylindrical duct with cross-sectional area $S$, the complex transmission line parameters $\Gamma$ and $Z_c$ vary with $\omega$ and $S$.

The $\Gamma$ and $Z_c$ are expressed in terms of an acoustical resistance $R_a$, inertance $I_a$, compliance $C_a$ and conductance $G_a$, with each variable expressed per unit length along the transmission line, and a viscous loss parameter ${\xi }_V$ and thermal loss parameter ${\xi }_T$ that are dimensionless constants explained below:

$$\begin{array}{c}{Z}_c=\sqrt{(j\omega I_a+{\xi }_V{R}_a)/(j\omega C_a+{\xi }_T{G}_a)},\\ \Gamma =\sqrt{(j\omega I_a+{\xi }_V{R}_a)(j\omega C_a+{\xi }_T{G}_a)}.\end{array}$$ (2)

Table I lists thermodynamic constants of air including the bulk modulus $B_a$, equilibrium density $\rho$, and square root of the dimensionless Prandtl number $\nu$. The phase velocity $c$ in air is calculated using $c=\sqrt{B_a/\rho }$. These constants were used to calculate $R_a$, $I_a$, $C_a$, and $G_a$ as functions of frequency based on Keefe (1984).¹

TABLE I.

Middle-ear model parameters. A blank entry for the unit of any parameter indicates a dimensionless value. A value in column named CODE is blank when estimated from published experimental values, $M$ when estimated in the morphometric optimization to determine the MACS geometry, $H$ for a high-loss condition, and $L$ for a low-loss condition. Sources of parameters include: tympanic cleft parameters (Singh, 2007) adjusted to the geometry of connected rectangular-side cavities, and thermodynamic air constants evaluated at a body temperature of 37 °C (Benade, 1968). The nominal value of S_e, which corresponds to the area of a circle with a 8-mm diameter, is between the average ear-canal area (0.442 × 10⁻⁴ m²) reported by Stinson and Daigle (2005) and the area (0.60 × 10⁻⁴ m²) used by Kringlebotn (1988).

Section	Code	Parameter	Value	Units (SI)
Ear canal		$S_e$	0.503 × 10−4	m2
Tympanic cleft		$L_{\text{itc}}$	1.2 × 10−2	m
		$S_{\text{itc}}$	0.525 × 10−4	m2
		$L_{\text{stc}}$	0.3 × 10−2	m
		$S_{\text{stc}}$	0.525 × 10−4	m2
		$L_{\text{ad}}$	0.1 × 10−2	m
		$S_{\text{ad}}$	0.0625 × 10−4	m2
		$L_{\text{an}}$	1 × 10−2	m
		$S_{\text{an}}$	0.55 × 10−4	m2
MACS	M	$N$	11
	M	$\sigma$	2.663
	M	$d$	9.171
	M	$\alpha$	1.709
	H	${\xi }_V$	19.8
	H	${\xi }_T$	8.79
	L	${\xi }_V$	2.88
	L	${\xi }_T$	1.78
Air constants		$\rho$	1.1369	kg m−3
		$B_a$	1.4173 × 105	kg m−1 s−2
		$\mathrm{\eta \backslash neth}$	1.8928 × 10−5	kg m−1 s−1
		$\gamma$	1.4014
		$\nu$	0.8393

The airways in the MACS are exceedingly complex, and the airway walls include a mucoidal layer. It is unknown whether the viscothermal losses within the MACS differ in the in vivo condition relative to measurements in human cadaver ears. For this reason, the model was evaluated using lower and higher amounts of viscothermal loss to examine how these losses might influence the measured impedances and pressure ratio. The viscous loss parameter ${\xi }_V>1$ and thermal loss parameter ${\xi }_T>1$ were incorporated within the model of Eq. (2) to describe the relative increases in viscothermal losses in the airways comprising the MACS compared to the losses predicted based by the ideal theory (with ${\xi }_V={\xi }_T=1$). This ideal theory for the one-dimensional propagation of sound through a cylindrical tube is based on linearized acoustics for a rigid-walled tube whose inner wall is maintained at a constant temperature. Biological airways are maintained at constant temperature in vivo, but the mucoidal layers in the small airways of the MACS are non-rigid and lossy. In the absence of empirical data, the ${\xi }_V$ and ${\xi }_T$ are each assumed to have a constant value across frequency.

The high-loss values of ${\xi }_V$ and ${\xi }_T$ listed in Table I are selected to model viscothermal losses in biological airways, such as are in the MACS, which might have much larger viscothermal losses than predicted by the ideal theory (whether they do or not is unknown). Corresponding low-loss values of ${\xi }_V$ and ${\xi }_T$ are also defined. The low-loss value of the excess viscous loss coefficient ${\xi }_V-1$ in Table I is defined as one-tenth of the high-loss value of ${\xi }_V-1$. The low-loss value of the excess thermal loss coefficient ${\xi }_T-1$ in Table I is defined as one-tenth of the high-loss value of ${\xi }_T-1$. Although smaller than the high-loss values, the low-loss values of ${\xi }_V$ and ${\xi }_T$ are larger than in the ideal theory.

In an alternative transmission-line model to Eq. (1), the length $L$ is discretized into multiple M > 1 short sections, each of length $\Delta L=L/M$. The original transmission matrix in Eq. (1) is transformed into one, or a concatenation of several, transmission matrices such that each represents a lumped circuit for a short length of the transmission line. The number of sub-matrices $M\ge 1$ in each transfer matrix is chosen to be sufficiently large that the length associated with each sub-matrix is small compared to the minimum acoustic wavelength ${\lambda }_{\text{min}}$ in the measurement bandwidth, i.e., $\Delta L<{\lambda }_{\text{min}}/10$. For a bandwidth of 20 kHz, this constraint takes the form

$$\Delta L<1.73\hspace{0.17em}\text{mm}.$$ (3)

This constraint ensures that standing wave effects are negligible within each sub-matrix. The rationale for using such sub-matrices is to avoid the use of transcendental functions of frequency, such as cosh and sinh in Eq. (1), which would complicate the calculation of an overall model in the time domain. Nonetheless, such a time-domain model is outside the scope of the present study.

The transfer matrix $\mathbf{T}$ in Eq. (1) to first order in smallness in $\Delta L$ is evaluated using Eq. (2) as

$$\mathbf{T}(\omega ;S,\Delta L,{\xi }_V,{\xi }_T)=(\begin{array}{cc}1& [j\omega I_a+{\xi }_V{R}_a]\Delta L\\ [j\omega C_a+{\xi }_T{G}_a]\Delta L& 1\end{array}),$$ (4)

such that its determinant is equal to one to first order in $\Delta L$. The original transmission matrix in Eq. (1) is then expressed as a matrix product of the form

$$\mathbf{T}(\omega ;S,L,{\xi }_V,{\xi }_T,M)={[\mathbf{T}(\omega ;S,L/M,{\xi }_V,{\xi }_T)]}^M,$$ (5)

such that each term $\mathbf{T}(\omega ;S,L/M,\xi )$ on the right side of the equation is calculated using Eq. (4). Numerical analyses verified that results generated using Eq. (5) were substantially identical to results generated using Eq. (1).

B. Tympanic cavity, aditus, and antrum

In an overall model of middle-ear function, $Z_{\text{cav}}$ is the acoustical input impedance in the tympanic cavity at the location of the tympanic membrane. Adopting a long-wavelength approximation, the pressure in the tympanic cavity is assumed to be constant over the surface area of the tympanic membrane, and $Z_{\text{cav}}$ is the ratio of this pressure to the total volume velocity swept out by the tympanic membrane into the tympanic cavity.

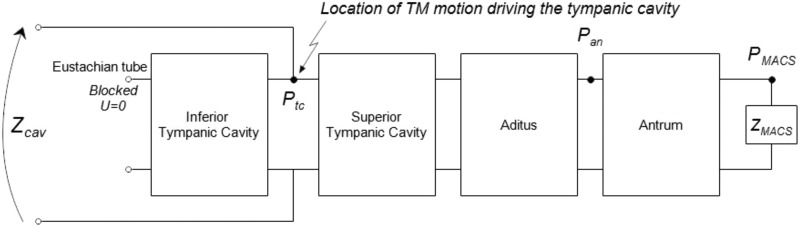
As shown in Fig. 1, $Z_{\text{cav}}$ is an input impedance of the parallel combination of an impedance of the inferior tympanic cavity terminated at its end by the closed Eustachian tube, and an impedance of an acoustical transmission line composed of the superior tympanic cavity, aditus (ad antrum), and antrum. The antrum is terminated by the input impedance $Z_{\text{MACS}}$ of the MACS. Other anatomical structures of smaller scale are present in the middle-ear cleft, but are not explicitly included in the model geometry of Fig. 1. The resulting model predictions take no account of such smaller structures, except for the MACS model described below.

FIG. 1.

Transmission line model of the tympanic cleft including the tympanic cavity inferior and superior to the center of the tympanic membrane (TM), aditus ad antrum, antrum, and the terminating input impedance of the MACS. The middle-ear cavity impedance $Z_{\text{cav}}$ is represented.

Using the expressions in Eqs. (4) and (5), the transfer matrix $\mathbf{T}$ for each acoustic chamber in the middle-ear cleft is a function of its cross-sectional area $S$ and length $L$, frequency, and additional viscothermal constants that are each assumed to equal one $({\xi }_V={\xi }_T=1)$ for all compartments in Fig. 1 except the MACS. Setting these constants equal to one corresponds to the ideal case of a uniform cylindrical duct with rigid, smooth walls. A more detailed notation $\mathbf{T}(\omega ;S,L)$ is sometimes used for each transfer matrix to make explicit the functional dependencies.

Each acoustic chamber is represented using a cylindrical geometry by a transfer matrix $\mathbf{T}$ in an one-dimensional transmission line model as follows: $S_{\text{itc}}$, $L_{\text{itc}},$ and $\mathbf{T}$ ($\omega$; $S_{\text{itc}}$, $L_{\text{itc}}$) for the inferior tympanic cavity, $S_{\text{stc}}$, $L_{\text{stc}},$ and $\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{stc}},\hspace{0.17em}{L}_{\text{stc}})$ for the superior tympanic cavity, $S_{\text{ad}}$, $L_{\text{ad}},$ and $\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{ad}},\hspace{0.17em}{L}_{\text{ad}})$ for the aditus ad antrum, and $S_{\text{an}}$, $L_{\text{an}},$ and $\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{an}},\hspace{0.17em}{L}_{\text{an}})$ for the antrum. All area and length values are listed in Table I.

Based on the circuit in Fig. 1, the input impedance $Z_{\text{in},\hspace{0.17em}\text{itc}}$ of the inferior tympanic cavity at the midpoint of the tympanic membrane is determined from the following matrix equation:

$$(\begin{array}{c}{P}_{\text{tc}}\\ Z_{\text{in},\text{itc}}^{-1}{P}_{\text{tc}}\end{array})=\mathbf{T}(\omega ;S_{\text{itc}},L_{\text{itc}})(\begin{array}{c}{P}_{\text{itc}}\\ 0\end{array}),$$ (6)

in which the volume velocity at the closed Eustachian tube is assumed to be zero and the pressure in the inferior tympanic cavity at the Eustachian tube is $P_{\text{itc}}$.²

The input impedance $Z_{\text{in},\text{stc}}$ looking into the superior tympanic cavity at the midpoint of the tympanic membrane is represented by a transfer matrix ${{}^{\text{stc}}\mathbf{T}}_{\text{an}}$ as follows:

$$(\begin{array}{c}{P}_{\text{tc}}\\ Z_{\text{in},\text{stc}}^{-1}{P}_{\text{tc}}\end{array})={\hspace{0.17em}}^{\text{stc}}{\mathbf{T}}_{\text{an}}(\begin{array}{c}{P}_{\text{MACS}}\\ Z_{\text{MACS}}^{-1}\hspace{0.17em}{P}_{\text{MACS}}\end{array}),$$ (7)

in which the pressure $P_{\text{MACS}}$ and input impedance $Z_{\text{MACS}}$ are defined relative to the entrance into the MACS (see Fig. 1). The model for $Z_{\text{MACS}}$ is described in Sec. II C 2. The transfer matrix ${{}^{\text{stc}}\mathbf{T}}_{\text{an}}$ from the superior tympanic cavity to the antrum is defined in terms of the circuit in Fig. 1 by

$$\begin{array}{c}{{}^{\text{stc}}\mathbf{T}}_{\text{an}}=\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{stc}},L_{\text{stc}})\hspace{0.17em}\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{ad}},\hspace{0.17em}{L}_{\text{ad}})\hfill \\ \times \mathbf{T}\hspace{0.17em}(\omega ;\hspace{0.17em}{S}_{\text{an}},\hspace{0.17em}{L}_{\text{an}}).\hfill \end{array}$$ (8)

To compare model predictions to measurements of the transfer function of pressure $P_{\text{an}}$ at the entryway to the antrum to $P_{\text{tc}}$, the above two equations are alternatively expressed by

$$\begin{array}{c}(\begin{array}{c}{P}_{\text{tc}}\\ Z_{\text{in},\text{stc}}^{-1}\hspace{0.17em}{P}_{\text{tc}}\end{array})=\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{stc}},\hspace{0.17em}{L}_{\text{stc}})\hspace{0.17em}\hspace{0.17em}\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{ad}},\hspace{0.17em}{L}_{\text{ad}})\hspace{0.17em}\hspace{0.17em}(\begin{array}{c}{P}_{\text{an}}\\ Z_{\text{in},\text{an}}^{-1}\hspace{0.17em}{P}_{\text{an}}\end{array}),\hfill \\ (\begin{array}{c}{P}_{\text{an}}\\ Z_{\text{in},\text{an}}^{-1}\hspace{0.17em}{P}_{\text{an}}\end{array})=\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{an}},\hspace{0.17em}{L}_{\text{an}})\hspace{0.17em}\hspace{0.17em}(\begin{array}{c}{P}_{\text{MACS}}\\ Z_{\text{MACS}}^{-1}\hspace{0.17em}{P}_{\text{MACS}}\end{array}),\hfill \end{array}$$ (9)

in which the input impedance into the antrum is $Z_{\text{in},\text{an}}$.

By applying Eq. (5), each transfer matrix on the right-hand sides of Eqs. (6) and (8) is expressed in terms of a product of one or more transfer sub-matrices, each comprised of a lumped element circuit. Based on the cavity dimensions in Table I, it suffices to choose $M=7$ sub-matrices for the inferior tympanic cavity, $M=2$ for the superior tympanic cavities, $M=1$ for the aditus ad antrum, and $M=6$ for the antrum. It follows that the transfer matrices in Eqs. (6) and (8) may be written as

$$\begin{array}{c}\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{itc}},\hspace{0.17em}{L}_{\text{itc}})={[\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{itc}},\hspace{0.17em}{L}_{\text{itc}}/7)]}^7,\hfill \\ {\hspace{0.17em}}^{\text{stc}}{\mathbf{T}}_{\text{an}}={[\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{stc}},\hspace{0.17em}{L}_{\text{stc}}/2)]}^2\times \mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{ad}},\hspace{0.17em}{L}_{\text{ad}})\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{[\mathbf{T}(\omega ;\hspace{0.17em}{S}_{\text{an}},\hspace{0.17em}{L}_{\text{an}}/6)]}^6.\hfill \end{array}$$ (10)

The input impedance of the middle-ear cleft at the midpoint of the tympanic membrane in the tympanic cavity is calculated from Eqs. (6)–(10) as (see Fig. 1)

$$Z_{\text{cav}}={[1/Z_{\text{in},\text{itc}}+1/Z_{\text{in},\text{stc}}]}^{-1}.$$ (11)

C. Mastoid air cell system

This section describes the calculation of $Z_{\text{MACS}}$ in Eqs. (7) and (9). Molvaer et al. (1978) measured the volume of the tympanic cavity and MACS to range in individual temporal bones between 2 and 22 cm³ with an average near 6.5 cm³. In terms of function, variations in the distribution of MACS volumes were associated with variations in the acoustical impedance of the MACS (Stepp and Voss, 2005).

An improved understanding of the function of the MACS may lead to a better understanding of how variability in the volume and total surface area of the MACS influence the transmission of sound energy through the normal middle ear. Such knowledge may inform future studies of development and of the effects of middle-ear disease. For example, the MACS increases in size and pneumatization during the process of maturation, and otitis media during childhood is associated with changes in the subsequent growth of the MACS (Park et al., 2000; Swarts et al., 2011). Differences in the morphology of the middle-ear cleft can increase the risk for chronic otitis media (Ars, 2008). Conversely, a history of otitis media may suppress the rate of growth and the pneumatization of the MACS (Park et al., 2000).

1. Morphometric model of the MACS

The mean volume and total surface area of the MACS were measured using x-ray computerized tomography (CT) scans of temporal bones (Park et al., 2000; Swarts et al., 2011). These data revealed a broad distribution of areas and volumes in individual temporal bones, for example, volumes ranged from 6.25 to 20.52 cm³ in Park et al. and from 0.7 to 21.4 cm³ in Swarts et al. Despite the differences in mean volume between these studies, the ratio of mean volume to mean total surface area was similar in the two studies. A binary symmetrical airway branching model of the MACS is constructed in the present study under the constraints that the total airway volume is 6.4 cm³ and total surface area is 107 cm²; these are close to the means reported by Swarts et al.

The MACS is formed by invasion of mucous epithelial tissue into cranial bone as a connected set of branching airways, which are assumed to have a self-similar geometry. That is, their linear dimensions are reduced in the model by a common factor at each level of branching. The measured fractal dimension of the airways is about 2.3 (Zollikofer and Weissmann, 2008), which suggests that branchings of the mastoid air cells are similar, but less complex, than those of the lung. No detailed anatomical measurements of the branching geometry of the MACS are available.

The antrum is the entryway into the MACS. All airways in the MACS are assumed to have a cylindrical geometry specified by airway length and radius. The antrum is termed generation 0 of the overall airway model, which branches in generation 1 of the airway tree into two airways with identical length and radius to one another. This binary, symmetrical branching is continued through the final generation $N$, to be determined, of the model. For each generation number $n$ from 1 up to $N$, the number of distinct airway branchings is 2ⁿ. The radius $r_n$ and length $l_n$ of each airway in the nth generation are equal to the radius and length, respectively, of any other airway in the same generation. The nth generation contributes a surface area $2^{n}2\pi r_n{l}_n$ to the total surface area of the branching model, and a volume $2^n\pi r_n^2{l}_n$ to the total volume of the branching model. The total surface area and volume of the MACS model are obtained by summing over all generations. The final generation N also adds to the total surface area an amount $2^N\pi r_N^2$, which equals the sum of the areas of the closed ends of the terminal airways.

The radius and length of the airways in each generation are assumed to scale as

$$\begin{array}{c}{r}_n=R_{\text{an}}{2}^{-n/\sigma },\hfill \\ L_n=d{R}_{\text{an}}{2}^{-\alpha n/\sigma },\hfill \end{array}$$ (12)

in which the fixed radius of the antrum is $R_{\text{an}}$ with cross-sectional area $S_{\text{an}}$ given in terms of its radius $r_{\text{an}}$ by

$$S_{\text{an}}=\pi r_{\text{an}}^2.$$ (13)

The numerical coefficients $\sigma$, $\alpha$, and $d$ were determined using a constrained nonlinear optimization.³ The constraints were that each coefficient was positive, and that $\sigma$ was in an interval whose upper value was slightly less than three. This is based on research on the anatomy of the vascular system (Murray, 1926) and lung (Mandelbrot, 1983), which show that systems of branching tubes in biological organs have $\sigma <3$.

The airway radii in the model decreased with increasing generation number. The number of generations $N$ was selected so that the airway radii in generation $N$ were not less than 0.19 mm. This dimension was on the order of the CT scan resolution as well as the size of pulmonary alveoli in the lung in which diffusion-limited gas exchange takes place between air and blood. Inasmuch as gas exchange between air and blood is a critically important function in both the MACS and the lung, this choice of minimum dimension appears reasonable in the absence of detailed empirical information.

The optimized set of scaling parameters $N$, $\sigma$, $d,$ and $\alpha$ are listed in Table I. The final N = 11 corresponds to 2048 airways in the final generation. This binary, symmetrical tree structure of branching airways is shown in Fig. 2. The antrum is the entryway into the MACS and the first branch occurs in generation 1. The airway radius and length in each generation are plotted in Fig. 3, which results in a total MACS volume of 6.41 cm³ and a total surface area of 107.0 cm². These are consistent with the physiological measurements described earlier. The sum of the lengths across all generations is 6.80 cm. The binary, symmetrical branching of the airways and the choice of numerical coefficients in Eq. (12) provide a morphometric model of the structural anatomy of the MACS.

FIG. 2.

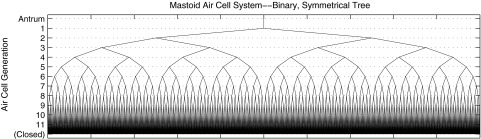
Binary, symmetrical airway branching model of the MACS with the antrum as the entryway. The airways in the lower order generations are all visually resolved, but airways in generations 10 and 11 are not resolved. The variation in the line thickness and length of the antrum and of each airway are not shown in this figure, which is intended to represent the connectivity of the branching airways.

FIG. 3.

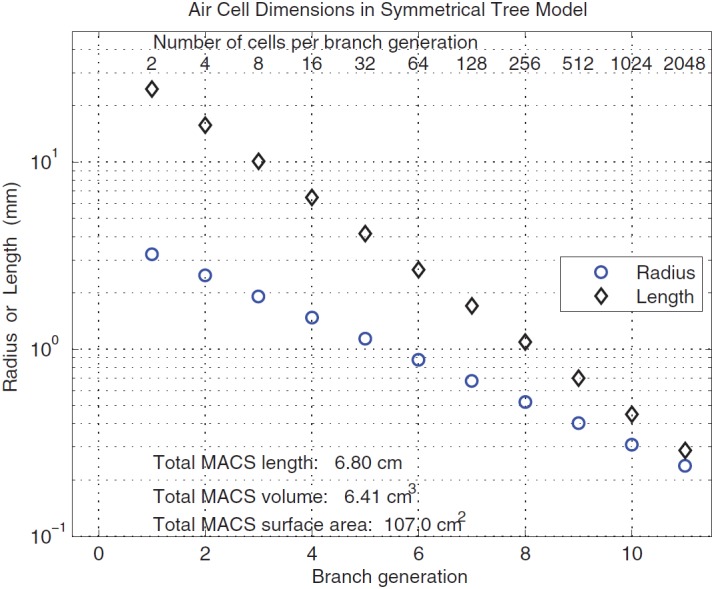
(Color online) Mastoid air cell dimensions (length and radius) in the binary symmetrical tree model with each air cell represented as a cylinder as a function of the branch generation of the tree model.

2. Acoustical model of the MACS

A binary symmetrical airway branching model of the MACS was also selected because sound transmission in such morphometric models is well understood in the case of the lung (Van Den Berg, 1960; Ishizaka et al., 1976). The input acoustic impedance $Z_{\text{MACS}}$ was calculated with recursion using an approach similar to those studies, except that an additional viscous loss coefficient ${\xi }_V$ and thermal loss coefficient ${\xi }_T$ were introduced. These coefficients were used to model larger viscothermal losses in the MACS compared to losses described by the idealized viscothermal boundary-layer theory. Each coefficient ${\xi }_V$ and ${\xi }_T$ was assumed to be constant in value across all generations of the airway branching model (i.e., each was assumed independent of $n$).

One other parameter needed to model the MACS is the acoustical conductance $G_{\text{end}}$ for the closed end of each airway in the terminal generation N of the binary branching airway tree. Each closed end has an area $S_N$ for $n=N$. The corresponding conductance $G_{\text{end}}$ associated with the thermal boundary layer is

$$G_{\text{end}}=\frac{(\gamma -1)}{B_a}\sqrt{\frac{{\kappa }_a\omega }{2\rho C_p}}{S}_N.$$ (14)

This equation includes the ratio of the thermal conductivity of air ${\kappa }_a$ and the specific heat of air at constant pressure $C_p$. The ratio $\kappa /C_p$ is calculated from parameters in Table I using the fact that ${\nu }^2=\eta C_p/{\kappa }_a$ for shear viscosity $\eta$. The wall conductance per unit area $G_{\text{end}}/S_N$ is assumed equal to the conductance per unit area for the thermal boundary layer of a planar surface. It is also equal to the conductance per unit area of a cylindrical tube $G_a$ in the low-frequency limit of the expressions in Keefe (1984), in which the area is the surface area $2\pi rl$ of a short section of tube of radius $r$ and length $l$.

The transmission model is initialized by relating the pressure $P_N$ and volume velocity $U_N$ at the entryway into the most peripheral airway generation $N$ to the pressure $P_{\text{end}}$ and volume velocity $U_{\text{end}}={\xi }_T{G}_{\text{end}}{P}_{\text{end}}$ at the opposite closed end of the airway. These pressures and volume velocities are related by a transfer matrix of a form given by Eq. (4), with $G_{\text{end}}$ given by Eq. (14). The matrix equation is expressed in terms of the airway length $L_N$, the resistance, inertance, compliance, and conductance per unit length in the Nth generation ($R_{a,N}$, $I_{a,N}$, $C_{a,N}$, and $G_{a,N}$, respectively), and ${\xi }_V$ and ${\xi }_T$ by

$$(\begin{array}{c}{P}_N\\ U_N\end{array})=(\begin{array}{cc}1& [j\omega I_{a,N}+{\xi }_V\hspace{0.17em}{R}_{a,N}]L_N\\ [j\omega C_{a,N}+{\xi }_T\hspace{0.17em}{G}_{a,N}]L_N& 1\end{array})(\begin{array}{c}{P}_{\text{end}}\\ {\xi }_T{G}_{\text{end}}\hspace{0.17em}{P}_{\text{end}}\end{array}).$$ (15)

These transmission line coefficients are evaluated for an airway area $S_N=\pi r_N^2$, with $r_N$ and $L_N$ given in Eq. (12). Using Eq. (15), the input admittance $Y_N$ at the entryway of any airway in generation $N$ is

$$Y_N=U_N/P_N=\frac{[j\omega C_{a,N}+{\xi }_T{G}_{a,N}]L_N+{\xi }_T\hspace{0.17em}{G}_{\text{end}}}{1+{\xi }_T{G}_{\text{end}}[j\omega I_{a,N}+{\xi }_V{R}_{a,N}]L_N}.$$ (16)

A transfer matrix of similar form calculates the pressure ${P_N}_{-1}$ and volume velocity ${U_N}_{-1}$ at the entryway into the next-to-last generation $N-1$ of airways in terms of the pressure $P_N$ and volume velocity $2U_N$ at the opposite end, where the airway branches into two similar airways, each with input pressure $P_N$ and volume velocity $U_N$. These two airways act in parallel so that the pressure is uniform and the total volume velocity is $2U_N$, or $2Y_N{P}_N$ using Eq. (16) for $Y_N$.

The recursive step is that the transfer matrix to calculate the pressure $P_n$ and volume velocity $U_n$ at the entryway of an airway in generation $n$ of the MACS has the same form for all $n$ from $n=N-1$ down to $n=1$. The general matrix equation relating these variables over this range of $n$ is

$$\begin{array}{c}(\begin{array}{c}{P}_n\hfill \\ U_n\hfill \end{array})=\mathbf{T}(\omega ;\hspace{0.17em}{S}_n,\Delta L_n)\hspace{0.17em}\hspace{0.17em}(\begin{array}{c}{P}_{n+1}\\ 2Y_{n+1}{P}_{n+1}\end{array}),\hfill \\ \mathbf{T}(\omega ;\hspace{0.17em}{S}_n,\Delta L_n)={(\begin{array}{cc}1& [j\omega I_{a,n}+{\xi }_V{R}_{a,n}]\Delta L_n\\ [j\omega C_{a,n}+{\xi }_T{G}_{a,n}]\Delta L_n& 1\end{array})}^{M_n},\hfill \\ \Delta L_n=L_n/M_n.\hfill \end{array}$$ (17)

The number of sections $M_n$ is selected as the smallest integer such that $\Delta L_n$ satisfies the inequality in Eq. (3). The resulting $M_n$ are 15, 10, 6, 4, 3, 2 for generations $n$ = 1 to 6, respectively, and $M_n=1$ for $n>6$. Representing the transfer matrix in Eq. (17) by its four ABCD elements as

$$\mathbf{T}(\omega ;\hspace{0.17em}{S}_n,\hspace{0.17em}{L}_n/M_n)=\left(\begin{array}{cc}{A}_n\hfill & B_n\hfill \\ C_n\hfill & D_n\hfill \end{array}\right)\hspace{0.17em},$$ (18)

the input admittance $Y_n$ at the entryway of an airway at generation $n$ is calculated from the top relation of Eq. (17) and from Eq. (18) as

$$Y_n=U_n/P_n=\frac{C_n+2Y_{n+1}\hspace{0.17em}{D}_n}{A_n+2Y_{n+1}\hspace{0.17em}{B}_n}.$$ (19)

Equations (17)–(19) form a recursive system initialized by Eqs. (15) and (16) to calculate $Y_1$. The resulting input impedance of the MACS is

$$Z_{\text{MACS}}={(2Y_1)}^{-1},$$ (20)

with the factor of 2 due to the fact that the total admittance of the MACS at the end of the antrum is the sum of the admittances of the pair of airways at generation 1.

III. RESULTS

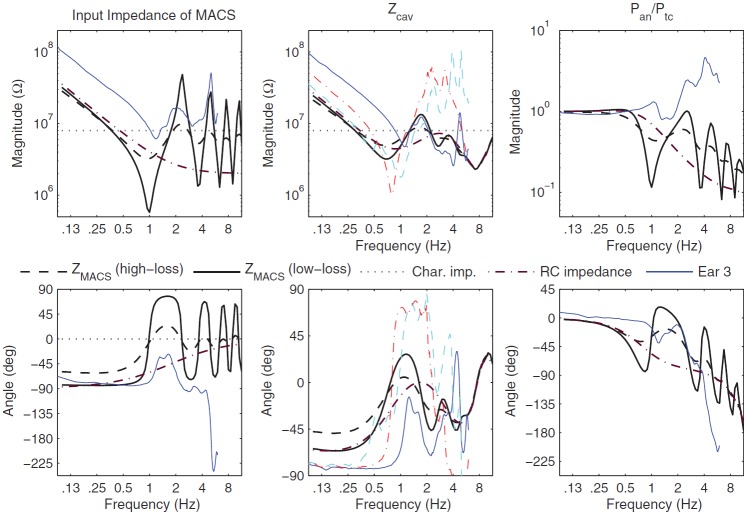
The resulting $Z_{\text{MACS}}$ (see left panels in Fig. 4) was compliance- and resistance-controlled below 0.7 kHz, and converged gradually at higher frequencies toward a value similar to the characteristic impedance $Z_{c,e}=\rho c/S_e$ of the ear canal, which is expressed in terms of the cross-sectional area $S_e$ of the ear canal. The reason for this similarity is that the cross-sectional areas of the antrum and ear canal are similar: Table I lists the antrum area as 0.55 × 10⁻⁴ m² and lists values of the average ear-canal area in the range from 0.44 × 10⁻⁴ to 0.60 × 10⁻⁴ m². The areas of the inferior and superior tympanic cavities ($S_{\text{itc}}$ and $S_{\text{stc}}$, respectively) are similar to the areas of the antrum and ear canal, so that their characteristic impedances are also in a similar range to $Z_{c,e}$. The exception is the more narrow aditus with its much smaller $S_{\text{ad}}$.

FIG. 4.

(Color online) Model predictions are shown with magnitude in the top row of panels and phase in the bottom row. A thick dashed line is used for plotting the high-loss model condition in the MACS model, a thick solid line for the low-loss model condition, and a thick dashed-dotted line when the RC impedance is used for $Z_{\text{MACS}}$ (see text). Left panels: $Z_{\text{MACS}}$ for the high- and low-loss model conditions, the measured Ear 3 of Stepp and Voss (2005) (thin solid line), and the RC impedance. Middle panels: $Z_{\text{cav}}$ for the high- and low-loss model conditions, the model condition with the RC impedance used for $Z_{\text{MACS}}$, and for the measurement in Ear 3 of Stepp and Voss (thin solid line). $Z_{\text{cav}}$ is also plotted for measurements in Ear 1 (thin dashed line) and Ear 2 (think dashed-dotted line) of Stepp and Voss (line styles for Ears 1 and 2 absent in legend). Right panels: Transfer function of antrum to tympanic-cavity pressure $P_{\text{an}}/P_{\text{tc}}$ for the high- and low-loss model conditions, the model condition with the RC impedance used for $Z_{\text{MACS}}$, and for the measurement in Ear 3 (thin solid line). For left and middle plots in top row, the constant dotted lines show the characteristic impedance of the adult ear canal.

The predicted $Z_{\text{MACS}}$ for the low-loss condition (see left panels in Fig. 4) was similar to the high-loss condition below 0.6 kHz, and had much larger resonant peaks and dips above 1 kHz than for the high-loss condition. The increased viscothermal loss coefficients in the high-loss condition substantially attenuated the magnitudes of the modal resonances and anti-resonances compared to the low-loss condition, and slightly reduced their frequencies. These changes were in the expected directions, and showed that the acoustical properties of the small airways changed the overall impedance $Z_{\text{MACS}}$, and thereby the impedance $Z_{\text{cav}}$ that influences the motion of the tympanic membrane.

Some middle-ear models have predicted the response of the MACS using a resistance and compliance in series. One such “RC impedance” prediction is shown in the left panels of Fig. 4 for a resistance of 2 $\mathrm{M}\mathrm{\Omega }$ or 2.0 × 10⁶ kg m⁻⁴ s⁻¹, and a compliance corresponding to an equivalent volume of 6.4 cm³. This equivalent volume was an approximate match to the total volume of the airways in the MACS model, and the RC impedance converged toward this resistance value at high frequencies.

A measured $Z_{\text{MACS}}$ is also shown for Ear 3 reported by Stepp and Voss (2005). The volume of the MACS in Ear 3 was 1.5 cm³; Stepp and Voss stated that Ear 3 may have had this unusually low volume due to early episodes of otitis media. As a result, the measured $\left|Z_{\text{MACS}}\right|$ was larger in the measured curve than the predicted curves below 1 kHz. The measured magnitude up to a maximum frequency of 6 kHz showed multiple minima and maxima that were absent in the RC impedance model. The predicted $Z_{\text{MACS}}$ for the low-loss condition showed minima and maxima that approximately coincided in frequency, but the minimum magnitudes in Ear 3 near 1 and 3 kHz were larger than predicted. In contrast, the predicted $Z_{\text{MACS}}$ for the high-loss condition showed minima and maxima with smaller changes in magnitude from the midline. While both were negative just below 1 kHz, the predicted phase exceeded the measured phase below 1 kHz, which was likely due to the much smaller MACS volume in Ear 3. The phase of Ear 3 was much more negative above 3 kHz than any model condition. The frequencies of the fine structure were similar in Ear 3 and the predicted $Z_{\text{MACS}}$ for the low-loss condition.

The predicted tympanic cavity impedance $Z_{\text{cav}}$ was calculated using Eq. (11), in which $Z_{\text{in},\text{stc}}$ was calculated in Eq. (7) in terms of $Z_{\text{MACS}}$. The middle panels in Fig. 4 show the predicted $Z_{\text{cav}}$ for the high- and low-loss conditions, with only modest differences in magnitude and phase that decreased with increasing frequency and converged above 3 kHz. Also shown in the middle panels is the predicted $Z_{\text{cav}}$ for the case in which the MACS impedance was replaced by the RC impedance (plotted in the left panels). The RC impedance eliminated the maxima and minima from $Z_{\text{MACS}}$, which had the effect of substantially attenuating the maxima and minima from the predicted $Z_{\text{cav}}$.

As shown in Fig. 4, Stepp and Voss (2005) measured $Z_{\text{cav}}$ in three temporal bones with an intact MACS over frequencies from 0.1 to 6 kHz. The volume of the MACS in their Ears 1 and 2 were 4.0 and 5.9 cm³, i.e., much larger than in Ear 3. Therefore, the model results for the low-loss condition were mainly compared with measurements in Ears 1 and 2. In reasonable agreement with the model, the measured $Z_{\text{cav}}$ was compliance dominated at low frequencies with a minimum magnitude ranging from 1 to 2 $\mathrm{M}\mathrm{\Omega }$ at a frequency of 0.7 to 1.1 kHz. Both ears had maxima close to 2 kHz and again at 3 to 4 kHz, similar to the frequencies of maxima in the model, but with larger magnitudes in the data than the model. The phase responses had similar signs in the model and measurements, but the measured phase extremals above 0.7 kHz were closer to +90 and −90 deg in the data compared to within +35 and −45 deg in the model. The measured phase in Ears 1 and 2 had large differences at frequencies above 3 kHz. The model successfully predicted the presence of multiple modes in $Z_{\text{cav}}$ with better agreement with measurements up to about 3 kHz, and larger discrepancies at higher frequencies up to 6 kHz.

The transfer function $P_{\text{an}}/P_{\text{tc}}$ measured in Ear 3 (Stepp and Voss, 2005) was close to unity at low frequencies, with generally increasing magnitude characterized by local maxima near 1.0, 2.6, and 4.5 kHz (see top right panel of Fig. 4). The predicted transfer-function magnitude using Eq. (9) for the low-loss condition had maxima near 0.4, 2.5, 4.8, and 7.1 kHz with a mid-line magnitude that decreased from unity at low frequencies to about 0.3 near 6 kHz. The peak spacings were relatively similar above 1 kHz in the data and model, but the model magnitudes were lower above 2 kHz.

In the lower right panel of Fig. 4, the measured transfer-function phase was close to 0 deg below 2 kHz, and decreased to −90 deg at 3.9 kHz (Stepp and Voss, 2005). The predicted phase for the low-loss condition slowly decreased from 0 deg at 0.125 kHz to a minimum of −85 deg at 0.8 kHz and a maximum of 17 deg at higher frequencies. Other peaks and dips appeared at higher frequencies, while the midline of the predicted phase decreased with increasing frequency to −99 deg at 6 kHz. Both measured and predicted phase responses showed a negative slope between about 2 and 6 kHz, although the measured slope was steeper above 4 kHz. The model responses for the high-loss condition followed the mid-line of the responses for the low-loss condition.

Also shown in the right panels is the predicted $P_{\text{an}}/P_{\text{tc}}$ for the case in which the MACS impedance was replaced by the RC impedance. The presence of the RC impedance for the MACS substantially attenuated the maxima and minima from the predicted transfer function.

It was difficult to draw firm conclusions for comparisons of $P_{\text{an}}/P_{\text{tc}}$, because Ear 3 had the smallest MACS volume of 1.5 cm³ compared to 6.4 cm³ in the model. Such a large volume difference would be expected to produce large shifts in $P_{\text{an}}/P_{\text{tc}}$. Nevertheless, the model predicted a multi-modal structure to $P_{\text{an}}/P_{\text{tc}}$ that was observed in measurements. As was the case for $Z_{\text{MACS}}$, the predicted $Z_{\text{cav}}$ and $P_{\text{an}}/P_{\text{tc}}$ in the low-loss condition agreed more closely with measured data than for the corresponding high-loss condition.

Stepp and Voss (2005) analyzed the measurements of $Z_{\text{cav}}$ in each ear and $P_{\text{an}}/P_{\text{tc}}$ in Ear 3 using a simple circuit model of the tympanic cleft, from which $Z_{\text{MACS}}$ was estimated. The authors cautioned that the estimated $Z_{\text{MACS}}$ included errors above 4 kHz. The measured and predicted results for $Z_{\text{MACS}}$ in the left panel of Fig. 4 were more similar for frequencies from 0.1 to 4 kHz than for higher frequencies.

IV. DISCUSSION

Acoustical modal resonances within the tympanic cleft were predicted in the one-dimensional transmission-line model of the tympanic cavity, aditus, antrum, and MACS (see Fig. 1), but additional families of three-dimensional standing-wave modal resonances may exist within the tympanic cavity. These were not considered in the present model.

A compliance or lossy compliance model of the MACS, as used in previous middle-ear models, lacked the multiple modal resonances observed in measured data and in the present model. The predicted $Z_{\text{cav}}$ for the low-loss condition in temporal bones had resonant peaks that were more similar to measured data (Stepp and Voss, 2005) than for the high-loss condition (Fig. 4). More research is needed to understand the role how variations in middle-ear cleft acoustics influence transmission through the middle ear and the acoustic transfer functions that are measured clinically in the ear canal.

It would not be possible to tune the MACS resonances in an overall acoustical model of middle-ear transmission, inasmuch as the underlying MACS geometry in the structural model was fixed, i.e., only ${\xi }_V$ and ${\xi }_T$ were varied in this study. An intriguing property of the x-ray CT scan analyses of the MACS (Park et al., 2000; Swarts et al., 2011) is that while there was a wide variation in the total area and volume of the MACS, the ratio of total volume to total area remained constant with a value of about 17 cm⁻¹ across all analyses (Swarts et al., 2011). The ratio in the present model was 16.7 cm⁻¹, in agreement with the ratio of mean volume to mean area. Despite repeated efforts in the present study, it was not possible to construct a family of binary symmetrical airway branching models that maintained this ratio over the range of total volumes observed in x-ray CT data. This suggests that some other type of morphometric model that left this ratio invariant as the volume of the MACS was varied might be identified in future research. Such an improved model might be applied to better understand the developmental growth of the MACS within an individual, and to relate the anatomical complexity of the MACS with its functional properties.

The results of this study identify potential areas of future research relevant to the acoustic function of the MACS in normal and diseased middle ears across the age range from infants to adults. A better understanding of the morphology and acoustics of the MACS may inform the study of ventilation and gas exchange in the MACS.

Air flows enter or leave the middle-ear cleft and influence overall pressure regulation according to three main pathways (Magnuson, 2003): air enters (or exits) the middle-ear cavity when the Eustachian tube opens intermittently, gases are continuously exchanged bi-directionally between the middle-ear cleft and the blood capillaries within the mucosa through diffusion, and there is a bi-directional, continuous exchange of fluid through the mucosa. The large surface area of the mucosa in the MACS compared to the mucoidal lining on the walls of the tympanic cavity and interior side of the tympanic membrane means that the MACS controls the latter two pathways.

Diffusion between air and blood is driven by the difference in partial pressures of each gas constituent (oxygen, carbon dioxide, nitrogen, argon, and water vapor) in air and blood (Ars et al., 2012). Capillaries with arterial blood remove oxygen from the air in the cleft, and capillaries with venous blood increase the carbon dioxide and water vapor in the air in the cleft. Due to diffusion times on the order of a couple minutes for oxygen, carbon dioxide, and water vapor, the partial pressure of each of these gases in the air of the middle-ear cleft is similar to its partial pressure in blood. Thus, air in the middle-ear cleft contains less oxygen, and more carbon dioxide and water vapor, than ambient air. Nitrogen diffuses much more slowly than these other gases, but it also diffuses from the air in the middle-ear cleft to the blood. These processes lead to an increased partial pressure of nitrogen in the cleft. When the Eustachian tube opens, the gas composition within the middle-ear cleft changes back in the direction toward ambient air.

The acoustical function of the MACS occurs over much shorter times than the characteristic diffusion times of the gases, so that the effect of sound may be limited to possibly enhancing the diffusive mixing of the gas constituents, about which more research is needed.

The overall effect of ventilation in a normal middle ear is a slightly decreased pressure of air within the middle-ear cleft compared to ambient air during the day when oxygen is used at a higher rate, and a slightly increased pressure during sleep when oxygen is used at a lower rate and the excess carbon dioxide in the blood increases its partial pressure in the air within the middle-ear cleft via diffusion (Magnuson, 2003). In the presence of Eustachian tube dysfunction, the tube does not open so that the air pressure is reduced within the middle-ear cleft. Such a pressure reduction would create a quasi-static pressure difference across the tympanic membrane which would stiffen the membrane and reduce sound transmission across it. Even in an ear with normal function, slight fluctuations during the 24-h day in the average air pressure in the middle-ear cleft, which occur due to the interplay of gas diffusion and transient opening of the Eustachian tube, contribute to intra-ear variability in acoustical ear-canal tests of middle-ear function.

The difference in partial pressures of the constituent gases in ambient air and the air within the middle-ear cleft would slightly perturb the values of the thermodynamic constants of dry ambient air listed in Table I. These perturbations were not considered in the numerical evaluations of the acoustical model in the present work.

The effect of the total volume of the MACS has been considered in models of pressure regulation and transmucosal gas exchange (Doyle, 2007), although potential effects related to MACS morphology have not been considered. It may be possible to construct a more detailed model of the MACS using a morphometric model of the airways comprising the MACS, including the effect of placing ventilation tubes (Fink et al., 2003) in the tympanic membrane in cases of otitis media. The surface area of the smaller airways in more remote generations of a branching airway model may equilibrate more rapidly the partial pressures of the constituent gases in the enclosed air and blood than in more peripheral generations. Large total volumes of the MACS would tend to be associated with more generations of airway branching, although the scaling of airway lengths and diameters across the generations may also differ with different total MACS volumes. Increased knowledge of this morphology in the form of a quantitative model may be useful in future analyses of more detailed MACS models of pressure regulation and transmucosal gas exchange.

In normal development, “the mastoid and antrum gas cells develop as an outgrowth of the antrum,” which develops beginning at age 22 weeks of fetal life; the “age at which gas cells develop is subject to huge individual variation” (Ars, 2008). Consistent with these general findings, the present model assumed that the MACS was connected with the other middle-ear air spaces via the aditus ad antrum. While this is the simplest case to model, it should be noted that Stepp and Voss (2005) studied one set of serial temporal bone sections with a “connection between the superior–anterior portion of the tympanic cavity and several air cells.” The case of a middle-ear cleft with multiple boundary surfaces between the tympanic cavity and the MACS requires further study.

V. CONCLUDING REMARKS

A morphometric model of the MACS was constructed using a binary symmetrical airway branching model with total volume and area equal to mean values from x-ray CT scans (Park et al., 2000; Swarts et al., 2011). Using this morphometric model, an acoustical model of the air spaces comprising the tympanic cleft with a closed Eustachian tube was constructed and analyzed. The approach used an acoustical transmission-line for the tympanic cavity, aditus, antrum, and terminated by the MACS. The input impedance of the MACS was calculated using a recursive transmission line model in two conditions with relatively smaller and larger viscothermal losses within the mastoid air cells.

The model was used to predict the impedance of the tympanic cleft at the tympanic membrane, the input impedance of the MACS, and the pressure transfer function between the antrum and tympanic cavity at the tympanic membrane. The predictions were compared with measurements reported by Stepp and Voss (2005). Both model predictions and measured data showed the presence of multiple modal resonances in the input impedances of the MACS and of the middle-ear cavities at the location of the tympanic membrane. The model outputs are well-suited for use within a more general model of sound transmission through the middle ear.