Abstract
The simultaneous–sequential method was used to test the processing capacity of establishing mean orientation summaries. Four clusters of oriented Gabor patches were presented in the peripheral visual field. One of the clusters had a mean orientation that was tilted either left or right while the mean orientations of the other three clusters were roughly vertical. All four clusters were presented at the same time in the simultaneous condition whereas the clusters appeared in temporal subsets of two in the sequential condition. Performance was lower when the means of all four clusters had to be processed concurrently than when only two had to be processed in the same amount of time. The advantage for establishing fewer summaries at a given time indicates that the processing of mean orientation engages limited-capacity processes (Experiment 1). This limitation cannot be attributed to crowding, low target-distractor discriminability, or a limited-capacity comparison process (Experiments 2 and 3). In contrast to the limitations of establishing multiple summary representations, establishing a single summary representation unfolds without interference (Experiment 4). When interpreted in the context of recent work on the capacity of summary statistics, these findings encourage reevaluation of the view that early visual perception consists of summary statistic representations that unfold independently across multiple areas of the visual field.
Keywords: summary statistics, ensemble representations, mean orientation, processing capacity limitations, simultaneous–sequential method
The visual system seems to deal with the vast amount of information that it receives from the natural world by summarizing visual properties across collections of similar items, to yield what are referred to as summary statistical representations or SSRs (Ariely, 2001; Balas, Nakano, & Rosenholtz, 2010; Chong & Treisman, 2003; 2005a; 2005b; Im & Chong, 2009). For instance, a beach scene with people, waves, and pebbles may be represented in terms of the mean facial expression, the mean size, and the mean color of items within groups of items. Under this view, when an SSR is established, information about the groups’ constituents become inaccessible (e.g., Corbett & Oriet, 2011; Haberman & Whitney, 2007; Parkes et al., 2001). In this way, the visual system has been likened to a statistician (e.g., Peterson & Beach, 1967; Pollard, 1984; Rosenholtz, 2011) in part because this summary process is similar to how the raw values in a dataset are lost when a descriptive statistic, such as the mean, is calculated.
The proposed function of SSRs is to reduce the computational demands that are placed on the system by a world that is rich with visual information. Representing the features that are present in a group of similar items by an abstracted summary value can be more efficient than representing each feature value individually, especially when those items appear in the periphery (e.g., Alvarez, 2011; Alvarez & Oliva, 2009; Chong & Treisman, 2005a; 2005b). Under this view, the rich perception of the world that we enjoy is thought to derive from the integration of summary representations that are low in detail and are produced by sampling redundant characteristics, and representations high in detail produced by sampling individual items at fixation (e.g., Chong & Treisman, 2003; Haberman & Whitney, 2009). The idea is that the so-called ‘Grand Illusion’, (e.g., Noë, 2002; Noë, Pessoa, & Thompson, 2000), whereby we feel as though we see more detail than we do, may simply be our experience of a coarse representation of feature averages that are established early within the stream of perceptual processing (e.g., Whitney, Haberman, & Sweeny, 2014).
More specifically, SSRs have been proposed as the underlying cause of a wide range of phenomena. A few examples include peripheral recognition, texture segmentation, perceptual stability, crowding, spatial vision, visual illusions, visual search, change blindness, visual working memory, and gist perception (e.g., Ariely, 2001; Ackerman & Landy, 2014; Balas, Nakano, & Rosenholtz, s2010; Brady & Alvarez, 2011; Cavanagh, 2001; Chong et al., 2008; Corbett & Melcher, 2013; Gillen & Heath, 2014; Rosenholtz, 2011; Whitney, 2009; Whitney, Haberman, & Sweeny, 2014). In the case of visual search, it has been shown that under some conditions, a model that predicts performance based on summary statistical representations of groups of items (e.g., Rosenholtz, 2011) can be more successful than models that predict performance based on individual items (e.g., Treisman & Gelade, 1980, Treisman & Souther, 1985; Wolfe, 1994; but see Wolfe et al., 2011 for a discussion on the role of both summary statistics and individual object processing in visual search under a variety of conditions).
If SSRs play this fundamental role in vision, then it follows that there should be substantial generality in the types of features and object properties that can be summarized. Consistent with this, accurate summaries are found to occur over space and time for both low-level stimuli and more complex objects, including mean brightness (Bauer, 2009), motion speed and direction (e.g., Watamaniuk, Sekular, & Williams, 1989), spatial position (e.g., Alvarez & Oliva, 2008), orientation (e.g., Dakin, 2001), height (Fouriezos, Rubenfeld, & Capstick, 2008), size over space (Ariely, 2001), size over time (Albrecht & Scholl, 2010), length (Weiss & Anderson, 1969), color (Demeyere et al., 2008), inclination (Miller & Sheldon, 1969), biological motion (Sweeny, Haroz, & Whitney, 2013), facial identity (e.g., de Fockert & Wolfenstein, 2009), facial attractiveness (Walker & Vul, 2014), and facial emotion and gender (e.g., Haberman & Whitney, 2007). Thus, it is clear that SSRs can be formed for a wide range of visual attributes, consistent with the suggestion that establishing SSRs is a fundamental early step in visual processing.
To summarize, SSRs are thought to play a central role in abstracting a large amount of visual information in a way that leads to rapid visual scene perception and the subjective impression that we see more than we do (e.g., Whitney, 2009; Rosenholtz, 2011). If true, then understanding SSRs is of considerable importance for theories of visual perception because these representations play a key role in both early vision and visual awareness (e.g., Corbett & Song, 2014; Haberman & Whitney, 2011; Whitney, Haberman, & Sweeny, 2014).
Parallel processing of SSRs
The proposed function of SSRs originates in part from evidence suggesting that they are established fast, independently, and in parallel across the visual field. This evidence derived mainly from tasks that measured how averaging performance changed as a function of the number of items in the set across which the average was computed (set size). Specifically, to the extent that performance is equal when sets of, for example, 4 vs 16 items are summarized, it has been concluded that those averages were established through spatially parallel, unlimited-capacity processes (Ariely, 2001; see also Chong & Treisman, 2003; 2005a). For example, Ariely (2001) presented visual displays that included a set of either 4, 8, 12, or 16 different-sized discs, and observers were asked to compare the perceived mean size of the set to the diameter of a subsequently presented probe disc. Observers could report whether the size of the probe was smaller or larger than the mean size of the group equally well for all set sizes. Similarly, Chong and Treisman (2003) found that judgments of mean size for sets of 12 heterogeneously sized circles were as accurate as those for single circles. The large number of studies showing equal accuracy between small and large set sizes has led to an endorsement of the view that statistical summaries are established by mechanisms that “…precede the limited capacity bottleneck…” (Chong & Treisman, 2005a, p. 899; see also Alvarez, 2011; Alvarez & Oliva, 2008; Ariely, 2001; Brady & Alvarez, 2011; Chong & Treisman, 2003, 2005b; Dakin & Watt, 1997; Demeyere et al., 2008; Oriet & Brand, 2013; Rosenholtz, 2011; Robitaille & Harris, 2011). An implication of this view is that summaries should depend almost exclusively on unlimited-capacity processes. That is, they should unfold independently of the number of stimuli to be processed.
Although many results from set-size experiments are consistent with an unlimited-capacity model of SSRs, the evidence is equivocal with regard to the issue of interference because of the way in which set size was manipulated. For example, Ariely (2001) varied set size between 4 and 16 items by varying the frequency of only four unique circle sizes. A set of 4 items contained four differently-sized discs while a set of 16 items contained those same four discs repeated four times each. Observers therefore did not have to sample all of the stimuli in a set to do the task. They could instead sample from only a portion of the display, effectively nullifying the set-size manipulation (Myczek & Simons, 2008). The high degree of item regularity, rather than efficient summary perception, may be one factor driving equal summary performance between small and large sets. Indeed, when size regularity across items was minimized, forcing observers to sample from the whole set, significant set size effects were observed (see Marchant, Simons, & de Fockert, 2013 for a discussion on this issue).
Based on the large set size effects found in Marchant et al. (2013), it is unclear whether statistical processing occurs with or without interference across stimuli. This is because set size manipulations generally simultaneously vary other factors as well, such as statistical decision noise, eye movements, exposure duration, and the ratio of relevant to irrelevant stimuli (Eckstein et al., 2000; Palmer, 1994; Shaw, 1980; Townsend, 1990). In the case of statistical decision noise, for example, the number of perceptual representations contributing to the decision process are greater at larger than smaller set sizes. The noise associated with the additional items increases the probability that an error will occur, and as a consequence, a true unlimited-capacity process may be interpreted as limited capacity because performance drops with the more items there are in the display to process (e.g., Palmer, 1995). It is for this and similar reasons that set size effects are not ideal for assessing the issue of processing independence (e.g., Huang & Pashler, 2005; Pashler, 1998; Wolfe, 1998). We turn to the simultaneous–sequential method instead.
Simultaneous–sequential method
The simultaneous–sequential method was developed to test the capacity limitations of perceptual processing in a way that avoids many of the problems associated with set size manipulations (Eriksen & Spencer, 1969; Shiffrin & Gardner, 1972). The overall number of to-be-processed stimuli remains constant in this method. Because of this fixed overall set size, decision factors and most sensory factors also remain constant and therefore cannot drive any observed differences in performance that occur. The factor that is varied in the simultaneous–sequential method is how many stimuli must be processed at any given time. In the simultaneous condition, all stimuli onset concurrently in a single frame and must be processed at the same time to perform the task. In contrast, the sequential condition presents half of the same display across two temporal frames, and therefore fewer stimuli require processing at any given time. Importantly every display is presented for the same amount of time in the simultaneous and sequential conditions (see Figure 1). Furthermore, the quick exposure duration of the critical displays and their subsequent masks serve to minimize eye movements and sequential shifts of attention. A direct comparison of accuracy performance between the simultaneous and sequential conditions, therefore, can then be made because the amount of time available for processing each item is constant between conditions and because the duration is fast enough to limit performance.
Figure 1.
Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 1. Observers saw four clusters of Gabor patches. One cluster consisted of tilted Gabors randomly sampled from a target distribution of orientations while the other three clusters consisted of Gabors sampled from a distractor distribution. Observers reported whether the mean orientation of the oddball cluster was tilted left or right relative to the others. The target cluster is tilted left and presented in the lower left corner in this example.
The simultaneous–sequential method tests the (in)dependence of processing multiple relevant stimuli. Unlimited-capacity models predict equal accuracy across the simultaneous and sequential conditions. This follows because if processing unfolds completely independently across multiple stimuli, then it should make no difference how many stimuli require processing. The quality or speed of processing will be constant. In contrast, limited-capacity models predict an advantage in accuracy for sequential over simultaneous presentation because the sequential condition allows fewer stimuli to engage the process at any one time. Processing is compromised by having to process additional items at the same time. Scharff et al. (2011a) has formulized these predictions.
An extended version of the simultaneous–sequential method, developed by Scharff et al. (2011a), includes a repeated condition that presents the entire array of items twice across two temporal frames. Assuming there is room for improvement over what can be processed during the single simultaneous display, performance should be better in the repeated condition when each item is available for twice the duration. The addition of the repeated condition provides two advantages over the original simultaneous–sequential design. First, in the event that processing is unlimited-capacity, this condition allows us to confirm that an effect could be obtained if it were there (i.e., there was room for improvement). The negative finding between the simultaneous and sequential conditions, in the context of better performance in the repeated condition, raises confidence that observers could have taken advantage of the sequential condition if processing was limited. Second, in the event that processing is limited capacity, the repeated condition allows us to test among a specific type of limited-capacity model, called the fixed-capacity model, which states that processing is limited to a fixed amount of information per unit time (e.g., only one item at a time). A fixed-capacity model predicts that performance in the sequential condition will be better than the simultaneous condition and equal to performance in the repeated condition (Scharff et al., 2011a).
The Current study
The view that SSRs are a fundamental aspect of early visual processing is dependent on the claim that summaries are computed over many items in the visual field independently. That is, they are assumed to depend entirely on unlimited-capacity processes. In the current study, we applied the extended simultaneous–sequential method (Scharff et al., 2011a) to ask whether establishing SSRs of mean orientation depends on limited-capacity processes or whether they can be established entirely through unlimited-capacity processes. In a recent study, we addressed this question for the establishment of mean size and found that representing mean size for multiple ensembles depended on limited-capacity processes (Attarha et al., 2014b). This finding presents a challenge to the hypothesis that the functional role of SSRs is to reduce complex information across the visual field to support later processes and the sense of perceptual continuity (e.g., Alvarez, 2011; Chong & Treisman, 2005a; Whitney, Haberman, & Sweeny, 2014).
Why follow up with orientation? One reason for considering the processing limitations of establishing SSRs for orientation, in particular, is that the visual search literature suggests that orientation information may be processed in a manner that is qualitatively different from other simple features. For example, when within-feature conjunctions are configured in a whole-part structure, attention can be guided by size (and color) but not by orientation. One possible explanation is that orientation may not be processed hierarchically to the same extent as other features (Bilsky & Wolfe, 1995; Wolfe, Friedman-Hill, & Bilsky, 1994; Wolfe et al., 1990). The results of this study and others (e.g., Cavanagh, Arguin, & Treisman, 1990; Lüschow & Nothdurft, 1993) suggest that orientation processing may be unique and thus it follows that any limitations or advantages observed for size may not generalize to orientation. If mean orientation SSRs can be established through unlimited-capacity processes, then it would provide evidence that at least some summary representations might serve in the role of abstracted information in the support of later visual processes (e.g., Alvarez, 2011; Rosenholtz et al., 2012). Alternatively, finding that orientation SSRs also depend on limited-capacity processes would challenge the widespread claim that SSRs precede or bypass the limited-capacity bottleneck.
A second, related, reason for considering the capacity limitations of establishing SSRs for orientations concerns a theoretical account of SSRs according to which summaries are generated at multiple levels and within separate pathways of the visual system (Haberman & Whitney, 2009; Haberman & Whitney, 2011; Whitney et al., 2014). According to this view, averages for some low-level surface features, such as orientation and brightness, may be established at the earliest stages of processing whereas SSRs for other attributes may not be established until later stages (Whitney et al., 2014; p. 702). Average object size and shape, for example, may be processed further along the ventral stream than mean orientation. Similarly, mean direction of motion and mean spatial position may be processed further along the dorsal stream than orientation. Still, other summary representations (e.g., biological motion or facial expression) may not be processed until after the ventral and dorsal pathways converge.
Under this multiple-site view of SSR formation, different SSRs will engage different subsets of processes; some may involve limited-capacity processing, whereas others may bypass all limited-capacity processes. For example, summaries of low-level features may be mediated by physiological mechanisms that pool the activity of a population of early feature channels in parallel, while summaries of more complex representations may involve more complex algorithms (e.g., this issue is discussed in Myzczek & Simons, 2008, p. 773; see also Marchant et al., 2013, p. 245). Although the algorithms by which summary statistics operate are currently unknown, linear pooling models have shown promise (Haberman & Whitney, 2011; Parkes et al., 2001). Specifically, for features that are explicitly represented in early visual stages, such as orientation, pooling mechanisms may combine the outputs of orientation-selective cells into a Gaussian-shaped population code, the center of which could be the basis of a summary percept (e.g., Suzuki, 2005; Whitney et al., 2014). Averaging across low-level feature detectors in this way may be an intrinsic aspect of visual processing that proceeds without capacity limitations. In contrast, more complex summaries (e.g., facial averaging) may require an additional step wherein summaries of multiple component feature populations are integrated into a superordinate population code. The additional step of integrating subordinate summaries may produce an information-processing bottleneck, thus limiting the processing capacity of such complex summaries. According to this framework, orientation averaging is a likely candidate for unlimited-capacity processing (Dakin, 2001; Dakin & Watt, 1997; see also Hubel & Wiesel, 1962; Webster & De Valois, 1985), whereas facial averaging is a likely candidate for limited-capacity processes.
By way of preview, the results from the current study are inconsistent with the hypothesis that orientation SSRs are established entirely through unlimited-capacity processes. That is, like size, the establishment of a representation of mean orientation cannot be done for multiple ensembles without interference. So far, there is little evidence that any SSRs bypass limited-capacity processes. As such, SSRs do not seem to be good candidates for the computation-saving representations that they are believed to serve as, at least not the versions tested so far using this method.
EXPERIMENT 1
Method
Observers
Twelve undergraduate volunteers from the University of Iowa participated in exchange for course credit (5 male, 7 female, age range: 18 – 28 years, 10 right-handed). A power analysis (N*; Cohen, 1988) based on a pilot run of this experiment indicated that only five subjects were needed to achieve at least 80% power. We made an a priori decision to run twelve to be consistent with a similar study that tested the capacity limitations of mean size summaries (Attarha et al., 2014b). All observers reported normal visual acuity and color vision.
Equipment
Stimuli were displayed on a cathode ray tube monitor (19-inch ViewSonic G90fB) controlled by a Macintosh Pro (Mac OS X) with a 512MB NVIDIA GeForce 8800 GT graphics card (1024 by 768 pixels, viewing distance of 61.5 cm, horizontal refresh rate of 100 Hz). Stimuli were generated using the Psychophysics Toolbox Version 3.0.11 (Brainard, 1997; Pelli, 1997) for MATLAB (Version 8.2, Mathworks, MA). Observers sat in a height-adjustable chair and used an adjustable chin rest to maintain a constant viewing distance from the monitor. The room was dimly lit.
Stimuli
Thirty-six Gabor patches (Gabor, 1946) of various orientations were presented on a neutral gray background (37.14 cd/m2) at the maximum contrast that could be produced by the monitor (50.06 cd/m2) (Figure 1). It has been previously established that orientation averaging can operate over Gabor stimuli (e.g., Dakin, 2001; Dakin & Watt, 1997; Parkes et al., 2001). All sinusoidal patches (1.58° in diameter) had a spatial frequency of 3 cycles per degree and were windowed by a symmetric Gaussian envelope with a spatial constant of 7 pixels. The Gabors were spatially grouped to give rise to the perception of four clusters, each centered on a corner of an imaginary square approximately 6.24° from fixation. The center of the Gabor closest to fixation was 2.89° away, while the center of the Gabor furthest from fixation was 9.94° away. A distance of 9.11° separated the clusters horizontally and vertically, center-to-center.
On every trial, the orientations of the Gabor patches within each cluster were chosen from a target or distractor distribution. Three of the four clusters were chosen randomly from a Gaussian distractor distribution (μ = 0°; σ = 15°), while the orientations of Gabors within the fourth cluster were chosen equally from either a Gaussian tilted-left distribution (μ = −30°; σ =15°), or a Gaussian tilted-right distribution (μ = 30°; σ = 15°). Vertical was 0°.
Procedure
Observers completed one 30-minute session. The session began with a practice block of 30 trials, followed by 6 experimental blocks of 48 trials each (96 observations per display type, 288 experimental observations per subject). Practice trials were excluded from all analyses.
All trials began with a centrally located fixation dot (2 pixel diameter) colored in black for 500 ms. Observers were instructed to maintain central fixation throughout the experiment. In the simultaneous condition, the fixation display was followed by the four clusters of Gabors for 200 ms. Each Gabor was subsequently masked by a square-shaped Gabor patch that was oriented horizontally at 90° (2.05° × 2.05°) for 100 ms. A blank screen with a question mark (“?”) at fixation followed the mask display and remained on the screen until a response was made (Figure 1A). In the sequential condition, fixation was followed by two clusters for 200 ms presented along either the positive or negative diagonal, masks for 100 ms, a blank ISI of 1,200 ms, the other two clusters for 200 ms presented along the opposite diagonal, masks again for 100 ms, and a blank screen with a question mark until response (Figure 1B). The repeated condition was the same as the sequential condition except that all four clusters appeared in both of the two 200 ms displays (Figure 1C). Written feedback (“correct”/“incorrect”) was given at fixation following each response for 500 ms. The next trial automatically began 1,000 ms after the feedback display.
The default exposure duration was 200 ms (see Whiting & Oriet, 2011). A coarse tracking procedure altered the exposure duration, block-by-block, on the basis of performance in the simultaneous condition only. If performance in the simultaneous condition was more than 90% on a given block, then the exposure duration for the simultaneous, sequential, and repeated conditions was decreased by 10 ms on the next block. Moreover, if performance was less than 60% in the simultaneous condition, then the exposure duration in all three conditions increased by 10 ms. The average adjusted exposure duration across all subjects was 190 ms.
Design
The full factorial combination of display type (simultaneous, sequential, repeated), target type (tilted left, tilted right), and target position (upper-left, upper-right, lower-left, lower-right) were randomly mixed within blocks of trials and appeared equally often. Which of the two diagonally opposite positions were presented first in the sequential display was constant for a given observer but varied across observers. Odd-numbered subjects saw clusters that first appeared along the negative diagonal and then along the positive diagonal. Even-numbered subjects saw clusters that appeared positive to negative. We kept the presentation of diagonal orders constant within an observer to eliminate uncertainty of the presentation positions.
Task
Observers reported whether the mean orientation of one cluster was tilted left or tilted right relative to the mean orientation of the other clusters by pressing the “F” or “J” key, respectively. Observers were instructed to respond as accurately as possible. Speed was not emphasized.
Method of analysis
All three models assume an advantage in the repeated condition where observers see the display twice compared to the simultaneous condition where observers see the display only once. Subjects who did not meet this criterion were omitted from further analyses and replaced until a total of 12 subjects in each experiment were collected. One, two, three, and five subjects failed to show a repeated advantage in Experiments 1–4, respectively.
Because of our sampling method, we filtered the small percentage of trials in which the perceptually correct response led to an “incorrect” feedback message. In Experiments 1–3, this meant that the mean orientation of a distractor cluster was tilted either more rightward (or leftward) than the mean orientation of the target cluster. The cluster that appeared to be the target was in fact a distractor on these trials. A total of 1, 0, and 0 out of 3,456 experimental trials across all twelve observers in Experiment 1, 2, and 3, were filtered, respectively. In Experiment 4, trials in which the mean of the entire set of thirty-six items was not tilted in the intended direction were filtered. A total of 8 out of 3,456 experimental trials (.0023%) were omitted. The elimination of these trials did not alter the results qualitatively.
After filtering, the accuracy data for the simultaneous, sequential, and repeated conditions were transformed to arcsin values to normalize their distributions and the underlying assumptions of the repeated-measures ANOVA were confirmed. Assumptions of normality and sphericity were confirmed using a one-sample Kolmogorov-Smirnov test and Mauchly’s test, respectively. When violations of sphericity were found, p-values were adjusted based on the Greenhouse-Geisser epsilon correction on degrees of freedom (Jennings & Wood, 1976). Two follow-up paired t-tests, one between the simultaneous and sequential conditions, and another between the sequential and repeated conditions, were used after significance of the final model was verified.
Results and Discussion
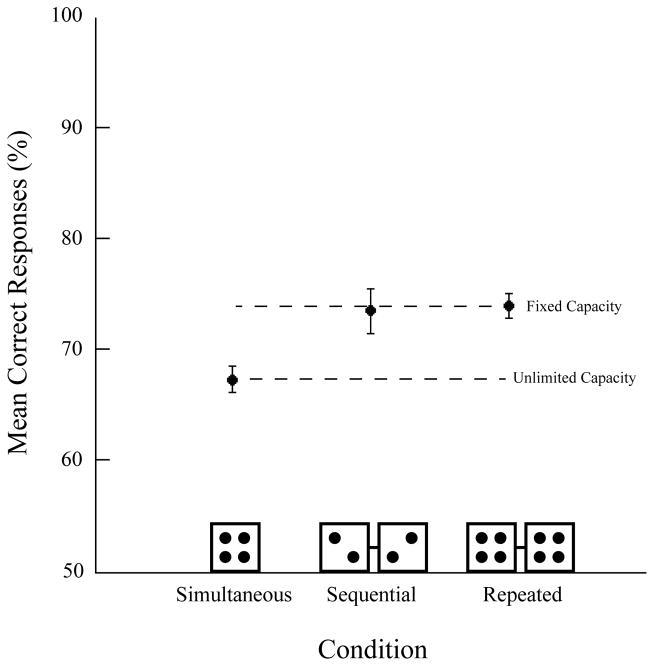
Figure 2 shows mean percent correct as a function of display, collapsed across all observers. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Moray, 2008). Notice that Figure 2 has two line labels. One of these lines defines the “unlimited capacity” prediction while the other defines the “fixed capacity” prediction. These lines can be thought of as boundary conditions. The simultaneous condition (where subjects see all four sets one time) provides a lower bound of processing performance whereas the repeated condition (where subjects see all four sets twice) provides an upper bound of performance. The “fixed capacity” and “unlimited capacity” labels define the theoretical model that is supported as a function of where performance in the sequential conditions falls (see Scharff et al., 2011a, Appendix, for details regarding predictions). Evidence of unlimited-capacity processing is concluded if the sequential condition falls on the line established by the simultaneous condition. In contrast, evidence of fixed-capacity processing is concluded if the sequential condition falls in line with the repeated condition. In Experiment 1, we found that sequential was equal to repeated performance and that there was a reliable decrement in the simultaneous condition. This pattern of results is consistent with a fixed-capacity model and inconsistent with an unlimited-capacity model.
Figure 2.
Mean correct responses (%) as a function of display collapsed across observers in Experiment 1. Performance in the sequential condition was better than performance in the simultaneous condition and equal to performance in the repeated condition. These results suggest that mean orientation SSRs for multiple sets engage fixed-capacity processes. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Moray, 2008).
Arcsin transformed values of mean percent correct were submitted to a one-way repeated-measures ANOVA with the simultaneous, sequential, and repeated display conditions as the within-subjects variable. The final model was significant, F(1.16, 12.72) = 5.64, p = .030, pη2 = .339, MSE = .007 (all Kolmogorov-Smirnov p > .766; Mauchly’s p = .001; Greenhouse-Geisser ε = .579). As predicted by fixed-capacity processing, performance in the sequential condition (73% ± 2.05) was significantly greater than performance in the simultaneous condition (67% ± 1.21), t(11) = 2.45, p = .032. Performance between the repeated (74% ± 1.11) and sequential conditions were equal, t(11) = 0.09, p = .927. We conclude that establishing SSRs of mean orientation for multiple ensembles depend on limited-capacity processes, some of which may even involve a fixed-rate processing bottleneck (see Scharff et al., 2011a)
Alternative explanations
The simultaneous–sequential method assumes that the simultaneous and sequential displays differ only with respect to how many stimuli must be processed at a given time. They did necessarily differ, however, in when the target appeared within the trial sequence. In the simultaneous condition the target always appeared in the “first” frame because that was the only frame, whereas in the sequential condition, the target appeared in either the first frame or the second frame. This difference might provide a disadvantage to the sequential condition if there are any memory differences across the two conditions. To assess this possibility, we compared performance in the sequential condition for trials on which the target appeared in the first and second frames. No reliable difference was found: 72% (first frame) vs. 75% (second frame), F(1,11) = 0.63, p = .446, pη2 = .054, MSE = .009 (all Kolmogorov-Smirnov p > .543).
With our stimulus design, there are two potential strategies that can be used to bypass a calculation of mean orientation. First, responses may be based on the orientation information of individual Gabor patches rather than on mean orientation. Specifically, if the most extreme orientation in the display points leftward, for example, then observers may use this information as a shortcut to a “tilted left” response without ever calculating a summary of each cluster. We used distributions with large standard deviations (see methods section) in order to minimize this potential strategy. Because of the large target-distractor overlap, the most tilted item in any given display may have originated from a distractor set and therefore an incorrect response would be obtained to the extent that observers used this information as a basis for their response. Observers may still use this strategy even if it is unreliable, however. If they had, we maintain that the results of Experiment 1 would have been consistent with an unlimited-capacity model. A later experiment in this paper tests the capacity limitations of processing the individual orientations unique to each cluster. Specifically, in Experiment 3, each cluster is represented by a single Gabor patch and the target patch was usually the most tilted item in the display. Observers could therefore exploit the tilt direction of individual orientations in these displays and base their response on the local item with the greatest tilt. We find evidence of unlimited capacity, which suggests that this strategy was not used in Experiment 1 since processing was limited.
Although using large standard deviations discouraged responses on the basis of local orientations, it is possible that the evidence of limited-capacity processing we observed is caused by having to establish an average without enough information. It may have been too difficult to extract the mean from orientation distributions with large variances using only nine items (e.g., Dakin, 2001). Summary extraction for multiple sets might proceed in parallel, unlimited capacity had the variance been smaller or the number of items per set larger. Unfortunately, it would be difficult to rule the use of local orientation cues as a potential strategy in this case since both would unfold without interference.
The second strategy is that the overall difference in the pattern of orientations across the target and distractor clusters may automatically direct attention to the target (see Figure 1). The Gabors within each distractor cluster will be, on average, composed of items that are tilted both left and right while the Gabors within the target clusters will be composed of orientations tilted in the same direction. The detection of pattern discontinuities is also an unlimited-capacity process (e.g., Huang, Pashler, & Junge, 2004). We conclude that both of these potential strategies would be of more concern had the data been consistent with unlimited-capacity processing. Given that it was not, it suggests that observers did not use such strategies.
Discussion of similar work on this topic
Chong and Treisman (2003, experiment 1) compared averaging performance across multiple ensembles under simultaneous versus sequential presentation conditions. They found equal performance across these two conditions, which appears to be at odds with the results and conclusions drawn in Experiment 1 of the present study. In that experiment, however, the simultaneous display was presented for 200 ms, whereas each frame of the sequential display was only 100 ms each. Therefore, the simultaneous condition was similar to the repeated condition of Experiment 1 in the current study (i.e., twice the duration of the other condition), and indeed performance in this double-duration condition achieved that of the sequential condition. We suggest that rather than conflicting with our results, the results from the Chong and Treisman experiment are, like ours, consistent with a fixed-capacity model of SSRs across multiple ensembles.
Experiment 1 also shares similarities with Halberda et al. (2006) who used a pre-post cueing paradigm to test the number of sets that could be enumerated simultaneously without interference. Observers saw multiple subsets of dots and estimated the number of dots in the cued set. When the relevant set was cued before the stimulus array (pre-cue), observers could use this information to focus on a single set and ignore the irrelevant sets. In contrast, when the relevant set was cued after the array was presented (post-cue), successful performance required the enumeration of all of the sets. Equal performance in the pre- and post-cue conditions in this design suggests parallel unlimited processing of the relevant information. Indeed, in the Halberda et al. (2006) study, performance was not reliably different between the pre- and post-cue conditions when two subsets of dots required enumeration (see also Emmanouil & Treisman, 2008; Im & Chong, 2014; but see Poltoratski & Xu, 2013 who obtained a pre-cue advantage for two subsets). Thus, evidence using a pre-cue/post-cue method has led to the conclusion of “unlimited-capacity” for SSRs for multiple sets of items, whereas evidence from the simultaneous–sequential method has led to the conclusion that establishing multiple sets depends on limited-capacity processes (Experiment 1). We suggest that this difference reflects a difference in what “capacity” is referring to. Specifically, the conditions of the Halberda et al. study were such that performance was limited by storage capacity, rather than online capacity. That is, processing was constrained by the number of sets that could be maintained in memory rather than the degree to which processing could be engaged independently by multiple stimuli. Indeed, Poltoratski and Xu (2013) and Im and Chong (2014) used a design similar to Halberda et al. and found that averaging performance is limited by, and cannot be separated from, visual working memory capacity. In contrast, the simultaneous–sequential method can be dissociated from storage capacity limits; if stimulus presentation conditions are such that performance is limited by how much information can be extracted from the display (e.g., because stimuli are presented briefly), then limited-capacity processing predicts a difference between simultaneous versus sequential even for one versus two items (i.e., less than the 3–4 item limit). Two versus four has been used in order to minimize contamination from differences in eye movements across conditions and to minimize contamination from sensory effects like crowding, but the logic is identical. Therefore we conclude that the apparent difference in results between the pre-post cueing paradigm and the simultaneous–sequential method likely arise from the different forms of capacity to which these methods measure.
EXPERIMENT 2
The conclusion that establishing SSRs of mean orientation is limited capacity relies on demonstrating that some other aspect of the task or design, unrelated to averaging, was not driving the observed advantage in the sequential condition. There are several potential factors to rule out, such as crowding of the Gabors within a set (Banno & Saiki, 2012; Bouma, 1970), low target-distractor discriminability across sets, and the involvement of limited-capacity comparison processes. To test the possibility that one or more of these factors was the cause of limited performance, we conducted a control experiment in which the task required all of the same processes except for actually calculating mean orientation.
The task in Experiment 2 was identical to that in Experiment 1; report the direction of average tilt (left or right) in the cluster with the non-vertical mean orientation. The orientations of Gabors within each cluster, however, were identical and all were set to the mean of their respective cluster from Experiment 1 (Figure 3). Because the mean of each group was provided directly, there was no need to compute an average orientation to do the task.
Figure 3.
Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 2. The mean orientation of each cluster was calculated after the orientations of Gabors within each cluster were sampled from their respective distributions. All Gabors within a given cluster was then adjusted according to that cluster’s mean. Establishing summary representations are no longer necessary to perform the task. The target cluster is tilted right and presented in the upper right corner in this example.
Multiple alternative explanations of the limited-capacity processing result that was obtained in Experiment 1 were tested using this design. First, the explanation that the crowding of items within each cluster impaired mean estimations (Banno & Saiki, 2012) more so in the simultaneous condition than in the sequential conditions can be ruled out as driving the observed limitation in Experiment 1 because the stimulus spacing in Experiment 2 was the same as in Experiment 1. Therefore the extent of crowding that would occur in Experiment 2 is at least physically equal to, and may even be perceptually greater than (Kooi et al., 1994), the crowding that occurred in Experiment 1. Second, target-distractor discriminability of the means is the same in this experiment as Experiment 1 because the mean values were identical across the two experiments. Finally, this experiment requires the same number of comparisons across clusters as Experiment 1. Despite these common aspects, we observed evidence of unlimited-capacity processing in Experiment 2 and limited-capacity processing in Experiment 1, suggesting that the source of the limitation in Experiment 1 was the need to calculate the mean orientation for each of the groups.
Method
All aspects of the method were identical to Experiment 1, with the exceptions noted below.
Observers
Twelve new undergraduate volunteers from the University of Iowa participated in exchange for course credit (2 male, 10 female, age range: 18 – 20 years, 11 right-handed).
Stimuli
The orientations of the Gabors within each of the four clusters were randomly chosen from the appropriate target or distractor distribution. The mean orientation for each cluster was then calculated and the orientations of all nine Gabors within a given cluster were set to that cluster’s mean prior to presentation (Figure 3). The orientations of the Gabors within each cluster were therefore identical.
Procedure
As before, the default exposure duration for the simultaneous, sequential, and repeated conditions was 200 ms. The average adjusted exposure duration for all subjects after tracking remained at 200 ms.
Results and Discussion
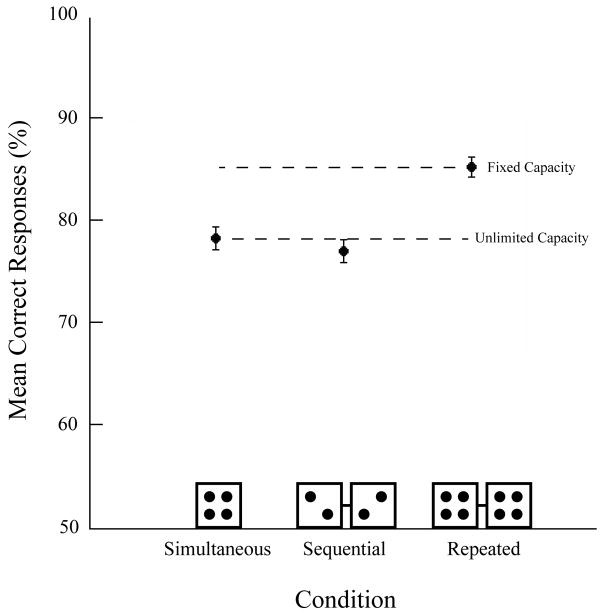
Figure 4 shows the mean percent correct as a function of display collapsed across all observers. Equal performance between the simultaneous and sequential conditions was observed. There was also an advantage in the repeated condition. In contrast to Experiment 1, the pattern of data in Experiment 2 is consistent with an unlimited-capacity model and inconsistent with a limited-capacity model.
Figure 4.
Mean correct responses (%) as a function of display collapsed across observers in Experiment 2. Performance was equal across the simultaneous and sequential conditions. There was also a reliable advantage in the repeated condition. Evidence consistent with unlimited-capacity processing was obtained when the task no longer required that subjects compute the average of each cluster. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Moray, 2008).
Arcsin transformed values were submitted to a one-way repeated-measures ANOVA with display as the within-subjects factor (all Kolmogorov-Smirnov p > .907; Mauchly’s p = .359). The final model was significant, F(2,22) = 17.76, p < .001, pη2 =. 618, MSE = .003. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (77% ± 1.11) than in the simultaneous condition (78% ± 1.13), t(11) = 1.17, p = .269. However, performance in the repeated condition (85% ± 0.92) was significantly higher than performance in the sequential condition, t(11) = 4.82, p < .001.
We again compared performance within sequential trials when the target was presented in the first frame versus the second frame. Performance across both frames were statistically equal, 75% (first frame) vs. 79% (second frame), F(1,11) = 2.55, p = .139, pη2 = .188, MSE = .006 (all Kolmogorov-Smirnov p > .865). Targets presented closer in time to response were not remembered better.
Everything about Experiment 2 was the same as that of Experiment 1 except for the need to establish an SSR of mean orientation. Whereas Experiment 1 yielded evidence of limited-capacity processing, Experiment 2 yielded evidence of unlimited-capacity processing. We conclude that processing was limited in Experiment 1 specifically because it required the computation of mean orientation to do the task, and therefore that establishing SSRs of mean orientation involves limited-capacity processes.
EXPERIMENT 3
In Experiment 2 the same orientation was repeated nine times within a given set. This redundancy may have had the unintended consequence of strengthening the represented average through probability summation. That is, it is possible that observers computed average orientations in Experiment 2, despite not having to do so in order to do the task. If they did, then the unlimited-capacity result might reflect an advantage for establishing SSRs on the basis of homogeneous sets compared to heterogeneous sets (Chong & Treisman, 2003; see also Utochkin & Tiurina, 2014), rather than reflecting them not doing the averaging process at all as we concluded. To test this possibility, we conducted a second control experiment in which a single Gabor patch was presented in lieu of the four ‘clusters’. If the evidence of unlimited-capacity processing persists when we remove the repeating orientations, then we could rule out that the averaging of homogeneous sets was the sole cause of the results in Experiment 2.
Method
All aspects of the method were identical to Experiment 2, with the exceptions noted below.
Observers
Twelve new undergraduate volunteers from the University of Iowa participated in exchange for course credit (1 male, 11 female, age range: 18 – 21 years, 11 right-handed).
Stimuli
The same displays presented in Experiment 2 were used except that only the center Gabor patch of each cluster was presented (Figure 5).
Figure 5.
Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 3. Observers were given the mean of each cluster, which was represented by the orientation of a single circle. The correct response is tilted right in this example.
Procedure
As before, the default exposure duration for the simultaneous, sequential, and repeated conditions was 200 ms. The average adjusted exposure duration for all subjects after tracking was 180 ms.
Results and Discussion
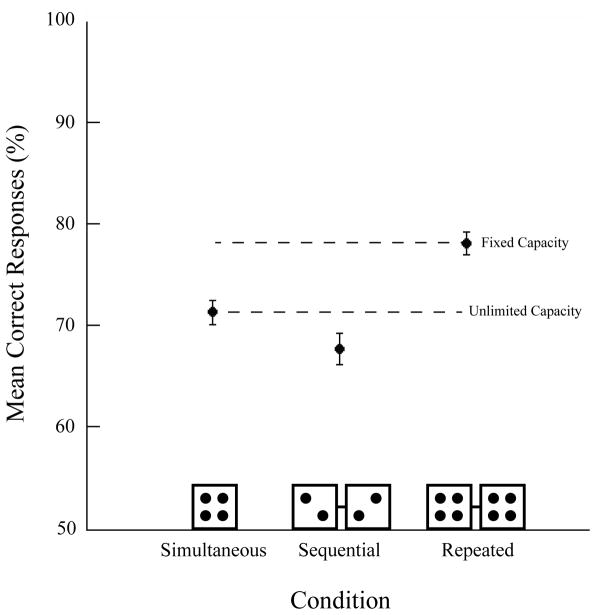
Figure 6 shows the mean percent correct as a function of display collapsed across all observers. The data were again consistent with an unlimited-capacity model and inconsistent with a limited-capacity model.
Figure 6.
Mean correct responses (%) as a function of display collapsed across observers in Experiment 3. Performance was equal across the simultaneous and sequential conditions and there was also a reliable advantage in the repeated condition. These results are consistent with the unlimited-capacity model. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Moray, 2008).
Arcsin transformed values were submitted to a one-way repeated-measures ANOVA with display as the within-subjects factor (all Kolmogorov-Smirnov p > .408; Mauchly’s p = .290). The final model was significant, F(2,22) = 18.06, p < .001, pη2 =. 621, MSE = .003. As predicted by unlimited-capacity processing, accuracy was equal between the sequential (68% ± 1.51) and simultaneous (71% ± 1.21) conditions, t(11) = 1.92, p = .081. However, performance in the repeated condition (78% ± 1.13) was significantly higher than performance in the sequential condition, t(11) = 5.65, p < .001.
Performance within sequential trials when the target was presented in the first frame versus the second frame were statistically equal, 69% (first frame) vs. 66% (second frame), F(1,11) = 1.12, p = .313, pη2 = .092, MSE = .006 (all Kolmogorov-Smirnov p > .639). There was no memory advantage for targets presented closer in time to response.
The results of this experiment provide further confidence in our original interpretation of the results of Experiment 1. That is, the evidence of limited-capacity processing found in that experiment can be attributed to the need to establish SSRs of mean orientation. When the task was the same, except that no average had to be computed, the results indicated unlimited-capacity processing. This was true in this experiment in which only a single item was presented in each cluster, and hence no average was needed, and in Experiment 2 in which every item in the cluster had the same orientation, and hence in principle no average was needed. The results from these three experiments combined strongly suggest that it is the averaging process that depends on limited-capacity processes.
EXPERIMENT 4
We now turn to the question of limited capacity with regard to what? Relatively few studies have made the distinction between establishing summary representations across multiple sets of stimuli versus establishing a single summary representation across multiple items within a single set (Halberda, Sires, & Feigenson, 2006; Poltoratski & Xu, 2013). The conclusion offered from the preceding experiments that establishing SSRs for mean orientation is limited capacity is in regard to multiple sets of multiple items. That is, the evidence so far indicates that people cannot simultaneously establish SSRs of mean orientation for multiple ensembles of stimuli without mutual interference. It is a separate question whether SSRs for multiple items within an ensemble can be established independently of the number of items within the ensemble. This is an important distinction to make because conclusions drawn from multi-set tasks (e.g., Banno & Saiki, 2012; Oriet & Brand, 2013) do not generalize to single-set tasks (e.g., Ariely, 2001; Robitaille & Harris, 2011). This may be because, as we recently showed for mean size (Attarha et al., 2014b), establishing SSRs for a given attribute may be limited with regard to multiple ensembles, but unlimited with regard to items within a single ensemble. We address this contrast with regard to orientation in Experiment 4.
Method
All aspects of the method were identical to Experiment 1, with the exceptions noted below.
Observers
Twelve new undergraduate volunteers from the University of Iowa participated in exchange for course credit (0 male, 12 female, age range: 18 – 22 years, 10 right-handed).
Stimuli
To create a single cluster, the four clusters of Gabor patches from Experiment 1 were placed on an evenly-spaced grid centered at fixation (Figure 7). Each patch was separated horizontally and vertically by 2.33° center-to-center. The size of the whole display was 13.91° × 13.91°.
Figure 7.
Trial events for the (A) simultaneous, (B) sequential, and (C) repeated conditions in Experiment 4. The four clusters from Experiment 1 were presented on an equally spaced grid to produce a single cluster with 36 items. Observers reported whether the mean orientation of the entire cluster was tilted left or right relative to vertical. The correct answer in this example is tilted left.
Procedure
A pilot of this experiment demonstrated that subjects could not perform the task above chance-levels at a viewing duration of 200 ms. The default exposure duration for the simultaneous, sequential, and repeated conditions was therefore set to 300 ms. The average adjusted exposure duration for all subjects was 310 ms.
Task
The task was to report whether the average orientation over the entire set of thirty six items was tilted left (“F” key) or right (“J” key) relative to vertical.
Results and Discussion
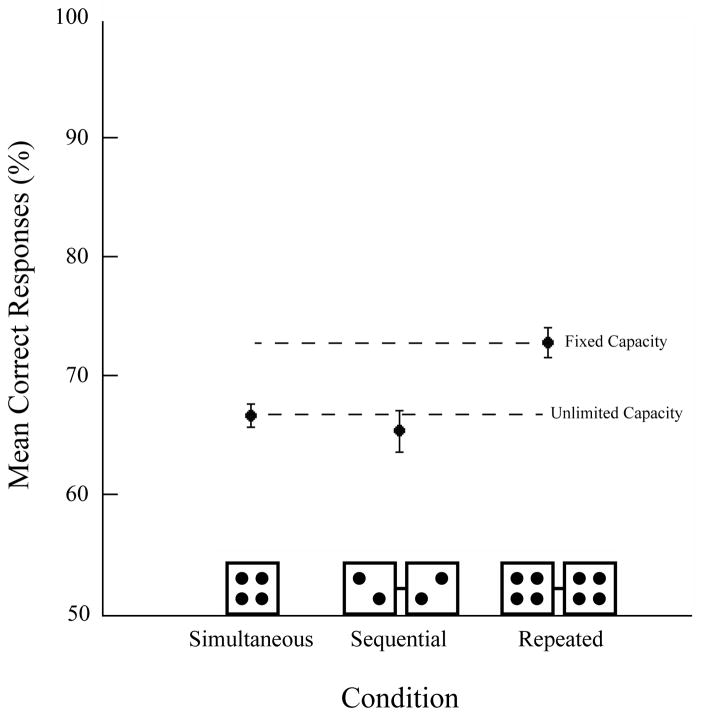
Figure 8 shows the mean percent correct as a function of condition collapsed across observers. The data were consistent with an unlimited-capacity model and inconsistent with a limited-capacity model.
Figure 8.
Mean correct responses (%) as a function of display collapsed across observers in Experiment 4. Evidence consistent with unlimited capacity was obtained when summary statistics were computed for a single set. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Moray, 2008).
Arcsin transformed values were submitted to a one-way repeated-measures ANOVA with condition as the within-subjects factor (all Kolmogorov-Smirnov p > .960; Mauchly’s p = .086, Greenhouse-Geisser epsilon = .721). The final model was significant, F(1.44,15.85) = 9.43, p = .004, pη2 = .462, MSE = .003. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (65% ± 1.71) than in the simultaneous condition (66% ± 1.00), t(11) = 0.57, p = .582. However, performance in the sequential condition was significantly lower than performance in the repeated condition (73% ± 1.21), t(11) = 3.39, p = .006.
Performance across both frames in the sequential condition were statistically equal, 65% (first frame) vs. 65% (second frame), F(1,11) = 0.01, p = .937, pη2 = .001, MSE = .006 (all Kolmogorov-Smirnov p > .687), suggesting that targets presented first did not suffer from more memory loss than targets presented closer in time to response.
In summary, although establishing summary representations of mean orientation for multiple sets depended on limited-capacity processes (Experiment 1), the results of Experiment 4 indicate that establishing a single summary representation of mean orientation, across multiple items, can unfold entirely through unlimited-capacity processes. This finding is consistent with the results of Halberda et al. (2006) who found that the enumeration of a single summary proceeds without cost (see also Chong & Treisman, 2005b).
GENERAL DISCUSSION
The visual system has been likened to a statistician that is capable of summarizing the features of similar items into efficient representations that guide behavior (e.g., Balas, Nakano, & Rosenholtz, 2010; Brady & Alvarez, 2011; Chong et al., 2008; Im & Chong, 2009; Joo et al., 2009; Rosenholtz, 2011; Rosenholtz et al., 2012). These representations are proposed to involve mechanisms that precede the limited bottleneck (Chong & Treisman, 2005a, p. 899; see also Alvarez, 2011; Chong & Treisman, 2003; 2005b; Oriet & Brand, 2013), which therefore implies that they are established through unlimited-capacity processes. We used the simultaneous–sequential method to test the capacity limitations of forming multiple SSRs of mean orientation, which is one of the main summaries for which the discussion of parallel processing is based. Performance was higher when fewer numbers of summaries had to be processed at a given time. The advantage for sequential over simultaneous presentation is consistent with a limited-capacity model and inconsistent with an unlimited-capacity model. Summaries of multiple ensembles may not be summarized independently, even for low-level features such as orientation. In contrast, when the same thirty-six items were grouped into a single cluster, the results were consistent with the opposite processing extreme, suggesting that averaging unfolds, without interference, regardless of the number of items that compose a single set (see also Halberda et al., 2006).
The same conclusion was reached in the case of mean size summaries. Attarha, Moore, and Vecera (2014b) used the simultaneous–sequential method and found that mean size summaries were highly limited in processing capacity. In that study, four sets of discs with various diameters were randomly sampled from their corresponding target or distractor distributions. The task was to report whether the mean size of one of the sets was larger or smaller than the three remaining distractor sets. Performance in the sequential condition was better than the simultaneous condition and equal to performance in the repeated condition, suggesting that size summaries are mediated by a fixed-rate bottleneck.
To the extent that the two most studied summary representations – mean size and mean orientation – are not unlimited-capacity, it decreases confidence in the view that SSRs drive a global sense of visual completeness in the periphery. A coarse representation of summaries would need to be established in multiple regions of the visual field, rather than only a single region, in order to meet this function.
Recent studies are contributing to the emerging picture that summaries may not be such an early aspect of perceptual processing after all. For example, accurate summary formation requires a ten-fold increase in exposure time when the displays are masked (Whiting & Oriet, 2011), two summaries cannot be computed concurrently without cost (Brand, Oriet, & Tottenham, 2012), large set size effects abound when the items within a set are sufficiently heterogeneous (Marchant, Simons, & de Fockert, 2013), and summaries are susceptible to modulation by visual stages beyond the initial registration of features (Jacoby, Kamke, & Mattingley, 2013; see also Poltoratski & Xu, 2013). The range of effects cited in the SSR literature may also be accounted for by known psychophysical principles (Allik et al., 2013) or by existing cognitive mechanisms, such as visual working memory (Myzczek & Simons, 2008). Taken together, these more recent findings suggest that summaries may not meet the basic criteria that constitute automatic processing (e.g., Brown, Gore, & Carr, 2002).
Interpreting the results of the current study within the context of other studies using the simultaneous–sequential method also points to the possibility that SSR formation commences at later stages of visual processing. Those processes found to engage unlimited-capacity processes in the simultaneous–sequential method include contrast discrimination (Scharff et al., 2011a), image shape (Scharff et al., 2013), size discrimination of individual items (Huang & Pashler, 2005), modal and amodal surface completion (Attarha et al., 2014a), symmetry detection (Huang, Pashler, & Junge, 2004), and letter identification (Shiffrin & Gardner, 1972). These processes have been implicated in sensory and segmentation aspects of visual processing. In contrast, processes found to engage fixed-capacity processes include summary statistics of mean size (Attarha et al., 2014b), object categorization (Scharff et al., 2011b), object shape identification (Scharff et al., 2013), word categorization (Scharff et al., 2011a) and now summary statistics of mean orientation. These processes appear to be involved in object and semantic processing. Although it is an open question as to whether there exists any summary statistic for which multiple sets are processed without interference, we conclude that at least the two most studied summaries (mean size and orientation) are not contenders for unlimited-capacity processing. It remains to be seen whether summaries of other low-level information, such as brightness, spatial position, or motion, can meet this requirement. If none do, then the foundational role that multiple ensembles are proposed to play in early visual perception would require revision and a shift to understanding the role of single ensembles in early visual perception would be warranted. The visual system cannot effortlessly generate multiple coarse representations of information in the peripheral visual field; a tradeoff exists between establishing summary statistics in one region and establishing them in another.
Acknowledgments
This research was supported by the NSF Graduate Research Fellowship awarded to M.A. and by grants BCS 08-18536 (NSF) and R21 EY023750 (NIH) to C.M.M.
Contributor Information
Mouna Attarha, Email: mouna-attarha@uiowa.edu.
Cathleen M. Moore, Email: cathleen-moore@uiowa.edu.
References
- Ackermann JF, Landy MS. Statistical templates for visual search. Journal of Vision. 2014;14(3):1–17. doi: 10.1167/14.3.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albrecht AR, Scholl BJ. Perceptually Averaging in a Continuous Visual World: Extracting Statistical Summary Representations Over Time. Psychological Science. 2010;21(4):560–567. doi: 10.1177/0956797610363543. [DOI] [PubMed] [Google Scholar]
- Allik J, Toom M, Raidvee A, Averin K, Kreegipuu K. An almost general theory of mean size perception. Vision Research. 2013;83:25–39. doi: 10.1016/j.visres.2013.02.018. [DOI] [PubMed] [Google Scholar]
- Alvarez GA. Representing multiple objects as an ensemble enhances visual cognition. Trends in Cognitive Sciences. 2011;15(3):122–131. doi: 10.1016/j.tics.2011.01.003. [DOI] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. The representation of simple ensemble visual features outside the focus of attention. Psychological Science. 2008;19(4):392–398. doi: 10.1111/j.1467-9280.2008.02098.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarez GA, Oliva A. Spatial ensemble statistics are efficient codes that can be represented with reduced attention. PNAS. 2009;106(18):7345–7350. doi: 10.1073/pnas.0808981106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariely D. Seeing sets: representation by statistical properties. Psychological Science. 2001;12(2):157–162. doi: 10.1111/1467-9280.00327. [DOI] [PubMed] [Google Scholar]
- Attarha M, Moore CM, Scharff A, Palmer J. Evidence of unlimited-capacity surface completion. Journal of Experimental Psychology: Human Perception and Performance. 2014a;40(2):556–565. doi: 10.1037/a0034594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attarha M, Moore CM, Vecera SP. Summary statistics of size: Fixed processing capacity for multiple ensembles but unlimited processing capacity for single ensembles. Journal of Experimental Psychology: Human Perception and Performance. 2014b;40(4):1440–1449. doi: 10.1037/a0036206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balas B, Nakano L, Rosenholtz R. A summary-statistic representation in peripheral vision explains visual crowding. Journal of Vision. 2010;9(12):1–30. doi: 10.1167/9.12.13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banno H, Saiki J. Calculation of the mean circle size does not circumvent the bottleneck of crowding. Journal of Vision. 2012;12(11):1–15. doi: 10.1167/12.11.13. [DOI] [PubMed] [Google Scholar]
- Bauer B. Does Stevens’s power law for brightness extend to perceptual brightness averaging? The Psychological Record. 2009;59:171–186. [Google Scholar]
- Bilsky AB, Wolfe JM. Part-whole information is useful in visual search for size x size but not orientation x orientation conjunctions. Perception & Psychophysics. 1995;57(6):749–760. doi: 10.3758/bf03206791. [DOI] [PubMed] [Google Scholar]
- Bouma H. Interaction effects in parafoveal letter recognition. Nature. 1970;226:177–178. doi: 10.1038/226177a0. [DOI] [PubMed] [Google Scholar]
- Brady TF, Alvarez GA. Hierarchical Encoding in Visual Working Memory: Ensemble Statistics Bias Memory for Individual Items. Psychological Science. 2011;22(3):384–392. doi: 10.1177/0956797610397956. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Brand J, Oriet C, Tottenham LS. Size and emotion averaging: Costs of dividing attention after all. Canadian Journal of Experimental Psychology. 2012;66(1):63–69. doi: 10.1037/a0026950. [DOI] [PubMed] [Google Scholar]
- Brown TL, Gore CL, Carr TH. Visual attention and word recognition in Stroop color naming: Is word recognition “automatic? Journal of Experimental Psychology: General. 2002;131(2):220–240. doi: 10.1037//0096-3445.131.2.220. [DOI] [PubMed] [Google Scholar]
- Cavanagh P. Seeing the forest but not the trees. Nat Neurosci. 2001;4:673–674. doi: 10.1038/89436. [DOI] [PubMed] [Google Scholar]
- Cavanagh P, Arguin M, Treisman A. Effect of surface medium on visual search for orientation and size features. Journal of Experimental Psychology: Human Perception and Performance. 1990;16(3):479–491. doi: 10.1037//0096-1523.16.3.479. [DOI] [PubMed] [Google Scholar]
- Chong SC, Joo SJ, Emmanouil TA, Treisman A. Statistical processing: not so implausible after all. Perception & Psychophysics. 2008;70(7):1327–1334. doi: 10.3758/PP.70.7.1327. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Representation of statistical properties. Vision Research. 2003;43(4):393–404. doi: 10.1016/s0042-6989(02)00596-5. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Statistical processing: computing the average size in perceptual groups. Vision Research. 2005a;45(7):891–900. doi: 10.1016/j.visres.2004.10.004. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Attentional spread in the statistical processing of visual displays. Perception & Psychophysics. 2005b;67(1):1–13. doi: 10.3758/bf03195009. [DOI] [PubMed] [Google Scholar]
- Cohen J. Statistical power analysis for the behavioral sciences. LEA; Hillsdale, NJ: 1988. [Google Scholar]
- Corbett JE, Melcher D. Characterizing ensemble statistics: mean size is represented across multiple frames of reference. Attention, Perception & Psychophysics. 2013;76(3):746–758. doi: 10.3758/s13414-013-0595-x. [DOI] [PubMed] [Google Scholar]
- Corbett JE, Oriet C. The whole is indeed more than the sum of its parts: perceptual averaging in the absence of individual item representation. Acta psychologica. 2011;138(2):289–301. doi: 10.1016/j.actpsy.2011.08.002. [DOI] [PubMed] [Google Scholar]
- Corbett JE, Song JH. Statistical extraction affects visually guided action. Visual Cognition. 2014;22(7):881–895. doi: 10.1080/13506285.2014.927044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cousineau D. Confidence intervals in within-subject designs: A simpler solution to Loftus and Masson’s method. Tutorials in Quantitative Methods for Psychology. 2005;1:42–45. [Google Scholar]
- Dakin SC. Information limit on the spatial integration of local orientation signals. Journal of the Optical Society of America a, Optics, Image Science, and Vision. 2001;18(5):1016–1026. doi: 10.1364/josaa.18.001016. [DOI] [PubMed] [Google Scholar]
- Dakin SC, Watt RJ. The computation of orientation statistics from visual texture. Vision Research. 1997;37(22):3181–3192. doi: 10.1016/s0042-6989(97)00133-8. [DOI] [PubMed] [Google Scholar]
- de Fockert J, Wolfenstein C. Rapid extraction of mean identity from sets of faces. The Quarterly Journal of Experimental Psychology. 2009;62(9):1716–1722. doi: 10.1080/17470210902811249. [DOI] [PubMed] [Google Scholar]
- Demeyere N, Rzeskiewicz A, Humphreys KA, Humphreys GW. Automatic statistical processing of visual properties in simultanagnosia. Neuropsychologia. 2008;46(11):2861–2864. doi: 10.1016/j.neuropsychologia.2008.05.014. [DOI] [PubMed] [Google Scholar]
- Eckstein MP, Thomas JP, Palmer J, Shimozaki SS. A signal detection model predicts the effects of set size on visual search accuracy for feature, conjunction, triple conjunction, and disjunction displays. Perception & Psychophysics. 2000;62(3):425–451. doi: 10.3758/bf03212096. [DOI] [PubMed] [Google Scholar]
- Emmanouil TA, Treisman A. Dividing attention across feature dimensions in statistical processing of perceptual groups. Perception & Psychophysics. 2008;70(6):946–954. doi: 10.3758/PP.70.6.946. [DOI] [PubMed] [Google Scholar]
- Eriksen CW, Spencer T. Rate of information processing in visual perception: some results and methodological considerations. Journal of Experimental Psychology. 1969;79(2):1–16. doi: 10.1037/h0026873. [DOI] [PubMed] [Google Scholar]
- Fouriezos G, Rubenfeld S, Capstick G. Visual statistical decisions. Perception & Psychophysics. 2008;70(3):456–464. doi: 10.3758/pp.70.3.456. [DOI] [PubMed] [Google Scholar]
- Gabor D. Theory of communication. J Inst Electr Eng. 1946;24:891–910. [Google Scholar]
- Gillen C, Heath M. Perceptual averaging governs antisaccade endpoint bias. Exp Brain Res. 2014;232:3201–3210. doi: 10.1007/s00221-014-4010-1. [DOI] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Rapid extraction of mean emotion and gender from sets of faces. Current Biology. 2007;17(17):R751–R753. doi: 10.1016/j.cub.2007.06.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Seeing the mean: Ensemble coding for sets of faces. Journal of Experimental Psychology: Human Perception and Performance. 2009;35(3):718–734. doi: 10.1037/a0013899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberman J, Whitney D. Ensemble perception: Summarizing the scene and broadening the limits of visual processing. In: Wolfe J, Robertson L, editors. A Festschrift in honor of Anne Treisman. Oxford University Press; 2011. [Google Scholar]
- Halberda J, Sires SF, Feigenson L. Multiple Spatially Overlapping Sets Can Be Enumerated in Parallel. Psychological Science. 2006;17(7):572–576. doi: 10.1111/j.1467-9280.2006.01746.x. [DOI] [PubMed] [Google Scholar]
- Huang L, Pashler H. Attention capacity and task difficulty in visual search. Cognition. 2005;94(3):B101–11. doi: 10.1016/j.cognition.2004.06.006. [DOI] [PubMed] [Google Scholar]
- Huang L, Pashler H, Junge JA. Are there capacity limitations in symmetry perception? Psychonomic Bulletin & Review. 2004;11(5):862–869. doi: 10.3758/bf03196713. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J Physiol. 1962;160(1):106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Im HY, Chong SC. Computation of mean size is based on perceived size. Attention, Perception & Psychophysics. 2009;71(2):375–384. doi: 10.3758/APP.71.2.375. [DOI] [PubMed] [Google Scholar]
- Im HY, Chong SC. Mean size as a unit of visual working memory. Perception. 2014;43(7):663–676. doi: 10.1068/p7719. [DOI] [PubMed] [Google Scholar]
- Jacoby O, Kamke MR, Mattingley JB. Is the whole really more than the sum of its parts? Estimates of average size and orientation are susceptible to object substitution masking. Journal of Experimental Psychology: Human Perception and Performance. 2013;39(1):233–244. doi: 10.1037/a0028762. [DOI] [PubMed] [Google Scholar]
- Jennings JR, Wood CC. The e-adjustment procedure for repeated- measures analyses of variance. Psychophysiology. 1976;13:277–278. doi: 10.1111/j.1469-8986.1976.tb00116.x. [DOI] [PubMed] [Google Scholar]
- Joo SJ, Shin K, Chong SC, Blake R. On the nature of the stimulus information necessary for estimating mean size of visual arrays. Journal of Vision. 2009;9(9):1–12. doi: 10.1167/9.9.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooi FL, Toet A, Tripathy SP, Levi DM. The effect of similarity and duration on spatial interaction in peripheral vision. Spatial vision. 1994;8(2):255–279. doi: 10.1163/156856894x00350. [DOI] [PubMed] [Google Scholar]
- Lüschow A, Nothdurft HC. Pop-out of orientation but no pop-out of motion at isoluminance. Vision Research. 1993;33(1):91–104. doi: 10.1016/0042-6989(93)90062-2. [DOI] [PubMed] [Google Scholar]
- Marchant AP, Simons DJ, de Fockert JW. Ensemble representations: Effects of set size and item heterogeneity on average size perception. Acta Psychol. 2013;142(2):245–250. doi: 10.1016/j.actpsy.2012.11.002. [DOI] [PubMed] [Google Scholar]
- Miller AL, Sheldon R. Magnitude estimation of average length and average inclination. Journal of Experimental Psychology. 1969;81(1):16–21. doi: 10.1037/h0027430. [DOI] [PubMed] [Google Scholar]
- Morey RD. Confidence intervals from normalized data: A correction to Cousineau (2005) Reason. 2008;4(2):61–64. [Google Scholar]
- Myzczek K, Simons DJ. Better than average: Alternatives to statistical summary representations for rapid judgments of average size. Perception & psychophysics. 2008;70(5):772–788. doi: 10.3758/pp.70.5.772. [DOI] [PubMed] [Google Scholar]
- Noë A. Is the visual world a grand illusion? Journal of Consciousness Studies. 2002;9(5–6):1–12. [Google Scholar]
- Noë A, Pessoa L, Thompson E. Beyond the grand illusion: What change blindness really teaches us about vision. Visual Cognition. 2000;7(1–3):93–106. [Google Scholar]
- Oriet C, Brand J. Size averaging of irrelevant stimuli cannot be prevented. Vision Research. 2013;79:8–16. doi: 10.1016/j.visres.2012.12.004. [DOI] [PubMed] [Google Scholar]
- Palmer J. Set-size effects in visual search: The effect of attention is independent of the stimulus for simple tasks. Vision Research. 1994;34:1703–1721. doi: 10.1016/0042-6989(94)90128-7. [DOI] [PubMed] [Google Scholar]
- Palmer J. Attention in visual search: Distinguishing four causes of set-size effects. Current Directions in Psychological Science. 1995;4:118–123. [Google Scholar]
- Parkes L, Lund J, Angelucci A, Solomon JA, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4(7):739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Pashler HE. The psychology of attention. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Pelli DG. The Video Toolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Peterson CR, Beach LR. Man as an intuitive statistician. Psychological bulletin. 1967;68(1):29–46. doi: 10.1037/h0024722. [DOI] [PubMed] [Google Scholar]
- Pollard P. Intuitive judgments of proportions, means, and variances: A review. Current Psychology. 1984;3(1):5–18. [Google Scholar]
- Poltoratski S, Xu Y. The association of color memory and the enumeration of multiple spatially overlapping sets. Journal of Vision. 2013;13(8):1–11. doi: 10.1167/13.8.6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robitaille N, Harris IM. When more is less: Extraction of summary statistics benefits from larger sets. Journal of Vision. 2011;11(12):1–8. doi: 10.1167/11.12.18. [DOI] [PubMed] [Google Scholar]
- Rosenholtz R. What your visual system sees where you are not looking. In: BER, Pappas TN, editors. SPIE: Human Vision and Electronic Imaging. XVI. 2011. p. 7865.p. 786510. [Google Scholar]
- Rosenholtz R, Huang J, Raj A, Balas BJ, Ilie L. A summary statistic representation in peripheral vision explains visual search. Journal of Vision. 2012;12(4):1–17. doi: 10.1167/12.4.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharff A, Palmer JP, Moore CM. Extending the simultaneous–sequential paradigm to measure perceptual capacity for features and words. Journal of Experimental Psychology: Human Perception and Performance. 2011a;37(3):813–833. doi: 10.1037/a0021440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharff A, Palmer JP, Moore CM. Evidence of fixed capacity in visual object categorization. Psychonomic Bulletin & Review. 2011b;18(4):713–721. doi: 10.3758/s13423-011-0101-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharff A, Palmer JP, Moore CM. Divided attention limits perception of 3-D object shapes. Journal of Vision. 2013;13(2):1–24. doi: 10.1167/13.2.18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw ML. Identifying attentional and decision-making components in information processing. Attention and Performance. 1980;8:277–296. [Google Scholar]
- Shiffrin RM, Gardner GT. Visual processing capacity and attentional control. Journal of Experimental Psychology. 1972;93(1):72–82. doi: 10.1037/h0032453. [DOI] [PubMed] [Google Scholar]
- Suzuki S. High-level pattern coding revealed by brief shape aftereffects. In: Clifford C, Rhodes G, editors. Fitting the mind to the world: Adaptation and aftereffects in high-level vision (Advantages in Visual Cognition Series) Vol. 2. Oxford University Press; 2005. [Google Scholar]
- Sweeny TD, Haroz S, Whitney D. Perceiving group behavior: Sensitive ensemble coding mechanisms for biological motion of human crowds. Journal of Experimental Psychology: Human Perception and Performance. 2013;39(2):329–337. doi: 10.1037/a0028712. [DOI] [PubMed] [Google Scholar]
- Townsend JT. Serial vs. parallel processing: Sometimes they look like Tweedledum and Tweedledee but they can (and should) be distinguished. Psychological Science. 1990;1:46–54. [Google Scholar]
- Treisman AM, Gelade G. A feature-integration theory of attention. Cognitive Psychology. 1980;12(1):97–136. doi: 10.1016/0010-0285(80)90005-5. [DOI] [PubMed] [Google Scholar]
- Treisman A, Souther J. Search asymmetry: A diagnostic for preattentive processing of separable features. Journal of Experimental Psychology: General. 1985;114:285–310. doi: 10.1037//0096-3445.114.3.285. [DOI] [PubMed] [Google Scholar]
- Utochkin IS, Tiurina NA. Parallel averaging of size is possible but range-limited: A reply to Marchant, Simons, and De Fockert. Actpsy. 2014;146(C):7–18. doi: 10.1016/j.actpsy.2013.11.012. [DOI] [PubMed] [Google Scholar]
- Walker D, Vul E. Hierarchical Encoding Makes Individuals in a Group Seem More Attractive. Psychological Science. 2014;25(1):230–235. doi: 10.1177/0956797613497969. [DOI] [PubMed] [Google Scholar]
- Watamaniuk SN, Sekuler R, Williams DW. Direction perception in complex dynamic displays: the integration of direction information. Vision Research. 1989;29(1):47–59. doi: 10.1016/0042-6989(89)90173-9. [DOI] [PubMed] [Google Scholar]
- Webster MA, De Valois RL. Relationship between spatial-frequency and orientation tuning of striate-cortex cells. J Opt Soc Am A. 1985;2(7):1124–1132. doi: 10.1364/josaa.2.001124. [DOI] [PubMed] [Google Scholar]
- Weiss DJ, Anderson NH. Subjective averaging of length with serial presentation. Journal of Experimental Psychology. 1969;82(1):52–63. [Google Scholar]
- Whiting BF, Oriet C. Rapid averaging? Not so fast! Psychonomic Bulletin & Review. 2011;18(3):484–489. doi: 10.3758/s13423-011-0071-3. [DOI] [PubMed] [Google Scholar]
- Whitney D. Vision: Seeing through the Gaps in the Crowd. Current Biology. 2009;19(23):R1075–R1076. doi: 10.1016/j.cub.2009.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitney D, Haberman J, Sweeny TD. From textures to crowds: Multiple levels of summary statistical perception. In: Werner JS, Chalupa LM, editors. The new visual neurosciences. Cambridge, MA: MIT Press; 2014. [Google Scholar]
- Wolfe JM. Guided Search 2.0 A revised model of visual search. Psychonomic Bulletin & Review. 1994;1(2):202–238. doi: 10.3758/BF03200774. [DOI] [PubMed] [Google Scholar]
- Wolfe JM. Visual search. In: Pashler H, editor. Attention. Hove, England: Psychology Press; 1998. [Google Scholar]
- Wolfe JM, Friedman-Hill SR, Bilsky AB. Parallel processing of part-whole information in visual search tasks. Perception & Psychophysics. 1994;55(5):537–550. doi: 10.3758/bf03205311. [DOI] [PubMed] [Google Scholar]
- Wolfe JM, Võ MLH, Evans KK, Greene MR. Visual search in scenes involves selective and nonselective pathways. Trends in Cognitive Sciences. 2011;15(2):77–84. doi: 10.1016/j.tics.2010.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM, Yu KP, Stewart MI, Shorter AD, Friedman-Hill SR, Cave KR. Limitations on the parallel guidance of visual search: Color × Color and Orientation × Orientation conjunctions. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:879–892. doi: 10.1037//0096-1523.16.4.879. [DOI] [PubMed] [Google Scholar]