Accurate typing of short tandem repeats from genome-wide sequencing data and its applications

Abstract

Short tandem repeats (STRs) are implicated in dozens of human genetic diseases and contribute significantly to genome variation and instability. Yet profiling STRs from short-read sequencing data is challenging because of their high sequencing error rates. Here, we developed STR-FM, short tandem repeat profiling using flank-based mapping, a computational pipeline that can detect the full spectrum of STR alleles from short-read data, can adapt to emerging read-mapping algorithms, and can be applied to heterogeneous genetic samples (e.g., tumors, viruses, and genomes of organelles). We used STR-FM to study STR error rates and patterns in publicly available human and in-house generated ultradeep plasmid sequencing data sets. We discovered that STRs sequenced with a PCR-free protocol have up to ninefold fewer errors than those sequenced with a PCR-containing protocol. We constructed an error correction model for genotyping STRs that can distinguish heterozygous alleles containing STRs with consecutive repeat numbers. Applying our model and pipeline to Illumina sequencing data with 100-bp reads, we could confidently genotype several disease-related long trinucleotide STRs. Utilizing this pipeline, for the first time we determined the genome-wide STR germline mutation rate from a deeply sequenced human pedigree. Additionally, we built a tool that recommends minimal sequencing depth for accurate STR genotyping, depending on repeat length and sequencing read length. The required read depth increases with STR length and is lower for a PCR-free protocol. This suite of tools addresses the pressing challenges surrounding STR genotyping, and thus is of wide interest to researchers investigating disease-related STRs and STR evolution.

Short tandem repeats (STRs) of 1–6 base pairs per motif constitute ∼3% of the human genome (Lander 2001). Due to the high incidence of polymerase slippage at STRs (Levinson and Gutman 1987; Abdulovic et al. 2011; Baptiste and Eckert 2012), these repeats have elevated germline mutation and polymorphism rates. After a certain threshold length, STRs are termed microsatellites (Kelkar et al. 2010; Ananda et al. 2013). The high level of polymorphism makes microsatellites attractive markers for population and conservation genetics studies (Jarne and Lagoda 1996; Sunnucks 2000; Wan et al. 2004; Kim and Sappington 2013) and for identifying individuals in forensics (Hagelberg et al. 1991; Chambers et al. 2014). Many STRs are involved in gene regulation and protein function (Li et al. 2004), with ∼17% of human genes containing STRs in their open reading frames (Gemayel et al. 2010). Although long microsatellites have attracted much attention, length alterations even within relatively short repeat tracts are sometimes associated with disease (Li et al. 2004). For instance, differences in the number of repeats at the (TG)_10-13(T)_5-9 STR located within the splicing branch/acceptor site of the CFTR gene (exon 9) can affect in-frame exon skipping and, as a result, can influence the severity of cystic fibrosis (Cuppens et al. 1990; Chu et al. 1991). The purity of STRs (the degree to which the perfect STR sequence remains uninterrupted) also has a functional effect. Interrupted STRs have lower mutation rates (Ananda et al. 2014), and this can diminish disease risk. For instance, ∼6% of Ashkenazi Jews have a T to A mutation in the APC gene (encoding for a tumor suppressor) that alters an interrupted STR (A)₃T(A)₄ into a perfect (A)₈ (Laken et al. 1997). This increases the probability of somatic frameshift mutation within the STR, leading to APC protein inactivation. As a result, Ashkenazi Jews have a higher colorectal cancer risk (Gryfe et al. 1999). Since even small changes in STR length and purity can have functional effects, accurate STR profiling is crucial.

Despite the importance of STRs in evolution and disease, their accurate genotyping from next generation sequencing (NGS) data has been challenging (for review, see Treangen and Salzberg 2012). Sequencing library construction frequently includes polymerase chain reaction (PCR) steps during which a polymerase might undergo slippage at STRs, leading to amplicons that differ in length due to expansion and contraction of repeat units (Ellegren 2004; Wang et al. 2011). Additionally, base calling by NGS instruments at repetitive regions is frequently imprecise. These factors result in high sequencing errors at homopolymer runs produced by the 454 (Roche) and Illumina instruments (Balzer et al. 2010; Albers et al. 2011).

From a bioinformatics perspective, if STR-containing reads are mapped in their entirety, some reads cannot be mapped because of high mismatch/indel penalties associated with STR lengths different than those at the corresponding positions in the reference genome. This obscures accurate estimation of allele frequency and underestimates the real level of STR variation in the genome. To alleviate this problem, a short-read alignment approach using nonrepetitive flanks of STR-containing reads has been proposed recently (lobSTR) (Gymrek et al. 2012). This tool has fast running time and takes into account PCR stutter noise during the genotyping stage. However, the entropy scanning implemented by lobSTR to detect STRs has low sensitivity for mononucleotide STRs and short STRs (<25 bp), which constitute a large proportion of STRs in the genome. Additionally, the allele frequency at STRs for genetically heterogeneous samples, for which a simple 1:1 ratio in allele frequency present in heterozygous diploids is not expected (e.g., for tumors, viral populations, and organelles), cannot be determined. Furthermore, lobSTR uses a fixed (embedded in the program) mapping algorithm. Novel short-read mapping and STR detection algorithms (Pellegrini et al. 2010; Lim et al. 2013) are constantly being developed; an STR-profiling tool that can be customized to incorporate emerging mapping algorithms is needed.

The recently released PCR-free Illumina library preparation protocol (hereafter called “PCR−”) is expected to improve STR genotyping accuracy. The direct advantage of limiting PCR steps during NGS is the increased uniformity of the sequencing depth (Kozarewa et al. 2009). Also, this protocol eliminates duplicate reads that obscure allele frequency profiling for heterogeneous genetic samples. Importantly, the degree to which the accuracy of calling STR alleles is improved using the PCR-free protocol has not been evaluated previously. Moreover, massive amounts of data have already been generated by the NGS technology with the PCR-containing library preparation protocol (hereafter called “PCR+”), and some such data cannot be regenerated due to the scarcity of samples and/or time and cost constraints. Therefore, universal methods are urgently needed that can evaluate and correct STR errors generated by NGS technology (both PCR− and PCR+) and accommodate evolving protocols and sequencing techniques.

Some efforts have been made to evaluate errors generated by NGS at STRs. For instance, errors at STRs sequenced with the PCR+ protocol vary with repeat number and motif size (Luo et al. 2012). However, an explicit quantitation of various sources of STR-related sequencing errors has been lacking, which hinders an unambiguous estimation of STR mutational properties. Indeed, as both mutation and sequencing error rates increase with STR length (Kelkar et al. 2008; Luo et al. 2012; Highnam et al. 2013), one cannot confidently decipher mutation rates without accounting for sequencing error rates. Recently, a tool to guide genotyping of STRs using informed error profiles from inbred Drosophila lines (RepeatSeq) has been released (Highnam et al. 2013). This tool utilizes reads mapped by other programs, such as BWA (Li and Durbin 2009) and Bowtie (Langmead et al. 2009), and predicts the most probable genotype at a locus based on STR motif, length, and base quality. However, RepeatSeq uses the whole-read mapping approach, which introduces a bias toward the STR length in the reference genome (Gymrek et al. 2012) and thus might obscure the true STR variation spectrum. Such biases can be accounted for by an error correction model based on the STR flank-based method.

To profile the full spectrum of STR lengths in the human and other genomes, and to correct for NGS-associated STR errors, we developed STR-FM (short tandem repeat profiling using a flank-based mapping approach), a flexible pipeline for detecting and genotyping STRs from short-read sequencing data. Our pipeline can detect STRs of any length, including short ones (as short as only two repeats), includes an error-correcting module, and can incorporate any NGS mapping algorithm with paired-end mapping capability, making it adaptable to new mapping methods as they become available. Applying this pipeline, we asked the following questions. First, what are the rates and patterns of sequencing errors associated with STRs of different motif sizes (mono-, di-, tri-, and tetranucleotides), motif compositions, and repeat numbers? These were contrasted between publicly available genome-wide data sets sequenced with PCR+ and PCR− protocols and validated with in-house generated, ultradeep sequencing of plasmids harboring individual STR sequences. Second, do technical errors have different patterns from true STR mutations? Third, based on the detailed knowledge of the error profiles, what is the minimum sequencing depth required for producing reliable STR genotypes for PCR+ and PCR− protocols? As a result, we provide the scientific community with STR-FM, a reproducible and versatile pipeline for genotyping STRs that incorporates an error correction model. To illustrate the utility of STR-FM, we applied it to the completely sequenced human genomes from the Platinum Genomes Project (Ajay et al. 2011) and determined human genome-wide germline mutation rates at STRs.

Results

The STR-FM pipeline

We designed the STR-FM pipeline as a collection of tools in Galaxy (Giardine et al. 2005; Blankenberg et al. 2010, 2014; Goecks et al. 2010), providing integration with various mapping algorithms and customization for a variety of applications. Either single-end or paired-end sequencing data can be utilized; for paired-end read data, each read is treated separately. The core of the pipeline consists of the following three procedures (Supplemental Fig. S1). First, STR-FM runs a short-read STR detection tool using a string comparison algorithm (see Methods for details). The algorithm can detect exact (pure, or uninterrupted) STRs (mono- through hexanucleotide STRs greater than or equal to two repeats), incomplete motifs (e.g., ATATATA), interrupted STRs (e.g., AAAATAAAAA), or multiple STRs in a read. Reads that do not have sufficient upstream or downstream sequences flanking the STRs are discarded (we used a threshold of 20 bp on each side of an STR). Next, each read is split into two “pseudoreads,” containing the upstream and downstream flanks surrounding the STR. These are mapped to the reference genome using a standard paired-end read-mapping algorithm, e.g., BWA (Li and Durbin 2009, 2010), Bowtie (Langmead et al. 2009), or Bowtie 2 (Langmead and Salzberg 2012), treating each pair of flanking sequences as a faux paired-end read. Finally, STR-FM runs a profiler tool, which groups all reads with STRs that are mapped to the same location in the reference genome. As a result, an array of all STR lengths from the reads mapping to a particular STR-containing locus is generated. The number of reads that completely cover an STR and its flanks is referred to as the “informative sequencing depth.” See Supplemental Text for details about running time and sensitivity of detection (Supplemental Tables S1–S5; Supplemental Fig S2).

Assessment of error profiles at STRs for PCR+ and PCR− library preparation protocols

The NGS errors at STRs were evaluated using two data sets. First, we utilized the PCR+ DNA sequencing data generated on a HiSeq instrument (150× depth) for a human male (SAMN00716185) sequenced as a part of the iPOP study (Chen et al. 2012). We combined the blood and saliva samples, as they had similar error profiles (see below). Second, we utilized the PCR− sequencing data generated on a HiSeq instrument (245× depth) for a human male blood sample (NA12882) sequenced as a part of the Platinum Genome Project (Ajay et al. 2011). The PCR− data were down-sampled to obtain the same number of filtered STRs (for each motif size) as present in the PCR+ data set for fair comparison, i.e., to obtain the 150× depth. These two data sets are comparable because both were generated on a HiSeq instrument using paired-end 100-bp reads. Therefore, the differences in their STR error profiles are expected to reflect the contribution of the PCR step during library preparation. To avoid heterozygous sites, we limited our analysis to the non-pseudoautosomal regions of Chromosome X. As this chromosome is hemizygous in males, any STR variability within an allele should result primarily from PCR and sequencing errors. We analyzed mono-, di-, tri-, and tetranucleotide STRs, which have lengths of at least 5, 6, 9, and 12 bp, respectively (the numbers of STRs analyzed are listed in Supplemental Table S6; fewer loci were detected in the regions occupied by Alu and L1 repetitive elements [Supplemental Table S5]). Only uninterrupted (perfect) STRs were considered. A stringent procedure was used to reduce bioinformatics errors (e.g., we removed nonuniquely mapped reads and reads with improper orientation between pairs, etc.; see Methods for details). For each STR locus in the reference genome's Chromosome X, we collected all mapped STR-containing reads using STR-FM and assigned the most frequent STR length as the major allele length for that particular locus. All STR lengths that differed from the major allele length were considered to represent sequencing errors. As the rate of sequencing errors correlates with STR length (Luo et al. 2012; Highnam et al. 2013), we grouped STR loci by the major allele length and evaluated their error profiles.

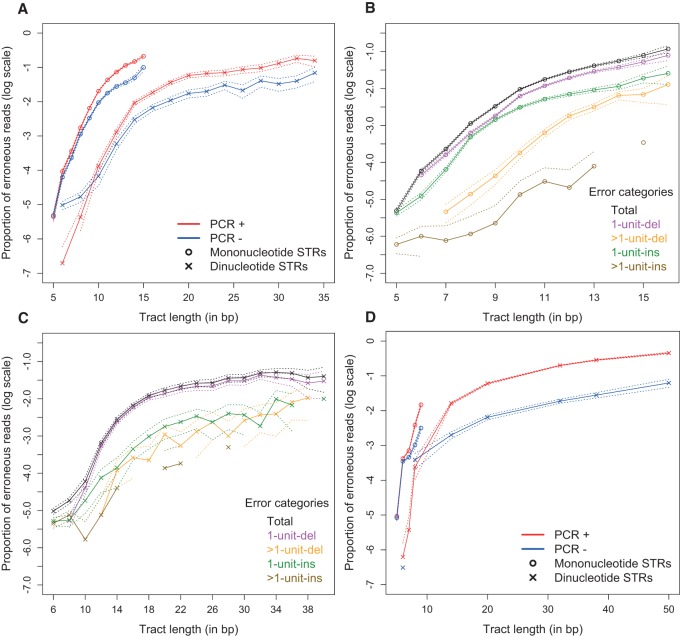
The PCR+ data had significantly higher error rates than the PCR− data for both mono- and dinucleotide STRs (Fig. 1A), except for very short ones (repeat number ≤5). For mononucleotide STRs, the difference in error rates increases until ∼11 bp, after which it plateaus at an ∼2.5-fold difference. For dinucleotide STRs, the difference increases until ∼16 bp, plateauing at an ∼3.6-fold difference. For most tri- and tetranucleotide loci studied (Supplemental Fig. S3), the PCR+ data also had higher error rates than the PCR− data; however, the confidence intervals of the two curves frequently overlapped. Blood and saliva PCR+ data had similar error profiles (Supplemental Fig. S4). Our overall results did not change considerably depending on whether we used the complete (245×) or down-sampled (150×) PCR− data (Supplemental Fig. S5); therefore, in the subsequent analyses we used the error rates from the complete (245×) PCR− data set, because it produces more narrow confidence intervals.

Figure 1.

Erroneous call rates for Illumina data. The dotted lines represent the 95% confidence intervals of the multinomial sampling. Only repeat lengths with ≥100 read support (all loci combined) were plotted. (A) Human male X Chromosome for PCR-containing (PCR+) and PCR-free (PCR−; down-sampled data) library preparation protocols. (B) PCR− mononucleotide STR error rates by error categories. See text for the explanation of the categories. (C) PCR− dinucleotide STR error rates by error categories. (D) Error rates for ultradeep sequencing of plasmids with PCR+ and PCR− protocols.

We observed several trends that were similar for both PCR+ and PCR− data. For all four repeat motif sizes, the error rates increased exponentially with repeat length and approached a plateau at longer repeats (Fig. 1A; Supplemental Figs. S3, S5), corroborating previous studies (Albers et al. 2011; Gymrek et al. 2012; Montgomery et al. 2013). For a fixed repeat length, error rates were highest for mononucleotide, intermediate for dinucleotide and trinucleotide, and lowest for tetranucleotide STRs (Fig. 1A; Supplemental Figs. S3, S5). We also classified sequencing errors into four categories: (1) shorter than the major allele length by one repeat (1-unit-del); (2) shorter by more than one repeat (>1-unit-del); (3) longer by one repeat (1-unit-ins); or (4) longer by more than one repeat (>1-unit-ins). The “1-unit-del” was the most common error category for all STRs (Fig. 1B,C; Supplemental Figs. S6, S7). For mono- and di-nucleotide STRs, the “1-unit-del” was followed (in the order of diminishing prevalence) by “1-unit-ins”, “>1-unit-del”, and “>1-unit-ins” (Fig. 1B,C; Supplemental Fig. S6A,B). For the other STRs, no further conclusions could be drawn due to the limited number of sites and overlapping confidence intervals (Supplemental Figs. S6, S7).

We also studied the effect of motif composition on the error rate. For dinucleotide STRs at least 14 bp (seven units) long, significantly higher error rates were observed at (AT/TA)_n repeats than at (AC/GT)_n, (AG/CT)_n, and (GC/CG)_n repeats, in both PCR+ and PCR− data (Supplemental Fig. S8B,D). For mononucleotide STRs, no significant differences in error rates between (A/T) and (G/C) repeats were observed for the lengths studied (Supplemental Fig. S8A,C). For tri- and tetranucleotide STRs, the number of loci was insufficient to evaluate the influence of motif composition on error rates.

Somatic mutations also might contribute to the STR variability in the two data sets analyzed here; however, both the PCR+ and PCR− data should be affected by them equally. Moreover, the somatic mutation rates of dinucleotide STRs estimated in previous studies (Hile et al. 2000; Baptiste and Eckert 2012) are 100- to 1000-fold lower than the error rates estimated here (for the same repeat number). Therefore, the contribution of somatic mutations to STR error rates estimation here is negligible.

Confirmation of STR error patterns via ultradeep sequencing of plasmids

The genome-wide PCR+ and PCR− data sets utilized above were generated in two different sequencing facilities, and this might have contributed to the discrepancy in their error rates, e.g., due to batch effect. We therefore sought to confirm our findings with an additional data set that we generated entirely in our own laboratory; namely, using both PCR+ and PCR− protocols, we sequenced STRs cloned in a plasmid vector. All data were generated in our facility using the same DNA samples, personnel, and equipment. We sequenced 11 plasmid libraries containing STR inserts (Supplemental Tables S7, S8) and a control vector plasmid library without an STR insert. We generated ∼100,000× depth on a MiSeq instrument, which has error rates comparable to those of HiSeq (Quail 2012). In addition to the inserts, all plasmid vector sequences contained 49, 14, and one mono-, di-, and trinucleotide STRs, respectively (Supplemental Table S8). Our plasmid analyses confirmed that PCR+ data had significantly higher STR error rates than PCR− data for mono- and dinucleotide STRs (Fig. 1D). The error rates between PCR+ and PCR− data were comparable for short STRs; however, for both mono- and dinucleotide STRs that were at least seven repeats long, the PCR+ data had consistently higher STR rates than PCR− data—by ∼4.2- and ∼9.3-fold for mono- and dinucleotide STRs, respectively. Our plasmid analysis also confirms that the “1-unit-del” is the most common category of errors (Supplemental Fig. S9).

Statistical model for genotyping STRs from NGS data

The error profiles estimated in this study can be used to correct for TR errors in several applications, including genotyping of diploid samples (distinguishing between homozygotes and heterozygotes) and of heterogeneous genetic samples (e.g., tumors, viral populations, and DNA-containing organelles). To achieve this, we developed an error correction model that takes STR features (repeat number and motif identity) into account (see Methods for details). Our error correction model can utilize error profiles (error rates depending on repeat numbers and motif identity) provided by the user (e.g., for novel sequencing technology), and thus is not limited to those generated by this study. The model determines the three most frequent STR lengths for an individual locus, and, based on the STR error array for this motif and repeat number, calculates the probability of generating this profile by a homozygote (all three possible homozygotes are evaluated) versus a heterozygote (all three possible heterozygotes are evaluated). For instance, the model is able to decipher the true genotype (A)₉/(A)₁₁, even in the presence of (A)₁₀ variant calls. It determines the most probable heterozygote and homozygote alleles at a locus from the NGS data and reports the log odds ratio between their probabilities, which can be interpreted as a confidence of genotyping (the higher this value is from 0, the more confidence we have in this genotype). For example, if for an STR locus sequenced at depth 9× we observed three, three, and three reads with (A)₉, (A)₁₀, and (A)₁₁, respectively, the most probable heterozygote is (A)₉(A)₁₁, and the most probable homozygote is (A)₁₀. According to the model, the log odds ratio for (A)₉(A)₁₁ compared to (A)₁₀ is 8.64 × 10⁴, strongly favoring a heterozygote in this case.

Accuracy of the genotyping model in diploid samples

To test the performance of our error correction model, we generated a pseudodiploid data set. For each class of STRs, we selected loci on the human male X Chromosome (from the same data sets that we used to evaluate the STR error profiles of the PCR+ and PCR− data above) that are supported by at least five reads. Then, we generated 10,000 sets of “homozygous” loci by randomly selecting two loci with the same motif and repeat number and combining their reads. Similarly, 10,000 “heterozygous” loci were generated by randomly selecting two loci with the same motif but different repeat numbers and combining their reads. We focused on the repeat numbers for which we could estimate error profiles with high confidence: length ranges of 6–15 bp, 8–23 bp, 12–20 bp, and 16–23 bp for mono-, di-, tri-, and tetranucleotide STRs, respectively (see Methods; Supplemental Tables S9, S10). Here we used error profiles from the human X Chromosome data as they include wider STR length range and higher resolution compared with the plasmid data.

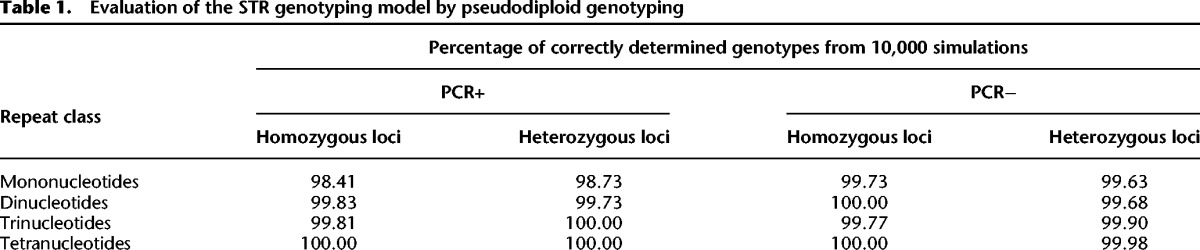
The genotyping model correctly determined the genotype for 98%–100% of both homozygotes and heterozygotes (Table 1). For STRs with motif size of at least two, our model's accuracy was at least 99.68%. Mononucleotide STRs were slightly more difficult to genotype correctly than the other STR classes (1%–2% lower accuracy) and were more difficult to genotype with PCR+ data than with PCR− data (∼1% lower accuracy). This is consistent with mononucleotide STRs having higher error rates (Fig. 1A,D; Supplemental Fig. S5).

Table 1.

Evaluation of the STR genotyping model by pseudodiploid genotyping

To investigate factors contributing to erroneous genotyping of mononucleotide STRs, we used logistic regressions with the correct prediction of an allele combination as the response and with four predictors: the read depth, STR length, the difference in the lengths of STR alleles (for heterozygotes), and the ratio of read depths supporting each allele (for heterozygotes; see Methods for details). A separate logistic regression was run for PCR+ and PCR− data and for heterozygous versus homozygous alleles. All four predictors were significant in at least one of the four models (Supplemental Table S11), although the sets of significant predictors and their relative contribution to the explained variability differed among models. However, we observed that high sequencing depth, small STR length, large difference between two alleles in heterozygotes, and similar ratio of read depths supporting each allele in heterozygotes increased the prediction power of each model (see Fig. 2 for examples).

Figure 2.

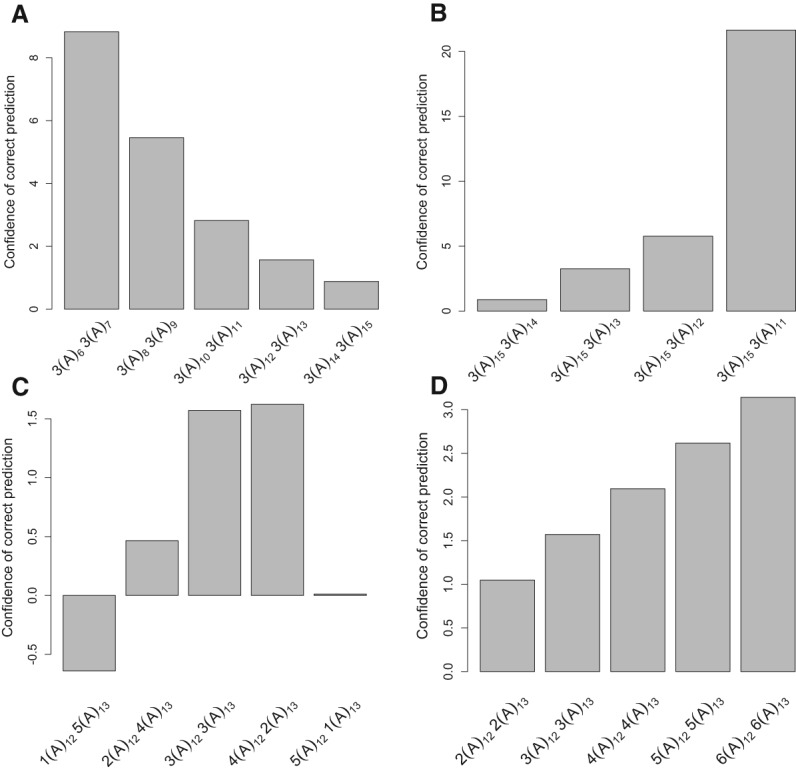
Factors that affect the accuracy of STR heterozygote genotyping, using the error correction model. (A) STR length. (B) The length difference in a heterozygote. (C) The ratio of read depths supporting each allele. (D) Read depth. All read profiles are generated from (A)_m (A)_n heterozygotes. The x-axis shows different STR length arrays, with the number of reads indicated for each genotype. The y-axis (confidence of correct prediction) shows the ratio of the probability for a locus to be a heterozygote versus a homozygote depending on the read length profile. The magnitude of the bar implies higher confidence in genotyping. The negative value indicates incorrect genotyping. PCR− error profiles from human X Chromosome data were used to calculate probabilities that the read profiles correspond to homozygous or heterozygous loci, which reflects the accuracy of genotyping, since the true genotype is a heterozygote.

We also evaluated the robustness of genotyping using technically replicated samples—two PCR− libraries (43× and 60×) of the whole genome for sample NA12882 from the Platinum Genome Project (Ajay et al. 2011). We profiled the STR lengths and genotyped those sites that had a minimum informative read depth of 5× in both samples. The ratio of loci that had different genotypes (the genotype discordance rate) between the two replicated libraries was only 0.29%.

Accuracy of the genotyping model in heterogeneous genetic samples

Our error correction model is able to accommodate applications other than standard diploid genotyping. For example, the allele contribution ratio can be modified to allow for a nondiploid allele frequency ratio commonly present in tumors and genomes of organelles (e.g., mitochondrial DNA). The user can find the percentage of heterogeneity that maximizes the likelihood of the observed STR length array or test the ratio that was suggested by a linked genetic marker (e.g., a SNP). To demonstrate this capability, we genotyped a sample of two plasmids with cloned mtDNA D-loop sequence, premixed at five different ratios—98:2, 99:1, 99.5:0.5, 99.75:0.25, and 99.9:0.1. The two plasmids differ at only one STR-containing region: the plasmid Z1-1 with a higher proportion of DNA in the mixture has a (C)₈ allele, whereas the lower proportion plasmid R2 has a (C)₇ allele (Rebolledo-Jaramillo et al. 2014). Each mixed DNA sample was sequenced on a MiSeq instrument using 250-bp paired-end reads at the depth of 300–2000× per site. Each mixture was sequenced twice to generate two replicates. We ran our STR-FM pipeline separately on each mixture and each replicate and genotyped the STR locus in each case. Since the plasmids were sequenced at a very high depth, the prediction should reflect the competency of the model to detect the rare allele and not the sequencing depth (see below). The minor allele was detected for both replicates at ratios of 98:2 and 99:1 and in one of the two replicates for the other three mixing ratios (Supplemental Table S12).

Genotyping disease-associated long trinucleotide STRs

We explored the abilities of the STR-FM pipeline and statistical model to genotype long trinucleotide repeats associated with diseases. Using the PCR−data described above (NA12882 sequenced with 100-bp reads at 245× depth) (Ajay et al. 2011), we genotyped 10 disease-related trinucleotide STRs from Supplemental Table S1 in Castel et al. (2010). Five of them had read depths above 5× (repeat length 16–48) and thus could be genotyped with confidence >90%. These included a 48-bp (homozygote) CAG repeat in the JPH3 gene (Wilburn et al. 2011), which is associated with Huntington's disease-like 2, and a 32-bp (also homozygote) CCG repeat in the RELN gene, which is associated with a higher risk of autism (Supplemental Table S13). For the remaining five loci (including those associated with spinocerebellar ataxia 6, Jacobsen syndrome, dentatorubral-pallidouysian atrophy, and Huntington's disease; repeat length of 34–55 bp), the informative read depth was below 5× preventing us from genotyping such loci with confidence (Supplemental Table S13).

STR germline mutation rates and patterns

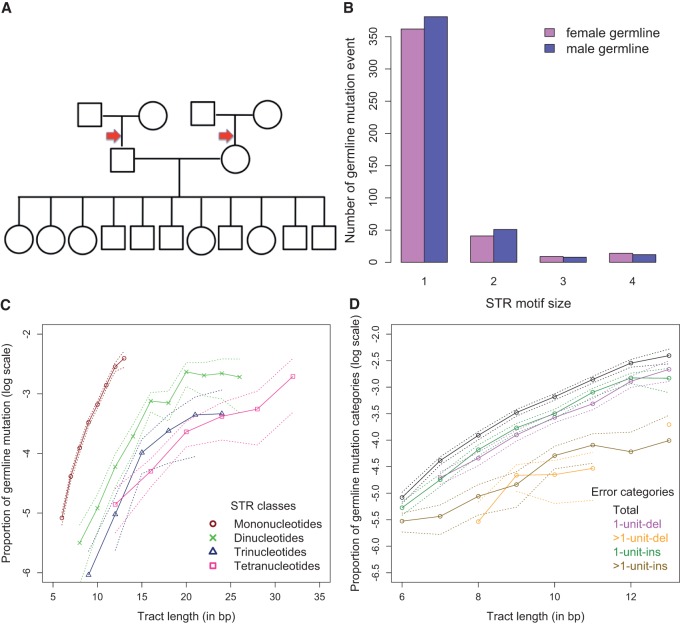
The germline mutation rate is a fundamental parameter in molecular evolution; however, it has not been evaluated for human STRs on a genome-wide scale. We utilized our genotyping model to estimate STR germline mutation rates using a three-generation pedigree—four grandparents, two parents, and 11 children (Fig. 3A)—sequenced at high depth (43–64×) with a PCR− protocol as part of the Platinum Genome Project (Ajay et al. 2011). For each sequenced individual, we detected and genotyped uninterrupted (perfect) STRs with at least 6, 8, 9, and 12 bp for mono-, di-, tri-, and tetranucleotide STRs, respectively.

Figure 3.

Germline mutation rate analyses using STR-FM. (A) Cartoon of the pedigree used, with arrows showing branches where mutations were detected. (B) The numbers of de novo mutations arising in the male and female germ lines. (C) The germline mutation rates for STRs with different length and motif size. The dotted lines represent the 95% confidence interval of the multinomial sampling. Only repeat lengths with ≥2000 loci support were plotted. (D) The frequencies of different mutation categories for mononucleotide STRs. The dotted lines represent 95% confidence intervals from multinomial sampling. Only repeat numbers with ≥2000 loci support were plotted.

Overall, the distribution of STR allele lengths as evaluated from sample NA12882 (one of the 11 children) was similar to that described in the recent studies (McIver et al. 2011; Payseur et al. 2011; Gymrek et al. 2012; Willems et al. 2014): The proportions of variable loci increased with repeat length and, at the same repeat length, were lower for STRs with longer motifs (Supplemental Fig. S10). Here we confirm these trends for mononucleotide STRs, which were removed from previous studies due to high sequencing error rates or inadequacy of error profiles. We also confirm that alleles at most heterozygous STRs differ by just one motif unit (Supplemental Fig. S11; Payseur et al. 2011; Gymrek et al. 2012). Thus, accurate genotyping of such heterozygotes is important.

We studied germline indel mutations (insertion or deletion of whole repeat units) in autosomes that occurred in transmissions from grandparents to parents and that were confirmed by genotypes of children (Supplemental Figs. S12, S13). To be scored as a germline mutation, the event was required to have the following characteristics: (1) a parent having an allele absent from his/her father or mother (a “putative mutant allele”); (2) a putative mutant allele present in at least two children to confirm that it is a germline variant; and (3) a putative mutant allele absent in the second parent (Supplemental Fig. S12A). If a variant STR allele is present in both parents, the child's genotype was required to unambiguously identify the parent of origin for the putative mutant allele (Supplemental Fig. S12B; Supplemental Table S14). We included all 11 children in our data set to capture the vast majority of germline mutations occurring between grandparents and parents. The cases when putative mutant alleles were present in only one child were not considered to reduce false positives resulting from incorrect genotyping in children.

We required STR-containing loci to be sequenced to at least 5× informative read depth in all children, parents, and grandparents (Fig. 3A). The number of loci satisfying this requirement totaled 9,726,196 (4,863,098 loci in father and 4,863,098 in mother, equal to 19,452,392 transmitted STR alleles, as one allele is transmitted from each grandparent). At such loci, we detected 1470 germline mutation events, which is equivalent to 7.6 × 10⁻⁵ mutations per locus per generation (Supplemental Tables S14, S15). Among these mutations, 452 and 426 occurred in the male and female germ line (Supplemental Table S14), respectively, corroborating male mutation bias (Kelkar et al. 2008; Sun et al. 2012). The parental origin of the remaining 592 de novo mutations could not be determined. The level of male mutation bias varied among STR classes and motifs (Fig. 3B; Supplemental Fig. S14). The germline mutation rate increased with repeat length and, among STRs of the same length, was highest for mononucleotide repeats (Fig. 3C). The STRs with C and AT motif are the most mutable among mono- and dinucleotide STRs (Supplemental Fig. S15), corroborating previous studies (Denver et al. 2004; Kelkar et al. 2008; Sun et al. 2012). For mono- and dinucleotide STRs, the “1-unit-ins” were only slightly more abundant than “1-unit-del” among STR de novo mutations (Fig. 3D; Supplemental Fig. S16); the confidence intervals highly overlapped. This is in contrast to STR NGS sequencing errors that were predominantly “1-unit-dels” (Fig. 1B,C; Supplemental Figs. S6, S7).

We next examined whether these mutations were distributed randomly along the genome. The observed number of mutant mononucleotide STR loci estimated in 50-Mb windows had high correlation with the number of mutations expected based on our estimated mutation rates by repeat number and corrected by the number of loci present in each window (Pearson correlation = 0.77; Spearman correlation = 0.79) (Supplemental Fig. S17), suggesting that these mutations were randomly distributed along the genome. Only two windows (Chr 6: 0–50000000 and Chr 11: 100000000–135006516) had a significantly higher number of mutations than expected (the P-value of the post-hoc binomial exact test of these two windows was 1.3 × 10⁻⁵ and 4.7 × 10⁻⁵, respectively) (Supplemental Fig. S17). Our data are insufficient to test the randomness of the distribution at smaller windows or for repeats with a larger motif size.

Required depth for accurate genotyping

The power to accurately genotype a locus depends on many factors (Fig. 2), including the length of true alleles, the combination of true alleles, the ratio of read depths supporting each allele, and the informative read depth at that locus. Based on the error profile we assessed and the genotyping model we formulated, we can estimate the minimal read depth required to correctly determine an allele combination for a locus, given the observed STR length array from the reads mapping to this locus. Recall that informative read depth at a locus is the number of reads that span the entire STR and possess ≥20-bp flanks on both of its sides.

We first evaluated the minimum informative read depth required to accurately genotype a locus as a function of the allele length. We focused on heterozygous loci with the two alleles containing consecutive repeat numbers, since these are the hardest cases to genotype. We used simulations (see Methods) to compute the minimal number of informative reads required to correctly genotype with 90% accuracy (Fig. 4; Supplemental Table S16). For instance, to correctly genotype (A)₁₃(A)₁₄, 13 informative reads are required for the PCR+ protocol, whereas only seven informative reads are required for the PCR− protocol. For PCR− data, only five informative reads per locus is required for genotyping of STRs for all motif sizes and repeat numbers up to nine. The PCR+ data usually requires a higher number of informative reads for mono- and dinucleotide STRs. For tri- and tetranucleotide STRs up to 11 repeats, the number of informative reads required is only five (Fig. 4), as they have lower error rates (Fig. 1A; Supplemental Figs. S3, S5). The sequencing depth requirements for longer tri- and tetranucleotide STRs could not be evaluated because we lacked error profile data for such long STRs. We also evaluated the effect of the motif itself, since some motifs are more error prone than others (Supplemental Table S16). For the STR lengths studied, we observed a difference in the number of informative reads required to genotype dinucleotides of allele combination 7/8—seven informative reads are required to genotype (AT)₇(AT)₈ but only five for (AC)₇(AC)₈ and (AG)₇(AG)₈. The trends for minimum informative read depth for genotyping with 95% accuracy are similar (Supplemental Table S17).

Figure 4.

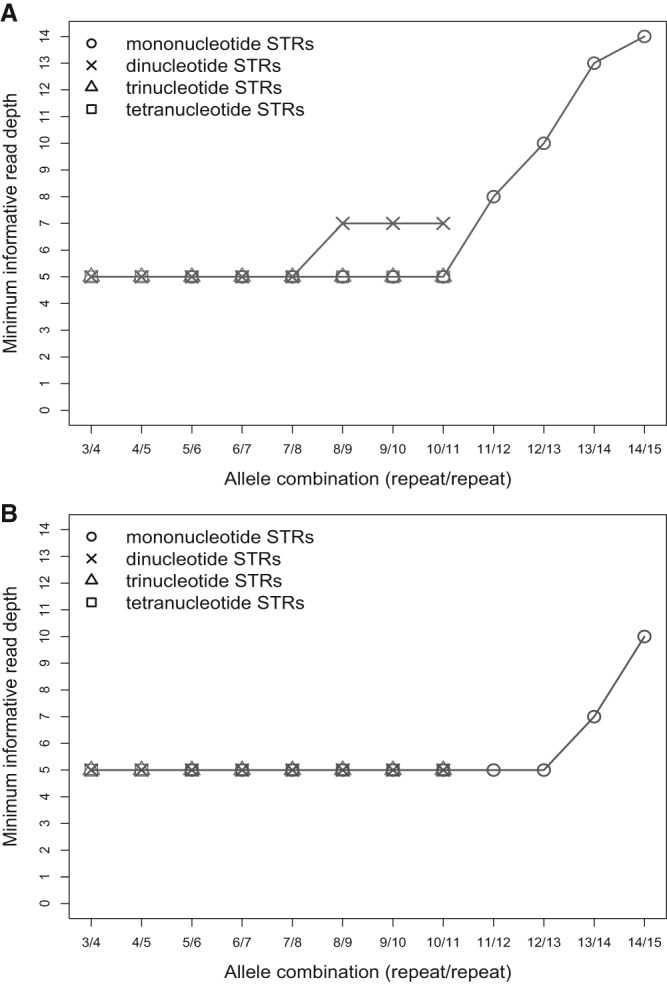
The minimal informative read depth required for correct genotyping of STR heterozygous alleles of consecutive repeat number with success rate of 90%. (A)_n was used for mononucleotide STRs, and (AC)_n for dinucleotide STRs. All tri- and tetranucleotide TRs were used. (A) PCR-containing library preparation protocol. (B) PCR-free library preparation protocol.

Next, we calculated the average genome-wide depth needed to achieve a given number of informative reads with 90% likelihood (see Methods). This depth is defined as the ratio of the number of sequenced bases to the genome length. The needed genome-wide depth is higher than the informative depth due to the randomness of the sequencing process and the need to have sufficiently long nonunique flanking regions. Because our calculations do not account for sequencing quality score, genome location sequencing bias, or mapping bias, they only serve as approximations for what is minimally needed in practice. Figure 5 shows the required average genome-wide depth as a function of repeat length of interest and read length utilized. The advantage of long reads is more pronounced for higher repeat lengths. For instance, to achieve 10× informative read depth for 10-bp STRs (independent of their repeat numbers), one needs to accomplish genome-wide sequencing depth of 26× and 17× for 100-bp and 300-bp single-end reads, respectively. However, to achieve the same depth for 50-bp STRs, one needs 104× and 21× genome-wide sequencing depth for 100-bp and 300-bp single-end reads, respectively.

Figure 5.

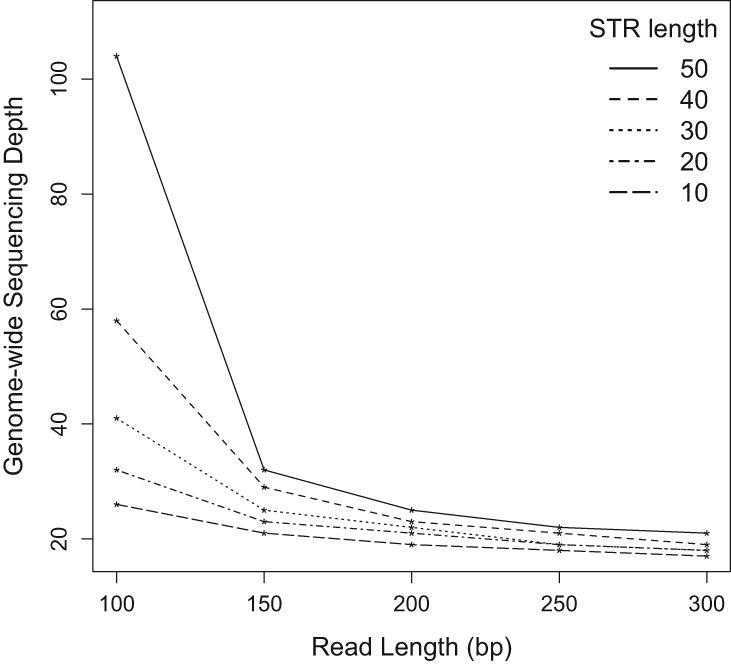
Genome-wide sequencing depth required for 10× informative read depth of 10–50 bp repeats with a success rate of 90% using different read lengths.

The conversion from informative to genome-wide sequencing depth substantially increases the difference in depth requirements between PCR+ and PCR− protocols. For instance, in the (A)₁₃(A)₁₄ genotyping example above, the difference in the required informative sequencing depth between PCR+ and PCR− protocols was only 6× (13× versus 7×). To achieve these informative read depths with 100-bp reads, the genome-wide sequencing depth required for PCR+ and PCR− protocols is 35× and 21×, respectively, leading to the difference of 14×. This result emphasizes the advantage of the PCR− library preparation protocol in STR genotyping.

Discussion

STRs are important causative agents of human diseases (Pearson et al. 2005; Castel et al. 2010) and are useful genetic markers (Wright and Bentzen 1994; Gupta and Varshney 2000; Miah et al. 2013; Abdul-Muneer 2014), but their genotyping with NGS technology is a challenge. To overcome this, we developed STR-FM, a versatile STR profiling method that is applicable to a wide range of STR lengths and motifs. We have thoroughly evaluated STR error profiles generated using Illumina PCR+ and PCR− library preparation protocols, using both computational and experimental approaches. As a result, we provide the scientific community with an STR genotyping tool, including an error correction model and a tool to evaluate the sequencing depth required for accurate genotyping of STR loci.

Factors that determine STR error rates and patterns

STR error profiles depend on repeat length (Fig. 1A,D; Supplemental Fig. S5), motif length (Fig. 1A,D; Supplemental Fig. S5), and motif composition (Supplemental Fig. S8), corroborating previous findings (Shinde et al. 2003; Highnam et al. 2013). For the STR length ranges considered in this study, mononucleotide STRs have the highest error rate, followed by di-, tri-, and tetranucleotide STRs, respectively (Fig. 1A,D; Supplemental Figs. S3, S5). The patterns of STR NGS errors we describe here are similar to those previously reported for STRs typed via gel electrophoresis (Murray et al. 1993; Walsh et al. 1996; Shinde et al. 2003): the most common STR error category resulting from slippage during PCR amplification is the “1-unit-del” (e.g., Murray et al. 1993; Walsh et al. 1996). The error rate from 10⁻⁶ to 10⁻⁵, observed by us here for five-unit mononucleotide STRs (Fig. 1), is consistent with an experimentally measured one-base deletion error rate within a five-base mononucleotide STR (∼1 error per 20,000 nucleotides) synthesized by Taq polymerase (Eckert and Kunkel 1990). Also, our results based on the NGS data (Supplemental Figs. S3, S5) agree with previous observations that tri- and tetranucleotide microsatellites have fewer stutter bands compared with di- and mononucleotide STRs (Ellegren 2004). The Illumina NGS data studied by us were generated using the Phusion polymerase (Ajay et al. 2011; Chen et al. 2012; Oyola et al. 2012); therefore the observed error patterns might be driven by the error profile of this enzyme. The error rates of the Phusion enzyme are ∼50-fold lower than those of the Taq polymerase (Frey and Suppmann 1995). However, the similarity between our error patterns and those of the Taq polymerase (Shinde et al. 2003) suggest that the error patterns of these two polymerases are comparable.

The PCR− library preparation protocol is expected to reduce bias in sequencing coverage (Kozarewa et al. 2009). Our findings reveal that eliminating the PCR step reduces STR errors as well. Based on our Chromosome X data, approximately a 1.5–2.8-fold and 2.0–3.7-fold error reduction was observed for mono- and dinucleotide STRs with greater than six and five repeats, respectively. This allows the PCR− protocol to achieve the equivalent power of the PCR+ with lower sequencing depth. For example, to distinguish (A)₁₄ from (A)₁₅ using 100-bp reads, we need 39× sequencing depth for PCR+ data, but we need only 29× depth for PCR− data.

Here we used the hg19 reference genome sequence. Mapping STRs to GRCh38 (Rosenbloom et al. 2015) might increase the number of loci that we will identify, but should not affect our overall conclusions. Indeed, we utilized stringent mapping parameters to map STR flanking regions without mismatches and indels. This minimized incorrect mapping to paralogous loci that are potentially more abundant in the new reference genome.

Minimum sequencing depth

We developed a method to estimate the informative and genome-wide sequencing depths required for STR genotyping. We demonstrate that the required sequencing depth depends on the STR error profile (as discussed above), sequencing read length, allele combination, and allele sequencing depth skew in a heterozygote. The depth-estimating tool integrated in Galaxy (Giardine et al. 2005; Blankenberg et al. 2010, 2014; Goecks et al. 2010) can be used for (1) selecting sequencing depth while planning a new project; and (2) evaluating which STRs can be accurately genotyped from a completed sequencing project (e.g., using a publicly available data set). The desired level of resolution contributes to determining the required read depth. For instance, for some questions (e.g., for studying allele spectrum in search of loci evolving under selection), distinguishing alleles of consecutive lengths in a heterozygote is important. For other questions (e.g., scoring normal versus premutation disease-causing alleles separated by several repeat numbers), such high resolution might not be needed. Therefore, the recommended minimal depth for accurate genotyping is not a fixed number and depends on the research question and STR loci of interest.

We found that to accurately (with 90% success rate) genotype STRs with less than nine repeats using the PCR− library protocol, the required informative read depth is only 5×, which corresponds to genome-wide sequencing depths of 15×, 17×, 21×, and 26× for mono-, di-, tri-, and tetranucleotide STRs, respectively (for 100-bp reads). These sequencing depths are comparable to those present in most publicly available data sets.

Our genotyping model and minimum sequencing depth study provide us with an opportunity to recommend the minimal depth needed for sequencing of disease-causing STRs. For instance, a change from 10 to 12–17 repeats at the (CGC)_n repeat, present at the gene PABPN1 encoding poly(A) binding protein, causes oculopharyngeal muscular dystrophy (OPMD) (Brais et al. 1998; Pearson et al. 2005). Running our simulations, we came to a conclusion that at least five informative reads are required to correctly genotype the (CGC)₁₀(CGC)₁₂ heterozygote with a 90% success rate. This corresponds to a genome-wide sequencing depth of 20× for 100-bp reads, using either the PCR+ or PCR− protocol.

Tools for STR length profiling

The STR-FM pipeline allows one to: (1) detect a broad range of STR lengths and motifs (including mononucleotide STRs and short STRs) (Supplemental Table S1); (2) clearly distinguish between perfect (uninterrupted) and interrupted STRs (Supplemental Table S2); and (3) be flexible with respect to the algorithm to be used for mapping the STR flanking sequences. Unlike other approaches, STR-FM can profile mononucleotide STRs, can profile heterogeneous genetic samples that do not follow a 50:50 allele frequency distribution (down to an allele frequency of 0.01), and can detect STRs in species without annotated STRs in the reference genome. Because STR-FM aligns only the flanking sequences and not the whole read, it is not susceptible to bias of STR length and can be used to compare the mutational spectrum across different lengths. Our pipeline is integrated into Galaxy (Giardine et al. 2005; Blankenberg et al. 2010, 2014; Goecks et al. 2010) and thus can be customized via a graphical user interface.

The STR-FM pipeline also could be used to extract STRs from mapped long reads generated by SMRT technology (Pacific Biosciences) (Roberts et al. 2013; Chaisson et al. 2015) or MinION (Oxford Nanopore) (Schneider and Dekker 2012). The long reads from these technologies would allow us to study longer microsatellites, which exceed the current read length of Illumina technology. Due to the differences in read lengths and sequencing errors between Illumina and these technologies, however, such data would require special mapping procedures and the development of separate error models. Alternatively, STR-FM can take mapped reads in standard SAM format, detect STRs in the mapped reads, and profile the STR length. Although the unbiased property of flank-based mapping will be lost this way, this demonstrates the versatility of the STR-FM in profiling STRs, even when an ad hoc mapping algorithm is utilized.

Germline mutation rates of STRs in the human genome

We report here the first genome-wide study of STR mutation rates. Using the NGS data, we genotyped >4.8 million STR loci, as compared to 2477 loci examined in a previous study (Sun et al. 2012). The pattern of de novo STR mutations we observed differs from that of STR sequencing errors (Figs. 1B,C, 3D; Supplemental Figs. S6, S7, S14), a result that demonstrates the importance of applying our error correction genotyping model when studying STR mutations in genomes. Specifically, germline mutations have comparable rates for expansions and deletions among the repeat lengths we studied, whereas STR sequencing errors have a very strong deletion bias.

The male mutation bias of dinucleotide STRs observed here is lower than that described in another recently published study (Sun et al. 2012), which was not genome-wide and included a higher proportion of AC-repeats than we find genome-wide (cf. Sun et al. 2012, Supplemental Table S3, with Supplemental Table S18 in the present study). Because AC-repeats have the highest male mutation bias among the dinucleotide repeats we studied (Supplemental Fig. S14), this could have inflated male mutation bias in the study by Sun et al. (2012). Also, a confounder in our study is that we could identify the parental origin for only 60% of de novo mutations. We could not assign a parental mutation bias when both grandparents carried an allele identical to the mutant allele in the next generation, e.g., mutation from (A)₆ to (A)₇ when both grandparents had (A)₆ allele, which could underestimate the real male mutation bias in our study.

The germline mutation rates we estimated for STRs are higher than recently obtained estimates (Sun et al. 2012). Several factors could contribute to this difference. We hypothesize that a major factor is that we used perfect (uninterrupted) STRs exclusively in this study, whereas the study of Sun et al. (2012) included interrupted STRs that, as we have shown, have significantly lower mutation rates genome-wide (Ananda et al. 2014). Additionally, our study presents a genome-wide analysis including all STR-containing loci in the genome for which we could obtain data of high depth. In contrast, Sun and colleagues analyzed loci used in large-scale gene-mapping studies, and thus potentially affected by ascertainment bias. Finally, our analysis is based on the analysis of a single family, whereas Sun et al. (2012) included hundreds of families, and this can also lead to differences in mutation rates.

We can apply these STR germline mutation rates and patterns in several areas. In population genetics, these rates can be used to estimate divergence times of recent population splits. Since STRs have higher mutation rates than SNPs (Ellegren 2004; Campbell and Eichler 2013), the former can accumulate many mutations in a short period of time and thus can provide higher resolution. In forensics, knowing mutation rates can aid in estimating the level of STR polymorphism, in computing the number of STR markers necessary for individual identification or kinship testing, and in computing the probability of relatives having different alleles due to a mutation. Also, in medical research, we can evaluate the likelihood of premutation STR loci to become disease-causing STRs in the next generation. Although most studied disease-causing STRs are long trinucleotide repeats (Pearson et al. 2005), some short STRs were also shown to have strong implications in several diseases (Cuppens et al. 1990; Chu et al. 1991; Pearson et al. 2005).

Methods

Data sets used to assess STR error rates

The PCR+ data were downloaded from the NCBI Sequence Read Archive (http://www.ncbi.nlm.nih.gov/sra) with accession numbers SRR345592–SRR345594. SRR345592 is a 100-bp paired-end data set sequenced from blood of a human male at the 50× depth. SRR345593 and SRR345594 are 100-bp paired-end data sets sequenced from saliva of a human male at the 100× depth.

The PCR− data were downloaded from the European Sequence Read Archive (http://www.ebi.ac.uk/ena/) with accession numbers ERR194151, and ERR174342–ERR174360. This male individual is a Utah resident (NA12882 from the CEPH collection) whose blood was sequenced at the 245× depth.

Using STR-FM to assess error profiles in the context of STRs for Illumina data

Detecting STRs in short reads

Our STR detection module for uninterrupted STRs executes the following three steps: (1) Scanning reads using sliding windows. For a given “k” (e.g., k = 2 for dinucleotide STRs), we compared consecutive k-mer window size sequences, with a step size of k. If a sequence at a given position matches the previous k-mer, it was marked with a plus and with a minus if otherwise. (2) Since we do not allow mutations in the reported STR, consecutive plus signal sequence means that a k-mer STR is present in this sample. (3) Report k-mer STRs if the length is larger than the threshold provided by the user.

The method to detect interrupted STRs can be found in the Supplemental Text. Using the STR-FM pipeline, we detected mono-, di-, tri-, and tetranucleotide STRs, with lengths ≥5, ≥6, ≥9, and ≥12 bp, respectively, in raw sequencing reads. These four classes of STRs were analyzed separately throughout the analysis. We also required that all bases in the STRs, and the 20 flanking bases on both sides have a Phred quality score of ≥20.

Mapping flanking bases of STRs to the reference genome

At least twenty bases flanking the STRs upstream and downstream in the STR-containing reads were extracted as FASTQ files and mapped to the human reference genome (GRCh37) with BWA version 0.7.5a-r405 (Li and Durbin 2009) as paired-end reads using aln and sampe mode. To minimize incorrect mapping, mismatches and indels were not allowed in mapping. The resulting alignments were filtered to retain only the uniquely mapping flank pairs with proper orientation of the upstream and downstream flanks. We discarded STRs that mapped to the Y Chromosome (pseudoautosomal regions) and human self-alignment regions from the UCSC Genome Browser to obtain only unique hemizygous loci on Chromosome X (reads mapping to autosomes were discarded). Duplicated reads were not removed throughout the analysis to get accurate magnitude of errors generated by the PCR+ and PCR− library preparation protocols.

Profiling STR length at each locus

At each STR locus in the reference genome (identified using the same script to detect STRs in reads starting from the FASTA-formatted human reference genome [GRCh37]), all mapped STR-containing reads were binned, and the STRs contained in these reads were collated. Only uninterrupted reference STR loci were considered. STRs with the same motif size (mono-, di-, tri-, or tetranucleotide repeats) on the X Chromosome that are closer than 10 bp were excluded to avoid incorrect STRs profiling from overlapping STRs. In total, 789,401, 378,730, 59,383, and 19,322 loci mono-, di-, tri-, and tetranucleotide STRs, respectively, were studied. The STRs were checked for motif compatibility with STR motifs in the reference genome. The major allele length for each locus was determined for each STR at each reference locus. Loci supported by <5 reads or with frequency of major allele <50% were removed. Then we grouped loci by their major allele lengths to evaluate their error profiles. Any STR length differences from the major allele length were considered to be erroneous calls.

Construction of bootstrap confidence intervals

For every STR motif size, motif composition, and allele length, using the observed counts of error variants of different lengths, we generated multinomially distributed random counts of error variants and computed the error rate using these counts. This was repeated 10,000 times, and the 95% confidence intervals for the error rate were constructed from the 2.5th to the 97.5th percentiles of the error rates. The bootstrap confidence intervals were not drawn when the sampling numbers of error counts at particular percentiles were zero. For example, several data points miss the lower bound of confidence intervals due to the small number of error counts.

Plasmid construction, sequencing, and analysis

The construction of plasmids containing artificially inserted tandem repeat sequences has been previously described (Eckert et al. 2002; Kelkar et al. 2010; Ananda et al. 2013, 2014; Baptiste et al. 2013). The standard procedures were used for library preparation and the sequencing on MiSeq. The analysis was performed using comparable parameters with the analysis in human X Chromosome. See Supplemental Text for complete description.

Building an error correction model for genotyping

The raw reads were processed to generate an STR length array using the STR-FM pipeline. The STR length array for each locus contained repeat length(s), number of repeats, and motif. The three most common STR lengths from the input STR length array of a single locus were considered for formulating homozygotes and heterozygotes.

The probability for any given allele length to be observed was retrieved from either PCR+ or PCR− error profiles generated from X Chromosome data. When the conversion could not be observed from an error profile, e.g., (AG)₃ was not observed to change to (AG)₈, the base substitution rate (Kong et al. 2012) was used. The probability value for all the repeat lengths in the input STR length array was multiplied to calculate the probability to generate the whole STR length array from either a homozygote or a heterozygote.

For homozygotes, each of the three most common STR lengths was considered. The allele that gave the highest probability to generate the observed STR array at a locus was considered to represent the probable homozygous allele. For heterozygotes, the three most common STR lengths were grouped into three sets of alleles. For each set, the probability of the two alleles to generate the observed repeat lengths was averaged. The most probable set of alleles was used as a probable heterozygous form. The log-odds ratio of the homozygous form to the heterozygous form was then reported, with a score greater than zero indicating a homozygote and a score below zero indicating a heterozygote.

Evaluation of the error correction model's correct prediction rate for diploid samples

We used the male X Chromosome sequencing data from the iPOP study (Chen et al. 2012) (for PCR+) and the Platinum Genome Project (Ajay et al. 2011) (for PCR−) to in silico generate pseudodiploid data to test the genotyping model (see Results). We generated 10,000 homozygous loci by combining two loci with the same motif and major allele length. Heterozygous loci were generated similarly. To ensure that the test data set had an error profile similar to the actual data, we focused on loci in which the major alleles were at least one repeat longer than our minimum cutoff (≥6, ≥8, ≥12, and ≥16 bp, for mono-, di-, tri-, and tetranucleotide STRs, respectively) to allow STR contractions, which are the major category of STR errors. We considered only the range of STR lengths that had at least 500 reads in both PCR+ and PCR− data in the STR genotyping model to ensure reliability of error rates. Motifs that had only one STR length that passed the criteria were removed because they would always have a 100% correct prediction and therefore would not be useful for evaluating our error correction model. The prediction was considered to be correct when the allele combination was determined correctly.

Logistic regressions were performed using the standard R package (R Core Team 2013). Pseudo R-squared of a model was calculated as (D_o − D)/D_o, where D_o is the null deviance and D is the residual deviance of the model. Relative contribution of each predictor to a model was calculated using [(D_o − D) − (D_o − D_(-p))]/(D_o − D), where D_(-p) is the deviance of a model obtained by removing the predictor of interest (Fungtammasan et al. 2012).

The genotype concordance/discordance rate was evaluated on libraries ERR194151 and ERR324433 from the European Sequence Read Archive (http://www.ebi.ac.uk/ena/). The genotype discordance was defined as the incongruence of at least one allele between genotypes of two replicated libraries (Pompanon et al. 2005). Minimum read depth was set at 5×.

Evaluation of the genotyping model's correct prediction rate for heterogeneous genetic samples

To assess the accuracy and precision of the error correction model, we prepared heterogeneous genetic samples by mixing DNA from two different plasmids (see Supplemental Text for details). The ratios of artificial heterogeneous genetic samples (clones R2 to Z1-1) were designed as 0.1%, 0.25%, 0.5%, 1.0%, and 2.0%. The sequencing data of mixed clones were profiled using the STR-FM pipeline described above. The sequences from the two plasmids were also profiled to check STR lengths in the inserted DNA region that were different between the two plasmids. The error correction and genotyping were performed using the error rates estimated from the two unmixed Z1-1 and R2 plasmids. Also, the ratios of contributed alleles were adjusted from 50:50 to the ratios present in each mixed sample.

Using an error correction model to evaluate germline mutation rates and patterns

PCR− whole-genome sequencing data of the three-generation pedigree from the Platinum Genome Project (Ajay et al. 2011) was downloaded from http://www.ebi.ac.uk/ena/data/view/ERP001960. This family consists of four grandparents, two parents, and 11 children. The data include libraries ERR194146–ERR194148, ERR194151–ERR194152, ERR194154–ERR194155, ERR194157–ERR194162, ERR218433, and ERR324432–ERR324435. Sequencing depth for each individual is 43.76–64.98×. We considered only autosomal STR-containing loci, which are sequenced to at least 5× informative read depth in all children, parents, and grandparents. STRs on sex chromosomes were excluded. We genotyped all individuals of the pedigree using error rates estimated from X Chromosome of PCR− data, which was evaluated from an individual of this pedigree (NA12882) to reduce potential differences due to batch effect. The germline mutations were classified by the gender of mutated germ line (male versus female), original length, and mutated length. The germline mutation rates were calculated as the fraction of mutations per the total number of transmissions (each locus has two transmissions). The expected numbers of mutations in 50-Mb windows were calculated using the germline mutation rates obtained in this study separately for different STR classes, lengths, and motifs multiplied with the numbers of corresponding STR loci that were genotyped in all members of the pedigree. The deviation from the expected number of mutations in 50-Mb windows was tested using a binomial exact test.

Computing minimum informative read depth required for accurate genotyping

We simulated a series of read profiles of all possible combinations of alleles with consecutive repeat numbers for 2–50×, 60×, 70×, 80×, and 100× depth for motifs A, T, AT, AC, AG, combined motif of trinucleotide STRs, and combined motif of tetranucleotide STRs. First, for each motif and STR length combination, we selected the range of observed STRs from our error profiles and generated all possible combinations of STR arrays. In this step, we did not include the observed STR lengths that have the probability of occurrence <0.01 (rare error form) to reduce computational time. We limited our study to a range of STR lengths for which we observed at least 500 reads in our error profiles in both PCR+ and PCR− data. Second, we used our error correction models to analyze these STR arrays and select only those that can be predicted to be heterozygotes. Third, we calculated the probability of our model to generate the observed STR arrays from predicted heterozygous allele pairs and multiplied by the number of all possible rearrangements in these STR arrays. A sum of these products was equal to the probability to detect heterozygous alleles for each allele pair at each depth.

Estimation of required sequencing depth

First, we derived an equation to calculate the locus-specific sequencing depth needed to achieve a certain informative read depth by assuming uniform sequenced reads along the genome. Suppose that the sequenced reads of length L uniformly represent parts of a genome that has an infinite size and no redundant sequences. If we place these reads on every position of this genome, the sequencing depth will be equal to read length L. If an STR of interest is r bp long, and we require at least F bp of flanking regions both upstream and downstream, there will be L + 2F + r − 1 reads that are associated with at least one base of STR or flanking regions. Among these reads, 2F + r start positions and 2F + r end positions of reads locate within STR or flanking regions. These positions are mutually exclusive as long as reads are longer than 2F + r. Thus, 2(2F + r − 1) reads do not cover at least one base of STR and F bases either upstream or downstream (−1 is the correction for start and end position at the outer edge of flanking regions which can still map). Since the reads that do not cover the whole STR of length r or do not cover at least the required minimum flanked bases are not useful for profiling, the informative read depth of L is L + (2F + r − 1) − 2(2F + r − 1) = L − (2F + r − 1). To achieve the informative read depth of X, an STR at a specific locus needs to be sequenced at depth

$$\frac{X\times L}{L-(2F+r-1)},$$ (1)

where L is read length; F is the number of flanked bases required at each flank; and r is the expected repeat length of an STR of interest. We will use y_required to represent this value. This equation is true for all flank-based mapping approach programs that require certain lengths for both flanking regions.

In reality, the sequenced reads are not evenly distributed along the genome. Therefore, we used Poisson distribution to estimate the required genome-wide sequencing depth (the average depth for all loci in the genome) that guarantees that a certain percentage of STRs in the genome (e.g., 90%) have at least a certain level of locus-specific sequencing depth and informative read depth. Using y to represent specific level of sequencing depth and λ to represent genome-wide sequencing depth, we can write the equation that the probability of observing a locus with depth y or P(Y = y) is

$$\frac{({\lambda }^y\times {\text{e}}^{-\lambda })}{y!}.$$ (2)

We are interested in finding the required genome-wide sequencing depth λ that gives sufficient informative read depth for a certain percentage (e.g., 90%) of the genome. In other words, we want to find the minimum value of λ that makes P(Y ≥ y_required) greater than or equal to a specific percentage of the genome. The P(Y < y_required) can be calculated from

$$P(Y=0)+P(Y=1)+\cdots +P(Y=y_{\text{required}}-1).$$ (3)

Each term of the Poisson distribution can be calculated from Equation 2, and y_required can be calculated from Equation 1. The tool to estimate locus-specific y_required and genome-wide sequencing depth “λ” is provided in the Galaxy toolshed.

Galaxy tool description

The tools from the STR-FM pipeline are freely available on Galaxy (https://usegalaxy.org/) (Giardine et al. 2005; Blankenberg et al. 2010, 2014; Goecks et al. 2010). Users can install local Galaxy and download all tools used in this research from repository “str_fm” (see Supplemental Text for details). These tools are also available at github (https://github.com/Arkarachai/STR-FM). The STR error rates estimated in this study can be downloaded from https://usegalaxy.org/u/guru%40psu.edu/h/error-rates-files.

Data access

The sequencing data of the plasmid containing artificially inserted tandem repeat sequences in both PCR+ and PCR− systems, all the ratios of heterogeneous genetic samples, and the original plasmids before mixing have been submitted to the NCBI Sequence Read Archive (SRA; http://www.ncbi.nlm.nih.gov/sra) under accession number SRP047377.