Graph-Based Airway Tree Reconstruction from Chest CT Scans: Evaluation of Different Features on Five Cohorts

Abstract

We present a graph-based framework for airway tree reconstruction from CT scans and evaluate the performance of different feature categories and their combinations on five lung cohorts. The approach consists of two main processing steps. First, potential airway branch and connection candidates are identified and represented by a graph structure with weighted nodes and edges, respectively. Second, an optimization algorithm is utilized for generating an airway detection result by selecting a subset of airway branches and connections based on graph weights derived from image features. The performance of the algorithm with different feature categories and their combinations was assessed on a set of 50 lung CT scans from five different cohorts, including normal and diseased lungs. Results show tradeoffs between feature categories/combinations in terms of correctly (true positive) and incorrectly (false positive) identified airways. Also, the performance of features in dependence of lung cohort was analyzed. Across all cohorts, a good trade-off with high true positive rate (TPR) and low false positive rate (FPR) was achieved by a combination of gray-value, local shape, and structural features. This combination enabled extracting 91.80% of reference airways (TPR) in combination with a low FPR of 1.00%. In addition, this variant was evaluated on the public EXACT’09 test set, and a comparison with other airway detection approaches is provided. One of the main advantages of the presented method is that it is robust against local disturbances/artifacts or other ambiguities that are frequently occurring in lung CT scans.

I. Introduction

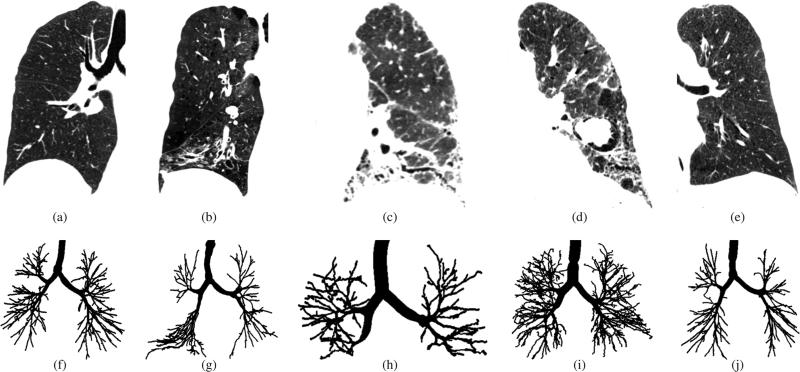
Segmentation of airway trees in chest CT scans is an important step in the analysis of various lung diseases like asthma and facilitates other image analysis tasks such as segmentation of lung lobes. In CT scans, airways appear as dark tubular structures, which are surrounded by a brighter airway wall. An example of a healthy human lung imaged with CT and the corresponding airway tree are depicted in Figs. 1(a) and 1(f), respectively. Airways branch recursively, following typical patterns of branching angles and diameter decreases. While the lumen of larger airways in CT scans is well contrasted, distinguishing small distal airways from lung parenchyma can be difficult, because of partial volume effects, noise and imaging artifacts. In addition, lung disease may alter the morphology and appearance of the airway tree and/or the surrounding parenchyma and can cause the obstruction of airways. Fig. 1 gives some examples, showing the impact of lung disease on airways and parenchyma.

Fig. 1.

Chest CT scans and corresponding airway tree segmentations in patients with different lung disease. (a)-(e) Coronal image slices of CT scans showing one of the lungs. All CT scans are visualized using the same gray-value window −1000 to −300 HU. (f)-(j) Corresponding airway tree reference standard segmentations. (a) and (f) Healthy individual. (b) and (g) Patient with chronic obstructive pulmonary disease. (c) and (h) Patient with asbestosis. (d) and (i) Patient with sarcoidosis. (e) and (j) Patient with severe asthma.

Several methods for segmentation of airways have been proposed in the literature. For a detailed overview, we refer to a recently published review article by Pu et al. [1]. Commonly used methods are region-growing variants based on gray-value features, where the segmentation starts from a seed point and adjacent regions are merged iteratively based on local image density or contrast. Such approaches tend to perform reasonably well for larger airways, but have limitations in identifying smaller weakly contrasted airways. Thus, alternatives have been investigated to improve the identification of smaller airways. For example, classification based on machine learning [2], [3] or methods that identify airways based on their tubular shape have been proposed. Airway identification can be achieved either directly in the image space utilizing bronchi-detection-filters (e.g. based on eigen-value analysis of the Hessian matrix [2]) or in a geometric space after iso-surface extraction [4].

Distinguishing airways from background based solely on local image features of the CT scan is difficult and may lead to leakage or undersegmentation due to ambiguities caused by poor image contrast, obstructions along the airway lumen, motion artifacts, etc. Some leakage can be prevented, or removed in a post-processing step by pruning, utilizing structural features such as local airway diameter increase or abrupt changes in branching angles [5]. However, dealing with situations where the local image information is ambiguous and the features do not justify classification as an airway is a more difficult issue. In case of region-growing like algorithms, this may result in a premature (local) termination of the algorithm, and consequently, whole airway subtrees could be missing in the segmentation result. Also, lung disease may alter the morphology and appearance of the airway tree as well as surrounding lung tissue (Fig. 1). Thus, typical assumptions incorporated into methods may become invalid.

Segmenting many generations of airways in CT scans in a robust way is a challenging task, as shown in a recent study based on a publicly available lung CT image database (EXACT’09) [6]. Even the best performing state-of-the-art methods were not able to identify more than approximately 60% of in the CT scans visible airways, on average, without producing major leakage. To facilitate research of lung diseases and development of new imaging-based biomarkers, algorithms are needed that allow segmentation of more smaller, distal airways and that perform robustly across various lung diseases. This requires methods that are able to deal with situations where the local image information is ambiguous.

Our previous work has addressed the issue of ambiguous local image information in the context portal vein [7] as well as simultaneous portal and hepatic vein [8] segmentation in contrast enhanced CT scans. Both methods reconstruct the vascular tree(s) in two steps. First, all tubular structures in the data set are identified based on their shape. Second, the tubular structures are connected into one [7] or several [8] vessel tree(s) based on properties between the individual tubular structures. During this process, gaps between the individual tubular structures that may result from local ambiguities or occlusions are closed. The method presented in [8] utilized a predefined set of rules with several hard thresholds to identify vessels and connect them into tree structures. Although the method was not designed for this application, evaluation of the method in the context of airway segmentation showed promising results on the EXACT’09 database [9], [6]. A similar approach for airway tree segmentation was recently utilized by Graham et al. [10]. First, the authors performed a region-growing based segmentation of larger airways. In subsequent processing steps, smaller airway cross-sections were identified, combined into airway segments, and then connected into an airway tree structure. The method was tested on lung CT scans acquired for bronchoscopy procedures [10], but was not evaluated on the public EXACT’09 database or a diverse set of lung CT scans that include different types of lung diseases.

Building on our previous work reported in [9], which utilized a graph-based approach for tree reconstruction, we make the following contributions in this paper. First, we have expanded the approach. Specifically, we now use different detectors for small and large airways, are less restrictive in defining potential connection candidates, define weights for airway branch and connection candidates, and introduce an optimization step that considers branch and connection candidates at the same time. Second, we substantially increased the number of features that are utilized to model the airway reconstruction problem in a graph and convert the majority of “hard” thresholds/requirements into “soft” features/weights that are now incorporated in the graph-based formulation of the problem. This is an important step, which allows us to better deal with ambiguities and variation caused by disease (Fig. 1), avoiding the issue of fine-tuning parameters (e.g., thresholds) for a specific cohort of lung diseases to achieve good results. Third, it is a priori not clear which features work best across different cohorts or for a given cohort. To address this issue, we assess and compare the detection performance of different feature combinations on a large set of lung MDCT scans, which includes data sets of normals and different lung diseases. In addition, for comparison with other airway segmentation approaches, we present an evaluation on the public EXACT’09 data set.

II. Image Data

For this work, two sources of image data were utilized, as described below.

1) CT scans from five different cohorts for training and evaluation

Chest CT scans of lungs with no significant abnormalities (normals), chronic obstructive pulmonary disease (COPD; including GOLD 1 to 4), asbestosis, sarcoidosis, and asthma (both severe and non-severe) were available for method development and evaluation. For each cohort, 20 scans were available, resulting in a data set of 100 chest CT scans. Fig. 1 shows a typical example of a CT cross-section for each cohort. This data set was divided by means of stratified random sampling into two disjoint sets, one for method development and one for evaluation, each consisting of 50 CT scans. The airway tree reconstruction approach was designed utilizing the development data set. Once this process was completed, a performance assessment utilizing the evaluation data set was performed. All CT scans were acquired at total lung capacity. Thirteen different CT scanners from Siemens, Philips, and GE Medical Systems were utilized for imaging. The images were reconstructed with different kernels, slice thickness, and pixel spacing. Pixel spacing ranged from 0.49 to 1.00 mm with a median of 0.5 mm. Slice thickness ranged from 0.5 to 1.3 mm with a median of 0.75 mm. Soft, medium, and hard image reconstruction kernels were utilized, but the majority of images were reconstructed with soft kernels.

2) Exact’09 data sets

The public EXACT’09 database [6] consists of 40 data sets; 20 for method development and 20 for evaluation. It consists of scans from patients with different lung diseases, which were acquired with CT scanners from all four major vendors using several different imaging protocols. The EXACT’09 test data set also contains low dose CT scans, scans acquired at full expiration or with intravenous contrast agent. The majority of scans were reconstructed using medium or hard image reconstruction kernels [6].

III. Graph-based Airway Tree Reconstruction

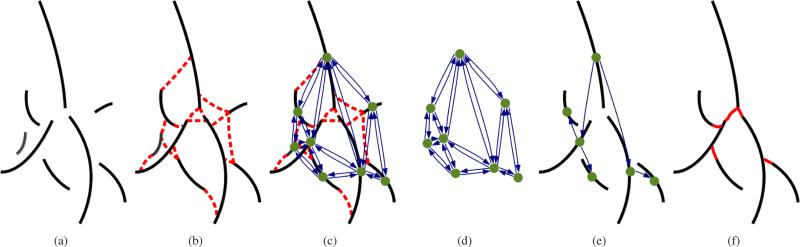
Distinguishing airways from background based only on local image information without any additional information is difficult. To address this problem, we utilize a graph-based optimization framework which considers potential airway branches and connections between them in a global context. The individual steps are illustrated in Fig. 2. First, we identify airway branch candidates based on the local appearance of airways in the CT scan (Fig. 2(a)) and plausible connection candidates between pairs of these airway branch candidates (Fig. 2(b)). Note that neither the detection of airway branches nor the detection of connections has to be perfect and may produce many false positives. In a next step, we represent airway branch and connection candidates as nodes and edges in a graph structure (Figs. 2(c) and 2(d)) and assign weights to each of them, which represent the confidence (weight) that the airway branch/connection candidate is actually part of the airway tree. Then, we utilize a graph-based optimization algorithm to select the airway branch and connection candidates that maximize the confidence in the resulting airway tree structure and remove false positive candidates (Figs. 2(e) and 2(f)). Because the optimization algorithm considers individual airway branch and connection candidates in the context of the whole tree structure and does not rely solely on local decisions, the segmentation process becomes more robust against local ambiguities present in the data set.

Fig. 2.

Airway tree reconstruction based on graph-optimization. (a) Airway branch candidate centerlines. (b) Airway branch connection candidate centerlines (red) and (c) corresponding graph structure. Each airway branch candidate is represented by a node and each connection candidate is represented by a pair of directed edges. (d) The graph structure alone, which is utilized for airway tree reconstruction. (e) Nodes and edges selected by the optimization algorithm. (f) Final airway tree.

In the following sections, we will describe in detail the detection of airway branch candidates (Section III-A) and plausible connection candidates (Section III-B), followed by the optimization algorithm (Section III-C). The definition of different features utilized to obtain graph-weights will be discussed separately in Section IV.

A. Detection of Airway Branch Candidates

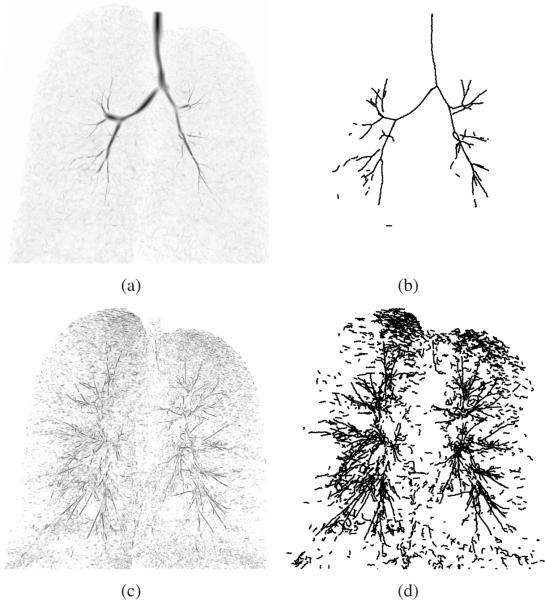
Airway branches appear as dark tubular structures in CT images. To identify them, we utilize tube detection filters (TDFs), which provide a measure of tube-likeliness for each voxel of the data set based on local shape information. Because large airways and small airways have different appearance, two different TDFs are utilized. Then, from the TDF results, centerline-based representations of individual airway branch candidates are extracted utilizing a height ridge traversal. Examples of the TDF results and the extracted airway branch candidates are shown in Fig. 3. For computational efficiency, all operations are performed only inside of a rough lung mask. The lung mask is obtained with region growing with a fixed threshold of −500 HU followed by a morphological closing operation with a spherical structuring element of 10 mm radius.

Fig. 3.

Examples of airway branch candidates. (a) Large airway TDF result shown as inverted Maximum Intensity Projection (MIP). (b) Large airway branch candidate centerlines. (c) Small airway TDF result shown as inverted MIP. (d) Small airway branch candidate centerlines.

Detection of large airways

Large airways appear typically well contrasted in CT images. We obtain a tube-likeliness measure for these airways by utilizing a multi-scale TDF [8]. The CT scans are preprocessed by truncating the voxel's density to a range of −1000 HU to −700 HU and inverting the gray-value range. Then, given the discrete range of radii r ∈ {0.5, 1.0, 1.5, ..., 10.0} mm, the filter calculates a response for each voxel. First, the filter estimates the tangent direction of the tubular structure for a given radius utilizing a Hessian scale space. Then, the method samples gradient information at the airways expected surface and center, which is then utilized to derive a tube-likeliness measure. For each voxel location, the maximum response over all test radii gives the final response together with a radius estimate. This filter allows robust extraction of large airways (Fig. 3(a)), but is not well suited for extraction of thin weakly contrasted airways that are surrounded by inhomogeneous tissue (e.g. in case of adjacent vessels of similar diameter).

Detection of small airways

For detection of small airways, we first apply a slice-based enhancement of cavities (small regions that are darker than the surrounding area) similar as in [11], [12], [10] followed by a single-scale tube-likeliness calculation. The cavity detection is applied to all axial, coronal and sagittal image slices individually and the results are then combined using the voxel-wise maximum operator to produce a 3D result. Cavities in individual 2D image slices are identified as follows. Starting from each local minimum in the 2D image slice, an associated cavity is identified. Therefore, a region growing method is applied where the threshold is continuously increased, until the associated area exceeds an area of 12 mm², thus only cavities up this this maximum size are identified. While increasing the threshold, the average gray-value of the associated segmented area and the minimum gray-value of the adjacent boundary pixels are monitored, and a cavity-score is calculated based on their difference. The threshold with the highest score and the associated region-growing segmentation is selected as the cavity area. All pixels of the cavity area are assigned the cavity-score in the cavity enhancement result image.

After combining the axial, coronal and sagittal cavity detection results, a single-scale 3D TDF response is calculated for each voxel. Therefore, we utilize Frangi's vesselness measure [13]. However, contrary to Frangi's method we do not utilize the eigenvalues of the Hessian matrix, but instead the eigenvalues obtained from the derivative matrix ∇Fⁿ(x) of a normalized image gradient vector field $F^n\left(\mathbf{x}\right)=\frac{F\left(\mathbf{x}\right)}{\mid F\left(\mathbf{x}\right)\mid }\frac{(min(\mid F\left(\mathbf{x}\right)\mid ,F_{max})}{F_{max}}$ where F = ∇(G_σ ⋆ I), I is the original image, G_σ is a Gaussian filter kernel at scale σ and F_max the normalization parameter. Utilizing such a normalized vector field leads to sharp responses directly at the center of tubular structures and makes the response less sensitive to inhomogeneities along the airway. The parameters utilized for obtaining the gradient vector field are σ = 0.5 mm and F_max = 50 HU. The parameters of Frangi's measure are α = 0.5, β = 0.5, and γ = 100. The resulting response of this small airway detection step is sensitive to thin, weakly contrasted elongated structures, but not very specific and may result in many false positive responses (Fig. 3(c)).

Centerline extraction

After calculation of the TDF responses, centerline-based representations of airway branch candidates are extracted utilizing a height ridge traversal method with hysteresis thresholding [8]. The centerlines for large airways and small airways are extracted separately, with thresholds adjusted such that the method provides centerlines for all structures that are potentially airways. For the large airways, t_high = 25 and t_low = 15 are used. For small airways, t_high = 0.008 and t_low = 0.002 were selected. While the estimated radii of large airway centerline points are determined by the TDF, for small airways it is set to a constant value of 0.5 mm. Centerlines shorter than 3 voxels are discarded as noise responses. Remaining centerlines are split at sharp turns. Thus, for each centerline point, an angle is calculated based on the relative location of neighboring centerline points and the centerlines are split at locations where the angle is above 90°. The TDFs only provide a measure of tube-likeliness. Separating all true airways from background based on a single threshold is generally not feasible because of ambiguities in the data. As a result, there might be many false positive airway candidates (Figs. 3(b) and 3(d)). These will be removed during the optimization step (Section III-C).

B. Finding Connection Candidates

The airway branch candidates are generally unconnected with gaps in between. These gaps may result from bifurcation locations (non-tubular shape), poor contrast, imaging artifacts, or occlusions along the airway lumen (stenosis or mucus, for example). To close these gaps and obtain a fully connected airway tree, the correct connection paths between the airway branch candidates need to be identified. In our approach, we obtain a set of potential connections between the airway branch candidates with two different approaches utilizing: (a) gray value information and (b) a continuation of an airway branch candidate beyond it's end points. Please note, that there might be several connection candidates between a pair of airway branch candidates (Fig. 4).

Fig. 4.

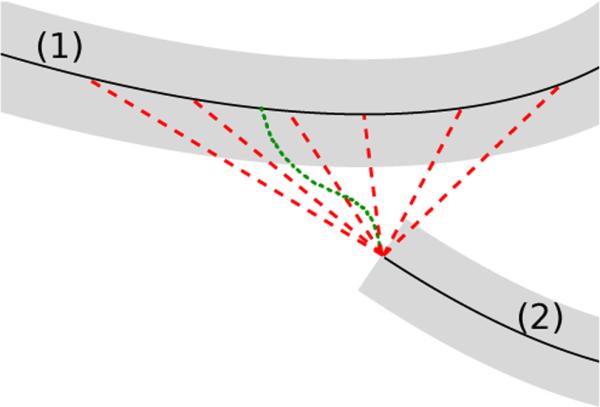
Connection candidates between two airway branch candidates (1) and (2). Dotted green line: minimum cost path connection candidate. Dashed red lines: several connection candidates representing continuation of the airway branch candidate.

Connections based on gray-value

The lumen of an airway is typically darker than the surrounding wall. Therefore, to identify suitable connection paths that stay inside of the airway lumen, a minimum cost path technique can be utilized. A suitable cost image is obtained based on the image gray-values, utilizing C(x) = max(I(x) + 1000, 0) where I(x) is the gray-value at location x in the original CT volume. Instead of calculating minimum cost paths between each pair of airway branch candidates separately, we utilize an approach based on the method described by Cohen and Deschamps [14]. Starting from a set of connected components (the airway branch candidate centerlines in our case), a geodesic distance transformation in the cost image is applied utilizing a fast marching algorithm. Then, saddle points in the distance image are identified and connection paths between the components are obtained using backpropagation in the distance image starting from the saddle points. This enables extraction of a set of minimum cost paths between the airway branch candidates in one processing step.

Connections representing a continuation of airway branch candidates

While above described minimum cost path approach is suitable to identify correct connections between airway branch candidates in many cases, such an approach does not necessarily succeed in cases of an occlusion or other disturbance along the airway lumen. Typically, each airway branch candidate continues beyond it's end point and connects to another airway branch along a short connection path. Therefore, to obtain suitable potential connections in cases of occlusions/disturbances along the airway, we also include connection candidates in our approach that extend from the end-point of an airway branch candidate to the centerline-points of other airway branch candidates, if the length of the connection is smaller than 30 mm. This may result in several connection candidates between the same two airway branch candidates, as indicated by the multiple red dotted lines depicted in Fig. 4. Limiting the distance to 30 mm avoids considering implausible connections between airway branch candidates that are too far apart, and thus, help reducing computation time.

C. Tree Reconstruction

After detection of airway branch and connection candidates, we utilize an optimization procedure to select the airway branch and connection candidates that represent the actual airway tree. Therefore, the airway branch and connection candidates are organized in a graph-structure G = (V, E) with a set of nodes V and a set of directed edges E. Each airway branch candidate corresponds to a node and each connection path candidate corresponds to a pair of directed edges. Different connection candidates between the same nodes are represented by different edge pairs. Each node v and edge e are assigned weights w^v and w^e, respectively (Section IV). Then, an optimization procedure identifies the airway tree in two steps. First, we optimize the selection of branch connections such that each airway branch candidate becomes connected to a parent branch by selecting one edge pointing towards the airway branch candidate (Section III-C1). Second, the final set of airway branch candidates is selected by pruning subtrees who's overall weight does not justify inclusion in the final airway tree (Section III-C2).

Weights

The node and edge weights represent the confidence to include or exclude an airway branch or connection candidate in the segmentation result. Positive weights encourage the selection of an airway branch or connection candidate and negative weights discourage the selection. The magnitude of the weight reflects the strength of the influence. The weights can be based on various features (Section IV), like for example branching angles. In order to calculate branching angles (and the resulting weights) in the tree structure correctly, it has to be known which end of the parent airway branch is closer (more proximal) to the trachea, as illustrated in Fig. 5. This information is not known a priori, but is obtained during the optimization process.

Fig. 5.

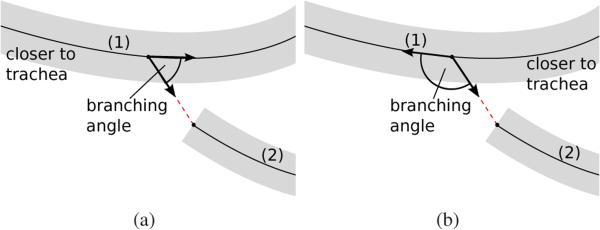
The branching angle between a parent branch (1) and a child branch (2) depends on which end of the parent branch is closer to the trachea. (a) Left end of parent branch is closer to trachea. (b) Right end of parent branch is closer to trachea.

1) Optimization of Connections

In the first optimization step, we reduce the initial graph to an optimized rooted directed spanning tree by selecting a subset of branch connections E′ ⊆ E where the sum of the associated weights is to be maximized. A rooted directed spanning tree is defined as a graph where each node (except the root) has one and only one incoming edge. The resulting graph G′ = (V, E′) is loop-free and contains all nodes of the initial graph G but only |V | − 1 edges. In our application, the root node is know as the trachea, which we can identify easily as the airway branch candidate with the largest volume starting in a fixed pre-defined area of the data set. Then, for optimization of the branch connections, we utilize Prim's minimum spanning tree algorithm [15] with the trachea as root node. Starting from the root node, the algorithm iteratively expands the tree structure until all nodes are merged based on the weights of adjacent outgoing edges. We calculate these weights on the fly, which allows correct calculation of branching angles and resulting weights.

2) Optimization of Branch Selection

As a result of the first optimization step described above, a fully-connected loop-free tree structure is obtained, which consists of true and false airway branch candidates. In the second optimization step, false airway branch candidates are removed by pruning the initial tree. This is accomplished by utilizing an approach that does not just consider weights of individual nodes or edges, but instead the overall combined weight of complete subtrees. For this purpose, we define a subtree weight for nodes, which is the overall sum of all node and edge weights in the subtree. Similar to individual weights, a positive subtree weight indicates that the subtree should be included in the final airway tree and a negative weight indicates that the subtree should be removed. The magnitude of the weight reflects the confidence. Then, subtrees who's subtree weight does not justify inclusion in the final airway tree are removed from the initial tree structure utilizing an adapted version of the global graph partitioning algorithm [10]. Because the original global graph partitioning algorithm may remove complete subtrees that have a high confidence in case of a single high cost connection to the parent branch, we introduce an additional criterion to preserve these structures. All nodes in the initial tree structure are sorted based on their depth in the tree. Starting from the distal ends of the tree, two tests are performed on each node. First, if a node has an overall subtree weight above a threshold t_conf = 100.0 we have a high confidence that this node (airway branch candidate) is part of the airway tree. Then, the airway branch candidate and it's whole path from the trachea should be included in the airway tree and all nodes on the path from the trachea are not further considered for pruning. Second, if a node has an overall subtree weight below zero, it should not be included in the airway tree and is pruned from the initial tree structure.

IV. Features and Weights

The weight of a node/edge in the graph can be based on different features, such as gray-value along the centerline, the TDF response, or structural properties. In the following, we define several suitable features $(x_1^v,\dots ,x_n^v)$ for nodes v ∈ V and $(x_1^e,\dots ,x_m^e)$ for edges e ∈ E that can be utilized to obtain graph weights (Sections IV-A to IV-C). All or a subset of these features are then normalized and combined into the final node and edge weights for the graph-optimization algorithm (Section IV-D). A priori it is not obvious which feature subset will produce the best results. Therefore, the influence of various feature combinations (Section V) on the segmentation result will be evaluated (Section VI). A complete list of all defined features and related weight terms is provided in Table I.

TABLE I.

List of individual features and weight terms for nodes and edges. A detailed description of features can be found in Sections IV-A- IV-C.

Parameters of normalization function $\mathcal{W}$ (Eq. 1)
Weight w	μ	σ	Description of feature x
Gray-value feature based weights (Section IV-A):
$w_{GRY1}^v=-\mathcal{W}\left(x_{GRY1}^v\right)$	–800	150	mean gray-value
$w_{GRY2}^e=-\mathcal{W}\left(x_{GRY2}^e\right)$	0.0	stdGRY(p(e))*	gray-value deviation on connection path
$w_{GRY3}^e=-\mathcal{W}\left(x_{GRY3}^e\right)$	0.0	stdGRY(p(e))*	gray-value deviation of child branch
Local shape feature based weights (Section IV-B):
$w_{TDF1}^v=+\mathcal{W}\left(x_{TDF1}^v\right)$	0.0
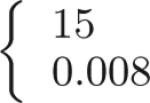
$w_{TDF2}^e=-3$	–	–	TDF counter-balance weight for connections
Structural feature based weights (Section IV-C):
$w_{STR1}^v=+\mathcal{W}\left(x_{STR1}^v\right)$	1.0	0.3	curvedness of branch centerline
$w_{STR2}^e=+\mathcal{W}\left(x_{STR2}^e\right)$	1.3	0.3	curvedness of connection path
$w_{STR3}^e=+\mathcal{W}\left(x_{STR3}^e\right)$	0.0	0.3	angle between parent and child branch
$w_{STR4}^e=+\mathcal{W}\left(x_{STR4}^e\right)$	0.0	0.3	angle between parent branch and connection path
$w_{STR5}^e=+\mathcal{W}\left(x_{STR5}^e\right)$	0.0	0.3	angle between connection path and child branch
$w_{STR6}^e=+\mathcal{W}\left(x_{STR6}^e\right)$	0.0	0.1	relative increase in airway radius

^*This parameter depends on properties of the parent airway branch candidate and is not a constant value.

A. Gray-Value Features

Gray-value based features such as the average density of a candidate airway branch or abrupt changes of density between connection candidates provide valuable information about what airway branch candidates to include and how to connect them to generate the final airway trees.

Let mean_GRY (p), std_GRY (p), min_GRY (p) and max_GRY (p) be the average, standard deviation, minimum and maximum density along the airway branch candidate centerline path or connection path p, respectively. Then, diff_GRY (p₁, p₂) = max{|max_GRY (p₂) − mean_GRY (p₁)|, |min_GRY (p₂) − mean_GRY (p₁)|} represents the maximum gray value deviation on centerline p₂ compared to the average of centerline p₁. p(e) and c(e) are the parent and child node of e, respectively. Then, we define the following three gray-value based features:

• $x_{GRY1}^v$ = mean_GRY (v) is the average density along the airway branch candidate.

• $x_{GRY2}^e$ = diff_GRY (p(e), e) is the largest difference in density along the connection path e relative to p(e).

• $x_{GRY3}^e$ = diff_GRY (p(e), c(e)) is the largest difference in density along the airway branch candidate c(e) relative to p(e).

B. Local Shape Features

The TDF responses utilized to identify large and small tubular structures in Section III-A provide information about the local shape of the airway candidate. We define the local shape feature $x_{TDF1}^v$:

• $x_{TDF1}^v$ = mean_TDF (v) is the mean TDF response along the airway branch candidate centerline path of v.

C. Structural Features

Besides the features described above, which consider information available for each voxel location, structural information of airway branch candidates or between airway branch candidates such as branching angles, radius change, or ”curvedness” of a centerline path, provide additional features on a higher abstraction level.

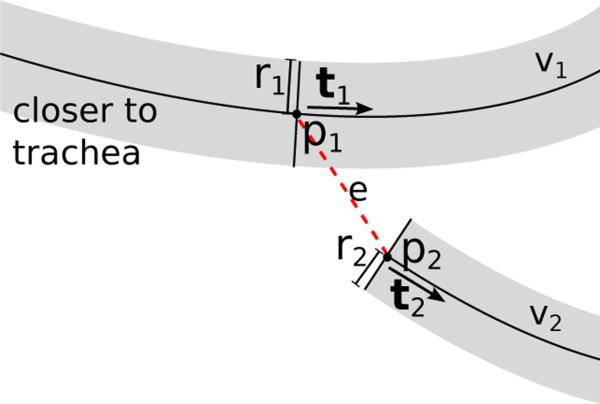
Let p₁ and p₂ be the start and end point of a connection path e between a potential parent airway branch candidate v₁ = p(e) and child branch candidate v₂ = c(e) with associated tangent directions t₁ and t₂ and radii r₁ and r₂, respectively (Fig. 6). We define a measure of line curvedness for a centerline path d as S(d) = centerline_length(d)/start_end_point_distance(d). In addition, we define the following six structural features:

• $x_{STR1}^v$ = S(v) is the curvedness of the airway branch candidate centerline.

• $x_{STR2}^e$ = S(e) is the curvedness of the connection path.

• $x_{STR3}^e=\angle (t_1,t_2)$ is the angle between the two airway candidates.

• $x_{STR4}^e=\angle (t_1,\overrightarrow{p_1{p}_2})$ is the angle between the airway branch candidate v₁ and the connection path e.

• $x_{STR5}^e=\angle (\overrightarrow{p_1{p}_2},t_2)$ is the angle between the connection path e and the airway candidate v₂.

• $x_{STR6}^e=\frac{h(r_2-r_1)}{r_1}$ is the relative increase in airway radius between the potential child and parent branch, where h(·) is the Heaviside step function.

Fig. 6.

Illustration of structural information utilized to obtain weights for an edge e between nodes v₁ and v₂.

D. Conversion of Features into Weights

To obtain the graph weights, all or just a subset of the features listed in Sections IV-A to IV-C may be utilized. However, a suitable normalization and aggregation of the feature values into a graph-weight w^v for each node v ∈ V and a weight w^e for each edge e ∈ E in the graph is required as described below.

Normalization

For normalization of each individual feature x, the following normalization function is utilized:

$$\mathcal{W}\left(x\right)=sign(x-\mu ){\left(\frac{x-\mu }{\sigma }\right)}^2.$$ (1)

Eq. 1 normalizes a feature value x based on parameters μ and σ that are related to the feature type. Equation 1 may result in positive or negative values with values close to 0 for measurements close to μ and values between −1 and +1 for measurements within the standard deviation. $\mathcal{W}\left(x\right)$ produces positive weights for feature values above μ and negative weights for feature values below μ. By utilizing $\mathcal{W}\left(x\right)$ the inverse behavior can be achieved. This allows us to define the weighting functions appropriately such that a suitable balance between positive and negative weights is obtained, which is required by the graph-optimization algorithm (Section III-C). The utilized weighting functions for all feature types are listed in Table I.

Combination

After transformation of the set of feature values $X^v=(x_1^v,\dots ,x_N^x)$ of a node into a set of weights $W^v=(w_1^v,\dots ,w_N^v)$, these are combined into a single weight for the node by averaging over all individual weights. The same applies to $X^e=(x_1^e,\dots ,x_M^e)$ of an edge and the resulting $W^e=(w_1^e,\dots ,w_M^e)$. Taking the average leads to a suitable balance between node and edge weights in the graph in case the number of individual node and edge weights are unequal. In addition, the weight of each node and edge is scaled proportionally by the length l(·) of the associated centerline of the airway branch candidate or connection path candidate, respectively. This gives longer centerlines a stronger influence compared to shorter centerlines. The final node and edge weights are obtained by:

$$w^v=l\left(v\right)\frac{1}{N}\sum _{i=1}^N{w}_i^v$$ (2)

and

$$w^e=l\left(e\right)\frac{1}{M}\sum _{i=1}^M{w}_i^e$$ (3)

E. Parameter Selection

The above features are weighted independently utilizing equation 1. Individual parameters μ and σ for each feature type were determined using statistical analysis on the development data sets described in Section II-1. The found parameters are listed in Table I.

V. Experimental Setup

A. Performance Comparison of Feature Combinations

To assess the performance of features introduced in Section IV, we utilized different feature combinations for graph-based airway reconstruction and evaluated the performance on the evaluation set described in Section II-1.

1) Feature Combinations

To generate meaningful feature combinations, all features were grouped into subsets of gray-value, local shape, and structural features, out of which seven feature combinations were generated, as summarized in Table II.

TABLE II.

Evaluated feature combinations.

Feature combination	Utilized features
	gray-value	local shape	structure
GRY	✓
TDF		✓
STR			✓
GRY+TDF	✓	✓
GRY+STR	✓		✓
TDF+STR		✓	✓
ALL	✓	✓	✓

Feature combination TDF contains only one feature (local shape) with positive weight values (Section IV-B). However, the optimization algorithm requires positive and negative weights for the pruning step (Section III-C2). In order to be able to study only structural features, we introduce a constant counter balance weight $w_{TDF2}^e$ and add it to the group of local shape weights (see Table I) for all further experiments, which involved local shape features. The value of this weight was determined in an experiment on the development data sets based on an ROC analysis. Using feature combination TDF, the value of $w_{TDF2}^e$ was varied until an optimal balance between leakage and undersegmentation was found at $w_{TDF2}^e=-3$.

2) Reference Standard

For performance evaluation, we established reference airway tree segmentations following a similar approach as selected by the organizers of the EXACT’09 segmentation challenge [6].

For each CT scan, all airway branches from all tree reconstruction results produced with the different feature combinations were visually inspected for correctness by a trained pulmonologist with several years experience in analyzing lung CT scans. The pulmonologist visually assessed each branch of each airway tree reconstruction result and labeled them as ’true airway’ or ’false airway’ using custom software . The software allows visualization of the 3D airway tree structure, selection of individual branches, and visualization of cross-sectional CT images around the branch for verification of it's correctness. Note that several of the branches included in the segmentations resulting from the different feature combinations are identical. To reduce the effort to inspect the same branches several times, branches that were previously assessed as ’true airways’ were automatically labeled. The visual evaluation required on average about 30 minute per data set.

After assessment of all segmentation results from the same data set, a reference airway tree was constructed as the union of all airway branches that were classified as ’true airways’. To obtain a clean structural representation of the reference airway tree without any duplicate centerlines, we utilized following procedure. Each ’true airway’ branch was individually transformed into a binary data set, using an inverse distance transformation based on a fast marching method [16], the individual binary segmentations were combined into one binary segmentation data set, from which we obtained clean centerline/radius based representations using skeletonization with pruning of surface-noise induced skeletonization artifacts [17] and distance transformation [18].

Average centerline lengths and number of branches of the resulting reference airway trees are summarized in Table III.

TABLE III.

Average centerline length and number of branches of reference airway trees.

Cohort	Centerline length (in cm)	Number of branches
normals	348.2	279.6
COPD	351.5	270.4
asbestosis	426.2	344.6
IPF/sarcoidosis	513.8	413.5
asthma	352.2	307.2
average	398.4	323.1

3) Performance Measures

Our performance measures focus on the structural correctness of the airway tree, which is represented as a set of centerline points T with associated radius information r(t) for each centerline point t ∈ T in the skeleton. Given a segmentation result T_S and a reference segmentation T_R, we use the true positive ratio T P R(T_S, T_R) = l(I(T_R, T_S))/l(T_R), which represents the percentage of the correctly identified reference airway tree, and the false positive ratio F P R(T_S, T_R) = l(I(T_S, T_R))/l(T_R), representing the percentage of airway branch/connection candidates that were falsely included in the segmentation. The function l(T ) represents the length of all centerlines in T and I(T₁, T₂) is the intersection between T₁ and T₂:

$$I(T_1,T_2)=\{t_1\in T_1\mid mi{n}_{t_2\in T_2}(\Vert \overrightarrow{t_2{t}_1}\Vert -r\left(t_2\right))<0\},$$ (4)

i.e. I(T₁, T₂) is the subset of T₁ that remains after removing from T₁ all centerline points that are outside of the volume covered by T₂. In addition, the overall length and number of branches of the tree structure are reported.

B. Evaluation on EXACT’09

For comparison of our approach with other airway segmentation methods, we applied our method on CT data sets from a publicly available database provided by the organizers of the EXACT’09 challenge [6]. During the EXACT’09 challenge, the organizers collected airway segmentation results obtained by several research groups with different segmentation algorithms on a common set of CT scans. Based on these individual segmentation results, the organizers constructed a reference segmentation for each CT scan by visual assessment of the individual airway branches. Using this approach allowed the organizers to measure and compare the performance of several state-of-the-art airway tree segmentation methods in a fair way. Algorithm developers can still submit new segmentation results for evaluation against this undisclosed standard. However, as mentioned by Lo et al. [6] “...some correctly segmented branches from newly submitted algorithms may be classified as incorrect if they are missing from the current [at the time of completion of the EXACT’09 competition] reference standard”. Thus, performance measures for newly submitted algorithms can partially be misleading in these cases.

We applied our method with all features included (feature combination ALL) to the CT scans in the EXACT’09 database. The EXACT’09 evaluation framework requires binary segmentations of the airway lumen for evaluation. To obtain such segmentations for the identified airway trees, we used an optimal surface finding method described in [19] to obtain a mesh-based segmentation of the inner and outer airway wall and voxelized the meshes representing the airway lumen surfaces. In addition, for two of the EXACT’09 evaluation data sets (Case 24 and Case 26), Hounsfield units in the airways were significantly off from expected values with some voxels in the trachea (air) having a gray value < −1200 HU. We adjusted those data sets, by shifting the gray-values before processing them. All binary segmentations were sent to the EXACT’09 organizers, who in return provided evaluation measurements for the 20 evaluation cases in the database. For exact definitions of the performance measures, we refer to the paper of Lo et al. [6].

VI. Results

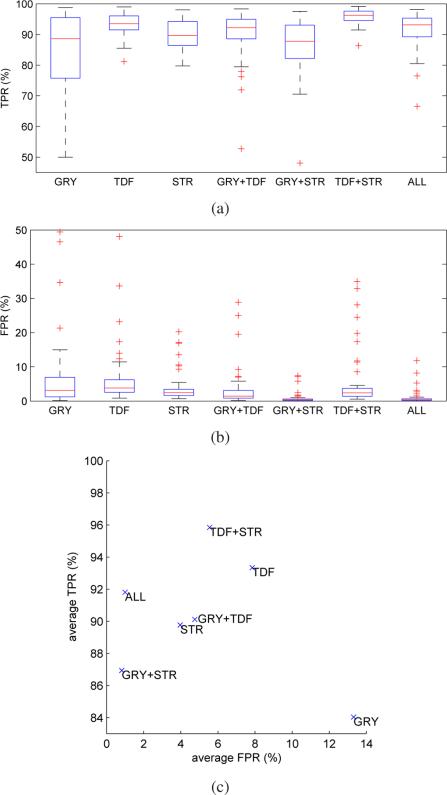
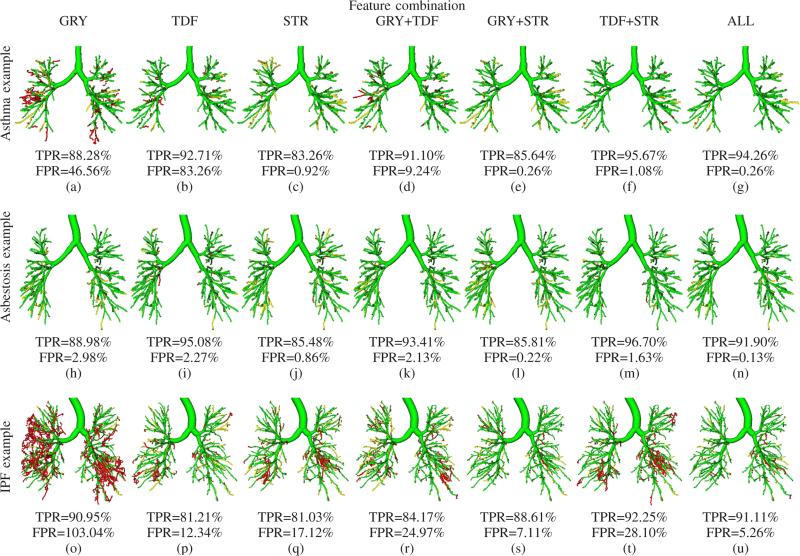
The average performances for each feature combination and cohort are summarized in Table IV. Figs. 7(a) and 7(b) show boxplots comparing TPR and FPR of the individual feature combinations, respectively. Fig. 7(c) compares the average TPRs and FPRs on all evaluation data sets. Some typical examples showing the impact of different feature combinations on the segmentation results are depicted in Fig. 8. Table V summarizes the average centerline lengths of correctly and falsely identified airway branches in the tree reconstruction results for feature combination ALL.

TABLE IV.

Average TPR and FPR for each feature combination.

Feature combination	normal		COPD		Cohort asbestosis		IPF/sarcoidosis		asthma		overall average
	TPR	FPR	TPR	FPR	TPR	FPR	TPR	FPR	TPR	FPR	TPR	FPR
GRY	94.43%	1.98%	85.51%	6.50%	82.93%	2.45%	80.17%	40.50%	77.13%	15.13%	84.03%	13.31%
TDF	94.42%	2.62%	94.32%	4.42%	94.31%	3.87%	89.59%	23.70%	94.07%	4.63%	93.34%	7.85%
STR	93.18%	1.96%	92.13%	2.55%	87.43%	1.96%	84.71%	10.08%	91.38%	3.29%	89.77%	3.97%
GRY+TDF	95.66%	0.74%	92.26%	1.99%	90.68%	1.42%	83.52%	14.87%	88.45%	4.75%	90.12%	4.75%
GRY+STR	93.74%	0.25%	88.94%	0.33%	85.48%	0.28%	81.78%	2.78%	84.77%	0.45%	86.94%	0.82%
TDF+STR	96.51%	1.53%	96.23%	2.27%	96.36%	2.27%	92.87%	18.18%	97.26%	3.50%	95.84%	5.55%
ALL	96.17%	0.25%	92.72%	0.43%	91.05%	0.29%	87.80%	3.65%	91.27%	0.40%	91.80%	1.00%

Fig. 7.

TPRs and FPRs for different feature combinations. (a) Boxplots of TPRs. (b) Boxplots of FPRs. (c) Average TPRs versus FPRs.

Fig. 8.

Influence of different feature combinations on tree reconstruction performance on three different CT scans. The images show the airway trees with true positives (green), false positives (red), and false negatives (yellow). Renderings of the airways are based on the centerline and radius estimate information.

TABLE V.

Average centerline length of correctly identified airway branches and false airway branches per data set for feature combination ALL.

Cohort	Length of correctly identified branches (cm)	Length of false positive branches (cm)
normals	334.9	0.9
COPD	325.9	1.5
asbestosis	388.1	1.2
IPF/sarcoidosis	451.1	18.8
asthma	321.5	1.4
average	365.7	4.8

For feature combination ALL, the median TPR was 93.14% and the 1st quartile was TPR 89.38% on all 50 evaluation data sets. Only 4 data sets had a TPR below 85%. The median FPR was 0.34% and the 3rd quartile was 0.63%. Only 3 data sets were found to have an FPR above 5%, all of which were IPF/sarcoidosis cases. Fig. 8(u) shows such a worst case scenario with an FPR of 5.26%.

The computation time on a single CT scan was about 10 minutes.

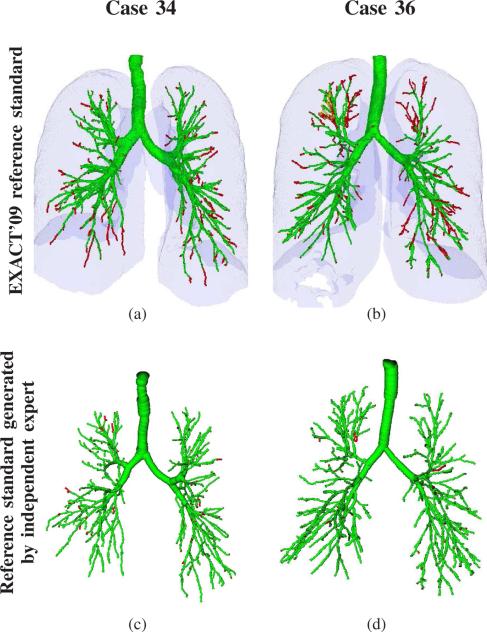
Evaluation results on the EXACT’09 database are provided in Table VI. The mean tree length was 162.8 cm and the mean tree length detection ratio was 71.6 %. The mean false positive rate was 9.75 %. Results for the two data sets with the highest leakage count (Case 34) and the largest leakage volume (Case 36) are shown in Figs. 9(a) and 9(b), respectively.

TABLE VI.

Evaluation results on the EXACT'09 evaluation set. The evaluation set consists of twenty cases from 15 different subjects (A-O). Imaging was performed with various acquisition parameters (tube voltage (TV), tube current (TC), reconstruction kernel, etc.) as well as scanner models (see Lo et al. [6] for details). Level of inspiration (LI) indicates whether the scan was a full inspiration (I) or full expiration (E) scan.

Case (Subject)	Imaging acquisition parameters				Evaluation results
	LI (-)	Kernel (-)	TV (kVp)	TC (mA)	Branch count (-)	Branch detected (%)	Tree length (cm)	Tree length detected (%)	Leakage count (-)	Leakage volume (mm3)	False positive rate (%)
CASE21 (A)	E	B50f	120	200.0	113	56.8	63.3	57.3	53	294.4	3.69
CASE22 (A)	I	B50f	120	200.0	332	85.8	290.3	87.8	188	2478.3	9.24
CASE23 (B)	I	B50f	120	200.0	262	92.3	232.6	89.4	181	2443.9	10.48
CASE24 (C)	I	FC12	120	10.0	164	88.2	146.3	90.0	119	2494.3	9.44
CASE25 (C)	I	FC10	120	150.0	188	80.3	199.8	79.3	144	1723.3	6.07
CASE26 (D)	I	FC12	120	10.0	34	42.5	28.4	43.2	41	1077.6	25.18
CASE27 (D)	I	FC10	120	150.0	56	55.4	42.4	52.3	21	2617.9	37.21
CASE28 (E)	I	B30f	120	348.0	95	77.2	81.2	74.1	59	810.0	8.37
CASE29 (E)	I	B50f	120	348.0	128	69.6	97.0	70.3	56	822.1	7.53
CASE30 (F)	I	D	140	120.0	130	66.7	104.2	68.2	45	520.6	5.41
CASE31 (G)	I	D	140	120.0	136	63.6	118.6	67.6	55	787.4	5.20
CASE32 (H)	I	D	140	120.0	183	78.5	175.4	80.5	91	2527.5	11.68
CASE33 (I)	I	B60f	120	103.6	134	79.8	110.4	75.1	64	337.2	3.84
CASE34 (J)	I	B60f	120	321.0	369	80.6	292.2	81.7	206	2879.5	8.75
CASE35 (K)	I	Stand.	120	411.5	282	82.0	246.3	79.6	178	1553.8	6.59
CASE36 (L)	I	C	120	206.0	289	79.4	339.5	82.4	199	4565.3	14.88
CASE37 (M)	I	B	140	64.0	151	81.6	142.7	80.3	116	1781.1	9.19
CASE38 (M)	E	C	120	51.0	33	33.7	28.0	42.2	19	186.6	2.93
CASE39 (N)	I	B70f	100	336.7	313	60.2	268.2	65.6	149	1427.3	5.83
CASE40 (O)	I	B70s	120	90.6	263	67.6	249.4	64.5	96	885.8	3.41
			Mean		182.8	71.1	162.8	71.6	104.0	1610.7	9.75
			Std. dev.		100.7	15.3	96.4	14.1	62.7	1119.7	8.17
			Min		33	33.7	28.0	42.2	19	186.6	2.93
			1st quartile		113	60.2	81.2	64.5	53	787.4	5.20
			Median		158	77.9	144.5	74.6	94	1490.6	7.95
			3rd quartile		289	82.0	268.2	82.4	181	2527.5	11.68
			Max		369	92.3	339.5	90.0	206	4565.3	37.21

Fig. 9.

Results on the two EXACT’09 data sets with the highest leakage count and volume when compared to the EXACT’09 reference standard segmentations. For comparison, we performed on the same data sets an evaluation of the segmentation results using independent expert branch-by-branch assessment as described in Section V-A. Airways classified as correct are shown in green, airways classified as leakage are shown in red. (a) CASE34 when compared to EXACT’09 reference standard (leakage count = 206). (b) CASE36 when compared to EXACT’09 reference standard (leakage volume = 4565.3 mm³). (c) CASE34 analyzed by independent expert (FPR = 3.08%). (d) CASE36 analyzed by independent expert (FPR = 1.78%). Renderings of the airway in (c) and (d) are based on the centerline and radius estimate information only, while the renderings in (a) and (b) are based on voxel-accurate delineations of the airway lumen.

VII. Discussion

A. Performance of Feature Combinations

The method presented in Section III translates airway detection/reconstruction in CT scans into a graph-based optimization problem. While this is a promising approach, its performance largely depends on the confidence assigned to possible branch and connection candidates. We have defined eleven features and grouped them into gray-value, local shape, and structural categories (Table I). Because it is not clear a prior which feature or feature combination is best suited for processing a specific cohort or a mixture of cohorts, we evaluated all possible combinations of feature groups regarding their TPR and FPR.

Ideally, a combination yielding 100% TPR and 0% FPR is preferable (point in the upper left corner in Fig.7(c). As can be seen in Fig. 7(c) and Table IV, no feature combination is totally error free and reaches this point. In absence of a perfect feature combination, a trade-off has to be made. Clearly, the best compromise depends on the target application. For example, for some applications (e.g., lung fissure detection) falsely detected airways can be critical and need to be avoided, while for others a higher detection rate (TPR) is more preferable (e.g., computer-aided measurement of airway diameters based on user selected path).

1) Performance across cohorts

The combination TDF+STR offers the highest airway detection performance (TPR), but at the cost of 5.55% falsely detected airways (FPR). The lowest FPR rates offer combinations GRY+STR and ALL, where ALL has a higher TPR (91.8%) versus GRY+STR (86.94%) at the cost of a slightly increased FPR (+0.18%). The differences in FPR and FPR were both found to be statistically significant in a signed rank test with p = 9.1e⁻¹⁰ and p = 7.6e⁻¹⁰, respectively.

The features TDF, STR, and GRY as well as the combination GRY+TDF are not recommended, because neither of them performs well regarding TPR or FPR. Out of these four constellations, the feature GRY, which only considers gray-value characteristics, is clearly the worst performer (lower right corner in Fig. 7(c)).

Note that all good performing feature combinations (ALL, GRY+STR, and TDF+STR) include the feature category STR, whereas STR alone is not performing well.

2) Performance per cohort

On normals, all feature combinations performed well with small differences among feature combinations (Table IV). However, for cohorts with lung dis ease, the performance variation amongst feature combinations is getting larger. In particular, on the cohort IPF/sarcoidosis, results obtained with most feature combinations showed a large amount of leakage (bottom row in Fig. 8). Only feature combinations TDF+STR and ALL had an average FPR≤ 5%, while all other feature combinations had an average FPR≥ 10% on IPF/sarcoidosis cases.

When looking at the results on individual cohorts, a similar picture emerges as described in Section VII-A1 above, with only a few exceptions. First, combinations GRY+STR and ALL show a good combination of high TPR and low FPR. On all five cohorts, the combination ALL shows a better TPR with a statisically significant improvement for all cohorts, as shown by a signed rank test with a significance level of 5%, while the differences in FPR were not statistically significant.

The feature combination ALL showed an FPR≥ 5% on only 3 data sets, all of which were IPF/sarcoidosis cases. One of these cases is shown in Fig. 8(u). IPF and sarcoidosis are diseases that can lead to progressive fibrosis of the lung parenchyma and in advanced stages to peripheral honeycombing (i.e., clustered cystic air spaces between 3-10 mm in diameter, which are usually sub-pleural and basal in distribution). These fibrotic changes lead to architectural distortions of the airway tree anatomy (Fig. 1(d)), making it difficult to distinguish true airways from the background of end-stage fibrotic lung parenchyma/honeycombing.

The top TPR across cohorts is delivered by the combination TDF+STR, but at the cost of statistically significantly higher FPR (p = 7.6e⁻¹⁰) compared to combination ALL. For this combination, the FPR is quite high for IPF/sarcoidosis (18.18%) in comparison to the results on the other four cohorts. As IPF and sarcoidosis can lead to substantial peripheral honeycombing of the lung parenchyma and to architectural distortions of the airway tree anatomy, local shape features (TDF) and structural features (STR) are affected.

B. Comparison with Other Methods

A direct comparison of our airway segmentation framework with other approaches is not straight forward. For example, we have tested it with feature combination ALL on the EXACT’09 challenge database [6], and the achieved results were presented in Section VI. However, when comparing these results to the EXACT’09 challenge results summarized in [6] (Table VII lists some best performing approaches including two of our previous published methods), the limitations discussed in Section V-B need to be taken into account. Because the EXACT’09 reference standard segmentations may not contain all true airways, airway branches that were correctly identified by our method might have been misclassified as leakage, as demonstrated in Fig. 9. For this example, the two EXACT’09 data sets with the highest reported leakage volume and leakage count were selected. The EXACT’09 classification is shown in Figs. 9(a) and 9(b). For these two cases, we asked an experienced pulmonologist to identify true leakage using the approach described in Section V-A2, which is similar to the EXACT’09 approach. The results of the expert assessment are depicted in Fig. 9(c) and 9(d). Based on this expert analysis, the leakage (FPR) would have been 3.08% and 1.78%, respectively. Independent of these limitations, our method performed well on the EXACT’09 data (Table VII). Thus, it could help improving the performance of approaches that fuse the results of different airway segmentations, as proposed by Lo et al. in [6].

TABLE VII.

Results of different methods on EXACT'09 database (see Lo et al. [6] for details).

Method	Tree length detected	False positive ratio	Comment
Evaluation on EXACT'09 after the challenge: false positives may be correct airways missing in the EXACT'09 reference standard (Section V-B)
Proposed method	71.60%	9.75%	with feature combination ALL
EXACT'09 challenge participants: false positives for these methods represent true leakage
Feuerstein et al. [20]	73.30%	15.56%	Adaptive region growing and local image enhancement
Tschirren et al. [21]	58.90%	1.19%	Automated region growing with manual branch adding and leak trimming which requires approximately 1 hour user interaction per data set
Bauer et al. [22]	58.40%	1.44%	Gradient vector flow
van Rikxoort et al. [23]	57.0%	7.27%	Multi-threshold region growing
Fetita et al. [24]	55.90%	1.96%	Morpholocial aggrevative
Bauer et al. [9]	55.20%	2.44%	Tube detection and linkage
Lo et al. [25]	54.00%	0.11%	Voxel classification and vessel orientation
... 8 more methods showed a lower tree length detected

In previous work we presented an other approach for reconstruction of airway trees from CT, which also identifies tubular structures and connects them into an airway tree [9]. The method imposed several hard constraints (thresholds) during the tree reconstruction to avoid leakage into non-airway structures. The decision whether an airway branch was connected or not was made for each airway branch/connection candidate individually, solely based on local image information, which can lead to missing airway subtrees. Further, the method utilized only structural features for weight calculation. In contrast, the new framework utilizes soft weights for airway branch/connection candidates. These weights are then utilized in the optimization algorithm, which considers the weights of airway branch/connection candidates in the context of the whole tree structure. This leads to an improved robustness against local ambiguities and thus to improved results (Table VII).

C. Computational Costs

Processing of a single CT scan takes approximately 10 minutes on a workstation with a 2.4 GHz processor and Tesla C-2070 card. Finding potential branch and connection candidates consumes the vast majority (97%) of the required computing time. Thus, finding a good performance tradeoff between computing time and detection performance has little practical impact, because the overall computation time is virtually independent of the utilized feature combination.

D. Parameters

The method utilizes two categories of parameters. The first kind is utilized to define airway branch and connection candidates (Sections III-A and III-B). For example, these parameters specify the expected airway diameter range or minimum required tube likeliness. Their values are set less restrictive, only discarding completely implausible airway branch or connection candidates. Thus, a number of false positive candidates are expected to remain after this processing stage. The second type of parameters are used for the feature weighting functions, which are utilized during the tree reconstruction step (Section III-C) to distinguish between true and false candidates. The parameters used for the weighting function (Equation 1) do not act as hard thresholds, but define a positive, neutral (weights close to 0), and negative impact range instead. These values were found based on a statistical analysis on the training data set (Section IV-E), and we observed that small variations of these values had little impact on detection results.

E. Imaging Protocol

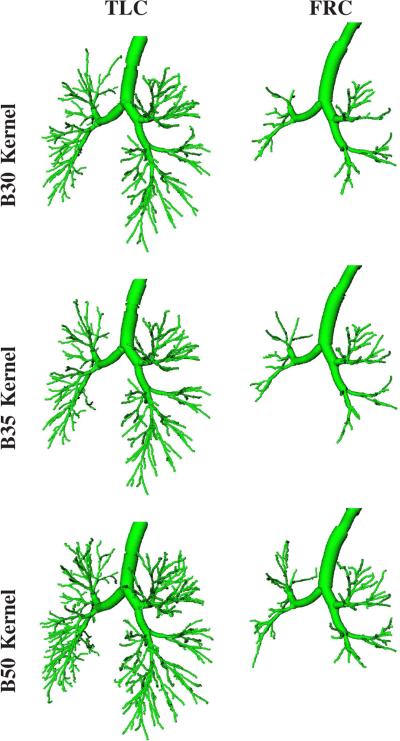
The vast majority of CT scans for detection, characterization, and quantitative assessment of lung disease is performed at inspiration (TLC). For example, the American College of Radiology (ACR) recommends that thoracic computed tomography for lung cancer screening should be obtained in a suspended state of full inspiration whenever possible.¹ Similarly, many large clinical trials follow a TLC only imaging protocol. In contrast, end-expiratory images are typically utilized to evaluate for air-trapping and are far less frequently performed. Consequently, our airway detection approach was developed for TLC lung CT scans. However, our approach is also applicable to expiratory lung CT scans (Fig. 10). Clearly, at functional residual capacity (FRC), less airways are visible compared to TLC, because of the reduced lung volume, and airway detection is more difficult. Further more, other aspects of the imaging protocol like utilized CT reconstruction kernel also impact achievable airway detection performance (Fig. 10). In this context, note that the results shown in Fig. 10 were produced without any adaptions of our method or its parameters. Thus, it is very likely that detection performance can be further optimized for a given imaging protocol.

Fig. 10.

Comparison of airway detection results generated with our method in dependence of utilized reconstruction kernel (B30, B35, and B50) and respiratory state (TLC and FRC) of a lung imaged with a Siemens Somatom Definition Flash scanner. All airways are rendered based on calculated centerline and estimated radius information.

F. Current Limitations

While there is a potential large number of features that could be utilized by the presented graph-based airway tree reconstruction method, we have focused on eleven features, which cover many features utilized by published airway detection/segmentation methods. Also, to reduce computational and other complexities of this effort, we have grouped these features into three categories. Nevertheless, we are not aware of similar studies that have systematically evaluated different features on several cohorts in the context of graph-based airway segmentation.

Results presented in this study are a good starting point for further investigations as well as development of new, powerful features for airway detection.

The method as presented obtains a structural representation of the airway trees, consisting of centerline points with radius estimates. In case, accurate airway lumen and wall surface segmentations are required, one can utilize the structural information obtained from our method as a shape prior to initialize a consecutive surface segmentation method such as that proposed by Liu et al. [19], for example.

VIII. Conclusion

We have presented a graph optimization based airway tree reconstruction framework and evaluated the utility of different features for this specific task. As demonstrated by evaluation results, a high airway detection rate in combination with a low number of false positives across different lung cohorts, including normal and diseased lungs, is achievable with our approach. A comparison with other methods on the EXACT’09 data set has shown that our approach is one of the top performers. In addition, it is very likely that additional discriminative features will allow us to further increase the airway detection rate, while reducing the number of false positives. Thus, future work will focus on studying new features and combinations thereof. One advantage of the presented framework is that it can be easily adapted to other application domains (e.g., vessel detection), mainly requiring the definition of suitable (gray-value) features.