The price elasticity of demand for heroin: matched longitudinal and experimental evidence

Abstract

This paper reports estimates of the price elasticity of demand for heroin based on a newly constructed dataset. The dataset has two matched components concerning the same sample of regular heroin users: longitudinal information about real-world heroin demand (actual price and actual quantity at daily intervals for each heroin user in the sample) and experimental information about laboratory heroin demand (elicited by presenting the same heroin users with scenarios in a laboratory setting). Two empirical strategies are used to estimate the price elasticity of demand for heroin. The first strategy exploits the idiosyncratic variation in the price experienced by a heroin user over time that occurs in markets for illegal drugs. The second strategy exploits the experimentally-induced variation in price experienced by a heroin user across experimental scenarios. Both empirical strategies result in the estimate that the conditional price elasticity of demand for heroin is approximately −0.80.

1. Introduction

Heroin abuse appears to be an increasingly significant problem in the United States. The number of past-year heroin users rose from 373,000 in 2007 to 620,000 in 2011 (as captured in the National Survey on Drug Use and Health (NSDUH) survey), and the number of people meeting criteria for heroin abuse or heroin dependence more than doubled during the same period, from 179,000 to 369,000 (Muhuri, Gfroerer and Davies, 2013). More broadly, the overall cost of illicit drug use in the US is approximately $200 billion per year, including crime, drug-related health care, and impact on productivity (NDIC 2011).

One factor that partly determines drug use is price. Heroin prices have fallen, in particular: by some measures, inflation-adjusted (2010 dollars) typical prices of one pure gram of heroin fell from over $1500 in the early 1980s, to $400 in the early 2000s, and have continued to gradually fall since then (ONDCP 2004; ONDCP 2012; Kilmer et al., 2014). In contrast, one goal of many policy responses to drug abuse problems is to increase the price. Therefore, it is important to understand the price responsiveness of drug consumption, otherwise known as the price elasticity of demand.

This paper reports estimates of the price elasticity of demand for heroin based on a newly constructed sample of information about regular heroin users. The newly constructed sample covers the period 2010 to 2012, and therefore is reflective of the recently low heroin prices, and other recent trends in heroin markets, including policies aiming to limit abuse of prescription opioid pain relievers, that may have shifted demand for heroin (Rudd et al., 2014; Muhuri, Gfroerer and Davies, 2013). Although our focus in this paper is on the collection of high quality data, and the implementation of appropriate empirical strategies to estimate the elasticity of demand for heroin, incidental contributions include “updating” the earlier estimates of the elasticity of demand for heroin to account for these recent aspects of heroin markets.

Our newly constructed dataset concerns 120 regular heroin users, and matches longitudinal information about real-world heroin demand at daily intervals with the results of a demand experiment. We focus our efforts on collecting data from regular heroin users because they simultaneously account for much of heroin consumption, and are difficult to capture in general population surveys (Dave 2008, 2006; van Ours and Pudney 2006; Saffer and Chaloupka 1999; Caulkins 1995).

The longitudinal component of the dataset has information at the level of individual drug demand collected via an interactive voice response (IVR) telephone system: actual price and actual quantity at daily intervals. Our longitudinal data therefore compares favorably with other datasets used to estimate elasticities of demand for illegal drugs, many of which rely on possibly misleading aggregated price and/or consumption data, indicators and/or proxies for drug use rather than transacted quantity data, time-series or cross-sectional data rather than panel data, and/or focus on general population surveys that under-represent regular heroin users. In the rest of the paper, we refer to this as “the IVR data.” We review the literature, and possible concerns about prior estimates, in more detail later in the paper.

Subjects also participated in a laboratory experiment in which they were given varying amounts of imitation money and asked to make hypothetical drug purchases at varying drug prices.¹ In the rest of the paper, we refer to this as “the experimental data.”

We motivate our preferred empirical strategies by first estimating the elasticity of demand for heroin using the IVR data treated as a pooled cross-sectional dataset. This results in an estimated conditional price elasticity of demand for heroin that is approximately −1.05.²

In this paper, we tend to focus on the conditional elasticity of demand for heroin, because in the IVR data we exploit transaction-level price data that does not exist for a given individual on a given day in the absence of a transaction. We can estimate a participation price elasticity of demand for heroin based on the experimental data, which we find to be small: approximately −0.07.

One concern with the −1.05 estimate of the conditional price elasticity of demand, which motivates our preferred empirical strategies, is the possibility that the price of heroin that an individual tends to experience is related to fixed factors that determine the quantity of heroin that individual tends to demand. In models of perfectly competitive markets, it is reasonable to assume that the price that an individual experiences is the “market price” that is unrelated to the characteristics of that specific individual, justifying the credibility of (pooled) cross-sectional estimates of price elasticity. However, in the context of the market for illegal drugs, it is possible that individuals that have fixed characteristics that make them “high demand” users of heroin also are individuals that tend to experience lower prices of heroin. For example, it could be that “high demand” users have more ability and financial incentive to search for, negotiate, and/or otherwise acquire a low price for heroin, perhaps due to learning from experience or the share of income spent on heroin (Reuter and Caulkins 2004; Galenianos et al. 2012).

If “high demand” users tend to experience lower prices of heroin, then the estimated elasticity based on (pooled) cross-section methods is biased. It is confounded by the fact that individuals that tend to experience high prices of heroin also tend to be those individuals that have low demand for heroin. By standard omitted variables bias arguments, that suggests that the demand for heroin is actually less price elastic than suggested by the estimate of −1.05.

We use two empirical strategies that address this concern. The first empirical strategy is a fixed-effects design based on the longitudinal IVR data, and exploits the idiosyncratic variation in price experienced by an individual over time. Even if, for example, “high demand” users tend to experience lower prices, because of the idiosyncratic nature of the market for illegal drugs³, they will occasionally experience higher prices. Our first empirical strategy estimates the elasticity of demand for heroin based on that within-individual idiosyncratic variation in price. The second empirical strategy is based on the experimental data, and exploits the experimentally-induced variation in price experienced by an individual across experimental scenarios.

Therefore, the two different empirical strategies aim to estimate the elasticity of demand based on two different sources of exogenous variation in price. Both empirical strategies result in an estimated conditional price elasticity of demand for heroin that is approximately −0.80, with no evidence of an economically or statistically significant difference in elasticities across the two empirical strategies.

Since our two preferred empirical strategies result in similar estimates, our estimates provide some support for the external validity of the experimental method for estimating illegal drug elasticities. More generally, our estimates add to the recent discussion about the credibility of experiments in general as a tool to recover features of the “real-world” in economics (e.g., Levitt and List 2007; Camerer 2011; and further references cited therein). However, it is important to recognize the possibility that participation in the study affected the behavior of the subjects, as in a Hawthorne effect (e.g., Zwane et al. 2010). For example, it is possible that being surveyed about price and quantity of heroin increases the salience of price, possibly changing the responsiveness to price. Consequently, it is not necessarily clear how the subjects would have behaved in the real world in the absence of the survey, or in an experiment that did not directly follow the collection of the real world data. Potentially, an experiment that is run separately from collection of real world data would exhibit less external validity than our results exhibit. Despite the evidence that such effects do exist in general, we suspect that our subjects are (relatively) unlikely to experience these effects in significant magnitude, because they have been using heroin for at least six months before participating in the study, and therefore have significant and repeated learned experience already with heroin prices that plausibly “outweighs” the additional experience of the study. Nevertheless, we cannot fully exclude the possibility that these effects are present in our study.

The novel features of our matched dataset are necessary ingredients in our preferred empirical strategies. To our knowledge, this is the first study to collect extended longitudinal data on: actual quantities purchased, actual transaction prices, and expected quality of purchased drugs. Furthermore, this is the first study to collect drug purchase data from users on a daily basis using an IVR system. Moreover, this is only the second study—and the first in several decades—to compare, based on the same sample of subjects, elasticity estimates obtained using real-world data to those obtained using hypothetical choice experiments.⁴ We also review alternative data designs in the literature review.

We also study, as extensions, heterogeneity in the elasticities, and cross-price elasticities.

Our paper proceeds as follows. Section 2 reviews the literature on heroin price elasticities. Section 3 describes our data. Section 4 presents the results, and Section 5 concludes.

2. Prior Studies of Heroin Price Elasticities

Because heroin is illegal, it is difficult to obtain the data necessary to estimate the price elasticity of demand (van Ours and Pudney 2006; Bretteville-Jensen 2006; Petry and Bickel 1998). See Gallet (2014) for an excellent review of 42 studies that collectively provide 462 elasticity estimates for heroin, cocaine, and marijuana.

One approach is to indirectly estimate the price elasticity of demand by focusing on outcomes related to heroin use (e.g., crime, arrests, emergency department visits). For example, Silverman and Spruill (1977) exploited the relationship between crime and the price of heroin in a monthly time series of 41 Detroit neighborhoods to estimate a long-term price elasticity of demand for heroin of −0.27. Caulkins (1995) used the percentage of arrestees testing positive for heroin in 24 US cities during 1987-1991, along with assumptions about the relationship between drug use and the probability of arrest, to estimate a heroin participation elasticity of −1.50 for arrestees.⁵ Dave (2008) used a similar approach to Caulkins (1995), though with a number of methodological differences, to estimate a heroin participation elasticity of −0.10 for arrestees in 42 US cities during 1988-2003. And Dave (2006) exploited the relationship between heroin-related visits to the emergency department (ED) and the price of heroin to estimate a heroin participation price elasticity of −0.11 in 21 US cities during 1990-2002. A major advantage of these “indirect” studies is that they rely on objective indicators of heroin use (e.g., urinalysis, drug purchases made by undercover narcotics agents) contained in administrative datasets (e.g., police records, NHSDA - National Household Survey on Drug Abuse, STRIDE - System to Retrieve Information from Drug Evidence, DUF - Drug Use Forecasting, ADAM - Arrestee Drug Abuse Monitoring, DAWN - Drug Abuse Warning Network).

An alternative approach combines large-scale self-report national household surveys that directly measure drug use with price data obtained from purchases made by undercover narcotics agents. A classic example of this approach is Saffer and Chaloupka (1999), who used consumption data on nearly 50,000 individuals from the National Household Survey on Drug Abuse (NHSDA, now called the National Survey on Drug Use and Health) and price data from STRIDE to estimate a heroin participation elasticity of −0.94 during 1988-1991.

Still another approach relies on aggregated historical records to estimate the relationship between drug use and price. For example, van Ours (1995) used data collected by the Dutch government in the Dutch East Indies during 1923-1938 to estimate price elasticities of −0.7 (short-run) to −1.0 (long-run) for opium consumption and −0.3 to −0.4 for opium participation. And Liu et al. (1999) used data collected by the Japanese colonial government in Taiwan during 1914-1942 to estimate price elasticities of −0.48 (short- run) to −1.38 (long-run) for opium consumption and −0.21 to −0.43 for opium participation. In addition, Liu et al. (1999) estimated the price elasticity for opium consumption, conditional on use, to be −0.27 (short-run) to −1.17 (long-run).

All of the studies described thus far rely on price data aggregated geographically (e.g., neighborhood, city, state). Another approach is to collect price and consumption data at the individual level to better reflect the experience of particular individuals, in particular given the heterogeneity in price even within geographic markets. For example, Bretteville-Jensen and Biorn (2003) applied a wide variety of econometric models and specifications to a two-period panel dataset (two waves of data collection separated by one year) comprising interviews with 78 active heroin injectors attending a needle exchange service in Oslo, Norway during 1997-1998. The median heroin price elasticities from this panel study were −0.71 and −0.91 for dealers and non-dealers, respectively. A later study based on 2,873 interviews with active heroin injectors attending the same needle exchange service during 1993-2006 estimated heroin price elasticities of −0.33 for dealers and −0.77 for non-dealers (Bretteville-Jensen 2006).⁶ And in the US, Roddy and Greenwald (2009) estimated a heroin price elasticity of −0.64 based on interviews with 100 chronic daily heroin users in Detroit, MI during 2004-2005.

All of the elasticity estimates described above are based on real-world data: administrative datasets (e.g., DUF, ADAM, STRIDE, etc.), historical records, or self-reported surveys and interviews. Collecting such real-world data is difficult, because, again, since heroin is illegal, heroin prices and heroin consumption are difficult to measure in real-world settings. To avoid the challenges of real-world data collection, researchers have adapted the laboratory method (Smith 1982) to the study of polydrug abuse. In the laboratory method, drug abusers are given imitation money, and prices of drugs are indicated on paper. Study subjects state the types and quantities of drugs they would buy. Changes in drug choices are then examined as a function of prices. Petry and Bickel (1998) used the laboratory method with 40 current or former opioid-dependent subjects in the US and estimated a heroin price elasticity of −0.87 when the unit price of heroin was low (less than $6/bag), −1.3 when the unit price of heroin was high (greater than $6/bag), and −1.04 overall. Jofre-Bonet and Petry (2008) used a similar approach with 41 heroin addicts in the US to estimate a heroin price elasticity in the range from −0.82 to −0.92. And Chalmers et al. (2010) used the laboratory method with 71 heroin-dependent subjects in Australia and estimated heroin elasticities in the range from −1.54 to −1.73.⁷ Laboratory experiments may provide valuable information when relatively little real-world market data or behavioral understanding exists (Chermak et al. 2013).

While each one of the above approaches has its merits, each has limitations as well. For example, the indirect approach relies on proxies for drug use, as opposed to actual drug use. Studies that aggregate price data geographically (instead of using individual level data) mask some of the heterogeneity of prices experienced by individuals within the market. Price data collected by undercover narcotics agents have been critiqued as unreliable for economic and policy analyses that require accurate measures of price levels and variations (Horowitz 2001). National surveys tend to under-represent regular heroin users, the group that consumes the bulk of heroin and imposes the highest social costs. Real-world data based on retrospective self-reports are subject to a number of well-known biases. And despite the demonstrated internal validity of the laboratory method (Jofre-Bonet and Petry 2008), its external validity has been questioned (Clare 2006; Reuter 1998; Glautier 1998). Because heroin is illegal, and therefore difficult to study empirically, such limitations are to be expected.

The present study reports two new estimates of the price elasticity of demand for heroin. The first estimate is derived from an individual-level panel dataset constructed from 120 regular heroin users. As already noted, individual-level datasets have several advantages over aggregated datasets. Moreover, to our knowledge, this is only the second time an individual-level panel dataset has been used to estimate the price elasticity of demand for an illegal drug. As noted above, Bretteville-Jensen and Biorn (2003) used a two-period panel dataset to estimate heroin price elasticities. Because our panel dataset asks each subject to report information in 28 different time periods (on 28 different days), we were able to collect much richer “within-subject” data than were Bretteville-Jensen and Biorn (2003). This additional within-subject data is desirable from the perspective of estimating the elasticity of demand for heroin based on our fixed effects approach, since that approach exploits within-subject variation, which relies on having many observations per subject. Moreover, and similarly, because Bretteville-Jensen and Biorn (2003) is concerned with “monthly” demand for heroin, there is less variability in price than in our dataset with demand data at daily intervals. Of course, Bretteville-Jensen and Biorn (2003) recognize these limitations, which are due to the practical difficulties (including cost and logistics) of collecting panel data on heroin users. Our approach based on an IVR system makes collecting panel data a more feasible task. The second estimate is derived from a traditional laboratory experiment using the same sample of 120 regular heroin users. By using the same subjects in both analyses, we are also able to investigate the external validity of the laboratory method. Note that our findings focus on regular heroin users; as such, they are not intended to generalize to the entire population, but rather emphasize (as discussed in the introduction) one of the most important subpopulations of the entire population.

3. Data

3.1 Subjects

Between 2010 and 2012, we recruited 120 regular heroin users from the greater Hartford, CT area using radio and newspaper advertisements, flyers distributed at low-income housing projects and social service agencies, and our contacts with community-based substance abuse treatment programs. Because the study spanned years, with each subject participating for a total of four weeks, only a few subjects were participating on any given day. Inclusion criteria included age greater than 18, and English speaking. Also, we include only regular heroin users (i.e., self-reported heroin use at least once per week during the past six months) in order to avoid complications associated with “new” heroin users who may have particularly unstable heroin use patterns. Consequently, we aim to estimate the elasticity that heroin users “converge to” after a possible initial learning process. Six months is a relatively small fraction of time compared to time spent using heroin: the average first-time admission to treatment for heroin users is approximately 12 years after first use of heroin (SAMHSA 2011). Moreover, regular heroin users simultaneously account for much of heroin consumption, and are difficult to capture in general population surveys (Dave 2008, 2006; van Ours and Pudney 2006; Saffer and Chaloupka 1999; Caulkins 1995).

We excluded users who reported “dealing drugs” as one of their top 3 sources of income, since we would expect dealers to have a potentially different response to changes in price, as they are not (exclusively) final consumers. Of 826 heroin users screened for participation in the study, only 35 (4%) were excluded due to “dealing drugs,” suggesting that including or excluding dealers from the sample would have relatively small effect on the estimated elasticity (but including dealers and estimating a single elasticity would undesirably mask the differences between non-dealers and dealers). Other exclusion criteria included active psychosis, suicidality, and inability to comprehend the study. Subjects provided written informed consent approved by the University of Connecticut Health Center Institutional Review Board. Subjects were informed that all information was confidential (via a Certificate of Confidentiality from the National Institute of Drug Abuse), including drug purchase data.⁸ Table 1 summarizes the study sample.⁹

Table 1.

Characteristics of subjects at beginning of each wave

	Wave 1 (n = 120)	Wave 2 (n = 92)
Male (%)	58	57
Race (%)
Caucasian	53	52
African American	42	43
Other	5	5
Years age	46 (9)	46 (9)
Years education	12 (2)	12 (2)
Income (all sources, last 30 days)	$1298 ($815)	$1297 ($1361)
Marital status (%)
Married	5	5
Widowed	4	5
Separated	5	1
Divorced	28	27
Never married	54	57
Cohabitating	3	4
Employment status (%)
Full-time	7	7
Part-time	6	7
Unemployed	49	54
Not in labor force	38	32
Lifetime serious depression (%)	63	68
Lifetime anxiety (%)	65	65
Lifetime suicidal thoughts (%)	29	29
Lifetime suicide attempt (%)	21	21
Lifetime dependence diagnosis (%)
Opioids	98	97
Cocaine	65	64
Marijuana	21	20
Alcohol	38	38
Lifetime substance abuse treatment (%)	86	90
Mental Health Inventory (MHI-5) score	20 (3)	19 (4)
Delay discounting rate (k)	.08 (.09)	.07 (.08)
Urine sample positive at beginning of wave (%)
Opioids	67	52
Cocaine	43	42
Marijuana	32	30
Urine sample positive at end of wave (%)	(n = 112)	(n = 88)
Opioids	66	48
Cocaine	38	44
Marijuana	34	33

Numbers in parentheses are standard deviations for non-binary characteristics.

Subjects participated in two distinct two-week waves of data collection, separated by six months. During each wave of data collection, the IVR telephone system made daily calls to subjects on their study-provided cellphones and asked them to report all drug purchases made since the previous call. At the end of each wave, subjects participated in a 30-minute laboratory experiment. Details of the data collection methods used by the IVR system and the laboratory experiment are described below. Subjects completed an interview and psychological testing at the start of each wave of the study. Subjects reported if they were currently receiving, or had ever received, substance abuse treatment excluding participation in self-help groups. Subjects also completed the Mental Health Inventory (MHI- 5), a 5-item subscale of the general health assessment SF-36 with items about depression and anxiety rated on a 6-point scale (Berwick et al. 1991; Ware et al. 2007). Our measure of mental health sums these item scores to produce a total score, with higher scores indicating greater mental health. Finally, we measure the subjects’ delay discounting rates using methods established by Kirby and colleagues (Kirby et al. 1999; Kirby and Marakovic 1996). A higher delay discounting rate, k, indicates more impulsive choices.

Subjects received $2.50 for each completed IVR call, and a $15 bonus for completing 12 or 13 calls in a given wave or a $25 bonus for completing all 14 calls in a given wave. Subjects received $25 for returning cellphones in working order at the end of each wave. Finally, subjects received $25 and $50 for completing the laboratory experiments at the end of the first and second waves, respectively. Conversely, subjects were removed from the study if they completed fewer than half of their IVR calls during a given wave or failed to participate in the laboratory experiment at the end of the first wave. Subjects were compensated an average of $181.96. It is possible that such additional income (approximately 15% of average monthly income) increases the overall level of quantity demanded, through an (anticipated) income effect. However, since the payment received by the subjects is not contingent on the price or quantity of heroin purchased, the receipt of compensation should not substantially affect the estimates of the price elasticity of demand. Appendix 3 in the online supplement demonstrates the high rate of compliance with study protocols: 73% (88/120) of the subjects completed both waves of the study (i.e., completed at least 50% of calls in each wave and completed the laboratory component in each wave). The final analysis sample concerns 1,130 subject-day observations of heroin transactions in the IVR data, and 1,390 subject-scenario observations in the experimental data (with heroin transactions in 1,041 subject-scenario observations).

3.2 IVR Data

An interactive voice response (IVR) system is a computerized telephone-based platform that allows participants to answer recorded questions (and follow-up questions that depend on previous responses) by pressing buttons on their telephone keypad. IVR systems typically yield high quality data, including drug use data, compared with interviews and questionnaires (Tucker et al. 2012; Mundt et al. 1997; Aiemagno et al. 1996; Perrine et al. 1995). IVR systems have been used to collect sensitive data from such populations as homeless crack cocaine addicts (Freedman et al. 2006), adolescents with alcohol and other substance use disorders (Kaminer et al. 2006), and economically-disadvantaged problem drinkers living with HIV/AIDS (Barta et al. 2008). IVR systems are perceived as anonymous compared with live interviewing, facilitating disclosure of sensitive information (Abu-Hasaballah et al. 2007).

Appendix 1 in the online supplement contains the portion of the IVR script for heroin, as well as some further details of implementation of the IVR system. Similar scripts were used for cocaine, marijuana, and beer: “secondary drugs” for heroin users. Data collected for each heroin purchase included total purchase price, units (bags, grams, etc.), number of units, percentage for own use, and expected quality.¹⁰

3.3 Experimental Data

At the end of each wave of IVR data collection, subjects participated in a laboratory experiment. Procedures for the laboratory experiment followed Petry and Bickel (1998). Subjects were given imitation money, and the prices of heroin, cocaine, marijuana and beer were indicated on paper. Subjects were then asked to choose the types and quantities of drugs they would buy. The experiment began with the research assistant reading aloud the instructions provided in Appendix 2 in the online supplement.

Subjects were exposed to the eight experimental scenarios shown in Table 2. The prices of cocaine, marijuana and beer were representative of street prices in Hartford, CT. One scenario was duplicated to assess the reliability of choices made in the experiment, discussed in Appendix 3 in the online supplement. Scenarios were presented in random order to avoid a possible order effect (Chang 2009).

Table 2.

Experimental Scenarios

Drug Budget $	Heroin Price $/bag	Cocaine Price $/bag	Marijuana Price $/joint	Beer Price $/bottle
30	1	10	5	1
30	3	10	5	1
30	5	10	5	1
30	10	10	5	1
30	15	10	5	1
15	5	10	5	1
30	5	10	5	1
60	5	10	5	1

Quality of all drugs is fixed at ‘7’. Scenarios were given to subjects in random order.

4. Results

4.1 Data analysis

We estimate a log-log demand function, thereby emphasizing the other novel features of our empirical strategies, “holding fixed” the conventional underlying functional form of demand.¹¹ Our main explanatory variable is the price of heroin measured in logs, and the own-price conditional elasticity of demand for heroin is estimated by the estimated coefficient on the log price explanatory variable.¹²

Our IVR dataset results in subject-by-day information on price and quantity of heroin. At least among our sample of regular heroin users, use of heroin on a given day seems to be roughly equal to the quantity of heroin acquired on that day.¹³ Consequently, the elasticity of demand for heroin at daily intervals is, at least approximately, interpretable also as the elasticity of daily use of heroin. Our IVR script collects data on the percentage of purchased heroin that the subject intends for own use. We scale the total purchase by that percentage, so that the measure of quantity that we use in our analysis is the quantity for personal consumption. This allows us to focus on the “final” demand for heroin, and avoids complications relating, for example, to “intermediate” demand for heroin due to resale. (As noted above, we also do not include dealers in our sample of heroin users.) Similarly, our experimental design instructs the subjects to imagine making the purchase exclusively for personal use.

In the IVR data, subjects could report the measurement units for heroin transacted as bags of heroin, weight of heroin, or other measurement units. We drop from the analysis sample any calls containing drug transactions that were not measured in bags of heroin, which is the predominant unit of measurement for heroin transactions in our sample (fewer than 1% of the calls (24 calls out of 2,620) were dropped for this reason). Our experiment measured heroin in bags of heroin. Typically, a “bag” of heroin is approximately 100mg (e.g., Roddy and Greenwald 2009), but despite the ubiquity of this unit of measurement, because of the nature of markets for illegal drugs, it is not a perfect measure of the quantity of heroin transacted (because of unavoidable concerns, like: the presence of substances other than pure heroin in the bag).

Our IVR script collects transaction-level price data.¹⁴ Therefore, in the IVR data we observe a price for a given drug on a given day for a given subject if and only if that subject actually purchased that drug on that day. Consequently, based on the IVR data, we estimate the own-price conditional elasticity of demand for heroin (which depends only on observed prices) but not the own-price unconditional elasticity of demand for heroin, or the own-price participation elasticity of demand for heroin (which depend on unobserved “prices” when there is no transaction).

However, in the experimental data, because we do observe the price of heroin even if there is no purchase of heroin, we can additionally estimate the own-price participation elasticity (or unconditional elasticity) of demand for heroin. In the experimental data, we find that the own-price participation elasticity of demand for heroin is small, implying that the own-price unconditional elasticity of demand for heroin is approximately equal to the own-price conditional elasticity of demand for heroin.

For the same reason, we cannot estimate cross-price elasticities of demand based on the IVR data, since the “cross-price” is observed if and only if that “cross-drug” is purchased. In the experimental data, we cannot estimate cross-price elasticities of demand for heroin with respect to the prices of the secondary drugs because, due to the time and mental cost imposed on the subjects for each additional “dimension” of the experiment, we varied only the price of heroin. However, in the experimental data, we can estimate cross-price elasticities of demand for the secondary drugs with respect to the price of heroin.

In the IVR data, subjects report the expected quality of purchased heroin, between 1 (“worst ever had”) and 9 (“best ever had”). In the experimental data, we fixed the quality of the drugs at 7, roughly the median of the expected quality of the heroin in the IVR data. In our analysis of the IVR data, we study demand for heroin with expected quality greater than or equal to 6. This corresponds to approximately the “best” 67% of heroin purchases, according to our IVR data. We treat such heroin as a “different good” from lower quality heroin, and therefore just as we take the conventional approach of studying demand for heroin abstracting from simultaneous demand for other goods (e.g., other drugs), we also take the approach of studying demand for heroin with expected quality greater than or equal to 6 abstracting from simultaneous demand for heroin with lower expected quality. In principle, it would be useful to estimate an elaborated model involving the tradeoffs between different qualities of heroin, but we are unable to do so as we do not observe the price of heroin except (at most) for the purchased quality of heroin, as mentioned above. An alternative method for accounting for the quality of the heroin could be to include the quality of the heroin as an explanatory variable. However, that model would still imply that the elasticity of demand for heroin is the same for all qualities of heroin, but it is not clear that should be true (Goudie et al. 2007).

4.2 Elasticity Estimates

We motivate our two preferred empirical strategies by first estimating the conditional price elasticity of demand for heroin using only the IVR data, treated as a pooled cross-sectional dataset. We report the results in Table 3. In the model reported in the first column, we include an indicator for an observation from Wave 2 of the study, which partly addresses the possibility of some forms of selection into Wave 2. In this model, we estimate the conditional price elasticity of demand for heroin to be approximately −1.05. As discussed in section 3.1, we observe in the dataset some characteristics of the subjects that might be “proxies” for factors that determine the typical demand for heroin. In the model reported in the second column, we add those characteristics as controls: an indicator for having ever participated in a substance abuse treatment program, a measure of psychiatric distress based on the MHI-5, a measure of delay discounting, and a measure of income over the past 30 days in logs. After adding these controls, we estimate the conditional price elasticity of demand for heroin to be approximately −0.92.

Table 3.

Conditional elasticities -- pooled cross sections in IVR data

	(1) Log(quantity)	(2) Log(quantity)
Log(price)	−1.049*** (0.21)	−0.921*** (0.19)
1[Wave2]	−0.042 (0.10)	−0.019 (0.10)
1[treatment]		−0.368* (0.22)
MHI score		−0.000 (0.02)
Delay discounting		1.475** (0.68)
Log(income)		0.376*** (0.09)
Constant	3.295*** (0.37)	0.631 (0.86)
Avg	7.113	7.113
R-squared	0.099	0.221
N	1130	1130

Robust standard errors clustered on subjects in parentheses

+ p<.20

++ p<.15

^*p<.10

^**p<.05

^***p<.01

In this and subsequent tables of estimates, we also report an “Avg” which is: in the case of models of conditional elasticities, the overall average quantity demanded (in bags), and in the case of models of participation, the overall probability of participation. All standard errors in this section are clustered on subjects.

One concern with these estimates, which motivates our preferred empirical strategies, is the possibility that the price of heroin that an individual experiences is related to fixed (but possibly unobserved) factors that determine the quantity of heroin that individual tends to demand. In particular, it is possible that individuals that have characteristics that make them “high demand” users of heroin also are individuals that tend to experience lower prices of heroin. For example, it could be that “high demand” users have more ability and financial incentive to search for, negotiate, and/or otherwise acquire a low price for heroin. If so, the estimated conditional price elasticity of demand based on (pooled) cross-section methods is biased because it is confounded by the fact that individuals that tend to experience high prices of heroin also tend to be those individuals that have low demand for heroin.

This suggests that (pooled) cross-section methods will overestimate the elasticity of demand for heroin. Indeed, we find that additional controls do reduce the estimated conditional elasticity of demand for heroin. These controls can “proxy” for the characteristics that make an individual “high demand.” However, it is possible that these controls are only imperfect “proxies,” suggesting the possibility that even with controls the elasticity of demand is overestimated, motivating the need for our two preferred empirical strategies.

However, despite these concerns, note that even these pooled cross-sectional estimates can compare favorably with some of the prior estimates in the literature, because our data compares favorably. So although we emphasize our preferred empirical strategies, it is important to note also that the data itself is novel and plays a major role in the credibility of the resulting estimates. Of course, as with any data concerning illegal drugs, the possibility of measurement error cannot be entirely ruled out, potentially resulting in attenuation bias of the estimated elasticity.

We use two preferred empirical strategies that address this concern about the relationship between price and fixed (but possibly unobserved) determinants of demand. The first empirical strategy is a fixed-effects design based on the longitudinal nature of the IVR data, and exploits the idiosyncratic variation in price experienced by an individual over time. The second empirical strategy is based on the experimental data, and exploits the experimentally-induced variation in price experienced by an individual across experimental scenarios.

Because the experimental design guarantees that price is unrelated to the characteristics of the subjects, we first present in Table 4 the results from the empirical strategy that uses the experimental data. The models reported in the first, second, and third columns are models of the conditional price elasticity of demand, and the models reported in the fourth, fifth, and sixth columns are models of participation. (We can estimate models of participation based on the experimental data, since we observe the price regardless of whether the subject makes a purchase.) The reported results on participation come from a linear probability model, but results from probit or logit specifications are similar and therefore not reported in the interest of space. The estimated coefficients in the models of participation in the fourth, fifth, and sixth columns are the estimated coefficients from the corresponding regression of participation on the explanatory variables, and consequently the coefficient on log price is the percentage point change in participation in response to a one percent increase in price. Consequently, the coefficients on log price divided by the overall average participation rate (0.749) result in the corresponding participation price elasticities of demand.

Table 4.

Conditional elasticities and models of participation in experimental data

	(1) Log(quantity)	(2) Log(quantity)	(3) Log(quantity)	(4) Participation	(5) Participation	(6) Participation
Log(price)	−0.793*** (0.02)	−0.794*** (0.02)	−0.795*** (0.02)	−0.054*** (0.01)	−0.054*** (0.01)	−0.054*** (0.01)
1[Wave2]	−0.003 (0.05)	−0.003 (0.05)	0.000 (0.05)	−0.115*** (0.04)	−0.115*** (0.04)	−0.112** (0.04)
Log(Budget) (lab only)		0.794*** (0.03)	0.793*** (0.03)		0.068*** (0.02)	0.068*** (0.02)
1[treatment]			0.045 (0.12)			0.117+ (0.09)
MHI score			0.020* (0.01)			−0.001 (0.01)
Delay discounting			0.770** (0.34)			0.425++ (0.29)
Log(income)			0.112*** (0.04)			0.079** (0.03)
Constant	2.589*** (0.06)	−0.121 (0.11)	−1.381*** (0.38)	0.885*** (0.03)	0.652*** (0.06)	−0.017 (0.30)
Avg	6.017	6.017	6.017	0.749	0.749	0.749
R-squared	0.523	0.639	0.659	0.028	0.031	0.059
N	1041	1041	1041	1390	1390	1390

Robust standard errors clustered on subjects in parentheses

⁺p<.20

⁺⁺p<.15

^*p<.10

^**p<.05

^***p<.01

The models in the first and fourth columns include only one explanatory variable other than the price of heroin in logs: an indicator for an observation from Wave 2, like the simpler specification from Table 3. The models in the second and fifth columns include also the experimental drug budget in logs. The models in the third and sixth columns additionally include the same controls used in the models based on the IVR data. The drug budget is not an experimental equivalent to the “income” of the subject, and therefore we do not interpret the coefficient on drug budget as an income elasticity. The “drug budget” is intended to anchor the subjects to making “reasonable” choices in the laboratory scenarios, for example to avoid subjects indicating a desire to buy “unlimited drugs” if there is no budget constraint. Since the “drug budget” is framed as the budget specifically for drugs, it is not the same as the “income” of the subject. As expected, Table 4 shows that the estimated price elasticities are not affected by the inclusion or exclusion of the lab budget as an explanatory variable, since the experimental price and experimental lab budget are effectively independent from each other, implying no omitted variables bias.

We find, unsurprisingly given the experimental design, that, unlike in the case of the models based on the IVR data, the addition of controls does not change the estimated elasticities. The estimated conditional price elasticity of demand is approximately −0.79, and the estimated participation price elasticity of demand is approximately −0.07 (= −0.054/0.749). Although we do not report the results, we also estimated these models with subject fixed effects, analogous to the subject fixed effects we use in our preferred empirical strategy based on the IVR data that we report below. We find, again unsurprisingly given the experimental design, that the estimates with fixed effects are (almost) numerically the same as the corresponding estimates without fixed effects.

Finally, we present in Table 5 the results based on the empirical strategy that uses the longitudinal nature of the IVR data. All of the models reported in Table 5 include subject fixed effects, implying that the price elasticity of demand is estimated off of the idiosyncratic within-subject variation in price over time. Therefore, unlike the pooled cross-section estimates based on the IVR data, the price elasticity of demand is not estimated off of the across-subject variation in price, avoiding the problems related to the possibility that such across-subject variation might be related to the characteristics of the subjects.

Table 5.

Conditional elasticities -- with fixed effects in IVR data

	(1) Log(quantity)	(2) Log(quantity)	(3) Log(quantity)
Log(price)	−0.801*** (0.23)	−0.799*** (0.18)	−0.772*** (0.17)
1[Wave2]	0.013 (0.09)	0.017 (0.08)	−0.021 (0.16)
1[treatment]		−0.302 (0.31)	−0.340 (0.32)
MHI score		−0.033 (0.03)	−0.034 (0.03)
Delay discounting		−0.452 (0.55)	−0.320 (0.49)
Log(income)		0.203** (0.10)	0.252** (0.12)
Constant	2.865*** (0.38)	2.370*** (0.79)	2.125*** (0.77)
Time effects	No	No	Yes
Avg	7.113	7.113	7.113
R-squared	0.058	0.078	0.085
N	1130	1130	1130

Robust standard errors clustered on subjects in parentheses

+ p<.20

++ p<.15

* p<.10

^**p<.05

^***p<.01

In the model reported in the first column, we include an indicator for an observation from Wave 2. In the model reported in the second column, we also include the controls. Consequently, the explanatory variables in the first two columns of Table 5 are the same as the explanatory variables in the corresponding columns of Table 3. It is possible to add the controls, even to the model with subject fixed effects, because the controls can change within-subject across waves of the study. However, we would not expect substantial change in the controls within-subject across waves, suggesting that including them in the model should have little effect on the estimated elasticity of demand. Indeed, across the two models, we estimate the conditional price elasticity of demand for heroin to be essentially the same: approximately −0.80. In the model reported in the third column, we additionally include time fixed effects (at the half-year level, for example first half of 2011), to account for time trends. Because our study spanned years, and each subject participated for only four weeks, time fixed effects at narrower intervals would come close to effectively being subject-by-day fixed effects, which would foreclose our empirical strategy. We find the estimated elasticity is essentially the same after including the time fixed effects. The R-squareds reported in Table 5 are within-R-squareds.

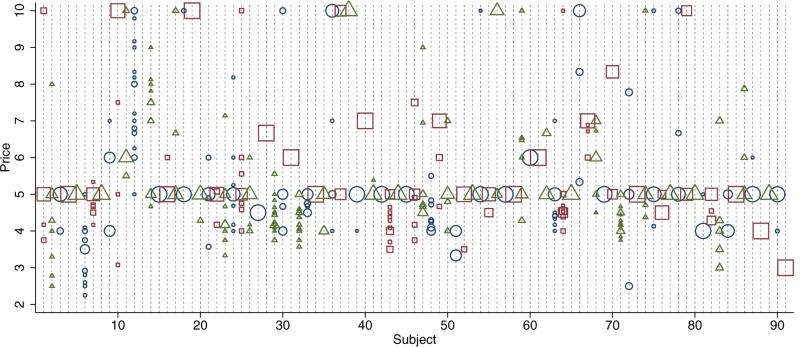
Figure 1 summarizes the within-subject variation in prices in the IVR data, based on the same sample restrictions previously described used in the analysis of the IVR data. Each “column” of the figure is a particular subject, with price displayed along the vertical axis. A marker displayed for a particular subject at a particular price indicates that subject experienced that price. The size of the marker indicates the frequency with which that subject experienced that price. The different shapes and colors of the markers help distinguish markers between adjacent subjects. The figure omits the less than 1% of prices that are less than 2, or greater than 10, because including such prices would obscure the detail in the more relevant range of prices. The overall average of price is 5.46. The overall standard deviation of price is approximately 1.7; the between-subject standard deviation of price (the standard deviation of subject-specific average price) is approximately 1.5; the within-subject standard deviation of price (the standard deviation of prices demeaned by subject-specific average price) is approximately 1.1. The within-subject standard deviation of price within wave 1 was approximately 0.95, and within wave 2 was approximately 0.85, suggesting the use of two waves (separated by six months, when prices might change) improves the key within-subject variation in prices.

Figure 1.

Distribution of Within-Subject Prices in the IVR Data. Note: each “column” displays the distribution of prices experienced by a particular subject in the IVR data. The size of a marker indicates the frequency with which that subject experienced that price. The figure reflects the sample restrictions on the IVR data used in the analysis of the IVR data. In particular, only subjects reporting ever purchasing heroin can be included.

Overall, therefore, both of our preferred empirical strategies result in an estimated conditional price elasticity of demand that is approximately −0.80. The fact that the estimated elasticity is smaller based on our preferred empirical strategies, compared to the estimate based on the pooled cross-section methods with controls, which in turn is smaller than the estimate based on the pooled cross-section methods without controls, is consistent with our concerns with (pooled) cross-sectional estimates.

We also estimated a model that pools the observations from the IVR component and the experimental component, in which we allow that the elasticity of demand could be different across the two components of the data. This allows us to test whether the difference in the estimates across the two preferred empirical strategies is statistically significant. Unsurprisingly, we cannot reject the null hypothesis that the elasticities are the same at any conventional level, since the p-value is 0.59. Moreover, although in general “economic significance” is subjective, it seems easy to conclude that the difference in the estimates across the two preferred empirical strategies is not economically significant.

We conclude therefore, on the basis of two different preferred empirical strategies, that the conditional price elasticity of demand for heroin is approximately −0.80.

4.3. Extension: Elasticity Estimates with Subject-Specific Elasticities

In section 4.2, we estimated standard models of demand that assume that the elasticity of demand is the same for all individuals. In this section, we estimate the elasticity of demand separately for each subject, which is possible because we have repeated measures of demand for each subject (pooling across both the IVR component and the experimental component of the dataset). As above, we continue to focus on conditional elasticities of demand.

If different individuals have different elasticities of demand, then the estimates from the models in section 4.2 (and the prior literature that uses similar models) can be interpreted to be the average elasticity of demand across individuals, primarily under the assumption that the subject-specific elasticities are mean-independent of the idiosyncratic variation in prices and other explanatory variables in addition to the other standard statistical assumptions typically used in the linear model (e.g., Wooldridge 2005). The estimates of the subject-specific elasticities are based on the sources of variation in price that we exploit in our preferred empirical strategies: the idiosyncratic variation in price that an individual experiences over time in the IVR data, and the experimentally-induced variation in price that an individual experiences across scenarios in the experimental data.

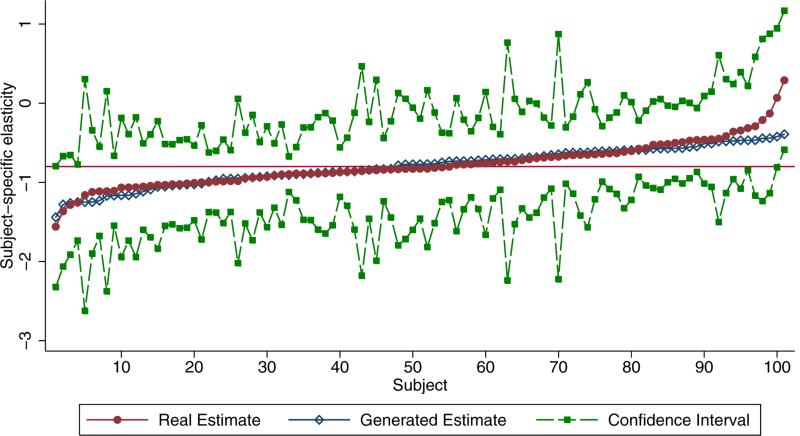
We report the results graphically in Figure 2. We display for each subject for whom we have sufficient information: the estimate of the conditional price elasticity of demand for heroin, and the 99% confidence interval. We display the estimate in red, with each red-filled circle representing an estimate for a particular subject. We display the endpoints of the confidence interval in green, again with each green-filled square representing a particular subject. (We also include in the figure another series that we display as empty blue diamonds, which we describe later. This series largely overlaps the series of estimates, and so is somewhat difficult to distinguish.) We have sufficient information for most but not all subjects: nine subjects in our dataset (across the IVR data and the experimental data) either never bought heroin, or bought heroin in response to only one price, making it mechanically impossible for us to estimate a conditional price elasticity of demand. Another subject only bought heroin twice, which is not sufficient information (it would result in a perfect fit for a linear regression), so we do not display the estimate corresponding to that subject. We also do not display the estimate corresponding to one other subject in our dataset, because the confidence interval for that subject is so wide that including it substantially changes the scale of the entire figure, obscuring the fine detail. (The estimate for that subject is not particularly extreme, however.) We ordered the displayed estimates so that the most positive estimates are on the right of the figure.

Figure 2.

Subject-Specific Elasticity Estimates

Overall, we find minimal evidence of statistically or economically significant heterogeneity in the conditional price elasticity of demand for heroin. The most negative estimated elasticity is -1.56 and the most positive estimated elasticity is 0.29. If we consider the width of the confidence intervals as a measure of the statistical precision of these estimates, it is not surprising that there are a few relatively extreme estimates, given that we are estimating 101 elasticities, and therefore we are likely to have a few “outlier” estimates due simply to sampling variation (a point we make more rigorously, below). If we therefore ignore the most extreme estimates, there is even less evidence of heterogeneity. The 5th quantile of the estimated elasticities is −1.12 and the 95th quantile of the estimated elasticities is −0.31. Further, the 10th quantile of the estimated elasticities is −1.06 and the 90th quantile of the estimated elasticities is −0.46.

Figure 2 also displays the 99% confidence interval for each of these subject-specific estimates of the elasticity of demand. The overall “average” estimate of −0.80, which is displayed as a horizontal red line, lies within all but one of those 99% confidence intervals, suggesting a lack of statistical evidence for heterogeneity. Indeed, note that we are estimating the elasticity for each of 101 subjects, so we are effectively testing 101 statistical hypotheses at the 99% significance level when we check whether −0.80 lies within each of the confidence intervals. Therefore, we would expect, even under the null hypothesis that each subject actually does have an elasticity equal to the overall “average” of −0.80, that we would reject that null hypothesis for approximately one subject, which is exactly our empirical result.

We also include in Figure 2 a randomly generated series of estimates from the estimated sampling distribution of these subject-specific estimates of the elasticity: that distribution is a normal distribution with mean −0.80 and standard deviation 0.22, which is the average standard deviation of these subject-specific estimates. The variation in these generated estimates reflects the sampling variation inherent in any estimation method: because we have to estimate the elasticity of demand, for each subject, based on a sample of data, we should expect some variation in the estimated elasticity of demand across subjects even if each subject actually had exactly the same elasticity of demand. We display those “generated” estimates in Figure 1 as empty blue diamonds. This series largely overlaps the series of “real” estimates, and so is somewhat difficult to distinguish from the series of “real” estimates. The fact that the series of “real” estimates basically overlaps the series of “generated” estimates is further evidence that there is minimal evidence of heterogeneity. This exercise shows that if there were no heterogeneity (each subject had elasticity −0.80), then because of sampling variation we should expect a series of estimates across subjects that has essentially the same characteristics as we actually find in our real empirical results. It is worth noting however that in the “real” estimates there seems to be a few more subjects with relatively more inelastic demand than would be suggested by this exercise. That is, the “most inelastic” (closest to zero) estimates from the “real” estimates seem to be more inelastic (closer to zero) than the “most inelastic” estimates from the “generated” estimates. However, again, these estimates have wide confidence intervals.

Based on this evidence, we do not claim that we can prove the nonexistence of heterogeneity. Indeed, it is highly implausible that all individuals share exactly the same elasticity, and our estimates do vary across subjects. Rather, we claim the more modest result that, to the extent that heterogeneity actually does exist, it seems to be relatively minimal, and evidently not sufficiently large to be statistically significant in our dataset.

4.3. Extension: Cross-Price Elasticities of Demand for Secondary Drugs with Respect to the Price of Heroin

So far, we have reported estimates of the own-price elasticity of demand for heroin, for a sample of regular heroin users. As a final extension, in this section we report estimates of the cross-price elasticity of demand for secondary drugs with respect to the price of heroin. These cross-price elasticities help to further answer the question: what do these regular heroin users do in response to a change in the price of heroin? In particular, the cross-price elasticities answer the question: do they change their demand for the secondary drugs? As we have already noted, since we observe the price of a given drug on a given day for a given subject in the IVR data only if the subject actually purchases that drug on that day, we cannot estimate cross-price elasticities based on the IVR data. However, we can estimate these cross-price elasticities of demand for secondary drugs based on the experimental data. Note that we have already provided some evidence for the external validity of the experimental method.

We report the results in Table 6. The models reported in the columns of Table 6 are essentially the same as the models reported in the third and sixth columns of Table 4, except that the outcome variables relate to the secondary drugs, rather than heroin.

Table 6.

Conditional cross-price elasticities and models of participation in experimental data

	(1) Log(marijuana)	(2) Log(beer)	(3) Log(cocaine)	(4) Participation Marijuana	(5) Participation Beer	(6) Participation Cocaine
Log(price)	0.003 (0.03)	0.088* (0.05)	−0.039* (0.02)	−0.003 (0.01)	−0.025** (0.01)	−0.038*** (0.01)
1[Wave2]	0.024 (0.10)	0.137 (0.15)	0.015 (0.07)	0.021 (0.03)	0.005 (0.03)	0.015 (0.03)
1[treatment]	−0.305*** (0.11)	0.002 (0.28)	−0.229** (0.09)	−0.033 (0.09)	−0.025 (0.07)	−0.075 (0.11)
MHI score	−0.025++ (0.02)	−0.030 (0.03)	−0.001 (0.01)	−0.008 (0.01)	0.003 (0.01)	−0.012+ (0.01)
Delay discounting	−0.934* (0.51)	−1.239 (1.15)	0.214 (0.31)	−0.492** (0.23)	−0.056 (0.32)	−0.499* (0.30)
Log(income)	−0.044 (0.11)	0.042 (0.17)	0.042 (0.05)	−0.000 (0.03)	−0.024 (0.04)	−0.005 (0.04)
Log(Budget) (lab only)	0.287*** (0.09)	0.223** (0.08)	0.453*** (0.05)	0.048*** (0.02)	0.085*** (0.02)	0.184*** (0.03)
Constant	0.529 (1.04)	0.627 (1.21)	−1.302*** (0.34)	0.213 (0.27)	0.104 (0.30)	0.120 (0.36)
Avg	1.798	4.643	1.510	0.150	0.222	0.310
R-squared	0.110	0.052	0.178	0.026	0.011	0.046
N	208	308	431	1390	1390	1390

Robust standard errors clustered on subjects in parentheses

⁺p<.20

⁺⁺p<.15

^*p<.10

^**p<.05

^***p<.01

In column one, we report the conditional cross-price elasticity of demand for marijuana with respect to the price of heroin. In column four, we report the effect of the price of heroin on participation with marijuana. (As before, these estimates can be divided by the overall average participation rate to get a participation elasticity of demand.) We find essentially zero cross-price elasticity, consistent with the notion that heroin and marijuana are unrelated goods, among regular heroin users. In column two, we report the conditional cross-price elasticity of demand for beer with respect to the price of heroin. In column five, we report the effect of the price of heroin on participation with beer. We find a modestly positive conditional cross-price elasticity, and a modestly negative participation cross-price elasticity (−0.113 = −0.025/0.222). The overall unconditional cross-price elasticity of demand (defined as the sum of the conditional and participation elasticities) is therefore approximately zero. This suggests that the overall demand for beer is approximately independent from the price of heroin, similar to the case of marijuana. However, unlike in the case of marijuana, this is the result of offsetting substitutions between heroin and beer at the intensive margin (positive conditional cross-price elasticity) and complementarities between heroin and beer at the extensive margin (negative participation cross-price elasticity). This suggests that, in response to an increase in the price of heroin, fewer regular heroin users will demand any beer, but considering those regular heroin users that do demand beer, those regular heroin users will demand more beer. Finally, in column three, we report the conditional cross- price elasticity of demand for cocaine with respect to the price of heroin. In column six, we report the effect of the price of heroin on participation with cocaine. We find that both elasticities are negative, suggesting that heroin and cocaine are complements, among regular heroin users, perhaps partly due to “speedballs” that combine heroin and cocaine.

5. Conclusion

Based on a sample of regular heroin users, we estimate based on two different preferred empirical strategies that the conditional price elasticity of demand for heroin is approximately -0.80. Our estimates are based on a newly constructed sample of information about regular heroin users. The dataset matches longitudinal information about real-world heroin demand with the results of a demand experiment. The longitudinal component has information on the actual price and actual quantity of heroin at daily intervals for each heroin user in the sample. The experimental component is the result of a demand experiment that elicits demand in experimentally-induced scenarios. The dataset provides us with two different empirical strategies, each of which aims to estimate the elasticity of demand based on a source of exogenous variation in price that is unrelated to the characteristics of the individuals. We also studied, as extensions, heterogeneity in the elasticities, and cross-price elasticities.

We note two limitations of the study.

First, because of the cost of collecting the data, we had to limit the scope of the study to estimating the elasticity of demand for heroin among regular heroin users in Hartford, CT. Therefore, strictly based on our data, it cannot be concluded with certainty whether or not our results generalize to other related research questions, for example: other geographic areas, or other primary drugs of abuse.

Nevertheless, it is useful to briefly speculate about the generalizability of our results. Our finding of a correspondence between the estimates from the two different empirical strategies (fixed effects design and experimental design) seems unlikely to be related to our restricted scope: it seems unlikely these particular people are more likely to generate data that “agrees” across these two data collection methods and empirical strategies than are any other people, but of course our data cannot rule out that possibility (and also the data cannot rule out the other explanations for that correspondence, discussed previously). There is somewhat less certainty about the generalizability of the numerical value of the estimate of the elasticity. It is possible that people in different geographic areas have different elasticities of demand. However, it is reasonable to think that, at a minimum, the elasticity would be similar across geographic areas with comparable demographics. (And of course most studies restrict attention to a certain geographic area, for example a particular country, or state, or city, so this limitation is not unique to our study.) Also, it is very likely that populations other than regular heroin users would have a different elasticity of demand for heroin, but as we discussed in the introduction, regular heroin users are arguably the most important population to study. Finally, it is very likely that people with other primary drugs of abuse would have different elasticities of demand for those other primary drugs of abuse.

Second, due to technological issues related to urinalysis testing, we were unable to validate the IVR call data with urinalysis. Specifically, because urinalysis can detect the presence of opioids for 2 to 4 days since the last use, we would be unable to determine specific days of use, and any use over a 2 to 4 day period may result in a positive test.

Nevertheless, our results can compare favorably with some prior estimates in the literature, partly because our data compares favorably, and partly because of the differences in the empirical strategy. Our results are somewhat in line with some earlier estimates, especially those using “low price” scenarios: either in the laboratory, such as Petry & Bickel (1998) that estimated a price elasticity of −0.87 when the price of heroin was relatively low, or that of Dave (2006) who made use of data from the 1990s and early 2000's to estimate participation elasticities of approximately −0.10 using arrestees or ED visits.

There are several important policy implications of our findings. First, to the extent that our findings are reflective of the overall population of regular heroin users, it appears that the participation elasticity of demand for heroin is quite small, and smaller than some estimates in earlier decades (based on estimates of the participation elasticity from older papers discussed in Section 2). Given the substantial costs involved in efforts to reduce the supply of heroin so as to increase heroin prices, this potentially suggests that policy responses with the goal of reducing the participation with heroin might consider alternative strategies that do not directly target price, and therefore may be more cost-effective. Examples include local market enforcement strategies that influence the search cost of obtaining heroin (Galenianos, Pacula and Persico, 2012) and expanding access to effective treatment (Sindelar and Fiellin, 2001; Rydell, Caulkins and Everingham, 1996).

Second, the cross-price effects suggesting complementarity between cocaine and heroin imply that effective strategies to reduce heroin use, particularly increasing prices, will have the additional benefit of reducing demand for cocaine. It is not clear from this study the extent to which regular heroin users reflect a small or large proportion of the cocaine market, but this finding of complementarity is consistent with evidence from other studies examining more casual users (Saffer and Chaloupka, 1999). Unfortunately, we did not include questions about prescription opioid abuse in this study, so it is not possible for us to consider the extent to which changes in the price of heroin would lead to more or less prescription opioid abuse. However, because many new heroin users appear to have initiated prescription drugs first (Rudd et al., 2014; Muhuri, Gfroerer and Davies, 2013), there is strong suggestive evidence these two drugs may be substitutes. Therefore, policy responses focused on treating regular users of heroin, rather than increasing heroin prices, might be more effective at reducing overall demand for both substances.

Finally, and most tentatively, our results provide some support for the external validity of the experimental method for estimating illegal drug elasticities, subject to previously discussed caveats, which suggests that laboratory experiments may be a useful tool for evaluating future policy strategies. However, we cannot fully rule out the possibility of a Hawthorne effect, in which case the results would not necessarily indicate evidence for the external validity of the experimental method.

Appendix 1 – IVR Implementation and Script for Heroin Purchases

We followed best practices as recommended by Abu-Hasaballah et al. (2007) and Mundt et al. (1997). The IVR system called subjects each day at a designated time specified by the subjects. Subjects were allowed (and encouraged) to call back if they were unavailable when the IVR call arrived. Compliance was monitored, and if a subject failed to complete two consecutive calls, a research assistant contacted the subject to re-engage him/her in the study. The IVR script contained filler questions so as not to reward subjects for answering incorrectly.¹⁵ Subjects received extensive training during the orientation session. Unrealistic responses were reconciled with the subject within 24 hours (whenever possible), and subjects were compensated (as described above) to encourage compliance with study procedures.

The portion of the IVR script for heroin begins by asking subjects for the number of times they purchased heroin since the previous call (Q1). For each purchase, subjects answer detailed questions about the total purchase price, units, number of units purchased, expected quality, and so on (Q2-Q10). If the subject did not purchase heroin since the previous call, the IVR script asks whether the subject attempted to do so, and if so, why he/she did not actually make a purchase (Q11-Q12).

	Script	Routing
Q1	During the [X] days since your last call, how many times did you buy heroin for your own use?	If Q1 = 0 → Q11
		If Q1 ≥ 1 → Q2
Q2	The [first/second/third/fourth/fifth] time you bought heroin, how much cash did you pay for it (in dollars)?
Q3	What units did you buy it in?
	Press: 1 for bags or balloons
	2 for grams
	3 for ounces
	4 for capsules
	5 for foil packets
	6 for lines
	7 for rocks
	8 for other
	0 for don't know
Q4	How many [bags/grams/ounces/capsules/etc.] did you get for that amount of money?
Q5	How much of this heroin was for your own use? Please enter your answer as a percentage: for example, 100 means all of it was for yourself; 50 means half of it was for yourself; 0 means none of it was for yourself.
Q6	When you bought the heroin, what did you expect its quality would be like? Please rate what you expected the quality of the heroin would be like when you bought it on a scale of 1 to 9, where 1 is the worst you've ever had and 9 is the best you've ever had. Press 0 for “don't know”.
Q7	Have you used any of the heroin from this buy?	If Q7 = 1 → Q8
	Press: 1 for yes	If Q7 = 2 → Q9
	2 for no
Q8	What was the quality actually like? Please rate the actual quality of the heroin from this buy, on a scale of 1 to 9, where 1 is the worst you've ever had and 9 is the best you've ever had. Press 0 for “don't know”
Q9	Who did you buy the heroin from?
	Press: 1 if from a regular source
	2 if from an occasional source
	3 if from a new source
Q10	Did you buy the heroin in the neighborhood where you live or outside your neighborhood?	If no more buys to report → END Otherwise, report next buy → Q2
	Press: 1 for in your neighborhood
	2 for outside your neighborhood
Q11	During the [X] days since your last call, did you try to buy any heroin, but you didn't actually buy any?	If Q11 = 1 → Q12
		If Q11 = 2 → END
	Press: 1 for yes
	2 for no
Q12	Why didn't you buy?
	Press: 1 if no dealers were available
	2 if dealers did not have any heroin
	3 if dealers did not have the quality you wanted
	4 if police activity kept you from the dealers
	5 if another reason stopped you from buying
END	END HEROIN PORTION OF IVR CALL

Appendix 2 – Instructions for Experiment

These questions are to find out your choices for drugs across changing drug prices and changing amounts of money to spend on drugs. This information is entirely for research purposes. First, think back to a typical day when you use drugs. In an average day, which drugs would you use, and how much of those drugs would you use? [pause to let subject think about this]

Now, we're going to use this sheet and fake money to play a type of game. Please answer the questions honestly and thoughtfully:

Assume you have $XX [state the subject's amount of money] that you can buy drugs with today. [give subject $XX]

The drugs you may buy with your $XX and their prices and qualities are listed on this sheet. You may buy any drugs listed on this sheet that you like with this money. [review the list of “drugs you can buy”]

So, assume that the only drugs you have access to today are those you buy with this $XX. You have no other drugs available to you. You cannot buy more drugs, or any other kinds of drugs except those you choose now. You cannot get drugs through any other source, other than those you buy with your $XX today.

Also, assume that the drugs you are about to buy are for your consumption only. In other words, you can't sell them or give them to anyone else. You also can't save them up and use them another day. Everything you buy is for your own personal use over the next 24 hours.

With this $XX, please indicate what you would buy, and I'm going to keep track of each drug as you buy it so you'll know what you've purchased.

Appendix 3 - Study Compliance/Attrition: IVR Calls, Laboratory Scenarios, and Cellphones

Table A3.1 shows subject retention throughout the study. One hundred and twenty regular heroin users were enrolled in Wave 1. Of these, 112 were eligible and able to continue to Wave 2. Reasons not eligible or able to continue were: did not complete at least 50% of calls in Wave 1 (n = 6), did not show to laboratory experiment at the end of Wave 1 (n = 1), and deceased (n = 1). Of the 112 subjects who were eligible and able to continue to Wave 2, 92 started it and 88 completed it. Reasons for not starting Wave 2 were: unable to contact (n = 18), relocated (n = 1), and incarcerated (n = 1). Four subjects did not complete at least 50% of calls in Wave 2 and so were ineligible for the laboratory component in Wave 2. Overall, 73% (88/120) of the subjects completed both waves of the study (i.e., completed at least 50% of calls in each wave and completed the laboratory component in each wave). Moreover, as Table 1 demonstrates, there do not seem to be any important significant differences between those who start Wave 1 (i.e., the overall starting sample) and those who start Wave 2 (i.e., those who both complete Wave 1 and actually do start Wave 2), further suggesting that attrition is plausibly unrelated to factors that are important to the study.

Subjects completed a total of 2,620 calls during the study. However, 56 of these calls were discarded due to either missing or suspect data that could not be reconciled within 1-2 days, resulting in a total of 2,564 calls with usable data out of a possible 3,360 calls (120 subjects X 14 calls per wave X 2 waves). At least one heroin purchase was reported on 56% (n = 1,432) of these calls.^16,17 In addition, the 2,564 calls with usable data covered drug purchases made on 2,741 (out of a possible 3,360) subject-days.¹⁸ Thus, overall, subjects covered 81% of the total possible number of subject-days throughout the study.¹⁹

As noted in section 4.1, we restrict analysis of the IVR data to only those heroin purchases with an expected quality of heroin greater than or equal to 6. We also discard calls containing heroin purchases in units other than bags (fewer than 1% of the calls (24 calls out of 2,620) were dropped for this reason), and made by subjects who started a given wave but did not participate in that wave's laboratory component (to ensure that the same subjects were responsible for both the IVR and experimental datasets), resulting in an analyzed IVR dataset comprising 1,130 subject-day observations.

Subjects completed 1,600 experimental scenarios (112 subjects in Wave 1 X 8 scenarios + 88 subjects in Wave 2 X 8 scenarios) out of a possible 1,920 scenarios (120 subjects X 8 scenarios X 2 waves). However, 12 scenarios were discarded due to incorrect scenario parameters provided to particular subjects, resulting in a final laboratory dataset comprising 1,588 experimental scenarios. Of those, 198 are the duplicate scenarios (two of the discarded scenarios were duplicates) that are dropped from the analysis sample, resulting in an analyzed laboratory dataset comprising 1,390 experimental scenarios. The duplicate scenarios showed high within-subject reliability. Correlations of the amounts of heroin, cocaine, marijuana, and beer chosen between the duplicate scenarios were 0.88, 0.76, 0.76, and 0.74, respectively.

Table A3.1.

Subject Retention

	Wave 1	Wave 2
Started	120	92
Completed	112	88