Staffing Subsidies and the Quality of Care in Nursing Homes

Abstract

Concerns about the quality of state-financed nursing home care has led to the wide-scale adoption by states of pass-through subsidies, in which Medicaid reimbursement rates are directly tied to staffing expenditure. We examine the effects of Medicaid pass-through on nursing home staffing and quality of care by adapting a two-step FGLS method that addresses clustering and state-level temporal autocorrelation. We find that pass-through subsidies increases staffing by about 1% on average and 2.7% in nursing homes with a low share of Medicaid patients. Furthermore, pass-through subsidies reduce the incidences of pressure ulcer worsening by about 0.9%.

I. Introduction

A difficult issue that arises in terms of the provision of public programs is how to keep down costs while at the same time ensuring that providers provide a level of quality that meets appropriate standards. User assessment of quality may not provide sufficient incentive if users do not have sufficient choice among alternative providers, if they cannot readily monitor quality or if providers are not otherwise able to benefit from improvements in quality in terms of higher prices (because of limits on out of pocket costs) or higher demand (if the reimbursement cost is close to the marginal cost of care). Direct monitoring of output quality is difficult and must often at least rely in part on self-reported data. In some cases it is more feasible to subsidize or regulate inputs that are thought to have a direct impact on quality. However, in such cases there is an obvious concern that providers may respond to such incentives by cutting back on other needed inputs, thus leading to little impact on quality.

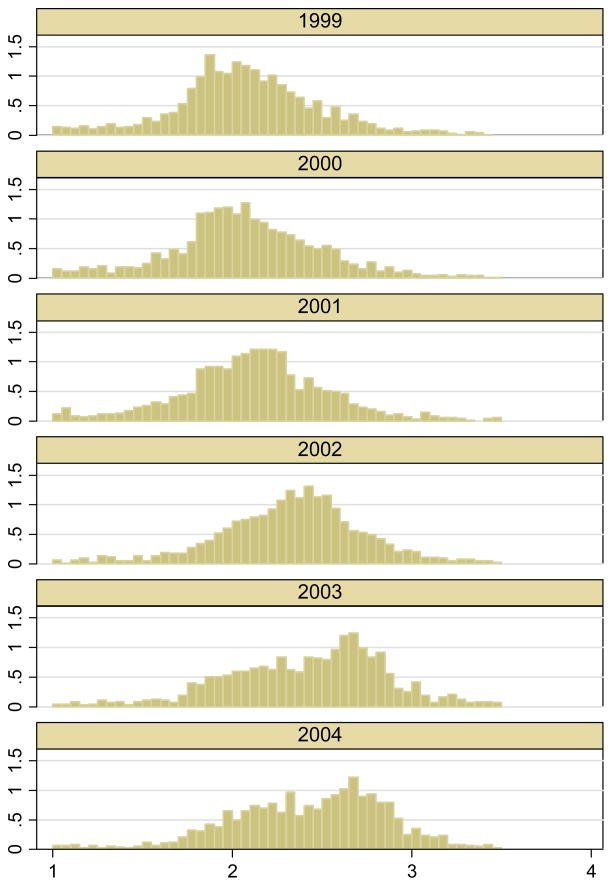
A particularly clear example of this problem arises in the context of nursing home care. Medicaid helps the poor gain access to old age long-term care by directly reimbursing nursing homes. However, Medicaid reimbursement rates are considerably lower than private-pay rates and in many cases barely cover the cost of care provided. Hence, nursing homes with a high percentage of Medicaid patients may have little incentive to increase quality beyond a level that would trigger unwanted attention (Scanlon 2001). Such concern, along with the sense that labor input is a primary determinant of the quality of care in nursing homes, has led to the wide-scale adoption by states of direct subsidies of nursing staff in the form of pass-through policies, in which Medicaid reimbursement rates are directly tied to staffing expenditure. States that adopt pass-through policies earmark additional funds to the direct-care staff, the majority of whom are Certified Nurse Assistants (CNAs), and generally require nursing homes to use the pass-through to increase wages, benefits, or the number of staff. Figure 1 shows the distribution of CNA hours from 1999 to 2004 for Florida, New York, and Massachusetts combined. These three states adopted the pass-through policy in 2002 and comprise some of the largest nursing home markets in the nation. A mean shift in CNA hours starting in 2002 is evident, suggesting a potential policy effect. Moreover, the distribution becomes bimodal, pointing to potential heterogeneous effects. The main question we ask in this paper is whether wage pass-through increases CNA staffing hours and ultimately the quality of care in nursing homes. An increase may occur at the mean but can also be more pronounced at certain parts of the distribution as suggested in Figure 1. We aim to identify both the average pass-through effects and the heterogeneous effects in this paper.

Figure 1. Distribution of Certified Nurse Aid (CNA) hours per patient day in Florida, New York, and Massachusetts Combined (1999–2004).

Notes: Florida, New York, and Massachusetts implemented the pass-through policy in 2002. Data is from the Online Survey Certification and Reporting (OSCAR) for years 1999 to 2004.

The literature has examined the relationship between the Medicaid reimbursement rate and the quality of nursing home care. Gertler (1989, 1992), utilizing 1980 New York data, finds that higher Medicaid payment rates increase Medicaid admissions but decrease the quality of care. In these papers, demand for nursing home care by Medicaid patients exceeds supply. Hence, nursing homes reduce cost by lowering service quality when it displaces a private pay patient with a Medicaid patient. Similarly, Nyman (1988) tests the excess demand hypothesis using 1979 Wisconsin data and finds that higher reimbursement rates are associated with lower quality of care. However, as Grabowski (2001) and Grabowski et al. (2004) point out, the nursing home market condition has changed considerably since the 1980s, with various long-term care options becoming available to patients. Using national data for 1996, Grabowski (2001) finds a positive effect of reimbursement on quality of care. Cohen and Spector (1996) also find a positive effect of reimbursement on staffing but no effect on quality.

Baughman and Smith (2010) examine the impact of wage pass-through on the wages of direct care workers. They use the Surveys of Income and Program Participation (SIPP) data and find that wages increase within states but are unable to find a wage increase when using individual fixed effects. Our focus is on nursing home behavior, specifically on how the pass-through policy affects nursing home staffing and patient outcomes. In a related paper Feng et al. (2010) estimates the impact of pass-through policy on the different nurse type staffing levels using a procedure outlined in an earlier version of this paper. In this paper we not only examine the average impacts but also the heterogeneous impacts on both staffing and various patient outcome variables. By doing so we identify a more nuanced policy impact. Another main contribution of this paper is that we motivate and explain the underlying estimation procedure and illustrate the efficiency gains of using different procedures in multi-level panel data sets. An important distinction from Feng et al. (2010) is that we examine the impact of state minimum staffing requirements in this paper. Many states enacted or increased minimum nurse staffing requirements during our study period. Bowblis (2011) and Lin (2014) find that CNA hours increase with minimum staffing requirements. Given the similar timing of the two policies, controlling for state minimum staffing requirements will be crucial to correctly identify the wage pass-through effect.

We construct a panel data set of nursing home characteristics and state policies from the 48 continental U.S. states over a six-year period from 1999 to 2004. Since the policy variables vary at the state level but the outcome variables vary at the nursing home level, state level shocks that are auto-correlated across time and correlation among nursing homes within each state are likely to impact the regression estimates. Hansen (2007) proposes a two-step FGLS method to account for the serial correlation and clustering problem. We simplify Hansen’s procedure so that the two-step FGLS method can be conveniently implemented by using an AR(1) structure. This method serves as an alternative to difference in difference (DD) methods that cluster standard errors at the state-level (Bertrand et al. 2004). We show analytically and by simulation that our two-step FGLS estimates reduce standard errors by about 30 to 45%. The method outlined in this paper can be generalized to many policy analyses that use multi-level panel data and can provide more efficient estimates than conventional difference in difference estimates.¹ We perform our analysis on the full sample and samples stratified based on each nursing home’s average share of Medicaid patients. We also non-parametrically estimate the heterogeneous policy impact over the distribution of the share of Medicaid patients. We find that pass-through increases staffing by about 1% on average and the impact is stronger for nursing homes with a low percentage of Medicaid patients, where staffing hours increase by 2.7%. For quality, we examine a multitude of patient outcome variables and primarily find results on the pressure ulcer worsening rate. Pass-through policy reduces incidences of pressure ulcer worsening by about 0.9%.

In the next section we discuss the wage pass-through policy and testable predictions. Section III describes our empirical strategy and the benefits of the two-step FGLS estimation procedure. Section IV describes the data. Section V discusses the main empirical results, Section VI the heterogeneous results, and Section VII the robustness tests. Section VIII concludes.

II. Background on the Pass-through Policy and Testable Predictions

Medicaid programs in many states have implemented a wage pass-through policy, which earmarks additional funds for the purpose of increasing compensation for direct-care workers in long-term care. In 1999, 6 states (California, Delaware, Michigan, Minnesota, South Carolina, and Wisconsin) had a wage pass-through policy in place. In the five-year period that followed, 17 additional states introduced a wage pass-through. States adopting a wage pass-through policy generally require a certain portion of the Medicaid reimbursement to be used to improve direct-care workers’ wages and/or benefits or to increase staffing level. How the wage pass-through policy is actually implemented varies widely from state to state, as do accountability procedures that monitor provider compliance. States often transfer a set dollar amount per staff hour or require a certain percentage of the reimbursement increase to be used for wages/benefits.

How might a wage pass-through policy affect staffing and quality? Pass-through could affect quality of care through changes in staffing level or worker effort². Staffing can change because the price of labor nursing homes face decreases with a wage pass-through. Worker effort can change because one’s effort depends on the wage one receives from the nursing home as well as one’s opportunity wage. An important element of our research is the distinction between increasing staffing and raising the quality of output per worker. It is unclear whether an increase in staffing would improve quality of care if the increase in staffing does not promote worker effort. Furthermore, given that states mandate a minimum level of staffing that nursing homes have to maintain, the introduction of a wage pass-through will likely have different implications depending on whether a nursing home is constrained by the staffing requirement.³

For unconstrained nursing homes, that is, nursing homes that optimally choose labor above the state minimum requirement, the first order effect of a wage pass-through would be the lower price of labor for nursing homes resulting in an increase in demand for labor. However, nursing homes that were constrained and were sub-optimally choosing staffing above its optimal level would be reluctant to use the pass-through to increase staffing but instead utilize the pass-through amount to increase wages for their staff. The relative increase in own wages would be larger for these constrained nursing homes, resulting in increased worker effort, and potentially quality of care. Though staffing increases in nursing homes that choose a high level of staffing, worker effort may not increase because own wages may not rise as much as the increase in market wages, which could result in minimal changes in worker effort.⁴ To put this idea into context consider two nursing homes: a high reputation nursing home with good facilities and management that attracts higher paying private-pay residents and less Medicaid patients, and a low reputation nursing home that caters mostly to Medicaid patients. When pass-through is introduced, the high reputation low Medicaid share nursing home, being unconstrained by the staffing mandate, would likely increase staffing hours. On the other hand, the low reputation high Medicaid share nursing home, which was already constrained by the staffing mandate, would be reluctant to increase staffing but instead utilize the pass-through subsidy to increase wages, potentially resulting in higher nurse effort and better patient outcomes.⁵

Empirically, we test whether there are differential impacts of wage pass-through on nursing homes based on the share of Medicaid patients, in addition to examining the average effect on CNA staffing and quality of care. Specifically, we test whether nursing homes with a lower share of Medicaid patients increase staffing when states introduce the pass-through policy. We also test whether nursing homes with a higher share of Medicaid patients are more responsive to the state minimum staffing requirements. If so, this would imply that nursing homes with higher share of Medicaid patients are indeed more constrained by the staffing mandates. Finally, we test whether pass-through improves quality of care more so in nursing homes with a higher share of Medicaid patients. We believe that examining the heterogeneous responses based on the share of Medicaid patients is reasonable during the time period we examine. The long-term care (LTC) market has become increasingly competitive, with more and more non-nursing home LTC providers, such as assisted living and other community-based services, competing with traditional nursing homes. The national average nursing home occupancy rate has fallen below 85% in recent years.⁶ Medicaid reimbursement policies likely had a more important impact on Medicaid patient admission when there was excess demand. However, the number of Medicaid patients in nursing homes nowadays is more determined by local market conditions (Grabowski 2008).

III. Empirical Research Design

Before discussing the data and empirical results, we discuss a simplified version of Hansen’s (2007) FGLS procedure that efficiently estimates state policy effects in facility-level panel data. We first discuss the serial correlation and clustering issues that arise in a multi-level panel and then describe our estimation strategy.

III.A Potential problems for estimation in a multi-level panel

Consider

$$y_{\mathit{ist}}={\mathrm{X}}_{\text{ist}}\mathrm{\beta }+{\mathrm{Z}}_{\text{st}}\mathrm{\gamma }+{\mu }_s+{\eta }_t+{\epsilon }_{st}+v_i+u_{\mathit{ist}}$$ (1)

where y_ist is the outcome variable (e.g., staffing level or patient outcome), X_ist is a vector of facility level variables including county characteristics, Z_st is a vector of state policy variables, μ_s represents state specific unobservables that determine staffing hour (e.g., other labor or health policies relevant to staffing level), η_t is a vector of year dummies, v_i reflects facility-level unobserved variables that determine our outcome (e.g., management style), ε_st and u_ist represent state-level and facility-level idiosyncratic factors. u_ist is assumed to be independent of all observable and unobservable factors in (1). We assume that ε_st is independent of Z_st, the state policy variables, and later examine this assumption using a duration model.

The parameter of interest is γ. However, there are several problems that complicate the consistent and efficient estimation of γ. First, facilities in the same state at a particular point in time are likely to face common shocks, such as, economic conditions or unobserved state policies. Thus, facilities in the same state and time cannot be treated as independent, i.e., E(u_istu_jst)≠0. This is the clustering problem. Second, these common shocks are likely to be serially correlated within states over time. So residuals at the state-level cannot be treated as independent over time, i.e., E(ε_stε_st−k)≠0. Lastly, there is an endogeneity problem because facility-level characteristics such as share of Medicaid patients or patient acuity may be influenced by state-year economic or environmental shocks, i.e., E(X_istε_st)≠0. Hence, regressions at the facility level may lead to biased estimates of these characteristics and thus lead to misleading policy effects.

A potential solution and widely used estimation method is to employ facility level difference in difference regression with Huber-White standard errors clustered at the state level (Bertrand et al. 2004). This method is robust to the clustering and autocorrelation problem but still suffers from endogeneity if the state-time level shocks are correlated with facility characteristics. Even if we assume E(X_istε_st)=0, this method is inefficient to the extent that the autocorrelation can be captured with an AR process as shown by Hansen (2007) using a two-step FGLS process. In this paper, we adapt and slightly modify Hansen’s procedure so that the two-step FGLS method can be easily implemented. The main modification is in the estimation of the AR(1) parameter which we discuss below. This method can be generalized to policy analysis settings that are susceptible to serially correlated state-year shocks, and in such cases provide more efficient estimates than conventional difference in difference estimates.

III.B Estimation Strategy: Two-step OLS and Two-step FGLS

The two-step estimation strategy in Hansen (2007) utilizes the fact that equation (1) contains variables that vary only at the state-year level, i.e., Z_stγ, μ_s, η_t, and ε_st. Lets capture all these variables and denote it as c_st. In other words, let c_st = Z_stγ + μ_s + η_t + ε_st. Then, we can rewrite equation (1) as

$$y_{\mathit{ist}}=X_{\mathit{ist}}\beta +c_{st}+v_i+u_{\mathit{ist}}.$$ (2)

Note that c_st captures the policy component as well as the state and year fixed effects. One of the main advantages of estimating a multilevel panel (facility level data with state level policy) in two steps is that we do not have to assume E(X_istε_st)=0. Time varying state shocks and facility level variables are likely to be correlated, i.e., E(X_istε_st)≠0. In our case, we have reasons to believe that year varying state economic shocks (e.g., unemployment) or weather shocks affect the share of Medicaid patients or patient acuity in nursing homes. However, many analyses using a multilevel panel assume away this possibility in estimating equation (1). The two-step process enables one to work around the potential endogeneity caused by the correlation between state level shocks and facility level variables.

In the first stage of the two-step estimation, one runs the OLS regression in equation (2) and retrieves estimates for c_st, i.e., the set of coefficient estimates on the state-year dummy variables. In order to cancel out the facility level fixed effects v_i, we first demean equation (2) at the facility level and then estimate the state-year fixed effects in

$${\stackrel{.}{y}}_{\mathit{ist}}={\stackrel{.}{\mathrm{X}}}_{\text{ist}}\mathrm{\beta }+{\stackrel{.}{c}}_{st}+{\stackrel{.}{u}}_{\mathit{ist}}={\stackrel{.}{\mathrm{X}}}_{\text{ist}}\mathrm{\beta }+{\mathrm{\sum }}_{\mathrm{s}}{\mathrm{\sum }}_{\mathrm{t}}{\stackrel{.}{c}}_{st}{\delta }_{st}+{\stackrel{.}{u}}_{\mathit{ist}}.$$ (3)

The dot indicates that variables are demeaned at the facility level (e.g., ẏ_ist = y_ist − ȳ_i) and δ_st are the set of state-year dummies. Note that ċ_st = c_st − c̄_s, where c̄_s is some state level constant. We first get estimates of ċ_st from equation (3), and then run a regression of ċ_st on the policy variables Z_st, and state and year fixed effects (the second stage). In other words, the second-stage estimation is

$${\stackrel{.}{c}}_{st}=Z_{st}\gamma +{\stackrel{\sim }{\mu }}_s+{\eta }_t+{\epsilon }_{st}$$ (4)

where μ̃_s = μ_s + c̄_s so c̄_s is subsumed as part of the state fixed effects.

What we refer to as the two-step difference in difference procedure estimates γ in (4) with OLS where standard errors are clustered at the state level to account for any potential correlation in the error terms within states over time.

The two-step DD returns consistent estimates of γ but is inefficient due to the serial correlation in the residuals. The two-step FGLS procedure, as documented in Hansen (2007), fits an AR(p) process on the residuals and improves the efficiency of the estimates (i.e., reduces the standard errors). In this paper, we model the serial correlation in ε_st as an AR(1) process and perform a standard FGLS estimation by first estimating the AR(1) coefficient ρ and then performing OLS on the ρ-differenced variables. We believe the serial correlation in the state-time level shocks in most policy or program analyses can be captured well with an AR(1) process even when there are further lags in the AR process. In section III.D we show that specifying the error terms as an AR(1) process still produces substantial efficiency gains even when the underlying process is of higher order. Estimating the AR(1) coefficient ρ requires caution. Here, we first illustrate the two-step FGLS procedure taking ρ as given and then in the next section describe how to get an unbiased estimate of ρ.

For the Two-step FGLS estimation, we demean variables at the state level in (4) to eliminate the state fixed effects μ̃_s, so that

$${\stackrel{.}{c}}_{st}-{\overline{\stackrel{.}{c}}}_s=(Z_{st}-{\overline{Z}}_s)\gamma +({\eta }_t-\eta )+({\epsilon }_{st}-{\overline{\epsilon }}_s).$$

Demeaning the left hand side simply returns ċ_st, because ${\stackrel{.}{c}}_{st}-{\overline{\stackrel{.}{c}}}_s=(c_{st}-{\overline{c}}_s)-({\overline{c}}_s-{\overline{c}}_s)$. η is subsumed in the constant term in the actual regression. We assume that ε_st follows a stationary AR(1) process so that ε_st = ρ ε_st−1 + e_st, where e_st is White noise, and hence ε̄_s = 0. Thus, we end up with the state-year level equation

$${\stackrel{.}{c}}_{st}={\stackrel{.}{Z}}_{st}\gamma +{\eta }_t+{\epsilon }_{st}.$$ (5)

With an unbiased estimate of ρ, we can ρ-difference equation (5), i.e., subtract a lagged equation (5) multiplied by ρ, run an OLS regression and get estimates of γ. That is, we estimate the equation

$${\stackrel{.}{c}}_{st}-\rho {\stackrel{.}{c}}_{st-\mathit{1}}=({\stackrel{.}{Z}}_{\text{st}}-\rho {\stackrel{.}{Z}}_{\text{st}-1})\gamma +{\xi }_t+e_{st}$$ (6)

where ξ_t = η_t − ρη_t−1. Allowing for the possibility that the error term in (6) could still be correlated within state across time, we additionally cluster standard errors by state. Note that the first observation in each state drops out of the panel when we ρ-difference the variables. We follow the standard procedure of normalizing the first observation by $\sqrt{1-{\rho }^2}$, so that the variance of ε_s1 equals the variance of e_st (Greene, 2002).

III.C Unbiased Estimation of the AR(1) Coefficient

In an NxT panel data with short T, estimating the AR coefficient by regressing the residual ε_st on its lags returns biased estimates. Consider our second stage equation ċ_st = Ż_sγ + η_t + ε_st and the AR(1) process ε_st = ρε_st−1 + e_st. Suppose we regress the estimated residual ε̂_st on its lag ε̂_st−1 to estimate ρ. Effectively we are regressing ${\epsilon }_{st}-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.{\sum }_{t=1}^T{\epsilon }_{st}$ on its lag. If we had a long panel with large T the term ${\overline{\epsilon }}_s=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.{\sum }_{t=1}^T{\epsilon }_{st}$ would converge to zero. However, in short panels this term becomes non negligible so that cov(ε_st, ε_st−1) ≠ cov(ε̂_st, ε̂_st−1) and ultimately ρ ≠ ρ̂. A simple example with T=2 illustrates this more concretely. In the case of T=2, ${\widehat{\epsilon }}_{s1}=\raisebox{1ex}{$({\epsilon }_{s1}-{\epsilon }_{s2})$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$ and ${\widehat{\epsilon }}_{s2}=\raisebox{1ex}{$({\epsilon }_{s2}-{\epsilon }_{s1})$}\!\left/ \!\raisebox{-1ex}{$2$}\right.$. So the correlation in the estimated residuals is −1 regardless of actual value of ρ. In general, the bias ρ̂ − ρ is negative with the absolute value of the bias decreasing in T.

Hansen (2007) develops a general method that calculates the magnitude of this bias and subtracts away the bias to get unbiased coefficient estimates of an AR(p) process. In this paper, we develop a simple method of moments approach that estimates an AR(1) coefficient. Hansen’s method has the advantage of being more generalizable to p^th-order processes, but our focus on AR(1) enables us to derive a simple one-step formula for the autocorrelation coefficient and does not require iteration as Hansen’s approach normally would. Since we use differences in the estimation we lose one degree of freedom for each state. However, comparison of our estimate with Hansen’s estimate when T=6 show minimal difference.

We now explain how one can obtain an unbiased estimate of the AR(1) coefficient ρ. We denote ε_st = ρ ε_st−1 + e_st as a stationary AR(1) process, where ε_st is the error term in (5). Since this process is stationary, the first differenced process Δε_st = ρ Δε_st−1 + Δ e_st (where, Δε_st corresponds to ε_st − ε_st−1) is also stationary. Denote the r^th autocovariance cov(Δε_st+r Δε_st) = h_r, and var(e_st) = σ_e². Multiplying the first differenced process by Δε_st−1 and Δε_st we get the following two equations:

$$\begin{array}{l}(\mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}}=\rho \mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}-1}+\mathrm{\Delta }{e}_{st})\times \mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}-1}\to h_{\mathit{1}}=\rho h_{\mathit{0}}-{{\sigma }_e}^{\mathit{2}}\\ (\mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}}=\rho \mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}-1}+\mathrm{\Delta }{e}_{st})\times \mathrm{\Delta }{\mathrm{\epsilon }}_{\text{st}}\to h_{\mathit{0}}=\rho h_{\mathit{1}}+(2-\rho ){{\sigma }_e}^{\mathit{2}}\end{array}$$

Solving for ρ from the two equations returns

$$\rho =1+2\frac{h_1}{h_0}.$$

Hence, the sample counterpart of the AR(1) coefficient is

$$\widehat{\rho }=1+2\frac{\mathit{cov}({\widehat{\epsilon }}_{st+2}-{\widehat{\epsilon }}_{st+1},{\widehat{\epsilon }}_{st+1}-{\widehat{\epsilon }}_{st})}{\mathit{var}({\widehat{\epsilon }}_{st+1}-{\widehat{\epsilon }}_{st})}.$$ (7)

In summary, one in practice would get the estimated residuals ε̂_st from equation (5), estimate ρ̂ by equation (7), and use the estimated ρ̂ in equation (6) to complete the two-step FGLS estimation. As mentioned before we employ either Huber-White standard errors clustered by state or jack-knife standard errors at the state level in order to ensure robustness against potential clustering that may still exist after accounting for the AR(1) serial correlation.

III.D Efficiency Gains of Two-step FGLS

Before we take the above estimation strategy to the data we first examine the efficiency gains from the two-step FGLS procedure both analytically and by simulation. First, consider y_it = x_itβ + u_it where T=2 and the residuals are serially correlated by an AR(1) process. If the autocorrelation for the residual is ρ and the autocorrelation for the regressor is κ then the percentage reduction in variance of FGLS relative to OLS as shown in the Appendix 1 is

$$1-\frac{1-{\rho }^2}{1-{\kappa }^2{\rho }^2}.$$

For ρ=0.7 and κ=0.5 this amounts to a 42% reduction in variance or 24% reduction in standard errors of the estimated β. Note that doubling the number of states should reduce variance by 50% or standard errors by 29%. Therefore, implementing the two-step FGLS results in similar efficiency gains as having a panel with twice as many states. Note that the efficiency gain crucially depends on the value of ρ. If ρ=0 then the efficient gain would be zero, which is quite intuitive. If there is no autocorrelation in the residuals then implementing the FGLS has no advantage over OLS. Hence, this points to when our proposed estimation procedure would be useful. If the estimated ρ from the data is large then the efficiency gains from the FGLS procedure will be large enough to warrant our proposed procedure. If the estimated ρ is small the efficiency gains become negligible. We confirm this pattern in our empirical result and will return to this point again.

Next, we perform a Monte Carlo simulation to examine the efficiency gains from two-step FGLS relative to two-step DD and standard DD estimation. The data generating process randomly generates facility variable x, policy variable z, and parameters roughly consistent with the data for 50 states, over 6 or 12 time periods, with 0–100 facilities per state. We set the true β, the coefficient on z, equal to one and carry out the exercise 100 times implementing (1) DD estimation with standard errors clustered at the state level, (2) two-step DD with standard errors clustered by states, (3) two-step FGLS with standard errors clustered by states, and (4) two-step FGLS with standard errors jack-knifed at the state level. The results in Table 1 clearly demonstrate the efficiency gains from the two-step FGLS approach. In the case of a panel with 6 time periods, the two-step FGLS results in standard errors that are about 40% smaller than the general DD estimation (Panel A). The efficiency gain increases with a longer panel of T=12 (Panel B) and remains similar even when we estimate an AR(2) error structure with an AR(1) process (Panel C). When there is no underlying AR process (Panel D), the two-step FGLS approach does slightly better than the traditional DD method that clusters by state, which is a conservative procedure. The difference between the two-step DD and FGLS are not large and not statistically different as one would expect when the AR coefficient is zero. Finally, in all simulations the standard deviations of the estimated coefficients are similar to the average standard errors of the coefficients, which illustrates that the estimation procedure is generating reliable standard errors.⁷

Table 1.

Efficiency Gains of the Two-Step FGLS procedure

Procedure		A		B		C		D
		N=50, T=6, AR(1), ρ=0.8		N=50, T=12 AR(1), ρ=0.8		N=50, T=12, AR(2) ρ1=0.6, ρ2=0.3		N=50, T=6 AR(0)
		Mean	SD	Mean	SD	Mean	SD	Mean	SD
I. Facility fixed effect	β	1.090	0.761	0.964	0.532	0.960	0.508	1.033	0.682
w/ clustered SE	SE of β	0.772	0.147	0.533	0.0803	0.485	0.0770	0.767	0.124
II. Two-step DD	β	1.088	0.597	0.945	0.458	0.913	0.427	1.050	0.548
w/ clustered SE	SE of β	0.699	0.102	0.484	0.0577	0.431	0.0546	0.693	0.0858
III. Two-step FGLS	β	1.055	0.423	0.994	0.306	0.925	0.336	1.039	0.535
w/ clustered SE	SE of β	0.473	0.0626	0.294	0.0328	0.341	0.0385	0.629	0.0798
IV. Two-step FGLS	β	1.055	0.423	0.993	0.306	0.925	0.336	1.039	0.535
w/ jackknife SE	SE of β	0.475	0.0408	0.205	0.0161	0.249	0.0222	0.591	0.0495
Efficiency Gain		39%		45%		30%		18%

Notes: Simulations are for 50 states, with 0–100 facilities per state, over 6 or 12 time periods. We set the true β equal to one and carry out the exercise 100 times implementing (I) DD estimation with standard errors clustered at the state level, (II) Two-step DD with standard errors clustered by states, (III) Two-step FGLS with standard errors clustered by states, and (IV) Two-step FGLS with standard errors jack-knifed at the state level. The underlying AR process for the first two columns is AR(1), the third AR(2), and the last AR(0). Efficiency gain calculates percentage reduction in the standard error of β from implementing procedure III relative to procedure I. SD and SE denote standard deviation and standard error, respectively.

Both the analytic exercise and the simulations show that two-step FGLS has considerable efficiency gains relative to conventional DD methods, resulting in 30–45% reduction in standard errors depending on the true underlying AR structure. These results are consistent with Hansen’s finding that the FGLS confidence interval decreases by 44% compared to the OLS case based on a simulation over resampled CPS-MORG data. In the following sections we implement our proposed two-step FGLS procedure using the nursing home data and empirically examine the impact of wage pass-through on staffing and the quality of care in nursing homes.

IV. The Nursing Home Data and Policy Variables

The main data source for this study comes from the Centers for Medicare and Medicaid Services’ (CMS) Online Survey Certification and Reporting (OSCAR) system from 1999 to 2004. OSCAR contains annual self-reported facility level information, including staffing, organizational characteristics and aggregate resident conditions, for all Medicare/Medicaid certified nursing homes in the U.S. Independent state surveyors verify and validate the information reported in OSCAR as part of the state survey process. Hence, the quality of the OSCAR data is better than traditional self-reported data. If surveys were conducted more than once a year for a given facility, we use the one closest to the year end. We exclude hospital-based nursing homes, which primarily serve short-stay, post-acute Medicare patients. Staff in these nursing homes is often provided by the affiliated hospital. We also exclude Medicare only certified facilities, which do not serve Medicaid patients in the main analysis. Bowblis et al. (2013) have found staffing patterns and the structure of the long term care market to differ considerably between urban and rural areas. We focus on urban nursing homes in the main analysis and present results for rural nursing homes in the appendix. Finally, we exclude the small number of facilities located outside the 48 contiguous U.S. states. State policy and local nursing home market information are then merged into the facility level data. State policy, such as the presence of a wage pass-through policy, minimum nurse staffing requirements, average Medicaid reimbursement rates, and the use of case-mix reimbursement, were collected from surveys of state Medicaid offices conducted by Brown University’s Community Health Department and the literature that examines minimum staffing laws (Bowblis 2011, Lin 2014). Lastly, the Bureau of Health Professions’ county-level Area Resource File provides local nursing home market characteristics.

Table 2 reports the variables used in the analysis and the descriptive statistics over the study period. Staffing level is defined as the total average hours per resident day (HPRD). We focus on CNAs, because they are the primary target of the wage pass-through program. In the empirical analysis we drop observations that report CNA staffing above 24 HPRD. We also examine total nurse hours in the main analysis to check if there were any substitution of CNAs with other, more expensive types of direct care staff, such as RNs and LPNs. Similarly, observations reporting total nurse hours above 24 HPRD are dropped.⁸

Table 2.

Summary Statistics

		Mean	SD	Min	Max	Obs
State policies	Wage pass-through:	0.25	0.44	0	1	53112
	State minimum nursing hours	1.95	1.07	0.30	3.67	53112
	Medicaid payment rate (2004)	14.27	2.92	8.29	21.55	53112
	Case-mix reimbursement	0.63	0.48	0	1	53112
Staffing	CNA hours per resident day	2.18	0.89	0	23.63	53101
	Total nurse hours per resident day	3.24	1.32	0.04	23.77	53065
Patient outcome	Pressure ulcer worsening rate	0.14	0.34	0	1.0	213663
	ADL decline rate	0.13	0.34	0	1.0	200381
	Persistent pain rate	0.13	0.34	0	1.0	211787
	Percent on antipsychotics	24.13	14.61	0	100	53112
	Percent on restraints	9.91	11.22	0	100	53112
	Percent with bowel incontinence	46.44	17.48	0	100	53112
	Percent with catheters	6.27	5.24	0	100	53112
	Percent with contractures	26.77	21.21	0	100	53112
	Percent receiving tube feeding	7.22	7.54	0	100	53112
Facility characteristics	Acuity Index	11.74	1.58	0	22.79	53112
	Nurse Practitioner/Physician Assistant	0.26	0.44	0	1	53112
	Alzheimer’s unit	0.19	0.39	0	1	53112
	Percent Medicaid	64.45	23.18	0	100	53109
	Percent Medicare	10.70	12.23	0	100	53109
	Occupancy rate	0.87	0.13	0.01	1	53072
	Total beds in facility	120.56	69.08	2.00	1389.00	53112
	For profit owner	0.73	0.44	0	1	53112
	Non-profit owner	0.25	0.43	0	1	53112
Market (county) conditions	HHI of residents	1.03	0.18	0.48	2.12	53135
	RNs per hospital bed	1.46	0.42	0.03	6.58	52190
	LPNs per hospital bed	0.18	0.10	0	1.33	52190
	Nursing home beds per 1000 elders	51.34	17.78	2.20	364.67	53112
	Managed care penetration rate (%)	16.82	14.46	0	55.32	53112
	Area wage index	1.03	0.18	0.48	2.12	53112

Notes: All variables, except for patient outcome variables are annual variables. Patient outcome variables are collected each quarter. Data comes from multiple sources including the Online Survey Certification and Reporting, Minimum Data Sets, Area Resource Files, and surveys of state Medicaid offices. Medicaid payment rate is in $10 increments.

For quality we examine a multitude of patient outcome variables.⁹ We examine pressure ulcer worsening rate, activities of daily living (ADL) decline rate, persistent pain rate, as well as percent on antipsychotics or restraints, percent with bowel incontinence, catheters, contractures, or tube feedings. These measure were constructed from the Minimum Data Set (MDS), a federally mandated resident assessment data. The pressure ulcer worsening rate, the ADL decline rate, and the persistent pain rate indicate the rate of a substantial decrease in each outcome while the patients were residents of the nursing home, and are quarterly variables as outlined in Mor et al (2011). The other patient outcomes are annual variables. Not all measures may well represent nursing home quality of care, since some conditions may worsen due to the patient’s inherent condition rather than the care given by nurses. The pressure ulcer worsening rate is considered a good measure of care in the literature because bedsores are generally preventable and treatable conditions (Grabowski 2008).

There are four state policy variables in our analysis. The key variable is the presence of a wage pass-through policy to nursing homes by Medicaid. Each state differs in how wage pass-through is actually implemented. We focus on the effect of introducing the pass-through policy and employ a single dummy variable that indicates the provision of wage pass-through payments in a given state and year over the period 1999–2004.¹⁰ Another important policy variable is the state minimum staffing requirements. Many states enacted or increased minimum nurse staffing requirements during our study period. Controlling for both the pass-through policy and minimum staffing requirement will be important for identification, given that many states implemented both policies at similar times. We also control for the annual state-average Medicaid reimbursement rate (per bed day) to nursing homes, a variable that the previous literature has focused on. The reimbursement rate not only varies among states but also varies within state over year depending on annual budgets. We use inflation adjusted 2004 dollar amounts in the analysis.¹¹ Lastly, we include an indicator variable for the presence of a case-mix adjusted reimbursement policy. States with a case-mix policy adjust Medicaid reimbursement rate based on the average acuity of patients in the nursing home.

We use county variables to proxy for nursing home market variables.¹² We construct a Herfindahl-Hirschman Index (HHI) of nursing home residents to proxy market competition. We include the number of Registered Nurses (RNs) and Licensed Practical Nurses (LPNs) per hospital bed, number of nursing home beds per thousand population over 65, the Medicare managed care penetration rate to capture the variations in local demand and supply factors pertaining to nursing home workforce, and a standardized hospital wage index to account for regional differences in the purchasing power of Medicaid payments and the price of medical and nursing services.

To control for facility level characteristics we include an acuity index which combines resident’s activity of daily living (ADL) dependencies and special treatment measures. Also, included are whether the facility employed or contracted for a nursing practitioner or physician assistant, and whether the facility operated an Alzheimer unit. We control for the payer mix of residents in each facility, as indicated by the percent of Medicaid residents. In addition, we control for occupancy rate, total beds in the facility, and dummy variables indicating whether the owner is for profit or non-profit, where the omitted category is government owned nursing homes.

V. Empirical Results

V.A Duration Analysis of Pass-through Policy Implementation

Before examining the effect of wage pass-through on staffing and quality, we do a simple duration analysis to examine whether the implementation of pass-through policy by states may be considered exogenous, i.e., whether E(Z_stε_st)=0. Though we cannot directly test for this exclusion restriction, we can examine whether the take-up of wage pass through by states is related to observables in our data. We estimate whether initial staffing level or the main quality of care variables affects the probability that a certain state implements a pass-through policy in the following years. In particular, we estimate a logit regression on the following semi-parametric equation,

$$y_{st}={\mathrm{X}}_{\mathrm{s}1999}\beta +d_{\mathit{2000}}+d_{\mathit{2001}}+d_{\mathit{2002}}+d_{\mathit{2003}}+d_{\mathit{2004}}+{\epsilon }_{st},$$

where y_st is a binary variable indicating whether state s had the policy in year t, X_s1999 is a vector of relevant covariates that include the staffing level, the patient outcome variables, and the market and facility characteristics variables for the base line year of 1999. The d’s are dummy variables equal to one in the subscript year. Table 3 presents the results. Column (1) includes the 1999 average CNA staffing, the other state policy variables, and the year indicators. Staffing hours is not significant. We include the facility and market level variables in column (2) and staffing remains insignificant. In column (3) we focus on the three main patient outcome variables and in column (4) we include both the staffing and patient outcome variables. The coefficients on all these variables are not statistically significant. Initial levels of staffing nor patient outcome in 1999 did not determine whether states take up the pass-through policy in following years. Though not reported in the table, the coefficient estimates on the facility and market level variables are not systematically significant. Table 3 suggests that policy endogeneity is unlikely a problem in analyzing the policy effects.

Table 3.

Duration Analysis on the Policy Variable

Dependent variable:	Pass-through policy
	(1)	(2)	(3)	(4)
log CNA hours (1999)	1.407 (5.039)	−8.184 (11.43)		−6.224 (10.25)
Pressure ulcer worsening rate (1999)			22.08 (15.69)	22.08 (15.69)
ADL decline rate (1999)			−7.656 (6.692)	−7.656 (6.692)
Persistent pain rate (1999)			15.56 (12.56)	15.56 (12.56)
State minimum nursing hours	−0.0140 (0.318)	0.128 (0.843)	−0.448 (0.825)	−0.291 (0.945)
Medicaid payment rate (1999)	−0.0219 (0.146)	0.128 (0.315)	0.157 (0.535)	0.137 (0.544)
Case-mix reimbursement (1999)	0.741 (0.563)	2.157 (1.440)	2.604* (1.435)	2.467* (1.374)
Dummy: 2 years later	−0.564 (0.741)	0.0288 (0.762)	0.326 (0.881)	0.317 (0.853)
Dummy: 3 years later	0.114 (0.643)	1.373** (0.692)	1.826** (0.780)	1.820** (0.773)
Dummy: 4 years later	−0.712 (0.848)	0.664 (0.889)	1.225 (0.963)	1.226 (0.968)
Dummy: 5 years later	−1.372 (1.115)	0.0132 (1.136)	0.552 (1.303)	0.552 (1.295)
Facility and market covariates	No	Yes	Yes	Yes
No. of observations	165	165	165	165

Notes: Initial policy, facility, and market covariates are 1999 averages. States that already had the pass-through policy in 1999 are dropped in the estimation. The excluded dummy variable is “one year later”. Robust standard errors are in parentheses. Medicaid repayment rate is in $10 increments. Facility and market variables listed in Table 2 were used as covariates in columns (2) to (4).

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

V.B Results on Staffing

Panel A of table 4 examines the effect of wage pass-through on log CNA hours. Column (1) presents results from the conventional DD model with standard errors clustered at the state level. Pass-through increases staffing hours by about 0.73% but is not statistically significant. As mentioned earlier, this estimate may be biased due to unobservable state level shocks and is potentially inefficient due to the autocorrelation of the residuals within states over time. Columns (2) to (4) report the second stage results of two-step DD and two-step FGLS models. Since the second stage results use the state year level variation the number of observation drops to 288, i.e., 48 states over six years. Column (3) uses Huber-White standard errors clustered by states and column (4) estimates the standard errors by jack-knifing over states. The standard error on pass-through further decreases to 0.0068 from 0.0095 in column (2) but the impact is still statistically insignificant. However, in the two-step FGLS result in column (3), the standard error on pass-through drops substantially to 0.0047 and the point estimate at 0.0096 is statistically significant at the 5% level. Wage pass-through increases CNA staffing by about 1%. The results are nearly identical when we use jack-knifed standard errors in column (4). The estimated AR(1) coefficient in Panel A is 0.85 indicating a high degree of serial correlation in the error term, and the two-step FGLS improves efficiency by over 50% relative to the standard DD estimates in Table 4.

Table 4.

Staffing Results

	Standard DID	Two-step DID	Two-step FGLS	Two-step FGLS
	(1)	(2)	(3)	(4)
A. Dependent variable: Log CNA hours
Wage pass-through	0.00734 (0.00952)	0.00693 (0.00678)	0.00962** (0.00465)	0.00962* (0.00490)
State minimum nursing hours	0.0386*** (0.00384)	0.0209** (0.00862)	0.0136*** (0.00430)	0.0136** (0.00526)
Medicaid payment rate	0.00192 (0.00233)	−0.00241 (0.00544)	−0.00213 (0.00346)	−0.00213 (0.00391)
Case-mix reimbursement	0.00768 (0.0105)	0.0127 (0.0130)	0.0158 (0.0109)	0.0158 (0.0124)
AR(1) coefficient			0.85	0.85
No. of observations	52,136	288	288	288
B. Dependent variable: Log total nurse hours
Wage pass-through	0.00630 (0.0117)	0.00620 (0.00719)	0.00940* (0.00472)	0.00940* (0.00502)
State minimum nursing hours	0.0349*** (0.00393)	0.0189** (0.00817)	0.0123*** (0.00429)	0.0123** (0.00533)
Medicaid payment rate	0.00162 (0.00212)	−0.000901 (0.00437)	−0.00127 (0.00309)	−0.00126 (0.00351)
Case-mix reimbursement	0.00539 (0.0100)	0.0119 (0.0121)	0.0132 (0.0104)	0.0132 (0.0119)
AR(1) coefficient			0.77	0.77
No. of observations	52,101	288	288	288

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Columns (1) to (3) use standard errors clustered by state and column (4) uses standard errors jack-knifed at the state level. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

The state minimum staffing requirements have statistically significant impacts on CNA staffing in all specifications. Column (3) indicates that increasing the staffing requirements by one nurse hour per patient day results in about a 1.4% increase in CNA staffing. Table 4 results indicate the importance of including minimum staffing requirements when examining pass-through policy. Many states implemented the pass-through policy and increased staffing requirements in similar years. Conditional on the other variables, Medicaid reimbursement rate and case mix policy on average do not have any significant effect on staffing level.

Panel B of Table 4 reports results on total nurse staffing which additionally includes RN and LPN staffing. One concern may be that wage pass-through enables nursing homes to switch to more expensive staff rather than increase CNA staffing per-se. The coefficient estimates in Panel B are very similar to that in Panel A. There does not seem to be any substitution towards RN or LPNs. Since CNAs comprise most of the nurse hours the staffing result is mostly driven by CNAs.

The literature has found that the markets for urban and rural nursing homes are structurally different and that rural nursing homes have lower level and quality of staffing (Bowblis et al. 2013). In Appendix Table 2, we examine the impact of wage pass-through on staffing for rural nursing homes. In general, we do not find any statistically significant impact of wage pass-through on CNA staffing. However, the magnitudes of the coefficients are similar to those for urban nursing homes. There seems to be a slightly smaller impact on total nurse staffing but the statistical precision is weak as well.

V.C Results on Quality of Care

We examine multiple patient outcome variables independently to examine the impact of pass-through policy on the quality of care. Table 5 presents results for pressure ulcer worsening, ADL decline and persistent pain rates. Table 6 examines percent on antipsychotics or restraints, percent with bowel incontinence, catheters, contractures, or tube feedings. In interpreting the numbers we remind the reader that a lower number implies better quality. We employ the same DD and FGLS estimation procedures as before. In table 5, we find that the introduction of wage pass-through reduces the rate of pressure ulcer worsening by about 0.9 percentage points. We do not find any statistically significant impact on ADL decline or persistent pain rates.¹³ An interesting point to note in Panel A is that the standard errors do not decrease when we implement the two-step FGLS procedure. This is because the efficiency gains from the two-step FGLS is small when the AR(1) coefficient itself is small, in this case 0.11. The AR(1) coefficient increases to 0.39 and 0.46 in Panels B and C, and the standard error reductions increase accordingly, but not to the degree we see in Table 4 where the AR(1) coefficient is 0.85. This empirically confirms that our proposed two-step FGLS procedure achieve meaningful efficiency gains when there is a high degree of serial correlation in the state error terms.

Table 5.

Quality Results

	Standard DID	Two-step DID	Two-step FGLS	Two-step FGLS
	(1)	(2)	(3)	(4)
A. Dependent variable: pressure ulcer worsening rate
Wage pass-through	−0.00857** (0.00375)	−0.00923** (0.00363)	−0.00868** (0.00344)	−0.00868** (0.00362)
State minimum nursing hours	−0.000647 (0.00248)	0.00265 (0.00496)	0.00283 (0.00479)	0.00283 (0.00574)
Medicaid payment rate	−0.00145 (0.00102)	−0.00174 (0.00161)	−0.00159 (0.00144)	−0.00159 (0.00152)
Case-mix reimbursement	0.00869 (0.00690)	0.0217** (0.0105)	0.0217** (0.00924)	0.0217** (0.01067)
AR(1) coefficient			0.11	0.11
No. of observations	193,370	288	288	288
B. Dependent variable: ADL decline rate
Wage pass-through	−0.0183** (0.00756)	−0.00616 (0.00887)	−0.00459 (0.00731)	−0.00459 (0.00778)
State minimum nursing hours	0.00116 (0.00332)	−0.00342 (0.00503)	−0.00298 (0.00460)	−0.00298 (0.00502)
Medicaid payment rate	0.00684*** (0.00192)	0.00697** (0.00287)	0.00531* (0.00272)	0.00531* (0.00289)
Case-mix reimbursement	0.00431 (0.0166)	0.0211 (0.0241)	0.0104 (0.0226)	0.0104 (0.0257)
AR(1) coefficient			0.39	0.39
No. of observations	181,651	288	288	288
C. Dependent variable: persistent pain rate
Wage pass-through	0.00139 (0.00955)	0.00797 (0.00937)	0.00666 (0.00657)	0.00666 (0.00708)
State minimum nursing hours	−0.00480 (0.00669)	−0.00453 (0.00685)	−0.00577 (0.00752)	−0.00577 (0.00923)
Medicaid payment rate	0.00672 (0.00506)	0.00484 (0.00643)	0.00317 (0.00504)	0.00317 (0.00555)
Case-mix reimbursement	−0.0303 (0.0209)	−0.0201 (0.0215)	−0.0108 (0.0169)	−0.0108 (0.0197)
AR(1) coefficient			0.46	0.46
No. of observations	191,694	288	288	288

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Columns (1) to (3) use standard errors clustered by state and column (4) uses standard errors jack-knifed at the state level. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

Table 6.

Additional Quality Measures

	Standard DID	Two-step DID	Two-step FGLS	Standard DID	Two-step DID	Two-step FGLS
	(1)	(2)	(3)	(4)	(5)	(6)
	A. Percent receiving antipsychotics			B. Percent physically restrained
Wage pass-through	0.239 (0.232)	−0.262 (0.327)	−0.181 (0.302)	−0.0819 (0.381)	−0.528 (0.522)	−0.237 (0.494)
State minimum nursing hours	0.356** (0.134)	−0.0348 (0.301)	−0.304 (0.296)	0.951*** (0.189)	0.691* (0.368)	0.967*** (0.328)
Medicaid payment rate	−0.163* (0.0908)	−0.151 (0.121)	−0.0718 (0.0979)	0.125 (0.229)	0.0128 (0.166)	0.00829 (0.130)
Case-mix reimbursement	0.603 (0.424)	0.811** (0.384)	0.369 (0.369)	1.052 (1.118)	1.262 (0.805)	1.104* (0.654)
AR(1) coefficient			0.51			0.44
	C. Percent with bowel incontinence			D. Percent with catheter
Wage pass-through	0.288 (0.200)	0.314 (0.343)	0.0498 (0.369)	−0.121 (0.0768)	−0.0494 (0.119)	−0.0565 (0.113)
State minimum nursing hours	−0.470* (0.253)	−0.519 (0.354)	−0.603* (0.314)	−0.123* (0.0647)	−0.166 (0.259)	−0.165 (0.225)
Medicaid payment rate	0.155 (0.0995)	0.248 (0.159)	0.222 (0.181)	0.0233 (0.0441)	0.0154 (0.0532)	0.0306 (0.0553)
Case-mix reimbursement	1.048 (0.686)	0.645 (0.592)	0.722 (0.512)	−0.285 (0.285)	−0.234 (0.337)	−0.221 (0.224)
AR(1) coefficient			0.52			0.38
	E. Percent with contractures			F. Percent receiving tube feedings
Wage pass-through	−1.014 (1.217)	−1.239 (0.804)	−0.264 (0.537)	−0.125 (0.116)	−0.146* (0.0792)	−0.139* (0.0823)
State minimum nursing hours	0.0661 (0.599)	−0.224 (1.412)	−0.184 (0.727)	−0.0892 (0.0665)	−0.0461 (0.0458)	−0.0162 (0.0472)
Medicaid payment rate	0.0254 (0.255)	0.120 (0.400)	0.386 (0.266)	−0.0128 (0.0382)	−0.0346 (0.0412)	−0.0327 (0.0353)
Case-mix reimbursement	4.554** (2.092)	2.679 (1.614)	1.215 (0.857)	−0.382* (0.196)	−0.265 (0.167)	−0.223 (0.141)
AR(1) coefficient			0.67			0.34
No. of observations	52,147	288	288	52,147	288	288

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Columns (1) to (3) use standard errors clustered by state and column (4) uses standard errors jack-knifed at the state level. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

The coefficient estimates on state minimum nurse hours are all insignificant in Table 5. Minimum staffing requirements increase staffing but do not impact patient outcomes. The increase in staffing levels without wage increases may not improve worker effort and quality of care. We also examine rural nursing homes in Appendix Table 3 and find that none of the state policy variables impact quality of care in rural nursing homes. Table 6 examines additional patient outcome variables. There is no evident wage pass-through impact on all quality variables other than percent receiving tube feedings, which exhibits a wage pass-through impact that is significant at the 10% level. Consistent with the nursing home literature, pressure ulcer rate seems to best proxy quality of care in our analysis as well. In the following stratified samples and non-parametric analysis, we focus on pressure ulcer decline rate as our main measure for quality of care.

VI. Heterogeneous Effects

As discussed in Section 2 the pass-through effect would likely differ between high-end nursing homes that cater to more private pay patients and low-end nursing homes that predominantly serve Medicaid patients. In this section, we examine the heterogeneous effects based on the nursing home’s average share of Medicaid patients, i.e., the number of Medicaid patients divided by the total number of beds in the facility. We use total number of beds rather than patients in the denominator, because total patient numbers and occupancy rates are susceptible to outside factors, whereas, the number of total beds is a reasonably fixed feature of a nursing home. We stratify the sample into quartiles and then estimate the policy effects on each quartile using the two-step FGLS procedure. One concern is that the share of Medicaid patients is distributed differently by state. If we stratify over the whole sample of nursing homes, some states may have nursing homes predominantly in the first quartile and others in another quartile. In order to overcome this problem we stratify the sample into quartiles within each state. Stratifying the sample provides an easy way to examine heterogenous effects but the estimates can be sensitive to the sample cut offs. Hence, we also examine the pass-through effects non-parametrically

VI.A Examination of Stratified Samples

Table 7 presents the results of the stratified analysis. We present standard DD estimates, two-step DD estimates, and two-step FGLS estimates. The 1^st quartile represents nursing homes with the lowest Medicaid share and the 4^th quartile represents nursing homes with the highest Medicaid share. Panel A of Table 7 indicates that wage pass-through increases staffing levels by about 2.7% in the first quartile, significant at the 1% level, and increases staffing by 2.8% in the second quartile, also significant at the 5% level. Note that this effect is much larger than the 0.96% found in the full sample. However, we find no pass-through impact on nursing homes with high Medicaid patient share. The policy effect on staffing is concentrated on the better, i.e., less Medicaid patient, nursing homes. Another interesting finding is that the minimum nurse hour impact on staffing is more pronounced on nursing homes with a higher share of Medicaid patients. This is consistent with the theoretical predictions in Section II. Low reputation nursing homes are likely to maintain staffing near the state minimum levels and hence are more likely to respond to the increase in minimum staffing requirements.

Table 7.

DD and FGLS Estimation Results on Samples Stratified into Quartiles by Average Quality

	1st Quartile			2nd Quartile			3rd Quartile			4th Quartile
	Standard DID	Two-step DID	Two-step FGLS	Standard DID	Two-step DID	Two-step FGLS	Standard DID	Two-step DID	Two-step FGLS	Standard DID	Two-step DID	Two-step FGLS
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)	(12)
Dependent variable: Log CNA hours
Wage pass-through	0.0149** (0.00734)	0.0195** (0.00789)	0.0272*** (0.00780)	0.00729 (0.00872)	0.0216* (0.0123)	0.0284** (0.0141)	−0.00117 (0.00905)	−0.0157 (0.0141)	−0.0183 (0.0146)	0.00804 (0.0113)	0.00896 (0.00927)	0.00698 (0.00980)
State minimum nursing hours	0.0298*** (0.00541)	0.0288* (0.0160)	0.0230 (0.0184)	0.0384*** (0.00537)	−0.00218 (0.0223)	−0.00660 (0.0201)	0.0420*** (0.00361)	0.0123 (0.0204)	0.0145 (0.0148)	0.0381*** (0.00461)	0.0247** (0.00970)	0.0198** (0.00923)
Medicaid payment rate	0.00371 (0.00486)	−0.00634 (0.0129)	−0.00676 (0.00797)	0.00198 (0.00222)	0.00373 (0.00225)	0.00331* (0.00176)	0.00146 (0.00238)	−0.000777 (0.00334)	−0.00172 (0.00308)	0.00376 (0.00338)	0.000628 (0.00525)	0.000976 (0.00408)
Case-mix reimbursement	0.0277 (0.0173)	0.0307 (0.0184)	0.0251* (0.0148)	0.000685 (0.0139)	−0.00825 (0.0180)	−0.0156 (0.0174)	0.00655 (0.00885)	0.00346 (0.0118)	0.00886 (0.0106)	−0.00463 (0.0150)	0.0166 (0.0234)	0.0229 (0.0238)
AR(1) coefficient			0.65			0.31			0.28			0.38
No. of obs.	12,218	288	288	13,263	288	288	13,524	288	288	13,131	288	288
Dependent variable: pressure ulcer worsening rate
Wage pass-through	0.00114 (0.00768)	0.00773 (0.0104)	0.00712 (0.0110)	−0.0119** (0.00472)	−0.0235* (0.0127)	−0.0254* (0.0129)	−0.00688 (0.00549)	−0.0205** (0.00862)	−0.0181** (0.00748)	−0.0141*** (0.00389)	0.00561 (0.0162)	0.00370 (0.0148)
State minimum nursing hours	0.00111 (0.00386)	−0.00118 (0.00647)	−0.00721 (0.00636)	0.00567 (0.00341)	0.0132** (0.00590)	0.0138** (0.00517)	−0.00295 (0.00434)	0.00620 (0.00909)	0.00906 (0.0106)	−0.00527 (0.00438)	−0.00663 (0.0146)	−0.00687 (0.0137)
Medicaid payment rate	0.000439 (0.00341)	0.00321 (0.00418)	0.00837* (0.00475)	0.000494 (0.00187)	−0.00263 (0.00360)	−0.00276 (0.00326)	−0.00291* (0.00167)	−0.00527 (0.00354)	−0.00427 (0.00335)	−0.00322 (0.00348)	−0.00182 (0.00478)	−0.00134 (0.00437)
Case-mix reimbursement	−0.00553 (0.01000)	−0.0224 (0.0197)	−0.0328 (0.0280)	0.00518 (0.00882)	0.0153 (0.0146)	0.0151 (0.0128)	0.0265 (0.0159)	0.0680** (0.0309)	0.0698** (0.0285)	0.00924 (0.0148)	0.0170 (0.0220)	0.0169 (0.0212)
AR(1) coefficient			0.48			0.2			0.21			−0.08
No. of obs.	42,259	288	288	50,996	288	288	51,763	288	288	48,352	288	288

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Share of Medicaid patients on the horizontal axes is a standardized measure of the number of Medicaid patients divided by the total number of beds in each nursing home. Standard errors clustered by state. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

Panel B presents results on pressure ulcer worsening rate. Pass-through does not reduce pressure ulcer worsening rate in the high-end nursing homes, i.e., in the 1^st quartile, but does so in the 2^nd and 3^rd quartile. In Section II we predicted that quality improvement from wage pass-through would be more pronounced in the lower quality nursing homes. Hence, we would have expected to see quality improvements in the 4^th quartile as well. The standard DD estimates indeed indicate a statistically significant quality improvement. However, the two-stage FGLS results do not. This is likely due to the negative and small AR(1) coefficient of −0.08. Such AR(1) coefficient estimate would not warrant performing a two-step FGLS procedure. Hence, we next turn to the non-parametric analysis that uses the full distribution of the data and is less likely influenced by the idiosyncrasies of partitioned samples.

V.D Non-parametric Estimation of Heterogeneous Effects

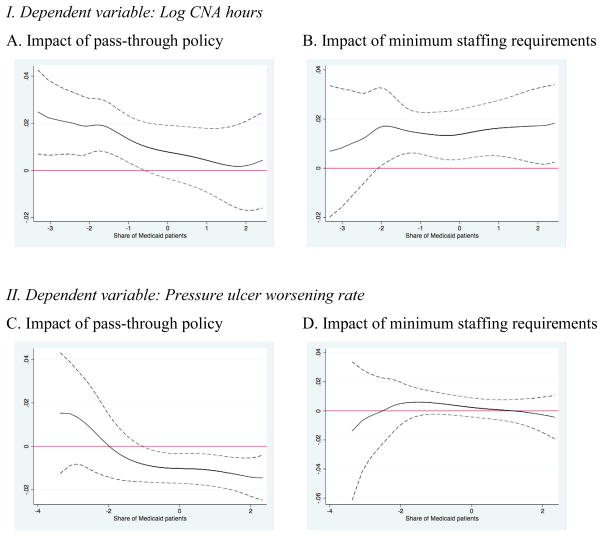
To illustrate the heterogeneous policy effects more generally, we non-parametically examine the pass-through effects along the full range of the Medicaid patient share distribution. We weight the data using a kernel around a Medicaid patient share value and then implement the two-step FGLS procedure to retrieve a coefficient on wage pass-through. We repeat this exercise over the entire distribution of Medicaid patient share and then plot the coefficients. Figure 2A illustrates the effect of pass-through on log CNA staffing. The solid line represents the mean effect and the dotted line the 95% confidence interval. Consistent with what we see in Table 7, the pass-through effect on staffing is positive and significant in nursing homes where Medicaid patient share is low. Visual inspection of the confidence interval bands suggests that the point estimates are statistically different between the low and high Medicaid patient share nursing homes. Figure 2B examines the impact of the minimum staffing requirements on staffing. Now the impact is positive and significant in nursing homes where Medicaid patient share is high. The patterns are again consistent with low-end nursing homes being constrained by the state minimum staffing mandate.

Figure 2. Non-parametric estimates of the impact of pass-through and minimum staffing requirements over the share of Medicaid patients.

Notes: Results are non-parametric estimates using a kernel density with a 0.3 bandwidth. Share of Medicaid patients on the horizontal axes is a standardized measure of the number of Medicaid patients divided by the total number of beds in each nursing home. The solid line presents the mean effects and the dashed lines indicate the 95% confidence intervals.

Figure 2C illustrates the effect of pass-through on pressure ulcer worsening rate, our main proxy for quality of care. The heterogeneous policy response is quite stark. Nursing homes with a higher share of Medicaid patients do see a significant reduction in pressure ulcer worsening and this pattern carries through to the part of the distribution that would correspond to the 4^th quartile in Table 7. Figure 2C illustrates the advantage of performing a non-parametric analysis to examine heterogeneous policy effects when using our proposed FGLS method. Stratifying the sample as we do in Table 7 is convenient but such strategy impacts the estimation of the AR(1) coefficient. The non-parametric approach has the advantage of using the full sample when estimating the AR(1) coefficient and returns more stable results. Figure 2D examines the impact of the minimum staffing requirements on pressure ulcer worsening, but the impact is not significant as we saw before. Figure 2 further supports Table 7 results and our earlier predictions on the heterogeneous pass-through effects on staffing and quality. Pass-through increases staffing in high-end nursing homes, which are less likely to be constrained by state minimum staffing requirements. However, pass-through increases quality of care in low-end nursing homes, which were likely hiring above their optimal level of staffing due to the state minimum requirements. Rather than increasing staffing levels, the low-end nursing homes with high Medicaid share use the subsidy to subsidize wages and better promote nurse staff effort.

VI. Robustness checks

We perform a few robustness checks to examine the sensitivity of the results. Though we find heterogeneous effects based on the share of Medicaid patients, wage pass-through should only affect nursing homes that actually admit Medicaid patients. We examine whether this is indeed the case by estimating the same procedures on a subset of nursing homes with zero Medicaid share. Panel A of Table 8 presents the result. Wage pass-through has no effect on both staffing and the pressure ulcer worsening rate.

Table 8.

Robustness tests

	Medicaid share 0%			Drop Medicaid payment rate
	Standard DID	Two-step DID	Two-step FGLS	Standard DID	Two-step DID	Two-step FGLS
	(1)	(2)	(3)	(4)	(5)	(6)
A. Dependent variable: log CNA hours
Wage pass-through	−0.00564 (0.0159)	0.0146 (0.0219)	0.0191 (0.0232)	0.00705 (0.00918)	0.00699 (0.00680)	0.00943** (0.00460)
State minimum nursing hours	0.0225 (0.0160)	0.0283* (0.0160)	0.0234** (0.0112)	0.0399*** (0.00426)	0.0199** (0.00915)	0.0132*** (0.00430)
Medicaid payment rate	0.00537 (0.00852)	0.00599 (0.00909)	0.0177 (0.0135)
Case-mix reimbursement	0.0369 (0.0345)	0.0395 (0.0462)	0.0391 (0.0333)	0.00765 (0.0104)	0.0134 (0.0133)	0.0163 (0.0110)
AR(1) coefficient			0.81			0.85
No. of obs.	2,311	243	231	52,136	288	288
B. Dependent variable: pressure ulcer worsening rate
Wage pass-through	0.0259 (0.0179)	0.00206 (0.0229)	0.00234 −0.0209	−0.00838** (0.00377)	−0.00919** (0.00361)	−0.00865** (0.00342)
State minimum nursing hours	0.00674 (0.0134)	0.0256 (0.0231)	0.0288 −0.0214	−0.00148 (0.00250)	0.00202 (0.00501)	0.00229 (0.00483)
Medicaid payment rate	0.00296 (0.00605)	−0.00443 (0.0112)	−0.00538 −0.00933
Case-mix reimbursement	0.152*** (0.0512)	0.175*** (0.0392)	0.182*** −0.0347	0.00870 (0.00706)	0.0220** (0.0108)	0.0221** (0.00949)
AR(1) coefficient			−0.11			0.11
No. of obs.	5571	222	215	193,370	288	288

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Standard errors clustered by state. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

Lastly, the Medicaid payment rate we use in the empirical analysis in general includes various forms of state Medicaid reimbursement policies including the wage pass-through. This may confound the point estimates we get on pass-through if the pass-through dummy and the Medicaid payment rate are highly correlated. The correlation is quite low at 0.04 and we believe multicolinearity is a not a concern in this context. However, we further examine the robustness of our results. In Table 8 Panel B, we drop the Medicaid payment rate from all estimation. The coefficient estimates are very similar to what we find in Table 4 and Table 5.

VII. Conclusion

A central question in health economics and public economics more generally is whether and under what conditions it is possible to achieve desired outcomes by subsidizing inputs. From an empirical perspective there are limited sources of policy variation that cover a sufficiently large area to create general equilibrium responses but a sufficiently small area to provide reasonable temporal and spatial variation. The states in the US provide a reasonable source of policy variation, but the need to control for autocorrelated state-wide shocks substantially reduces power, at least when standard state-clustering methods are used.

In this paper we address this issue in the context of an analysis of the effects of Medicaid pass-through regulations on nursing home staffing and patient outcomes. We implement a simplified version of Hansen’s model for small-T panels with autocorrelated shocks and fixed effects. In particular, we develop a simple consistent estimator of the AR(1) parameter and then show, using simulation, that this alternative method leads to substantial improvements in efficiency relative to the usual approach of simply clustering on states. Implementation of the procedure using nursing home data leads to reductions of standard errors of over 50%, even when clustering is used in addition to Feasible GLS to ensure robustness against autocorrelation that is greater than AR(1).

Wage pass-through led to greater staffing in nursing homes with a low share of Medicaid patients, but had little effect on staffing on nursing homes with a high share of Medicaid patients On the other hand, wage pass-through led to improvements in the quality of care in nursing homes with a high share of Medicaid patients. Nursing homes that were constrained and were sub-optimally choosing staffing above its optimal level are reluctant to use the pass-through to increase staffing but instead utilize the pass-through amount to increase nurse wages and effort, and ultimately the quality of care. The results indicate that pass-through can be an effective instrument for improving nursing home quality among nursing homes already constrained by existing staff constraints. More generally, the results point out the importance of input subsidies that work in tandem with existing constraints to limit possibilities of substitution.

Appendix

Appendix 1. Efficiency gain of FGLS relative to OLS

Denote $E(U^{\prime }U)=\mathrm{\Omega }=\left[\begin{array}{cc}1& \rho \\ \rho & 1\end{array}\right],X=\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]$, A = E(X′X)⁻¹ E(X′ΩX)E(X′X)⁻¹ and B = E(X′Ω⁻¹X)⁻¹ where A is variance of β under clustered OLS and B is the variance of β under FGLS. Let Ex₁² = Ex₂² = σ_x² where the subscripts on x indicate the time periods T=1, 2. Then Ex₁x₂ = κ · σ_x². Substituting these into A and B we get A=(1 + κρ)(2σ_x²)⁻¹ and B=(1−ρ²)(2σ_x²(1−κρ))⁻¹. Calculating the percentage reduction by (A−B)/A returns $1-\frac{1-{\rho }^2}{1-{\kappa }^2{\rho }^2}$.

Appendix Table 1.

Simulation result with a different sampling seed

Procedure		A		B		C		D
		N=50, T=6, AR(1), ρ=0.8		N=50, T=12 AR(1), ρ=0.8		N=50, T=12, AR(2) ρ1=0.6, ρ2=0.3		N=50, T=6 AR(0)
		Mean	SD	Mean	SD	Mean	SD	Mean	SD
I. Facility fixed effect	β	0.974	0.725	0.939	0.556	0.967	0.591	1.023	0.678
w/clustered SE	SE of β	0.780	0.153	0.548	0.0833	0.480	0.0737	0.785	0.127
II. Two-step DD	β	0.990	0.628	0.943	0.479	0.979	0.501	1.002	0.600
w/clustered SE	SE of β	0.683	0.0937	0.493	0.0577	0.427	0.0543	0.689	0.0861
III. Two-step FGLS	β	0.971	0.496	0.997	0.275	0.984	0.392	1.004	0.595
w/clustered SE	SE of β	0.472	0.0623	0.293	0.0366	0.339	0.0434	0.627	0.0793
IV. Two-step FGLS	β	0.971	0.496	0.997	0.275	0.983	0.392	1.004	0.595
w/jackknife SE	SE of β	0.470	0.0405	0.203	0.0179	0.245	0.0209	0.586	0.0448
Efficiency Gain		40%		63%		49%		25%

Notes: We use a different seed number from Table 1 for the random sampling. Simulations are for 50 states, with 0–100 facilities per state, over 6 or 12 time periods. We set the true β equal to one and carry out the exercise 100 times implementing (I) DD estimation with standard errors clustered at the state level, (II) Two-step DD with standard errors clustered by states, (III) Two-step FGLS with standard errors clustered by states, and (IV) Two-step FGLS with standard errors jack-knifed at the state level. The underlying AR process for the first two columns is AR(1), the third AR(2), and the last AR(0). Efficiency gain calculates percentage reduction in the standard error of β from implementing procedure III relative to procedure I. SD and SE denote standard deviation and standard error, respectively.

Appendix Table 2.

Staffing Results – Rural nursing homes

	Standard DID	Two-step DID	Two-step FGLS	Two-step FGLS
	(1)	(2)	(3)	(4)
A. Dependent variable: Log CNA hours
Wage pass-through	0.00698 (0.00532)	0.00675 (0.00668)	0.0110 (0.00668)	0.0110 (0.00704)
State minimum nursing hours	0.0267*** (0.00952)	0.0306** (0.0123)	0.0221** (0.00893)	0.0221* (0.0113)
Medicaid payment rate	0.00199 (0.00266)	−0.00128 (0.00347)	−0.00284 (0.00309)	−0.00284 (0.00333)
Case-mix reimbursement	−0.000789 (0.00605)	0.000638 (0.00893)	−0.00393 (0.00790)	−0.00393 (0.00932)
AR(1) coefficient			0.72	0.72
No. of observations	29,085	276	276	276
B. Dependent variable: Log total nurse hours
Wage pass-through	0.0101* (0.00572)	0.00575 (0.00771)	0.0110* (0.00611)	0.00110 (0.00652)
State minimum nursing hours	0.0267*** (0.00867)	0.0302** (0.0121)	0.0215** (0.00820)	0.0215** (0.0105)
Medicaid payment rate	0.00176 (0.00238)	0.000576 (0.00338)	0.000419 (0.00244)	0.000420 (0.00264)
Case-mix reimbursement	−0.000870 (0.00534)	0.000542 (0.00918)	−0.00449 (0.00656)	−0.00450 (0.00768)
AR(1) coefficient			0.61	0.61
No. of observations	28,995	276	276	276

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Columns (1) to (3) use standard errors clustered by state and column (4) uses standard errors jack-knifed at the state level. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.

Appendix Table 3.

Quality Results – Rural nursing homes

	Standard DID	Two-step DID	Two-step FGLS
	(1)	(2)	(3)
A. Dependent variable: pressure ulcer worsening rate
Wage pass-through	−0.00325 (0.0172)	0.00942 (0.0230)	0.00968 (0.0205)
State minimum nursing hours	−0.00319 (0.0281)	0.00443 (0.0153)	0.00337 (0.0138)
Medicaid payment rate	−0.00654 (0.00679)	−0.00686 (0.0111)	−0.00679 (0.00968)
Case-mix reimbursement	−0.000922 (0.0180)	0.00787 (0.0302)	0.00581 (0.0270)
AR(1) coefficient			0.01
No. of observations	4,244	119	118
B. Dependent variable: ADL decline rate
Wage pass-through	0.00313 (0.0132)	−0.0139 (0.0235)	−0.0131 (0.0217)
State minimum nursing hours	0.0224 (0.0220)	0.00557 (0.0222)	0.00478 (0.0196)
Medicaid payment rate	0.00395 (0.00566)	−0.00116 (0.0121)	−0.00108 (0.0106)
Case-mix reimbursement	−0.00916 (0.0214)	0.0258 (0.0406)	0.0233 (0.0366)
AR(1) coefficient			−0.03
No. of observations	3,976	118	116
C. Dependent variable: persistent pain rate
Wage pass-through	0.00796 (0.0284)	0.0544 (0.0697)	0.00396 (0.0441)
State minimum nursing hours	0.00100 (0.0170)	−0.0421 (0.0347)	−0.0317 (0.0222)
Medicaid payment rate	−0.00494 (0.0118)	0.000348 (0.0201)	0.000401 (0.0181)
Case-mix reimbursement	0.0505 (0.0384)	0.107 (0.103)	0.153 (0.117)
AR(1) coefficient			−0.65
No. of observations	4,185	119	118

Notes: All specifications include facility and year fixed effects. All facility and market variables listed in Table 2 are included in the standard DD procedure and the first-step of the two-step procedures. Columns (1) to (3) use standard errors clustered by state and column (4) uses standard errors jack-knifed at the state level. Medicaid repayment rate is in $10 increments.

^{*, **, and ***}indicate significance at the 10%, 5%, and 1 % level, respectively.