Abstract
We have developed a method for the simultaneous estimation of local diffusion and the global fiber tracts based upon the information entropy flow that computes the maximum entropy trajectories between locations and depends upon the global structure of the multi-dimensional and multi-modal diffusion field. Computation of the entropy spectrum pathways requires only solving a simple eigenvector problem for the probability distribution for which efficient numerical routines exist, and a straight forward integration of the probability conservation through ray tracing of the convective modes guided by a global structure of the entropy spectrum coupled with a small scale local diffusion. The intervoxel diffusion is sampled by multi b-shell multi q-angle DWI data expanded in spherical waves. This novel approach to fiber tracking incorporates global information about multiple fiber crossings in every individual voxel and ranks it in the most scientifically rigorous way. This method has potential significance for a wide range of applications, including studies of brain connectivity.
Keywords: Magnetic Resonance Imaging, Diffusion Weighted Imaging, Fiber Tractography, Brain Connectivity
I. Introduction
A problem of significant interest in basic neuroscience research and in a wide range of clinical applications is the reconstruction of tissue fiber pathways from volumetric diffusion weighted magnetic resonance imaging (DW-MRI) data. This is an inherently ill-posed problem because the local (voxel) diffusion measurements are noisy and made on a scale significantly greater than the underlying fibers and thus there are a multitude of possible neural pathways between any two given points in the imaging volume that might be consistent with the experimental data. The question then is to find the paths that are most probable. Current fiber tractography methods generally fall into two categories: 1) deterministic methods, typically based on some form of streamline construction (e.g., [1]–[3]) or 2) probabilistic methods, also generally based on streamline construction, but with the most likely principal diffusion direction determined from a posterior distribution of principal diffusion directions (e.g., [4]–[7]). These algorithms are ”local” in the sense that the computations are done at each voxel and some small neighborhood around it and thus are not informed by the final path that is created, and thus are not capable of assessing the probability of the final path amongst all possible paths. In most cases, these algorithms are inherently based upon some underlying relation to a random walk which guides the evolution of the trajectories.
Recently, interest has grown in more ”global” methods that aim to take into account the probabilities of the final paths by incorporating the path probabilities into the estimation process. These methods typically are based upon parameterizations of the diffusion field, or the anatomical connections they imply, that extend spatially beyond the voxel dimensions and subsequently take the form of either improving the local computations by the incorporation of more spatially extended path lengths (e.g., [8], [9]) or on the extremization of a cost function over a multitude of possible paths [10]–[13]). These global methods usually (with some exceptions [11]) do not take the random walk viewpoint but rather view the entire system as possessing some underlying structure, characterized by local interactions or potentials, that can be elucidated by optimizing some cost function (e.g., energy) over multiple configurations of that system.
The original diffusion tensor imaging (DTI) model assumes that the measurements in each voxel provide an estimate of a single real, 3 × 3 symmetric diffusion tensor D from whose eigenstructure can be derived both a meaningful measure of the anisotropy (here characterized by the fractional anisotropy FA [14]) and a principal eigenvector that can be used as a proxy for the fiber orientation [14]. Then DTI is the simplest underlying model for diffusion data, is predicated on a single fiber model for the voxel content, and is equivalent to a Gaussian model for diffusion (e.g., [14]). (To be more accurate, DTI can be viewed as the next simplest mathematical framework, while a scalar framework is the simplest that can be used for modeling diffusion data. Also, there may be significant deviations from Gaussian diffusion both on microscopic and on meso-scales. Thus, effectively even DTI may have a deviations from Gaussian due to i.e. cellular boundaries with less than 100% permeability). However, the DTI model is not sufficient to capture more realistic possibilities of complex fiber crossings needed for clinical applications [15]. To estimate local diffusion directions in each voxel (streamline directions) several high angular resolution diffusion imaging (HARDI) [16] methods are typically used. These methods represent an extension of the original DTI acquisition framework [17] to higher angular resolutions appropriate not only for detection of main fiber orientation, but also for attempting to resolve more complex intravoxel fiber architecture such as multiple crossing fibers [18]–[22].
In recent years, there has been significant interest in developing DW-MRI methods capable not only of estimating angular fiber distributions from multidirectional diffusion imaging (multiple q-angles) [16], [19]–[23]), but also find spatial scales with multiple diffusion weightings (multiple b-shells) [24]– [28]. While it has long been recognized that the most general nonparametric (model-free) approach is to measure the dis-placement probability density function or diffusion propagator directly [29], [30], the natural extension of this to imaging wherein 3D Cartesian sampling of q-space is used to obtain the 3D displacement probability density function (dPDF) at each voxel [24], is prohibitively expensive from the standpoint of data acquisition. This recognition has recently spawned more practical methods for obtaining an estimate of the dPDF, often called the ensemble average propagator (EAP), from more practical multi-shell, multi-directional acquisitions [25]–[28].
Nevertheless, despite these advances, a critical simplification that is made in all current methods used to estimate either the intravoxel diffusion characteristics (via the EAP, for example) or to estimate the underlying global structure (tractography) is the assumption that these two estimation procedures are independent. Thus one first estimates the intravoxel diffusion, then applies a tractography algorithms. For example multiple b-shell effects, used in obtaining the EAP, are used only to infer directional multiple fiber information for input into streamline tractography algorithms (see e.g. [31]). However, this distinction between local and global estimation is artificial and limiting, since both the local (voxel EAP) information and the global structure (tracts) are from the same tissue, just seen at different scales. In practical applications of human DW-MRI data this artificial division of information on local and global gives rise to problems at the data interpretation stage: e.g. spurious white matter loss due to local underestimation of fiber anisotropy, incorrect tracking of fiber orientation due to apparent overlapping of angular distributions, etc.
In this paper we revisit the problem of local diffusion estimation and fiber tractography with the specific goal to include multiple spatial and temporal scales that can be deduced from multiple b-shell DW-MRI measurements in addition to just angular (multi-)fiber orientation [32], [33]. In many practical applications, either one or two spatial locations (or regions) are known a priori. In neuroscience applications, for example, two regions may be functionally connected (as measured, perhaps, by FMRI) and the diffusion weighted MRI data is being used to assess the degree (if any) of the structural connectivity between two functionally connected regions. We therefore reconsider two common formulations of fiber tractography: (1) – initial value, i.e. finding fibers that start at some chosen area of the brain, (2) – boundary value, i.e. finding fibers that connect two preselected brain regions. Thus we recast the fiber tractography algorithm as the determination of the most probable path either starting at a selected location or connecting two spatial locations, and seek a general probabilistic framework that can accommodate various local diffusion models and yet can incorporate the structure of extended pathways into the inference process. In this case, the problem of tractography from DWI data can be reformulated as the determination of the probability of paths on a 3D lattice between two given points where the probability of a path passing through any particular point is not equiprobable, but is weighted according to the locally measured diffusion characteristics.
The essential problem at the core of the tractography problem is the estimation of macroscopic structure from microscopic measurements. In this paper we present a formulation of the tractography problem based upon a recently formulated general theory for understanding information flow in a disordered lattice. This theory, called entropy spectrum pathways, or ESP [34], is used to infer the spectra of the most probable global pathways (in this case, fiber tracts) in a non-uniform lattice (the sampled DWI data) based upon prior information about the local coupling structure of lattice (in this case estimated from the local measurements of the diffusion). The method is generalized to utilize multi–scale diffusion information that is available in multi–shell DWI datasets by extending the mechanism of streamlines generation using a Hamiltonian formalism and a diffusion-convection (FokkerPlank) description of signal propagation though multiple scales [34]–[36].
II. Reformulation of the EAP problem
As shown below, the ESP framework allows for the incorporation of both measured data and prior information into the estimation procedure. It is thus essential that the description of the data be as general and complete as possible. A general description of the measured DW-MRI data is provided by the EAP formalism [25]–[28]. In this section we reformulate the problem in order to provide a very general characterization amenable to numerical implementation, and to bring out some of the essential spatial scales that inform our application of ESP.
The DW-MRI signal W (r, q) measured in both r and q space can be expressed in terms of both the spin density ρ(r) and the average propagator pΔ(r, R) using the narrow pulse approximation [30] as
| (1) |
where r is the voxel coordinate, q = γGδ/2π, with G and δ being the strength and duration of the diffusion-encoding gradient and γ the gyromagnetic ratio of protons and the function W (r, q) is the Fourier transform (in the diffusion displacement coordinate R, defined as a change in particle position over time t, R = r(t0 + t) − r(t0)) of the weighted spin density function [23]
| (2) |
that scales (or weights) the spin density with the average propagator pΔ(r, R) at each observed voxel.
To find an expression for the spin density function Q(r, R) we will use the plane wave expansion in spherical coordinates with ,
| (3) |
where jl(qR) is the spherical Bessel function of order l and is the spherical harmonic with θq and φq being the polar and azimuthal angles of the vector q, and similarly for the vector R.
The product jl(qx)(x̂) represents the basis function for the spherical wave expansion [37]. These basis functions can be obtained as solutions of Helmholtz’s wave equation [38]:
| (4) |
This representation suggests an interesting possibility of treating the problem of fiber tractography for diffusion weighted MRI data using the techniques of geometrical optics in in-homogeneous media [39]. We will discuss this point in more details in section III-C.
The above basis functions are composed of radial (spherical Bessel jl) and angular (spherical harmonic ) parts, where the spherical harmonics are the eigensolution of the angular part of the Laplacian with the eigenvalues λl = −l(l+1):
| (5) |
The spherical harmonic of degree l and order m allows separation of the θ and φ variables when expressed using associated Legendre polynomials of order m as
| (6) |
where cl,m is the normalization constant
chosen to guarantee the orthonormality condition
The radial component jl(qx) of Eqn 3 is obtained as the eigenfunction of the radial Laplacian
| (7) |
with the orthonormality conditions
This allows us to reconstruct the spin density function Q(r,R) using the spherical wave decomposition as
| (8) |
where
| (9) |
This representation offers a concise and intuitively clear quantitative description of the local diffusion in terms of a clearly defined expansion order on which can be based decisions of optimal fitting. We would like to mention, that although there are several different bases proposed to describe MR signal in q-space [25], [40], [41], finding the best representation of q-signal on partially acquired grid was not an intent of our paper. We reused existing fast and robust algorithms that we have developed for this computation [37]. Our implementation is flexible and does have a choice of several filters able to significantly reduce ringing artifacts.
It should be kept in mind that the typical scales for the voxel coordinate rand for the dynamic displacement Rin current diffusion weighted MR experiments are vastly different. For the time scale over which the individual measurements in DWI are typically made (≈ 50 ms) the free diffusion root mean squared distance is x2 1/2 ≈ 20µ and thus much smaller than typical voxel dimensions (≈ 1 mm3, at best). Hence, with high degree of accuracy it can be assumed that the average propagator in the spin density function Q(r, R) only influences the nearest neighbor voxels through the dynamic displacement R dependence. The entropy spectrum pathway (ESP) formalism presented in [34] is well suited for taking nearest neighbors into account. We would like to emphasize that although the spin density function Q(r, R) only influences the nearest neighbors through the dynamic displacement Rdependence in the current sample acquisition framework, it also contains the global scale variations through the rdependence. Hence, even in the limit when the diffusions times are vanishingly small (such as in high gradient strength systems) our approach does not break down, but simply operates as a global method.
III. Tractography Guided by Entropy Spectrum Pathways
A. Summary of ESP theory
The entropy spectrum pathways (ESP) theory [34] is an extension of the maximum entropy random walk [42], [43] and concerns the very general problem of random walks on a defective or disordered lattice. There are several key findings provided by the ESP theory. First, the pathways of the random walk are determined by prior information concerning the structure and relationships of the lattice points, and therefore the ESP represents a flow of information, rather than representing an actual physical process. This view facilitates the use of ESP within a wide range of practical problems related to connectivity. Second, it is possible to characterize multiple pathways, ranked according to their entropy, all of which contribute to the flow of information on the lattice. Thirdly, the interesting localization phenomenon previously noted [42], [43] can be understood in terms of the eigenstructure of the lattice. Fourthly, the local interactions that inform the generation of global structure can be based upon whatever coupling information the user has available. This coupling can take on a general form, and it was shown that this property can be understood in terms of potential theory [34]. In the case of nearest neighbor coupling with a ”binary” potential (on or off), the problem reduces to the computation of the eigenstructure of the adjacency matrix of accessible (non-defective) lattice locations. But the more general formulation of ESP facilitates the use in practical applications such as we present here. In this section we will briefly summarize and reformulate the ESP formalism within the context of the tractography problem.
The objective is to calculate the probability that a spin, or ”particle”, starting from an initial spatial location x(t0) at initial time t0 = 0 diffuses to a second location x(t) at a later time t. While the underlying structure we wish to estimate is assumed continuous (being comprised of tissue fibers), the spatial locations x at which the measurements are acquired are assumed to be from DWI images and thus discretized to a 3D Cartesian spatial grid. However, the temporal discretization to be employed is a fictitious construct used to implement a random walk model, due to the above mentioned difference in scales of the voxel coordinates and the dynamic displacement. Our space-time points are defined on the true voxel spatial grid but on a di-ffusion pseudo-time grid whose increments are much larger than the experimen-tal time scale. Simulating diffusion in this way lends itself to two differe-nt interpretations. One view of this process is to see it as diffusion that is allowed to take place for much longer than the measurement time, or, equivalently, that the process is in equilibrium and thus long time behavior is well-represented by the snapshots in time provided by the experimental data. However, another viewpoint, that of ESP, and the one we adopt, is that the simulation is of the flow of information constrained by the physical measurements. The entire process is one of estimating a macroscopic phenomena from local measurements, using by prior information.
The ESP theory ( [34]) ranks the optimal paths within a disordered lattice according to their path entropy. Associated with the k’th path is a transition probability
| (10) |
| (11) |
where λk and are eigenvalues and eigenvectors of the coupling matrix Q defined as
| (12) |
Hence each transition probability is associated with a standard eigenvalue equation
| (13) |
This matrix defines the interactions between locations on the lattice and is called the coupling matrix. The λij are Lagrange multipliers that define the interactions that can be seen as local xij on the lattice. For each transition matrix Eqn 11 there is a unique stationary distribution associated with each path k:
| (14) |
that satisfies
| (15) |
the first of which, µ(1), corresponds to the maximum entropy stationary distribution. Considering only µ(1), note that if the Lagrange multipliers take the form
| (16) |
then Q becomes simply an adjacency matrix, the single maximum entropy distribution constructed from this adjacency matrix is maximum entropy random walk [42]. However, one major significance of the ESP theory to the present problem is that is ranks multiple paths, and these paths can be constructed from arbitrary coupling schemes through Qij . For each of the stationary distributions is associated a path related to the localization of information related to the eigenstructure of the disordered lattice. The key feature is that the local transition probabilities between nodes depend on the global structure of the graph through the eigenvectors ψ(k). In practical applications, the lattice can be described in terms of n pathways constructed from the first n eigenvectors of the potential matrix (in decreasing order of the eigenvalues).
We emphasize that we do not presume to be explicitly modeling the diffusion over the paths, since we know that the diffusion length over the typical time-scale of a DWI experiment is typically far smaller than a voxel dimensions. Rather, this procedure is viewed as one of estimation and thus the construction of the ranked maximum entropy paths - those that are most unbiased with respect to the measured data and the prior information (the lattice couplings) while satisfying the initial and/or final conditions. In this view the problem is one of estimating the global connectivity from the local diffusion characteristics.
B. Multiple scale coupling
The estimation of the local and global tissue structure over multiple scales using DW-MRI data can be investigated within the ESP framework by viewing the data as measurements on a 3D lattice in which each voxel is ascribed a ”potential” that is related to its coupling with neighboring voxels. An important feature of the ESP theory is that this potential is very general in form. This is critical to its application in the current problem. While it was shown for a binary coupling (i.e. wherein the coupling matrix reduced to the adjacency matrix with 0/1 elements) [34], in the current problem we will incorporate a strength of coupling that reflects the local interaction of voxel data. In order to do this we first symmetrize the spin density function
| (17) |
where l represents the dimensionless ratio of scales of dynamic displacement Rto the spatial (voxel) scales r, and, then sum all relevant scales included in the spin density function Q(r;R) by the dependence on the dynamic displacement R:
| (18) |
Here, we used a symmetric input from voxels i and j by taking the line integral of the spin density function Q(r, RR) along account only a subset of spatial scales that can contr-ibute to this interaction (from lmin to lmax). Since the typical scales for the voxel coordinate r in current diffusion weighted MR experiments are much larger then the scales for the dynamic displacement R(20µ vs 1mm), the coupling can be limited to nearest neighbor effects taking lmin = 0 and lmax = ∞ to calculate a coupling potential .
We would like to emphasize, that in nearest neighbor coupling evaluation (Eqn 18) we do not use solid angle integration. The appropriate choice of filters and order of angular resolution in the SWD allows us to replace the costly integration of geometrically complex coupling between noisy multiple peaked dODF from neighboring voxels with the fast and simple line integration across all radial scales.
This form of the coupling potential is then used in Eqn 13 to obtain the relevant eigenvalues and eigenvectors
| (19) |
The k-th eigenvalue and eigenvector can be used to generate the transition probabilities (Eqn 11) but in addition we also generate the scale dependent transition probabilities
| (20) |
that will be equal to the total transition probability Pij when integrated over all scales l. As those probabilities only describe transitions between nearest neighbors they can be expressed as a scale dependent function Pl(r, R). We will also generate the equilibrium probabilities µ(k) = [ψ(k)]2.
As a concluding remark to this section, we would like to reiterate that the general problem of tractography is necessarily one of multiple scales because the local diffusion occurs on the microscale and the tracts are on a macroscale. The entire point of our approach is that it enables a characterization of the problem in terms of information at these multiple scales.
C. Generation of optimal paths
Our goal is either to construct a pathway between an initial spatial location a and a final spatial location b or to trace a pathway incrementally starting from an initial location a. In both cases we are interested in “the most probable” pathways, i.e. we would like to constrain our local search by the global entropy structure. Therefore, our interest is not in the final equilibrium distribution µ∗ but in the pathway to it. We are therefore interested in the dynamics of the probability and want to compute the path that maximizes the entropy at each step, and thus results in the final (equilibrium) distribution µ∗at time τ.
The scale dependent transition and equilibrium probabilities obtained in the previous section can naturally define the global entropy field that shapes the flow of information and allow finding optimal paths. In the limit of long pathway lengths (or large time τ ) and under the Markovian assumption, the rate of entropy change SR(ri) can be expressed at each location ri as [44], [45]
| (21) |
The most straight forward way to include this multi scale structure of the global entropy field is by taking into account that the conservation of probability in general includes not only the diffusive component (as for example used by [30] for obtaining the expression of EAP in single mode homogeneous self-diffusion), but also has the convective part [34]–[36]
| (22) |
here P is the probability, S is the entropy, and L and D are coefficients (in general either tensors or functions of the coordinates) that characterize local convective and diffusive scales (L = κD). This Fokker-Planck equation, with the potential equal to the entropy, connects the global structure of the probability with the local structure of the lattice through the local structure of the entropy.
The current state-of-the-art approaches used for fiber tractography in DTI/DWI data require splitting this problem in two parts: first, obtain the EAP from the diffusion only subsystem,
| (23) |
and second, solve the convective part (averaged over all the dynamic displacement scales R)
| (24) |
by simple local tracing of one (DTI) or several (DWI) principal fiber directions. Unfortunately, this decoupling results in only the local diffusion information derived from EAP being used at the fiber tracking stage To illustrate this point, we will first assume the entropy gradient fixed and will show how it leads to the current tractography. In this case the convective part of Eqn 22 in the eikonal approximation provides a simple expression for the Hamiltonian H(ω, k, r) – the function of canonical co-ordinates that defines the dynamics. (For mechanical systems this function is simply the total energy, which is conserved in motion. For more complex systems it does not necessarily corresponds to energy, but still describes conservation laws of the system).
| (25) |
where an input from all dynamic displacement scales is included, as formally both L and S may depend on both R and r Finding the characteristics (or rays) of Eqn 22 will describe how the signals propagate and can be accomplished by integrating a set of ordinary differential equations of the Hamilton-Jacobi type:
| (26) |
The current fiber tractography methods in general do not emphasize or discuss the notion of global entropy, but implicitly assume the local behavior of the entropy gradient, directing it along some of the major axes of the local diffusion/convection tensor L = κD, i.e. ∇S = ψ, where ψis the eigenvector of L· ψ = λψ. Under the assumption of scale independent diffusion (i.e. D(r, R) ≡ D(r)) the Hamiltonian Eqn 25 then becomes
| (27) |
and the ray tracing equation simplifies to the following form
| (28) |
Ignoring the spatial dependence of the diffusion propagator (i.e. C = const) this equation is exactly in the form of Frenet equation commonly used for fiber tracking [3]. Thus, the current fiber tractography can be regarded as a fixed scale and spatially homogeneous limit of the more general Fokker-Plank formalism – Eqn 22.
To develop a more general entropy based tractography several assumptions will be made. First, only solutions with the high enough probability will be considered, i.e. it will be assumed that in the region of interest the probabilities are sufficiently close to 1, so that it is possible to linearize both the probability and the entropy as
| (29) |
where S0 = −P0 ln P0 and the scale dependent transition probability Pl(r, R) (Eqn 20) can be substituted for P0. Second, it is assumed that P1 is a small correction to the equilibrium probability (i.e. P1 ******* P0). The linearized convective part of Eqn 22 can then be written
| (30) |
Third, use of the scale dependent transition probability Pl(r, R) for P0 allows us to omit L in these expressions, as the diffusion anisotropy is already included in ESP calculations of PR(r, R) from the spin density function Q(r, R) obtained with the spherical wave decomposition using Eqns 8 and 9. Fourth, no time dependence is assumed to be present in P0 as it is time stationary, hence ∂tP0 ≡ 0. Fifth, we also have omitted the last term ∇ · D∇P1 from the Eqn 22 as it won’t appear in eikonal approximation used for obtaining the ray tracing equations.
Eqn 30 is a linear inhomogeneous hyperbolic equation, hence it has traveling wave solutions propagating along the characteristics. In order to formally find those characteristics we will assume a plane wave solution for P1 [39], [46] in the form
| (31) |
and then obtain a more general expression for the Hamiltonian
| (32) |
where , and, again we averaged over all dynamic displacement scales.
Hence, taking into account the global entropy gradient as well as the scale dependence of the diffusion coefficient, the fiber tracking in the geometrical optics limit can be represented in more general form, using Eqns 26 and 32, as
| (33) |
| (34) |
The first equation (Eqn 33) traces the characteristics (rays) of the convective part of the original Fokker-Plank equation (Eqn 22) under the influence of a local diffusion coupled with a global entropy gradient. This coupling is locally described by a vector X. A second term (with 2kY ) provides some smoothing by adding “a push” in the direction of the wave vector k. It also ensures that in voxels with isotropic diffusion (or with many fibers of different directions crossing) and without a global entropy gradient the ray will continue following this kdirection. In the second equation (Eqn 34) the spatial gradients are responsible for a change of the wave vector kdirection and magnitude.
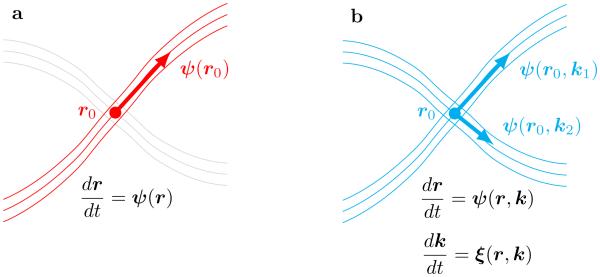
A schematic illustration of differences between traditional fiber tracking and geometrical optics–like tracking is shown in Figure 1. The traditional approach defines tracts by integration of position–only function ψ, that assigns the tangential direction of tracts to each location r. For the geometrical optics approach, the integration takes into account both the orientation and multiple scales, through the dependence of ψ on directional angle k/|k| and magnitude |k|.
Fig. 1.
Schematic illustration of (a) traditional fiber tracking based on integration of a single Frenet equation vs (b) fiber tracking that uses the geometrical optics analogy. (a) In the first case the fiber orientation vector ψonly depends on spatial location r0, hence, even at location of fiber crossing only single the most important fiber can be followed (point r0 uniquely selects single family of fibers oriented along ψ(r0)). (b) The geometrical optics approach automatically includes dependence of ψon both orientation k/|k| and scale |k|, hence it can effectively proceed through difficult areas of crossings of multiple fibers (the choice of fiber direction at point r0 depends on the value of the parameter k, with k1 selecting the same fiber direction as in (a), and k2 corresponding to the alternative crossing family of fibers).
IV. Results
To evaluate practical aspects and performance of ESP guided fiber tractography we used our method to process several multiple shell multiple angle diffusion weighted MRI datasets acquired using either realistic MR phantom or real brain samples.
A practical realization of the method used in all of the experiments includes several stages that were implemented in C++ with multithreading (using pthread libraries) and runs both on Linux and Mac OS X. The ESP framework uses our spherical wave decomposition approach (SWD) [37] based on the fast Fourier and on the fast spherical Bessel transforms. The tracking algorithm uses the standard fourth order Runge– Kutta integration applied to six dimensional (r,k) space.
The high resolution full brain tractography processing of typical 140x140x96 diffusion weighted MRI volume with 4 shells of 552 q-vectors using Intel® CoreTM i7-4930K six cores (twelve threads) 3.40GHz CPU produces around 190K fiber tracts in 15 minutes. The spherical wave decomposion part of processing takes six minutes for obtaining 600 spherical wave modes at each voxel using Lmax (or spherical harmonics order) of 10, and Nmax (or spherical Bessels order) of 6. The tractography part uses full 140x140x96 spatial grid and 7x7x7 resampled k-grid and outputs ~190K of fiber tracts in under 9 minutes. The medium resolution full brain processing produces ~90K tracts in 5 minutes, with the ESP stage taking around 3 minutes.
The first dataset is of the well-known ”fiber cup” MR phantom extensively used for testing and performance evaluation of various fiber tractography approaches [47]. The phantom consists of seven fiber bundles confined in a single plane by squeezing them in between two solid disks. Diffusion-weighted image data of the phantom was acquired on the 3T Tim Trio MRI system with 3 mm isotropic resolution on 64 × 64 × 3 spatial grid. Three diffusion sensitizations (at b-values b = 650/1500/2000 s/mm2) were collected two times for 64 different diffusion gradients uniformly distributed over a unit sphere. Several baseline (b = 0) images were also recorded [47].
Our initial stage of processing includes restoration of the spin density function Q(r, R) using Eqns 8 and 9 from section II. The spin density function is then used to generate symmetric scale integrated input to the coupling potential with Eqns 17 and 18. Eigenvectors and eigenvalues of the coupling potential then used for obtaining the transition probabilities using Eqn 11.
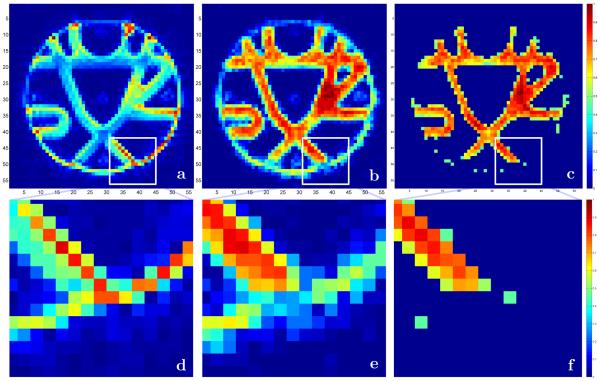
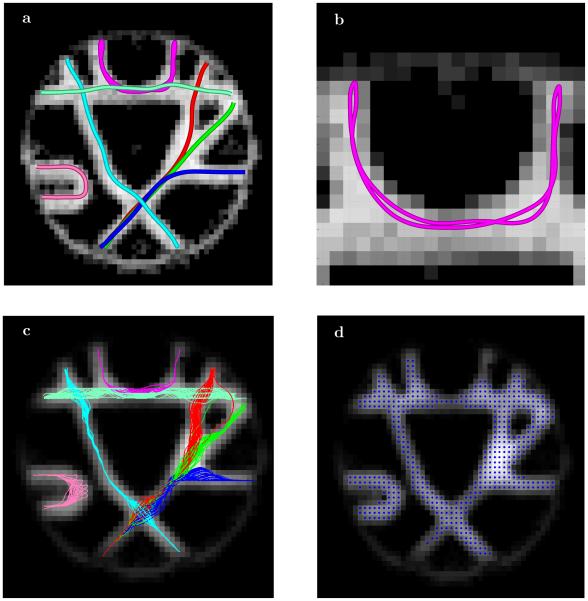
We included one of the baseline images of the fiber cup phantom in Figure 2a to emphasize an interesting and important feature of the ESP approach. The baseline image (as well as other diffusion weighted images not shown here) clearly shows bright artifacts at the interface boundaries of the disks used for phantom manufacturing. The overall effects of these artifacts are significant with the brightest spots located either at the very ends of the fiber bundles where they are cut by the disks or even at the circular boundary of the disks themselves. The expanded version of one of these areas is shown in Figure 2d.
Fig. 2.
Central 5horizontal 64 × 64 slice of 64 × 64 × 3 MR fiber cup phantom [47]; (a) one of the baseline b=0 images and (d) the expanded version of the white square area clearly showing strong signal at the fiber end and at the circular disc interface; (b) the map of the largest ESP transition probability values with (e) the enlargement of the same area showing the resolution of the fiber end; (c) and (f) the map of equilibrium probability distribution (µ∗ = [φ(1)]2) thresholded at 0.45 with perfect identification of all fiber ends and overall area occupied by fiber bundles.
The currently standard analyses that are based on the maps of the apparent diffusion coefficient (ADC) and the fractional anisotropy (FA) (available in Figure 2 of [47]) also favor those regions by assigning higher anisotropy and diffusion values. As a result many of the current streamline tracing tractography approaches do not see the actual ends of the fiber bundles and continue tracts through the circular disks interfaces.
But the transition probability map shown in Figure 2b that was generated by the ESP clearly emphasizes the separation between the fiber bundles and the circular disk interface (with the same area enlarged in Figure 2e). Using simple thresholding (Figure 2c and Figure 2f) allows identification of the ends for all of the fiber bundles. What is equally important is that ESP correctly restores the contrast that has been lost at the crossing fiber areas that can clearly be seen in b0 as well as in the diffusion weighted images for different gradient directions. As previously mentioned, this helps the geometrical optics algorithm to find the correct continuation of rays in voxels with isotropic diffusion (or with many fibers of different directions crossing).
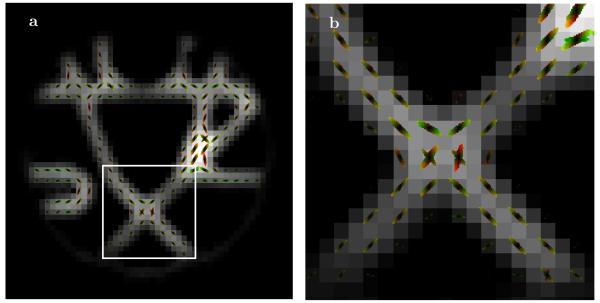
The local samples of multiple scales of the transition probabilities calculated by the ESP method are presented in Figure 3. One of the crossing fiber areas, enlarged in the right panel, clearly shows existence of different fiber directions in different scales of the transition probabilities.
Fig. 3.
(a) Local samples of different scales of transition probabilities obtained by the ESP, with (b) blow up of the center crossing fibers area.
We would like to stress two important aspects of our method. First, Figure 3 shows the multi-scale transition probabilities (as expressed by Eqn 20) rather than the EAP (or dPDF). The transition probabilities were derived not just from the local diffusion (used in EAP/dPDF). It also takes into account the nonlocal coupling between voxels by calculating the global eigenmodes and updating the probabilities according to the structure of the corresponding global eigenvectors. In this respect, the transition probabilities are more fundamental quantities than the locally derived EAPs or dPDFs.
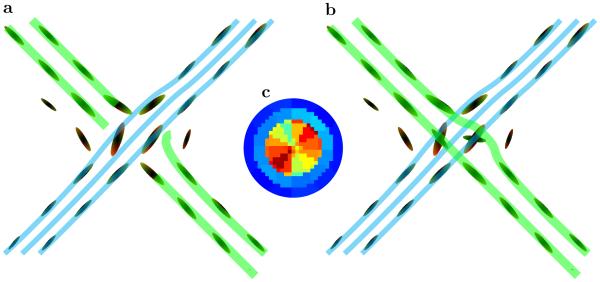
Second, the use of multiple scales enables the geometrical optics–like approach presented here to find the correct path even when the angular resolution is relatively low. To illustrate this fact we included in Figure 4 two possible tracking scenarios, (a) using just single scale transition probabilities, and (b) with transition probabilities that include multiple scales. The single scale tracking finds only one bundle of fibers, and either breaks the second set of fibers or wrongly connects it to the first bundle. But with multiple scale transitional probabilities, the second set of fibers is found correctly with the geometrical optics–like tracking even at this relatively low angular resolution.
Fig. 4.
(a) One possible tracking through fiber crossing area shown in Figure 3b using only single scale transition probabilities. With low angular resolution only a single set of crossing fibers can be identified, and the second bundle will either be broken (or connected to the first one). (b) Tracking with multiple scales and coupling information are used in obtaining transition probabilities. Even with this relatively low angular and radial resolution the presence of multiple scales enables geometrical optics–like tracking through the difficult area. (c) A map of EAP–like function for a single voxel from the crossing area. The map was obtained using only local diffusion data from the original shell of 60 direction q-values with high angular resolution 72 mode spherical harmonics expansion. The map shows that even with high angular resolution only one fiber direction can be reliably identified. Our multi-scale approach incorporating global connectivity information can reliably identify crossing in the calculated transition probabilities.
Utilization of high angular resolution locally (in an isolated voxel) and without the incorporation of multiple scales and global connectivity does not necessarily guarantee detection of crossing fibers. For example, it is not possible to detect the second direction of fibers in an EAP–like function (Figure 4c) of a single voxel from the crossing area of Figure 3b. This EAP–like map was obtained from single voxel diffusion data using the original shell of 60 direction q-values with high angular resolution 72 mode spherical harmonics expansion. Importantly, our approach using multi scale transition probabilities and global connectivity information can identify crossings from significantly lower angular and radial resolution.
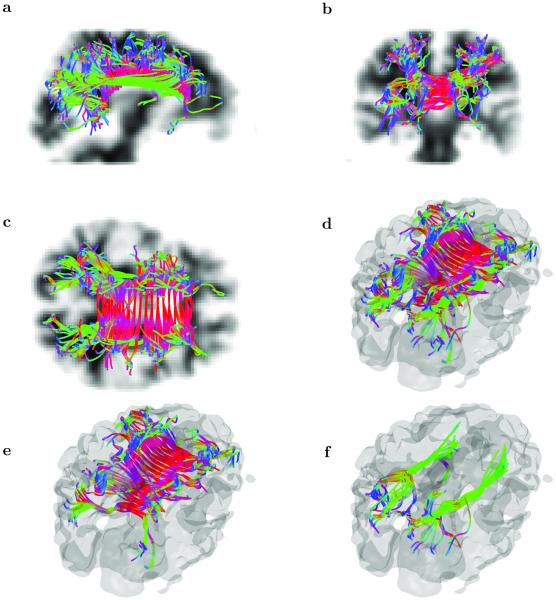
A direct comparison with the fiber cup results is shown in Figure 5a. Several possible fiber tracts obtained by integrating the equations of geometrical optics rays for Fokker-Plank formalism (Eqns 33 and 34) are displayed. The phantom includes several different types of fiber crossings (at different angles), as well as kissings and splits/joints. To illustrate one peculiar feature of the approach based on geometrical optics we included the blow up of one of the fiber tracts. In the boundary area where the underlying fibers end abruptly the ray tracing algorithm may produce a reflection of the ray from the interface and proceed following the same (or neighboring) fiber backwards. In Figure 5b the reflection happens at two ends of the fiber and results in a closed horseshoe-like loop that is being transversed back and forth many times. Of course, we included this close-loop tract only as an example as identifying the reflection regions and cutting the fibers at these points instead of reflecting would be a fairly easy task.
Fig. 5.
(a) Several fiber tracts produced by geometrical optics ray tracing of the Fokker-Plank equation using the ESP equilibrium probability distribution shown in Figure 2. (b) Blow up of one of the tracts showing an interesting property of the ray tracing: the tracts reaching the fiber ends can get reflected at the boundary and form a closed cycle repeating itself again and again. (c) All fiber tracts obtained using seeds (d) selected with single threshold from the ESP equilibrium probability distribution. The processing of 512 total seed produced 372 fiber tracts with only two (one red and one green) incorrectly finished at the neighboring ending point. These results correspond to slightly more than 0.5% false positive rate.
To generated fiber tracts we selected seed points (Figure 5d) by thresholding the map of the ESP equilibrium probabilities. Using all 512 selected seed points the algorithm produced 372 total fiber tracts. All but two fiber tracts are topologically equivalent to one of the seven tracts shown in Figure 5a. Two fiber tracts (one red and one green) show the end points switched. These two incorrect tracts give 0.5% false positive error rate. In general simple post processing can remove even those two outliers using, for example, the total fiber tract length or the distinct change in the fiber curvature as a source of discrimination. Also all those fibers can be evaluated using for example Tracktometer [48]. We will surely be using it when/if we are directly involved in developing, tuning, optimizing a full-fledged tractography processing pipeline. However, the main intention or this paper is to show the feasibility of a new tracking paradigm. Our motivation for using the FiberCup data was precisely because it facilitates comparison of our results with previously published results, which we have successfully demonstrated. Further detailed analysis on a phantom that has a rather limited connection to human brain data is ultimately of little importance.
For human brain ESP tractography we collected multi b-shell multi q-angle DWI dataset on the GE MR750 3T scanner at the UCSD Center for FMRI using a multi-band blipped-CAIPI EPI method [49] with a GRAPPA reconstruction [50]. Each data set was collected with both forward and reversed phase encoding polarity in order to perform a ”topup” distortion and eddy current correction [51] using FSL [52]. The dataset contains three shells at b = 1000, 2000 and 3000 s/mm2. Each b-shell uses different number of q-values, with 30 angles for b = 1000 s/mm2, 45 angles for b = 2000 s/mm2, and the largest at 60 angles for b = 3000 s/mm2.
Several slices of three dimensional eigenvector map obtained by the ESP solution are shown in Figure 6. The local samples of transition probabilities are shown by directionally colored ellipsoids. The multi-scale structure of the ESP approach can be used for identifying fiber crossings – it can be seen clearly in many of these samples that different scales show different main fiber direction.
Fig. 6.
Different slices of three dimensional equilibrium probabilities µ(1), or square of the first ESP eigenvector Eqn 14 (shown by grayscale background), obtained using diffusion weighted images of human brain with local samples of different scales of transition probabilities shown by directionally colored ellipsoids.
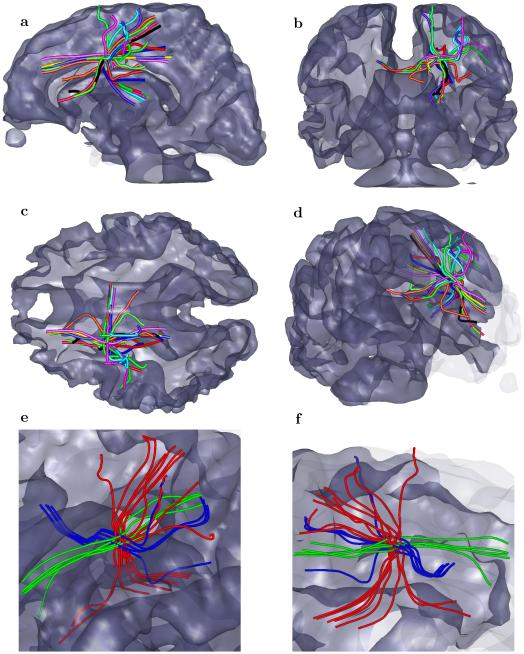
To illustrate the practical ability of geometrical optics–like tracking of fibers though those “difficult” areas of multiple fibers with different orientations we generated fiber tracts for several sets of seed points (Figure 7) located in the areas of corpus callosum and longitudinal fasciculus that are known to have multiple overlaps in both inferior and fronto-occipital regions [53]. The 135 corpus callosum seed points were grouped in blocks of three consecutive voxels coronally and two or three voxels vertically. In the fasciculus region two sets of seed were selected in left and right hemispheres with 30 seeds each again grouped in blocks by three consecutive voxels vertically and five consecutive voxels coronally. The total number of seeds were 195 voxels resulting in 195 distinct fiber tracts.
Fig. 7.
Selected fiber tracts obtained by geometrical optics–like processing of ESP guided tractography, with ESP equilibrium probability distribution shown by grayish transparent background. A subset of seed points has been used to initialize fiber tracts, with 135 seeds located in corpus callosum (arranged in blocks of three consecutive voxels coronally and two or three voxels vertically), and two sets of 30 seeds localized in left and right hemispheres around the inferior fronto-occipital fasciculus areas (also blocked in by three consecutive voxels vertically and five consecutive voxels coronally), giving 195 seeds total. Panels (a)-(d) corresponds to different projections and panes (e) and (f) shows tracts with seeds in corpus callosum and fasciculus respectively. The corpus callosum originating fibers and fibers going through longitudinal fasciculus are crossing in areas occupying multiple voxels and the ESP tractography with geometrical optics–like tracking is able to correctly proceed through those voxels.
All the seeds were selected in mostly in the regions with predominantly single fiber orientation. In the multi–scale ESP guided geometrical optics–like approach, the tracking algorithm is able to follow tracts across voxels that contain a mixture of fibers of different orientations and select the correct path based on the combination of local and global parameters (Figure 7).
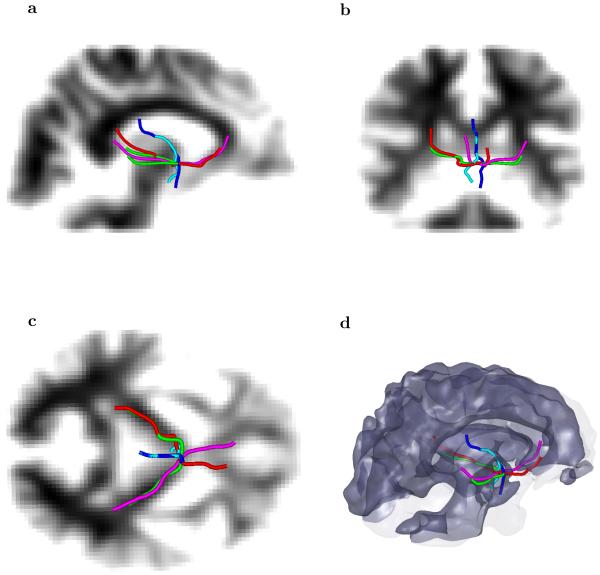
For a more “difficult” starting point we first have chosen several seed voxels in the area around the splenium of the corpus callosum and up to the internal capsule. The five fiber tracts, shown in Figure 8, clearly demonstrate the ability of the algorithm to detect separate fibers crossing through rather small regions at different directions. In this figure, the fibers passing though the chosen location include those from latero– lateral (left to right and right to left), anterior–posterior, and dorsal–ventral. That example shows that the multiple scales used by ESP guided geometrical optics–like approach can help resolve crossing of multiple fibers in a small area of only several voxels extent.
Fig. 8.
Five fiber tracts going through a small region where a mixture of different fiber orientations emphasizes different directions at different scales. The five chosen tracts show coexistence of orientations ranging from a latero–lateral (left to right and right to left), an anterior–posterior, a dorsal–ventral direction, and a combinations of them.
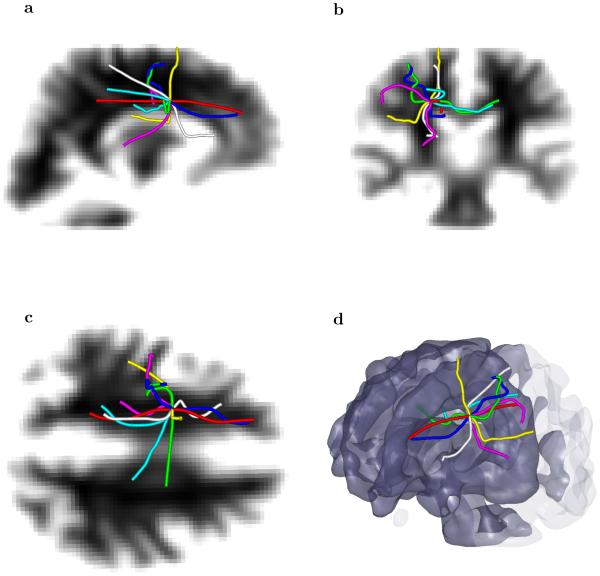
To study behavior of our approach in even more difficult conditions, we selected a single seed voxel that is located into a region where the corticospinal tract crosses the corpus callosum. This is a region that is well known for crossing fiber problems, and appears often in the DTI literature. Even starting with just a single voxel seed in the “difficult” area, the multi-scale multi-modal approach is able to find and distinguish several fibers that go into different regions of brain (Figure 9). For comparison we included in Figure 9 a fiber tract that should be produced by a standard tractography approach with a single scale integration of the principal direction of the diffusion tensor (shown by white/gray tract).
Fig. 9.
Seven fiber tracts with the same single voxel seed located in the area where the corticospinal tract crosses the corpus callosum. The geometrical optics–like approach with different scales parameterized by the vector produces a latero–lateral, an anterior–posterior, a dorsal–ventral (and mixed) tracts that originate in the same voxel. For comparison we included a fiber tact that would be traced by the standard method (shown by white/gray color) with the same voxel as a seed.
Using several seeds in the small vicinity of the single seed voxel used in Figure 9 gives more complicated behavior with a bundle of fibers going in and out of the corpus callosum, a bundle coming to/from the corticospinal tract, a bundle connecting anterior posterior regions, and some bundles going to outer regions of the brain (Figure 10).
Fig. 10.
Several bundles of fiber tracts obtained when seeded by several voxels in the vicinity of a single seed voxel used in the previous Figure 9. Panels (a)-(c) show coronal, sagittal and axial planes, panel (d) shows 3D view and panels (e)-(f) show different projections of zoomed area with fibers grouped in going from/to corpus callosum (blue), coming to/from the corticospinal tract (red), and longitudinal fibers (green).
Finally, we applied our method to one of the diffusion imaging datasets (MGH 1010) available from the Human Connectome Project [54]. This dataset was collected on the customized Siemens 3T Connectom scanner, which is a modified 3T Skyra system (MAGNETOM Skyra Siemens Healthcare), housed at the MGH/HST Athinoula A. Martinos Center for Biomedical Imaging (see [55] for details of the scanner design and implementation). A 64-channel, tight-fitting brain array coil [56] was used for data acquisition. The dataset contains 96 slices of 140x140 matrix at four levels of diffusion sensitizations (b-values b = 1k, 3k, 5k and 10k s/mm2) distributed over 552 total q-vectors.
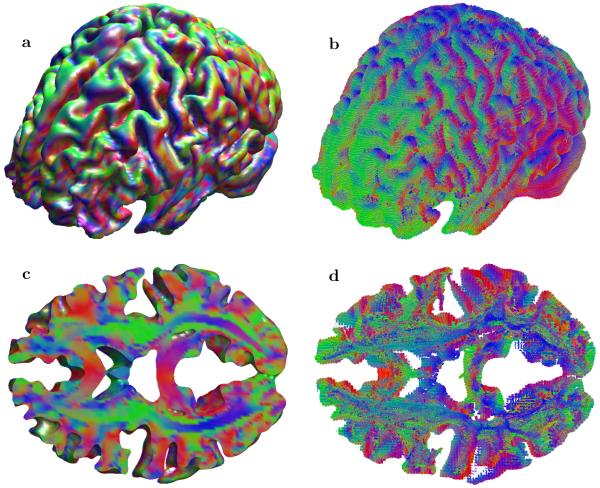
Figure 11 shows both anisotropy maps for the primary directions of the transition probabilities and full brain tractography for the whole volume as well as for a selected set of slices. Fibers cut out through set of slices in panel (d) in general show good agreement with the primary direction of the transition probability (panel (c)), at the same time clearly indicating that many areas with seemingly single fiber direction may contain a mixture of different orientations.
Fig. 11.
Results of full brain ESP tractography obtained using the Human Connectome Project diffusion imaging dataset (MGH 1010). Panel (a) shows anisotropy maps for primary direction of the transition probabilities for the whole volume and panel (b) shows full brain tractography also for the whole volume. Panel (c) and (d) provide detailed views of for a set of slices (46 ≤ z ≤ 51).
V. Discussion and Conclusion
We have developed a novel diffusion estimation and fiber tractography method that is based on simultaneous estimation of global and local parameters of neural tracts from maximum entropy principles and sorting them into a series of entropy spectral pathways (ESP). The method uses local coupling between sub–scale diffusion parameters to compute the structure of the equilibrium probabilities that define the global information entropy field and uses this global entropy to update the local properties of neural fiber tracts.
We have also developed an efficient way to trace individual tracts that utilizes the multi–scale and multi–modal structure of the local diffusion-convection propagation by means of an approach reminiscent of the geometrical optics ray tracing in dispersive media (either elastic or viscoelastic). This geometrical optics–like approach naturally includes multiple scales that allows fiber tracing to continue fibers through voxels with complex local diffusion properties where multiple fiber directions are unable to be adequately resolved.
One of the most important aspects of our method is that it is ”global” in the sense that data from spatially extended brain structures are being used to inform both the local diffusion and generation of tracts. The typical workflow of majority of other global algorithms used in tractography, including algorithms based on the well known shortest-path algorithm on graphs by Dijkstra [57]–[60], represent the brain as a graph, where each voxel is a node, in which they have a local estimation of the diffusion process that they use as a speed function to guide a front evolution evolving from a seed point. Then, the geodesic or shortest-path between this point and any other location in the brain can be easily computed with backtracking. While there might appear to be similarities with our method, we point out that both the theoretical foundations and the numerical implementation for our approach are quite different from these schemes. It is important to realize that our method does not represent the brain as a graph. Rather, only nearest neighbor coupling has been used. However, as we have shown in [34], this is sufficient to produce long-range correlations. The local estimation of the diffusion process is not used as a speed function. Rather, the prior coupling is used to find the global eigenvalues/vectors, rank those information pathways based on a maximum entropy, and spread this global information about pathways to every voxel. This global information we use in every voxel is more than just an analog of a locally inferred speed function – it is more akin to a dispersion of fibers. For each voxel this function includes both angular and radial (scale) distributions obtained as a collective effect of all fibers that cross in a single voxel.
Our tracking process, although it might appear to look like a front evolution, is not. Our approach does not need an explicit front evolution step at all. The eigensystem calculation of the connectivity matrix provides more complete and accurate path information, than is available from the typical front evolution methods, and does more efficiently. Our tracking is performed in 6 dimensional coordinate and momentum space. Not only is the position of each fiber updated on each step, but a momentum equation is used to update the local fiber orientation as well as a rate of orientation change based on a globally constructed distribution/dispersion of fibers. All the current tracking algorithm, including the shortest-path algorithms [58]–[60], only update a position of fiber assuming its orientation defined by static (fixed at each voxel position) speed function.
Although we presented here both the theoretical foundation and a number of practical examples that characterize performance and accuracy of our approach, the main limitation of the method and of the overall study is the lack of a system wide analysis of a role of different parameters that can be updated both during data acquisition and during reconstruction stages on the optimality of diffusion estimates as well as on the overall tractography results.
It is important to reiterate that we have formulated the analysis problem in this paper as one of inference where the goal is to make the most accurate estimates of both the local diffusion and the extended fiber tracts based only upon the available data and any relevant prior information. This is just the logic of probability theory [61] and the theoretical basis for our method is a probabilistic analysis of information flow in a lattice [34]. The key result of that paper is that local coupling information provides significant information about global pathways, which thus forms the important connection between local phenomena (diffusion) and global structures (fiber tracts). Moreover, the dynamics of how local effects inform global structures was shown to be characterized by a Fokker-Planck equation with a potential equal to the entropy [34], a formulation that had previously been put forth in a general theoretical framework [35], [36], but here finds a very practical manifestation, as it facilitates a geometric–optics tractography scheme where the relationship between the local diffusion measurements and the global fiber tract structure is made explicit.
Perhaps the most important result of our analysis is that the connection between the local and the global properties of the diffusion field are mediated by the transition probability, which emerges as a more fundamental quantity than the traditional diffusion PDF. In effect, our approach makes explicit a fact that is often implicitly assumed in diffusion analysis papers but rarely explicitly addressed: There is a fundamental logical flaw in estimating the local diffusion as if it were taking place in independent, isolated voxels, but then using it to generate connections between voxels based on their assumed dependence. Our formulation naturally incorporates the continuum of spatial scales, from local to global, and avoids unnecessary arguments related to the fact that the actual diffusion is occurring on a scale much smaller than the measurement process, and thus far smaller than the scale of the fiber structures, since we are only requiring that our macroscopic predictions from microscopic phenomena are consistent with our data and prior information.
This method has potential significance for a wide range of applications that employ diffusion weighted imaging, including studies of brain connectivity.
ACKNOWLEDGMENTS
LRF and VLG were supported by NSF grants DBI-1143389, DBI-1147260, EF-0850369, PHY-1201238 and NIH grant R01 MH096100. Data used for preparation of Figure 11 were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Vitaly L. Galinsky, Center for Scientific Computation in Imaging, and Electrical and Computer Engineering Department, University of California at San Diego, La Jolla, CA 92093, USA
Lawrence R. Frank, Center for Scientific Computation in Imaging, Center for Functional MRI, University of California at San Diego, and VA San Diego Healthcare System, La Jolla, CA 92093, USA
References
- [1].Mori S, Crain B, Chacko V, van Zijl P. “Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 1999 Feb;45(2):265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- [2].Conturo T, Lori N, Cull T, Akbudak E, Snyder A, Shimony J, McKinstry R, Burton H, Raichle M. “Tracking neuronal fiber pathways in the living human brain. Proc. Natl. Acad. Sci. USA. 1999 Aug;96:10 422–10 427. doi: 10.1073/pnas.96.18.10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Basser P, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. “In vivo fiber tractography using (DT MRI) data. Magn. Reson. Med. 2000;44:625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- [4].Behrens T, Berg H, Jbabdi S, Rushworth M, Woolrich M. “Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? NeuroImage. 2007;34(1):144–155. doi: 10.1016/j.neuroimage.2006.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Jones D. Tractography gone wild: probabilistic fibre tracking using the wild bootstrap with diffusion tensor MRI. Medical Imaging, IEEE Transactions on. 2008;27(9):1268–1274. doi: 10.1109/TMI.2008.922191. [DOI] [PubMed] [Google Scholar]
- [6].Descoteaux M, Deriche R, Knosche T, Anwander A. Deterministic and probabilistic tractography based on complex fibre orientation distributions. Medical Imaging, IEEE Transactions on. 2009;28(2):269–286. doi: 10.1109/TMI.2008.2004424. [DOI] [PubMed] [Google Scholar]
- [7].Ratnarajah N, Simmons A, Hojjatoleslami A. Novel Approach for Improved Tractography and Quantitative Analysis of Probabilistic Fibre Tracking Curves. Medical Image Analysis Journal. 2011 doi: 10.1016/j.media.2011.07.005. [DOI] [PubMed] [Google Scholar]
- [8].Jbabdi S, Woolrich MW, Andersson JLR, Behrens TEJ. A Bayesian framework for global tractography. NeuroImage. 2007 Aug.37:116–129. doi: 10.1016/j.neuroimage.2007.04.039. [DOI] [PubMed] [Google Scholar]
- [9].Aganj I, Lenglet C, Jahanshad N, Yacoub E, Harel N, Thompson P, Sapiro G. A Hough transform global probabilistic approach to multiple-subject diffusion MRI tractography. Medical Image Analysis. 2011 doi: 10.1016/j.media.2011.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Mangin J, Poupon C, Cointepas Y, Riviere D, PapadopoulosOrfanos D, Clark C, Régis J, Bihan DL. A framework based on spin glass models for the inference of anatomical connectivity from diffusionweighted MR data–a technical review. NMR in Biomedicine. 2002;15(78):481–492. doi: 10.1002/nbm.780. [DOI] [PubMed] [Google Scholar]
- [11].Kreher B, Mader I, Kiselev V. Gibbs tracking: a novel approach for the reconstruction of neuronal pathways. Magnetic Resonance in Medicine. 2008;60(4):953–963. doi: 10.1002/mrm.21749. [DOI] [PubMed] [Google Scholar]
- [12].Fillard P, Poupon C, Mangin J. A novel global tractography algorithm based on an adaptive spin glass model. Medical Image Computing and Computer-Assisted Intervention–MICCAI. 2009;2009:927–934. doi: 10.1007/978-3-642-04268-3_114. [DOI] [PubMed] [Google Scholar]
- [13].Reisert M, Mader I, Anastasopoulos C, Weigel M, Schnell S, Kiselev V. Global fiber reconstruction becomes practical. NeuroImage. 2011;54(2):955–962. doi: 10.1016/j.neuroimage.2010.09.016. [DOI] [PubMed] [Google Scholar]
- [14].Basser P, Pierpaoli C. Microstructual and physiological features of tissues elucidat ed by quantitative diffusion tensor MRI. J. Magn. Reson. B. 1996;111:209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- [15].Farquharson S, Tournier JD, Calamante F, Fabinyi G, Schneider-Kolsky M, Jackson GD, Connelly A. White matter fiber tractography: why we need to move beyond DTI. J. Neurosurg. 2013 Jun;118(6):1367–1377. doi: 10.3171/2013.2.JNS121294. [DOI] [PubMed] [Google Scholar]
- [16].Tuch D, Reese T, Wiegell M, Makris N, Belliveau J, Wedeen V. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn. Reson. Med. 2002;48:577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- [17].Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994 Jan;66(1):259–267. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Tuch DS. Q-ball imaging. Magn Reson Med. 2004 Dec;52(6):1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- [19].Frank L. Characterization of anisotropy in high angular resolution diffusion weighted MRI. Magn Reson Med. 2002 Jun;47(6):1083–1099. doi: 10.1002/mrm.10156. [DOI] [PubMed] [Google Scholar]
- [20].Ozarslan E, Mareci T. Generalized diffusion tensor imaging and analytical relationships between diffusion tensor imaging and high angular resolution diffusion imaging. Magn. Reson. Med. 2003;50(5):955–965. doi: 10.1002/mrm.10596. [DOI] [PubMed] [Google Scholar]
- [21].Anderson A. Measurement of fiber orientation distributions using high angular resolution diffusion imaging. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2005;54(5):1194–1206. doi: 10.1002/mrm.20667. [DOI] [PubMed] [Google Scholar]
- [22].Descoteaux M, Angelino E, Fitzgibbons S, Deriche R. Apparent diffusion coefficients from high angular resolution diffusion imaging: Estimation and applications. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine. 2006;56(2):395–410. doi: 10.1002/mrm.20948. [DOI] [PubMed] [Google Scholar]
- [23].Yeh FC, Wedeen VJ, Tseng WY. Generalized q-sampling imaging. IEEE Trans Med Imaging. 2010 Sep;29(9):1626–1635. doi: 10.1109/TMI.2010.2045126. [DOI] [PubMed] [Google Scholar]
- [24].Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weis-skoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005 Dec;54(6):1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- [25].Descoteaux M, Deriche R, Le Bihan D, Mangin JF, Poupon C. Multiple q-shell diffusion propagator imaging. Med Image Anal. 2011 Aug;15(4):603–621. doi: 10.1016/j.media.2010.07.001. [DOI] [PubMed] [Google Scholar]
- [26].Merlet SL, Deriche R. Continuous diffusion signal, EAP and ODF estimation via Compressive Sensing in diffusion MRI. Med Image Anal. 2013 Jul;17(5):556–572. doi: 10.1016/j.media.2013.02.010. [DOI] [PubMed] [Google Scholar]
- [27].Hosseinbor AP, Chung MK, Wu YC, Alexander AL. Bessel Fourier Orientation Reconstruction (BFOR): an analytical diffusion propagator reconstruction for hybrid diffusion imaging and computation of q-space indices. Neuroimage. 2013 Jan;64:650–670. doi: 10.1016/j.neuroimage.2012.08.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].White NS, Leergaard TB, D’Arceuil H, Bjaalie JG, Dale AM. Probing tissue microstructure with restriction spectrum imaging: Histological and theoretical validation. Hum Brain Mapp. 2013 Feb;34(2):327–346. doi: 10.1002/hbm.21454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Cory D, Garroway A. Measurement of translational displacement probabilities by NMR: An indicator of compartmentation. Magn Res Med. 1990;14:435. doi: 10.1002/mrm.1910140303. [DOI] [PubMed] [Google Scholar]
- [30].Callaghan PT. Principles of nuclear magnetic resonance microscopy. Oxford University Press; 1993. [Google Scholar]
- [31].Tefera GB, Zhou Y, Juneja V, Narayana PA. Evaluation of fiber tracking from subsampled q-space data in diffusion spectrum imaging. Magn Reson Imaging. 2013 Jul;31(6):820–826. doi: 10.1016/j.mri.2013.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Vos SB, Viergever MA, Leemans A. Multi-fiber tractography visualizations for diffusion MRI data. PLoS ONE. 2013;8(11):e81453. doi: 10.1371/journal.pone.0081453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Jbabdi S, Sotiropoulos SN, Savio AM, Grana M, Behrens TE. Model-based analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn Reson Med. 2012 Dec;68(6):1846–1855. doi: 10.1002/mrm.24204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Frank LR, Galinsky VL. Information pathways in a disordered lattice. Phys. Rev. E. 2014 Mar;89:032142. doi: 10.1103/PhysRevE.89.032142. [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevE.89.032142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Grabert H, Green M. Fluctuations and nonlinear irreversible processes. Physical Review A. 1979 Apr.19(4):1747–1756. [Google Scholar]
- [36].Jaynes E. Macroscopic prediction. In: Haken H, editor. Complex Systems - Operational Approaches in Neurobioloy, Physics, and Computers. Springer-Verlag; Berlin: 1985. pp. 254–269. [Google Scholar]
- [37].Galinsky VL, Frank LR. Automated Segmentation and Shape Characterization of Volumetric Data. NeuroImage. 2014;92(0):156–168. doi: 10.1016/j.neuroimage.2014.01.053. [Online]. Available: http://www.sciencedirect.com/ science/article/pii/S1053811914000834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Lebedev N. Special functions and their applications. In: Silverman Richard A., editor. Unabridged and corrected republication. New York; Dover Publications, Inc.: 1972. Revised edition, translated from the Russian and edited by. [Google Scholar]
- [39].Kravtsov YA, Orlov YI. Geometrical Optics of Inhomogeneous Media. Springer-Verlag; Berlin: 1990. [Google Scholar]
- [40].Ozarslan E, Shepherd TM, Koay CG, Blackband SJ, Basser PJ. Temporal scaling characteristics of diffusion as a new MRI contrast: findings in rat hippocampus. Neuroimage. 2012 Apr;60(2):1380–1393. doi: 10.1016/j.neuroimage.2012.01.105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Ozarslan E, Shepherd TM, Vemuri BC, Blackband SJ, Mareci TH. Resolution of complex tissue microarchitecture using the diffusion orientation transform (DOT) Neuroimage. 2006 Jul;31(3):1086–1103. doi: 10.1016/j.neuroimage.2006.01.024. [DOI] [PubMed] [Google Scholar]
- [42].Burda Z, Duda J, Luck J, Waclaw B. Localization of the maximal entropy random walk. Phys. Rev. Lett. 2009;102(16):160602. doi: 10.1103/PhysRevLett.102.160602. [DOI] [PubMed] [Google Scholar]
- [43].Burda Z, Duda J, Luck J, Waclaw B. The various facets of random walk entropy. 2010 Arxiv preprint arXiv:1004.3667. [Google Scholar]
- [44].Shannon C. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:379423–623656. [Google Scholar]
- [45].McMillan B. The basic theorems of information theory. Ann. Math. Stat. 1953;24(2):196–219. [Google Scholar]
- [46].Lax PD. Asymptotic solutions of oscillatory initial value problems. Duke Mathematical Journal. 1957;2412(4):627–646. [Online]. Available: http://dx.doi.org/10.1215/S0012-7094-57-02471-7. [Google Scholar]
- [47].Fillard P, Descoteaux M, Goh A, Gouttard S, Jeurissen B, Malcolm J, Ramirez-Manzanares A, Reisert M, Sakaie K, Tensaouti F, Yo T, Mangin JF, Poupon C. Quantitative evaluation of 10 tractography algorithms on a realistic diffusion MR phantom. Neuroimage. 2011 May;56(1):220–234. doi: 10.1016/j.neuroimage.2011.01.032. [DOI] [PubMed] [Google Scholar]
- [48].Côté M-A, Girard G, Boré A, Garyfallidis E, Houde J-C, Descoteaux M. Tractometer: Towards validation of tractography pipelines. Medical Image Analysis. 2013;17(7):844–857. doi: 10.1016/j.media.2013.03.009. [DOI] [PubMed] [Google Scholar]
- [49].Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Res Med. 2011 Aug.67(5):1210–1224. doi: 10.1002/mrm.23097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA) Magn Res Med. 2002 Jun.47(6):1202–1210. doi: 10.1002/mrm.10171. [DOI] [PubMed] [Google Scholar]
- [51].Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage. 2003 Oct.20(2):870–888. doi: 10.1016/S1053-8119(03)00336-7. [DOI] [PubMed] [Google Scholar]
- [52].Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, Niazy RK, Saunders J, Vickers J, Zhang Y, De Stefano N, Brady JM, Matthews PM. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004 Jan.23:S208–S219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- [53].Catani M, Thiebaut de Schotten M. A diffusion tensor imaging tractography atlas for virtual in vivo dissections. Cortex. 2008 Sep;44(8):1105–1132. doi: 10.1016/j.cortex.2008.05.004. [DOI] [PubMed] [Google Scholar]
- [54].Sotiropoulos SN, Moeller S, Jbabdi S, Xu J, Andersson JL, Auerbach EJ, Yacoub E, Feinberg D, Setsompop K, Wald LL, Behrens TEJ, Ugurbil K, Lenglet C. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion mri: Reducing the noise floor using sense. Magnetic Resonance in Medicine. 2013;70(6):1682–1689. doi: 10.1002/mrm.24623. [Online]. Available: http://dx.doi.org/10.1002/mrm.24623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab J, Keil B, Tisdall M, Hoecht P, Dietz P, Cauley S, Tountcheva V, Matschl V, Lenz V, Heberlein K, Potthast A, Thein H, Horn JV, Toga A, Schmitt F, Lehne D, Rosen B, Wedeen V, Wald L. Pushing the limits of in vivo diffusion {MRI} for the human connectome project. NeuroImage. 2013;80(0):220–233. doi: 10.1016/j.neuroimage.2013.05.078. mapping the Connectome. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1053811913005788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Keil B, Blau JN, Biber S, Hoecht P, Tountcheva V, Setsompop K, Triantafyllou C, Wald LL. A 64-channel 3t array coil for accelerated brain mri. Magnetic Resonance in Medicine. 2013;70(1):248–258. doi: 10.1002/mrm.24427. [Online]. Available: http://dx.doi.org/10.1002/mrm.24427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Dijkstra E. A note on two problems in connexion with graphs. Numerische Mathematik. 1959;1(1):269–271. [Online]. Available: http://dx.doi.org/10.1007/BF01386390. [Google Scholar]
- [58].Parker GJ, Wheeler-Kingshott CA, Barker GJ. Estimating distributed anatomical connectivity using fast marching methods and diffusion tensor imaging. IEEE Trans Med Imaging. 2002 May;21(5):505–512. doi: 10.1109/TMI.2002.1009386. [DOI] [PubMed] [Google Scholar]
- [59].Jbabdi S, Bellec P, Toro R, Daunizeau J, Pelegrini-Issac M, Benali H. Accurate anisotropic fast marching for diffusion-based geodesic tractography. Int J Biomed Imaging. 2008;2008:320195. doi: 10.1155/2008/320195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Zalesky A. DT-MRI fiber tracking: a shortest paths approach. IEEE Trans Med Imaging. 2008 Oct;27(10):1458–1471. doi: 10.1109/TMI.2008.923644. [DOI] [PubMed] [Google Scholar]
- [61].Jaynes E. Probability Theory: The Logic of Science. Cambridge University Press; New York: 2003. [Google Scholar]