Bayesian Modeling and Prediction of Accrual in Multi-Regional Clinical Trials

Abstract

In multi-regional trials, the underlying overall and region-specific accrual rates often do not hold constant over time and different regions could have different start-up times, which combined with initial jump in accrual within each region often leads to a discontinuous overall accrual rate, and these issues associated with multi-regional trials have not been adequately investigated. In this paper, we clarify the implication of the multi-regional nature on modeling and prediction of accrual in clinical trials and investigate a Bayesian approach for accrual modeling and prediction, which models region-specific accrual using a nonhomogeneous Poisson process (NHPP) and allows the underlying Poisson rate in each region to vary over time. The proposed approach can accommodate staggered start-up times and different initial accrual rates across regions/centers. Our numerical studies show that the proposed method improves accuracy and precision of accrual prediction compared to existing methods including the NHPP model that does not model region-specific accrual.

1 Introduction

With advances in medical research, fairly effective treatments have been developed and have become the standard of care for many diseases in recent years, including some life-threatening conditions. As a result, the clinical research on new investigational treatments generally needs to aim at demonstrating a meaningful improvement in the therapeutic effect over an active control treatment, rather than a placebo. As the bar for drug development rises, it presents a challenge to the industry in that the clinically meaningful improvement in therapeutic efficacy of a promising investigational treatment over an existing treatment is likely to be moderate in scale. This usually translates into substantial sample sizes in phase III clinical trials, noting that, unlike phase I/II trials^1-3, adequate power is essential for phase III trials. In practice, these phase III trials easily require thousands of patients, if not more. Consequently, it is hardly practical or even possible to enroll all patients from one region within an acceptable timeframe that is suitable for the drug development strategy.

In addition, differences in regulatory requirements exist between different countries, in spite of regular as well as ad hoc conversations between health agencies across different countries (such as the Food and Drug Administration in the United States, the European Medicines Agency, the Japanese Ministry of Health and Welfare, and the States Food and Drug Administration in China). Among many factors that contribute to the differences, an important one is the concern on differential treatment effects across different racial designations. When such concern is warranted, it may become a mandate to recruit patients from different regions or racial groups. Generally speaking, few sponsors are adequately resourced to conduct a separate registrational trial for each region, nor is it an efficient or ethical way of drug development; usually, one large trial with multiple participating regions that accommodates most of the regulatory requirements is employed.

Multi-regional trials require substantial investment of resources and present some unique challenges, which have drawn considerable interest in recent years; most notably, a recent special issue in Pharmaceutical Statistics⁴ explored some of these challenges. In practice, slower than expected accrual is common in clinical trials⁵, which can be costly to the industry, in particular, in multi-regional trials; as a result, proper monitoring and prediction of patient accrual is very important in multi-regional trials. Although patient enrollment by region is routinely tracked by the operational team, its inherent randomness is rarely accounted for. A proper monotoring/prediction tool of region-specific accrual may provide informative and reliable guidance on the quantity of drug supply, distribution of laboratory kits, and allocation of clinical staff, etc. In addition, the regions usually vary not only in their enrollment capacity but also in their accrual pattern over time. Moreover, the regions are subject to their respective Institutional Review Board (IRB) and regulatory agency for the approval of the protocol, which may cause delay in the kick-off of enrollment in the respective region and hence additional complexity when monitoring the overall recruitment of the trial.

Researchers have investigated modeling patient accrual in clinical trials with a goal of better prediction of future accrual and better allocation of resources; Barnard et al.⁶ provided a nice review of models for predicting accrual in multicenter clinical trials with a focus on the utility of the existing methods in practice. Senn⁷ investigated modeling the accrual process in multicenter trials as a homogeneous Poisson process (HPP) with a fixed accrual rate across all centers. Similarly, Gajewski⁸ developed a Bayesian model for accrual assuming the waiting time between two consecutive recruits are independently and identically distributed (i.i.d.) exponential random variables, which is equivalent to an HPP model. Anisimov and Fedorov⁹ investigated a Gamma-Poisson model for accrual in multicenter trials, and Mijoule et al.¹⁰ extended this model to a Pareto-Poisson model and discussed a sensitivity analysis; in both papers, the enrollment at each center is assumed to follow an HPP. However, accrual in real trials often does not follow an HPP^11,12. To address this issue, Tang et al.¹² proposed an accrual model for multicenter trials in which the overall accrual rate was modeled as piecewise linear or constant with pre-specified or estimated change-points; their model for the overall accrual rate was specifically tailored to and worked well for their data example and, though, is still rather restrictive for general use. Alternatively, Zhang and Long¹¹ proposed to use the non-homogeneous Poisson process (NHPP) to model patient accrual, where a smooth nonparametric function was adopted for the underlying true accrual rate; for brevity, we refer to this NHPP model as NHPPS throughout. With the flexibility of a nonparametric fit, the NHPPS model implicitly accommodates different region start-up times and non-constant accrual pattern within each region. It was shown¹¹ that the NHPP approach outperformed the HPP approach substantially when the assumption underlying HPP was not met; their subsequent investigation also revealed that the performance of these two approaches was comparable when the underlying accrual rate was constant over time. Both the HPP model and the model proposed by Tang et al.¹² can be considered a special case of this NHPPS model.

When used in multi-regional trials, the NHPPS approach¹¹, however, has some limitations. It does not take advantage of the region-specific accrual information. Furthermore, when a region first clears the IRB/regulatory hurdles and is ready for recruitment, this usually brings a “boost” to the overall enrollment, i.e., a sudden increase in the overall accrual rate; this sudden increase then translates into a discontinuity in the underlying overall accrual rate, noting that the NHPPS approach assumes that the overall accrual rate is continuous and smooth over time and hence cannot accommodate discontinuity. In other words, when the staggered region start-up times are combined with initial jump in accrual within each region, the overall accrual rate is not only non-constant but also discontinuous, whereas the accrual rate within each region can be still considered continuous though often not constant over time. In such settings, statistical methods based on constant accrual rates are inadequate; in addition, while a smooth nonparametric function may be adequate for modeling the accrual rate within each region, it is often not adequate for modeling the overall accrual rate.

In this article, we clarify the impact and implication of the multi-regional nature on monitoring and prediction of patient accrual in clinical trials, investigate flexible modeling of patient accrual in multi-regional trials, and contrast the proposed approach with the NHPPS approach. The proposed approach borrows strength of the accrual profiles across regions and accommodates staggered and different regional start-up times and initial jump in accrual within each region, overcoming limitations of existing methods including those noted by Barnard et al.⁶. In this approach, the accrual rate within each region is assumed to be continuous over time, but no continuity is assumed for the overall accrual rate over time, a more realistic assumption compared to existing methods. In addition, the proposed approach will provide region-specific prediction of accrual, which is not available from the NHPPS approach, and improve accuracy and precision of the prediction of overall accrual. Consequently, the proposed method will allow for better resource allocation, e.g., drug supply, distribution of laboratory kits, and regional staff assignment.

We note that the term “region” in multi-regional clinical trials is used loosely throughout this article; it can represent a geographic region, a collection of sites that are believed to share some commonalities in their enrollment profiles. In particular, our proposed approach can be readily applied to multi-center clinical trials with each center considered as a “region”. The remainder of the article is organized as follows. In Section 2, we describe the proposed approach, which models multi-regional trial enrollment with a region-specific non-homogeneous Poisson process. In Section 3, we conduct simulation studies to investigate the performance of the proposed approach and compare it with the NHPPS approach. In Section 4, we illustrate the proposed approach using a real clinical trial for colon cancer. We conclude this manuscript with some discussion remarks in Section 5.

2 Methodology

Suppose a multi-regional clinical trial plans to enroll a total of n patients in J participating regions. Let j (1 ≤ j ≤ J) index the regions; without loss of generality, let t (t = 1, 2, ⋯) index the time in days with the date of the study start as the reference point (i.e., t = 1). We write the number of patients enrolled in region j on day t as N_jt, which is subject to the randomness of the enrollment process; by definition, N_jt is a random variable. We denote its realization in the current trial, or the observed value, by n_jt. Suppose an interim look of accrual occurs at time T, we write the observed enrollment from all J regions by that time as n = {n_jt : j = 1, ⋯, J, t = 1, ⋯, T}. The total number of patients enrolled across all regions on day t can be written as a random variable $N_{.t}={\sum }_{j=1}^J{N}_{\mathit{jt}}$, with its realization $n_{.t}={\sum }_{j=1}^J{n}_{\mathit{jt}}$ (n_jt = 0 for regions that have not started enrollment by time t). We are interested in predicting the time when at least a total of n patients are enrolled across all regions, namely, $\tau ={\mathrm{arg\; min}}_r\left({\sum }_{t=1}^r{n}_{.t}\ge n\right)$.

Since the patients are independent individuals, the number of patients enrolled each day in any given region can be modeled as a random variable following a Poisson distribution. We denote the underlying Poisson rate of region j at time t by λ_jt, and write the vector of the underlying accrual rate for all regions by time T as λ = {λ_jt : j = 1, ⋯, J, t = 1 ⋯, T}. The distribution of the observed data then follows, i.e.,

$$\mathrm{Pr}\left(\mathrm{N}=\mathbf{n}\mid \mathit{\lambda }\right)=\prod _{j=1}^J\prod _{t=1}^T\frac{e^{-{\lambda }_{\mathit{jt}}}{\lambda }_{\mathit{jt}}^{n_{\mathit{jt}}}}{n_{\mathit{jt}}!}.$$ (1)

2.1 Modeling Region-Specific Accrual Rate Using Nonparametric Method

To model region-specific accrual, we assume that the underlying accrual rate within each region is continuous over time, or close to continuous, which can be approximated with a cubic B-spline¹³. We define the B-spline basis at time t as ϕ(t) = (ϕ₁(t), ⋯, ϕ_q(t))^T. Note that the dimension of the B-spline (i.e., the number of basis functions), q, is determined by the number of knots, p, i.e., q = p + 4. We denote the B-spline coefficients for region j by β_j and write the coefficients for all regions as β = (β₁, ⋯, β_J)^T. It follows that the true accrual rate from region j at time t is ${\lambda }_{\mathit{jt}}={\mathit{\beta }}_j^T\mathit{\varphi }\left(t\right)$.

In real life multi-regional trials, it is rare for enrollment to initialize in all regions at the same time. The kick-off of the enrollment usually depends on the regional IRB/regulatory schedules and processes. As a consequence, region start-up times usually stagger. It is not uncommon that some regions may lag behind for months, or even longer, in the trial initialization activities compared to other regions. To address this, we introduce an offset time for each region, i.e., $t_j^0$ for region j, which represents the time when the specific region (j) starts enrollment (relative to the study start) and is fixed based on the observed data. This conceptually divides the underlying accrual rate of region j into two periods, one before $t_j^0$ and the other one afterwards. Clearly, patients can only be enrolled into the study during the latter period, i.e., $t\ge t_j^0$. The underlying accrual rate of region j is then expressed as

$${\lambda }_{\mathit{jt}}={\mathit{\beta }}_j^T\mathit{\varphi }({(t-t_j^0)}_{+}),$$ (2)

where t₊ = t when t ≥ 0 and t₊ = 0 when t < 0. We note that the proposed model encompasses the NHPPS model as a special case when J = 1. The comparison of the two models will be elaborated in Section 2.4.

We assign a common prior distribution to govern the region-specific B-spline coefficients, β_j. More specifically, we assume β_j ~ MVN_q(ν, Γ), for all j = 1, ⋯, J, that is,

$$f({\mathit{\beta }}_j\mid \mathit{\nu },\mathbf{\Gamma })\propto {\left|\mathbf{\Gamma }\right|}^{-1/2}\exp \left\{-.5{({\mathit{\beta }}_j-\mathit{\nu })}^T{\mathbf{\Gamma }}^{-1}({\mathit{\beta }}_j-\mathit{\nu })\right\},$$

where ν and Γ are pre-specified values. It follows that

$$f(\mathit{\beta }\mid \mathit{\nu },\mathbf{\Gamma })=\prod _{j=1}^{J}f({\mathit{\beta }}_j\mid \mathit{\nu },\mathbf{\Gamma })\propto {|\mathbf{\Gamma }|}^{-J/2}\exp \left\{-.5\sum _{j=1}^J{({\mathit{\beta }}_j-\mathit{\nu })}^T{\mathbf{\Gamma }}^{-1}({\mathit{\beta }}_j-\mathit{\nu })\right\}.$$ (3)

2.2 Specification of ν and Γ

We now discuss how to determine the values of ν and Γ in the prior distribution of β_j. In a general setting of Bayesian analysis, when there is no or limited prior knowledge on model parameters, a noninformative prior distribution may be preferred. However, this is usually not the case with accrual modeling. At the design stage, some information regarding the regional recruitment capacity should exist, for instance based on the recruitment history from earlier trials for a similar indication, from the investigators’ judgement, or a combination of the two. Those can then serve as a reasonable basis for the values of ν and Γ. Additionally, sensitivity analyses may be conducted to evaluate the choice of those parameter values.

Following Zhang and Long¹¹, we use A_max to denote the anticipated maximum accrual rate across all regions. Assuming regions of equal enrollment capacity a priori, this suggests a maximum accrual rate of A_avg = A_max/J from each region. We thereby let ν = (A_avg, ⋯, A_avg)^T. Next, we introduce a coefficient of variation (cv), ρ (0 ≤ ρ ≤ 1), to quantify the variability across the regions in their deviation from the average accrual rate. That is, Γ = diag(ρ²ν²), with larger value of ρ indicating larger variability in the enrollment profiles across the regions. On an empirical note, many multi-regional trials consist of a few high-enrollers (i.e., regions that each contribute a large number of patients) and many poor-enrollers (i.e., regions that each contribute a small number of patients). If this is expected to be the case, it is desirable to use a relatively large value of ρ or pool multiple poor-enrollers to form a more robust entity.

2.3 Estimation and Prediction

Given Equations (1), (2), and (3), the joint distribution of the model parameters and the data is

$$\begin{array}{lll}f(\mathit{\beta },\mathbf{n}\mid \mathit{\nu },\mathbf{\Gamma })& \propto & \exp \left\{-.5\sum _{j=1}^J{({\mathit{\beta }}_j-\mathit{\nu })}^T\mathbf{\Gamma }({\mathit{\beta }}_j-\mathit{\nu })-\sum _{t=1}^T\sum _{j=1}^J{\mathit{\beta }}_j^T\mathit{\varphi }({(t-t_j^0)}_{+})\right\}\\ & & \times {\prod _{t=1}^T\prod _{j=1}^J\left[{\mathit{\beta }}_j^T\mathit{\varphi }({(t-t_j^0)}_{+})\right]}^{n_{\mathit{jt}}}.\end{array}$$

The value of β_j for each region can then be updated from the following conditional posterior distribution using the Adaptive Rejection Metropolis Sampling algorithm implemented in the arms function in the R package HI¹⁴,

$$f({\mathit{\beta }}_j\mid ·)\propto \exp \left\{-.5{({\mathit{\beta }}_j-\mathit{\nu })}^T{\mathbf{\Gamma }}^{-1}({\mathit{\beta }}_j-\mathit{\nu })-\sum _{t=1}^T{\mathit{\beta }}_j^T\mathit{\varphi }({(t-t_j^0)}_{+})\right\}{\prod _{t=1}^T\left[{\mathit{\beta }}_j^T\mathit{\varphi }({(t-t_j^0)}_{+})\right]}^{n_{\mathit{jt}}},$$

where f(β_j ∣ ·) denotes the conditional posterior distribution of β_j given all the other parameters and the observed enrollment by time T.

We are interested in the posterior predictive distribution of τ, the time when the enrollment target n is reached, f(τ ∣ n), which follows from the posterior predictive distribution of the future region-specific enrollment, f(ñ ∣ n) where ñ = {ñ_jt, J = 1 ⋯, J, t > T}. By definition, f(ñ | n) = ∫ f(ñ | λ̃)f(λ̃ | n)dλ̃. The future accrual can then be generated from n̄_jt ~ Poisson(λ̃_jt) for t > T. We write λ̃ = {λ̃_jt, j = 1, ⋯, J, t > T} as the future region-specific accrual rate. It is known that spline models can be unstable when used to make extrapolation, i.e., λ̃_jt for t > T. Therefore, we propose to set λ̃_jt = λ_jT for t > T, where λ_jT comes from the posterior distribution of f(λ | n), i.e., assuming the underlying accrual rate within each region remains constant beyond the day of the interim look, T. This approach is generally conservative, i.e., it tends to underestimate the future accrual rate, as the patient enrollment within a region usually increases before reaching a plateau (i.e., the maximum enrollment capacity), and consequently this approach tends to overestimate the time to reach the overall enrollment goal. Compared to a naive approach of projecting the observed accrual at time T as the future accrual rate, i.e., n̄_jt = n_jT for all j and t > T, the proposed approach properly models the randomness in the observed daily enrollment and avoids projecting random highs or lows as the future accrual rate for t > T.

We comment that, in the above, we illustrate as an example how to make prediction for τ using the proposed model. If quantities other than τ are of interest, such as the number of subjects enrolled by a given time in the future, they can be derived from the posterior predictive distribution of f(λ̃ | n) following the similar lines. Furthermore, as we noted in Section 2.2, sensitivity analyses can be performed based on different prior assumptions on the maximum accrual capacity, A_max, and/or the variability across regions, ρ.

2.4 Comparison with the NHPPS Model

We compare the proposed model (denoted by NHPPM) with the original NHPP model¹¹ that does not model individual accrual rate within each region (denoted by NHPPS). Following the notation in Section 2, it can be readily shown from the properties of Poisson distributions that the overall enrollment on day t, N_.t, also follows a Poisson distribution, i.e., N_.t ~ Poisson(λ_.t) with ${\lambda }_{.t}={\sum }_{j=1}^J{\lambda }_{\mathit{jt}}$, where λ_jt’s are defined in Equation (2). It follows that {N_.t, t = 1, 2,⋯} can be modeled using a NHPP with a time-dependent accrual rate, λ_.t. Again, we emphasize that the NHPPS model has some limitations in the case of multi-regional trials. Specifically, if there is delay in the enrollment initiation (namely, $t_j^0$) in some regions, then the overall accrual rate across all regions, λ_.t, may not be smooth; if, in addition, the accrual rate at the enrollment initiation (namely, $t_{j{t}_j^0}$) is greater than 0, then λ_.t is not even continuous. As a j result, a key assumption underlying the NHPPS model, namely, that the overall accrual rate λ_.t is smooth and can be modeled using splines, may not hold in multi-regional clinical trials. While one could still use the NHPPS model, the performance may suffer as a result of these complications. On the other hand, the region-specific accrual rate in the current model, λ_jt, is assumed to be continuous over time within each region, but the proposed model does not require continuity in the overall accrual rate, λ_.t; hence, it allows for extra flexibility compared to the NHPPS approach. The comparisons between these two types of models will be further evaluated in our simulation studies.

3 Simulation Studies

As noted in Introduction, it has been shown^11,12 that accrual in real trials often does not follow an HPP, in particular in the initial and final stages¹², in which case an NHPP model outperforms an HPP model. In addition, the model proposed by Tang et al.¹² can be considered as a special case of the NHPPS model¹¹. As a result, we first focus on the comparisons of the proposed method (NHPPM) and the NHPPS model¹¹ in our simulations.

Suppose that we are interested in a multi-regional trial with a targeted sample size of 3000 and a targeted maximum daily accrual of 12 patients across all regions, i.e., n = 3000 and A_max = 12. The true accrual rate over time within each region follows the shape of the cumulative distribution function (c.d.f.) of a Gamma random variable. This choice of the true accrual function over time is flexible with five parameters for each region j, including two parameters of the Gamma c.d.f. (a_j > 0 and b_j > 0), two parameters to scale the c.d.f. (c_j > 0 and 0 ≤ d_j ≤ 1), and one parameter to denote the region start-up time ( $t_j^0\ge 0$), i.e.,

$${\lambda }_{\mathit{jt}}=d_j{c}_j+(1-d_j)c_j\frac{b_j^{a_j}{\left[{(t-t_j^0)}_{+}\right]}^{a_j-1}\exp \left[-b_j{(t-t_j^0)}_{+}\right]}{\mathrm{\Gamma }(a_j)},\mathrm{for}t=1,2,\dots ,$$

where t₊ is defined as in Section 2.1. In other words, c_j is the maximum true accrual capacity of region j and d_j represents the ratio of the accrual rate at the start of the enrollment relative to the maximum enrollment capacity. Within each region, a_j, b_j, and c_j are drawn from the following distributions, a_j ~ Unif(0.04, 0.12), b_j ~ Unif(2, 6), and c_j ~ Unif(8/J, 16/J). These parameters allow for a considerable heterogeneity in the simulated true accrual rate across the regions. When all J regions have reached the maximum capacity (i.e., the respective c_j), the overall accrual capacity is in the neighborhood of A_max = 12. d_j is set to either 0 (i.e., the underlying overall accrual rate (λ_.t) is continuous over time throughout) or 0.5 (i.e., there is discontinuity in the underlying overall accrual rate whenever a region first starts enrollment). We conducted three sets of simulations. In the first set of simulations, the regions have different, staggered start-up times. Without loss of generality, we set the start-up time of one region as the study start, or Day 1 ( $t_{j\prime }^0=1$ for region j′) and drew the start-up times for the rest regions from $t_j^0~\mathrm{Unif}\left(1,150\right)$ for j ≠ j′. In the second set of simulations, all regions start accrual at the same time, i.e., $t_j^0=1$ for all j. In the first two settings of simulations, we conducted two interim analyses of the accrual, one at 40% of the total targeted enrollment and the other one at 70%. In the third set of simulations, start-up times are drawn from two uniform distributions in two intervals: the first interval is (0.5, 100.5) and the second interval is (150.5,250.5), (250.5,350.5), or (350.5,450.5), corresponding to interval settings 1-3, respectively; the time for the interim look is fixed at 470 days. This setting mimics situations where some centers start accrual right before the interim look time, likely presenting challenges to the proposed method. Settings with J = 2, 5, or 30 regions are included in the first two sets of simulations and settings with J = 20 or 50 regions are included in the third set of simulations. Figure 1 present representative true accrual rates used to generate observed accrual data in all three settings.

Figure 1.

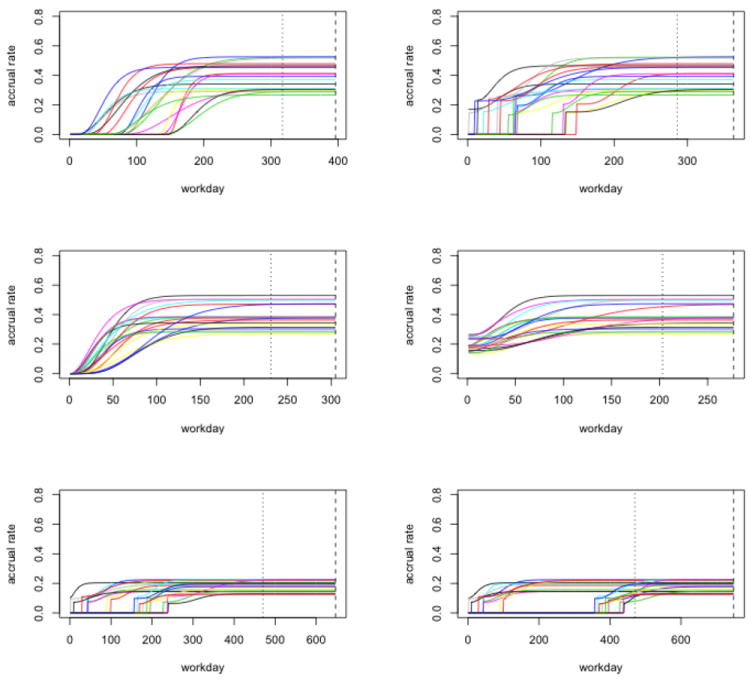
Representative true accrual rates used to generate observed accrual data in the simulation studies. The dotted vertical line represents the interim look and the dashed vertical line represents the end of enrollment. The first row is for the set of simulations in which participating regions have different start-up times, with the left side for d_j = 0 and the right side for d_j = 0.5. The second row is for the second set of simulations in which all participating regions initialize accrual at the same time, with the left side for d_j = 0 and the right side for d_j = 0.5. The third row is for the third set of simulations (d_j = 0.5), with the left side for interval setting 1 and the right side for interval setting 3. In addition, ρ = 0.3 and pct. = 70% for all.

We denote the observed time to reach a total of n patients in the simulated dataset by τ_true. We set the prior parameters at ν = (A_max/J, ⋯, A_max/J)^T and ρ = 0.1 or ρ = 0.3. Both the proposed model (NHPPM) and the NHPPS model were fitted using a cubic B-spline with three equally spaced internal knots, i.e., T/4, T/2, and 3T/4. For each simulated dataset, we ran 5000 iterations for both models after discarding 1000 iterations of burn-in. We present the median of the posterior draws of τ as the predicted time of full accrual (sub-sampled to every fifth draw for a total of 1000 posterior draws), T_exp. The posterior credible interval of τ is then computed as the 2.5^th and 97.5^th percentile of the posterior draws of τ within each dataset, denoted by T_L and T_U. We denote the width of the 95% posterior credible interval (CI) by w = T_U − T_L.

We ran a total of 1000 simulated trials under each setting and compared the proposed NHPPM approach with the NHPPS approach¹¹ using the following summary statistics: root mean squared prediction errors, calculated as rMSPE = {E(T_exp − τ_true)²}^1/2, mean coverage rate of the 95% posterior CI, calculated as CR = E(I(T_L ≤ τ_true ≤ T_U)), where I(A) is the index function with value 1 when A is true. In addition, we present the mean width of the posterior CI of each method across the 1000 simulated datasets, namely w, as well as the percentage of simulated trials in which NHPPM produces tighter posterior CI than NHPPS.

Table 1 presents the results for NHPPS and NHPP when the initiation of accrual is staggered among regions. We first focus on the settings where there are two regions (J = 2). In all cases, the proposed approach (NHPPM) leads to smaller rMSPE, e.g., rMSPE₂ = 7.72 for the proposed method when d_j = 0 and ρ = 0.1 at the first interim look, compared to rMSPE₁ = 8.71 for NHPPS. In addition, the proposed method produces tighter posterior CIs, on average, than the NHPPS method, e.g., w̄₂ = 29.15 compared to w̄₁ = 49.44 when d_j = 0 and ρ = 0.1 at the first interim look. The proposed method almost always yields tighter CI, i.e., Pr(w₁ > w₂) = 1.00, under the same d_j = 0 and ρ = 0.1 at both the first and the second looks. At the same time, the proposed method provides comparable, if not better, CR as the NHPPS method despite its tighter posterior CIs, e.g., 98.9% versus 99.3% at the second look when dj = 0 and ρ = 0.1. When a more diffused prior distribution is utilized, i.e., ρ = 0.3 instead of ρ = 0.1, the results from both methods become more variable with higher rMSPE and w̄; nevertheless, the impact on the proposed method is more modest compared to the NHPPS method. For example, the rMSPE of the NHPPS method increases from 8.71 to 17.97, which is more than doubled, when ρ increases from 0.1 to 0.3 with d_j = 0 at the first look, compared to a moderate increase from 7.72 to 11.69 with the proposed method. We also note that the performance of both methods improves as information accumulates for the prediction, i.e., from the first look with 40% observed enrollment to the second one with 70%. The performance of both methods is generally similar when d_j = 0.5 compared to the respective ones under d_j = 0.

Table 1.

Comparison of root mean squared prediction errors (rMSPE), mean coverage rates (CR), and mean width of the 95% posterior CI (w̄) of the proposed method (NHPPM) and the original NHPP method (NHPPS), as well as the probability of the proposed method having tighter 95% CI than NHPPS (Prob.), i.e., Pr(w₁ > w₂), based on 1000 simulated trials with J = 2, 5 or 30 regions, when participating regions have different start-up times.

Settings				Summary Measures
dj	ρ	pct.	Method	rMSPE	CR	w	Prob.
			NHPPS	8.71	0.99	49.44
		0.4	NHPPM, J=2	7.72	0.94	29.15	1.00
			NHPPM, J=5	5.02	0.98	22.27	1.00
	0.1		NHPPM, J=30	3.84	0.97	15.73	1.00
			NHPPS	4.74	0.99	23.68
		0.7	NHPPM, J=2	3.28	0.99	15.54	1.00
			NHPPM, J=5	2.78	0.98	12.68	1.00
0			NHPPM, J=30	2.58	0.97	10.44	1.00
			NHPPS	17.97	0.96	74.88
		0.4	NHPPM, J=2	11.69	0.96	49.91	0.99
			NHPPM, J=5	9.41	0.96	38.24	1.00
	0.3		NHPPM, J=30	5.55	0.99	23.70	1.00
			NHPPS	8.12	0.95	32.34
		0.7	NHPPM, J=2	5.27	0.98	24.00	0.98
			NHPPM, J=5	3.84	0.99	18.34	1.00
			NHPPM, J=30	2.81	0.99	12.94	1.00
			NHPPS	8.53	1.00	50.80
		0.4	NHPPM, J=2	6.80	0.98	34.11	1.00
			NHPPM, J=5	4.47	0.99	23.39	1.00
	0.1		NHPPM, J=30	3.90	0.97	15.74	1.00
			NHPPS	4.45	1.00	24.19
		0.7	NHPPM, J=2	3.28	1.00	17.41	1.00
			NHPPM, J=5	2.84	0.99	13.21	1.00
0.5			NHPPM, J=30	2.59	0.97	10.47	1.00
			NHPPS	18.73	0.96	80.27
		0.4	NHPPM, J=2	13.37	0.97	59.99	0.98
			NHPPM, J=5	9.61	0.98	42.67	1.00
	0.3		NHPPM, J=30	5.68	0.99	24.49	1.00
			NHPPS	7.92	0.97	33.99
		0.7	NHPPM, J=2	5.78	0.98	26.76	0.97
			NHPPM, J=5	4.23	0.98	19.86	1.00
			NHPPM, J=30	2.78	0.99	13.25	1.00

In the simulation settings with five regions (J = 5), the above observations still hold. Moreover, the proposed method provides even smaller rMSPE and tighter posterior CI compared to the respective results with two regions. For instance, the rMSPE reduces to 5.02 (J = 5) from 7.72 (J = 2) when d_j = 0 and ρ = 0.1 at the first look, whereas the average width of the posterior CI also reduces to 22.27 (J = 5) from 29.15 (J = 2). Nevertheless, the performance of the NHPPS method remains similar. This further demonstrates the improvement in efficiency of the proposed method by properly utilizing the regional accrual information. Similar patterns are also observed as J increases to 30.

Tables 2 and 3 present the results for the second set of simulations where all regions start accrual at the same time, i.e., $t_j^0=1$ for all j, and for the third set of simulations where some regions start accrual very close to the interim analysis. The main findings in Table 1 also hold for Tables 2 and 3.

Table 2.

Comparison of root mean squared prediction errors (rMSPE), mean coverage rates (CR), and mean width of the 95% posterior CI (w̄) of the proposed method (NHPPM) and the original NHPP method (NHPPS), as well as the probability of the proposed method having tighter 95% CI than NHPPS (Prob.) based on 1000 simulated trials with J = 2, 5 or 30 regions, when all participating regions initialize accrual at the same time.

Settings				Summary Measures
dj	ρ	pct.	Method	rMSPE	CR	w	Prob.
			NHPPS	8.24	1.00	50.16
		0.4	NHPPM, J=2	4.78	1.00	28.44	1.00
			NHPPM, J=5	4.09	0.99	21.77	1.00
	0.1		NHPPM, J=30	3.65	0.98	15.57	1.00
			NHPPS	4.63	0.99	24.45
		0.7	NHPPM, J=2	3.18	0.99	15.97	1.00
			NHPPM, J=5	2.68	1.00	12.90	1.00
0			NHPPM, J=30	2.62	0.96	10.41	1.00
			NHPPS	18.21	0.96	79.32
		0.4	NHPPM, J=2	10.00	0.99	50.58	1.00
			NHPPM, J=5	7.40	0.99	39.69	1.00
	0.3		NHPPM, J=30	4.24	1.00	23.52	1.00
			NHPPS	8.38	0.97	34.88
		0.7	NHPPM, J=2	5.37	0.99	25.81	0.98
			NHPPM, J=5	3.90	0.99	20.30	1.00
			NHPPM, J=30	2.87	0.98	13.25	1.00
			NHPPS	8.09	1.00	51.65
		0.4	NHPPM, J=2	5.39	1.00	37.91	1.00
			NHPPM, J=5	4.11	1.00	26.68	1.00
	0.1		NHPPM, J=30	3.96	0.97	16.10	1.00
			NHPPS	4.63	0.99	24.92
		0.7	NHPPM, J=2	3.58	1.00	19.87	1.00
			NHPPM, J=5	2.83	0.99	15.16	1.00
0.5			NHPPM, J=30	2.66	0.97	10.75	1.00
			NHPPS	18.38	0.97	85.21
		0.4	NHPPM, J=2	14.13	0.98	72.22	0.96
			NHPPM, J=5	9.33	1.00	55.84	1.00
	0.3		NHPPM, J=30	4.35	1.00	27.14	1.00
			NHPPS	8.45	0.98	36.24
		0.7	NHPPM, J=2	7.06	0.98	32.54	0.88
			NHPPM, J=5	5.00	1.00	26.63	1.00
			NHPPM, J=30	2.90	1.00	15.28	1.00

Table 3.

Comparison of root mean squared prediction errors (rMSPE), mean coverage rates (CR), and mean width of the 95% posterior CI (w̄) of the proposed method (NHPPM) and the original NHPP method (NHPPS), as well as the probability of the proposed method having tighter 95% CI than NHPPS (Prob.) based on 1000 simulated trials with J = 20 or 50 regions, when ρ = 0.3 and using three different sets of intervals to generate start-up times. The interim look time is 470 days.

Settings			Summary Measures
dj	Interval Setting	Method	rMSPE	CR	w	Prob.
		NHPPS	30.49	0.96	131.80
	1	NHPPM, J=20	9.17	0.99	46.80	1.00
		NHPPM, J=50	8.55	0.98	39.79	1.00
		NHPPS	40.75	0.96	170.21
0	2	NHPPM, J=20	10.46	0.99	55.35	1.00
		NHPPM, J=50	9.35	0.98	45.56	1.00
		NHPPS	50.39	0.94	192.51
	3	NHPPM, J=20	12.67	0.99	66.19	1.00
		NHPPM, J=50	8.88	1.00	51.38	1.00
		NHPPS	26.07	0.97	117.47
	1	NHPPM, J=20	8.48	0.99	43.08	1.00
		NHPPM, J=50	7.89	0.99	36.82	1.00
		NHPPS	35.01	0.97	152.67
0.5	2	NHPPM, J=20	9.85	0.99	51.67	1.00
		NHPPM, J=50	8.81	0.98	42.64	1.00
		NHPPS	43.69	0.96	182.2
	3	NHPPM, J=20	11.94	0.99	62.6	1.00
		NHPPM, J=50	9.71	0.98	48.54	1.00

We conducted additional simulation studies comparing NHPPM, NHPPS, HPPM and HPPS as well as another NHPPM approach denoted by NHPPM-bspline which uses direct extrapolation from the B-spline fit for prediction. The order, from the best to the worst, of the prediction performance is NHPPM, NHPPS, HPPM and HPPS, lending further support to the notion that the use of non-homogeneous Poisson process and modeling accrual in individual regions improves prediction; prediction from NHPPM-bspline is substantially worse than the other methods, confirming that direct extrapolation using NHPPM is unstable and unsuitable for prediction. In addition, we also show in simulation studies that NHPPM outperforms HPPM in terms of estimation of λ_jt.

In summary, the proposed method not only provides region-specific accrual prediction, but also produces smaller rMSPE and tighter posterior CI of τ_true. The advantage of the proposed approach compared to the NHPPS method can impact multiple aspects of trial operations, such as regional drug supply and distribution of laboratory kits, as well as proper allocation of clinical staff within each region, all attributable to the granularity of regional accrual adjusted for in the proposed model. More importantly, the tighter CIs produced by the proposed method translate into less uncertainty regarding the projected accrual, and hence better confidence when addressing issues such as slow accrual.

4 Data Example: a Cancer Trial

In this section we retrospectively apply the proposed method to a real oncology trial¹⁵ and, again, focus on comparisons with the NHPPS method¹¹. In this randomized Phase III study of adjuvant treatments of colorectal cancer, a total of 1794 Stage III patients were planned to be enrolled from 32 countries. Although Stage II patients satisfying certain criteria were later on also enrolled per a protocol amendment, they were not included in the primary analysis, and the enrollment goal was only tracked for Stage III patients. Therefore, for the purpose of illustration, we only focus on the Stage III patients in this analysis. Under a reasonable expectation of an enrollment duration of 24 months (523 workdays, excluding weekends), a daily enrollment of 3.45 patients is assumed. The accrual goal was met on Day 570 with a total of 1801 patients, i.e., τ_obs = 570.

We illustrate a retrospective enrollment monitoring/prediction using the proposed method at two interim looks with 40% and 70% of patients enrolled, which should occur on Days 386 and 474, respectively. We use an ad hoc determination of A_max based on the observed accrual in the past 20 workdays at the time of the interim look and consider different cv values. Among all countries participated in this study, one country contributed 30% of the patients. Therefore, we first consider grouping all countries into two regions, i.e., this one country contributing the most enrollment vs. the rest of the world. The results are shown in Table 4. The predicted T_exp generally excludes the originally planned 523 days, indicating that it is highly unlikely to meet the original accrual goal given the observed data. In addition, the predictive CI from NHPPS does not include the observed truth (τ_obs = 570) whereas NHPPM does when ρ = 0.1, noting that the maximum overall daily accrual rate across all regions is much higher than the anticipated A_max = 3.45. When the prior distribution is more diffused, e.g., ρ = 0.3 or 0.5, both NHPPS and NHPPM cover τ_obs. In other words, one can still make a reasonable accrual projection based on the data despite a dubious yet diffused prior distribution. As in the simulation studies, we observe tighter posterior CIs using NHPPM compared to NHPPS.

Table 4.

Data Example: 95% posterior CIs of the predicted accrual duration (τ) and w = T_U − T_L which is the width of the 95% posterior CI, using the proposed method (NHPPM) versus the original NHPP method (NHPPS).

Real data		NHPPS		NHPPM
				Two regions		Three regions		Thirty-two regions
cv	pct.	CI	w	CI	w	CI	w	CI	w
0.1	40%	[594, 660]*	66	[547, 587]	40	[550, 584]	34	[552,578]	26
	70%	[578, 611]*	33	[552, 574]	22	[552, 570]	18	[552,568]*	16
0.3	40%	[533, 593]	60	[528, 585]	57	[526, 583]	57	[570,609]	39
	70%	[553, 589]	36	[549, 581]	32	[546, 576]	30	[559,580]	21
0.5	40%	[525, 594]	69	[522, 582]	60	[518, 567]*	49	[581,628]*	47
	70%	[548, 591]	43	[552, 587]	35	[549, 579]	30	[560,586]	26

^*denotes the 95% posterior CI does not cover the true value (τ = 570).

Following the highest enrolling country, there were five countries each contributing between 5% and 11% of the patients. The rest of the countries each contributed a maximum of 4% patients. Hence, based on the enrollment capacity, we conduct a second analysis after grouping all countries into three categories, i.e., high enrolling region (the one country with the most enrollment), medium enrolling region (the five countries with moderate enrollment), and low enrolling region (the rest of the countries). We also conduct a third analysis using all 32 regions without any grouping. As shown in Table 4, NHPPM with J = 3 or 32 produces even tighter CIs compared to NHPPM with j = 2, though in three settings the CIs barely miss τ. In addition, as cv increases the length of CI generally increases.

Overall, the proposed method performs well with tighter posterior CIs and smaller rMSPE compared to the NHPPS approach. In addition, the sensitivity analyses based on ρ (ρ = 0.1, 0.3 and 0.5) as well as the number of regions (J = 2, 3, and 32) suggest the robustness of the proposed method. If an interim monitoring had been conducted during this trial, it would have allowed the study team to detect issues with accrual and identify potential enrollment problems with certain regions relatively early and alerted the study team, or the coordinating data center, for proper actions.

5 Discussion

In this paper, we propose a Bayesian approach for modeling and predicting patient accrual in multi-regional clinical trials, which models region-specific accrual using a nonhomogeneous Poisson process. Compared to the existing methods, the proposed approach accommodates different start-up times and different initial accrual rates across regions/centers and allows for discontinuity in the overall accrual rate. In numerical studies, the proposed method is shown to improve accuracy and precision of accrual monitoring and prediction compared to the NHPPS approach that does not model region-specific accrual rates¹¹. In practice, this translates into improved accuracy and precision and hence improved decision making on resource allocation. The flexible B-spline model for region-specific accrual rates provides good prediction in the simulation studies as well as the real data example. The proposed method would allow a research team to identify potential enrollment problems with certain regions using prediction results from individual regions and enable the research team to use a more targeted approach, such as addressing detected deficiency in recruitment in certain regions or adding satellite regions to increase enrollment.

Along the lines of Zhang and Long¹¹, Deviance Information Criterion (DIC) can be used to perform model selection to select optimal models for regions or region specific accrual rates and evaluate goodness of fit for the proposed model. In particular, a model assuming that the region specific accrual rate is constant, i.e., λ_jt = λ_j is a special case of the proposed model, which could be selected by DIC in cases where the constant accrual rate assumption is indeed met. In the numerical studies, we observe that the choice of the prior parameters (A_max and ρ) has an effect on the results to certain degree. Therefore, we recommend a possibly iterative approach to adjust the prior parameters. For instance, if the fitted profile of the underlying accrual rate deviates substantially from the initial guess, as in the real data example, one may want to adjust the values of A_max and/or ρ accordingly and refit the model. Alternatively, one may resort to an ad hoc determination of A_max as discussed in Section 4, e.g., taking A_max as the average of the recent observed accrual. The proposed approach can be readily extended to accommodate the cases where accruals in some regions/centers may terminate at different times.

In clinical trials with time-to-event endpoints, the statistical power is primarily driven by the number of events observed. In such cases, monitoring and prediction of accrual is not enough and monitoring and prediction of event times is equally important, which has also been investigated in the literature^16-18. It is of future interest to extend the proposed approach to monitor and predict both patient accrual and event times in multi-regional clinical trials.