A high-performance keyboard neural prosthesis enabled by task optimization

Abstract

Communication neural prostheses are an emerging class of medical devices that aim to restore efficient communication to people suffering from paralysis. These systems rely on an interface with the user, either via the use of a continuously-moving cursor (e.g., mouse) or the discrete selection of symbols (e.g., keyboard). In developing these interfaces, many design choices have a significant impact on the performance of the system. The objective of this study was to explore the design choices of a continuously-moving cursor neural prosthesis and optimize the interface to maximize information theoretic performance. We swept interface parameters of two keyboard-like tasks to find task and subject specific optimal parameters as measured by achieved bitrate using two rhesus macaques implanted with multielectrode arrays. In this report, we present the highest performing free-paced neural prosthesis under any recording modality with sustainable communication rates of up to 3.5 bits per second (bps). These findings demonstrate that meaningful high performance can be achieved using an intracortical neural prosthesis, and that, when optimized, these systems may be appropriate for use as communication devices for those with physical disabilities.

I. INTRODUCTION

NEURAL prostheses translate brain activity into control signals for guiding assistive devices such as robotic arms and computer cursors. One goal of these systems is to restore efficient communication to those with motor impairment. Several reports of neural prostheses have shown promising proof-of-concept demonstrations [1]–[11], but clinically-useful performance remains a challenge despite recent advances. [12]–[14] A central measure of any communication system is information throughput. The higher the throughput of the system, the faster it can transmit information, yielding a more useful clinical tool. A theoretic upper-limit known as channel capacity estimates the maximum bitrate of a channel assuming infinitely long channel codes and infinite symbols transmitted. Channel capacity for short selection chains was calculated in prior work [5], and provided an upper bound of 6.5 bps for the bitrate in that system. This previous study from our group used a system-paced, delayed center-out discrete selection task where selections were made in short chains followed by real arm reaches to keep the monkey engaged in the task and preserve time-locking. A follow on study reported ways that this system could be run without external knowledge of timing (system timing), but importantly this was an open-loop offline study as opposed to a closed-loop online study [15]. Many electroencephalographic (EEG) studies also commonly report channel capacity, labelling it as the system’s information transfer rate (ITR) [16]. These EEG systems have often been used to demonstrate information rates using a system-paced task, usually by flashing symbols at a fixed rate and measuring event potentials, such as P300. One such system averaged an ITR of 0.09 bps in this manner [17]. Another P300 study achieved 0.38 bps using a checkerboard pattern of flashing characters [18]. Most recently, EEG BCI studies based on code modulation of visual evoked potentials have achieved ITRs of 1.8 bps [19] and 2.4 bps [20]. However, channel capacity and ITR, while important and useful, are not the same as achieved bitrate in a closed-loop system [21]. The achievable bitrate of these systems has not been well demonstrated, while the channel capacity has not exceeded 2.4 bps for EEG or electrocorticographic (ECoG) studies [17]–[20], [22]–[25]. Additionally, many of these systems are paced by the computer as opposed to being paced by the subject, increasing cognitive demand and making them less suitable for extended use.

A task that is paced by the user is more desirable because it allows the user to set the pace of symbol transmission and pause as desired. Further, although task optimizations are common in the EEG studies, they are relatively rare in intracortical systems. These types of optimizations may be important to the successful development of intracortical neural prostheses. In fact, we recently reported conference abstracts of keyboard applications with intracortical electrode arrays in a person with ALS as part of the BrainGate2 FDA pilot clinical trial [26], [27], which further emphasizes the need to optimize these systems for maximum performance and ease of use.

The aim of this study was to demonstrate the maximum achievable, sustained bitrate on a free-paced typing-like task that would closely mimic a clinical system. As such, the use of complex channel codes may overestimate the achievable bitrate. Further, the clinical use case is unlikely to involve the transmission of channel codes greater than one or two symbols because they are difficult for people to remember and use. While channel codes are considered best practices for data integrity in electronic transmission systems, they are not practical when used by people. Notably, a conventional computer keyboard primarily employs a single-symbol channel code: each key selection encodes an independently meaningful piece of information to the computer. Thus, in this study, achieved bitrate was measured using a single-symbol channel code.

Designing a keyboard interface also involves many design choices that would impact performance. These design choices are not obvious, and thus to find the optimal interface, parameter optimization is necessary. Since performance can only reliably be measured online in a closed-loop setting [28], this optimization must occur iteratively. As such an optimization has never been performed to our knowledge, we elected to exhaustively explore the parameter space when searching for optimal parameters.

II. MATERIALS & METHODS

A. Experimental Setup

All procedures and experiments were approved by the Stanford University Institutional Animal Care and Use Committee (IACUC). Experiments were conducted with adult male rhesus macaques (L and J), implanted with 96 electrode Utah arrays (Blackrock Microsystems Inc., Salt Lake City, UT) using standard neurosurgical techniques. Electrode arrays were implanted in arm motor regions of primary motor cortex (M1) and dorsal premotor cortex (PMd), as estimated visually from local anatomical landmarks [5]. Monkey L was implanted with a single array at the M1/PMd border on 2008-01-22, whereas Monkey J had two arrays implanted, one in M1 and the other in PMd on 2009-08-24. In Monkey J, only the M1 array was used in this study. Implantation targets were shoulder and brachium areas. We found that in both monkeys we had neural responses to shoulder, brachium, antebrachium, and carpus regions as evaluated by passive movement. Monkey L’s array was placed in the right hemisphere. Monkey J’s arrays were placed in the left hemisphere.

The monkeys were trained to make point-to-point reaches in a 2D plane with a virtual cursor controlled by the contralateral arm or by a neural decoder, as diagrammed in Figure 1a. The ipsilateral arm was restrained in these experiments. From arm movement sessions, a neural prosthesis decoder was trained using the ReFIT-KF algorithm [13]. Briefly, this involved 500 trials of center-out and back arm reaches followed by 500 trials of a first-pass neural control training set before the final ReFIT-KF decoder was ready. During neural control sessions, the contralateral arm was left unbound and typically continued to move. This approach was preferred because it minimized any behavioral (and thus neural) differences between the testing set (neural prosthesis session) and the training set (arm control sessions). This animal model was selected because we believe it more closely mimicked the neural state of a human subject employing a neural prosthesis in a clinical study [29], and has previously demonstrated comparable performance to the dual arm-restrained animal model [13]. Specifically, this animal model most closely mimics the neural state of a human subject utilizing a neural prosthesis because it does not place any constraints on neural activity. With respect to neural activity, it is the closest animal model possible to a human subject without resorting to means of temporarily or permanently paralysing the monkey. A paralyzed human subject’s cortex can explore any desired and achievable neural state and yet, because of their paralysis (e.g., spinal cord injury), their limb would not move. Requiring the monkey’s arm to remain motionless or otherwise restraining it necessitates a more constrained neural state (i.e., there are some neural states that are off-limits for the monkey because they lead to movement). This discrepancy results in differences in the neural states between the monkey and the human subject, and since the goal is to mimic a human subjects neural activity and not their behavior, artificial constraints on the monkey’s behavior is non-ideal. Despite the arm being free, during experimental blocks, the cursor was continuously and always under neural control. Nevertheless, to adress the potential concern of the role of somatosensory feedback driving the decoder, we also conducted a smaller optimization sweep with both arms restrained in both monkeys.

Fig. 1.

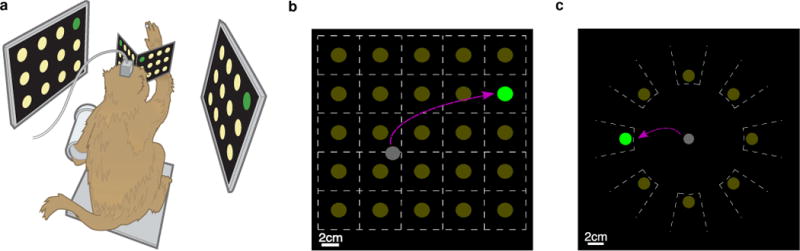
Experimental Setup. a Diagram of monkey in experimental rig interacting with virtual workspace. b Diagram of grid task configured for 25 targets. Dashed white lines are drawn for illustration purposes to denote the boundaries of the acceptance regions and were not shown to the monkey. The gray cursor was under neural control and the task was to navigate and hold the cursor over the green target. c Diagram of the radial task with 8 targets. Dashed white lines again are for illustration purposes only.

The virtual cursor and targets were presented in a 3D environment (MSMS, MDDF, USC, Los Angeles, CA) [30]. Hand position was measured with an infrared reflective bead tracking system (Polaris, Northern Digital, Ontario, Canada) polling at 60 Hz. Neural data were initially processed by the Cerebus recording system (Blackrock Microsystems Inc., Salt Lake City, UT) and were available to the behavioral control system within 5 ± 1 ms. Spike counts were collected by applying a single negative threshold, set to 4.5 × root mean square of the voltage of the spike band of each neural channel per the Cerebus software’s thresholding [12]. Behavioral control and neural decode were run on separate PCs using the Simulink/xPC platform (Mathworks, Natick, MA) with communication latencies of 3 ms. This system enabled millisecond-timing precision for all computations. Visual presentation was provided via two LCD monitors with refresh rates at 120 Hz, yielding frame updates within 7 ± 4 ms. Two mirrors, setup as a Wheatstone stereograph, visually fused the monitors into a single 3D percept for the monkey, although all task relevant motion was limited to two dimensions [28]. Datasets are referenced by monkey-date format: a dataset from Monkey J would be JYYMMDD.

B. Tasks

Two keyboard-like tasks were investigated in this experimental setup with both monkeys: the grid task and the radial task. These tasks were designed as cursor-based keyboard interfaces that a human subject could use when controlling a neural prosthetic cursor. The same ReFIT-KF decoder was used for both tasks. This decoder was retrained at the start of each experimental day and used for the duration of that day. The goal of both tasks was to acquire a green target among possible yellow targets. Targets were prompted in random with replacement fashion for both tasks, and thus repeated targets were allowed, mimicking the situation where the user may want to select the same character twice. Each task had two parameters that were swept when performing the optimization. This was a free-paced task because trial lengths were determined by how quickly selections were made by the monkey. There were no breaks between trials of an experimental block, such that a new target appeared immediately after a selection was made.

Although some task parameters would lead to layouts with less than 26 keys (i.e. the number of letters in the English alphabet), the goal of this study was to thoroughly sweep the parameter space to find the optimal bitrate. Further, this type of preclinical work directly informs the subsequent design, testing, and optimization of the relevant parameters in clinical keyboard systems as we recently demonstrated in a bench-to-bedside methodology [26], [27], [31]. Monkeys were given a liquid reward at the end of each correct target acquisition.

1) Grid Task

The layout of the grid task, shown in Figure 1b, resembled traditional keyboard interfaces. It uniformly divided a 24×24 cm workspace into contiguous, non-overlapping, square acceptance regions each containing a potential target in yellow. Within this workspace, the cursor was always in the acceptance region of a possible target. The goal of this task was to navigate the cursor onto the green target and maintain it within the acceptance region for a required hold time. Dwelling over an incorrect target region resulted in an incorrect selection, akin to striking the wrong key on a keyboard. The grid task had a five second time out, resulting in a failed trial if no selection was made during the alloted time. Once a selection was made, a 200 ms lockout period was enforced during which no target could be selected. Without this lockout period, the monkey would often fail a subsequent trial very quickly after a selection because the cursor tended not to move out of the acceptance region of the prior target while the monkey searched to find the next target. This 200 ms lockout period, which is on the order of reaction time [32], was too short for the monkey to attend and acquire the next target, and thus did not slow down performance unless the same target was prompted twice.

2) Radial Task

The radial task, depicted in Figure 1c, was a keyboard interface inspired from the human computer interface community [33]. It divided the workspace equally into pie slices, each slice having one yellow target. In this task, the goal was to navigate the cursor into the acceptance region in the direction indicated by the green target. A selection would immediately be made once the cursor moved into an acceptance region; no hold time was required. The cursor would then be reset to the center of the workspace and the next trial would begin. A fixed gap size of $\frac{\pi }{16}$ was present between all acceptance regions to allow some tolerance at the edges of the pie slices.

C. Optimization

In both tasks, each trial prompted the selection of a single correct target in green, while many other potential choices appeared in yellow. Therefore, each selection conveyed information equal to the binary logarithm of the number of all possible targets on the screen. Viewing the BMI as a communication channel, the information transmitted over time represents the throughput of the system. Task parameters must thus be optimized with the aim of maximizing throughput. A common adjustable parameter in both tasks was the number of targets. A successful trial conveyed more information when the number of targets increased, but this increased the task’s difficulty, consequently lowering the success rate. In addition, each task had a second, unique, adjustable parameter. In the case of the grid task, this parameter was the hold time required to select a target. A long hold time slowed the overall rate of target selection, whereas a short hold time increased it but lowered the threshold for inadvertent selections while navigating to the prompted target. In the radial task, the distance to the targets was the second adjusted parameter: targets further from the center decreased the selection rate, while placing them closer to the center increased it at the expense of a higher error rate.

For each task, we found experimentally, by virtue of directly measuring the performance achieved at every combination of parameters, the optimal task parameters that yielded the highest information throughput, as measured in bits per second (bps). These optimal parameters struck the best balance between success and selection rates. Parameters were swept across several days in a random-without-replacement block fashion.

There were 16 parameter pairs tested for the grid task with both monkeys. For the radial task, there were 20 parameter pairs tested with Monkey L and 25 parameter pairs tested with Monkey J. Each block consisted of a random parameter pair (e.g., grid task: 49 targets at 450 ms hold time) that was run for approximately 200 trials (3–6 minutes). Some parameter pairs were unusable because of high error rates (e.g. short hold times with large acceptance regions), resulting in a communication rate of 0 bps, and were stopped early to prevent monkey frustration.

D. Bitrate

Neural prosthetic performance on these tasks was evaluated using information theoretic measures. The primary measure used in this study was achieved bitrate. This was calculated by measuring the net rate at which correct symbols were transmitted. For the purposes of a communication neural prosthesis, evaluating bitrate required the transmission of a single-symbol out of multiple potential choices, where every symbol had an equal likelihood of being prompted, including sequentially repeating symbols. To mirror the primary use-case and avoid overestimation, we assumed a channel code of a single-symbol and calculated only achieved bitrate. In conventional keyboards, there is the occasional, limited use of multi-symbol channel codes with keyboards such as the Shift, Ctrl, and Alt keys (e.g., Ctrl+C for copy); however, these were not addressed in this study.

An important additional issue in calculating achieved bitrate was how to handle error. To conservatively address incorrect symbol transmissions, we used only the net number of correct symbol transmissions as the measure of total meaningful symbols transmitted during an experimental session. Any incorrect transmissions (e.g., selecting the wrong key) had to be followed by the respective number of correct transmissions (i.e., simulating the delete key) before meaningful information transfer could be resumed. This is very similar to the usage of a keyboard for typing, where incorrect key selections are corrected by the use of the delete key before resuming character transmission. The formula for achieved bitrate, B, under these conditions is described by Equation 1.

$$\mathbf{B}=\frac{{\log }_2(N)\max ((S_c–S_i),0)}{t}$$ (1)

In Equation 1, N is the total number of targets on the screen, S_c is the number of correct selections, S_i is the number of incorrect selections, and t is the time elapsed. In this study, t was measured as the total time elapsed between the start of the first trial of a block to the end of the block’s last trial. All inter-trial time was counted as part of the elapsed time. If the quantity (S_c − S_i) < 0, then the bitrate is set to a floor of 0 bps since it cannot be negative. Note that trials where a selection was not made (i.e., the cursor was out of the workspace or the trial timed out) were not errors in symbol transmission and thus they were not counted in S_i since no symbol was transmitted. However, the time spent during such a trial was included in the elapsed time and consequently decreased bitrate appropriately. Thus, the achieved bitrate calculated in the optimization sweeps was the bits per trial for that task condition, multiplied by the net total number of successful trials across all blocks of all days for a given parameter pair divided by the total time spent across all blocks of all days for that given parameter pair.

Equation 1 is the most conservative measure for evaluating bitrate and thus a good estimate of the minimum expected neural prosthetic performance. In the context of a typing task, word completion algorithms would be employed to elevate typing rate, but this is not a measure of raw performance. It should be noted that neural prostheses achieving a 50% success rate that may otherwise appear functional would nonetheless have an information rate of 0 bps under these metrics.

This approach in is contrast to the measurement of ITR as defined in earlier work [16]. ITR, since it is a measure of channel capacity, will be nonzero for a 50% success rate, possibly significantly so, contingent on the structure or pattern of the errors. However, such a measurement is potentially misleading as it requires a multi-symbol channel code (e.g. at least two selections per symbol transmitted [16]). This is not the natural use case for conventional typing keyboards and confounds the measurement by complicating the task structure. In this study, we sought to measure achieved bitrate in the simplest and most conservative way with as straightforward a task as possible using a single-symbol channel code. Despite the harsh penalty for errors, this approach more accurately measures the clinical utility of a neural prosthesis, as transmitting text involves similar challenges and penalties (e.g. the use of the delete key) when used in the clinical setting.

E. Dual arm restrained optimization

Additionally, as a control, for a limited set of parameters, we conducted optimization sweeps on both tasks with both monkeys where both arms were restrained during the neural control experiments. This was done to serve as a control experiment to demonstrate that in the arm free condition, decoder performance is not a function of somatosensory input. Under this model, both of the monkey’s arms were gently restrained at the start of the experimental day and held throughout the experiment. The arms were monitored via an infrared camera and noted not to be moving while restrained in these experiments. A ReFIT-KF decoder was built with initial kinematics seeded off of a computer controlled cursor while the monkey passively observed. After this step of passive observation of automatic cursor movements, the second step decoder training was under neural control and the same as in the main experiment. We note that this decoder and training protocol is identical to the dual arm restrained animal model decoder control tested in prior work [13].

III. RESULTS

The results of the optimization for both tasks are presented in two figures. Figure 2 shows the results of the grid task optimization and Figure 3 shows the results of the radial task. Each row of each figure plots the results of one monkey. The parameter optimization is plotted as a heatmap in the middle figure of each row (panels b and e of Figures 2, 3). Additionally, complete numerical reports of the optimization sweeps appear in Supplementary Tables 1–4. As hypothesized, varying task parameters had a significant impact on performance. A two-sample unpaired t-test demonstrated statistical significance for the optimal parameters versus every other parameter pair evaluated (p < 0.05) on both tasks with Monkey L. On the same t-test, Monkey J’s optimal parameters met statistical significance for all parameters except for the 49 target, 450 ms hold time parameter pair on the grid task (p-value 0.07), and the following distances on the 12 target radial task: 9 cm, p-value 0.19; 11 cm, p-value 0.29; 13 cm, p-value 0.11. This is likely because Monkey J had a wider range of parameters that he performed well at on the radial task compared to Monkey L. Points for this t-test were collected by calculating the instantaneous bitrate across bins of 10 non-overlapping trials of a given parameter pair from the optimization data. These were the same points used to calculate the standard deviation of bitrate in the supplementary tables. The histogram on the left (panels a and d of Figures 2, 3) is the distribution of the time to target of all trials collected during the optimization sweep for the optimal parameters. These histograms reflect the expected right skew normal distributions for target acquisition time in tasks like these [4], [13]. The time-series plot on the right (panels c and f of Figures 2, 3) plots the exhaustive, sustained performance of the optimal parameters on a single day where those were the sole parameters evaluated. Example videos of the optimal parameters for both tasks with both monkeys are presented as supplementary videos.

Fig. 2.

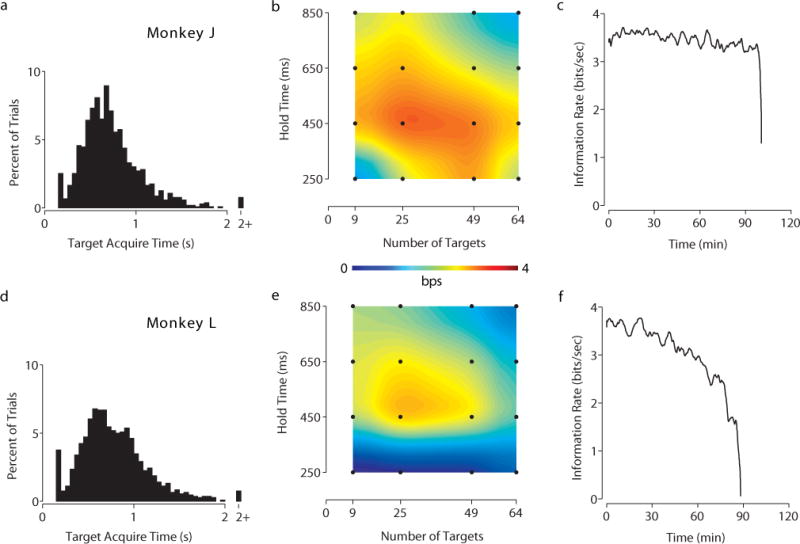
Experimental data of grid task. Monkey J: a–c. Monkey L: d–f. a Acquire time histogram of grid task with task parameters of 25 targets and 450 ms hold time. The peak at 0.2 s represents trial targets that were randomly repeated. This time represents the moment of successful target acquisition and does not include the hold time. b Bitrate heatmap of task parameters swept for grid task. Each point in black represents a tested pair of task parameters, with the colors interpolated between points. Data from datasets J100913 – J100917 and J100928 – J100930, comprising of 20716 trials. c Information plot of sustained performance across an experimental session for the grid task. The line plots the average overlapping 50 trial smoothed bitrate as a function of time. Data from dataset J101013. d Acquire time histogram of grid task with 25 targets and 450 ms hold time. e Bitrate heatmap as in b. Data from datasets L100913 – L100917, L100920, and L100929 – L100930; comprising of 17677 trials. f Information plot as in c. Data from dataset L101014.

Fig. 3.

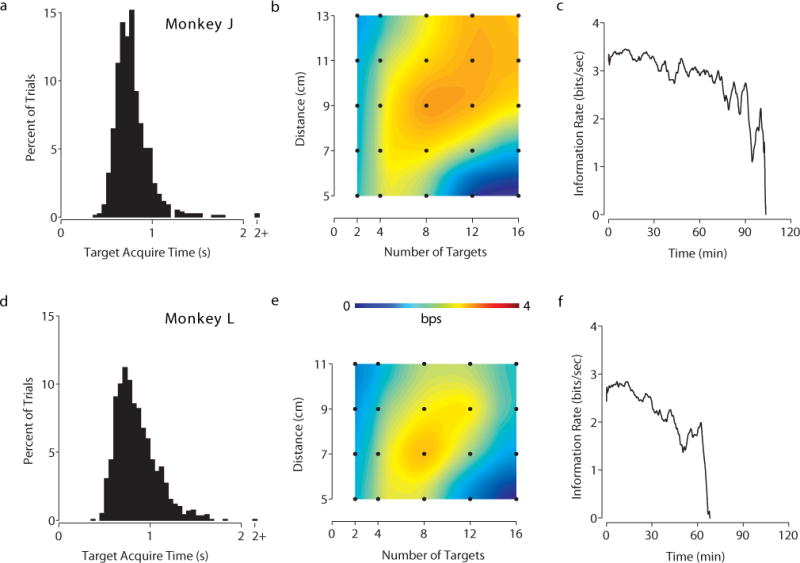
Experimental data of radial task. Monkey J: a–c. Monkey L: d–f. a Acquire time histogram of radial task with task parameters of 8 targets and 9 cm distance. b Bitrate heatmap of task parameters swept for radial task. Each point in black represents a tested pair of task parameters, with the colors interpolated between points. Data from datasets J100901 – J100903 and J100906 – J100907, comprising of 16754 trials. c Information plot of sustained performance across an experimental session for the radial task. The line plots the average bitrate as a function of time. Data from dataset J101014. d Acquire time histogram of radial task with 8 targets and 7 cm distance. e Bitrate heatmap as in b. Data from datasets L100831 – L100903 and L100906; comprising of 14684 trials. f Information plot as in c. Data from dataset L101013.

On the grid task, for Monkey J, the optimal task parameters were 25 targets with a 450 ms hold time, achieving an average bitrate of 3.4 bps at these parameters. On the same task, Monkey L had similar optimal parameters, achieving an average bitrate of 3.0 bps. Monkey J sustained around 3.5 bps for over an hour and a half when tested exhaustively with these optimal parameters before tiring out and stopping. Monkey L had about the same initial performance and lasted about the same time, however his work ethic, and not the decoder quality, diminished gradually over the course of the 90 minutes.

On the more fast-paced radial task, Monkey J’s optimal task parameters were 8 targets at a distance of 9 cm, achieving an average bitrate of 3.1 bps. Monkey L had different optimal parameters, averaging 3.0 bps with 8 targets and a distance of 7 cm. Sustained performance for the radial task was lower than the grid task for both monkeys. We speculate that this may be because the radial task required more concentration and engagement than the grid task, and was thus more fatiguing and variable in performance.

For comparison, on the grid task with the optimal parameters under arm control, Monkey J achieved 100% success rate with acquire times around 450–600 ms, corresponding to a bitrate in the range of 4.5–5.2 bps. Monkey L could also achieve 100% success rate with comparable bitrates under arm control. The maximum achievable bitrate varies based on the task parameters. The upper limit on bitrate on the grid task with optimal parameters (25 targets at 450 ms hold time) is 7.1 bps (i.e., ${\log }_2(25)·\frac{1000}{650}=7.1$), but this would require near instantaneous movement to each prompted target. The maximum bitrate for the easiest parameter pair on the grid task (9 targets at 850 ms hold time) is 3.0 bps. The maximum bitrate for the hardest parameter pair on the grid task (64 targets at 250 ms hold time) is 13.3 bps. The bitrate is not infinite because of the required hold time and the 200 ms post-selection lockout time.

As an additional reference point to the established literature, we also calculated information transfer rate (ITR) for the optimal parameters we found in this study. The ITR for the optimal parameters on the grid task was 3.4 bps (Monkey J) and 3.0 bps (Monkey L) with optimal parameters of 25 targets and 450 ms for both monkeys. The ITR for the optimal parameters on the radial task was 2.9 bps (Monkey J, 8 targets and 9 cm) and 2.8 bps (Monkey L, 8 targets and 7 cm). To our knowledge, these ITRs are higher than previously reported in the literature with the exception of [5].

Results of the dual arm restrained limited optimization sweep are detailed in Supplementary Tables 5–8. For the grid task, these are from datasets J101007-J101008 and L101005-L101008. For the radial task, these are from datasets J101008, J101011, J101015, L101008, L101011, and L101015. In this animal model as well we found that the choice of parameter pairs had an impact on the achieved bitrate of the system. These optimization parameters were different than that found in the main experiment, likely due to the different quality of cursor control under this animal model, again demonstrating the importance of task optimization for a given level of neural cursor control. While it is difficult to summarize the performance difference (and thus supplementary tables are provided), when comparing the maximum bitrate achieved for each task (grid/radial), for each monkey (J/L), and for each model (unrestrained/restrained arm), we found and average of 29% lower bitrate with arms restrained versus arms unrestrained. This is generally consistent with our previous report comparing these two animal models [13].

IV. DISCUSSION

The tasks performed in this study are considered free-paced tasks because they are not bound to rigid system-based timing cues required of fixed-timing trial-based tasks, but instead controlled by the user. Although the monkeys did not voluntarily take breaks from the task, the self-paced nature of the system allows for user-controlled breaks by simply not selecting any targets. In a clinical system, this may be made more explicit by the direct use of a pause button at the edge of the workspace, but this is an abstract idea not within easy reach of monkey behavior and was thus not implemented in this study. This system also demonstrated flexibility to conform to a user’s desired task rate, as the tempo of the task was set by the monkeys’ target acquisition rate, which was guided by the monkeys’ intention and desire for reward. A human user could select targets as fast or as slow as comfortable without any adjustment to the design of system or task structure.

The parameter sweep findings demonstrated that the choice of parameters had a significant impact on the information transmitted. Incorrect selection of parameters led to severalfold slower communication rates, or, in the worst case, no meaningful throughput at all. In general, higher bitrate tasks also had higher success rates. Careful tuning of these parameters is important for maximizing the utility of the communication channel. The findings of the optimal parameters for the grid task performed here served as the basis task for a set of later experiments exploring how well the high performance achieved here could be sustained across time without resorting to retraining the decoder [34].

It should also be noted that each subject had their own optimal parameters for a given task. Thus, a parameter search should be done on a per subject basis. This need not be exhaustive, as was done in this study, but could instead be informed based on prior subjects with only a speedy local search around typical parameters to find the best set for a given subject. Moreover, it is essential that parameter optimizations be performed and clinically-relevant metrics be utilized in studies to facilitate comparison. Without optimization and standardized, appropriate metrics, it is unclear how the field will advance performance through the years if some studies do not state their best (optimized) results and use comparable, meaningful measures.

The two tasks required different control strategies by the monkeys. The grid task was a continuous control task where the cursor was always moving smoothly, requiring both accurate movements as well as accurate stopping ability. The radial task however did not require any stopping ability and simply needed fast and accurate movements to the correct threshold before being reset to the center. This lack of a need to stop made the radial task more tolerant of decoders with poor control, as simpler decoders like the velocity Kalman filter will work reasonably well for movements towards the intended direction of a target (e.g., Figure 1e in [13]). This also suggests that a higher velocity gain on the decoder may have resulted in higher performance with the radial task, however this was not explored in this study. Thus, although the same ReFIT-KF decoder was used for both tasks, it is likely that different or optimized decoders may be better suited for different tasks. This may partially explain why the maximum achieved bitrates for the radial task are slightly lower than those achieved in the grid tasks across both monkeys. Nonetheless, in using the same decoder, the ReFIT-KF algorithm, in both tasks, we demonstrated generalizability of the algorithm. This may be an important feature for clinical translation as this single decoder may perform well in a variety of cursor control use cases.

Additionally, the experiments shown in panels c and f of Figures 2, 3 demonstrate that optimal parameters can lead to sustained high performance across a day. These sustained performance experiments were performed only with the optimal parameter pairs because entire experimental days were devoted to them, unlike the block structure of the optimization sweep. The performance falloff seen at the end of these experiments is consistent with monkey behavior and not representative of decoder performance. Monkeys, just like humans, will work consistently for a fixed period on a given task and then stop abruptly. Similar performance falloff is seen in arm controlled sessions (e.g., Figure 3b in [13]), indicating that this is a behavioral phenomenon. These optimal parameters facilitate the most effective communication rates and minimize subject frustration, enabling over hour-long sessions. Attempts to use non-optimal parameters (i.e., at or near 0 bps) led to rapid subject frustration and refusal to participate. This reinforces the need to carefully select task parameters, not only for the highest instantaneous communication rates, but also for enabling long-running sessions that maximize ease of use.

V. CONCLUSION

Taken together, these results demonstrate the highest reported sustained communication rates of any neural prosthesis under any measurement modality (i.e., EEG, ECoG, or intracortical electrodes) [22]–[25].

Sustainable high performance is a central factor in the successful translation of neural prosthetics and the findings here suggest that careful task optimization can lead to significant increases in communication rates. The sustained high communication rates found here also suggest that these systems are capable of transmitting meaningful information for hours at a time, an important feature of clinical neural prostheses. Further work is still necessary to explore the application of these information theoretic optimization findings to directly clinically-appropriate measures and settings as neural prostheses march closer to clinically therapeutic use.

Biographies

Paul Nuyujukian (S05–M13) received the B.S. degree in cybernetics from the University of California, Los Angeles, in 2006. He received an M.S. and Ph.D. degrees in bioengineering and M.D degree from Stanford University in 2011, 2012, and 2014, respectively. He is currently a postdoctoral scholar in the department of Neurosurgery at Stanford University. His research interests include the development and clinical translation of neural prostheses.

Joline M. Fan received a B.S. degree in Chemical Engineering from Princeton University in 2009, and a M.S. degree in Bioengineering from Stanford University in 2011. She is currently pursuing an M.D. degree at University of California San Francisco. Her interests include neural prostheses and clinical translation.

Jonathan C. Kao (S13) received the B.S. and M.S. degree in electrical engineering from Stanford University in 2010. He is currently pursuing his Ph.D. degree in electrical engineering at Stanford University. His research interests include algorithms for neural prosthetic control, neural dynamical systems modeling, and the development of clinically viable neural prostheses.

Stephen I. Ryu received the B.S. and M.S. degree in electrical engineering from Stanford University, Stanford, CA, in 1994 and 1995, respectively, and the M.D. degree from the University of California at San Diego, La Jolla, in 1999. He completed neurosurgical residency and fellowship training at Stanford University in 2006. He was on faculty as an Assistant Professor of Neurosurgery at Stanford University until 2009. He now practices at the Palo Alto Medical Foundation in Palo Alto, CA. His research interests include brainmachine interfaces, neural prosthetics, minimally invasive neurosurgery, and stereotactic radio-surgery.

Krishna V. Shenoy (S87-M01-SM06) received the B.S. degree in electrical engineering from U.C. Irvine in 1990, and the M.S. and Ph.D. degrees in electrical engineering from MIT, Cambridge, in 1992 and 1995, respectively. He was a Neurobiology Postdoctoral Fellow at Caltech from 1995 to 2001 and then joined Stanford University where he is currently a Professor in the Departments of Electrical Engineering, Bioengineering, and Neurobiology, and in the Bio-X and Neurosciences Programs. He is also with the Stanford Neurosciences Institute. His research interests include computational motor neurophysiology and neural prosthetic system design. He is the director of the Neural Prosthetic Systems Laboratory and co-director of the Neural Prosthetics Translational Laboratory at Stanford University. Dr. Shenoy was a recipient of the 1996 Hertz Foundation Doctoral Thesis Prize, a Burroughs Wellcome Fund Career Award in the Biomedical Sciences, an Alfred P. Sloan Research Fellowship, a McKnight Endowment Fund in Neuroscience Technological Innovations in Neurosciences Award, a 2009 National Institutes of Health Director’s Pioneer Award, the 2010 Stanford University Postdoctoral Mentoring Award, and the 2013 Distinguished Alumnus Award from the Henry Samueli School of Engineering at U.C. Irvine.