Discounting of Delayed Rewards: (A)theoretical Interpretation of the Kirby Questionnaire

Abstract

111 participants, recruited from Amazon’s MTurk worker pool, completed Kirby’s (2009) monetary choice questionnaire, which involves choosing between immediate, but smaller rewards and delayed, but larger rewards. Individual participants’ responses were scored in three ways: first, by calculating the proportion of choices of the delayed rewards; second; using the scoring procedure described by Kirby, Petry, and Bickel (1999) to estimate discounting rate (i.e., the value of the k-parameter in a hyperbolic discounting function); and third, using logistic regression to estimate discounting rate (Wileyto, Audrain-McGovern, Epstein, & Lerman, 2004). Individuals’ scores calculated using the proportion measure and the logarithms of their estimated k values were very strongly correlated (rs > .97). In addition, the proportions of choices of small, medium, and large amounts of the delayed rewards were strongly correlated (rs > .80). Taken together, these results suggest that the relative ease of calculating the proportion measure does not require sacrificing reliability. Moreover, the proportion measure is atheoretical and very easy to calculate whereas estimating an individual’s discounting rate requires assuming a theoretical model that may not be appropriate. Significant differences in the proportion of delayed reward choices were observed between the small, medium, and large delayed reward amounts, with smaller rewards being discounted more steeply than larger ones, replicating previous findings of magnitude effects. These results provide further validation of the proportion of delayed reward choices on the Kirby questionnaire as a measure of individual and group differences in discounting.

Individuals differ greatly in the degree to which they discount the value of delayed rewards, and steep discounters (i.e., those for whom a delayed reward has a relatively low subjective value) are often described as being more impulsive than shallow discounters. Consistent with this view, groups of smokers, alcoholics, and users of illegal drugs tend to discount delayed rewards more steeply than control groups (MacKillop, Amlung, Few, Ray, Sweet, & Munafò, 2011; Yi, Mitchell, & Bickel, 2010). Because of this, and because of the relevance of discounting to issues of self-control and decision making in general, the relation between individual differences in discounting and other behaviors has become a major topic of research (for a review, see Green & Myerson, 2010).

Individual differences research, particularly studies using contemporary methods such as confirmatory factor analysis and structural equation modeling (Floyd & Widaman, 1995), requires much larger samples than those that typically have been used in studies examining individual differences in discounting (Odum & Baumann, 2010), and thus the development of efficient ways to measure discounting is critical. Kirby and his colleagues (Kirby, Petry, & Bickel, 1999) developed a brief 27-item questionnaire for this purpose that meets psychometric standards for reliability and stability, with 1-year test-retest correlations similar to those obtained with tests designed to assess personality traits (Kirby, 2009). In addition, the difference in test scores observed between psychoactive substance users and controls attests to the questionnaire’s construct validity (e.g., Kirby & Petry, 2004; Kirby et al., 1999). Further evidence of construct validity is provided by the finding of a magnitude effect, a benchmark result in delay discounting research (Frederick, Loewenstein, & O’Donoghue, 2002; Green & Myerson, 2004): Steeper discounting is observed on responses to questions involving smaller delayed amounts than on responses to questions involving larger amounts (Kirby & Maroković, 1996).

Although the reliability and validity of the Kirby questionnaire are now established, there remain problems with its scoring. Following Kirby et al. (1999), the usual approach involves matching individual patterns of responses to those predicted based on individual differences in the rate parameter (k) of a hyperbolic discounting function:

$$V=A/(1+kD),$$ (1)

where V is the subjective value of a reward of amount A that is available after a delay of D time units (Mazur, 1987). This scoring method assigns individuals to one of 10 categories, 8 of which are associated with specific ranges for k, whereas the other 2 indicate k values that are either less than the minimum or more than the maximum that can be assessed with the questionnaire. Assigning individuals to these categories may be useful, but it is obviously a limitation of the original scoring method because such a small number of discrete categories limits the resolution with which discounting can be measured. Moreover, the steepness with which individuals discount is usually assumed, at least implicitly, to vary along a continuous dimension.

Wileyto, Audrain-McGovern, Epstein, and Lerman (2004) proposed using logistic regression to score the Kirby (2009) questionnaire, an approach that, in principle, allows for continuous estimates of k. However, Wileyto et al. reported that logistic regression did not yield parameter estimates for 8% of the individuals they tested. Moreover, like the original scoring method, their use of logistic regression assumes a one-parameter discounting function, namely, the simple hyperbola (Eq. 1). Considerable evidence now suggests that the hyperbola is not the best theoretical model (for a review, see Green & Myerson, 2004), and a number of two- and three-parameter discounting functions have been proposed (Laibson, 1997; Prelec & Loewenstein, 1991; Myerson & Green, 1995; Rachlin, 2006; van den Bos & McClure, 2013).

Motivated by the strengths of the Kirby (2009) questionnaire (i.e., its quick, easy administration, relative absence of problems with floor and ceiling effects, and established reliability and validity) as well as by potential problems and limitations of current scoring methods and their theoretical underpinnings, we examined a simple alternative approach to scoring individuals’ responses that builds on the logic of Kirby’s original approach. The advantages of this alternative approach derive not only from the simplicity of its straightforward scoring method, but also from the fact that it potentially provides for more precise measurement of individual differences in discounting. Importantly, as we will show, this alternative approach does not rely on theoretical assumptions regarding the mathematical form of the discounting function. The primary goal of the present study was to assess the reliability and validity of this alternative scoring method. For this purpose, we collected data online from a sample recruited using Amazon’s Mechanical Turk (MTurk), a source which Jarmolowicz, Bickel, Carter, Franck, and Mueller (2012) have shown can yield reliable and valid data when the Kirby questionnaire is scored using the original method.

Method

Participants

A sample of 111 participants (58.7% female; age: M = 34.1 years, SD = 12.9; education: M = 15.1 years, SD = 2.55; individual annual income: M = $29,593, SD = 25,510; household income = $59,433, SD = 41,977) was recruited from the pool of workers maintained by MTurk. Participation in the study was restricted to individuals using a computer with an IP address in the United States who had a previous MTurk approval rate of at least 95%, meaning that 95% or more of an individual’s previous efforts had been approved by requesters (i.e., those offering jobs through MTurk).

Procedure

In the MTurk request for the current study, participants were informed that the task would take approximately 15 minutes (although the actual mean duration to complete the task was approximately 6 minutes, with the majority of participants taking less than 8 minutes) and that on completion of the task, they would receive $0.20 deposited into their Amazon account. A link to Qualtrics (Provo, UT) was included in the MTurk request.

After agreeing to participate and receiving instructions, participants completed the Kirby (2009) questionnaire. Each of the 27 questions (which were presented in the order specified in Kirby, 2009) asked participants to choose between a smaller, immediate reward and a larger, delayed reward. In addition, we added a final, 28^th question, similar in form as well as in the amounts and the delay involved, which served as a catch trial: “Which would you prefer to receive, $59 now or $21 in 139 days?” All 111 participants chose the “$59 now” alternative. Following completion of the questionnaire, participants answered a series of demographic questions, after which they were provided with a password to use to arrange for their payment from MTurk.

Materials

The 27 questions of the Kirby (2009) questionnaire can be divided into three sets of 9 each, based on whether the delayed reward is small ($25, $30, or $35), medium ($50, $55, or $60), or large ($75, $80, or $85). Alternatively, the 27 questions can be divided into 9 groups of 3 each, with one small amount question, one medium amount question, and one large amount question for each of 9 values of k. When divided into sets of 9 based on the amount of the delayed reward, the questions in each set yield nine logarithmically spaced values of the k-parameter in Equation 1, ranging from approximately 0.00016 to approximately 0.25. This may be seen in Table 1, which reproduces the amounts of the immediate and delayed rewards together with the delays for the set of nine questions involving the small reward amounts. The k values were calculated based on the equation $k=[(A/V)-1]/D$, which is Equation 1 solved for k (note that when the immediate and delayed rewards are equal in subjective value, V and A represent their respective amounts).

Table 1.

Immediate (I) and Delayed (D) Reward Amounts and Their Ratio (I/D), Delay to the Larger Reward (in days), and Values of k for the Small Delayed Rewards Questions.

I($)	D($)	Ratio	Delay	k
34	35	.97	186	0.00016
28	30	.93	179	0.00040
22	25	.88	136	0.0010
25	30	.83	80	0.0025
19	25	.76	53	0.0060
24	35	.69	29	0.016
14	25	.56	19	0.041
15	35	.43	13	0.10
11	30	.37	7	0.25

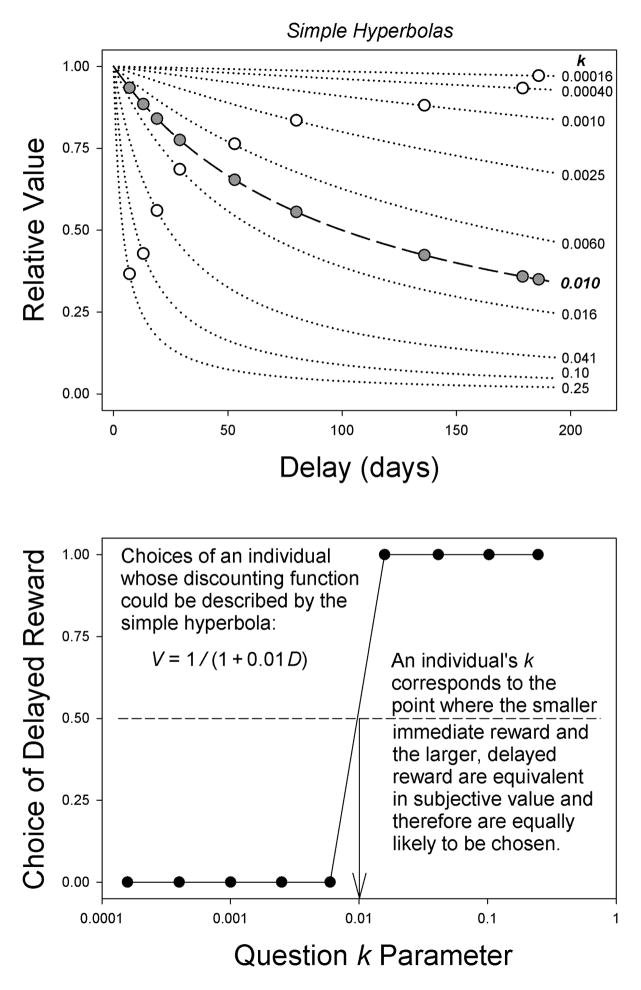
Figure 1 illustrates the logic underlying the Kirby (2009) questionnaire, its scoring and analysis. Each open circle in the top panel corresponds to one of the nine questions that involve a small amount ($25–$35) of delayed reward (Table 1); similar graphs would describe the nine questions for the medium and large amounts. The X-coordinate of the circle indicates how long one would have to wait for the delayed reward, and the Y-coordinate indicates how much one could have immediately (as a proportion of the delayed amount) if one decided not to wait. Each circle lies along a dashed line that represents the hyperbolic discounting curve (Eq. 1) for an individual with a specific k (indicated on the right side of the top graph), one who would find that pair of immediate and delayed rewards to be equal in subjective value. For example, the leftmost circle corresponds to the question about small reward amounts that has the shortest delay (see Table 1), a choice between $11 now and $30 after 7 days, for which the immediate reward has a relative value of 11/30 or .37.

Figure 1.

Graphs illustrating the logic underlying the Kirby (2009) questionnaire. In the top panel (modeled after Figure 2A in Wileyto et al., 2004), the value of the immediate reward, expressed as a proportion of the amount of the delayed reward, is plotted as a function of delay for the nine questions involving a small amount of delayed reward (white circles). The dotted curves represent the simple hyperbolic discounting functions associated with each of these pairs of immediate amounts and delays; the values of the k parameter in these discounting functions are indicated at the right. The solid curve represents the discounting function V=1/(1+kD) where k = 0.010, and the dark circles represent the values predicted by this function for each of the nine questions. The bottom panel shows the probability of choosing the delayed reward (solid circles) predicted by the hyperbolic discounting function of the hypothetical individual depicted in the top panel.

The questionnaire is scored based on the assumption that if a circle lies above an individual’s discounting curve, then the amount available now is more than the subjective value of the delayed reward, and the individual would choose the immediate reward; if the circle lies below an individual’s discounting curve, then the amount one could have now is less than the subjective value of the delayed reward, and the individual would choose to wait. Thus, for individuals who are such steep discounters that their discounting functions are below the lowest dotted line, the immediately available amount in the nine Kirby questions is always more than the subjective value of the delayed amount, and they would never choose the delayed option. In contrast, for individuals who are such shallow discounters that their discounting functions are above the highest dotted line, the immediately available amount is always less than the subjective value of the delayed reward, and they would always choose to wait for the larger, delayed reward. Someone with a discounting function corresponding to a more typical value of k, however, would show a switch in preference from the immediate alternative to the later alternative as the k value associated with a question increased.

More specifically, someone with a k parameter of 0.010 (i.e., someone whose discounting function corresponds to the dashed curve, V = 1 / (1 + 0.01D), in the top panel of Figure) would choose the immediate amounts on the questions corresponding to the four highest k values (represented by the four circles in the lower left portion of the graph), but would choose the delayed reward on the questions corresponding to the five lowest k values (represented by the five circles in the upper right portion of the graph). This pattern of choice is depicted in the lower panel of Figure 1. The observed sequence of five 0s and four 1s corresponding to the nine questions is appropriate for analysis with logistic regression (also known as logit regression). Such analysis estimates the parameter values that produce the best-fitting regression equation: $\text{logit}(P)=b+m\ast log(k)$, where the logit transformation converts a probability to the logarithm of the odds. This equation then may be solved to determine the value of k at which the probability of choosing the delayed reward is .50 (i.e., when logit(P) = 0, and log(k) = −b/m), which corresponds to the value of k in a simple hyperbolic discounting function that would give rise to the observed sequence.

Data Analysis

At the group level, the responses to the Kirby (2009) questionnaire were analyzed by calculating the proportion of participants choosing the larger, delayed reward on each question, and then fitting logistic growth functions using nonlinear regression with a least squares criterion. If individual participants show patterns of choices similar to those assumed in the development of the Kirby questionnaire, but k varies across participants, then the proportion choosing the delayed reward should increase sigmoidally across questions as the k associated with the questions increases.

At the individual level, participants’ responses to the Kirby (2009) questionnaire were scored in three different ways. First, individual participants’ k-parameter values were estimated using the method described by Kirby et al. (1999) in which each participant was assigned to a range of k-parameters that yielded the highest proportion of choices consistent with that value. There are 10 such ranges for the Kirby questionnaire: k less than 0.00016, k between 0.00016 and 0.0004, k between 0.0004 and 0.0010, etc., with the tenth range being k greater than 0.25 (see Table 1). Following Kirby et al., k-parameter values for participants assigned to the lowest and highest ranges were estimated to be 0.00016 and 0.25, respectively, and other participants’ k parameters were estimated as the geometric midpoint of the range to which they were assigned.

Second, when possible, individual participants’ k-parameter values also were estimated using logistic regression (Wileyto et al., 2009). Third and finally, each individual’s responses were scored as the proportion of questions on which the individual chose the larger, delayed reward over the smaller, immediate one (i.e., number of choices of a delayed reward divided by the number of questions).

The correlation between the logarithms of individual k-parameter estimates and the proportion of the 27 questions on which individuals chose the delayed reward provided an assessment of the concurrent validity of the proportion measure. In addition, the three amount conditions were taken as alternate test forms, and correlations among individuals’ choices in the three conditions were used to assess the reliability of the proportion measure of individual performance on the Kirby questionnaire. Finally, choices in the three amount conditions were compared in order to determine whether the amount of the delayed reward had effects on the proportion measure consistent with previously reported magnitude effects.

Results

Figure 2 depicts the proportion of participants choosing the larger, delayed option on each question of the Kirby questionnaire, plotted as a function of the k value associated with that question. As may be seen, the proportion of choices of a delayed reward of a given size (i.e., small, medium, or large) increased systematically as a function of the logarithm of the k values for the set of nine questions that concerned that amount. That is, choice of the delayed reward increased as either the delay to that reward, or the size of the immediate alternative, or both, decreased (see Table 1). For all three sizes of delayed reward, the increase was sigmoidal in nature and was well described by a logistic growth function (all three R²s > .98):

$$V=1/[1+{\mathrm{e}}^{-(x-x_0)r}],$$ (2)

where x is the logarithm of the k-parameter values associated with the various questions, x₀ is an intercept parameter that shifts the curve horizontally, and r is a rate parameter that describes the rate of increase in the proportion of later choices.

Figure 2.

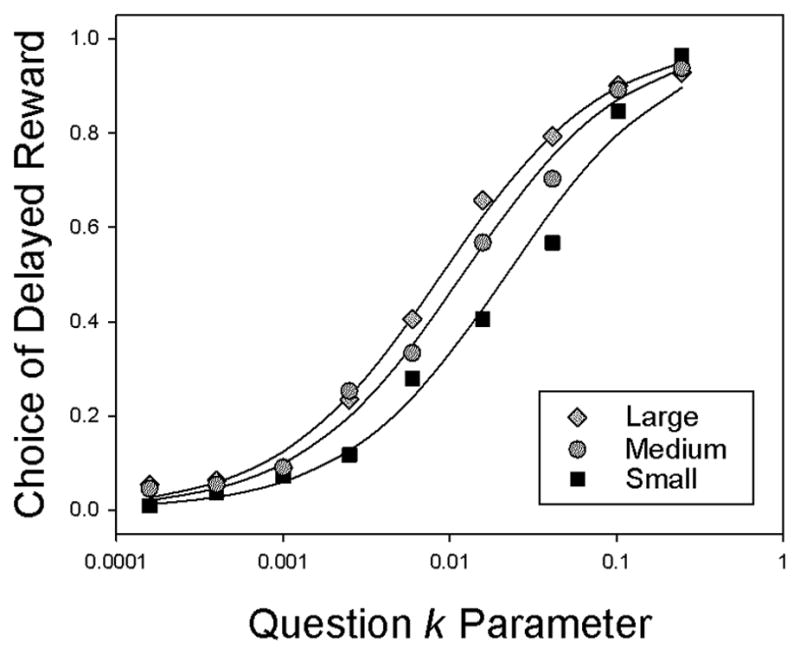
The proportion of participants choosing the larger, delayed reward on the 27 questions of the Kirby (2009) questionnaire, plotted as a function of the values of k associated with those questions. The curves represent the fit of a four-parameter logistic growth model (see text).

Visual inspection of Figure 2 suggests that while the shape of the growth curves remained the same across the three amount conditions, the curve for the small delayed reward was shifted to the right of the curve for the medium delayed reward, which was to the right of the curve for the large delayed reward. As a result, at any value of k, the proportion of choices of the delayed reward tended to be greater for the larger delayed amount than for the medium amount, and greater for the medium amount than for the small amount. Such shifts correspond to magnitude effects like those reported in previous studies of the discounting of delayed gains (Frederick et al., 2002; Green & Myerson, 2004), with discounting becoming progressively shallower as the amount increased.

The rightward shift of the logistic function as the amount of delayed reward decreased that is apparent in Figure 2 may be captured mathematically by decreases in the x₀ parameter of the function. Indeed, when three logistic functions with the same value for the r parameter and three different amount-dependent values of x₀ to be estimated, for a total of four free parameters, were fit to the data from the three amount conditions simultaneously (see Figure 2), these functions accounted for 99.2% of the variance. Because the logistic growth function closely approximates the cumulative normal (i.e., the Gaussian distribution function), these results suggest that the distribution of k across individuals is log normal, with similar standard deviations but different means for the different amounts of reward.

To this point, our analysis has focused on group data (proportions of the sample choosing the delayed reward on each question). Further analyses of our internet data at the individual level used three different measures of the degree to which individuals discount delayed rewards. First, following the procedure described by Kirby et al. (1999), each individual’s choices were assigned to the range of k-parameter values that yielded the highest proportion of choices consistent with a value of k in that range; second, following Wileyto et al. (2004), we analyzed each participant’s data using logistic regression to obtain individual estimates of the k parameter, and third, we calculated the proportion of questions for which each individual chose the larger, later reward.

The proportion measure builds on the same logic that underlies both Kirby et al.’s scoring system (1999) and Wileyto et al.’s (2004) logistic regression approach. This logic assumes a pattern of responses similar to that depicted in the lower panel of Figure 1, with the logarithm of an individual’s k marking the midpoint of that individual’s switch from choosing the immediate reward on questions associated with smaller values of k to choosing the larger delayed reward on questions associated with higher values of k. If this logic is correct, then the higher an individual’s k is, the fewer questions on which that individual will pick the delayed reward option. In fact, regardless of how individual ks are estimated, the number of questions on which one chooses the delayed option should be a negative linear function of the logarithm of one’s k value, a testable prediction independent of whether either measure reveals the expected magnitude effect.

The distribution of proportion measures was approximately Gaussian, as evidenced by the close correspondence of the mean and median proportions (.418 and .407, respectively), skewness of 0.301, and kurtosis of 0.099, and nonsignificant results of the Shapiro-Wilk and Komogorov-Smirnov tests of normality (both ps > .17). Moreover, the mean was approximately in the center of the range of possible scores (from .00 to 1.00), with a standard deviation small enough (0. 199) to minimize problems with floor and ceiling effects. In contrast, the distribution of individual log k parameters estimated using the Kirby et al. (1999) procedure (M = −1.930, SD = 0.745), although similarly symmetrical (median = −2.009, skewness = −0.305, kurtosis = −0.318) differed significantly from normal by Shapiro-Wilk and Komogorov-Smirnov criteria (both ps = .001 or less)). Notably, the average k value for the current sample recruited and tested over the internet was 0.012, nearly identical to the average k value of 0.013 reported for the 60 participants in the control group of the Kirby et al. study who were recruited using newspaper advertisements and who were of similar age (M = 35.4 years) to the present sample.

As predicted, the correlation between the logarithms of individual k-parameters estimated using Kirby et al.’s (1999) procedure and the proportions of delayed reward choices was negative and extremely strong (r = −.97). In addition, the correlation between the proportions of delayed reward choices and the logarithms of individual k-parameter estimates obtained using logistic regression (Wileyto et al., 2004) was also negative and extremely strong (−.99), although there were 6 participants for whom k could not be estimated this way. The pattern of extremely strong correlations among the discounting measures suggests that they are measuring the same construct.

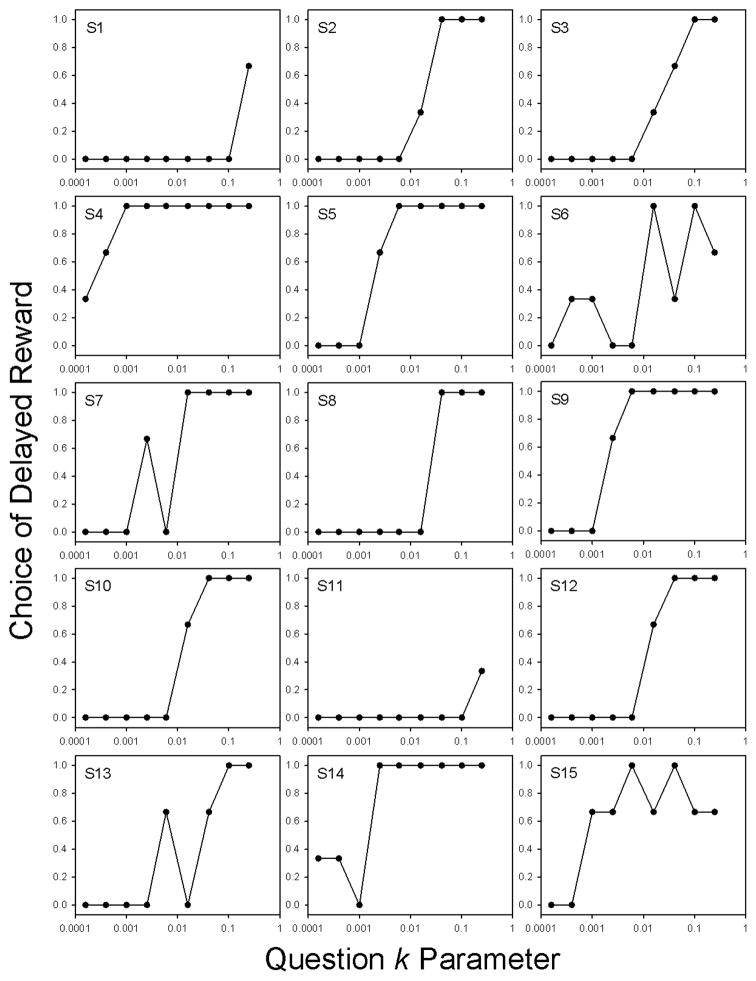
At the individual level, the pattern of results may be illustrated using the data from the first 15 participants in the present study. As may be seen in Figure 3, which plots the proportion of choices of the delayed reward as a function of the value of k for each group of three questions with approximately the same value of k, all of the first 15 participants tended to show the predicted pattern of response, switching from choices of mostly the immediate reward on questions associated with low values of k to choices of mostly the delayed reward on questions associated with high values of k, although they varied considerably in what k value the switch in preference occurred at and how clean the transition was. Even the participant (S11) who only chose the delayed reward once out of the 27 opportunities did so on the question associated with the highest value of k, as would be expected for such an ‘impatient’ individual. It should be noted, however, that this participant was one of those whose data could not be fit using logistic regression. At the other extreme, another of the first fifteen participants (S4) chose the delayed reward on twenty-four questions, and as expected for such a ‘patient’ individual, these were questions associated with the lowest and next-to-lowest k values. Overall, the proportions of choices of a delayed reward were tightly coupled to the estimated k values for the fourteen of the first fifteen individuals whose k could be estimated using logistic regression, as evidenced by a correlation between the proportion measure and the logarithm of k equal to −.99.

Figure 3.

The proportions of choices of the larger, delayed reward on the Kirby questionnaire for the first 15 participants in the present study.

In addition to each individual’s proportion of delayed reward choices for all 27 questions, the proportion of delayed reward choices was calculated for each amount separately. The correlations between individuals’ delayed choice proportions for the three different amount conditions, each of which may be thought of as an alternative form of the Kirby (2009) questionnaire, reflect the reliability of the proportion measure. These correlations were all greater than .83, indicating that the questionnaire meets psychometric standards of reliability when it is scored using the proportion of delayed choices measure.

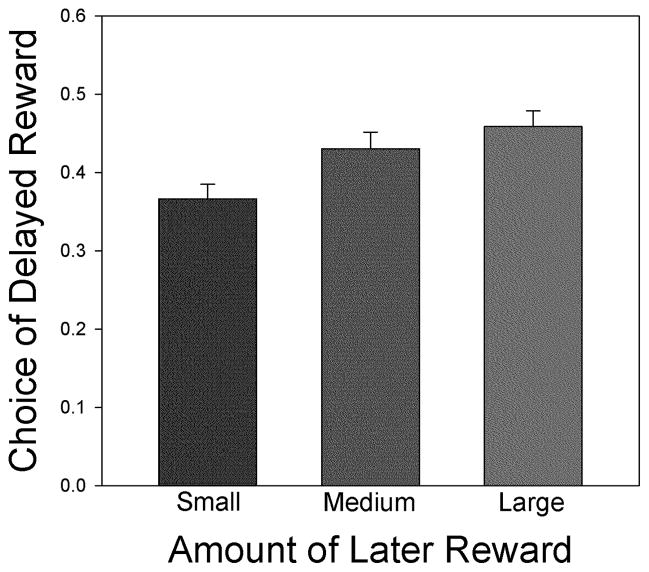
Planned contrasts revealed that individuals’ proportions of choices of the delayed reward on small amount questions differed significantly from their proportions of such choices on medium amount questions (t(110) = 6.04, p < .001), which in turn differed significantly from their proportions of choices on large amount questions (t (110) = 2.77, p = .006). The observed differences, which may be seen in Figure 4, reflect systematic increases in the proportion of choices of the delayed reward as its amount increased from small to medium and again from medium to large. These results, which are consistent with the well-established magnitude effect in delay discounting (Green & Myerson, 2004), provide further evidence of the validity of the Kirby (2009) questionnaire with scoring based on the proportion of choices of the delayed reward.

Figure 4.

The proportions of participants (with standard error bars) choosing the larger, delayed gain on the small, medium, and large amount questions of the Kirby questionnaire.

Discussion

Taken together, the present results suggest that the proportion of choices of delayed rewards provides a measure of individuals’ delay discounting that is much simpler to calculate and applicable to more individuals than are estimates of individual k parameters. Importantly, these advantages may be achieved without sacrificing validity, either criterion validity, as indicated by the strong correlation between log k and the proportion of choices of delayed rewards, or construct validity, as evidenced by the significant effects of amount on the proportion measure of discounting. Moreover, the advantages of the proportion measure do not require sacrificing reliability, as evidenced by the strong correlations among measures for the different amounts. As noted previously, the questions involving each of the three delayed amounts (small, medium, and large) may be thought of as representing alternate short forms of the Kirby (2009) questionnaire, and the correlations among them provide estimates of their reliability. Using the Spearman-Brown prophesy formula and the reliability of these short forms, the reliability of the complete 27-item Kirby questionnaire using proportion scores is estimated to be at least .94.

The goal of the present effort was to assess the reliability and validity of an alternative approach to measuring how steeply individuals discount the value of delayed rewards. This measurement approach was of interest in part because it offered the possibility of a simple, straightforward scoring method that might increase measurement precision while facilitating the study of individual differences in discounting using very large samples. Equally important, however, was to establish an alternative to measures that seek to characterize individuals by estimating the k parameter of their individual discounting functions.

Extensive research has shown that a simple hyperbola is often not the best way to describe delay discounting functions at either the individual or the group level (Myerson & Green, 1995; Green & Myerson, 2004). A number of alternatives have been proposed, including exponential decay functions which, like the hyperbola, have only a single free parameter to be estimated, two-parameter hyperboloid discounting functions (Green, Fry, & Myerson, 1994; Prelec & Loewenstein, 1991; Rachlin, 2006), as well as forms with three free parameters, like the quasi-hyperbolic (or beta-delta; Laibson 1997; McClure, Laibson, Loewenstein, & Cohen, 2004) and the double-exponential discounting functions (van den Bos & McClure, 2013). Theoretically grounded measures may be the ultimate goal, but such measures assume a degree of consensus that does not yet exist in the field of discounting research.

Moreover, the theoretical models on which such measures are based may provide more detailed descriptions than are necessary or even desirable in certain applications. This can occur when the relation between the parameters of a model is such that estimating multiple parameters necessarily entails less accurate estimation of individual parameters, as is likely to be the case with current discounting models. One approach designed in response to this issue is the area-under-the-curve measure (Myerson, Green, & Warusawitharana, 2001), which provides a theoretically neutral way to describe discounting data consisting of multiple indifference points. However, the efficiency of the Kirby (2009) questionnaire is derived from the fact that it does not require determining indifference points, and thus if one wants the advantages that Kirby’s questionnaire provides, a different approach to theoretically neutral measurement is needed.

We have described such an alternative here – one that, although it builds on the logic of Kirby’s original approach (Kirby & Maraković, 1996), does not rely on assumptions regarding the mathematical form of the discounting function. Although the Kirby (2009) questionnaire may appear to have been designed with a simple hyperbolic discounting function in mind, the underlying logic, while compatible with this model, is much more general. Indeed, Kirby and Maraković intended their original questionnaire to be theoretically neutral, at least in the sense of being compatible with both hyperbolic and exponential discounting functions, although they believed the evidence clearly favored the former. In fact, they pointed out that the consistency scores on which their scoring method is based are themselves relatively neutral because they will be the same regardless of whether one assumes hyperbolic or exponential discounting (or, for that matter, other systematically decreasing functions). Thus, there is no inherent contradiction between consistency scores and measuring discounting using the proportion of choices of a delayed reward, and a computer program could easily provide researchers with both kinds of information.

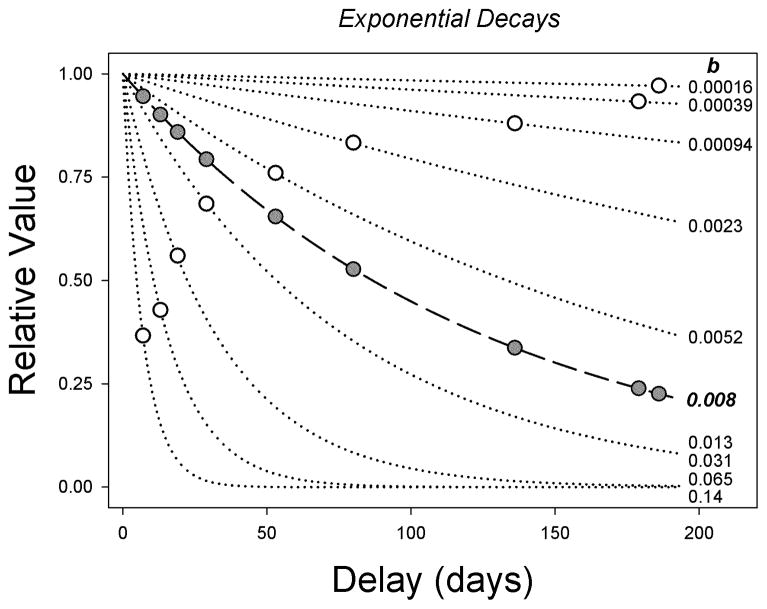
Consider Figure 5, for example, in which each of the nine small amount questions is characterized by a different rate parameter, b, in an exponential decay function (V = A e ^−bD), rather than by the rate parameter, k, in a hyperbola (Eq. 1). A hypothetical individual with an exponential discounting function like that depicted would show the same pattern of responses, five immediate choices followed by four later choices, as the hypothetical individual with a hyperbolic discounting function depicted in Figure 1. Moreover, based on their response patterns, both individuals could be characterized in terms of either an exponential or a hyperbolic discounting rate, regardless of whether the form of the individual’s discounting function was itself exponential or hyperbolic. Indeed, so could an individual whose discounting functions were hyperboloid in form.

Figure 5.

Graphs illustrating the logic underlying the Kirby (2009) questionnaire using exponential discounting functions. The amount of the immediate reward, expressed as a proportion of the delayed amount, is plotted as a function of delay for the nine questions involving a small amount of delayed reward (open circles). The dotted curves represent the exponential discounting functions associated with each of these pairs of immediate amounts and delays; the values of the rate parameter, b, in these discounting functions are indicated at the right. The solid curve represents the discounting function V = e ^−bD with b = 0.008.

For example, an individual whose discounting of small reward amounts was best described by the equation $V=1/{(1+0.03D)}^{0.5}$ would also have the same pattern of responses depicted in the bottom panel of Figure 1. This person would respond this way despite the fact that the equation predicts lower subjective values at brief delays and higher subjective values at longer delays than the simple hyperbola with k=0.01 that describes the hypothetical individual in that figure. In principle, one could calculate the discounting rates for a hyperboloid with an exponent of 0.5 (or any other exponent) that would correspond to each of the Kirby (2009) questions, and then score individuals’ responses using those discounting rates, rather than the values of k provided by Kirby or the exponential decay rates given in Figure 5.

We do not recommend doing so, however, but only raise the possibility in order to further demonstrate the arbitrariness of assigning discount rates to specific questions. That is, such assignments depend on specific assumptions regarding the form of individual discounting functions, a form that is still the subject of debate (e.g., Green, Myerson, Oliveira, & Chang, 2013; McClure et al., 2004; McKerchar, Green, & Myerson, 2010). Moreover, the actual rates at which individuals discount hypothetical monetary rewards are irrelevant for the purposes for which the questionnaire is most commonly used – determining whether those individuals or the groups to which they belong differ in their discounting of other types of rewards (e.g., drugs of abuse), rewards which are known to be discounted at rates that are different than those at which monetary rewards are discounted (e.g., Kirby & Petry, 2004).

Fortunately, as the present results demonstrate, it is unnecessary to wait for consensus on the form of the discounting function. Instead, one can simply take the Kirby (2009) questionnaire at face value as a series of choices between immediate and delayed rewards that is extremely efficient in determining whether a person is more or less likely than other individuals to be willing to wait for a larger reward. In short, the Kirby questionnaire itself is theoretically neutral, making its considerable advantages potentially available to all regardless of theoretical position. To those advantages, we propose adding a simple, straightforward scoring procedure that does an end run around both the potential difficulty and the theoretical baggage of other scoring methods. As the present results demonstrate, the combination of the Kirby questionnaire and our proposed measurement approach offers ease of administration and scoring, combined with valid and reliable assessment, that should facilitate the application of contemporary psychometric approaches to the study of individual and group differences in the discounting of delayed rewards.

• The Kirby questionnaire was scored using the proportion of delayed reward choices.

• Validity was evidenced by strong correlations with the logarithm of participants’ k values (r >.97).

• Reliability was evidenced by high correlations among scores for different amounts.

• Magnitude effects provided further validation of the simple proportion measure.

• The proportion measure is easy to calculate and does not require assuming a theoretical model.