Evaluating model based imputation methods for missing covariates in regression models with interactions

Abstract

Imputation strategies are widely used in settings that involve inference with incomplete data. However, implementation of a particular approach always rests on assumptions, and subtle distinctions between methods can have an impact on subsequent analyses. In this paper we are concerned with regression models in which the true underlying relationship includes interaction terms. We focus in particular on a linear model with one fully observed continuous predictor, a second partially observed continuous predictor, and their interaction. We derive the conditional distribution of the missing covariate and interaction term given the observed covariate and the outcome variable, and examine the performance of a multiple imputation procedure based on this distribution. We also investigate several alternative procedures that can be implemented by adapting multivariate normal multiple imputation software in ways that might be expected to perform well despite incompatibilities between model assumptions and true underlying relationships among the variables. The methods are compared in terms of bias, coverage and confidence interval width. As expected, the procedure based on the correct conditional distribution (CCD) performs well across all scenarios. Just as importantly for general practitioners, several of the approaches based on multivariate normality perform comparably to the CCD in a number of circumstances, although, interestingly, procedures that seek to preserve the multiplicative relationship between the interaction term and the main-effects are found to be substantially less reliable. For illustration, the various procedures are applied to an analysis of post-traumatic-stress-disorder symptoms in a study of childhood trauma.

1. Introduction

The issue of missing data is ubiquitous in both experiments and observational studies and can lead to substantial inferential bias if it is not appropriately addressed [1]. In regression settings, situations may arise where the dependent variable is missing, some of the covariates are missing, or both. When the focus is solely on inference about the regression parameters and only the outcome variable is missing, complete-case analysis is valid [2], although it may not be fully efficient compared to the alternative of using auxiliary information; the situation is more complicated when covariates are missing [3]. Multiple imputation [4–6] has emerged as a leading strategy for handling missing data primarily because it can provide a general purpose solution for a diverse set of problems under standard modeling assumptions. It has been implemented in many widely-available statistical software packages including SAS, Stata, and R [7–9]. All procedures for handling missing data make assumptions, whether implicitly or explicitly, about the joint distribution of the variables under consideration. One broad strategy for producing multiple imputations, represented in several ways in the text by Schafer [8], is to develop a joint model for the multivariate data distribution and generate imputations based on the corresponding conditional distributions using Markov-Chain Monte Carlo (MCMC) computational methods. One example of this approach is SAS PROC MI, which assumes multivariate normality among the available variables; such an approach can be expected to work well when the data are approximately multivariate normal, but would be expected to deteriorate in modeling situations which involve multiple variable types, require transformations, or need interactions terms to reflect the patterns in the data.

Another broad strategy, which can be motivated by analogy with MCMC methods for generating imputations from joint models, is to specify overlapping conditional distributions without regard for whether those distributions are consistent with a valid joint distribution [10–12]. Examples of this strategy include MICE [10, 11], ICE in Stata [13–15], and IVEWare [12]. Although such approaches have the flexibility to handle multiple variable types, questions about compatibility with a joint distribution can be regarded as an inherent weakness of methods based on specifying overlapping conditional distributions.

There has been recent attention to the importance of considering possible interactions among variables when performing imputation [16–18]. However, the various approaches that have been proposed do not necessarily respect implied constraints and relationships among the variables in the joint distribution function. Specifically, among methods that impute one variable at a time, the existence of interaction effects adds a layer of incompatibility to the procedure, e.g., if a provisional value of the interaction product term is treated as “just another variable” for imputing a missing covariate, the multiplicative relationship between the main effects and interaction is not enforced as a constraint. Accordingly, this paper instead considers a joint modeling strategy for producing multiple imputations in the context of a regression problem where the relationships among variables include interactions.

We focus on providing a systematic treatment of the case where the underlying model is a linear regression with interaction terms, although the basic approach could be extended to other contexts involving composite variables. Specifically, we examine a setting where one of the primary predictors and an interaction term involving that predictor are missing. We consider two main approaches for producing multiple imputations in this setting. The first strategy involves preserving the multiplicative relationship between the primary predictors and the interaction term by deriving the correct conditional distributions for the missing values from the joint distribution of the variables. The second strategy involves approximating the correct conditional distribution (CCD) using standard imputation software [17–19], in order to investigate whether existing multiple imputation software using a multivariate normal model can be adapted to perform well. Candidate approximations include multivariate normal imputation models with or without interaction term in the model, where the relationship of the interaction term may or may not be constrained to be a product of the two predictors. Log transformations are also considered in the imputation model to account for nonlinearity of the interaction term.

In Section 2, we derive the bivariate conditional distribution for a missing covariate and a related interaction term in a regression setting with two continuous covariates and present an MCMC imputation procedure based on this conditional distribution. In Section 3, we consider candidate approximations based on multivariate normal (MVN) imputation, and compare the performance of the imputation procedures through a simulation study. In Section 4, the procedures are applied to analyses of post-traumatic-stress-disorder symptoms in a study of childhood trauma, and finally, in Section 5 we give a discussion on imputation methods for accommodating interactions in regression models with missing covariates.

2. Methods for Imputation Via a Joint Model in the Presence of An Interaction

We restrict our attention specifically to the setting of a linear regression model with two continuous predictors, X₁ and X₂, and their interaction, X₁₂ = X₁ × X₂. Without meaningful loss of generality, we assume that the dependent variable is completely observed. For the theoretical development that follows, we assume a monotone pattern of missingness in the primary covariates, whereby X₁ is fully observed and X₂ is partially missing. The interaction term, X₁₂ is necessarily missing if and only if X₂ is missing, given the deterministic relationship among the model terms. The goal is to impute the values of the missing X₂ and X₁₂. We begin by deriving the conditional distribution of X₂ and X₁₂. We assume here that each of X₁, X₂ and the residual errors are normally distributed, although similar derivations could be done for other covariate distributions. However, the non-linear relationship between the interaction term and the predictors means that the variables in the imputation model are not jointly multivariate normal.

2.1. Derivation of the Correct Conditional Distribution

The conditional distribution of [X₂|X₁, Y] can then be derived using the Bayes theorem. Specifically, let

$$\left(\begin{array}{c}{X}_1\\ X_2\end{array}\right)~N\left(\right(\begin{array}{c}{\mu }_1\\ {\mu }_2\end{array}),(\begin{array}{cc}{\sigma }_1^2& \rho {\sigma }_1{\sigma }_2\\ \rho {\sigma }_1{\sigma }_2& {\sigma }_2^2\end{array}\left)\right)$$

and

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_1{X}_2+\mathit{\in },\mathit{\in }~N(0,{\sigma }_{\mathit{\in }}^2).$$

Then Y has a multivariate normal distribution conditional on X₁ and X₂ given by

$$[Y|X_1{X}_2]~N({\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_1{X}_2,{\sigma }_{\mathit{\in }}^2).$$

To impute the missing values for X₂ and X₁₂, we use draws from the conditional distribution [X₂|Y, X₁] and calculate X₁₂ = X₁X₂ using the observed X₁ and the drawn value of X₂. This can be shown to be equivalent to drawing from the the joint conditional distribution of X₂ and X₁₂ given X₁ and Y, which will be given later in this section.

By Bayes Theorem, P(X₂|X₁, Y) ∝ P(Y|X₁, X₂)P(X₂|X₁). For variables that are jointly normally distributed, the conditional distribution of X₂ given X₁ has a normal distribution of the form

$$[X_2|X_1]~N({\mu }_2+\rho {\sigma }_2/{\sigma }_1(X_1-{\mu }_1),{\sigma }_2^2(1-{\rho }^2)).$$

Therefore, the conditional distribution can be expressed as follows:

$$\begin{array}{c}P(X_2|Y,X_1)\propto P(Y|X_1,X_2)P(X_2|X_1)\\ \propto exp[-\frac{1}{2}(X_2^2(\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2})-2X_2(\frac{{\mu }_2+(X_1-{\mu }_1)\rho {\sigma }_2/{\sigma }_1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{(Y-{\beta }_0-{\beta }_1{X}_1)({\beta }_2+{\beta }_3{X}_1)}{{\sigma }_{\mathit{\in }}^2})\left)\right].\end{array}$$

This shows that [X₂|X₁, Y] has a normal distribution with a mean and variance that depend on the joint distribution of X₁ and X₂ as well as on the regression parameters and observed values X₁ and Y:

$$[X_2|X_1,Y]~N(E(X_2|X_{1}Y),\mathit{Var}(X_2|X_1,Y))$$

$$E(X_2|X_1,Y)=\frac{\frac{{\mu }_2+(X_1-{\mu }_1)\rho {\sigma }_2/{\sigma }_1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{({\beta }_2+{\beta }_3{X}_1)(Y-{\beta }_0-{\beta }_1{X}_1)}{{\sigma }_{\mathit{\in }}^2}}{\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2}},$$

$$\mathit{Var}(X_2|X_{1}Y)={[\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2}]}^{-1}.$$

The interaction term, X₁₂, can be calculated by multiplying the observed X₁ and the value of X₂ drawn from the above conditional distribution. It can be shown that this is equivalent to drawing the missing X₂ and X₁₂ as a pair from the joint conditional distribution of X₂ and X₁₂ given the observed X₁ and Y, which has the following distribution.

$$[X_2,X_{12}|X_1,Y]~N(E(X_2,X_{12}|X_1,Y),\mathit{Var}(X_2,X_{12}|X_1,Y))$$

$$E(X_2,X_{12}|X_1,Y)=(\frac{\frac{{\mu }_2+(X_1-{\mu }_1)\rho {\sigma }_2/{\sigma }_1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{({\beta }_2+{\beta }_3{X}_1)(Y-{\beta }_0-{\beta }_1{X}_1)}{{\sigma }_{\mathit{\in }}^2}}{\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2}},X_1\left[\frac{\frac{{\mu }_2+(X_1-{\mu }_1)\rho {\sigma }_2/{\sigma }_1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{({\beta }_2+{\beta }_3{X}_1)(Y-{\beta }_0-{\beta }_1{X}_1)}{{\sigma }_{\mathit{\in }}^2}}{\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2}}\right])$$

$$\mathit{Var}(X_2,X_{12}|X_1,Y)={[\frac{1}{{\sigma }_2^2(1-{\rho }^2)}+\frac{{({\beta }_2+{\beta }_3{X}_1)}^2}{{\sigma }_{\mathit{\in }}^2}]}^{-1}(\begin{array}{cc}1& X_1\\ X_1& X_1^2\end{array}).$$

Note that if β₃ = 0 this reduces to a standard linear regression model and draws from the above conditional distribution are consistent with the multivariate-normal models used in standard software implementations such as PROC MI.

2.2. An MCMC Imputation Procedure Using Draws from the Correct Conditional Distribution

This section outlines an MCMC imputation procedure based on the correct conditional distribution (CCD). In the initial cycle calculations are based on the values from the complete cases only, while in subsequent cycles all observed values plus the imputed values from the previous step are used. This procedure can be employed to obtain multiple completed data sets, which can then be analyzed using standard complete data methods and the results combined to form a single inference.

Algorithm

1. Draw Σ^(t)|X₁, $X_2^{(t)}$, Y ∼Inverse-Wishart (n–1,(n–1)S^(t)), where $S^{(t)}={\sum }_{i=1}^n[X_i^{(t)}-{\overline{X}}^{(t)}]{[X_i^{(t)}-{\overline{X}}^{(t)}]}^{\prime }$, and

   $$X_i^{(t)}=\left(\begin{array}{c}{X}_{i1}\\ X_{i2}^{(t)}\end{array}\right)\text{and}{\overline{X}}^{(t)}=\left(\begin{array}{c}{\overline{X}}_1\\ {\overline{X}}_2^{(t)}\end{array}\right)$$

   are derived from the sample.

2. Draw μ^(t)| X₁, $X_2^{(t)}$, Y, ${\sum }^{(t)}~N({\overline{X}}^{(t)},\frac{1}{n}{\sum }^{(t)})$

3. Draw ${\sigma }_{\mathit{\in }}^{2\left(t\right)}|X_1,X_2^{(t)}$, Y ∼ Scaled-Inverse ${\chi }_{n-4}^2$ With ${\sigma }_{\mathit{\in }}^{2(t)}~(n-4)\frac{s^{2(t)}}{{\chi }_{n-4}^2}$, where $s^{2(t)}=\mathit{var}(Y-b_0^{(t)}-b_1^{(t)}{X}_1-b_2^{(t)}{X}_2^{(t)}-b_3^{(t)}{X}_{12}^{(t)})$, and $b_0^{(t)},b_1^{(t)},b_2^{(t)},b_3^{(t)}$ are fitted values of regression coefficients.

4. Draw β^(t)| X₁, $X_2^{(t)}$, Y, ${\sigma }_{\mathit{\in }}^{2(t)}~\mathit{\text{MVN}}(\widehat{{\beta }^{(t)}},{\sigma }_{\mathit{\in }}^{2(t)}{(X^{\prime }X)}^{-1})$ where

   $$X=\mathit{\text{array}}(\underset{\_}{1},X_1,X_2^{(t)},X_{12}^{(t)}),\widehat{{\beta }^{(t)}}=\left(\begin{array}{c}{b}_0^{(t)}\\ b_1^{(t)}\\ b_2^{(t)}\\ b_3^{(t)}\end{array}\right)$$

5. Draw $X_2^{(t+1)},X_{12}^{(t+1)}|X_1$, Y, μ^(t), Σ^(t), β^(t), ${\sigma }_{\mathit{\in }}^{2(t)}$ jointly by drawing $X_2^{(t+1)}$ from the conditional distribution, and then calculating the product, $[X_{12}^{(t+1)}|X_1,X_2^{(t+1)}]=X_1\times X_2^{(t+1)}$.

6. Update $X_2^{(t+1)},X_{12}^{(t+1)}$, μ^(t), Σ^(t), β^(t), ${\sigma }_{\mathit{\in }}^{2(t)}$ and iterate.

Note that in Step 3, having a regression model with different number of predictors would affect the degrees of freedom.

3. Candidate Approximations Using Adaptations of Standard MVN Imputation and their performance relative to the Correct Conditional Distribution

3.1. Adapting Standard MVN Imputation

First we consider the candidate approximation procedures that would be readily available to data analysts, some of which were considered in Seaman [18], Von Hippel [17], as well as Kim [19], others not previously appeared in the literature. Some of these procedures preserve the structure of the interaction term as a product of the covariates, while others do not enforce the constraint. Because of the nonlinearity of the interaction term, we also investigate performing log transformations prior to imputation and then transforming back after imputation. This is motivated partly by the fact that the log transformation translates multiplicative effects to additive effects and pulls in extreme values and partly because it may help to limit propagation of errors when multiplying large quantitites (e.g. computing X₁₂ from X₁ and imputed X₂) or dividing by values near 0 (e.g. computing X₂ from X₁ and an imputed X₁₂). Eight different imputation methods, described below, are considered as candidates for comparison:

1. Just Another Variable (JAV): Impute X₂ and X₁₂, as separate variables; equivalent to ‘Impute All Unconstrained (IAU)’ in Kim [19]

2. Passive Imputation (PSI): Impute X₂ only and calculate X₁₂ = X₁ × X₂; equivalent to Impute and Calculate Constrained (ICC) in Kim [19]

3. Impute All, Recalculate by Multiplication (IARM): Impute X₂ and X₁₂, drop X₁₂, and recalculate X₁₂ = X₁ × X₂

4. Impute All, Recalculate by Division (IARD): Impute X₂ and X₁₂, drop X₂, and recalculate X₂ = X₁₂ ÷ X₁

5. Log Just Another Variable (logJAV): Take logs [log Y, log X₁, log X₂, log X₁₂], and impute log X₂ and log X₁₂

6. Log Passive Imputation (logPSI): Take logs [log Y, log X₁, log X₂], and impute log X₂ only, and calculate log X₁₂ = log X₁ + log X₂

7. Log Impute All, Recalculate by Multiplication (logIARM): Take logs [log Y, log X₁, log X₂, log X₁₂], and impute log X₂, log X₁₂, drop log X₁₂, and recalculate log X₁₂ = log X₁ + log X₂

8. Log Impute All, Recalculate by Division (logIARD): Take logs [log Y, log X₁, log X₂, log X₁₂], and impute log X₂, log X₁₂, drop log X₂, and recalculate log X₂ = log X₁₂ − log X₁.

As indicated above, Kim [19] used different naming conventions for these procedures, with JAV equivalent to “Impute All Unconstrained” and PSI equivalent to “Impute and Calculate Constrained”. Here, we have updated the labels of these procedures to agree with names used by other authors in recently published work [17, 18]. We note that JAV includes all four variables (Y, X₁, X₂, X₁₂) in the imputation model and places no constraints on the interaction term. This implies that the imputed values of X₁₂ will not in general be equal to the product of the observed X₁ and the imputed value of X₂. On the other hand, procedures PSI, IARM, and IARD preserve the relationship by recalculation of either X₂ or X₁₂ after imputation. In logJAV, logPSI, logIARM, and logIARD, imputations are performed on the log scale and the results are then transformed back to the original scale by exponentiation prior to analysis.

3.2. A Comparison of the Candidate Approximations

Prior to comparing their performance to CCD in detailed manner the eight candidate approximations are evaluated in a preliminary study. Specifically, we use PROC MI for imputation, and vary the means, variances and the correlation between X₁ and X₂. The mechanism is chosen to be MCAR, since if the methods do not perform well in this straightforward setting they are unlikely to be appropriate for general use. We consider a regression setting

$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_1{X}_2+\mathit{\in },$$

where ∊ ∼ N(0, υ_e), assuming that the true value for each regression coefficient equals 1. Each data set consists of 500 observations for which X₁ and Y are completely observed while 20% of X₂ and X₁₂ values are missing. We use the following combinations of parameter values in the simulations:

• Mean of (X₁, X₂) = (0,0), (0,5), (5,5)

• Variance of X₁ = 1

• Variance of X₂ = 1, 4

• Error Variance = 16

• Corr(X₁, X₂) = 0, 0.5, 0.9

The location of the X's may affect the performance, particularly for recalculation methods that involve multiplying large values or dividing by values near 0. The means of X₁ and X₂ are varied in pairs to be (0,0), (0,5) or (5,5) to test for such effects. The variance of X₁ is fixed at 1 while the variance of X₂ is varied be either 1 or 4 to determine whether the relative variance of the predictors is important. The error variance is fixed to be 16, while Corr(X₁, X₂) is allowed to take on the values (0, 0.5, and 0.9) to cover a wide range of possible relational effects. For each simulated data set we create 5 imputed versions using SAS PROC MI, fit the corresponding regression models for the imputed sets using PROC REG and then combine the results using PROC MIANALYZE. To evaluate the performance of the candidate approximate imputation procedures, we compute bias, confidence interval width, and confidence interval coverage for each of the regression coefficients [β₀, β₁, β₂, β₃].

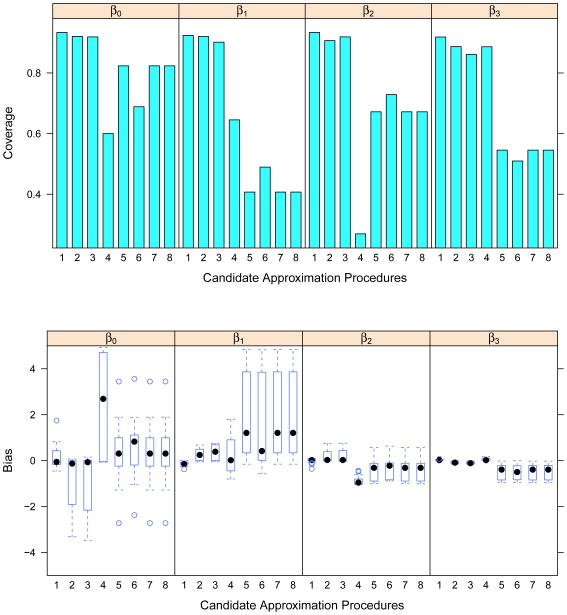
Figure 1 shows the performance of the eight candidate approximations based on the confidence interval coverage and bias. The values given are means across the scenarios considered as discussed above. JAV tends to yield the highest confidence interval coverage across all regression coefficients. IARD is unstable when the mean of X₁ is small, since it involves division by numbers close to zero. The procedures involving log transformations, namely logJAV, logPSI, logIARM and logIARD, display below nominal coverage. Out of the eight candidate approximations we considered, the results suggest that JAV tends to perform the best, which is consistent with the recommendation given in recent studies for treating the interaction term as just another variable [17, 18]. PSI and IARM are also stable, although they tend to yield lower CI coverage and larger bias compared to JAV. The three stable candidates, namely JAV, IARM, and PSI, are used in the simulation study in the next section. Given that methods 4-8 perform poorly across all scenarios with MCAR, these are not considered in the detailed comparison with CCD which includes a broader array of scenarios.

Figure 1. Comparisons of Candidate Approximation Procedures.

1. JAV, 2. PSI, 3. IARM, 4. IARD, 5. logJAV, 6. logPSI, 7. logIARM, 8. logIARD

3.3. Comparison of the Correct Conditional Distribution and selected Multivariate Normal Approximation Procedures

Simulation results presented in this section compare imputation based on the correct conditional distribution (CCD) with three MVN approximation procedures which had adequate performance on MCAR scenarios.

1. MVN Just Another Variable (JAV): Impute X₂ and X₁₂ without constraint

2. MVN Passive Imputation (PSI): Impute X₂ only and calculate X₁₂

3. MVN Impute All, Recalculate by Multiplication (IARM): Impute X₂ and X₁₂, recalculate X₁₂

In addition to varying means, variances and correlations as in the previous section, we investgate how much missing data the methods can tolerate and how sample size and the missing data mechanism affect performance by allowing sample size, the percentage of missing data, and the missingness pattern, and features of the missing data mechanism to vary. Specifically, the sample size for each data set is taken to be 100, 500 or 1000. We use missingness fractions of 20 percent or 50 percent for X₂ and X₁₂ missing, and generate the missing data mechanism under both missing completely at random (MCAR) and missing at random (MAR) assumptions. In particular, we consider two scenarios for MAR mechanisms, generated using logistic regression with weaker and stronger relationships between the observed variables and the missingness. Odds ratios of 1.5 and 5 (scaled by the standard deviation of each variable) was used to generate weaker and stronger relationships, respectively. A summary of factors fixed or varied in the simulation are listed below:

• β₀ = β₁ = β₂ = β₃ = 1

• Error Variance = 16

• Mean(X₁,X₂) = (0,0), (0,5), (5,5)

• Var(X₁)=1

• Var(X₂)=1,4

• Corr(X₁,X₂) = 0, 0.5, 0.9

• Mechanism: MCAR, MAR OR 1.5, MAR OR 5

• Sample size: 100, 500, 1000

• Percent missing: 20, 50

We again fix the number of imputations at five and replicate each scenario 200 times, with bias, CI widths, and CI coverage of regression coefficients recorded for evaluation of performance. Increasing the number of imputations to 25 does not tend to affect the results in our scenarios. The theoretical margin of error for 0.95 coverage with 200 replications is 0.0302.

Table 1 presents results averaged across all scenarios for each of the coefficients in the regression model in the forms of means and standard deviations of each of the performance metrics. As expected, the CCD procedure yields highest mean confidence interval coverage across all regression coefficients; values range from 0.946 to 0.949 for CCD compared to 0.889-0.933 for JAV. The other MVN procedures (PSI and IARM), which attempt to constrain the interaction term to be a product of the primary predictors, result in lower mean coverage, with results ranging from 0.640-0.776 for the four regression coefficients, well below the nominal 0.95. In addition, standard deviations are smallest for CCD and greater for the PSI and IARM procedures, suggesting that CCD not only has the best average coverage, but is also stable with small variation in the results with good mean coverage, compared to that of other procedures that fluctuate more widely from scenario to scenario.

Table 1. Overall CI Coverage/Bias/CI Width Across Scenarios for CCD and MVN Procedures.

	Imputation Strategy	β0		β1		β2		β3
		Mean	SD	Mean	SD	Mean	SD	Mean	SD
Coverage	CCD	0.947	0.016	0.948	0.016	0.946	0.018	0.949	0.016
	JAV	0.910	0.116	0.889	0.134	0.933	0.034	0.928	0.043
	PSI	0.776	0.266	0.731	0.301	0.754	0.270	0.645	0.332
	IARM	0.771	0.268	0.726	0.304	0.756	0.274	0.640	0.334
Bias	CCD	0.01	0.27	0.02	0.14	-0.01	0.06	-0.01	0.04
	JAV	-0.46	1.48	0.28	0.48	0.10	0.26	-0.01	0.08
	PSI	-1.68	3.69	0.99	0.85	0.34	0.88	-0.26	0.17
	IARM	-1.67	3.70	1.01	0.86	0.32	0.87	-0.26	0.17
Width	CCD	9.6	11.7	3.6	2.8	2.4	2.4	0.8	0.6
	JAV	11.5	15.6	4.3	3.9	2.9	3.3	1.1	0.9
	PSI	9.6	11.2	3.7	2.7	2.4	2.2	0.8	0.5
	IARM	9.6	11.3	3.6	2.7	2.4	2.2	0.8	0.5

Values are means across 324 scenarios.

Low coverages considering margin of error are highlighted in bold.

CCD: Correct Conditional Distribution

JAV: Just Another Variable

PSI: Passive Imputation

IARM: Impute All Recalculate by Multiplication

Similarly, mean bias tends to be smaller in magnitude for CCD compared to the MVN procedures, and among the MVN procedures, JAV yields the smallest bias. Again, the standard deviations of bias are small for CCD, suggesting that it is stable with low bias, whereas PSI and IARM have more variation in the results. CI widths are similar for most of the procedures, except for JAV which produces the widest intervals. This suggests that JAV achieves better coverage than other MVN methods by making up for bias with lower precision in some situations.

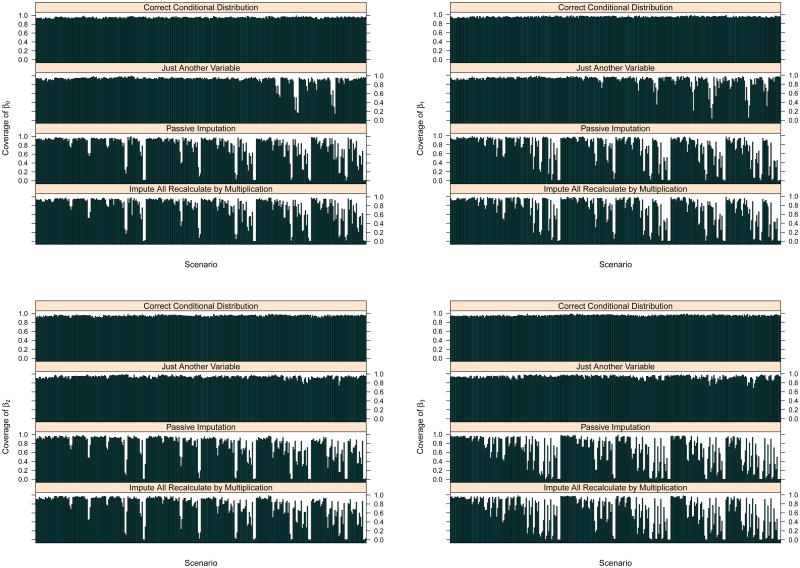
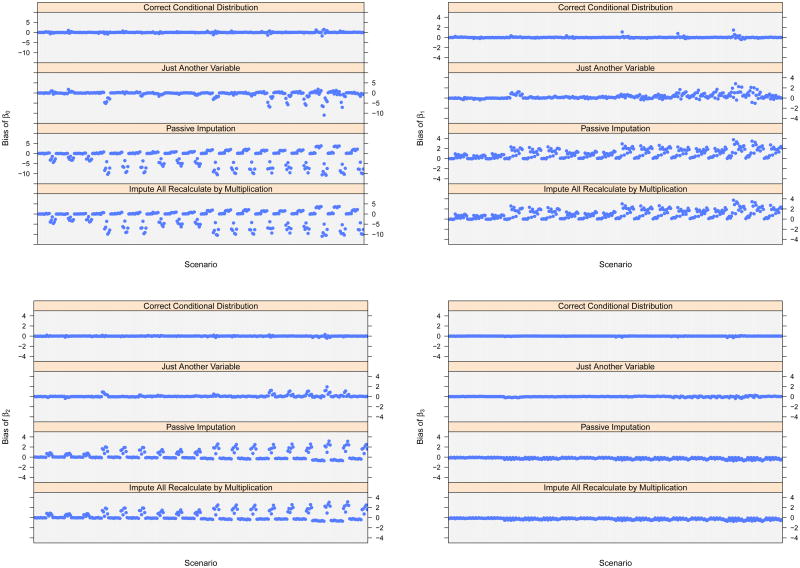
Figures 2, 3 and 4 present CI coverage, bias, and CI widths by scenario. Each bar in the coverage plots and each dot in bias and width plots represents the mean from 200 replications of a scenario. The figures illustrate that CI coverage tends to be consistently high across the scenarios for CCD, whereas coverage is below the nominal level for some of the scenarios for PSI and IARM procedures. JAV tends to perform well in terms of coverage for most of the MCAR scenarios, but coverage may be low with MAR mechanisms, particularly for scenarios with large sample sizes where observed variables are strongly predictive of missingness. Bias is shown to be stable and small in magnitude for CCD across scenarios and across the four regression coefficients. Among the MVN approximations, JAV tends to perform better in terms of bias compared to PSI and IARM, although there are some fluctuations. Plots of CI widths show similar interval widths for CCD, PSI, and IARM, whereas JAV tends to have larger CI widths for some of the scenarios.

Figure 2. Confidence Interval Coverage by each scenario.

(Nominal coverage is 95%.)

Figure 3. Bias by scenario.

*Note that the axes are not equal.

Figure 4. Confidence Interval Width by Scenario.

*Note that the axes are not equal.

Generally, the conditions that led to deficiencies in coverage for ad hoc methods based on MVN approximations were (1) the extent of the departure from MCAR where an MAR mechanism with substantial dependence on covariates led to worse coverage, (2) the sample size of the scenario, where a larger sample size gave rise to worse coverage, i.e. a higher proportion of the mean squared error was due to bias, (3) larger percentage of missing data led to worse coverage, (4) larger means of the covariate distributions, which translated into a greater degree of non-linearity when a product term was incorporated in the regression model, and (5) higher correlation between covariate values.

Overall, the results suggest that the CCD method performs well across all the scenarios. This is not surprising given the alignment of the scenarios with CCD assumptions, but it is still useful to understand the degree of likely variation in practical applications. In contrast, PSI and IARM result in low coverage for various combination of the factors we considered. JAV performs better than PSI and IARM for most scenarios, even though this procedure does not in general preserve the relationship of the interaction term as a product of predictor variables. However it sacrifices precision to maintain good coverage and low bias.

4. Application to a Study of Childhood Trauma

The National Child Traumatic Stress Network (NCTSN) Core Data Set [20] consists of 14,088 subjects who were seen at participating clinics in the United States. Variables in the data set include patient demographic characteristics, a trauma history profile, and the score on the Post-Traumatic Stress Disorder Reaction-Index (PTSD-RI) [21, 22] along with other mental-health related scores.

For illustration, we investigate the regression relationship of the outcome variable, PTSD-RI total score, on age, a measure of trauma burden, and their interaction. The trauma variable is defined as the average number of types of traumas experienced per year, which is computed by summing across twenty different trauma categories and then scaling by the age of the child. The resulting trauma variable can range between 0 and 20. The twenty trauma types include: sexual abuse, sexual assault, physical abuse, physical assault, emotional abuse, neglect, domestic violence, political violence inside the U.S., political violence outside the U.S., traumatic illness, serious injury, natural disaster, kidnapping, traumatic loss or bereavement, forced displacement, impaired caregiver, extreme interpersonal violence, community violence, school violence, and other trauma.

An interaction effect is investigated in order to see whether the relationship between PTSD-RI and trauma differs as a function of age using the following model:

$$\mathit{\text{PTSD}}={\beta }_0+{\beta }_1\mathit{\text{Age}}+{\beta }_2\mathit{\text{Trauma}}+{\beta }_3\mathit{\text{Age}}\times \mathit{\text{Trauma}}.$$

This study includes a subset of children aged between 7 and 18 with a confirmed trauma history, i.e., subjects who endorsed at least one confirmed trauma on one of the twenty possible trauma types. For illustrative purposes, we further limit the subjects to those with complete PTSD-RI scores, which leads to a sample of 6,291 children. Age is completely observed in this subset, but the trauma variable is missing for 47% of the children (leaving n=3,338 complete cases). This is due to the fact that the standardized trauma history profile was completed not by study personal but by local clinicians who did not always collect the information. Mean age of the subjects in the study is 12.7 (sd=3.1), mean of the trauma burden based on 3,338 observations is 12.1 (sd=14.3), and the correlation between age and trauma is 0.22. With the trauma variable missing, the interaction term is also missing for the corresponding 47% of the cases. We multiply impute the missing covariate and the interaction term based on both the CCD procedure and the approximate MVN procedures. We also consider results obtained using complete-case (CC) analysis.

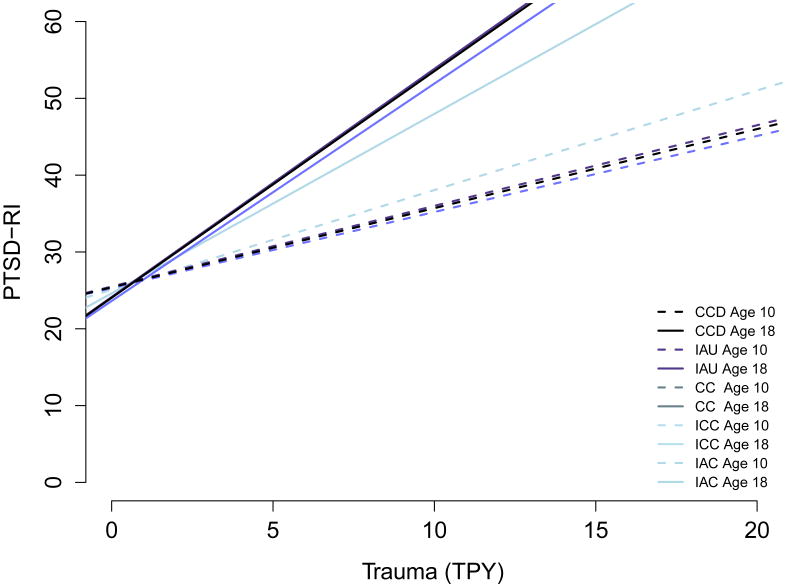
The CCD procedure was implemented in R, and the MVN imputations were run using SAS PROC MI, PROC REG and PROC MIANALYZE. Table 2 gives a comparison of results using CCD and the various alternatives. The parameter estimates are similar in magnitude for the CCD and JAV procedures. For CCD, the coefficients of Age and the Age*Trauma interaction are significant at the 0.05 level, and Trauma is marginally significant (P=0.077). For the JAV procedure, the Age*Trauma interaction is significant (P=0.002), Age is marginally significant (P=0.08), but Trauma is not (P=0.173). For the PSI and IARM procedures, the signs are consistent for each parameter estimate but the magnitudes differ from those of CCD and JAV. Complete-case (CC) analysis using the 3,338 completely observed cases yields results similar to the JAV method in this example, although biases emerging from CC analysis are apt to be unpredictable and could differ in other settings. Figure 5 illustrates the difference in trauma slopes for age=10 and age=18 for each of the procedures. PSI and IARM give similar results with overlapping lines with smaller differences in slopes for ages 10 and 18, whereas CCD and JAV depict greater differences in slopes.

Table 2. Comparison of Results from CCD and MVN Procedures.

	Intercept		Age		Trauma		Age*Trauma
	Est	P	Est	P	Est	P	Est	P
CCD	27.1	<.0001	-0.17	0.04	-1.37	0.077	0.24	0.001
JAV	27.2	<.0001	-0.17	0.08	-1.35	0.173	0.24	0.002
PSI	25.7	<.0001	-0.06	0.52	-0.004	0.996	0.13	0.047
IARM	25.7	<.0001	-0.06	0.51	-0.004	0.996	0.13	0.044
CC	27.4	<.0001	-0.21	0.06	-1.31	0.179	0.23	0.002

CCD: Correct Conditional Distribution

JAV: Just Another Variable

PSI: Passive Imputation

IARM: MVN Impute All Recalculate by Multiplication

CC: Complete Case analysis

Figure 5.

Plots of PTSD-RI for ages 10 (dashed) and 18 (solid). CCD and JAV (with dark colors) depict greater differences in slopes with a highly significant age*trauma interaction, illustrating the importance of correctly handling the missing values.

5. Discussion

The possibility of interactions in regression relationships adds substantial complexity to handling missing data in multivariate settings. In this paper, we studied several methods for accommodating such interactions in imputation procedures. Our proposed approach makes use of the correct conditional distribution of the missing continuous predictor given the observed outcome and observed predictor, preserving the relationship of the interaction term as a product of the two predictors. It performs well across a full range of settings in which we have a completely observed continuous predictor and a missing continuous predictor in the model.

Including interaction terms in missing data models is suggested and discussed in Graham [16], and more recently, passive imputation (PSI) and just another variable (JAV) approaches have been proposed for settings in which a model includes terms that are functions of the base variables such as through power transformations or multiplicative interactions [17, 18]. In these methods, the composite variable is, respectively, calculated after the fact from the imputed values of the base variables or else treated as if it was exchangeable with the base variables under a joint multivariate normal distribution. Kim [19] independently proposed the PSI and JAV methods as part of a set of approximation methods based on multivariate normality under the names impute and calculate (IAC) and impute all unconstrained (IAU). While these methods have the advantage that they can be implemented using standard software, it is important to understand how their performance, both theoretical and practical, is affected by the mis-specification of the underlying joint distribution. For example, Seaman [18] showed that JAV method is consistent for linear models if the data are missing completely at random but otherwise produces asymptotically biased results, consistent with the findings from our simulation studies. The scope of the work by Seaman et al. is broader in certain respects as it considers quadratic predictors as well as interactions, and considers predictive mean matching in addition to JAV and PSI methods, but it is narrower in that it does not include MCMC methodology for imputation using the correct conditional distribution. Seaman et al. [18] concluded that JAV was the best of a set of imperfect methods for adapting existing software to the imputation task.

One of the challenges we have noted in recent explorations is that even the extension from two to three predictor variables involves a meaningful additional layer of complexity. Specifically, when two or more predictor variables are missing on an individual, the conditional distribution of these variables given other variables and current parameter values is not in general multivariate normal. It still is possible to accommodate the three predictor version of the model in an MCMC estimation framework, drawing missing values one at a time from non-normal distributions using appropriate statistical computing methods, but one would need to remain attentive to convergence issues. Extensions to realistic but much larger numbers of predictors are apt to give rise to additional complexities. Looking beyond the scope of the present work, we regard methodological development in this area as a high priority.

The simulation results suggest that the multivariate normal JAV procedure shows robustness in various scenarios with an MCAR mechanism; however, CI coverage can drop to below nominal level for some situations, such as in MAR scenarios in which there is a strong relationship between the observed variables and the missingness of a covariate, or when the sample size is large. A weakness of the JAV approach is that the product term induces a violation of the multivariate normality assumption; another weakness is that there is no constraint for the imputations to be a product of the values of the variables contributing to the interaction. Trying to enforce the constraint for the interaction, either by imputing X₂ only and calculating X₁₂ as in PSI, or imputing all then recalculating X₁₂ as in Impute All Recalculate by Multiplication (IARM) can lead to biased results with low coverage. Therefore, some caution is needed when trying to preserve the relationship of the interaction as the product of the variables using an approximation procedure; the CCD procedure, of course, explicitly incorporates the interaction constraint without assuming multivariate normality of the variables.

As noted earlier, imputation with chained equations [12, 13, 23] is a competitor approach that gives an implicit representation of interaction relationships. There is an ambiguity in chained-equation approaches, which typically impute variables one at a time, about how to handle products of more than one variable. We would encourage the development of chained-equation approaches that are specifically tailored to settings with potential interactions, after which it would be helpful to consider comparisons of joint-modeling strategies such as the CCD method with chained-equation approaches.

Throughout the paper, we assume a linear relationship between the regression outcome and predictors, a bivariatenormal covariate distribution, and a monotone missing-data pattern with the outcome and a predictor fully observed and only one of the predictors and the corresponding interaction term missing. The ability to relax these assumptions would clearly be appealing; extension of the methods to more general models with potentially larger numbers of predictors also remains an interest for future research.