Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2015 Feb 26;119(11):6414–6420. doi: 10.1021/acs.jpcc.5b00210

Structure-Directed Exciton Dynamics in Templated Molecular Nanorings

Juliane Q Gong †,*, Patrick Parkinson †, Dmitry V Kondratuk ‡, Guzmán Gil-Ramírez ‡, Harry L Anderson ‡, Laura M Herz †,*
PMCID: PMC4418736  PMID: 25960822

Abstract

graphic file with name jp-2015-00210e_0004.jpg

Conjugated polymers with cyclic structures are interesting because their symmetry leads to unique electronic properties. Recent advances in Vernier templating now allow large shape-persistent fully conjugated porphyrin nanorings to be synthesized, exhibiting unique electronic properties. We examine the impact of different conformations on exciton delocalization and emission depolarization in a range of different porphyrin nanoring topologies with comparable spatial extent. Low photoluminescence anisotropy values are found to occur within the first few hundred femtoseconds after pulsed excitation, suggesting ultrafast delocalization of excitons across the nanoring structures. Molecular dynamics simulations show that further polarization memory loss is caused by out-of-plane distortions associated with twisting and bending of the templated nanoring topologies.

Introduction

Conjugated polymers have been studied extensively because of their semiconducting and optical properties, which offer great potential for a diverse range of applications1 such as organic light-emitting diodes,2,3 field-effect transistors,4,5 and polymer solar cells.6,7 Recently, macrocycles have attracted increasing attention as quasi-infinite π-conjugated systems exhibiting unique electronic and optical behavior.8 Several studies have investigated electron or energy transfer, nonlinear optical phenomena, and topological effects in these structures.9−14

A promising approach to synthesis of nanosized fully π-conjugated macrocycles based on porphyrin units has been developed using template-directed self-assembly.15,16 However, the difficulty of synthesizing suitable templates has greatly limited the size of macrocycles accessible. To this end, Vernier effects were exploited to direct synthesis of large nanorings using multiple smaller templates.17 Vernier templating not only proves to be a powerful new strategy to construct large nanorings, but also renders shape-persistent structures with diverse geometries.18 Exciton delocalization and emission depolarization processes are expected to be strongly affected by the change of geometry in the structures.19

Conformational effects on photophysical properties have been examined extensively using both experimental20,21 and theoretical methods22 on a variety of conjugated polymer systems, such as PPV,23,24 P3HT,25,26 and dendrimers.27 In particular, effects on polarization memory loss18,23 and energy transfer28,29 have attracted much attention.

At the center of our study, we address the question of how deliberate distortion of a molecular nanoring influences the emissive properties of a molecule following excitation. We examine to what extent out-of-plane distortions of a particular nanoring topology affect the polarization memory of the transition dipole moment and whether such effects can be predicted by molecular mechanics simulations. In search for answers to these questions, a range of conjugated zinc porphyrin nanorings of similar size but different conformations are examined using ultrafast time-resolved spectroscopy and the results are compared to molecular dynamics simulations of ring structures.

Experimental Section

Materials

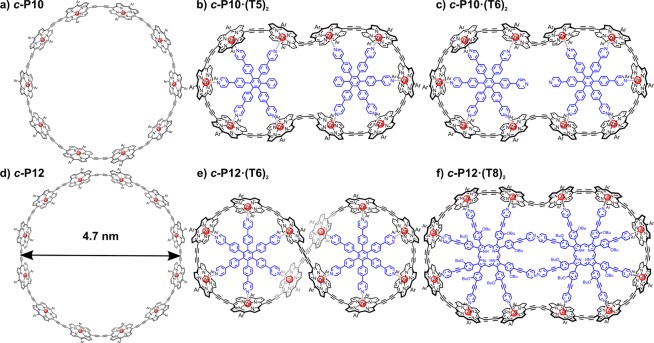
The synthesis and characterization of the nanoring templates and complexes are described in detail elsewhere.15,17,30−32 Figure 1 introduces the porphyrin nanorings under investigation, which comprise porphyrin units joined by butadiyne bridges. Through insertion of templates binding to the porphyrin units, a range of different molecular shapes are created with spatial extent on the nanometer scale. Untemplated nanorings c-P10 and c-P12 only differ slightly in ring diameter and have almost identical conformation and absorption/emission spectra (further information in the Supporting Information (SI)). Both samples are prepared in toluene/1% pyridine solution to prevent aggregation. Templating changes the geometry considerably by rigidifying the nanoring into two smaller porphyrin “loops” and introducing significant out-of-plane distortions, such as bending and twisting. Molecular mechanics simulations (vide infra) show that c-P10·(T5)2 and c-P10·(T6)2 have similar structures, with the main difference being in the shape of templates as shown in Figure 1b,c. The angle between the mean template planes in c-P10·(T5)2 is calculated to be θ = 72°. The twist in c-P12·(T6)2 is even more pronounced and has the form of a figure-of-eight, with θ = 28°, as shown from crystal structure data in a previous study.17 On the other hand, c-P12·(T8)2 is planar and not expected to exhibit any substantial twist. These conformations have been deduced from molecular mechanics and dynamics simulation using HyperChem, which will be described later in detail. Samples with template complexes were prepared in pure toluene solution, as the templates would otherwise be displaced by competition with pyridine.

Figure 1.

Figure 1

Open in a new tab

Chemical structures of the budadiyne-linked zinc porphyrin nanoring assemblies under investigation: (a) c-P10, (b) c-P10·(T5)2, (c) c-P10·(T6)2, (d) c-P12, (e) c-P12·(T6)2, and (f) c-P12·(T8)2. Templates are indicated in blue, and zinc atoms are denoted in red. All compounds have octyloxy side chains (Ar) which are omitted in the graphic for clarity.

Time-Resolved Photoluminescence Spectroscopy

The photoluminescence (PL) upconversion technique was engaged to investigate PL dynamics of sample solutions held in quartz cuvettes as described in detail elsewhere.18,33 An excitation pulse was generated by a mode-locked Ti:sapphire laser with pulse duration of 100 fs and a repetition rate of 80 MHz. PL is collected and optically gated in a beta-barium-oxide (BBO) crystal by a vertically polarized time-delayed gate beam. The upconverted signal, which consists of sum-frequency photons from the gate pulse and the vertical component of the PL, was collected, dispersed in a monochromator, and detected using a nitrogen-cooled CCD. Using a combination of a half-wave plate and a Glan-Thompson polarizer, the polarization of the excitation pulse was varied and PL intensity dynamics were recorded separately for components polarized parallel (I∥) and perpendicular (I⊥) to the excitation pulse polarization. The PL anisotropy is defined using γ = (I∥ – I⊥) /(I∥ + 2I⊥) and calculated from the measured components. The full-width-half-maximum (FWHM) of the instrumental response function (IRF) was measured to be ∼270 fs, which gives the time-resolution limit of the system (further details in the SI). By recording the IRF with both polarizations, a temporal shift of ∼15 fs between I∥ and I⊥was found, and thus, the calculation of γ(t) was adjusted accordingly (further information in the SI).34

To investigate PL decay dynamics at longer delay time after excitation (>1 ns), electronic gating through time-correlated single-photon counting (TCSPC) technique was explored, using a Becker & Hickl module. Here, emission was detected with a silicon single-photon avalanche diode, yielding a temporal resolution of around 40 ps. By fitting the experimental data to a single exponential decay model IPL = A exp(−t/τ), the lifetime τ of the excitation was extracted.

Steady-state absorption and time-integrated PL spectra at room temperature were recorded using a PerkinElmer Lambda 1050 UV/Vis/NIR spectrometer and a Horiba FluoroLog fluorimeter, respectively.

Results and Discussion

Absorption and Emission Spectra

In order to gain basic insight about the photophysical and electronic properties of the nanorings, steady state absorption and emission spectroscopy was performed. The resulting spectra for c-P12 and c-P12·(T6)2 are compared in Figure 2; spectra for further structures are provided in the SI. Zinc porphyrin monomers exhibit a strong S0 → S2 transition at ∼400 nm (Soret band) and a weaker S0 → S1 transition at ∼550 nm (Q-band).35 For the nanorings, π-conjugation extends through the butadiyne bridges, lifting the degeneracy in both the lowest-energy Q band and Soret band of the porphyrin monomers. Transitions polarized parallel (Qx) and perpendicular (Qy) to the acetylenic backbone can therefore be observed (see Figure 2). When the nanorings bind to the templates, Qx is observed to be red-shifted with respect to the Soret band, while Qy shows no considerable change. In addition, a significant sharpening of features in both emission and absorption spectra can be observed for the templated complexes. Templates bring rigidity to the system; the molecules are less prone to interporphyrin torsional motions and the molecular backbone may be planarized,18 resulting in the observed red shift of Qx. The four templated nanorings hence exhibit similar spectral features (see also further spectra in the SI).

Figure 2.

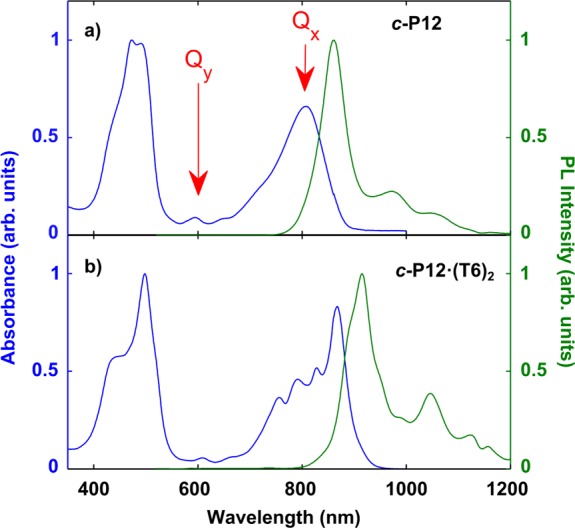
Figure 2

Open in a new tab

Normalized steady-state absorption (blue lines) and time-integrated photoluminescence (green lines) spectra at 295 K for (a) c-P12 in toluene/1% pyridine and (b) c-P12·(T6)2 in toluene solution. The emission spectra were recorded after excitation at 520 nm (into the Soret band). The Qx and Qy transitions are indicated by red arrows.

Photoluminescence Intensity and Polarization Anisotropy Dynamics

PL upconversion under ambient condition was performed to reveal the extent of emission depolarization following photoexcitation with a linearly polarized laser pulse. The templated nanorings were excited at 820 nm and the untemplated rings at 760 nm, with emission being monitored at the peak wavelength for each nanoring. To avoid PL quenching via exciton–exciton annihilation,36 the excitation fluence was kept low (0.08 μJ cm–2). Figure 3 depicts the time-dependent PL of c-P12 and c-P12·(T6)2 over the first 15 ps after excitation with a pulse polarized either parallel (I∥) or perpendicular (I⊥) to the polarization of the detected emission. Corresponding data for all investigated molecules are given in the SI. For c-P12, the PL intensity remains constant over the experiment time window after the onset of the signal at t = 0, whereas c-P12·(T6)2 shows a slight decaying trend, in agreement with the shorter lifetime obtained using TCSPC (shown in Table 1).

Figure 3.

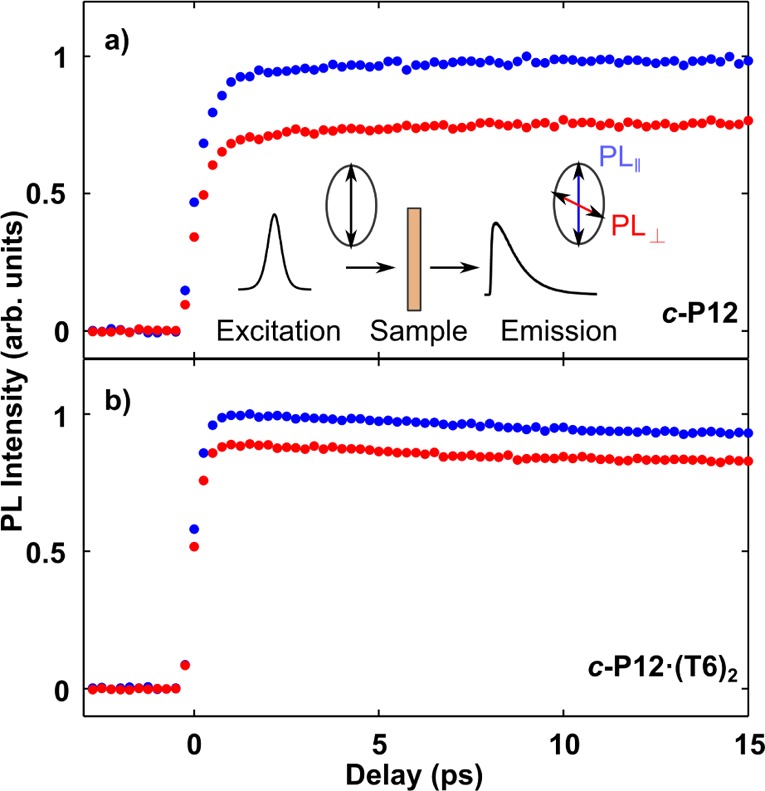
Figure 3

Open in a new tab

Time-resolved PL dynamics of (a) c-P12 in toluene/1% pyridine (concentration 0.2 mM) and (b) c-P12·(T6)2 in toluene solution (concentration 0.4 mM). Samples were excited by excitation pulse polarized either parallel (blue dots) or perpendicular (red dots) to the detection polarization, as illustrated in the inset.

Table 1. Experimentally Obtained PL Lifetimes τ and Anisotropy γ Values for All Nanorings under Investigation, as Well as the Root-Mean-Squared Values of the Distortion angles α (Twisting) and β (Bending) Obtained for the Templated Rings from Molecular Dynamics Simulation using HyperChema.

molecule τ ± 5% (ps) γ ± 0.02 γs (⟨α 2⟩)1/2 (⟨β 2⟩)1/2
c-P10 683 0.11 0.10 – –
c-P12 792 0.10 0.10 – –
c-P10·(T5)2 471 0.05 0.03 68° 54°
c-P10·(T6)2 463 0.05 0.03 60° 62°
c-P12·(T6)2 448 0.04 0.06 24° 44°
c-P12·(T8)2 543 0.07 0.08 27° 14°
Open in a new tab
a

Using a simplified model based on the results from HyperChem as described in the main text, simulated anisotropy values γs are given.

Selective excitation near the Qx band of a rigid butadiyne-bridged porphyrin oligomer is expected to result in an excited state with a transition dipole moment along the molecular backbone.18 In the absence of any depolarization mechanisms, emission will occur in the same polarization direction as the absorption, and for a randomly oriented distribution of such molecules in solution, an initial anisotropy value of 0.4 is expected.37,38 However, for a complete depolarization of the transition dipole moment within the 2D plane, as may be the case for the untemplated rings, a PL anisotropy value of 0.1 should be found.37,38 Other effects, such as out-of-plane distortion, could further lower the value toward zero.38

Figure 4 shows the temporal dependence of the anisotropy γ(t) for a number of the investigated nanoring topologies. Data for the remaining structures are provided in the SI. For all nanoring topologies investigated, the anisotropy is found to be static over the first 20 ps after excitation, within the temporal resolution of 270 fs. These dynamics were recorded for excitation near the middle of the Qx band. It is possible that excitation near the band edge (∼900 nm) may lead to creation of localized states that have higher anisotropy and/or slower PL depolarization;19 however, we are unable to probe such effects here. These transients therefore indicate that while an initial ultrafast depolarization process may occur within the first hundred femtoseconds after excitation, slower effects such as molecular reorientation are absent over these time scales.18 The values extracted in this way for the initial PL anisotropy γ are listed in Table 1 for all molecules investigated. These values have been independently determined multiple times at 5 ps after excitation, and an overall accuracy of ±0.02 was achieved. The untemplated rings c-P10 and c-P12 display anisotropy values around 0.1, as expected for a complete memory loss in the 2D plane and in the absence of significant out-of-plane distortions of the rings.19 For all templated rings on the other hand, a significant reduction of γ below the value of 0.1 was observed.

Figure 4.

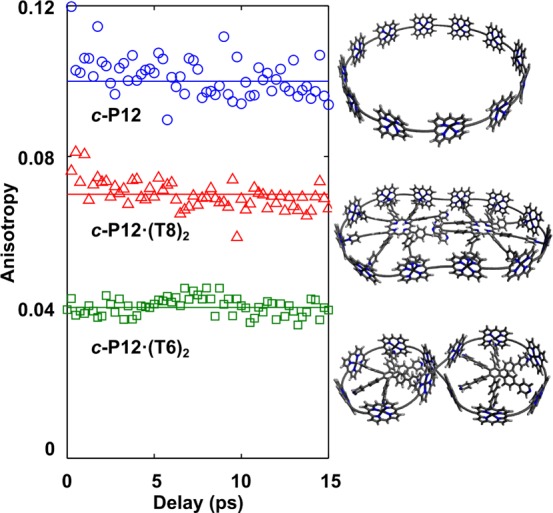
Figure 4

Open in a new tab

PL polarization anisotropy as a function of time after excitation at 820 nm for c-P12 (blue circles, detection at 872 nm), c-P12·(T8)2 (red triangles, detection at 904 nm), and c-P12·(T6)2 (green squares, detection at 914 nm). The structures shown on the right are energy minimized geometries calculated using a modified form of MM+ force field in HyperChem. Side chains are not shown in the diagram but were included in the simulations.

These results suggest that the excitation can access any segment on the rings, both templated and untemplated, within the first few hundred femtoseconds after excitation. Such dynamics may be accounted for by either of two different mechanisms. In the first possible scenario, excitons are initially fully delocalized over the entire ring in the absorbing state,18,39 but may subsequently self-localize following geometric relaxation.10,40−44 In the second scenario, the absorbing state is only delocalized over a subset of monomers, but excitons are subject to ultrafast energy migration along the ring within hundreds of femtoseconds and thus beyond the time-resolution of the upconversion system, similar to observations reported in LH2 antenna complexes.45 It has recently been shown that as the size of untemplated porphyrin nanorings increases, a shift from the former to the latter scenario may gradually occur.14,19

We find that the measured anisotropy values below 0.1 for the templated nanorings can be explained by the presence of significant out-of-plane distortions. Molecular dynamics simulations discussed in detail below show that the measured γ is closer to zero for nanoring topologies with larger distortions. As illustrated in Figure 4, the rigid planar c-P12·(T8)2 has an appreciably higher anisotropy (γ = 0.07) than the other three templated nanorings which are found to display significant out-of-plane distortions.

Molecular Dynamics and PL Depolarization Simulation

To quantitatively examine the distortions present in the different nanoring topologies, molecular dynamics simulations were conducted for the templated nanorings with side chains using HyperChem. The starting configurations were energy-minimized geometries (at 0 K) calculated using a modified form of HyperChem’s MM+ force field. Additional bond stretch, angle bend, and torsion terms were added to describe metalloporphyrins,46,47 alkynes,48 and butadiynes.49

Molecular dynamics simulation were conducted assuming ambient vacuum at two constant temperatures, 300 and 600 K. Simulations ran in time steps of 1 fs for a time window of 500 ps, which gave a representative average. Since the templates are fairly rigid, it can be assumed that distortions mainly originate from motions between two template planes where two fundamental motions can be distinguished: twisting and bending, as illustrated in Figure 5a,b for the case of 300 K. Corresponding results for 600 K are shown in the SI. The corresponding angles α and β are introduced in the figure to quantitatively describe the deviation of the structure from a planar conformation. All starting configurations hold β(0) ∼ 0°. The distortion angles of the conformations in the 500 ps simulation window are plotted as a histogram, and the results are summarized in Figure 5c–f, with the root-mean-square (RMS) values listed in Table 1. Due to the nature of the simulations and the ambiguity in defining the distortion angles, these results only provide a good estimate of the overall trend. It is remarkable that, compared to the bending angle β, the spread in the twisting angle α is generally much narrower and the RMS remains closer to the energetically optimized values, which indicates that, in the molecular dynamics, thermal energy has a greater influence on the bending motion than the twisting motion. c-P10·(T5)2 and c-P10·(T6)2 show large out-of-plane distortions in twisting (around 65°) as well as bending motion at 300 K, consistent with the experimentally observed low PL anisotropy values of γ = 0.05. c-P12·(T6)2 and c-P12·(T8)2 both show similar distributions in α around ∼25°, much lower than that for the templated c-P10 topologies in comparison and in good agreement with structures obtained from crytallographic investigations.17 These simulations explain the only slight decrease in γ from 0.1 to 0.07 experimentally observed for c-P12·(T8)2. However, c-P12·(T6)2 has a much lower PL anisotropy, which can be accounted for by its large bending angle similar to c-P10·(T5)2 and c-P10·(T6)2. In contrast, c-P12·(T8)2 remains rigid: β is narrowly distributed around the planar starting conformation.

Figure 5.

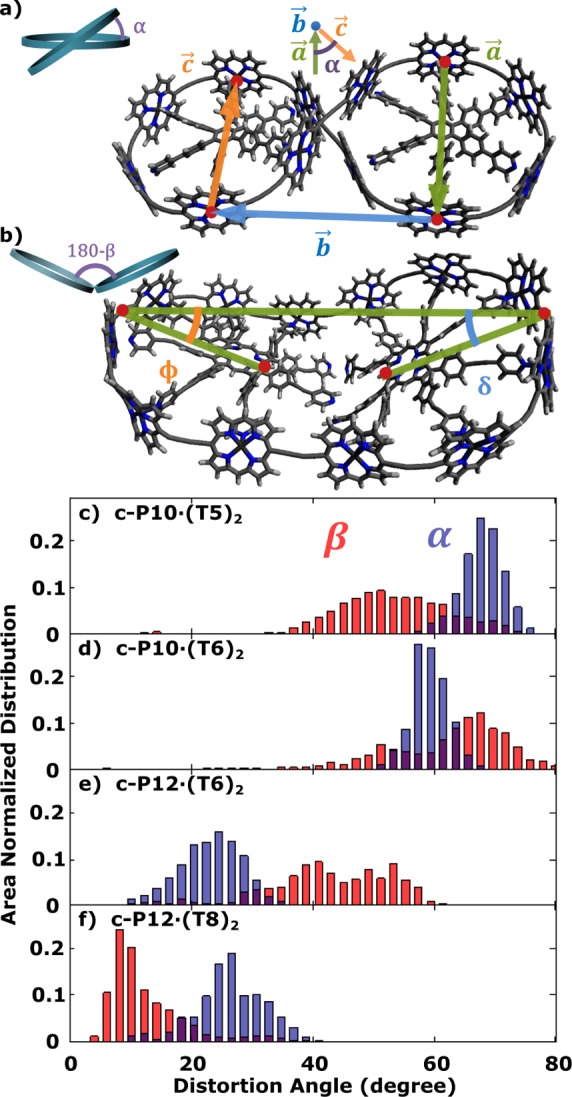
Figure 5

Open in a new tab

(a,b) Definition of the distortion angles. (a) The twisting angle α between two template planes is defined using c-P12·(T6)2 as an example. Four atoms on the porphyrin ring (red) are chosen to form three vectors a⃗ , b⃗ , and c⃗, with a⃗ and c⃗ lying approximately parallel to each other when the molecule does not exhibit any twist. α is the torsional angle defined by the four atoms and is the angle between the planes formed by a⃗, b⃗ and b⃗, c⃗. α represents the twisting angle from a planar position. (b) The bending angle β is illustrated using c-P12·(T8)2 as an example. Four atoms (red) are chosen as shown. Two angles ϕ and δ are calculated, where β = ϕ + δ describes the deviation from a planar position. Simulations were carried out with octyloxy side chains, which are omitted in the diagram for clarity. (c–f) Area normalized histogram of twisting angle α (blue) and bending angle β (red) for (c) c-P10·(T5)2, (d) c-P10·(T6)2, (e) c-P12·(T6)2, (f) c-P12·(T8)2. Molecular dynamics simulation carried out using HyperChem at 300 K for 500 ps, as described in detail in the text.

In summary, the molecular dynamics simulations reveal that the templates provide an effective means to control the nanoring structure, as can be seen in the narrow distribution in Figure 5c–f as well as in the close resemblance between RMS values at 300 K and the energetically optimized values at 0 K for all nanorings. Furthermore, a good correspondence is evident between simulated conformations and measured PL anisotropy: the more pronounced the out-of-plane distortions in both twisting and bending motions, the further the anisotropy is found to be lowered from 0.1.

To link the value experimentally obtained for the PL anisotropy with the calculated molecular structures, simple simulations were performed using a distributed point-dipole model.38,50,51 The porphyrin units in each nanoring are assumed to be arranged in two smaller circles around each template as a result of the template’s rigidity, with their transition dipole moments aligned along the molecular backbone, as shown in the schematic in the SI. The angle between the two template planes in the calculation is taken to be the RMS values simulated by HyperChem at 300 K. Corresponding values for 600 K are given in the SI and exhibit similar trends. For simplicity, the emitting and absorbing states are assumed to extend over one monomer unit. This approximation seems sensible as the PL depolarization dynamics are observed to be sufficiently fast (<300 fs) to suggest that all sites are visited with similar probability. Therefore, the calculated average based on contributions from individual monomers will yield representative results, independent of the extent of exciton wave function delocalization. The polarization anisotropy is then calculated using38

graphic file with name jp-2015-00210e_m001.jpg 1

with the only parameter being κ, the angle between absorbing and emitting dipole moments. Excitation can access any segment of a nanoring, and so each monomer can act as absorbing or emitting site with equal probability. Therefore, angles between dipoles of any two porphyrin monomers on the rings are considered and the average of γ is calculated according to eq 1. Even though this model is rather simplified and primarily focuses on the effect of bending and twisting distortions on the PL anisotropy, the results agree well with the experimental findings. The calculated anisotropy results γs are listed in Table 1 and lie within the error range of the experimental values. This correspondence confirms that the out-of-plane distortion is in fact the major contribution causing the lowered anisotropy value from 0.1. The modeled values tend to be slightly lower than the experimental values, but are surprisingly close, given the simplicity of the model. Deviations between experimental and simulated values may arise because simulations were carried out assuming vacuum conditions (screening of intermolecular interactions arising from the solvent was not taken into account) and because of some variation with the molecular mechanics potential chosen. In addition, a more complete description of exciton depolarization dynamics ought to include effects such as exciton localization dynamics,41 for example, to sites that are preferred through specific local geometries. However, the good agreement between the experimental results and the simple simulation performed here ultimately results from the intimate link between the topology of the molecule to the polarization directions its emitting state can explore.

Conclusion

π-Conjugated nanorings containing 10 or 12 porphyrin units have been investigated to explore the influence of molecular topology on exciton dynamics and polarization memory loss. It is found that excitations can access any part of the templated nanorings, despite their twisted conformations, thus showing similar exciton dynamics to their more planar untemplated counterparts. Time-dependent ultrafast spectroscopy reveals that all nanorings exhibit static PL anisotropy transients within the first 20 ps after excitation, but with an anisotropy much lower than the value of 0.1 found for untemplated rings. Molecular dynamics simulations show that this phenomenon can be fully explained and well described by the out-of-plane distortions of the rings from a planar conformation. Numerical simulations of the PL anisotropy taking into account such distortions yield values that correlate well with the experimentally obtained results. In summary, template-directed synthesis not only plays a vital role in the synthesis of large porphyrin rings, but it also rigidifies the nanorings and introduces a means to control their geometric structures while maintaining excellent π-conjugation. These findings open exciting new possibilities for fast and directional energy transfer in nanoscale molecular structures.

Acknowledgments

The authors thank Martin D. Peeks for modification of HyperChem MM+ force field for porphyrins. Support from European Research Council (COSUN) and the Engineering and Physical Sciences Research Council (EPSRC) is gratefully acknowledged.

Supporting Information Available

Absorption and emission spectra of all compounds. Characterization of PL upconversion response function. PL transients and anisotropy dynamics of all compounds. Details of anisotropy modeling. Molecular Dynamics and PL Depolarization at 600K. This material is available free of charge via the Internet at http://pubs.acs.org/.

The authors declare no competing financial interest.

Supplementary Material

jp5b00210_si_001.pdf (571KB, pdf)

References

  1. Guo X.; Baumgarten M.; Müllen K. Designing π-Conjugated Polymers for Organic Electronics. Prog. Polym. Sci. 2013, 38, 1832–1908. [Google Scholar]
  2. Burroughes J. H.; Bradley D. D. C.; Brown A. R.; Marks R. N.; Mackay K.; Friend R. H.; Burn P. L.; Holmes A. B. Light-Emitting Diodes Based on Conjugated Polymers. Nature 1990, 347, 539–541. [Google Scholar]
  3. Gong X.; Wang S.; Moses D.; Bazan G. C.; Heeger A. J. Multilayer Polymer Light-Emitting Diodes: White-Light Emission with High Efficiency. Adv. Mater. 2005, 17, 2053–2058. [Google Scholar]
  4. Bronstein H.; Chen Z.; Ashraf R. S.; Zhang W.; Du J.; Durrant J. R.; Tuladhar P. S.; Song K.; Watkins S. E.; Geerts Y.; et al. Thieno[3,2-b]thiophene-Diketopyrrolopyrrole-Containing Polymers for High-Performance Organic Field-Effect Transistors and Organic Photovoltaic Devices. J. Am. Chem. Soc. 2011, 133, 3272–3275. [DOI] [PubMed] [Google Scholar]
  5. Chen H.; Guo Y.; Yu G.; Zhao Y.; Zhang J.; Gao D.; Liu H.; Liu Y. Highly π-Extended Copolymers with Diketopyrrolopyrrole Moieties for High-Performance Field-Effect Transistors. Adv. Mater. 2012, 24, 4618–4622. [DOI] [PubMed] [Google Scholar]
  6. Boudreault P.-L. T.; Najari A.; Leclerc M. Processable Low-Bandgap Polymers for Photovoltaic Applications. Chem. Mater. 2011, 23, 456–469. [Google Scholar]
  7. Blouin N.; Michaud A.; Gendron D.; Wakim S.; Blair E.; Neagu-Plesu R.; Belletête M.; Durocher G.; Tao Y.; Leclerc M. Toward a Rational Design of Poly(2,7-carbazole) Derivatives for Solar Cells. J. Am. Chem. Soc. 2008, 130, 732–742. [DOI] [PubMed] [Google Scholar]
  8. Iyoda M.; Yamakawa J.; Rahman M. J. Conjugated Macrocycles: Concepts and Applications. Angew. Chem., Int. Ed. Engl. 2011, 50, 10522–10553. [DOI] [PubMed] [Google Scholar]
  9. Aratani N.; Kim D.; Osuka A. Discrete Cyclic Porphyrin Arrays as Artificial Light-Harvesting Antenna. Acc. Chem. Res. 2009, 42, 1922–1934. [DOI] [PubMed] [Google Scholar]
  10. Aggarwal A. V.; Thiessen A.; Idelson A.; Kalle D.; Würsch D.; Stangl T.; Steiner F.; Jester S.-S.; Vogelsang J.; Höger S.; et al. Fluctuating Exciton Localization in Giant π-Conjugated Spoked-Wheel Macrocycles. Nat. Chem. 2013, 5, 964–970. [DOI] [PubMed] [Google Scholar]
  11. Yamamoto T.; Tezuka Y. Topological Polymer Chemistry: A Cyclic Approach Toward Novel Polymer Properties and Functions. Polym. Chem. 2011, 2, 1930–1941. [Google Scholar]
  12. Yang J.; Yoon M.-C.; Yoo H.; Kim P.; Kim D. Excitation Energy Transfer in Multiporphyrin Arrays with Cyclic Architectures: Towards Artificial Light-Harvesting Antenna Complexes. Chem. Soc. Rev. 2012, 41, 4808–4826. [DOI] [PubMed] [Google Scholar]
  13. Parkinson P.; Knappke C. E. I.; Kamonsutthipaijit N.; Sirithip K.; Matichak J. D.; Anderson H. L.; Herz L. M. Ultrafast Energy Transfer in Biomimetic Multistrand Nanorings. J. Am. Chem. Soc. 2014, 136, 8217–8220. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Parkinson P.; Kondratuk D. V.; Menelaou C.; Gong J. Q.; Anderson H. L.; Herz L. M. Chromophores in Molecular Nanorings: When Is a Ring a Ring?. J. Phys. Chem. Lett. 2014, 5, 4356–4361. [DOI] [PubMed] [Google Scholar]
  15. Hoffmann M.; Wilson C. J.; Odell B.; Anderson H. L. Template-Directed Synthesis of a Pi-Conjugated Porphyrin Nanoring. Angew. Chem., Int. Ed. 2007, 46, 3122–3125. [DOI] [PubMed] [Google Scholar]
  16. Hoffmann M.; Kärnbratt J.; Chang M. H.; Herz L. M.; Albinsson B.; Anderson H. L. Enhanced Pi Conjugation Around a Porphyrin[6] Nanoring. Angew. Chem., Int. Ed. 2008, 47, 4993–4996. [DOI] [PubMed] [Google Scholar]
  17. Kondratuk D. V.; Sprafke J. K.; O’Sullivan M. C.; Perdigao L. M.; Saywell A.; Malfois M.; O’Shea J. N.; Beton P. H.; Thompson A. L.; Anderson H. L. Vernier-Templated Synthesis, Crystal Structure, and Supramolecular Chemistry of a 12-Porphyrin Nanoring. Chem.—Eur. J. 2014, 20, 12826–12843. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Chang M.-H.; Hoffmann M.; Anderson H. L.; Herz L. M. Dynamics of Excited-State Conformational Relaxation and Electronic Delocalization in Conjugated Porphyrin Oligomers. J. Am. Chem. Soc. 2008, 130, 10171–10178. [DOI] [PubMed] [Google Scholar]
  19. Yong C.-K.; Parkinson P.; Kondratuk D. V.; Chen W.-H.; Stannard A.; Summerfield A.; Sprafke J. K.; O’Sullivan M. C.; Beton P. H.; Anderson H. L.; et al. Ultrafast Delocalization of Excitation in Synthetic Light-Harvesting Nanorings. Chem. Sci. 2015, 6, 181–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kanimozhi C.; Naik M.; Yaacobi-Gross N.; Burnett E. K.; Briseno A. L.; Anthopoulos T. D.; Patil S. Controlling Conformations of Diketopyrrolopyrrole-Based Conjugated Polymers: Role of Torsional Angle. J. Phys. Chem. C 2014, 118, 11536–11544. [Google Scholar]
  21. Adachi T.; Vogelsang J.; Lupton J. M. Chromophore Bending Controls Fluorescence Lifetime in Single Conjugated Polymer Chains. J. Phys. Chem. Lett. 2014, 5, 2165–2170. [DOI] [PubMed] [Google Scholar]
  22. Hestand N. J.; Spano F. C. The Effect of Chain Bending on the Photophysical Properties of Conjugated Polymers. J. Phys. Chem. B 2014, 118, 8352–8363. [DOI] [PubMed] [Google Scholar]
  23. Dykstra T. E.; Hennebicq E.; Beljonne D.; Gierschner J.; Claudio G.; Bittner E. R.; Knoester J.; Scholes G. D. Conformational Disorder and Ultrafast Exciton Relaxation in PPV-Family Conjugated Polymers. J. Phys. Chem. B 2009, 113, 656–667. [DOI] [PubMed] [Google Scholar]
  24. Huser T.; Yan M.; Rothberg L. J. Single Chain Spectroscopy of Conformational Dependence of Conjugated Polymer Photophysics. Proc. Natl. Acad. Sci. U. S. A. 2000, 97, 11187–11191. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Adachi T.; Lakhwani G.; Traub M. C.; Ono R. J.; Bielawski C. W.; Barbara P. F.; Vanden Bout D. A. Conformational Effect on Energy Transfer in Single Polythiophene Chains. J. Phys. Chem. B 2012, 116, 9866–9872. [DOI] [PubMed] [Google Scholar]
  26. Parkinson P.; Müller C.; Stingelin N.; Johnston M. B.; Herz L. M. Role of Ultrafast Torsional Relaxation in the Emission from Polythiophene Aggregates. J. Phys. Chem. Lett. 2010, 2788–2792. [Google Scholar]
  27. Maus M.; Mitra S.; Lor M.; Hofkens J.; Weil T.; Herrmann A.; Müllen K.; De Schryver F. C. Intramolecular Energy Hopping in Polyphenylene Dendrimers with an Increasing Number of Peryleneimide Chromophores. J. Phys. Chem. A 2001, 105, 3961–3966. [DOI] [PubMed] [Google Scholar]
  28. Bolinger J. C.; Traub M. C.; Brazard J.; Adachi T.; Barbara P. F.; Vanden Bout D. A. Conformation and Energy Transfer in Single Conjugated Polymers. Acc. Chem. Res. 2012, 45, 1992–2001. [DOI] [PubMed] [Google Scholar]
  29. Larsen J.; Brüggemann B.; Khoury T.; Sly J.; Crossley M. J.; Sundström V.; Akesson E. Structural Induced Control of Energy Transfer within Zn(II)-Porphyrin Dendrimers. J. Phys. Chem. A 2007, 111, 10589–10597. [DOI] [PubMed] [Google Scholar]
  30. Liu S.; Kondratuk D. V.; Rousseaux S. A. L.; Gil-Ramírez G.; O’Sullivan M. C.; Cremers J.; Claridge T. D. W.; Anderson H. L. Caterpillar Track Complexes in Template-Directed Synthesis and Correlated Molecular Motion. Angew. Chem., Int. Ed. 2015, 10.1002/anie.201412293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hogben H. J.; Sprafke J. K.; Hoffmann M.; Pawlicki M.; Anderson H. L. Stepwise Effective Molarities in Porphyrin Oligomer Complexes: Preorganization Results in Exceptionally Strong Chelate Cooperativity. J. Am. Chem. Soc. 2011, 133, 20962–20969. [DOI] [PubMed] [Google Scholar]
  32. O’Sullivan M. C.; Sprafke J. K.; Kondratuk D. V.; Rinfray C.; Claridge T. D. W.; Saywell A.; Blunt M. O.; O’Shea J. N.; Beton P. H.; Malfois M.; et al. Vernier Templating and Synthesis of a 12-Porphyrin Nano-Ring. Nature 2011, 469, 72–75. [DOI] [PubMed] [Google Scholar]
  33. Chang M.; Hoeben F.; Jonkheijm P.; Schenning A.; Meijer E.; Silva C.; Herz L. Influence of Mesoscopic Ordering on the Photoexcitation Transfer Dynamics in Supramolecular Assemblies of Oligo-p-Phenylenevinylene. Chem. Phys. Lett. 2006, 418, 196–201. [Google Scholar]
  34. Montgomery N. A.; Hedley G. J.; Ruseckas A.; Denis J.-C.; Schumacher S.; Kanibolotsky A. L.; Skabara P. J.; Galbraith I.; Turnbull G. A.; Samuel I. D. W. Dynamics of Fluorescence Depolarisation in Star-Shaped Oligofluorene-Truxene Molecules. Phys. Chem. Chem. Phys. 2012, 14, 9176–9184. [DOI] [PubMed] [Google Scholar]
  35. Anderson H. L. Building Molecular Wires from the Colours of Life: Conjugated Porphyrin Oligomers. Chem. Commun. 1999, 2323–2330. [Google Scholar]
  36. Herz L. M.; Daniel C.; Silva C.; Hoeben F. J. M.; Schenning A. P. H. J.; Meijer E. W.; Friend R. H.; Phillips R. T. Exciton Dynamics in Supramolecular Assemblies of p-Phenylenevinylene Oligomers. Synth. Met. 2003, 139, 839–842. [Google Scholar]
  37. Lakowicz J. R.Principles of Fluorescence Spectroscopy, 3rd ed.; Springer: New York, 2006. [Google Scholar]
  38. Valeur B.; Berberan-Santos M. N.. Molecular Fluorescence: Principles and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
  39. Sprafke J. K.; Kondratuk D. V.; Wykes M.; Thompson A. L.; Ho M.; Drevinskas R.; Chen W.; Yong C. K.; Joakim K.; Bullock J. E.; et al. Belt-Shaped π -Systems: Relating Geometry to Electronic Structure in a Six-Porphyrin Nanoring. J. Am. Chem. Soc. 2011, 133, 17262–17273. [DOI] [PubMed] [Google Scholar]
  40. Ruseckas A.; Wood P.; Samuel I. D. W.; Webster G. R.; Mitchell W. J.; Burn P. L.; Sundström V. Ultrafast Depolarization of the Fluorescence in a Conjugated Polymer. Phys. Rev. B 2005, 72, 115214 1–5. [Google Scholar]
  41. Adamska L.; Nayyar I.; Chen H.; Swan A. K.; Oldani N.; Fernandez-Alberti S.; Golder M. R.; Jasti R.; Doorn S. K.; Tretiak S. Self-Trapping of Excitons, Violation of Condon Approximation, and Efficient Fluorescence in Conjugated Cycloparaphenylenes. Nano Lett. 2014, 14, 6539–6546. [DOI] [PubMed] [Google Scholar]
  42. Beljonne D.; Hennebicq E.; Daniel C.; Herz L. M.; Silva C.; Scholes G. D.; Hoeben F. J. M.; Jonkheijm P.; Schenning A. P. H. J.; Meskers S. C. J.; et al. Excitation Migration Along Oligophenylenevinylene-Based Chiral Stacks: Delocalization Effects on Transport Dynamics. J. Phys. Chem. B 2005, 109, 10594–10604. [DOI] [PubMed] [Google Scholar]
  43. Schmid S. A.; Abbel R.; Schenning A. P. H.; Meijer E. W.; Herz L. M. Impact of Nuclear Lattice Relaxation on the Excitation Energy Transfer Along a Chain of π-Conjugated Molecules. Phys. Rev. B 2010, 81, 085438 1–5. [Google Scholar]
  44. Schmid S. A.; Abbel R.; Schenning A. P. H.; Meijer E. W.; Sijbesma R. P.; Herz L. M. Analyzing the Molecular Weight Distribution in Supramolecular Polymers. J. Am. Chem. Soc. 2009, 131, 17696–17704. [DOI] [PubMed] [Google Scholar]
  45. Kennis J. T. M.; Streltsov A. M.; Vulto S. I. E.; Aartsma T. J.; Nozawa T.; Amesz J. Femtosecond Dynamics in Isolated LH2 Complexes of Various Species of Purple Bacteria. J. Phys. Chem. B 1997, 101, 7827–7834. [Google Scholar]
  46. Marques H. M.; Cukrowski I. Molecular Mechanics Parameters for the Modelling of Four-Coordinate Zn(ii) Porphyrins. Phys. Chem. Chem. Phys. 2003, 5, 5499–5506. [Google Scholar]
  47. Marques H. M.; Cukrowski I. Molecular Mechanics Modelling of Porphyrins. Using Artificial Neural Networks to Develop Metal Parameters for Four-Coordinate Metalloporphyrins. Phys. Chem. Chem. Phys. 2002, 4, 5878–5887. [Google Scholar]
  48. Goldstein E.; Ma B.; Lii J.-H.; Allinger N. L. Molecular Mechanics Calculations (MM3) on Nitriles and Alkynes. J. Phys. Org. Chem. 1996, 9, 191–202. [Google Scholar]
  49. Jarowski P. D.; Diederich F.; Houk K. N. Structures and Stabilities of Diacetylene-Expanded Polyhedranes by Quantum Mechanics and Molecular Mechanics. J. Org. Chem. 2005, 70, 1671–1678. [DOI] [PubMed] [Google Scholar]
  50. Westenhoff S.; Beenken W. J. D.; Yartsev A.; Greenham N. C. Conformational Disorder of Conjugated Polymers. J. Chem. Phys. 2006, 125, 154903-1–8. [DOI] [PubMed] [Google Scholar]
  51. Kasha M. Energy Transfer Mechanisms and the Molecular Exciton Model for Molecular Aggregates. Radiat. Res. 1963, 20, 55–70. [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp5b00210_si_001.pdf (571KB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES