A hybrid biomechanical intensity based deformable image registration of lung 4DCT

Abstract

Purpose

Deformable Image Registration (DIR) has been extensively studied over the past two decades due to its essential role in many image-guided interventions (IGI). IGI demands a highly accurate registration that maintains its accuracy across the entire region of interest. This work evaluates the improvement in accuracy and consistency by refining the results of Morfeus, a biomechanical model-based DIR algorithm.

Methods and Materials

A Hybrid DIR algorithm is proposed based on, a biomechanical model–based DIR algorithm and a refinement step based on a B-spline intensity-based algorithm. Inhale and exhale reconstructions of 4DCT lung images from 31 patients were initially registered using the biomechanical DIR by modeling contact surface between the lungs and the chest cavity. The resulting deformations were then refined using the intensity-based algorithm to reduce any residual uncertainties. Important parameters in the intensity-based algorithm, including grid spacing, number of pyramids, and regularization coefficient, were optimized on 10 randomly-chosen patients (out of 31). Target Registration Error (TRE) was calculated by measuring the Euclidean distance of common anatomical points on both images after registration. For each patient a minimum of 30 points/lung were used.

Results

Grid spacing of 8 mm, 5 levels of grid pyramids, and regularization coefficient of 3.0 were found to provide optimal results on 10 randomly chosen patients. Overall the entire patient population (n = 31), the Hybrid method resulted in mean±SD (90^th%) TRE of 1.5±1.4 (2.9) mm compared to 3.1±1.9 (5.6) using biomechanical DIR and 2.6±2.5 (6.1) using intensity-based DIR alone.

Conclusions

The proposed hybrid biomechanical modeling intensity based algorithm is a promising DIR technique which could be used in various IGI procedures. The current investigation shows the efficacy of this approach for the registration of 4DCT images of the lungs with average accuracy of 1.5 mm.

1. INTRODUCTION

Deformable Image Registration (DIR) has become a necessary tool in a wide range of image-guided interventions. Researchers have used various deformable transformation models and optimization strategies to achieve accurate and reliable registration results [1], [2]. The transformation models are typically classified as physical models (e.g., linear elasticity, viscous fluid flow, and optical flow) or basis functions (e.g., radial basis functions, B-Splines, and wavelets) [3]. Each transformation model has advantages and disadvantages that are specific to each clinical application. A continuum biomechanical model is a general method to study the complex mechanical behavior of non-linear soft tissues. Linear elasticity is a simplified assumption that can be used in all or in parts of a general biomechanical model. Previous researchers have shown promising results for anatomical sites such as the lungs using biomechanical models [4]–[6]. For the lung application, a biomechanical based DIR can efficiently model the biomechanics of respiration through the breathing motion, the sliding interface between the lungs and the chest cavity, and the nonlinearity of heterogeneous lung soft tissues. Alternatively, intensity based methods typically use basis functions or optical flow as their transformation models, and often regularize the image intensity similarity measure with a specific operator (e.g., Laplacian, Navier-Lamé, Huber, Lp norm, etc.) to avoid singularity in the deformation field in order to achieve physically plausible results [7]–[10].

Intensity based registration methods are a naturally suitable candidate for respiration correlated, or 4D, CT data of the lungs which contains a wealth of image signal contrast. Different groups have addressed the problems of local intensity changes and mass preservation using various methods [11], [12]. Accounting for the sliding motion of the lung against the chest wall often represents a challenge for these algorithms [13]. Researchers have attempted to address the sliding interface between the lungs and the chest cavity using modifications to intensity based methods. Wu et al. [13] separated the lungs from the rest of the images using a mask, performed the registration separately in the lungs and outside of the lungs, then combined the deformations. Schmidt et al. [14] developed a demons based algorithm by decoupling normal and tangential regularizations based on discontinuities of the displacement field to allow sliding in the boundary of the lungs. Vandemeulebroucke et al. [15] developed a fully automated segmentation of the motion mask without the need for a manual segmentation. Although the accuracy of the results of these works is promising, they do not incorporate the physical modeling of the sliding motion integrated into the registration.

The first biomechanical model of the lungs using Finite Element Modeling (FEM) was developed by West and Matthews [16]. They used canine lung material properties in their simple lung model. After this work, development of lung FEM was investigated by many researchers over the past decades [4], [6], [17]. Brock et al. [17] developed a multi-organ FEM algorithm, Morfeus, to register inhale and exhale MR images. The preliminary results of the algorithm were obtained by considering only surface based boundary conditions in the form of vector displacements. Al-mayah et al. extended Morfeus to include hyperelastic [5], heterogeneous materials [18], and modeling the sliding interface [19] between the lungs and the chest cavity using frictionless contact surfaces. Werner et al. [6] applied a negative pressure to expand the lungs from exhale to inhale while in contact with the chest cavity using homogeneous models. Despite the general capability of biomechanical modeling, many of these implementations only consider some of the physiological aspect of respiratory motions with simplified assumptions.

To benefit from the capabilities of both intensity-based and biomechanical modeling approaches Zhong et al. [20] combined the demons algorithm with a homogeneous linear elastic FEM technique in low contrast regions derived based on 4DCT images. In their work, the boundary conditions for constructed FEMs of low contrast regions were derived based on the displacement field of the initial demons registration. Their method allowed correcting the artifacts of the demons driven deformations such as irregular curvatures with the help of the FEM component in low contrast regions. The accuracy of the FEM component was directly dependent on the demons registration, leading the authors to caution that the displacement of the low contrast region boundary nodes should be pre-evaluated before being used for FEM correction. Recently, Li et al. [21] proposed a hybrid DIR method for lung 4DCT images which is based on a varying intensity flow (VF) metric in a block matching framework and a voxel-wise heterogeneous linear elastic FEM. The boundary conditions for FEM were determined by spatial correspondence between the surfaces of the inhale and exhale lungs using the block matching registration with the help of VF similarity model. Moreover, the heterogeneity of the lungs was determined using a novel iterative approach based on the displacement field.

Both of the previous hybrid strategies utilized the intensity-based component only in a part of the image domain. In this work, the goal is to combine the biomechanical modeling approach with the inclusion of contact surfaces to model lung sliding motion and heterogeneous material models as presented in [22], (referred to as Morfeus hereafter) with a validated intensity-based method based on discrete Markov Random Field (MRF) proposed by Glocker et al. [23] referred to as Drop. The general idea is to perform the registration initially in Morfeus, and then refine the displacement field by Drop registration to improve registration accuracy in the entire image domain. The main motivation behind the work as introduced earlier is to benefit from the advantages of biomechanical modeling while utilizing the remarkable image signal contrast in 4DCT data by means of an intensity-based algorithm.

2. METHODS AND MATERIALS

Morfeus Algorithm

Inhale and exhale reconstructions of the 4D CT images of the lungs were obtained with voxel size of 1.0 × 1.0 × 2.5 mm from 31 lung cancer radiotherapy patients. A subset of 10 patients were obtained from DIR-lab (http://www.dir-lab.com/) public datasets [24] while the remaining 21 patients were obtained through a Research Ethics Board (REB) approved study at the Princess Margaret Cancer Centre, Toronto, Canada. For simplicity these 21 patients are referred to as internal patients. For each patient, the boundary of the lungs, body and tumor(s) were semi-automatically contoured in a treatment planning system (PINNACLE, Philips Radiation Oncology Systems, Madison, WI), and were exported as binary mask images. Triangular surface meshes were created using the binary masks by an implementation of marching cube algorithm (Interactive Data Language, IDL, Research Systems Inc). The volumetric tetrahedral mesh for each organ was then generated using HYPERMESH (version 11.0, Altair Engineering, Troy, MI). The interface of the lungs and the chest cavity was then modeled using frictionless contact surface allowing the sliding of the lungs in the pleural cavity [19]. The lungs, tumors, and body were assigned Young’s moduli of 7.8KPa, 78KPa, and 1.5KP, respectively and Poisson’s ratio of 0.4 with the assumption of linear elasticity [26]. Finally, a surface projection algorithm (HYPERMORPH, Altair Engineering, Troy, MI) was performed between the chest cavity surfaces to calculate the boundary conditions in the form of displacement vectors for the surface nodes of primary (inhale) model. In the contact region, the nodes of the body and the lung surface nodes are distributed such that each lung surface node has a duplicate body node. The boundary conditions are then applied to the body nodes, and thus the two sets of nodes are free to slide against each other [5]. After constructing the biomechanical model, a Finite Element Analysis (FEA) software (ABAQUS version 6.9, ABAQUS Inc, Pawtucket, RI) was used to find the nodal displacement vectors (U) in a linear system of equations KU = F, derived based on Hook’s law, with zero external force (F = 0) and known global stiffness matrix (K). U is essentially equivalent of a Displacement Vector Field (DVF) in the nodal locations rather than Cartesian grid of the images. In order to obtain the deformed inhale image, it is necessary to compute the inverse DVF on the Cartesian image grid of the exhale image. Let $X^m={(x_i^m,y_i^m,z_i^m)}^T$, i =1…N be the spatial position of the inhale FEM nodes. The spatial position of the image coordinates in the Cartesian system is also denoted by X^c. Y^m and Y^c are similarly defined for the exhale image. The DVF for the inhale to exhale registration in the FEM mesh coordinate is denoted by ${{}_{ex}{}^{in}T}^m$. It follows that

$${\stackrel{\sim }{X}}^m=X^m+{{}_{ex}{}^{in}T}^m,$$ (1)

where X̃^m is the displaced position of the inhale nodes. To determine the inverse DVF on the image grid, a GPU accelerated implementation of linear interpolation was performed on the negative of DVF in the exhale image coordinate to get the DVF on the Cartesian exhale image grid (Y^c),

$${{}_{in}{}^{ex}T}^c=\text{interp}({\stackrel{\sim }{X}}^m,-{{}_{ex}{}^{in}T}^m,Y^c),$$ (2)

where the arguments of interpolation algorithm are the function evaluation points, function values, and the new function evaluation points, respectively. The interpolation algorithm first finds the corresponding Cartesian grid points inside a given tetrahedron. Using barycentric coordinates of the tetrahedral elements, the displacement vectors can then be interpolated. Next, the deformed inhale image was obtained by warping the inhale image using ${{}_{in}{}^{ex}T}^c$,

$${\stackrel{\sim }{I}}^{in}=\text{warp}(I^{\text{in}},X^c,{{}_{in}{}^{ex}T}^c,Y^c),$$ (3)

where Iⁱⁿ and Ĩⁱⁿ are the image intensities of the inhale and the deformed inhale images, and the arguments of the warp algorithm are the input image intensities, the location of the intensities in the Cartesian system, the inverse DVF in the Cartesian system, and the location of the deformed image intensities, respectively. Figure 1 summarizes various steps involved in the Hybrid registration pipeline.

Figure 1.

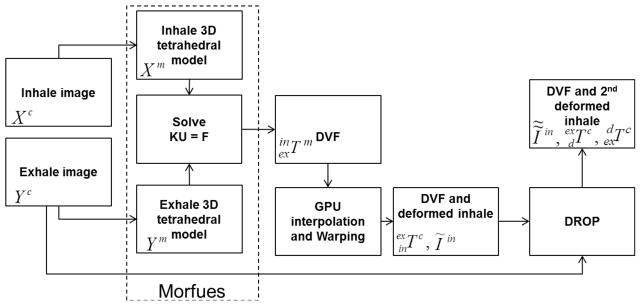
Overview of the Hybrid algorithm.

Drop algorithm and the refinement step

In the refinement step. Ĩⁱⁿ undergoes a deformable registration in order to be more precisely matched with the exhale image without distorting the biomechanical properties (i.e, non-negative Jacobians) of the original $\text{DVF}{(}_{ex}^{in}{T}^m)$. This is ensured in the chosen intensity based algorithm (Drop) by setting a B-spline control point maximum displacement of 0.4 times the grid spacing [23]. The maximum allowed displacement limit for each control point guarantees a non-negative Jacobian enabling a physically plausible transformation. This algorithm is based on discrete MRF and provides a fast and reliable B-spline based registration with a variety of similarity measure choices [23]. Drop does not require calculation of a similarity measure derivative due to its incremental deformation estimation functionality. It also enables a maximum displacement magnitude for the B-spline control points to avoid foldings (or singularities in the Jacobian matrix), and ensures a diffeomorphism DVF.

Optimization of the Drop parameters

Most of the parameters required for the Drop refinement step, were set to the default parameters according to the original settings suggested in [23]. The similarity measure was set as Sum of Absolute Difference (SAD) since the images were from the same modality (4DCT). No significant changes to the performance of SAD were noticed due to local intensity variations in (Hounsfield units) of the images. Three important parameters including spacing of the B-spline control point grid, number of image and B-spline grid pyramid levels in the multi-resolution optimization approach, and regularization coefficient were explicitly adjusted by measuring the average mean and 90^th percentile Target Registration Error (TRE) amongst 10 randomly selected patients (out of the total of 31). TRE is defined as the Euclidean distance between homologous anatomical points (typically, bifurcation points) selected on the inhale and exhale images after registration. Interested readers are encouraged to refer to the original paper by Glocker et al. for more information on the rest of the parameters and their influence on the registration [23]. The outputs of Drop were ${\widetilde{\stackrel{~}{I}}}^{in},{{}_{ex}{}^{d}T}^c$, and ${{}_d{}^{ex}T}^c$ where the first term is the refined Morfeus-deformed inhale image (final deformed image using the Hybrid method) and the latter two transformations are the inverse of each other, and represent the DVF from the deformed inhale image (previously using Morfeus) to the exhale image and vice versa, respectively (see figure 1).

Evaluation metrics

As a sanity check for the final transformation of this Hybrid method in terms of any clear violation of the biomechanics of the lung tissue, the determinant of the Jacobian matrix for ${{}_{ex}{}^{d}T}^c$ and the overall ${{}_{ex}{}^{in}T}^c+{{}_{ex}{}^{d}T}^c$ was calculated. Furthermore, a minimum of 30 pairs of airway and vessel bifurcation landmark points per each lung for each patient on inhale and exhale images were identified by an experienced radiation therapist (MV) to quantitatively assess the registration accuracy by calculating TRE. The efficacy of the Hybrid algorithm was demonstrated by comparing TRE results between Morfeus and Drop. To avoid bias, the three important Drop parameters (spacing of the B-spline control point grid, number of image and grid pyramids, and regularization coefficient) were separately optimized for direct registration of inhale to exhale images, and for the refinement registration step from deformed image to exhale image. Also, Dice index and mean surface distance (D_s) were used to assess the accuracy of tumor alignment. The Dice index is defined as:

$$I_{\mathit{Dice}}=\frac{2\mid V_2\cap V_1\mid }{\mid V_2+V_1\mid },$$ (4)

where V₁ and V₂ are the tumor volumes on the exhale (secondary or target) and the deformed images. D_s is defined as the average minimum distance between the surface nodes of the deformed and the secondary tumor meshes:

$$D_s=\frac{{\displaystyle \sum _{i=1}^N}min\left({\displaystyle \sum _{j=1}^M}\sqrt{{(x_i^{m1}-x_j^{m2})}^2+{(y_i^{m1}-y_j^{m2})}^2+{(z_i^{m1}-z_j^{m2})}^2}\right)}{N},$$ (5)

where N and M are the total number of nodes in tumor triangular mesh representations of the inhale and exhale images, respectively, and superscripts m1and m2 of Cartesian components of the nodes relate to the deformed inhale tumor and the exhale tumor representations.

3. RESULTS

3.1 Parameter selection

The relevant Drop parameters for both direct Drop and Hybrid registrations were optimized by performing a series of registrations on a subset of 10 randomly selected patients out of the 31 total cases. The parameters include the number of image and B-spline grid pyramid levels in the multi-resolution optimization approach, the B-spline control point grid spacing, and the regularization coefficient. Figures 2.a–c show the average mean and 90^th percentile TRE values of all 10 patients using different parameters for the refinement step in the hybrid method while figures 2.d–f illustrate the results of the similar experiments for the direct Drop registration. The experiments were performed from left to right, and the optimized parameter at each step was used for the remaining set of experiments. For the first experiment (effect of grid spacing) a one-level pyramid was used. Based on both the average and 90^th percentile TRE, as the grid spacing is reduced the registration accuracy improves (Figures 2.a and 2.d). As illustrated in figure 2.a, grid spacing of 8 mm results in improved accuracy in the registrations compared to the 4 mm grid spacing, as the optimization likely got stuck in local optima. A similar pattern is observed for the direct Drop registration with an optimal 16 mm grid spacing (Figure 2.d). Figures 2.b and 2.e show that the average and 90^th % TRE were generally reduced if more image and B-spline control points grid pyramid levels were used. This is in accordance with previous studies, which showed multi-resolution registration leads to more accurate and robust results [27]. Based on the average 90^th percentile, a 5-level pyramid was selected to reduce the larger uncertainties in the registrations (the same number was chosen based on Figure 2.e). Finally, Figures 2.c and 2.f indicate that regularization coefficients of 3.0 and 0.25 were the proper choices overall for these 10 patients (for better visualization the log scale was used for the regularization coefficient axis). The error bars for each mean TRE value shows the standard deviation of the obtained average and 90^th %TRE emphasizing on the uncertainties involved in the process of parameter selection. The final value for each parameter is the one that resulted in the best average mean and 90^th % TRE among these 10 patients. The standard deviations for regularization coefficient in the experiments of figure 2.c and 2.f were 9.5 and 4.6, respectively. It should be noted that in all the experiments, Sum of Absolute Differences (SAD) was chosen as the similarity measure. Therefore, the optimal values for regularization coefficient allowed suitable amount of deformations with good accuracy for both the Morfeus refinement and direct Drop registrations, only if SAD is used. The final parameter selection for both refinement and direct Drop registrations are summarized in Table 1. These experiments showed the sensitivity of registration accuracy with respect to a subset of Drop parameters.

Figure 2.

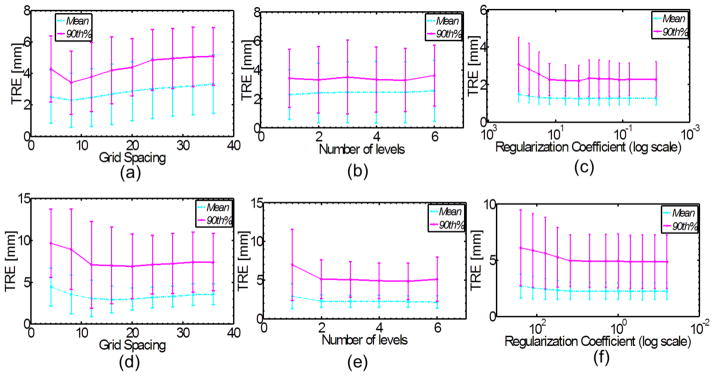
Parameter optimization for the hybrid refinement step (a–c) and Drop algorithm (d–f).

Table 1.

Selected parameters for the refinement step in the Hybrid algorithm and Drop.

	Grid Spacing [mm]	Number of pyramid levels	Lambda (regularization coefficient)	Similarity measure
Direct Drop	16	5	0.25	SAD
Hybrid-refinement	8	5	3.0	SAD

3.2 Overall TRE results

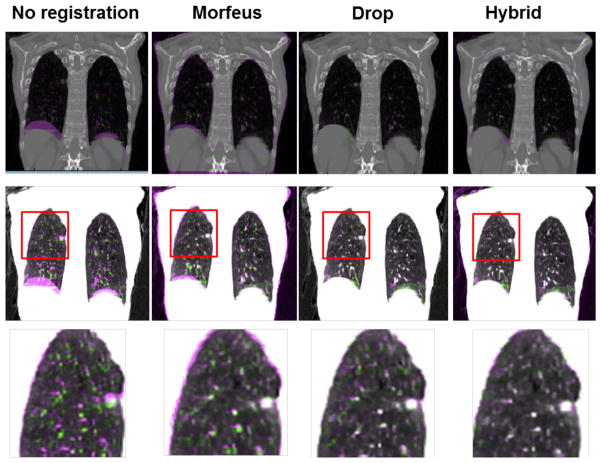
Table 2 summarizes the overall TRE and the TRE within a 20 mm margin of the tumor boundary for 21 internal patients. The main purpose of reporting the TRE values in such tumor regions is to provide detailed information regarding the approximate alignment of the tumor neighborhood in addition to the tumor itself where there is a possibility of microscopic disease. Overall, the TRE improved using the Hybrid method compared to either Morfeus or Drop alone, for both the overall TRE and within 20 mm of the tumor boundary. The results within 20 mm of the tumor boundary should be interpreted with caution since on average patients had only 5 TRE points were identified in the tumor proximity. Figure 3 illustrates overlays of coronal slices of patient 6 with different contrast settings before and after all three registrations. The first row shows how the diaphragm, bony structures (mainly the ribs), and other major vessels and airways are registered. The second row displays the same slice with a differentiated contrast highlighting smaller airways of the bronchial trees. The third row further scales up the red rectangle area in the second row, showing how the Hybrid method helps such small but important structures are more accurately aligned.

Table 2.

Overall and 20 mm neighborhood of tumor TRE, and tumor volume for internal patients. The number of points to calculate the TRE is shown in a column after the TRE results for each patient.

	Overall			20 mm Neighborhood of Tumor
Patient #	Morfeus Mean SD	Drop Mean SD	Hybrid Mean SD	# of Points	Morfeus Mean SD	Drop Mean SD	Hybrid Mean SD	# of Points	Tumor #
1	2.6±1.8	2.6±2.1	1.3±1.2	71	1.4±0.4	0.9±0.6	0.6±0.4	5	1
2	3.3±1.2	1.5±0.9	1.2±0.6	62	1.7±0.2	0.9±0.7	1.2±0.3	3	2
3	2.8±3.2	2.5±3.0	1.7±2.5	67	-	-	-	0	3
4	4.1±3.0	3.4±4.1	2.0±3.2	66	2.9±1.0	1.0±0.7	0.9±0.3	6	4
5	2.3±1.0	2.0±1.4	1.4±1	67	3.0±1.4	2.5±2.1	1.9±1.8	16	5
6	2.5±1.3	3.5±3.4	1.2±0.9	65	1.5±0.6	1.0±0.9	1.2±0.6	6	6
7	1.8±1.1	1.6±1.5	0.8±0.4	63	2.5±0.1	1.0±0.1	0.7±0.1	2	7
8	2.7±1.3	1.3±0.9	1.1±0.6	62	0.7±0.3	0.5±0.1	0.6±0.1	2	8
9	2.2±0.8	1.7±1.2	1.1±0.5	60	2.9±0.0	2.6±0.0	0.5±0.0	1	9
10	2.7±1.3	2.1±1.5	1.0±0.6	63	4.8±0.8	3.6±1.8	1.0±0.4	4	10
11	3.2±2.6	2.2±2.4	1.5±1.7	68	2.7±2.6	2.1±1.5	1.4±1.2	7	11
12	3.9±3.5	2.7±2.7	1.5±1.6	63	4.4±3.0	2.5±3.3	2.1±3.2	5	12
13	2.6±1.7	1.9±2.1	1.1±1.2	107	0.7±0.0	0.5±0.0	0.8±0.0	1	13
14	2.9±2.3	2.6±2.6	1.4±1.1	79	1.1±0.6	0.9±0.5	0.8±0.4	12	14
15	4.0±3.0	3.6±4.2	1.8±1.9	63	2.0±0.5	0.6±0.2	0.5±0.2	11	15
16	3.6±2.2	2.4±2.1	1.8±1.7	70	1.8±1.2	1.7±1.1	1.4±0.9	8	16,17
17	2.3±1.3	1.3±1.5	1.0±0.8	86	1.9±0.2	1.1±0.1	1.0±0.4	3	18
18	5.2±3.6	2.9±2.7	1.7±1.5	64	4.4±1.3	1.0±0.5	0.7±0.5	3	19
19	4.8±2.4	5.1±6.3	2.1±2.1	62	2.2±1.2	0.8±0.4	0.9±0.1	3	20
20	1.6±0.6	1.7±1.2	1.0±0.6	67	1.1±0.3	1.4±0.1	0.9±0.4	2	21
21	2.5±1.0	1.6±1.5	1.3±1.2	59	3.7±0.8	1.1±0.5	1.4±0.9	3	22,23
Avg.	3.0±1.9	2.4±2.4	1.4±1.3	86	2.9±1.7	2.0±1.7	1.2±1.1	5

Figure 3.

Overlay of coronal (first row) and axial (second row) inhale and exhale slices before and after registrations. In the misalignment regions, the exhale and inhale intensities are in purple and green colors, respectively.

Figure 4 illustrates the cumulative TRE curves using over 4430 landmark points indicating the substantial improvement in accuracy of the Hybrid method compared to Morfeus and Drop. It should be noted in order to avoid bias as a result of difference in number of identified points for each patient, the point errors are normalized per patient in the distribution calculations. The average mean TRE values in the Left-Right (LR), Anterior-Posterior (AP), and Superior-Inferior (SI) directions were 0.5, 0.6, and 1.0 mm, respectively using the Hybrid method, compared to 1.0, 1.5, 2.0 mm by Morfeus, and 0.7, 0.9, 2.0 mm by direct Drop registrations. It should be noted that the average intra-observer variation in the point selection was 0.7±0.4 mm (mean±SD) for internal patients (#1–21) and 0.9±1.3 mm for DIR-lab patients [24].

Figure 4.

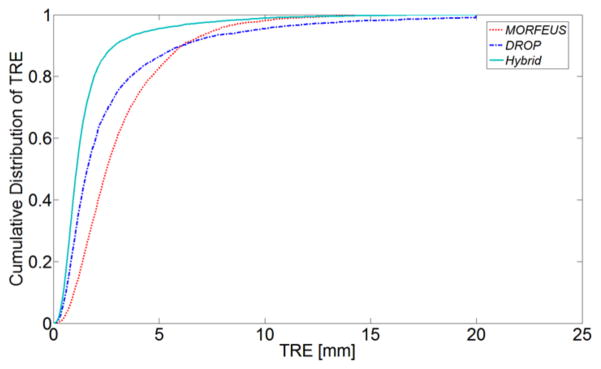
The cumulative distribution of TRE for all the points in all the patients. The influence of each patient is normalized by the individual patient’s number of points.

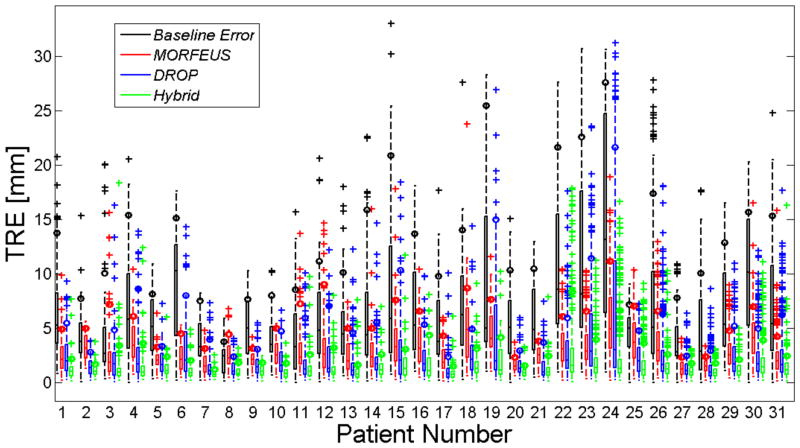
Figure 5 illustrates the result of the TRE analysis in the form of boxplots for all patients. A paired two-sided two-sampled Wilcoxon test were used to assess the median difference between Hybrid, Morfeus, and Drop mean, standard deviation, and 90^th TRE results. The average mean±SD was 1.5±1.4 mm using the hybrid method compared to 3.1±1.9 mm and 2.6±2.5 mm by Morfeus and Drop, respectively (p<0.00001). Furthermore, by looking at the 90^th percentile (shown using a small color circle on the whisker of each box) the hybrid method reduced the residual TRE values for all patients with the only exception of patient 22. Overall, the 90^th percentile TRE was 5.6 mm and 6.1 mm using Morfeus and Drop, respectively. This was significantly reduced using the Hybrid method to 2.9 mm (p<0.00001).

Figure 5.

The boxplot representation of all patients’ baseline error and TRE using all three methods. The small color-filled rectangles show the 90^th percentile for each box data.

3.3 Tumor alignment

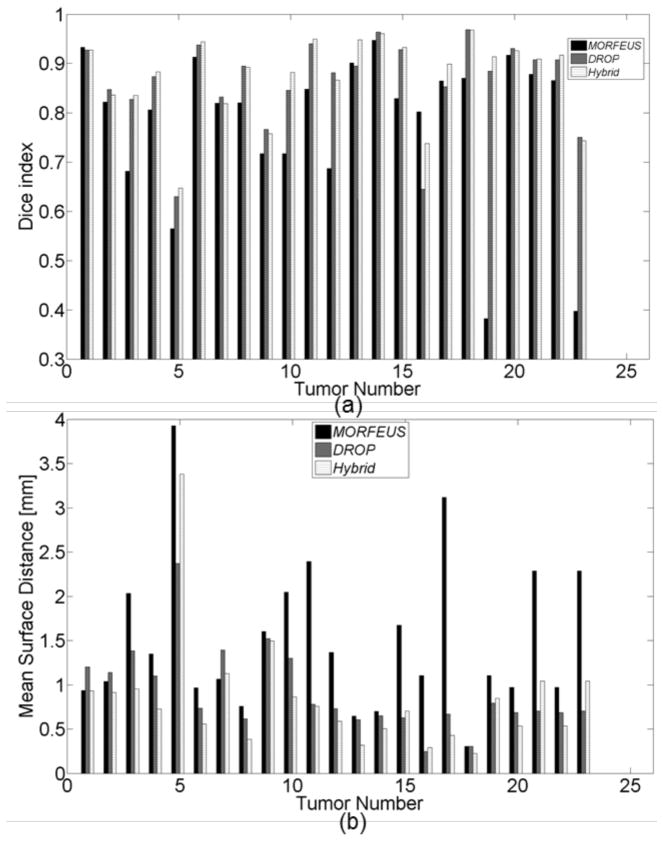
Dice coefficients and the mean surface distance were calculated to measure the accuracy of aligning tumors. Figure 6.a and 6.b illustrate the performance of each algorithm for a total of 23 tumors across 21 internal patients. The correspondence between the tumor and patient numbers is presented in the last column of Table 2. Overall, the mean Dice coefficient was increased from 0.78 using Morfeus to 0.88 using the Hybrid method (p<0.001). The average increase in the Dice index between Drop (0.86) and the Hybrid method (0.88), was marginally significant (p = 0.05) and may not have any clinical significant. Similarly, the Hybrid method reduced the surface distance (D_s) between the tumor delineations from an average of 1.5 and 1.0 mm Morfeus and Drop respectively to 0.8 mm (p<0.01).

Figure 6.

(a) Dice index of each tumor using all three algorithms. (b) Mean Surface Distance of the aligned tumors for each tumor using all three algorithms.

The computation times for Morfeus, Drop, and Hybrid, on average were 1500s, 100s, and 2950s, respectively, on a quad core 3.0GHz Intel Xeon with 16Gb of RAM. The run time for Morfeus algorithm excluded the pre-processing steps such as contouring and triangular mesh creations.

4. DISCUSSION AND CONCLUSION

In this work, a hybrid deformable image registration combining biomechanical modeling and intensity-based approaches was presented. In the first step, Morfeus finds the approximate physical deformation of the lungs based on linear elastic materials for the lungs and surface matching as the boundary condition to the biomechanical model. Morfeus also allows a contact surface between the lungs and the chest cavity to model the sliding motion of the lungs in the thin pleural cavity. This provides a large displacement of the diaphragm and deformation in the lungs while accounting for the differential movement of the ribs. In the second step, the intensity based algorithm, Drop, allows reduction of the residual errors while preserving the desired properties of Morfeus through small magnitude B-spline refinements. The proposed Hybrid method significantly reduced the overall TRE compared to Morfeus and Drop. Considering the benefits provided by the Hybrid method, it is worthwhile to investigate possible solutions to increase the speed of the algorithm. Previous researchers have shown that GPU-based parallel programming implementation of FEM-based and B-spline intensity-based DIR methods could significantly reduce the computational time from several minutes to just a few seconds [28], [29]. Thus, in the future the hybrid approach presented in this work could be significantly accelerated.

Deformable image registration is an ill-posed problem [30]. However, numerous evaluation methods have been proposed to determine the uncertainty of the DVFs provided by various DIR techniques [31]. One of the most common ways of estimating the uncertainty is to calculate the distance of anatomical landmarks before and after registration which is known as TRE. In this paper, it was ensured that at least 30 anatomical points were selected for TRE calculations in each lung. The evaluation of the intra-observer variation indicated that the uncertainty in the landmark selection is within the voxel size of the images. The proposed Hybrid method significantly reduced the overall TRE compared to Morfeus and Drop. TRE results showed that Morfeus has a slightly larger mean error compared to Drop (mean TRE difference = 0.5 mm). However, this study shows that it registers the images more consistently as indicated by smaller overall TRE standard deviation compared to Drop (TRE standard deviation difference = 0.6 mm). Drop also tends to have more random errors with larger 90^th % TRE values compared to Morfeus and Hybrid (in 15 patients Drop had the largest 90^th% TRE). The Hybrid method reduced the average TRE results from Morfeus by at least 1.5 mm for patients with more than 20 mm deformation magnitude, which shows the effectiveness of the algorithm in registering large deformations. The average mean TRE obtained by the Hybrid method is half of voxel size in the LR direction, close to a half for the AP direction, and less than a half for the SI direction (voxel size = 1.0 × 1.0 × 2.5 mm). This is a significantly high accuracy since the half of the physical length of each voxel in the images is the practical limit for measuring the accuracy, and thus identifying any reliable lesion.

Dice index and the mean surface distance were used to illustrate the accuracy of the hybrid method for aligning the tumor within the images. The tumor alignment measurements showed that the hybrid method results in a better alignment compared to Morfeus. However, the differences between the direct application of Drop and the Hybrid method were subtle. These results are aligned with the strengths and weaknesses of the algorithms. In these clinical cases, the tumor presents on the CT image as a dense, spherical object of high intensity surrounded by a low intensity background. This makes it a prominent focus of the intensity based registration, as shown by the high Dice value for Drop. The complexities of the tumor biomechanics in the lung likely vary between patients and are not well understood. They are also not specifically included in the biomechanical model. The variation in the structural relationship between the boundary of the tumor and the surrounding normal lung, and the inaccuracies of the model to incorporate this, is likely contributing to the lower Dice value following the Morfeus alignment alone. The combination of Morfeus followed by Drop allows the intensity based refinement to correct for the unknown biomechanics of the tumor within the normal lung.

The current investigation has provided promising preliminary results for the proposed Hybrid DIR method. However there are still areas that can be improved to ensure consistently accurate registration across the entire image for all patients. For instance, in a small number of patients, shown in Figure 5, (e.g., patient 22) the maximum TRE using Hybrid method is larger than Morfeus (shown as outlier points). Visual inspection of the images and analysis of the TRE in LR, AP, and SI directions reveals that the biomechanical model based component produces inaccurate deformation in AP and SI directions in the interior lobes of both lungs especially within the superior region. This observation suggests a potential limitation of the current implementation of the biomechanical model based component which does not model either the lobes or the interaction between the lobes. For these patients the misalignment of the deformed image using the biomechanical component and the exhale image is too large to be accurately recovered using the final refinement step in the hybrid method. For future investigations, more sophisticated biomechanical models could be constructed which include modified lung material models (nonlinear heterogeneity due to the presence of the lobes rather than linear elastic homogeneity of the current model) and more complex boundary condition (through modeling the interaction between the lobes).

Previously, Zhong et al. [20] investigated a combination of biomechanics and intensity based registration. In their approach, a demons registration was initially performed and was then further improved in low-contrast regions using biomechanical modeling to have a combined registration methodology. They validated their model using a single benchmark mathematical phantom with known deformations showing an average accuracy of 1.1 mm. This is within the range of average accuracy that was seen in our cohort of 31 clinical patients (0.8 – 3.1 mm). Our proposed method has also resulted in comparable accuracies in the registration of 10 publically available lung cases (patients 22–31) as achieved by recently developed algorithms in [9], [14], [15]. The mean±SD TRE [mm] for this subset of 10 patients using the hybrid method was 1.8±1.6 compared to 1.4±1.1, 2.1±1.8, and 2.0±1.4 using MRF-based ventilation model [9], direction dependent with automatic slipping detection [14], and motion mask [15], respectively. In this limited number of cases, the Hybrid method proposed here performs at the level of accuracy of other techniques. A Multi Institution Deformable Registration Accuracy Study (MIDRAS) [32] reported a range of average accuracies of 1.0 – 3.0 mm across 21 different algorithms ran independently on the same 4DCT lung dataset, with max errors of up to 1.2 cm observed following DIR. The average accuracy of 1.4 mm and average maximum error of 7.1 mm presented here indicates that the Hybrid technique performs as well or with some advantage (specifically in reduced maximum errors) compared to these established algorithms. An overview of accuracy of DIR algorithms for lung 4DCT provided in [33] reports a submillimeter to 3 mm range of average accuracies with the majority of algorithms being able to achieve less than 2 mm in each direction compared to the performance of the proposed hybrid method with submillimeter average error in each direction. Strengths of the Hybrid method are not limited to the 4DCT lung data. The algorithm has the potential to be a powerful tool in applications where there is a limited Field of View (FOV) in one imageset. For example, in CT to cone-beam CT (CBCT) registration which is the focus of another ongoing investigation in our group, parts of the lungs are often cut off in the CBCT due to the location of the tumor, the treatment plans, and other tradeoffs in the data acquisition. In such cases, the biomechanical component of the Hybrid method helps establish a reliable deformation model in the cut-off regions based on the biomechanical properties of the lung tissues and the remaining boundary conditions determined in the regions where the data is available. Next, the intensity based refinement increases the accuracy in the overlapping regions by matching any residual misalignments.

An important application for an accurate DIR algorithm is dose accumulation, where the radiation dose is accumulated over the course of the treatment ranging from one to several weeks. An appropriate DIR adds minimum uncertainty in the process, and can subsequently help identify the remaining uncertainties in the treatment delivery and/or planning. Correlative pathology is another important example where accurate DIR plays a crucial role. For instance, recent studies show that there is significant deformation between the in vivo MRI of the prostate and the histopathology reconstructed images of the specimen after routine histology processes [34], [35]. A hybrid biomechanical intensity based registration may aid in determining an accurate deformation map between the two images which will then enable comparison of gold standard of pathology with in vivo imaging.