Self-aligned deterministic coupling of single quantum emitter to nanofocused plasmonic modes

Significance

Control and optimization of interaction between light and single quantum emitters are a crucial issue for cavity quantum electrodynamics studies and quantum information science. Although considerable efforts have been made, reliable and reproducible coupling between quantum emitter and cavity mode still remains a grand challenge due to the uncertainty of the size, i.e., the emission wavelength, and position of the quantum emitter. Here, we demonstrate an unprecedented approach of the self-aligned deterministic coupling of single quantum dots (QDs) to nanofocused plasmonic modes on an entire wafer. Spatial precision is better than any nanopositioning techniques, and almost all processed QDs exhibit outstanding spontaneous emission rate enhancement. This reliable approach eliminates a major obstacle in the implementation of practical solid-state quantum emitters.

Abstract

The quantum plasmonics field has emerged and been growing increasingly, including study of single emitter–light coupling using plasmonic system and scalable quantum plasmonic circuit. This offers opportunity for the quantum control of light with compact device footprint. However, coupling of a single emitter to highly localized plasmonic mode with nanoscale precision remains an important challenge. Today, the spatial overlap between metallic structure and single emitter mostly relies either on chance or on advanced nanopositioning control. Here, we demonstrate deterministic coupling between three-dimensionally nanofocused plasmonic modes and single quantum dots (QDs) without any positioning for single QDs. By depositing a thin silver layer on a site-controlled pyramid QD wafer, three-dimensional plasmonic nanofocusing on each QD at the pyramid apex is geometrically achieved through the silver-coated pyramid facets. Enhancement of the QD spontaneous emission rate as high as 22 ± 16 is measured for all processed QDs emitting over ∼150-meV spectral range. This approach could apply to high fabrication yield on-chip devices for wide application fields, e.g., high-efficiency light-emitting devices and quantum information processing.

Solid-state quantum photon sources based on semiconductor quantum dots (QDs) are a promising platform to realize scalable quantum technology (1–7). However, owing to the extremely small size of QDs (a few tens of nanometers) compared with the wavelength of light (a few hundreds of nanometers), the QD interaction with the photon field is very poor. This poor interaction results in rather low intrinsic spontaneous emission (SE) rates (8, 9), limiting the optical properties of single QDs: low repetition rate, higher sensitivity to thermally activated nonradiative processes and to dephasing from solid-state environment, etc. To overcome these limitations, there have been extensive efforts during the past decade to achieve deterministic coupling of a QD to intense photonic modes for strong Purcell effect (10–13), which demands spectral and spatial overlap between them. Due to the uncertainty of the size and position of the QD, it is still quite challenging and requires sophisticated control techniques, such as scanning probe microscopy and nanoscale positioning system (12, 14, 15). Therefore, demonstration of deterministic coupling is limited to few devices because the process has to be customized for each QD on the wafer.

Nanofocusing of surface plasmon polaritons, beyond the light diffraction limit, has recently seen rapid development. This nanofocusing can be achieved using various tapered metallic structures, such as a sharp metal edge, V-shaped wedges, and tapered waveguides (16–21). Tapering a metallic structure in all three dimensions, instead of only two, is considered ideal for ultimate light focusing (20, 21). The resulting extremely small mode volume can permit strong coupling to a nanosized single emitter. Moreover, the broad spectral bandwidth of plasmonic nanofocusing could cover the broad QD spectral distribution (∆λ/λ > 10⁻¹), whereas precise spectral matching between QD and the dielectric cavity is crucial, typically on the order of ∆λ/λ ∼ 1/Q ∼ 10⁻³ (Q is cavity quality factor). In return, positioning of nanofocused plasmonic mode with respect to the QD at the nanometer-scale accuracy is prerequisite for optimized coupling. For these reasons, control of the QD sites and of their overlapping with nanofocused light has become a significant issue for the wide application of single quantum emitters such as plasmonic cavity quantum electrodynamics experiments and integrated on-chip quantum devices.

Here, we demonstrate how both spectral and spatial matching between nanofocused plasmonic modes and array of single QDs can be achieved with two relatively simple technologies: site-selective growth of pyramidal QDs on a nanohole-patterned mask and thin metal film deposition on a QD wafer. The plasmonic modes are highly focused in close proximity to each single QD formed on the pyramid apex, in a self-aligned fashion with lateral spatial accuracy better than 5 nm. As a result, the decay time is reduced down to 0.2 ± 0.1 ns for processed QDs, compared with 4.4 ± 2.2 ns for as-grown QDs. This SE rate enhancement (22 ± 16) has been obtained for all measured QDs distributed over a spectral range of ∼150 meV across the entire wafer.

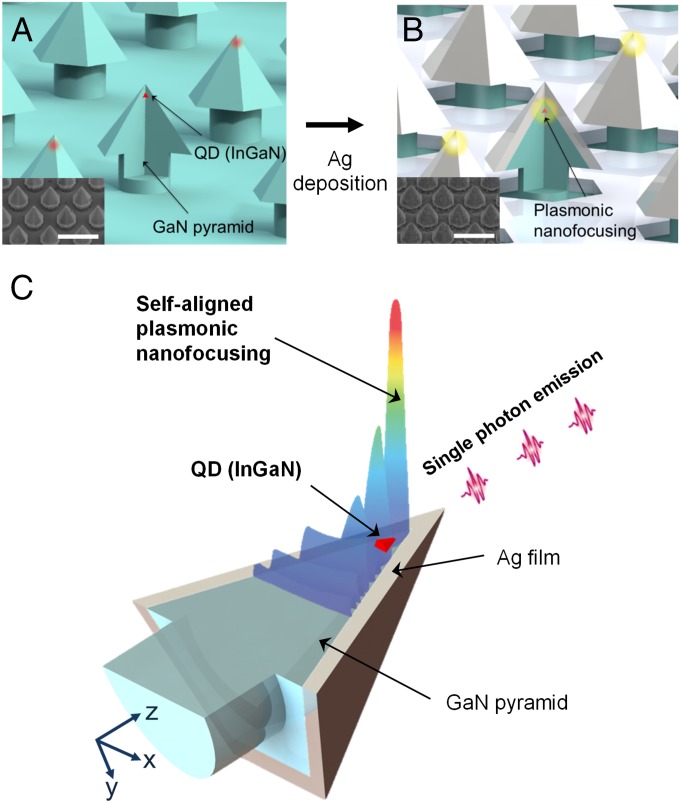
A schematic illustration of the proposed self-aligned coupling between plasmonic modes and single QDs is shown in Fig. 1. Submicrometer-sized GaN hexagonal pyramid structures were laterally overgrown on a hole-patterned Si₃N₄ mask by metal-organic chemical vapor deposition, as described in our previous work (22). They were subsequently covered by an InGaN layer and a GaN barrier layer, leading to the formation of 2.5-nm-thick InGaN quantum wells (QWs) at the pyramid facets and single QDs on pyramid apexes thanks to the 3D confinement of the exciton wave function at the apex, as shown in Fig. 1A (22–24). The QD sizes (diameter, 10–20 nm; height, 5–7 nm) are comparable to those of Stranski–Krastanov mode InGaN QDs (25, 26). Before depositing the silver film, the Si₃N₄ pattern was removed using an HF solution to obtain better confinement of plasmonic fields. Finally, a silver film with 40-nm thickness, optimized for local electric field enhancement and out-coupling to the far-field radiation (SI Text), was deposited on the pyramid wafer (Fig. 1B). For each QD at the pyramid apex, the six silver-coated facets act as 3D metallic tapered structures to generate strongly focused plasmonic modes at the apex (Fig. 1C). As a consequence, owing to the wide spectral range of the plasmonic resonance, both geometrical and spectral matchings are naturally realized between intense plasmonic fields and individual QDs over the entire wafer. The thickness of the GaN capping layer, serving as a spacer between the InGaN QDs and the silver film, was about 10 nm to ensure strong coupling to plasmonic nanofocused modes while minimizing metallic (nonplasmonic) quenching (i.e., nonplasmonic excitations in the metal such as interband absorption, electron scattering losses, and electron–hole excitations) (27, 28).

Fig. 1.

Structure of the site-controlled single QD array deterministically coupled to a plasmonic system. (A) A schematic and a scanning electron microscope (SEM) image of site-controlled InGaN QD array. The bottom diameter and height of the pyramid structure are around 260 and 220 nm, respectively. (Scale bar in SEM image: 500 nm.) (B) A schematic of self-aligned nanofocused plasmonic modes on single QD array and a SEM image of pyramid array after Ag deposition. The thickness of Ag film is ∼40 nm. (C) A conceptual image of how three-dimensionally nanofocused plasmonic modes and single QD could be spatially matched in a self-aligned fashion.

Results and Discussion

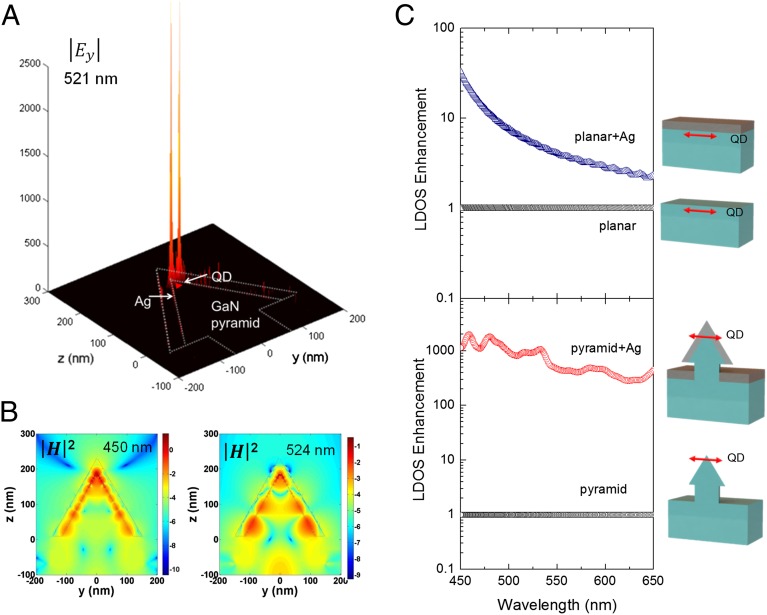
We undertook numerical modeling of the silver-coated nanopyramid structures by solving Maxwell equations using the 3D finite-difference time-domain method. Fig. 2A shows the electric field distribution inside the silver-coated pyramid structure, which has a dipole source polarized along the y axis near the apex of the pyramid (see Fig. 5B) (29, 30). As clearly shown in the magnetic field profiles (Fig. 2B), plasmonic modes in the tapered geometry of the pyramid structure generate strong enhancement of the local fields at the metal/dielectric interface over a wide spectral region. The silver-coated pyramid facets are similar in concept to previously reported cases of tapered plasmonic waveguides (17–19).

Fig. 2.

Numerical simulation of the pyramid-plasmonic system. (A) A surface plot of the absolute value of the electric field component along dipole direction (E_y) at 521 nm. The local electric fields are sharply enhanced near the apex of the pyramid structure, which is in close proximity to the QD position. (B) Cross-sectional intensity profile of the magnetic field in log scale at 450 and 524 nm. Dashed guided lines represent the position of the silver film on the pyramid. (C) Relative LDOS enhancement at the position of the dipole in silver-coated planar and pyramid systems with respect to those without silver film.

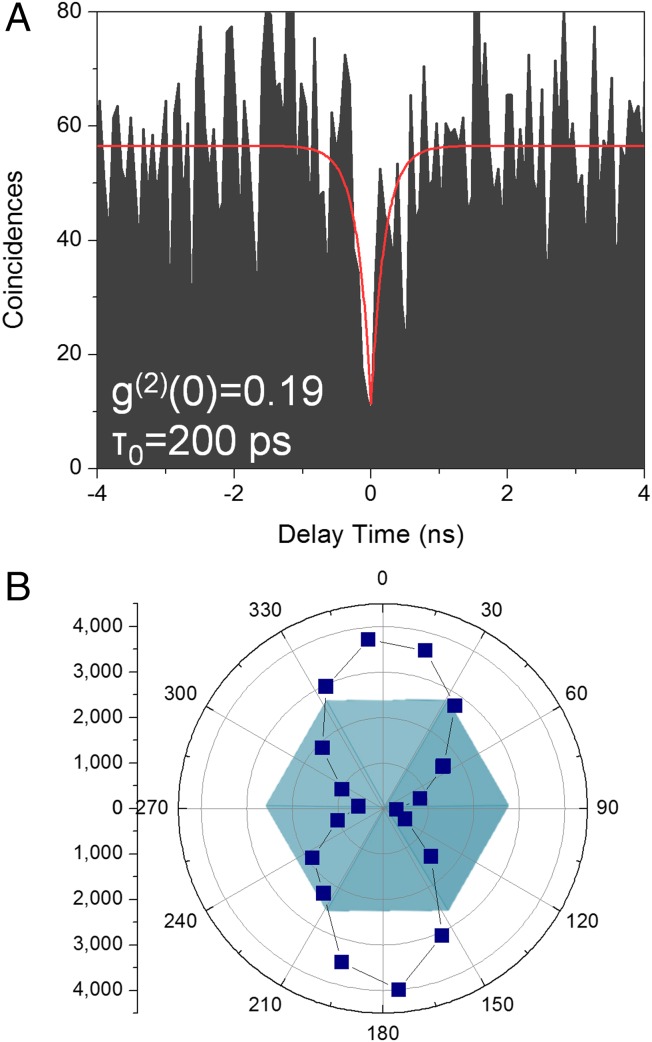
Fig. 5.

Optical characteristics of the single QD-plasmonic coupled system. (A) Photon-correlation measurement under CW excitation. The red curve was fitted using a second-order coherence function (B) Polar plot of the single QD PL intensity as a function of the polarization direction of the emission. Emissions from QDs are linearly polarized along the <$10\overline{1}0$> direction and have a high polarization ratio ∼0.93, defined as P = (I_max – I_min)/(I_max + I_min), where I_max is the maximum PL intensity and I_min is the minimum PL intensity. This polarization characteristic is also observed in QD emissions without a silver film.

To study the influence of these plasmonic modes on the SE rate of pyramid QDs, we calculated the local density of optical states (LDOS) for a dipole located at the apex of a pyramid structure with and without a silver film. The LDOS is proportional to the power emitted by the dipole, and thus to its SE rate (31). To appreciate the importance of the tapered geometry, calculations were also performed for the dipole in a planar structure, mimicking a self-assembled QD. Results were normalized to the case of structures without the silver film and plotted in Fig. 2C. The LDOS is clearly enhanced in silver-coated structures. However, this enhancement is much larger in the pyramid structure, as a result of highly focused plasmonic modes at the pyramid apex.

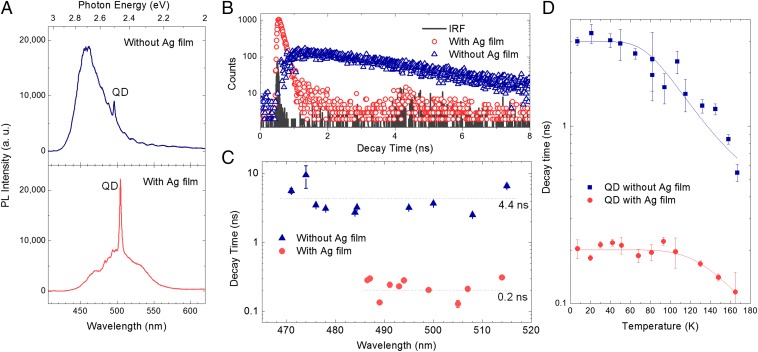
Samples with and without silver film were examined by microphotoluminescence (PL) measurements at 7 K, using both continuous-wave (CW) and pulsed excitations at 405 nm in the continuum bands of InGaN QDs and QWs. Fig. 3A shows the micro-PL spectra of pyramids with and without the silver film. The sharp line and the broader band observed for each pyramid are due to radiative recombination of excitons in the QD at the pyramid apex and in the QWs at the pyramid facets, respectively. In the as-grown pyramid, the QW emission is dominant over the QD emission. Remarkably, the QD emission increases significantly with respect to the QWs in the silver-coated pyramid, indicating an overall increase of the QD emitting power.

Fig. 3.

Experimental observation of Purcell effect of a single QD coupled to plasmonic modes. (A) Micro-PL spectra of QD pyramids without and with a silver film measured at 7 K. (B) Micro-PL decay dynamics measured at 7 K. The decay time is 4 ns for the single QD without a silver film, and 0.14 ns for the QD with a silver film. The black line shows the instrument response function of our system. (C) Scatter plot of measured single QD decay times at 7 K versus emission wavelengths. Error bars indicate the standard error of monoexponential decay fitting. The average decay time was 4.4 ± 2.2 ns for QDs without a silver film, and 0.2 ± 0.1 ns for QDs with a silver film, as shown by dotted lines. The signs of “±” indicate a standard deviation. (D) Measured exciton decay times of single QDs with and without Ag film as a function of temperature.

Quantitative analysis of QD PL measurements is not straightforward, because the measured PL intensity depends on several factors, which are likely to be modified upon the silver film deposition: in-coupling of the excitation laser, QD decay rate, out-coupling of the emitted light to the far field (including extraction to the far field and detection of far-field radiation pattern). However, one can get rid of the in-coupling factor by working under saturation condition, i.e., under excitation at level high enough to saturate the QD emission. Then, assuming the internal quantum efficiency of QDs equal to 1 (see discussion on QD decay dynamics below and SI Text), the saturated PL intensity under CW excitation would be proportional to the SE rate times the emission out-coupling, whereas for pulsed excitation (with an excitation repetition rate smaller than the PL decay rates), the saturated PL intensity is only governed by the out-coupling factor (see SI Text for details). By random probing QDs across the wafer, we measured out-coupling to the far-field radiation reduced by a factor of 0.5 ± 0.3 in silver-coated QDs compared with as-grown pyramid QDs. Modeling of our pyramid QDs shows that, with respect to bare pyramid QDs, the extraction efficiency to the far-field radiation would be strongly reduced to 0.2, but partly counterbalanced by a more favorable coupling (approximately $\times$ 2) toward our micro-PL setup for an overall reduction of 0.4, in good agreement with the measured value 0.5 ± 0.3. Despite this reduction, the saturated PL intensities of silver-coated QDs under CW excitation are enhanced by a factor 13 ± 8, giving evidence of remarkable enhancement of their SE rate. Combining both measurements, we obtain an enhancement of the SE rate equal to 26 ± 22 in silver-coated pyramid QDs (the large data dispersion observed here could be assigned to fluctuations of the pyramid shape; see below).

A more direct determination of the SE rate could be provided by time-resolved PL experiments. Exciton recombination dynamics were measured at 7 K, using low excitation power to avoid any state filling, which would yield wrong decay dynamics. As displayed in Fig. 3B, PL decays of QDs are monoexponentials, but dynamics of silver-coated QDs are much faster. A scatter plot of QD decay times versus wavelengths is shown in Fig. 3C. Outstanding shortening of the decay times are observed for all of the measured silver-coated pyramid QDs. Decay times averaged over the measured spectral range of ∼150 meV are 4.4 ± 2.2 ns for uncoated pyramid QDs and 0.2 ± 0.1 ns for coated ones, yielding an enhancement of decay rate by 22 ± 16, in good agreement with the PL saturation measurements.

At this stage, we need to confirm whether the internal quantum efficiency of QD is equal to 1 or not at low temperature. Therefore, to ascertain the radiative (or nonradiative) nature of the QD decay, we studied its decay dynamics as function of the temperature, and a typical result is plotted in Fig. 3D. Decay times of as-grown pyramid QDs and silver-coated ones are constant at low temperatures, and then become shorter above ∼50 K for the former and ∼100 K for the latter. The existence of a plateau in the exciton decay at low temperatures clearly indicates that the temperature-dependent part of the nonradiative decay channel is negligible at low temperature. Its temperature-independent part is usually neglected also in as-grown QDs. However, for QDs strongly coupled to plasmonic modes, temperature-independent nonradiative decay processes (nonplasmonic quenching due to the metal) should be taken into account. This is the case of emitters at close proximity to the metal surface, typically at distances below 5 nm (27, 28). In this work, however, QDs are separated by ∼10 nm from the silver film, which should be enough to minimize metallic quenching while ensuring strong interaction with nanofocused plasmonic modes. This speculation is supported by the strong enhancement of the QD PL intensity in silver-coated QDs despite reduced out-coupling efficiency. Therefore, we have fitted data (solid lines in Fig. 3D) by considering an exciton recombination process that is dominantly radiative at low temperatures and nonradiative at elevated temperatures (32): 1/τ = 1/τ_r + 1/τ_nr, where τ is the measured total exciton decay time, τ_r is the spontaneous radiative decay time (supposed to be independent of temperature in the studied temperature range), and τ_nr = τ₁ exp(E_a/kT) is the nonradiative exciton decay time corresponding to a thermally activated loss process (e.g., thermal carrier escape out of the QD) characterized by a time constant τ₁ and an activation energy E_a. In case of silver-coated pyramid QD, τ_r would be replaced by τ_p, the spontaneous emission time in the presence of plasmonic modes (SI Text). From the fit, decay rates are found to be accelerated in silver-coated QDs, but more strongly for the SE rate part (approximately $\times$ 22) than for the nonradiative part (approximately $\times$ 5 at 180 K), making them more “stable” at higher temperatures. As a consequence, the measured decay rate above (at 7 K) would be dominated by SE rate rather than nonradiative exciton decay rate, we extract the SE rate enhancement equal to (1/τ_p,pyramid+Ag)/(1/τ_r,pyramid) = 22 ± 16.

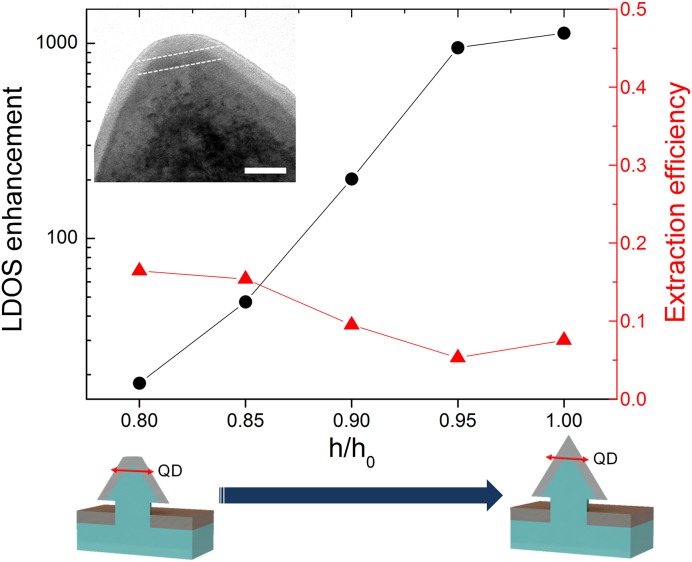
The SE enhancement observed here is remarkable considering that it has been achieved over a wide spectral range (∼150 meV) across the whole QD wafer, requiring no precise positioning or complex technology but only simple thin-film deposition. However, it is still much lower than the predicted values shown in Fig. 2C. Notably, the actual enhancement is very sensitive to any imperfections of the pyramid shape. We used transmission electron microscopy (TEM) to examine the pyramid shapes (Inset of Fig. 4). As shown in the TEM image, the pyramid tip is not so perfectly sharp as modeled in Fig. 2 but is more or less rounded. We have modeled pyramids featuring this type of imperfection by truncated pyramids and plotted their LDOS enhancement factor F_LDOS = LDOS_pyramid+Ag/LDOS_pyramid in Fig. 4 (solid circles). As shown in this figure, the enhancement factor F_LDOS varies dramatically with the pyramid sharpness, reflecting the extreme sensitivity of plasmonic nanofocusing on the facet taper shape. For truncated pyramids with heights reduced by 20% with respect to the perfect pyramid (similar to the pyramid shown in TEM data), the SE enhancement would be around 18, which is consistent with our measured SE rate enhancement ∼22 ± 16. This strong dependence of plasmonic nanofocusing on the pyramid shape also affects the extraction efficiency of plasmonic modes toward the far field: average extraction efficiency of QDs emitting at 470- to ∼540-nm increases from 8% for the perfect pyramid to 16% for the truncated pyramid (Fig. 4, solid triangles). We note that the shape of pyramid can be further improved by optimizing growth conditions and high-precision nanopatterning process.

Fig. 4.

Influence of the pyramid sharpness on the calculated LDOS enhancement and extraction efficiency (i.e., far-field radiated power/total emitted power), which is averaged over 470∼540 nm. The pyramid sharpness is characterized by the ratio h/h₀, where h₀ is the height of the perfect pyramid structure, whereas h is that of the truncated pyramid structure. (Inset) TEM image of the apex of the InGaN/GaN pyramid structure without a silver film. (Scale bar: 20 nm.) Two dotted lines indicate the QD height. For the structure with h/h₀ = 0.8, similar to the structure in the TEM image, the calculated LDOS enhancement is ∼18.

Finally, we observed nonclassical photon statistics from silver-coated pyramid QD by measuring the second-order correlation function (with Hanbury Brown–Twiss setup). Fig. 5A presents a coincidence histogram under CW excitation as a function of the delay time. The photon correlation data were fitted with the function $G^{\left(2\right)}\left(\tau \right)=A[1-(1-g^{\left(2\right)}\left(0\right))\exp \left(-\left|\tau \right|/{\tau }_0\right)]$ with the fitting parameters $A$, $g^{\left(2\right)}\left(0\right)$, and ${\tau }_{\mathrm{0}}$ (26). Under weak excitation, the radiative recombination rate is dominant over the pumping rate, and hence τ₀ ∼ τ_r. The fitting result of ${\tau }_{\mathrm{0}}$ was 200 ± 60 ps, which agrees well with the average decay time of silver-coated QDs in Fig. 3C. The fitting result of $g^{\left(2\right)}\left(0\right)$ was 0.19 ± 0.17, which provides unambiguous evidence of nonclassical photon antibunching from our silver-coated pyramid QDs. Fig. 5B shows the polarization dependence on the single-photon emission. The observed linear polarization is caused by the anisotropy potential of QDs on the pyramid structure (30). It can be controlled for various applications such as quantum information processing by growing elongated pyramid QDs as demonstrated in ref. 33.

Conclusion

In conclusion, we have shown that pyramid QD facets can serve as self-aligned 3D tapered waveguides for plasmonic nanofocusing at pyramid apexes. By depositing a thin silver film layer on the pyramid QD wafer, we have obtained an enhancement ∼22 ± 16 of the QD SE rate, together with a far-field radiation increased by one order of magnitude, over the QD spectral distribution ∼150 meV. The fabrication process proposed in this work is extremely simple and can be applied to not only pyramid structures but also any tapered structures. Moreover, this single QD in metal-coated nanostructure could be easily detached from its wafer and integrated with on-demand on-chip device. The mass fabrication of single emitter–light coupled devices with this simple approach is an essential technological step toward the development of quantum on-chip devices and opens up possibilities of achieving practical quantum information devices.

Materials and Methods

Growth and Fabrication.

An n-type GaN template was prepared on a c-plane sapphire substrate by metal-organic chemical vapor deposition (MOCVD). Si₃N₄ hole patterns were produced on the n-type GaN template, after which hexagonal pyramidal GaN structures were laterally overgrown on the hole-patterned mask by MOCVD. An InGaN single-quantum well layer and a GaN barrier layer were grown on GaN pyramid structures to achieve a single QD on the top of the pyramid. Single QDs were naturally formed on each apex of pyramids as a result of the 3D confinement of the exciton (electron–hole pair) wave function at the apex. The fabricated pyramid structures have base radius of 127 ± 3 nm and height of 161 ± 17 nm. Before depositing the silver film, the Si₃N₄ pattern was removed using an HF solution [50% (wt/wt)] for 15 min to obtain better confinement of plasmonic fields. The silver film, with a thickness of 40 nm, was directly deposited by an e-beam evaporator.

Numerical Modeling.

Three-dimensional numerical modeling by solving Maxwell equations was done using a commercial finite-difference time-domain method program (Lumerical Solutions). We used refractive indices experimentally determined by Johnson and Christy (34) for silver and by Barker and Ilegems (35) for GaN. We assume real and imaginary parts of the silver refractive index are temperature independent in case of thin films (36). Dimensions of simulated pyramid QDs were those observed in SEM and TEM images: pyramids with 260-nm base diameter, and rounded tips. Our pyramids are modeled by perfect pyramid and truncated pyramids (characterized by the ratio h/h₀ ∼0.8, with h indicating height of the truncated pyramid, and h₀, height of the perfectly sharp pyramid). A single dipole was positioned close to the pyramid apex, 11 nm below the silver film, as in TEM data. The dipole was adjusted to be linearly polarized along the <$10\overline{1}0$> direction, as experimentally measured. As a reference structure, the dipole embedded in a planar GaN structure was also simulated. The LDOS and the far-field radiation (from the top and the bottom of the pyramid structure) were calculated as a function of the silver film thickness, the dipole emission wavelength, and the pyramid sharpness (h/h₀).

Single QD Spectroscopy.

A low-temperature micro-PL setup was used to study the optical properties of single QDs. The sample was mounted in a low-vibration cryostat with tunable temperatures ranging from 7 K to ∼300 K. A semiconductor laser diode was used for CW excitation, whereas a Ti:sapphire laser [full width at half-maximum (FWHM), 200 fs; repetition rate, 80 MHz] was used for pulsed excitation; both lasers operated at a wavelength of 405 nm to selectively excite in the continuum bands of InGaN QDs and QWs. A microscope objective lens with a long working distance (Mitutoyo; 100×; N.A., 0.5) was used to excite an area of ∼1 μm² of the pyramidal structures and to collect the PL from the samples in the normal direction. The PL spectrum was measured using a monochromator (Acton; SP2500) in conjunction with a CCD detector with spectral resolutions of 0.03 and 0.2 nm using 1,200 and 150 lines per mm, respectively. To eliminate the polarization dependence error from the optics system, we used a controlled half-wave plate in front of a fixed linear polarizer for the polarization measurement. To measure the decay time, the selected spectral region of the signal was detected with a rapid avalanche photodiode (APD) (temporal resolution, 40 ps; ID Quantique) coupled to a time-correlated single-photon counting (TCSPC) (Picoharp300; Picoquant) system. The FWHM of our instrument response function was 49 ps, and the time bin of our measurement setting was 8 ps. To obtain the second-order photon correlation function, two rapid APD pairs (temporal resolution, 40 ps; ID Quantique) with a 50:50 beam splitter were used for the Hanbury Brown–Twiss setup. Coincidence histograms of the delay times between detected photons were measured using a TCSPC system.