HCN channels enhance spike phase coherence and regulate the phase of spikes and LFPs in the theta-frequency range

Significance

The impact of the pacemaking hyperpolarization-activated cyclic-nucleotide–gated (HCN) channels on local field potentials (LFP) has not been analyzed. Here, employing a neuropil of several morphologically precise hippocampal neuronal models that received systematically randomized rhythmic synaptic inputs, we demonstrate that HCN channels alter the phase, but not the amplitude, of LFPs. Further, it is known that the spike timings of individual neurons follow the beat of the LFPs and fire at precise phases of the LFP beat. We demonstrate that the presence of HCN channels alters this phase and enhances the precision to which the spikes follow the LFP beat. These results unveil several important roles for HCN channels, extending their regulatory potential beyond single-neuron physiology.

Abstract

What are the implications for the existence of subthreshold ion channels, their localization profiles, and plasticity on local field potentials (LFPs)? Here, we assessed the role of hyperpolarization-activated cyclic-nucleotide–gated (HCN) channels in altering hippocampal theta-frequency LFPs and the associated spike phase. We presented spatiotemporally randomized, balanced theta-modulated excitatory and inhibitory inputs to somatically aligned, morphologically realistic pyramidal neuron models spread across a cylindrical neuropil. We computed LFPs from seven electrode sites and found that the insertion of an experimentally constrained HCN-conductance gradient into these neurons introduced a location-dependent lead in the LFP phase without significantly altering its amplitude. Further, neurons fired action potentials at a specific theta phase of the LFP, and the insertion of HCN channels introduced large lags in this spike phase and a striking enhancement in neuronal spike-phase coherence. Importantly, graded changes in either HCN conductance or its half-maximal activation voltage resulted in graded changes in LFP and spike phases. Our conclusions on the impact of HCN channels on LFPs and spike phase were invariant to changes in neuropil size, to morphological heterogeneity, to excitatory or inhibitory synaptic scaling, and to shifts in the onset phase of inhibitory inputs. Finally, we selectively abolished the inductive lead in the impedance phase introduced by HCN channels without altering neuronal excitability and found that this inductive phase lead contributed significantly to changes in LFP and spike phase. Our results uncover specific roles for HCN channels and their plasticity in phase-coding schemas and in the formation and dynamic reconfiguration of neuronal cell assemblies.

Local field potentials (LFPs) have been largely believed to be a reflection of the synaptic drive that impinges on a neuron. In recent experimental and modeling studies, there has been a lot of debate on the source and spatial extent of LFPs (1–9). However, most of these studies have used neurons with passive dendrites in their models and/or have largely focused on the contribution of spike-generating conductances to LFPs (7, 8, 10, 11). Despite the widely acknowledged regulatory roles of subthreshold-activated ion channels and their somatodendritic gradients in the physiology and pathophysiology of synapses and neurons (12–17), the implications for their existence on LFPs and neuronal spike phase have surprisingly remained unexplored. This lacuna in LFP analysis is especially striking because local and widespread plasticity of these channels has been observed across several physiological and pathological conditions, translating to putative roles for these channels in neural coding, homeostasis, disease etiology and remedies, learning, and memory (16, 18–23).

In this study, we focus on the role of hyperpolarization-activated cyclic nucleotide-gated (HCN) channels that mediate the h current (I_h) in regulating LFPs and theta-frequency spike phase. From a single-neuron perspective, HCN channels in CA1 pyramidal neurons play a critical role in regulating neuronal integration and excitability (14, 24–27) and importantly introduce an inductive phase lead in the voltage response to theta-frequency oscillatory inputs (28), thereby enabling intraneuronal synchrony of incoming theta-frequency inputs (29). Given these and their predominant dendritic expression (25), we hypothesized HCN channels as regulators of LFPs through their ability to alter the amplitude and phase of the intracellular voltage response, thereby altering several somatodendritic transmembrane currents that contribute to LFPs. The CA1 region of the hippocampus offers an ideal setup to test this hypothesis, given the regular, open-field organization (4, 6, 7) of the pyramidal neurons endowed with well-established somatodendritic gradients in ion channel densities (16). As this organization enables us to assess the role of location-dependent channel expression profiles on LFPs across different strata, we tested our hypothesis, using a computational scheme involving morphologically realistic, physiologically constrained conductance-based model neurons. Our results positively test our hypothesis and provide specific evidence for novel roles for HCN channels and their inductive component in regulating LFP and spike phases, apart from enhancing spike-phase coherence. These results identify definite roles for HCN channels in phase-coding schemas and in the formation and dynamic reconfiguration of neuronal cell assemblies and argue for the incorporation of subthreshold-activated ion channels, their gradients, and their plasticity into the computation of LFPs.

Results

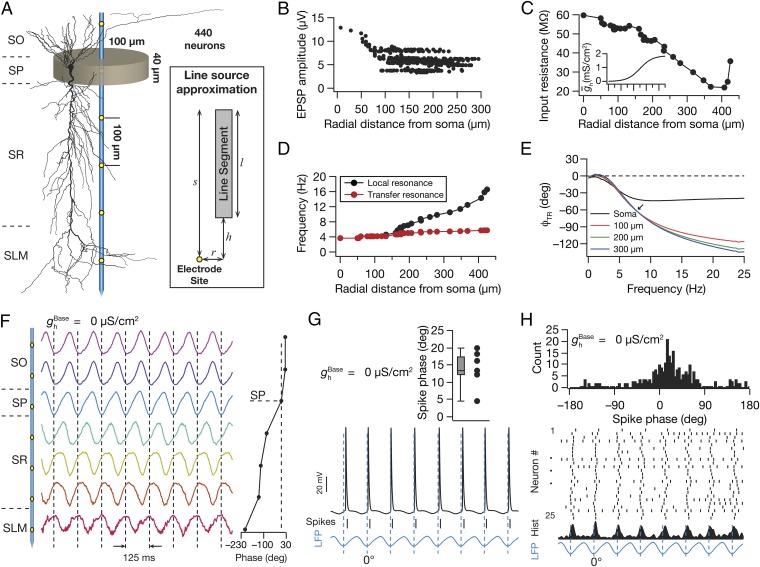
We performed our experiments on a neuropil containing 440 morphologically realistic, conductance-based CA1 pyramidal neuronal models, whose somata were distributed within a cylindrical volume of 200 µm diameter and 40 µm height (Fig. 1A). We stimulated the neuronal compartments with theta-modulated (8 Hz) excitatory and inhibitory inputs, with an experimentally constrained synaptic distribution (Fig. 1B). The passive properties and the gradient in HCN-channel density (Fig. 1C) were set to match the functional maps of input resistance (R_in) (Fig. 1C), local (f_R), and transfer (f_TR) resonance frequencies (Fig. 1D), apart from setting the synchronization frequency (Fig. 1E) at ∼8 Hz (16, 25, 26, 28, 29).

Fig. 1.

Model components and computation of local-field potentials and spike theta phase. (A, Left) A single electrode with seven recording sites, located at the center of the cylindrical neuropil, spanned all strata of the CA1 (SO, stratum oriens; SP, stratum pyramidale; SR, stratum radiatum; and SLM, stratum lacunosum moleculare). (A, Right) The line source approximation method. Shown is a single line segment of length l, separated by a radial (perpendicular) distance r from a recording site. The nearest distance between the compartment and the perpendicular is denoted by h and s = l + h. (B) Distribution of unitary somatic EPSP amplitudes (v_uEPSP) as a function of radial distance from the soma, depicting distance invariance of v_uEPSP. (C and D) Input resistance (C) and local and transfer resonance frequency (D) in the presence of a sigmoidal gradient of HCN conductance (C, Inset), all plotted along the somatoapical trunk. (E) Transfer impedance phase profile for four different locations along the somatoapical trunk. Arrow indicates the synchronization frequency at ∼8 Hz. (F, Left) Normalized LFP traces (1 s) computed using LSA for SO, SP, SR, and SLM. (F, Right) LFP phase (mean ± SEM, 10 cycles) at each recording site, with reference to the SP LFP. (G, Bottom) SP LFP with spikes (ticks) and intracellular voltage for a single neuron. (G, Top) Distribution of spike phases of the neuron, at various cycles, with reference to the SP LFP. (H, Bottom) Raster plot for 25 neurons and corresponding spike time histogram and SP LFP. (H, Top) Histogram of the spike phases with reference to the SP LFP for the population of 25 neurons.

As a first step, we removed all voltage-gated ion channels (VGIC) from the entire neuronal population and computed LFPs, using the line-source approximation method (4, 6–8, 30, 31). As a direct consequence of theta-modulated synaptic inputs (8 Hz) that drove the neuronal compartments, the LFPs across strata depicted theta-band modulation (Fig. 1F). With an open-field dipole oriented with the sink in the stratum radiatum (SR) and a source around the perisomatic region (4, 6, 7), the theta-frequency LFP recorded across different sites exhibited a progressive phase shift across recording sites adding to ∼180° (Fig. 1F). Next, we introduced Na⁺ and delayed-rectifier K⁺ channels into the somatodendritic arbor of these neurons and recorded somatic intracellular voltages to calculate neuronal spike phases with reference to the stratum pyramidale (SP) LFP (Fig. 1G). We found that neuronal spikes were triggered at specific theta phases close to the trough of the SP LFP (Fig. 1 G and H). These conclusions on phase shifts in cross-strata theta-frequency LFPs and spikes aligned to specific phases of the SP LFP are consistent with experimental measurements from rodent hippocampus (32–35).

HCN Channels Introduced a Phase Lead in LFPs Across Strata.

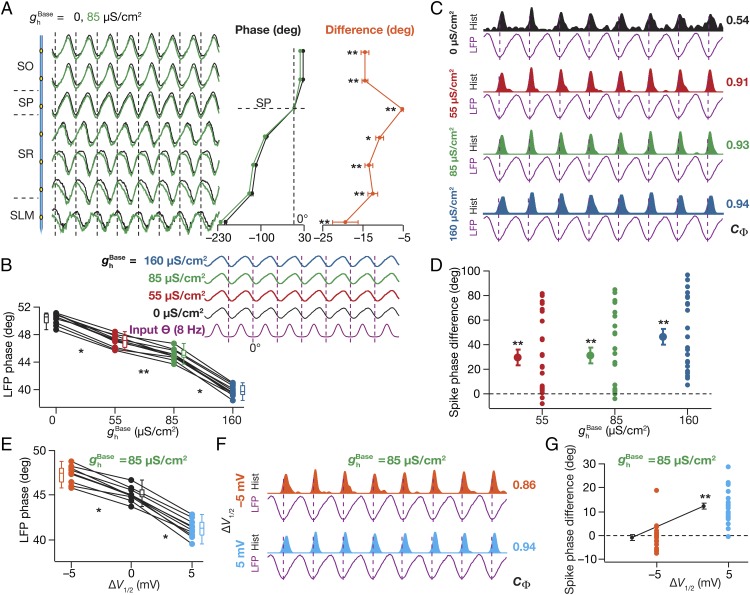
To assess the role of HCN channels and their graded plasticity (16, 22–24, 26, 28) on LFPs, we next measured LFPs in models with three different base values ($g_h^{\text{Base}}$ = 55 µS/cm², 85 µS/cm², and 160 µS/cm²) for the somatodendritic gradient (Fig. 1C) of HCN channels, set across the arbor of all constituent neurons (Fig. S1 A–C). Because of the domination of the underlying rhythmic high-conductance state (36), the LFP amplitudes across recording sites were not significantly different with the insertion of HCN channels. However, the incorporation of HCN channels introduced a significant location-dependent phase lead in the LFPs across all recording sites, when compared with corresponding LFPs computed in the absence of HCN channels (Fig. 2A). Assessing the mechanistic basis for this, we noted that the incorporation of HCN channels introduced an inductive lead in the intracellular local response voltage (28, 29) with reference to the response voltage in the passive neuron. Consequently, the transmembrane leak current in these compartments (which, by definition, followed the local voltage) exhibited a phase lead with reference to the leak current recorded in the absence of HCN channels. As LFPs are correlated with the net transmembrane current, LFPs computed in the presence of HCN channels showed a phase lead across all strata in comparison to the LFPs computed in their absence (Fig. 2A). The phase of the local leak current and its somatodendritic distribution, in conjunction with the density of HCN channels (higher in distal apical dendrites) and the differential activation of HCN channels as a consequence of the relative phase difference and localization profiles of synaptic types (inhibition induces perisomatic hyperpolarization, whereas excitation induces SR depolarization, with a 60° phase shift) then explains the location dependence of LFP phase lead introduced by HCN channels. Consistent with this inference, we found that the LFP phase lead was graded and increased progressively with increase in HCN conductance (Fig. 2B), suggesting a graded influence of global HCN-channel plasticity on LFP phase.

Fig. 2.

Incorporating HCN channels resulted in a location-dependent lead in the LFP phase, a lag in the spike phase, and a reduction in spike-phase jitter. (A, Left) Normalized LFP traces (1 s) for different strata in the presence ($g_h^{\text{Base}}$ = 85 µS/cm²) and in the absence ($g_h^{\text{Base}}$ = 0 µS/cm²) of HCN channels. (A, Center) LFP phase (mean ± SEM over 10 cycles) with reference to the stratum pyramidale (SP) LFP for corresponding traces in A, Left. (A, Right) Strata-wise cycle-matched difference (mean ± SEM) between the LFP phase obtained with $g_h^{\text{Base}}$ = 85 µS/cm² and 0 µS/cm². (B, Top) Normalized LFP traces (1 s) for different $g_h^{\text{Base}}$ values depicted with reference to the excitatory input θ. (B, Bottom) LFP phase (SP recording site) with reference to the excitatory input θ, plotted for different $g_h^{\text{Base}}$ values. (C) Population spike time histograms (1 s) with corresponding SP LFP, plotted for different $g_h^{\text{Base}}$ values. (D) Spike-phase difference (cycle matched for 8 cycles; mean ± SEM) between the spike phase for the said $g_h^{\text{Base}}$ value and for the case where $g_h^{\text{Base}}$ = 0 µS/cm² (n = 24 neurons for $g_h^{\text{Base}}$ = 85 µS/cm² and 160 µS/cm²). (E) LFP phase with reference to the excitatory input θ (mean ± SEM, 10 cycles) for baseline $V_{1/2}$ ($\mathrm{\Delta }{V}_{1/2}$ = 0 mV) and hyperpolarized ($\mathrm{\Delta }{V}_{1/2}$ = –5 mV) and depolarized $V_{1/2}$ ($\mathrm{\Delta }{V}_{1/2}$ = +5 mV) of HCN-channel activation. (F) Population spike time histograms (1 s) with corresponding SP LFP with $\mathrm{\Delta }{V}_{1/2}$ = –5 mV and $\mathrm{\Delta }{V}_{1/2}$ = +5 mV. (G) Spike-phase difference (cycle matched for 8 cycles; mean ± SEM) between the spike phase for the case where $\mathrm{\Delta }{V}_{1/2}$ = –5/+5 mV and those with $\mathrm{\Delta }{V}_{1/2}$ = 0 mV (n = 24 neurons). (A, B, and E) *P < 0.05, **P < 0.005 (Wilcoxon signed-rank test). (D and G) **P < 0.005 (Student’s t test on the null hypothesis of no spike-phase difference).

HCN Channels Induced a Lag in the Spike Phase and Enhanced Neuronal Spike Phase Coherence.

How does the presence of and plasticity in (26, 27) HCN-channel conductance alter the theta phase of neuronal spikes? We plotted the population spike-timing histogram and the corresponding SP LFP for each HCN-channel density under consideration (Fig. 2C). With increase in $g_h^{\text{Base}}$, we observed that the jitter associated with spike phases decreased, thereby enhancing their coherence with reference to the SP LFP (Fig. 2C). To quantify this, we calculated spike-phase coherence, $C_{\mathrm{\Phi }}$ (37), and observed that $C_{\mathrm{\Phi }}$ increased with increasing $g_h^{\text{Base}}$. This is consistent with earlier observations that HCN channels reduce temporal summation (14, 24–26), in effect reducing the temporal window for spike-generating coincidence detection (38, 39), a property that critically depends on their ability to introduce an inductive component (38). Specifically, the presence of HCN channels constricts the ability of a neuron to spike across a large span of the theta oscillation, thereby leading to enhanced spike-phase coherence (Fig. 2C). Finally, we found that the theta phase of the spikes showed a progressive and significant lag with increase in HCN-channel density (Fig. 2D), implying a graded influence of global HCN plasticity on spike phase.

Apart from changes in conductance, plasticity and cyclic nucleotide-dependent modulation of HCN channels have been demonstrated (40–43) to also manifest as shifts in their half-maximal activation voltage (V_1/2). To assess the impact of such shifts on LFP and spike phase, we repeated our simulations and analyses with different values of HCN-channel V_1/2 (Fig. 2 E–G). We found that depolarization of V_1/2 resulted in an increased lead in LFP phase (Fig. 2E and Fig. S1 D and E), an increased spike-phase coherence (Fig. 2F), and an increased lag in spike phase (Fig. 2G). We noted that our observations with depolarization of V_1/2 were similar to those with increase in $g_h^{\text{Base}}$ (Fig. 2 A–D). This should be expected given that I_h increases either with increase in $g_h^{\text{Base}}$ or with depolarization of V_1/2, given similarities in the impact of either change on several intrinsic properties (26, 28).

Regulation of LFP and Spike Phases by HCN Channels Was Invariant to Changes in Neuropil Size and to Morphological Heterogeneity.

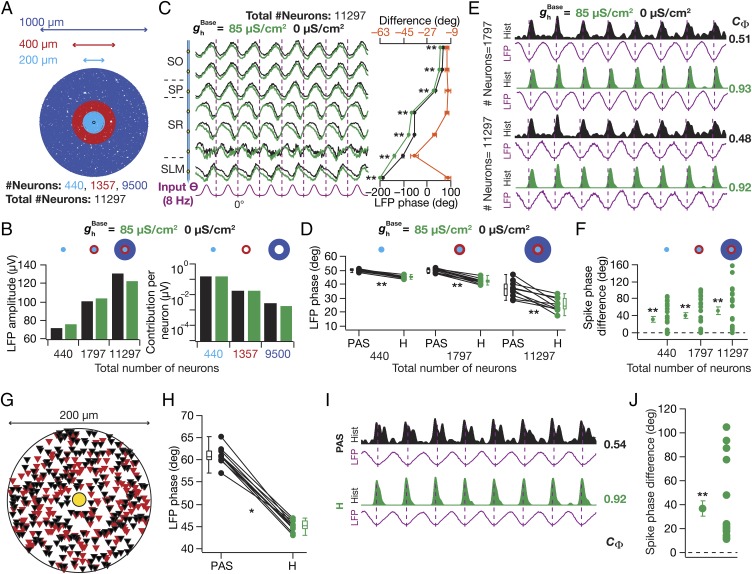
Our analyses thus far were performed with a small 200-µm diameter cylindrical neuropil in an effort to reduce computational burden. How dependent were our conclusions on the size of the neuropil? To address this, we repeated our simulations with two additional neuropils with 400 µm diameter (total number of neurons: 1,797) and 1,000 µm diameter (total number of neurons: 11,297; Fig. 3A), while retaining the same density of neurons across neuropils and with identical electrode location at the center of the neuropil. As expected (7), the LFP amplitude increased with increase in neuropil size (Fig. 3B, Left and Fig. S2). However, the contribution per neuron from the distal annuli decreased by orders of magnitude (Fig. 3B, Right), suggesting minimal contribution of neurons from these annuli to the LFP. Importantly, the introduction of an HCN-channel gradient (Fig. 1 C–E) into the constituent neurons resulted in a lead in the LFP phase without significant changes in LFP amplitude (Fig. 3 B–D and Fig. S2), an increase in spike-phase coherence (Fig. 3E), and a lag in the associated spike phase (Fig. 3F) across all tested neuropils.

Fig. 3.

HCN-channel–induced changes in LFP and spike phases were invariant to changes in neuropil size and to morphological heterogeneity. (A) Three neuropils of different sizes, used for analyses presented in B–F, depicted with the distribution of neurons. (B, Left) SP LFP amplitude computed in the presence ($g_h^{\text{Base}}$ = 85 µS/cm²) and in the absence ($g_h^{\text{Base}}$ = 0 µS/cm²) of HCN channels, for three different neuropil sizes. (B, Right) Per neuron contribution to the LFP amplitude computed with $g_h^{\text{Base}}$ = 0 µS/cm² and 85 µS/cm² for the three annuli (A). (C, Left) Normalized LFP traces (1 s) for different strata with $g_h^{\text{Base}}$ = 0 µS/cm² and 85 µS/cm² for the largest (1,000 µm diameter) neuropil. (C, Right, Bottom axis) LFP phase with reference to the excitatory input θ (mean ± SEM, 10 cycles) for corresponding traces in C, Left. (C, Right, Top axis) Strata-matched phase difference between LFPs obtained with $g_h^{\text{Base}}$ = 85 µS/cm² and 0 µS/cm². (D) LFP phase with reference to the excitatory input θ for three different neuropil sizes computed in the absence (PAS) and the presence (H) of HCN channels. Note the increased variability in the LFP phases (computed across cycles) with increase in neuropil size, a consequence of increased jitter in LFP traces with increase in neuropil size (Fig. S2). (E) Population spike-time histograms (1 s) with corresponding SP LFP for different neuropil sizes for $g_h^{\text{Base}}$ = 0 µS/cm² and 85 µS/cm². (F) For three neuropil sizes, cycle-matched difference between spike phases obtained with $g_h^{\text{Base}}$ = 85 µS/cm² and with $g_h^{\text{Base}}$ = 0 µS/cm², for 24 different neurons (mean ± SEM). (G) Distribution of 440 neurons with n123 (red, N_n = 214) and ri04 (black, N_n = 226) morphological reconstruction, used for the analyses in H–J. (H) SP LFP phase with reference to input θ (mean ± SEM, 10 cycles), computed in the absence (PAS) and the presence (H) of HCN channels. (I) Population spike-time histograms (1 s) with corresponding SP LFP. (J) Cycle-matched difference between spike phases obtained in the presence and in the absence of HCN channels, for 22 different neurons (mean ± SEM). (C, D, and H) *P < 0.05, **P < 0.005 (Wilcoxon signed rank test). (F and J) **P < 0.005 (Student’s t test on the null hypothesis of no spike-phase difference).

Next, although our analyses thus far were performed with independently rotated versions of a morphological reconstruction with randomly located probabilistic synaptic input (7), they were derived from a single morphological reconstruction (n123; Fig. 1A). To address the impact of morphological heterogeneity, we employed an additional morphological reconstruction (ri04; Fig. S3A), tuned its intrinsic and synaptic properties along its somatodendritic arbor to match with experimental observations (Fig. S3 B–E), and uniformly distributed the two morphologies with random rotations across the neuropil (Fig. 3G). Comparing LFPs and spikes obtained in the absence and the presence of HCN channels, we found the impact of HCN channels in introducing a lead in LFP phase (Fig. 3H and Fig. S3 F and G), an increase in spike-phase coherence (Fig. 3I and Fig. S3H), and a lag in spike phase (Fig. 3J) to be invariant to morphological heterogeneity. Together, these results suggested that the impact of HCN channels on LFP phase, spike phase, and spike coherence was invariant to changes in neuropil size and to morphological heterogeneity.

Regulation of LFP and Spike Phases by HCN Channels Was Invariant to Changes in Synaptic Parameters.

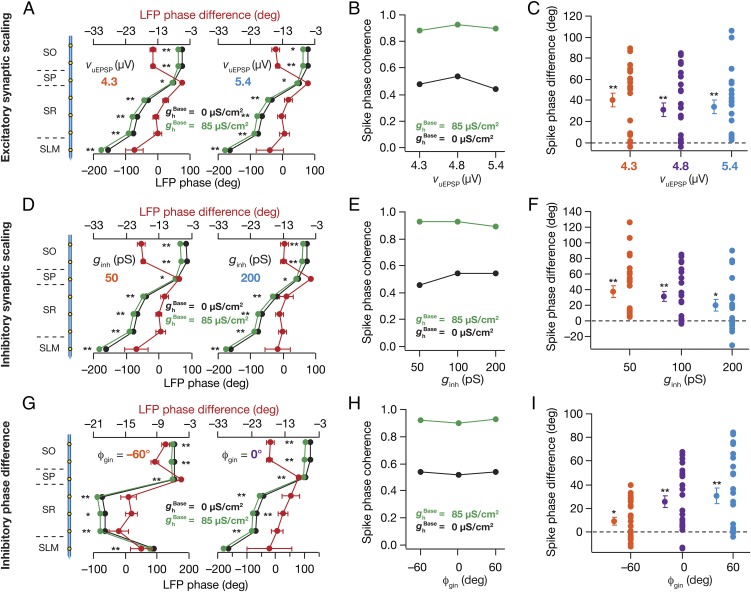
Were our conclusions on the role of HCN channels in altering LFP and spike phases (Figs. 2 and 3) specific to our choice of parameters associated with the excitatory and inhibitory drive? To address these, we performed detailed sensitivity analyses on parameters (Fig. 4 and Figs. S4–S7) associated with excitatory and inhibitory synapses. We found that the introduction of HCN channels resulted in a lead in the LFP phase, an enhancement in spike-phase coherence, and a lag in the spike phase, irrespective of up- or down-regulation of excitatory (Fig. 4 A–C) or inhibitory (Fig. 4 D–F) synapses. Next, we reanalyzed the data presented in Fig. 4 A–F to ask whether synaptic scaling of excitatory or inhibitory inputs altered LFPs and spikes. Whereas increasing AMPAR conductances induced a lag in the SP LFP and a lead in the spike phase (Fig. S4), increase in GABA_AR conductances resulted in a lead in the SP LFP and a lag in the spike phase (Fig. S5). We noted that the spike-phase coherence was not significantly altered by synaptic scaling (Fig. 4 B and E and Figs. S4 and S5).

Fig. 4.

HCN-channel–induced changes in LFP and spike phases were invariant to changes in synaptic properties. (A, Bottom axis) LFP phase with reference to the excitatory input θ (mean ± SEM, 10 cycles), computed in the presence ($g_h^{\text{Base}}$ = 85 µS/cm²) and in the absence ($g_h^{\text{Base}}$ = 0 µS/cm²) of HCN channels for different unitary EPSP (v_uEPSP) values. Default value of v_uEPSP = 4.8 µV. (A, Top axis) Strata-matched phase difference between LFPs obtained with $g_h^{\text{Base}}$ = 85 µS/cm² and 0 µS/cm². (B) Spike-phase coherence plotted for different v_uEPSP values, for $g_h^{\text{Base}}$ = 0, 85 µS/cm². (C) Cycle-matched difference between spike phases obtained with $g_h^{\text{Base}}$ = 85 µS/cm² and with $g_h^{\text{Base}}$ = 0 µS/cm² for different neurons (mean ± SEM), plotted for each v_uEPSP. (D–F) Same as A–C, but for different values of inhibitory synaptic conductance (g_inh). Default value of g_inh = 100 pS. (G–I) Same as A–C, but for different values of phase difference (ϕ_gin) between the excitatory and inhibitory theta-frequency synaptic inputs. Default value of ϕ_gin = 60°. Spike phases: n = 22 neurons for v_uEPSP = 4.3 µV, n = 23 neurons for g_inh = 200 pS, n = 24 neurons for v_uEPSP = 4.8 µV, for g_inh = 100 pS and for ϕ_gin = 0° and 60°. (A, D, and G) *P < 0.05, **P < 0.005 (Wilcoxon signed-rank test). (C, F, and I) **P < 0.005 (Student’s t test on the null hypothesis of no spike-phase difference).

How dependent were our conclusions on the specific choice of the phase difference, ϕ_gin, between the excitatory and inhibitory theta-frequency synaptic inputs, thus far fixed at 60°? We changed ϕ_gin to various values and compared LFPs and spike phases across different values of ϕ_gin in neurons, in the presence or the absence of HCN channels. We found that the introduction of HCN channels resulted in a lead in the LFP phase, an enhancement in spike-phase coherence, and a lag in the spike phase, irrespective of the specific value of ϕ_gin (Fig. 4 G–I). Next, we reanalyzed the data presented in Fig. 4 G–I to ask whether changes in ϕ_gin altered LFPs and spikes. We observed a striking shift in the SP LFP phase on changing ϕ_gin, with the LFP phase leading by ∼120° when ϕ_gin shifted from –60° to 60°, a magnitude of shift that strictly followed magnitude of change in ϕ_gin (Fig. 4G and Fig. S6). Although we did not observe any significant difference in the population spike-phase coherence on changing ϕ_gin (Fig. 4H and Fig. S6), spike phase displayed a dependence that would be expected from the shift in SP LFP. Specifically, shifting ϕ_gin from –60° to 60° resulted in ∼120° lag in the spike phase (Fig. S6). Finally, we performed a sensitivity analysis on the reversal potential of the GABA_A receptor and found that except for the expected change in LFP amplitude due to changes in driving force, our conclusions on the impact of HCN channels were invariant to changes in the reversal potential of the GABA_A receptor (Fig. S7).

Together these results suggest that our conclusions on HCN-channel regulation of LFPs and spikes were invariant to changes in synaptic parameters. Further, these results also reveal an important role for synaptic scaling and for temporal structure of excitatory–inhibitory inputs in regulating LFP and spike phases, but not in spike-phase coherence.

A Single Neuron Can Shift Its Spike Phase Through HCN Plasticity.

The kind of global changes in HCN channel density spanning a large set of neurons that we assessed thus far have been shown to occur only under pathophysiological conditions (18–20, 22, 23). Under physiological conditions, neurons are known to shift their spike phase over a course of time, either as part of a behavioral task or in the process of the neuron being reassigned to another cell assembly (33–35). As HCN plasticity has been demonstrated to accompany bidirectional synaptic plasticity (16, 22, 24, 26–28) and plasticity in one or few neurons is physiologically more plausible, we asked whether plasticity in HCN channel density of a single neuron was sufficient to alter its spike phase.

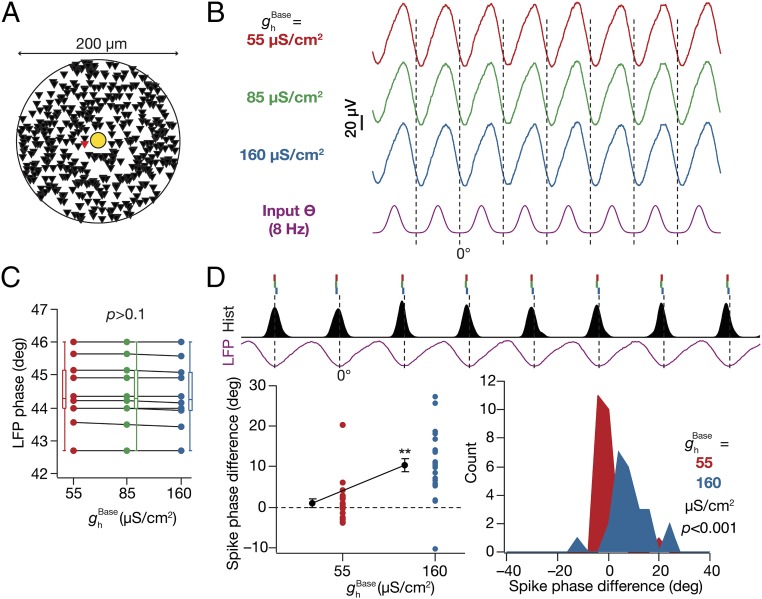
We altered the $g_h^{\text{Base}}$ of a single neuron whose soma was located among those closest to the electrode to three different values (as in Fig. 2 B–D), while $g_h^{\text{Base}}$ of all other neurons was set at 85 µS/cm² (Fig. 5A). Despite such proximal positioning, we observed no significant difference in the LFP amplitude (Fig. 5B) or phase (Fig. 5C) with plasticity in HCN channels of the neuron. This was to be expected because the LFP was calculated using compartments from 440 neurons, and a change in HCN-channel density in one neuron should not alter the LFP significantly. Next, we computed the spike phase of the chosen neuron with reference to the corresponding LFPs and compared them across different values of its $g_h^{\text{Base}}$ (Fig. 5D). We found no significant difference in the spike phase of the neuron when $g_h^{\text{Base}}$ was decreased, but observed a significant lag in the spike phase with higher $g_h^{\text{Base}}$. We repeated the procedure across all input structures that elicited spikes (24 of 25), by replacing the neuron at the specified location (Fig. 5A) by each of the remaining 23 spiking neurons, and found our conclusions to be robust across different input structures (Fig. 5D). These results suggested that HCN-channel plasticity could act as a putative mechanism for a neuron to shift its spike phase with reference to an externally driven theta oscillation (4, 33, 35, 44).

Fig. 5.

Plasticity in HCN channels of an individual neuron shifted its spike phase. (A) Top view of the neuropil (Fig. 1A) depicting the location of the neuron undergoing plasticity (red), which is among the neurons closest to the electrode (yellow). (B) SP LFP (1 s), shown with reference to excitatory input θ, computed with $g_h^{\text{Base}}$ for the chosen neuron set to one of three values: 55 µS/cm², 85 µS/cm², or 160 µS/cm². $g_h^{\text{Base}}$ value for the other (439) neurons was set at the baseline value of 85 µS/cm². (C) SP LFP phase across cycles computed (with reference to excitatory input θ; mean ± SEM, 10 cycles) for corresponding traces shown in B. P > 0.1, Kruskal–Wallis test. (D, Top) Ticks representing spike timings of the single neuron undergoing plasticity with reference to SP LFP. Color codes of ticks correspond to the different values of $g_h^{\text{Base}}$ (B). Histogram of spike timings of the other 23 neurons not undergoing plasticity is also shown (black). (D, Bottom Left) Cycle-matched difference between the spike phase of the chosen neuron computed with $g_h^{\text{Base}}$ = 55 µS/cm² or 160 μS/cm² and the spike phase of the same neuron obtained with $g_h^{\text{Base}}$ = 85 μS/cm². The different data points (n = 24; also mean ± SEM) correspond to this spike-phase difference computed by placing different neurons at the specified location. **P < 0.005 (Student’s t test on the null hypothesis of no spike-phase difference). (D, Bottom Right) Histogram of the spike-phase differences obtained across these 24 trials.

A Faster HCN Channel Nullified Inductive Impedance Without Altering Intrinsic Excitability.

The presence of HCN channels introduces two distinct sets of changes in a neuronal compartment. First, they reduce intrinsic excitability (24–26, 45), and second, they introduce an inductive component to the impedance profile. Whereas the former reflects as a reduction in R_in and in the impedance amplitude across several frequencies, the latter manifests as resonance in impedance amplitude and a lead in impedance phase (28, 46, 47). The manifestation of the inductive component of HCN channels requires their (de)activation time constant be slower than that of the membrane time constant (28, 46, 47). Concordantly, an ideal method to test the relative contribution of intrinsic excitability vs. inductive component of the HCN channel to any measurement is to render the channel activation faster than the membrane time constant with an unaltered voltage-dependent gating profile. To address the question of what specific property of the HCN channel explains its impact on LFP and spike phases, we reduced the (de)activation time constant of HCN channels (in what follows, we call them HCNFast channels) to around 7 ms [from ∼33 ms, at –65 mV (25)], thereby nullifying theta-frequency resonance and the inductive phase lead (Fig. S8 A and B). As our analysis was confined to theta-modulated synaptic inputs (8 Hz), we matched neuronal excitability at 8 Hz at ∼250 µm from the soma to find appropriate values of $g_{hF}^{\text{Base}}$ (for the HCNFast channels) corresponding to each $g_h^{\text{Base}}$ analyzed earlier (Fig. S8 C–E). By doing this, we ensured that all distance- and voltage-dependent properties of HCNFast channels (including their reversal potential) and their impact on excitability were matched to the HCN counterparts, with the only exception that the presence of these channels would not introduce an inductive component onto the neuronal compartments.

Fast HCN Channels Revealed a Differential Role for Inductive and Excitability Changes Introduced by HCN Channels.

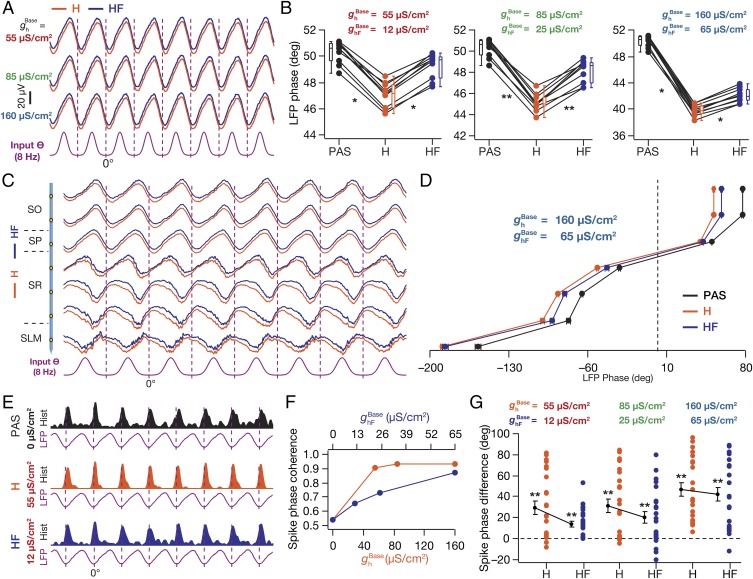
To discern the roles of the inductive vs. the excitability component in altering LFPs, we replaced HCN channels with their fast counterparts, computed SP LFP for different $g_{hF}^{\text{Base}}$ values, and compared them with the LFPs computed with the corresponding (Fig. S8) $g_h^{\text{Base}}$ values (Fig. 6A). Consequent to excitability not being altered by channel replacements (Fig. S8), we found that there was no significant difference in the LFP amplitudes (Fig. 6A). However, across strata, we found the lead observed in LFP phase in the presence of HCN channels was significantly reversed in the presence of HCNFast channels (Fig. 6 B–D), suggesting that the inductive properties of HCN channels played a critical role in regulating the LFP phase lead. Further, we also noted the amount of HCNFast-induced reversal decreased with increase in conductance density (Fig. 6 B–D), implying a role of changes in intrinsic excitability dominating in the presence of higher HCN conductances. When compared across HCNFast conductance values, LFP phase lead increased with an increase in HCNFast conductance (Fig. S8F), albeit with lower values for the phase lead in comparison to those obtained with HCN channels (compare Fig. 2B).

Fig. 6.

The inductive component of HCN channels played a critical role in regulating LFP and spike phase as well as spike-phase jitter. (A) SP LFP traces (1 s) for different $g_h^{\text{Base}}$ values (H) and corresponding $g_{hF}^{\text{Base}}$ values (HF), shown with reference to the excitatory input θ (A, Bottom). (B) LFP phase (with reference to excitatory input θ; mean ± SEM, 10 cycles) across cycles plotted for three different values of $g_h^{\text{Base}}$ and corresponding values of $g_{hF}^{\text{Base}}$. PAS, $g_h^{\text{Base}}$ = $g_{hF}^{\text{Base}}$ = 0 µS/cm²; H, HCN channels inserted with the depicted value of $g_h^{\text{Base}}$; HF, faster HCN channels inserted with the depicted value of $g_{hF}^{\text{Base}}$. (C) Normalized LFP traces (1 s) for different strata for $g_h^{\text{Base}}$ = 160 µS/cm² and $g_{hF}^{\text{Base}}$ = 65 µS/cm², with reference to excitatory input θ. (D) For each recording site (C), quantification of the LFP phase with reference to the excitatory input θ (mean ± SEM, 10 cycles) for $g_h^{\text{Base}}$ = $g_{hF}^{\text{Base}}$ = 0 µS/cm² (PAS), $g_h^{\text{Base}}$ = 160 µS/cm² (H), and its faster counterpart $g_{hF}^{\text{Base}}$ = 65 µS/cm² (HF). (E) Population spike-time histograms (1 s) with corresponding SP LFP for $g_h^{\text{Base}}$ = $g_{hF}^{\text{Base}}$ = 0 µS/cm² (PAS), $g_h^{\text{Base}}$ = 55 µS/cm² (H), and its faster counterpart $g_{hF}^{\text{Base}}$ = 12 µS/cm² (HF). (F) Spike-phase coherence, $C_{\mathrm{\Phi }}$, plotted as functions of $g_h^{\text{Base}}$ and $g_{hF}^{\text{Base}}$. (G) Cycle-matched difference (8 cycles; mean ± SEM) between the spike phase for the said $g_h^{\text{Base}}$ (H) or the corresponding $g_{hF}^{\text{Base}}$ (HF) value and the case where $g_h^{\text{Base}}$ = 0 µS/cm² (n = 24 neurons for $g_h^{\text{Base}}$ = 85 µS/cm² and 160 µS/cm² and $g_{hF}^{\text{Base}}$ = 65 µS/cm²). (B) *P < 0.05, **P < 0.005 (Wilcoxon signed-rank test). (G) **P < 0.005 (Student’s t test on the null hypothesis of no spike-phase difference).

Next, we compared the population of spikes and their theta phases in the presence of HCN or HCNFast channels, across different conductance values (Fig. 6 E–G). We observed that the presence of HCNFast channels reduced the spike-phase coherence compared to the presence of HCN channels (Fig. 6 E and F), but with coherence values higher than those obtained with the passive case (Fig. 6F). Further, the amount of HCNFast-induced reduction in spike-phase coherence was higher for lower conductance values than for higher conductance values (Fig. 6F). Finally, the lag in theta phase of spikes introduced by HCN channels was reduced in the presence of HCNFast channels at lower HCN/HCNFast conductances, whereas when the conductance value increased, this lag remained intact (Fig. 6G).

To further assess the role of the (de)activation time constant of HCN channels in regulating LFPs and spike phase, we increased the (de)activation time constant to ∼100 ms (HCNSlow) (Fig. S9A) and matched neuronal excitability at 8 Hz (Fig. S9B). This resulted in an increase in the impedance amplitude but at a lower resonance frequency (Fig. S9C) (28). As a direct consequence of the nonmonotonic changes in inductive phase lead with increase in the time constant (28), the LFP phase lead introduced by HCN channels across different strata was partially reversed by their slower counterparts but not as much as by their faster counterparts (Fig. S9 D and E). The spike phase obtained with HCNSlow channels, however, exhibited a lag that was larger than that in the presence of HCN channels, owing to the reduced impedance at the soma in the presence of the altered HCNSlow channels (Fig. S9F). Finally, the spike-phase coherence achieved with HCNSlow channels was lower than that in the presence of HCN channels (Fig. S9 G–I).

How would neuronal spike phases and their dependencies on HCN/HCNFast channels change if we used LFP from a stratum other than the SP for computing spike phases? We noted a significant shift in the spike phase, apart from changes in the actual value of HCN-channel–induced phase lag in the spike phase, when we used LFPs from other strata as the reference (Fig. S10). Although these results emphasize the importance of electrode location with reference to the source-sink dipole for spike-phase computation, our overall conclusions on HCN channels and their inductive components remained intact. Next, to confirm the validity of our results for a frequency other than 8 Hz, we repeated our experiments (Figs. 2 and 6) with 5-Hz modulated synaptic inputs (Fig. S11) and found these results to be consistent with previous results.

In summary, these results suggested that the inductive lead induced by the presence of HCN channels and its regulation of transmembrane currents across the dendritic arbor critically contributed to the LFP phase lead, spike-phase lag, and enhancement of spike-phase coherence, especially at lower values of HCN conductance.

Discussion

The prime conclusion of our study is that HCN channels can significantly alter LFP phase and the associated theta-phase of neuronal firing, apart from enhancing spike-phase coherence. Importantly, we found that the ability of HCN channels to introduce an inductive phase lead in intracellular voltage responses to theta-modulated synaptic currents played a significant role in altering LFP and spike phases. These, in conjunction with our results on the implications for altering the kinetic and voltage-dependent properties, together emphasize a critical role for the unique voltage dependence and kinetic properties of HCN channels in regulating LFP and spike phases. Apart from demonstrating that our conclusions on HCN channels were robust to changes in several model parameters, we also report that synaptic scaling and excitatory–inhibitory phase difference could alter LFPs and spike phase, but not spike-phase coherence.

Phase Coding and Somatodendritic Ion Channels.

LFPs have been referred to as the internal clocks for several neuronal circuits, and groups of cells have been shown to synchronize their spike timings to specific phases of the LFP, thus forming cell assemblies. The temporal/phase coding schema revolves around the fact that LFPs and specific timings of the spike with reference to these LFPs can convey information about the inputs that drove the spike, with behavioral relevance such as the animal’s spatial location (4, 33, 35, 44). In this context, our results establish that the existence of and various forms of plasticity in HCN channels and AMPA and GABA_A receptors could regulate the emergence and the evolution of the phase code in response to behavioral states, through state dependence and neuromodulation of their properties. The differences in spike phase introduced by plasticity/modulation in either HCN channels or the synaptic conductances are significant and large, spanning up to around 100° (Figs. 2 D and G; 3 F and J; 4 C, F, and I; 5D; and 6G). From the phase-coding perspective, especially with reference to theta–gamma coupling and gamma cell assemblies, the physiological and behavioral implications for such large differences in spike phases are enormous (4, 32, 33, 35, 44, 48–50). Together, our results argue for the incorporation of subthreshold-activated ion channels, their subcellular gradients, and their plasticity into the physiological and pathological studies on LFPs, phase coding, and neuronal cell assemblies. Our predictions on spike-phase coherence and about shifts in spike phases with reference to LFPs could be experimentally tested by introducing specific pharmacological agents (that intracellularly alter channel properties) through an in vivo whole-cell patch pipette, in a configuration that involves awake-behaving extracellular and whole-cell recordings (51).

These very conclusions also imply that a group of cells can undergo specific forms of plasticity to synchronize their spike phases, thus configuring a new cell assembly. Apart from global changes, our results delineate specific roles for physiologically plausible localized changes in channel densities in altering the phase code and in allowing a neuron to switch cell assemblies by altering its spike phase, without significantly altering the external oscillator or its readout, the LFP (Fig. 5). Additionally, given such a multitude of mechanisms that can reconfigure phase codes and cell assemblies, these results also emphasize that the interpretation of experiments with pharmacological agents to block channels or with transgenic animals lacking genes encoding channel subunits should be done with utmost care. Such interpretation should account for our observation that upon blockade of channel currents, not only do spike timings change, but also the local reference LFP phase could change, thus resulting in a different reference point for the local temporal code. Finally, it is important that the interpretation of results with knockouts incorporates the differential impact of all compensatory mechanisms (52, 53) on LFPs and spike generation before attributing a specific role for a channel/subunit.

Limitations of the Analyses and Future Directions.

First, similar to several previous studies (7, 8), our model assumes a homogenous and resistive extracellular field in arriving at the local field potentials. Although biophysical and experimental studies point to nonresistive components and nonhomogeneities in the extracellular fields, the impacts of these nonhomogeneities and nonresistive components are largely confined to higher frequencies (54–56). From these analyses, it stands to reason that the resistive and homogeneity assumptions are not debilitating for the conclusions drawn in our study where the range of frequencies is much lower, in the theta range.

Second, our study does not incorporate ephaptic coupling across neurons in the overall analysis (4, 57). Although it is clear that these ephaptic interactions, despite their small-amplitude deflections, can entrain action potentials at lower frequencies (57), the impact of such interactions on our conclusions is expected to be minimal. The reasons behind this are threefold: First, the presence of HCN channels did not significantly alter the amplitude of the LFPs (Figs. 2 and 3). Because volume conduction critically relies on the amplitude of the field signal, the impact of ephaptic interactions is not expected to change significantly in the presence or absence of HCN channels. Second, the open-field organization of hippocampal pyramidal neurons ensures that the somato-dendritic gradient in HCN channels is aligned with the source-sink dipole along the neuronal axis. If ephaptic coupling were present under a scenario where such alignment was absent, adjacent compartments from different neurons with huge differences in HCN-channel density would interact ephaptically, resulting in possible nullification of the impact of HCN channels on the LFP. However, given the alignment, our conclusions are not expected to change even in the presence of an additional distance-dependent ephaptic coupling across neurons with their compartments endowed with similar gradients in HCN-channel density. Third, with reference to spike-phase coherence, although the presence of ephaptic interactions might further enhance the spike-phase coherence across neurons (57), our results are entirely related to the presence or absence of HCN channels. Specifically, the enhanced spike-phase coherence observed in the presence of HCN channels is a direct consequence of the ability of these channels to reduce the temporal window for spike-generating coincidence detection (38, 47) and is expected to be present even with ephaptic coupling in place.

Finally, our study was limited to HCN channels. However, our results call for the necessity to incorporate the wide array of somatodendritic subthreshold-activated channels (e.g., A-type K⁺, T-type Ca²⁺), given their ability to regulate several aspects of neuronal physiology (15–17, 21, 58–62). Future studies should therefore focus on how the localization and targeting of these channel types are maintained across the somatodendritic arbor toward location-dependent regulation of LFPs, spike phases, and their coherence. In this context, it would be interesting to ask whether analogous LFPs and spike phases, and thereby analogous phase codes and cell assemblies, can be achieved with different channel/receptor combinations (58–60, 63).

Models and Methods

A detailed version of the simulated models and the methods employed is provided in SI Models and Methods. Briefly, we employed a forward modeling scheme with morphologically realistic neuronal models toward understanding the impact of active dendritic conductances on LFPs and spike theta phase of hippocampal pyramidal neurons. LFPs were constructed through line-source approximation (7, 8, 30, 31) of neuronal compartments from 440 (or 1,797 or 11,297; Fig. 3) morphologically realistic CA1 pyramidal neuron models. Two 3D reconstructions of a CA1 pyramidal neuron (n123, ri04) obtained from NeuroMorpho.Org (64–66) were employed (Fig. 1A and Fig. S3A) and were compartmentalized into 1,247 (n123)/1,351 (ri04) compartments. Somatodendritic passive, active, and synaptic parameters were set to match experimental data from somatodendritic recordings (26, 28, 29, 67, 68), with kinetics for the channels adopted from cell-attached recordings from soma and dendrites of hippocampal pyramidal neurons (25, 62, 69, 70). Specifically, the parameters were set to match normalization of somatic excitatory postsynaptic potential (EPSP) amplitudes, functional maps in input resistance, local and transfer resonance frequencies, and the synchronization frequency (Fig. 1 B–E for n123 and Fig. S3 B–E for ri04). To account for the variability in theta-frequency LFP and in spike phase as the animal navigates in an arena (51), balanced rhythmic high-conductance state at theta frequency (default 8 Hz) was introduced through systematic randomization of the spatiotemporal activation of excitatory and inhibitory synapses distributed across the somatodendritic arbor. A phase difference (default 60°) was introduced in the perisomatic inhibitory inputs with reference to the predominantly dendritic excitatory inputs (34, 71, 72). All simulations were performed in the NEURON simulation environment (73) with an integration time constant of 25 µs. Computation of line-source approximated (LSA) currents was performed using MATLAB R2011a (Mathworks), and analyses of LFP and spike phases were performed using MATLAB R2011a and Igor Pro (Wavemetrics). All statistical tests were performed using the R statistical package (www.r-project.org).