Cu_3-xP Nanocrystals as a Material Platform for Near-Infrared Plasmonics and Cation Exchange Reactions

Abstract

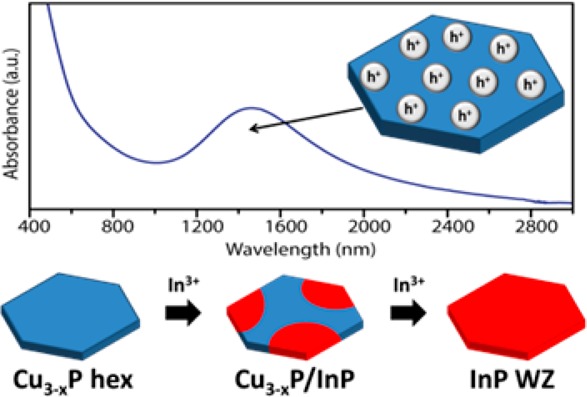
Synthesis approaches to colloidal Cu₃P nanocrystals (NCs) have been recently developed, and their optical absorption features in the near-infrared (NIR) have been interpreted as arising from a localized surface plasmon resonance (LSPR). Our pump–probe measurements on platelet-shaped Cu_3-xP NCs corroborate the plasmonic character of this absorption. In accordance with studies on crystal structure analysis of Cu₃P dating back to the 1970s, our density functional calculations indicate that this material is substoichiometric in copper, since the energy of formation of Cu vacancies in certain crystallographic sites is negative, that is, they are thermodynamically favored. Also, thermoelectric measurements point to a p-type behavior of the majority carriers from films of Cu_3-xP NCs. It is likely that both the LSPR and the p-type character of our Cu_3-xP NCs arise from the presence of a large number of Cu vacancies in such NCs. Motivated by the presence of Cu vacancies that facilitate the ion diffusion, we have additionally exploited Cu_3-xP NCs as a starting material on which to probe cation exchange reactions. We demonstrate here that Cu_3-xP NCs can be easily cation-exchanged to hexagonal wurtzite InP NCs, with preservation of the anion framework (the anion framework in Cu_3-xP is very close to that of wurtzite InP). Intermediate steps in this reaction are represented by Cu_3-xP/InP heterostructures, as a consequence of the fact that the exchange between Cu⁺ and In³⁺ ions starts from the peripheral corners of each NC and gradually evolves toward the center. The feasibility of this transformation makes Cu_3-xP NCs an interesting material platform from which to access other metal phosphides by cation exchange.

Introduction

Cu₃P is a copper-rich alloy that is commonly used in soldering, and it has been additionally investigated as anode material in lithium ion batteries.^1,2 Some reports indicate that Cu₃P is a semiconductor (with a gap of 1.3–1.4 eV according to scanning tunneling spectroscopy³ or around 0.8 eV according to optical spectroscopy⁴), while other works have shown that this material has a behavior closer to that of a metal.^5,6 A study by Olofsson in 1972 on the Cu–P alloy system demonstrated that the homogeneity range lies between Cu_2.867P and Cu_2.755P.⁷ Upon detailed crystal structure analysis, it emerged that the deviation from the 3:1 Cu:P stoichiometry was associated with Cu vacancies on the two 6(c) copper positions in the cell.⁷ Our group has recently developed synthetic approaches to Cu₃P nanocrystals (NCs) in shapes that depended on the type of the synthesis (either platelets or truncated hexagonal bipyramids).⁸ Soon after that, Pradhan et al. reported a detailed study on platelet-shaped Cu₃P NCs³ in which the optical absorption band in the 1–3 μm region of the spectrum was interpreted as due to a localized surface plasmon resonance (LSPR). The claim was supported by the dependence of the spectral position of the absorption band on the refractive index of the solvent in which the particles were dissolved. It is likely that such plasmonic behavior arises from the presence of copper vacancies (as described by Olofsson⁷), a finding that would go hand in hand with recent developments on plasmonic copper chalcogenide NCs, in which the LSPR can arise from a high density of free holes in the valence band, due to the many Cu vacancies that these structures can sustain.⁹⁻¹²

We have carried out density functional calculations on the formation energy of Cu vacancies in Cu₃P. The results of our calculations indicate indeed that the formation energy of Cu vacancies in 6(c) copper positions is negative, and therefore they are thermodynamically favored (in line with the findings of Olofsson),⁷ and henceforth this enables us to refer to the Cu₃P NCs, with which we will deal in this paper, as having a “Cu_3-xP” stoichiometry. Also, hot-probe thermoelectric measurements on films of platelet-shaped Cu_3-xP NCs (synthesized by us) pointed to a metallic p-type behavior for such NCs. We then studied the time-dependent evolution of the optical absorption of Cu_3-xP NCs in the NIR, which was supportive of a LSPR, as first reported by Pradhan et al.³ Our studies demonstrate that most likely both the p-type metallic character and the presence of a LSPR in the NCs stem from the thermodynamically favored substoichiometry in Cu. These findings make Cu_3-xP NCs a new and alternative promising material if compared to copper chalcogenide NCs.

Furthermore, inspired by the recently discovered ability of cadmium phosphide NCs¹³ to undergo cation exchange with a variety of cations (with preservation of NC size, shape, and often of the anion framework) we explored the feasibility of such reactions on Cu_3-xP NCs. This is further supported by the possibility to partially displace Cu⁺ with Li⁺ ions in Cu₃P (leading to Cu_3-zLi_zP) via electrochemical lithiation.¹ We demonstrate here that the hexagonal anion framework of Cu_3-xP can accommodate for Cu⁺ cations to be displaced by In³⁺ cations without considerable distortions and allows for the formation of metastable wurtzite (WZ) InP NCs even at mild reaction conditions. The exchange reaction starts on the peripheral corners of each NC and proceeds toward the center forming as intermediate steps multidomain Cu_3-xP/InP heterostructures.

Computational and Experimental Section

Computational Details

All calculations have been performed in the framework of the Kohn–Sham density functional theory^14,15 (DFT) using the pseudopotential approximation and the PBE functional.¹⁶ The codes PWSCF¹⁷ and CP2K¹⁸ were used. More details on the calculations can be found in the Supporting Information (SI).

Chemicals

Copper(I) chloride (CuCl, 99.999%), trioctylphosphine oxide (TOPO, 99%), and tri-n-octylphosphine (TOP, min. 97%) were purchased from Strem Chemicals. Indium(III) bromide (InBr₃, 99.999%), oleylamine (Olam, 70%), octylamine (Octam, 99%), tetrachloroethylene (TCE, anhydrous, ≥99%), tri-n-butylphosphine (TBP, 97%), and 1-octadecene (ODE, 90%) were purchased from Sigma-Aldrich. Anhydrous chloroform, toluene, and ethanol absolute were purchased from Carlo Erba reagents. All chemicals were used without further purification.

Synthesis of Cu_3-xP Nanocrystals

The synthesis of Cu_3-xP NCs was carried out following our previous work with minor modifications.⁸ In a typical synthesis, a solution of CuCl (3.2 mmol), degassed Olam (4.8 mL), and degassed Octam (0.8 mL) was prepared under inert atmosphere and then heated to 140 °C for 1 h to get a clear solution. A mixture of 8 g of TOPO and 12 mL of TOP was degassed in a reaction flask for 2 h at 130 °C under vacuum using a standard Schlenk line. The copper solution was then then rapidly injected into the reaction flask at 380 °C. After the injection the temperature dropped, and the solution was heated to 350 °C for 50 min and then slowly cooled to room temperature. The Cu_3-xP NCs were washed twice by dispersion in toluene followed by precipitation by addition of ethanol. Extra Olam (100 μL) was added at each cleaning step to optimize the colloidal stability of the NCs. Eventually the Cu_3-xP NCs were dispersed in toluene and stored in a glovebox under inert atmosphere.

Exchange Reactions Involving In³⁺ Ions

In order to exchange Cu⁺ with In³⁺ ions we followed the method reported by Beberwyck et al.¹³ with various modifications. In a typical cation exchange reaction, a solution of InBr₃ (0.2 mmol), TOP (1.5 mL), and ODE (3.5 mL) was degassed at 130 °C for 1 h and then heated to 200 °C. At this point a solution of Cu_3-xP NCs in degassed ODE (1 mL), containing 0.2 mmol of Cu atoms (that is a In:Cu molar ratio of 1:1), was added to the reaction flask, and the solution was allowed to react for 15 min at 200 °C. The NCs were washed twice by dissolution in chloroform followed by precipitation upon addition of ethanol. In the first cleaning step a small amount of degassed Octam (1 mL) was added in order to better stabilize the colloidal suspension. The InP NCs were eventually dispersed in toluene and stored in a glovebox.

Structural Characterization and Elemental Analysis

TEM Measurements

The samples were prepared by dropping dilute solutions of NCs onto carbon coated gold grids that were then placed in a pumping station in order to let the solvent evaporate completely and preserve them from oxidation. Low resolution transmission electron microscopy (TEM) measurements were carried out on a JEOL-1100 transmission electron microscope operating at an acceleration voltage of 100 kV. High Resolution TEM (HRTEM) was performed on a JEOL JEM-2200FS microscope equipped with a Schottky emitter at 200 kV and an in-column Omega filter. The chemical composition of the NCs was determined by Energy Dispersive X-ray Spectroscopy (EDXS) analysis performed in high angle annular dark field scanning TEM mode (HAADF-STEM) with a JEOL JED-2300T detector, using the Cliff-Lorimer method.

X-ray Diffraction (XRD)

XRD measurements were performed on a Rigaku SmartLab X-ray diffractometer operating at 40 kV and 150 mA. The diffractometer was equipped with a Cu source and a Gobel mirror in order to have a parallel beam, and it was used in the 2-theta/omega scan geometry for the acquisition of the data. Specimens for the XRD measurements were prepared in the glovebox by dropping a concentrated NCs solution onto a zero-background silicon substrate.

Elemental Analysis

This was carried out via Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES), using a iCAP 6500 Thermo spectrometer. Samples were dissolved in HCl/HNO₃ 3:1 (v/v). All chemical analyses performed by ICP-AES were affected by a systematic error of about 5%.

Raman Analysis

The pristine NCs were dropcast on glass substrates under inert atmosphere. Raman measurements were performed under inert atmosphere by fluxing nitrogen through a closed chamber (by Linkam) in order to avoid oxidation of the samples under laser irradiation. Raman spectra were collected using a Renishaw InVia MicroRaman spectrometer that excites the samples with a diode laser (λ = 785 nm) focused through a 50× magnification microscope objective at a nominal power of 200 mW and integration times up to 60 s.

X-ray Photoelectron Spectroscopy (XPS)

Samples for XPS were prepared under inert atmosphere by dropcasting a solution of NCs onto a highly oriented pyrolytic graphite (HOPG, ZYB grade, NT-MDT) substrate. Sample preparation was performed in a N₂-filled glovebox, and the specimens were then transferred into the XPS setup via a transfer vessel to avoid exposure to air. Measurements were performed on a Kratos Axis Ultra DLD spectrometer, using a monochromatic Al Kα source (15 kV, 20 mA). High resolution narrow scans were performed at constant pass energy of 10 eV and steps of 0.10 eV. The photoelectrons were detected at a takeoff angle of Φ = 0° with respect to the surface normal. The pressure in the analysis chamber was maintained below 7 × 10^–9 Torr for data acquisition. The data was converted to VAMAS format and processed using CasaXPS software, version 2.3.16. The binding energy (BE) scale was internally referenced to the C 1s peak (BE for C–C = 284.8 eV).

Thermoelectric Measurements

Cu_3-xP NCs stabilized with Olam and dissolved in toluene were dropcast on microscope glass slides and allowed to dry in a glovebox under inert atmosphere. To improve the conductivity of the films, the samples were annealed on a hot plate at 200 °C for 30 min under nitrogen atmosphere. This annealing process promotes a partial removal of the residual organic in excess and results in a significant improvement of the film conductivity. Subsequently, ohmic contact pads (∼2 mm²) were deposited on the films by sputtering 20 nm of Au (99.99%) in an Ar-filled chamber (Cressington Sputter Coater 208HR) with a metal shadow mask tightly mounted on the top of the sample (see Figure S4 for the linear current–voltage curves measured between these pads). The hot-probe thermoelectric measurements were performed under nitrogen atmosphere. The samples were mounted on a copper heat sink to facilitate the heat dissipation from the substrate.

Optical Spectroscopy

UV–vis-NIR Absorption

The NCs (dispersed in toluene) were dried under nitrogen flux to remove the solvent, and they were then redispersed in anhydrous TCE to perform the measurements. The UV–vis-NIR absorption spectra of the NCs solutions were recorded using a Varian Cary 5000 UV–vis-NIR absorption spectrophotometer.

Pump–Probe Absorption Spectroscopy

The laser system employed for ultrafast pump–probe measurements was based on a Ti:sapphire chirp pulse amplified source, with maximum output energy of about 1 mJ, 1 kHz repetition rate, central wavelength of 800 nm (1.59 eV), and pulse duration of about 180 fs. Excitation pulses at 1300 nm (0.95 eV) were generated by noncollinear optical parametric amplification (NOPA) in a β-Barium borate (BBO) crystal, with pulse duration of around 150 fs. Pump pulses were focused in a 200 μm diameter spot. Probing was done in the near IR region (870 nm–1500 nm) by using white light generated in a thin sapphire plate. Chirp-free transient transmission spectra were collected by using a fast optical multichannel analyzer (OMA) with dechirping algorithm. We used a InGaAs Bayspec SuperGamut NIR Spectrometer with a spectral range from 870 to 1650 nm. The measured quantity is the normalized transmission change, ΔT/T. Excitation energy per pulse has been kept in the linear regime at around 450 nJ (measured at 1300 nm), in order to get ∼360 μJ/cm² fluence. All measurements were performed at room temperature on sealed samples prepared under nitrogen atmosphere by dispersing Cu_3-xP NCs (containing 0.005 mmol of Cu⁺) in 0.7 mL of toluene.

Results and Discussion

Synthesis

The Cu_3-xP NCs resulting from our synthetic route are typically polydispersed hexagonal shaped platelets with a diameter ranging from ∼10 nm to ∼50 nm. Higher reaction times (i.e., more than 50 min) result in larger NCs that can be grown as large as 100 nm, albeit with a broader size distribution.⁸ The XPS analysis of the as-synthesized Cu_3-xP NCs is consistent with the presence of Cu⁺ and P^3– species (giving a rough estimation of the Cu:P ratio of 2.9:1) and excludes any trace of Cu²⁺ ions (see the SI and Figure S7 for further details). According to their XRD pattern (reported later in this work in Figure 4c and in Figure S8), the NCs crystallize in a hexagonal phase (space group P63cm, see Figure 1a-b). Refinement of the structural parameters using the fundamental parameter (FP) method¹⁹ yielded the following lattice parameters: a = 6.9507 Å and c = 7.1428 Å (see Figure S8) that are consistent with a Cu₃P structure substoichiometric in copper, as shown by Olofsson.⁷

Figure 4.

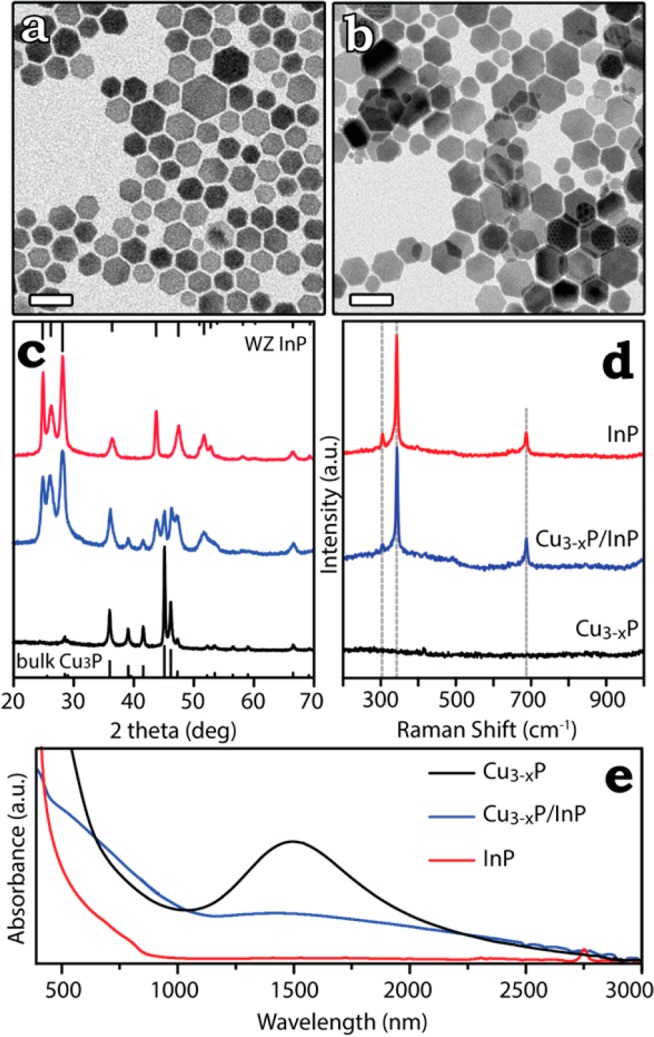
Low resolution TEM images of hexagonal platelet-shaped (a) Cu_3-xP and (b) InP NCs after cation exchange. The scale bar in each image is 50 nm. (c) XRD patterns and (d) Raman spectra obtained from dropcast solutions of Cu_3-xP, Cu_3-xP/InP, and InP NCs. In (c) the bulk reflections of Cu_3-xP (ICSD card no. 15056) and WZ InP, the latter calculated from the ICSD card no. 180911, are also reported. From the Raman spectra in (d), labeled as Cu_3-xP/InP and InP, it can be noticed the presence of transverse optical (TO, at 304 cm^–1) and longitudinal optical (LO, at 343 cm^–1) phonon first order modes and of the LO phonon second order mode at 687 cm^–1 of InP, in accordance with literature data.³⁶ At a deeper analysis, it is possible to note that the LO peak, even if characterized by a narrow profile (fwhm = 5 cm^–1), shows an asymmetric broadening at lower frequencies, associated with contributions from the surface modes of the crystals.³⁶ (e) UV–vis-NIR absorption curves of solutions of Cu_3-xP, Cu_3-xP/InP, and InP NCs dispersed in TCE.

Figure 1.

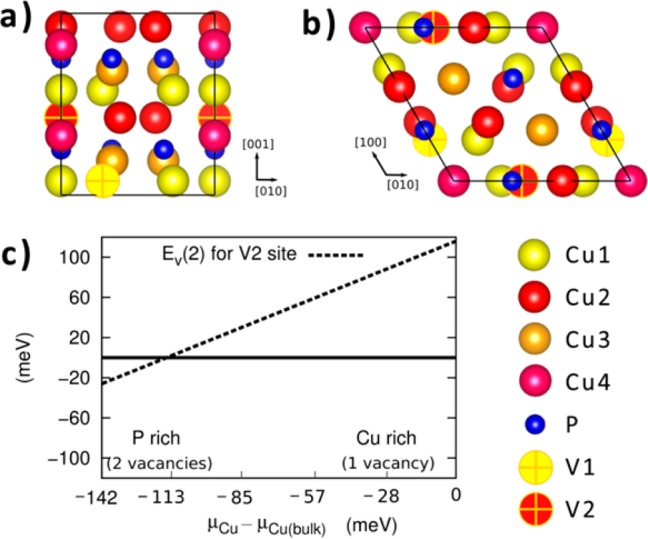
(a) [100] and (b) [001] views of the Cu₃P lattice. The projection of the primitive unit is given by the solid black line. (c) Free energy profile for E_v(2) at the V2 site, as a function of μ_Cu. The value of E_v(2) is given relative to E_v(1). The line y = 0 is also shown to help distinguish regions in the free energy profile where 1 or 2 vacancies are energetically favored.

Calculations

The asymmetric unit of Cu₃P is composed of one P atom and four Cu atoms. Along the [001] direction, the different irreducible Cu positions can be grouped in adjacent layers (see Figure 1a). P atoms are arranged in a hexagonal sublattice, which is intercalated between the Cu3 and Cu4 layers. The resulting structure can be described in terms of small aggregated subunits composed of one P atom coordinated with 11 Cu sites, with an average P–Cu crystallographic distance of 2.513 Å (see also Figure S1).⁷ The structural anisotropy leads to partial ionic bonding in the compound, as evidenced by our atom-in-molecule analysis (see the computational details section in the SI). According to the Bader partitioning scheme, charge transfer occurs in Cu₃P, leading to a charge depletion of 0.2 e^– on each Cu atom and a charge excess of 0.6 e^– on P atoms. These values are smaller than the respective formal charges, consistent with the mixed ionic/covalent character of the compound. The calculated lattice parameters for the stoichiometric Cu₃P cell were a = 7.04 Å and c = 7.32 Å. These parameters are slightly larger than the bulk experimental values (a = 6.96 Å, c = 7.14 Å) which are indeed very close to the parameters extrapolated for our Cu_3-xP NCs (a = 6.95 and c = 7.14, see previous section). A slight overestimation of lattice parameters is expected for PBE calculations on solids.²⁰

In the systems with one vacancy (either in Cu1, Cu2, Cu3, or Cu4 sites) the cell contracted slightly along the c axis (optimized lattice parameters were a = 7.04 Å, and c = 7.18 Å). We computed the values of the single vacancy formation energy E_v(1) (see the SI for details), in either Cu1, Cu2, Cu3, or Cu4 sites. The vacancy formation energy has been estimated in the range of values for the Cu chemical potential, μ_Cu, compatible with the thermodynamic stability of Cu₃P (see also the SI for a more in-depth explanation). The higher and lower bounds of μ_Cu correspond, respectively, to the Cu-rich condition, i.e. μ_Cu = μ_Cu(bulk), and P-rich condition, i.e. μ_P = μ_P(bulk), where μ_Cu(bulk) and μ_P(bulk) represent the chemical potentials of the elemental bulk Cu and P. For values of μ_Cu larger than μ_Cu(bulk), Cu₃P is unstable and copper precipitates into the pure elemental solid. Similarly, for values of μ_Cu smaller than the lower bound, Cu₃P is unstable and elemental solid phosphorus forms. Values of E_v(1) at Cu-rich conditions are shown in Table S1. The vacancy formation energies E_v(1) are negative in Cu1 (−117 meV) and Cu2 (−99 meV) sites, while they are positive in Cu3 (162 meV) and Cu4 (54 meV) sites.

From these calculations we can conclude that even in copper rich conditions at least one vacancy would form, preferably in Cu1 sites, which corroborates the substoichiometric nature of the material proposed by Olofsson.⁷ Starting from the lowest energy system with one single vacancy, we introduced one additional vacancy in one of the remaining 17 nonequivalent Cu sites. Cell optimization led again to a small decrease of the lattice parameters (a = 7.02 Å, c = 7.16 Å) in the lowest energy structure. The formation energies of the second vacancy E_v(2), in Cu-rich conditions are shown in Table S1 of the SI. Our calculations always predicted positive E_v(2) under Cu-rich conditions. The stability of the second vacancy can be increased by moving to P-rich conditions. This can be seen in Figure 1c, where we show that the formation energy of the second vacancy becomes negative in the P-rich corner. The most stable vacancy pair found in our DFT calculations is therefore the one corresponding to the unoccupied sites Cu1 and Cu2, denoted as V1 and V2 and described in Figure 1a-b. These results are again in close agreement with the crystallographic refinement presented by Olofsson,⁷ where it was indicated that Cu1 and Cu2 are below full occupancy. The computed values for E_v(3) are instead positive over the whole stability range of Cu₃P, suggesting that the presence of one or two vacancies per cell is the most likely situation in Cu_3-xP.

This set of results confirms the scenario that Cu₃P is natively substoichiometric and that its composition varies from 16 Cu and 6 P atoms per unit cell (Cu_2.667P) in P-rich conditions to 17 Cu and 6 P atoms (Cu_2.833P) in Cu-rich conditions. Similarly, Olofsson estimated the homogeneity range to lie between Cu_2.755P and Cu_2.867P.⁷ Another interesting aspect of consistence between our calculations and the work of Olofsson⁷ is represented by the experimental sharp change in the lattice parameter upon increase of the compositional P atomic percentage. This structural transition is explained by our calculations, which reproduce a quantitatively similar change in the lattice parameter upon increasing the number of copper vacancies from one to two.

Because of the large number of possible Cu vacant sites in Cu₃P, we expect that the configurational entropy strongly favors the increase of vacancies in the system with temperature. Consistent with this view, the statistical model presented in the SI suggests that the formation of vacancies in the Cu-rich side of the stability diagram is strongly activated by temperature. At T = 500 K for instance the content of Cu vacancies at μ_Cu = μ_Cu (bulk) increases by about 20% with respect to the T = 0 K case (see the black curve in Figure S2), within the level of modeling used. The marked dependence of the total number of vacancies on temperature correlates with the necessity of working at about 500 K in the Cu₃P-InP cation exchange experiments (see later).

Thermoelectric Measurements on Cu_3-xP NC Films

Hot-probe thermoelectric measurements on Cu_3-xP NC films were carried out to determine the majority carriers in our NCs. The setup of the measurements is illustrated in Figure 2a. In order to ensure that no alteration of the NCs occurred in the annealing process that preceded the electrical measurements, XRD patterns and XPS analyses of the NC films were acquired before and after the heat treatment (see Figures S5 and S7). In the thermoelectric measurements, the voltage difference between probe 1 and probe 2 was recorded over a period of time (typically ∼100 s) by a voltmeter (Agilent 34410A) with its positive terminal connected to the hot probe and the negative terminal to the room temperature (RT) probe. A soldering iron was used as a heating source. In the first few seconds of each measurement the sample was not heated up yet. Then the iron was carefully brought in contact with the glass substrate and heated up to 380 °C. Being the iron closer to probe 1, it created a temperature gradient between probe 1 and probe 2. After ∼50 s the heating iron was quickly removed from the substrate surface, allowing the sample to cool down to room temperature.

Figure 2.

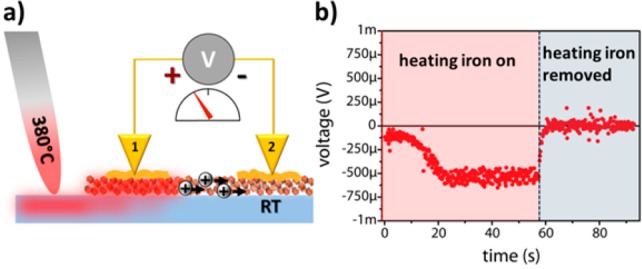
(a) Sketch illustrating the thermoelectric measurement setup on a Cu_3-xP NC film. The numbers 1 and 2 indicate Au-plated tungsten probes. An iron soldering tip is in contact with the glass substrate in close proximity to probe 1 on the NC film. The voltage drop across the two gold pads is measured by means of a voltmeter. The circled positive signs represent the holes diffusing from the hot probe to the probe at RT. (b) Thermovoltage across the gold pads measured over time while heating the soldering iron from RT up to 380 °C (red area) and then quickly removing it from the glass substrate (light blue area).

In the thermoelectric measurements, the majority carrier type of the film can be identified from the polarity of the thermoelectric voltage that manifests between the cold and the hot probes.²¹ For the Cu_3-xP NC films a positive space charge builds up at the cold probe (leading to a negative voltage drop as shown in Figure 2b), which can be rationalized by a diffusion of positive majority carriers from the hot to the cold probe, thus pointing to p-type conduction (see also control experiments in Figures S6 on Si wafers with known conductivity type). When the heating iron was removed from the substrate at t = 57 s, the thermoelectric voltage dropped quickly back to zero, suggesting efficient heat dissipation from the sample to the surrounding environment.

The results of the thermoelectric measurements indicate that our Cu_3-xP NCs behave as semiconductors and that holes are the majority carriers. We believe that their conductivity arises from the large number of Cu vacancies in the Cu_3-xP lattice (at least one per unit cell) that create a large number of acceptor levels close to the valence band. On the other hand, our DFT calculations point to a ground state of Cu₃P that is semimetallic for both stoichiometric and substoichiometric systems, although the presence of Cu vacancies affects the DFT electronic structure by enhancing the energy difference between the highest occupied and lowest unoccupied band of the system (see the SI for more details). The experimental semiconducting state may be obtained by the use of quasi-particle corrections to the standard DFT results and/or after introducing structural disorder in the system. Similar considerations have been used to describe the 2-fold metallic/semiconducting character observed in some copper chalcogenides, such as CuS and Cu₂S.^22,23

Pump–Probe Measurements

As mentioned in the Introduction, previous works supported the presence of LSPR in Cu₃P NCs, which should be elicited by free carriers (holes).³ For a further verification of the plasmonic nature of the NIR resonance that is also characterizing our Cu_3-xP NCs (see Figure 3a), we performed transient absorption (TA) measurements in the region of the NIR resonance. We pumped at 1300 nm by generating pulses of around 150 fs through a NOPA in a BBO crystal, which is close to the maximum NIR resonance, and we probed in the NIR, around 870–1500 nm, by using a white light generated in a thin sapphire plate (see Figure 3a). A nonlinearity was observed in the region of the NIR resonance. Figure 3b displays a contour plot showing the wavelength (y-axis) versus time (x-axis) of the differential transmission (ΔT/T %). As demonstrated also in the time trace in Figure 3c, an instantaneous bleach signal was observed at 1500 nm. The bleach maximum, at around 1500 nm, was very close to the steady state NIR absorption maximum.

Figure 3.

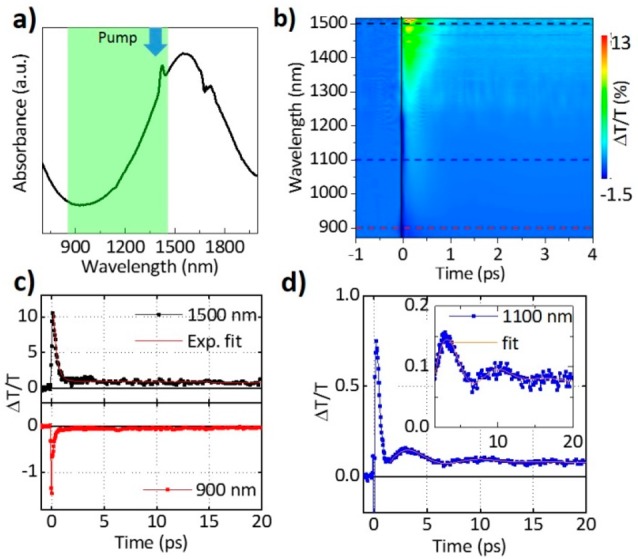
(a) Steady-state absorption of the Cu_3-xP NCs; the arrow indicates the pump wavelength while the probe region is marked in green. (b) Contour plot of the differential transmission versus wavelength (y-axis) and time (x-axis). Horizontal dashed lines in black, blue, and red indicate the wavelength of representative differential transmission decay dynamics as given in (c) at 1500 nm (black curve) together with a biexponential fit (red curve, upper plot), and 900 nm (red curve, lower plot) and (d) at 1100 nm (blue curve) together with a fit to the oscillation as described in the main text (orange curve).

The observed nonlinearity was dominated by a two-step decay, having a fast initial component with a time constant of around 1 ps and a second slower decay of around 50 ps (the biexponential fit is given in Figure 3c (red curve) upper panel together with the 1500 nm decay in black). To the blue end of the spectrum a photoinduced absorption signal was found. This negative feature is represented by the decay dynamics at 900 nm (red curve in Figure 3c, lower panel). It showed a similar temporal behavior as the bleach maximum. We interpreted the bleach and the photoinduced absorption signals as an excitation-induced damping and broadening of the plasmonic resonance due to the pump pulse that induced heating of the carrier gas. This in turn led to an induced absorption in the transient spectra to the red and the blue end of the plasmon resonance, and a decrease of intensity around the plasmon maximum, detected as a bleach signal in the TA measurements.²⁴⁻²⁶ While we observed the bleach signal close to the LSPR maximum and the photoinduced absorption to the blue end, between ∼870 and 1200 nm, an evaluation to the red was not possible, due to a limited white light generation in this spectral region.

The observed time-dependent evolution of the optical spectra in the region of the NIR resonance is clearly reminiscent of the typical two step decay dynamics observed in plasmonic nanostructures,²⁶⁻²⁹ and it can be understood in the following way: the initial very intense pump pulse excites the free carriers in the system to a nonthermal energy distribution, which then thermalize within the duration of the laser pulse. This leads to a Fermi distribution at a higher carrier temperature, which results in the maximum of the TA signal observed. Thereafter, the carriers relax within a couple of picoseconds by releasing their energy through the emission of phonons, leaving the lattice at an elevated temperature. This step corresponds to the first initial decay observed in the transient spectra. Afterward, the lattice cools down with a slower decay through the interaction with the surrounding medium until it reaches its equilibrium after a couple of hundreds of picoseconds.²⁶⁻²⁹ In the dynamic trace at 1100 nm (blue curve in Figure 3d) oscillations are found up to 20 ps. To extract the period of the oscillation we fitted the dynamics at several wavelengths, starting from delays greater than 1.5 ps and by previously subtracting the slowly varying second exponential decay. Then the period T and the damping τ were extracted by using a damped cosine function, which describes the oscillatory behavior³⁰

1

where A and ϕ are free parameters to obtain a valuable fit (Figure 3d, orange curve). The extracted values are T = 6.936 ps and τ = 3.825 ps. For plasmonic NCs the oscillatory behavior of the TA signal is related to an instantaneous increase in the lattice temperature due to the carrier phonon interaction, which in turn causes a small expansion of each single NC. As a consequence of the activation of its vibrational modes an oscillating and periodic change of its dimension, shape, and volume is induced.^27,31 As the plasmonic resonance depends both on the particle geometry and the density of the carriers, a modulated absorption of the pumped NCs is detected.²⁶⁻³¹ Importantly, our results demonstrate that our NCs contain a sufficient concentration of free carriers to absorb the energy of the high intensity pump pulse and to transfer it to the lattice efficiently leading to the coherent excitation of the breathing modes in the NCs. Similar results have been found in the recently examined copper chalcogenide NCs,³²⁻³⁵ where a high hole density was responsible for the observed nonlinearity. Our TA results thus show the typical time dependent spectral behavior characteristic of plasmonic nanostructures and confirm the plasmonic nature of the NIR resonance in Cu_3-xP NCs.

Cu_3-xP to InP Cation Exchange

The partial ionic character of Cu_3-xP, as calculated and discussed earlier, suggested that the replacement of the Cu(I) cation sublattice in this material should be feasible. We developed a procedure to exchange Cu⁺ ions with In³⁺ ions in Cu_3-xP NCs, by adapting a procedure reported by Beberwyck et al. on Cd₃P₂ NCs.¹³ On Cu_3-xP NCs, the exchange occurred at conditions that were milder than those tested on Cd₃P₂ NCs (typically carried out at 300 °C and with large excess of incoming ions with respect to Cd²⁺ ions).¹³ For example, a total conversion of Cu_3-xP to InP NCs could be achieved at temperatures as low as 200 °C and with a molar ratio of In³⁺ precursor to Cu⁺ ions present in the NCs as low as 1:1 (that is, three times the required stoichiometric ratio). Figure 4 reports XRD, Raman, and TEM data on initial, intermediate, and final samples of an exchange reaction (TEM images refer only to the initial and final samples) (see the SI for more details on partial exchange experiments).

According to TEM, both size and morphology of the Cu_3-xP NCs were retained, even after complete exchange (compare panels a and b in Figure 4). XRD patterns of the initial, intermediate, and final samples are reported in Figure 4c. An evolution can be evinced from the hexagonal Cu_3-xP phase (ICSD card no. 15056) of the initial sample (Figure 4c, bottom pattern in black) to a phase that could be indexed to WZ InP (ICSD card no. 180911) for the fully exchanged sample (Figure 4c, top pattern in red), passing through an intermediate sample with a mixed pattern of Cu_3-xP and WZ InP phases (Figure 4c, middle pattern in blue), with no additional phases present. As a note, in order to have a good fit of the experimental data for WZ InP, we had to refine the structural parameters (using the FP method), which yielded a = 4.1420 Å and c = 6.8095 Å. Therefore, the WZ InP phase of our exchanged InP NCs was characterized by slight compression along both the ab plane (0.2%) and the c direction (1.5%) with respect to the reference WZ InP phase from the database.³⁷

Here, as in a previous work of ours,³⁸ Raman analysis turned out to be a valid tool to assess whether alloyed crystals or heterostructures were formed in the intermediate steps. Raman analysis of the same initial, intermediate, and final sample (reported in Figure 4d) supported a Cu₃P→ InP transformation, upon exchange with In³⁺ ions, with no presence of alloys nor other compounds other than Cu₃P and InP at the intermediate step: while the pristine Cu_3-xP NCs (Figure 4d, bottom spectrum in black) did not exhibit any Raman feature, both the intermediate (Figure 4d, middle spectrum in blue) and the final (Figure 4d, top spectrum in red) spectra were characteristic of the InP phase (see caption of Figure 4 for more details).³⁶

Further insights over the cation exchange process could be deduced from the optical absorption spectra of solutions containing initial Cu_3-xP NCs, the intermediate sample, and the final InP NCs, respectively. As shown in Figure 4e, the initial copper phosphide NCs (black curve) were characterized by a LSPR absorption peak (as already discussed earlier). A weaker NIR absorption in the intermediate sample (blue curve in Figure 4e), with a maximum still at about 1500 nm, most likely arose from the residual Cu_3-xP domains in the partially exchanged heterostructures. The final InP NCs (red curve) did not show any feature in the NIR region and exhibited instead an absorption edge having its maximum at ∼800 nm from which we extrapolated a bandgap of 1.55 eV. This value is slightly larger than the bulk band gap of WZ InP (832 nm, 1.49 eV),³⁹⁻⁴³ thus we believe that a quantum confinement of carriers might take place in our InP NCs. Since the Bohr radius of bulk zinc-blende InP is around 110 Å (11 nm),⁴⁴ the confinement in our InP nanoplatelets should be along their (001) direction (the one perpendicular to the basal facets). This is reasonable, as the thickness of some NCs could be as low as 5 nm (see Figure 6b), while the lateral dimensions were much larger.

Figure 6.

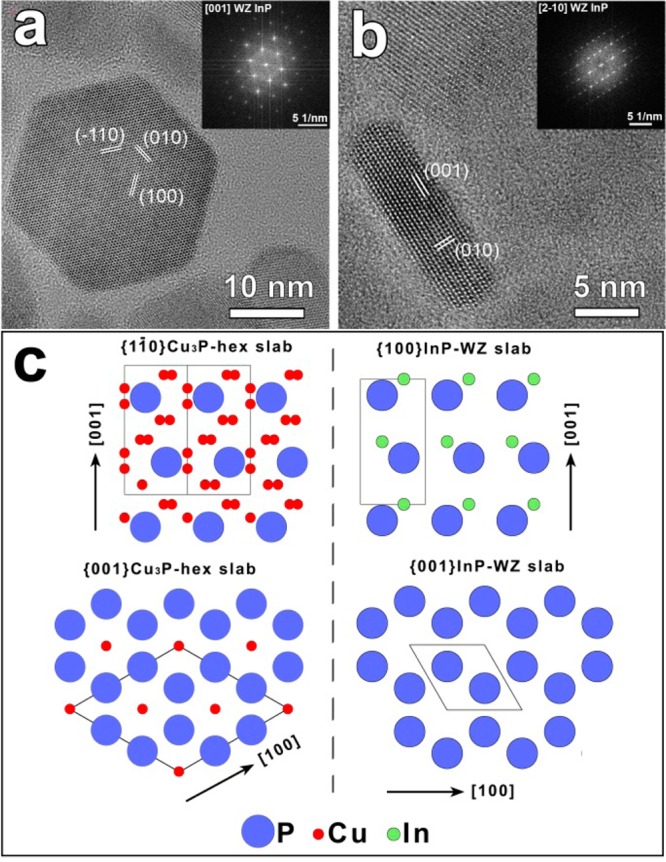
(a-b) HRTEM images and the corresponding FFT (of platelet-shaped InP NCs). The WZ structure can be directly inferred from the top (a) and the side (b) views. (c) Atomic sketches representing (left panel) [11̅0] and [001] lattice slabs of hexagonal Cu_3-xP and (right panel) [100], [001] lattice slabs of WZ InP. The structural isomorphism of the two phases is evident, with preservation of the anion sublattice. The projection of the primitive unit cell is depicted with a solid black line in both structures.

A detailed TEM analysis was carried out on the intermediate and final samples. The intermediate sample was a mixture of totally exchanged WZ InP nanocrystals and of partially exchanged Cu_3-xP/InP heterostructures. Typical HAADF-STEM images of partially exchanged Cu_3-xP NCs (Figure 5a-c) evidence the presence of two different types of domains inside each NC. The brighter domains are Cu_3-xP, while the darker ones are InP (verified from EDXS maps). From the sequence of HAADF images, which capture three NCs at different stages of conversion, it can be seen that the exchange starts preferentially from some of the corners of the hexagonal platelets (Figure 5a). One possible explanation of this side selectivity would be that, while the upper and lower facets of each Cu_3-xP platelet are almost atomically flat (see also our previous work on Cu_3-xP NCs⁸), the lateral edges and especially the corners contain more low-coordination species, that is highly reactive sites. In particular, in the direction of the six corners of the platelets (i.e., [11̅0] and the other five equivalent directions) straight Cu atomic columns can form preferential avenues for the inflow/outflow of cations (see also the sketches in Figure 6) with a small perturbation of the anion sublattice. This can explain why a preferential substitution is seen starting from the sides of the NCs rather than from the top/bottom. The exchange then progressed to yield heterostructures that were often of the “pie” type reported in Figure 5b.

Figure 5.

(a-c) HAADF-STEM of Cu_3-xP/InP heterostructures at different cation exchange states. The scale bar in each image is 20 nm. (d-e) HRTEM images at different magnifications of the heterostructure shown in panel (b), exhibiting two different crystalline domains: Cu_3-xP in the two central wedges and InP in the upper and lower wedges of the platelet. (f) Detail of an interface between a Cu_3-xP and an InP domain in the heterostructure, clearly showing the preservation of the anions sublattice. (g) FFTs from the Cu_3-xP domain and the InP domain. The InP WZ cell is obtained from a 30° rotation of the Cu_3-xP hexagonal cell, so that Cu_3-xP (1̅20) planes become InP (11̅0) planes (following the notation used in Figure 6c). (h) Schematic representation of the cation exchange reaction involving Cu_3-xP NCs and In³⁺ ions.

HRTEM images of a typical pie-shaped Cu_3-xP/InP NC are displayed in Figure 5d-f. This heterostructure, with quite sharp Cu_3-xP/InP interfaces (Figure 5f), further supports our XRD and Raman analysis that no other alloys/compounds seem to be formed during exchange. Also, from the FFT of the HRTEM images of partially exchanged Cu_3-xP NCs (see for example Figure 5g and S10) a clear 30° rotation relationship between the Cu_3-xP and InP unit cells can be extrapolated, from which we can infer the epitaxial relation between the two structures: (100) InP || (21̅0) Cu_3-xP and (001) InP || (001) Cu_3-xP. In this way the anions sublattice (brighter columns⁴⁵ in the intensity image of Figure 5f) is preserved at the interface. The formation of Cu_3-xP/InP NC heterostructures is well supported by the experimental evidence that in the bulk there are no known stable Cu–In–P alloys, and even if Cu is a typical dopant for InP,^44,46 attempts to diffuse Cu into bulk InP above doping levels (typically smaller than 5 × 10¹⁵ cm^–3) resulted in the formation of Cu–In metallic precipitates in InP.⁴⁶⁻⁴⁸

At later stages of exchange, the NCs had domains that were often of the type reported in Figure 5c (the nonexchanged Cu_3-xP domains were further confined toward the center of the crystal or at domain boundaries), after which complete cation exchange was accomplished (see also the scheme in Figure 5h). In the fully exchanged samples, HRTEM analysis revealed that the cation exchange process led to the formation of monocrystalline InP NCs exhibiting the expected WZ structure, as shown in Figure 6a-b, with no detectable defects. The lattice parameters extrapolated from the HRTEM images (a = b = 4.21 Å and c = 6.80 Å) were in good agreement with the values calculated for the WZ InP phase. EDXS elemental analysis performed on such InP NCs gave typical elemental compositions of the following: P = 42%, In = 57%, and Cu = 1% (see also Figure S9 of the SI). These are in agreement with ICP elemental analysis, which corroborated the complete exchange of copper with indium, with a residual amount of Cu in the samples that did not exceed 2%.

Figure 6c reports atomic sketches representing the [11̅0], [001] lattice slabs of hexagonal Cu_3-xP and [100], [001] lattice slabs of WZ InP. The similarity in the P anion frameworks of the two structures is indeed noteworthy: as a consequence of replacement of Cu⁺ ions with In³⁺ ions, the initial Cu_3-xP lattice undergoes an expansion of ±3% along the ab plane (a_Cu3-xP = 6.95 Å and √3a_InP = 7.17 Å) and a contraction of −5% along the c direction (c_Cu3-xP = 7.14 Å and c_InP = 6.81 Å). Such a close match in anion sublattices for the two structures may help to explain why the P^3– anion sublattice remained unaltered during the whole process, and single domain crystalline InP NCs were obtained at the end.

It is known that Cu⁺ ions can rapidly diffuse in bulk InP (both bulk and nanocrystalline) through interstitial sites⁴⁶ allowing for Cu doping of InP NCs even at very low temperatures (i.e., 50 °C).⁴⁹ On the other hand, it is not clear whether In³⁺ diffusion in Cu_3-xP proceeds likewise interstitially or it is instead dominated by Cu vacancy diffusion. We believe that the diffusion of In³⁺ in the Cu_3-xP phase is most likely mediated by Cu vacancies and that a “minimum” vacancy generation rate in Cu_3-xP NCs is required for the effective In³⁺ diffusion. This can be achieved by increasing the reaction temperature, as we estimated in our calculations (details are reported in the SI). At room temperature, there is on average one Cu vacancy per unit cell. At 200 °C the mean value increases to 1.2, that is, there are ∼20% more vacancies available for the ions diffusion (see the black curve in Figure S2). Thus, it is likely that the limiting step of the exchange process in our system is the In³⁺ diffusion inside the Cu_3-xP lattice that is directly connected to the amount of Cu-vacancies. Clearly, higher reaction temperatures (with respect to room temperature, at which no cation exchange was observed) can trigger other processes that are required for the exchange to take place, for example a more frequent detachment of the ligand molecules at the surface of the NCs, allowing for the insertion and the removal of ions.

Additional control experiments were run in order to establish the best reaction conditions for the In³⁺ → Cu⁺ exchange reaction. Interestingly when TBP was employed instead of TOP, at the same reaction conditions, the resulting NCs exhibited a very low InP conversion (see the SI). While TBP has been shown to be a good soft base for the transformation of ionic CuX (X = S, Se, Te) into II–VI crystals,⁵⁰ it appears that its efficacy is limited on phosphides. This can be explained considering that the Cu₃P → InP conversion requires a larger driving force in order to take place and optimized reaction conditions are necessary. These experiments prove that the soft acidity of Cu⁺ ions is best matched by the basicity of TOP rather than TBP.

Finally, worthy of note is that, up to now the metastable WZ InP phase^51,52 has been observed almost only in nanowires grown by molecular beam epitaxy or by chemical vapor deposition methods with the vapor–liquid–solid (VLS) technique.^{39−43,53,54} The formation of WZ InP phase has been observed as a polytype in nanowires growing along the [111] direction. Its formation is most likely due to the lower surface energy of the parallel side facets of the WZ wires compared to that of the ZB ones, and the interface energies involved in the VLS three-phase technique.⁵⁵ We therefore report here for the first time a colloidal approach to obtain WZ InP NCs.

Conclusions

We have reported a systematic study on Cu_3-xP NCs. Theoretical calculations on bulk Cu_3-xP and experimental evidence from different techniques indicate that Cu_3-xP NCs are plasmonic and that the LSPR arises from the collective motion of positive charge carriers (holes). We have studied, by means of TA measurements, the plasmon dynamics of Cu_3-xP NCs (from which a possible use of these NCs for ultrafast NIR switching can be envisaged).^56,57 It is possible that the plasmonic behavior stems from the presence of a large number of Cu vacancies in the NCs (on average one Cu vacancy per unit cell at room temperature). The presence of vacancies, and the partial ionic character of the Cu_3-xP lattice (as calculated by us), is perhaps the reason for the ability of such NCs to undergo cation exchange to InP. The exchange proceeds through Cu_3-xP/InP intermediated heterostructures (given the immiscibility of Cu_3-xP and InP) and is likely mediated by Cu vacancy diffusion. The close match in the anion frameworks for the two materials entails little distortion of the NC lattice during the transformations and facilitates the formation of single crystalline InP NCs in the wurtzite phase, which is unusual for colloidally synthesized NCs. Progress in this direction may come from the exploitation of similar features in Cu₃As and Cu₃Sb NCs.

Supporting Information Available

Computational details, estimation of the bond order and charge transfer in Cu₃P, calculation of vacancy formation energies, estimation of the temperature dependence of the vacancy density; additional details on thermoelectrical measurements, X-ray photoelectron spectroscopy (XPS) analysis, refinement of the structural parameters with the FP method, energy dispersive X-ray spectroscopy (EDXS) analysis, partial cation exchange experiments, and cation exchange experiments with TBP. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.