Identifying the Structure of the Intermediate, Li_2/3CoPO₄, Formed during Electrochemical Cycling of LiCoPO₄

Abstract

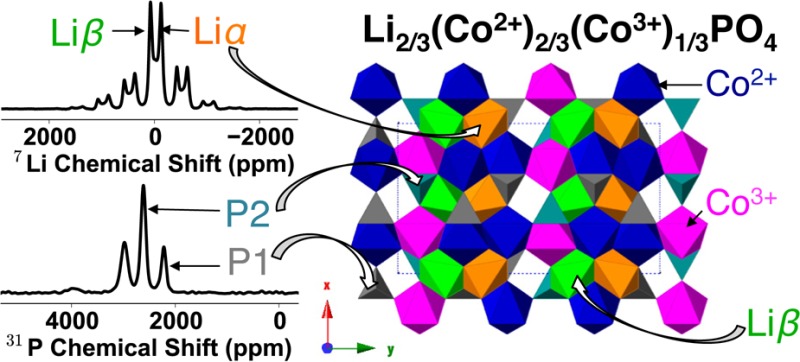
In situ synchrotron diffraction measurements and subsequent Rietveld refinements are used to show that the high energy density cathode material LiCoPO₄ (space group Pnma) undergoes two distinct two-phase reactions upon charge and discharge, both occurring via an intermediate Li_2/3(Co²⁺)_2/3(Co³⁺)_1/3PO₄ phase. Two resonances are observed for Li_2/3CoPO₄ with intensity ratios of 2:1 and 1:1 in the ³¹P and ⁷Li NMR spectra, respectively. An ordering of Co²⁺/Co³⁺ oxidation states is proposed within a (a × 3b × c) supercell, and Li⁺/vacancy ordering is investigated using experimental NMR data in combination with first-principles solid-state DFT calculations. In the lowest energy configuration, both the Co³⁺ ions and Li vacancies are found to order along the b-axis. Two other low energy Li⁺/vacancy ordering schemes are found only 5 meV per formula unit higher in energy. All three configurations lie below the LiCoPO₄–CoPO₄ convex hull and they may be readily interconverted by Li⁺ hops along the b-direction.

Introduction

Olivine-type LiFePO₄¹ has been extensively studied as a promising cathode material for Li-ion batteries, due to its good reversibility, safe operating voltage (3.45 V vs Li/Li⁺) and high reversible capacity² of 160 mAh/g (compared to the practical capacity of 140 mAh/g for LiCoO₂,³ the commonly used cathode in the portable communications industry). However, the low operating voltage of LiFePO₄ leads to an energy density that is considered low for use in electric transportation. Substituting Fe²⁺ with a transition metal that has a higher redox potential (e.g., Mn²⁺, Co²⁺, or Ni²⁺ with redox potentials of 4.1, 4.8, and 5.1 V, respectively, vs Li/Li⁺)⁴⁻⁶ increases the theoretical energy density of the olivine cathode material. However, LiMnPO₄, LiCoPO₄, and LiNiPO₄^7,8 have more sluggish kinetics than isostructural LiFePO₄, and are more difficult to fully lithiate and delithiate. LiCoPO₄ has the lowest hole polaron migration barrier of the high voltage olivines and subsequently has the highest electronic conductivity among LiMnPO₄, LiCoPO₄ and LiNiPO₄.⁹⁻¹² Furthermore, the high redox potential of the Co²⁺/Co³⁺ couple means that LiCoPO₄ has a high theoretical energy density of 800 Wh/kg, as compared with 580 Wh/kg for LiFePO₄, but is not as affected as LiNiPO₄ by the electrolyte decomposition that occurs at high voltages.^13,14

Bramnik et al. in 2007 studied the electrochemical reaction of LiCoPO₄ using in situ X-ray diffraction (XRD) and observed an intermediate Li_0.7CoPO₄ phase, where the composition was determined based on Vegard’s Law (i.e., assuming a linear relationship of the unit cell parameters to Li content).¹⁵ However, a later study combining X-ray and neutron diffraction determined an intermediate Li_0.6CoPO₄ stoichiometry.¹⁶ Thus, the Li content of this phase likely lies in the range 0.6 and 0.7, but it is not clear whether the difference in Li content arises from the ability of the intermediate phase to tolerate some degree of solid solution, or whether it reflects differences in the approaches used to estimate the Li content. Loss of long-range order was also observed, which agrees with the chemical delithiation results of Wolfenstine et al.^17,18

The observation of intermediates in the olivine system is not unique to LiCoPO₄. Intermediates of Li_xFePO₄ (0.5 < x < 0.7) have been observed on cooling the solid solution phases formed at elevated temperatures,^19,20 from chemical oxidation²¹ and more recently, during electrochemical cycling of micron-sized particles.²² The isolated intermediates generally have a Li content of between 0.6 and 0.7, the Li content again being typically inferred using Vegard’s Law. First-principles density functional theory (DFT) calculations performed on the Li_0.6FePO₄ phase found that it is energetically favorable for Li vacancies to be ordered in pairs.²¹ An A_2/3 intermediate (A = Na, Li) has also been observed during charging of the polyanionic materials NaFePO₄ and LiVPO₄F.^23,24 The crystal structure of the Na phase, Na_2/3FePO₄ (space group Pnma), was originally proposed to have a (3a × 3b × c) supercell (relative to the parent olivine unit cell),^25,26 in which the Fe³⁺ cations are aligned in the (110) and (220) planes and the Na⁺ vacancies reside between the Fe³⁺ ions for charge balance.^26,27 Boucher et al., on the basis of TEM and synchrotron data showed, however, that this cell could be redrawn using a smaller “(a−b × 3b × c)” monoclinic P21/n superstructure, which is only 3 times larger in volume than the original cell.²⁸ DFT calculations suggested that Li_2/3FePO₄ adopts the same superstructure.²⁸

The LiCoPO₄–CoPO₄ system exhibits complex magnetic properties, the magnetic data providing insight into the electronic structures of the end and intermediate members, and of direct relevance to the present study, often aiding the interpretation of the nuclear magnetic resonance (NMR) spectroscopy. Ehrenberg et al. carried out an experimental magnetic study on the end member LiCoPO₄ and CoPO₄ phases, and on their intermediate Li_xCoPO₄ (x = 0.6) phase, and showed that the electronic ground state of all three compositions is high spin.¹⁶ High-spin LiCoPO₄ and CoPO₄ ground states had also previously been predicted using DFT plus Hubbard U (DFT+U) calculations, and self-consistently calculated effective Hubbard U parameters for Co²⁺ and Co³⁺.²⁹ The result for the fully delithiated Co³⁺-only phase is not necessarily expected given that the electronic configuration of Co³⁺ is d⁶, for which a low spin configuration (corresponding to a fully occupied t_2g orbital set in octahedral coordination) is typically lower in energy than the high spin (t_2g)⁴(e_g)² configuration. Additionally, an intermediate spin Co³⁺ has been reported to exist at the surface of LiCoO₂, owing to changes in the Co–O coordination near and at particle surfaces,³⁰ and in Li-excess LiCoO₂ materials.³¹ A magnetic and neutron diffraction study on a LiCoPO₄ polycrystalline sample reported an antiferromagnetic alignment of the Co spins, along the [010] vector in the Pnma unit cell.³² Ehrenberg et al.’s neutron diffraction study confirmed this alignment of spins, and found a similar alignment of the Co spins in their intermediate Li_xCoPO₄ (x = 0.6) phase.¹⁶ The neutron diffraction data acquired on a sample with average composition of Li_0.2CoPO₄ was interpreted in terms of an additive contribution from all three stable phases (LiCoPO₄, Li_0.6CoPO₄, and CoPO₄), and the magnetic structure of CoPO₄ was found to comprise of Co spins aligned antiferromagnetically along the [100] direction of the CoPO₄ unit cell (i.e., perpendicular to the spin alignment in the LiCoPO₄ cell).

In situ X-ray (powder) diffraction is a valuable tool for monitoring the evolution of the long-range order of crystalline battery materials during electrochemical cycling.³³⁻³⁵ Solid-state NMR, on the other hand, yields insight into the local coordination of the nucleus being studied and is also proven to be a fundamental technique for the study of battery materials.³⁶⁻³⁸ The paramagnetic Co²⁺ and Co³⁺ ions in the olivine structure result in hyperfine interactions between the unpaired electrons and the nucleus under study (⁷Li and ³¹P in this case), and these interactions dominate the NMR response. The strongly covalent P–O bonds in the olivine structure lead to a large transfer of electron density onto the P atom via Co–O–P pathways, the resulting through-bond or supertransferred Fermi contact interaction leading to very large ³¹P isotropic shifts (e.g., δ_iso ≈ 3000 ppm for LiCoPO₄).³⁹ The through-space nuclear-electron interaction (i.e., the dipolar interaction) in these systems results in broad spinning sideband manifolds, even when fast magic angle spinning (MAS) is used. The presence of multiple chemical environments invariably complicates the spectra, as the isotropic resonance due to one environment may overlap with spinning sidebands from another, and so pulse sequences that separate sidebands from isotropic resonances are particularly useful in such cases. For example, both the magic angle turning phase adjusted sideband separation (MATPASS) and the adiabatic magic angle turning (aMAT) experiments have been used to study related paramagnetic cathode materials;^40,41 the former method is used in this work.

This paper builds on our preliminary report of the ³¹P spectra and XRD patterns of Li_xCoPO₄⁴² and on the work recently published by Kaus et al.⁴³ We combine the complementary experimental techniques of NMR and XRD with first-principles DFT calculations to study the electrochemical (de)lithiation of LiCoPO₄. We obtain invaluable insights into not only how LiCoPO₄ delithiates, but also into the Co²⁺/Co³⁺ ordering and the Li composition of the Li_xCoPO₄ intermediate phase. Because only limited information is obtained experimentally on Li⁺/vacancy ordering in the intermediate phase, we use DFT calculations to evaluate the lowest energy configurations, within the Co²⁺/Co³⁺ ordering determined from the experimental NMR and XRD data on the intermediate phase. The effect of the magnetic ordering and spin states of the Co²⁺ and Co³⁺ cations on the phase energetics is explored by DFT, first for the end member phases, and then for the intermediate Li_xCoPO₄ structure.

Experimental and DFT Details

Synthesis and Characterization

Carbon-coated LiCoPO₄ (C-LiCoPO₄) was synthesized via the solid-state method using cobalt oxalate (Sigma-Aldrich), lithium carbonate (Sigma-Aldrich, 99.997%), ammonium dihydrogen phosphate (Sigma-Aldrich, 99.999%) and 10 wt % Ketjen black (AzkoNobel) in a stoichiometric mixture. After high-energy ball milling for 20 min, the reaction mixture was pelletized and heated to 600 °C under flowing argon. The precursors were heated for 6 h, cooled and reheated for 11 h twice, before a final 24 h heating step.⁴⁴ The additional heating and cooling steps were carried out to decrease the amount of impurities present in the final product.

Phase purity was confirmed using powder X-ray diffraction with a PANalytical Empyrean X-ray diffractometer with a Cu Kα source. The total scan time was 9 h and 52 min, using a step size of 0.017° over a 2θ range from 5 to 140°. The TOPAS software was used to perform the Rietveld refinement.⁴⁵

Film Fabrication and Battery Assembly for Electrochemical Testing and ex Situ NMR

The electrode was prepared by ball milling 80 wt % C-LiCoPO₄, 10 wt % carbon super P Li (Timcal) and 10 wt % polyvinylidene fluoride (Kynar) for 1 h. Dry N-methyl pyrolidene (Sigma-Aldrich) was added dropwise to the mixture to make a slurry. A 150 μm spreader was used to cast the film onto aluminum foil, which was dried in an oven at 60 °C overnight. A circular punch of 7/16 in. diameter was used to cut the cathode (∼2 mg). For the ex situ NMR studies, the as-synthesized C-LiCoPO₄ powder (∼10–20 mg) was used as the cathode. A coin cell-type battery was assembled in an argon-filled glovebox, using Li metal (Sigma-Aldrich) as the counter electrode, a Whatman GF/B borosilicate microfiber filter as the separator and 1 M LiPF₆ solution in a 1:1 mixture of ethylene carbonate/dimethyl carbonate as the electrolyte.

Film Fabrication and Battery Assembly for in Situ XRD

The electrode was prepared by mixing 85 wt % C-LiCoPO₄, 5 wt % Super P carbon (Alfa Aesar), 5 wt % carbon black (Vulcan XC-72, Cabot Corporation) and 5 wt % polytetrafluorethylene (Sigma-Aldrich). The powder was pressed into a 13 mm-diameter pellet of ∼150 μm thickness and weighing ∼22 mg. The pellet was assembled into the AMPIX⁴⁶ in situ cell in an argon-filled glovebox, using Li metal as the counter electrode, a Whatman GF/B borosilicate microfiber filter as the separator, and 1 M LiPF₆ solution in a 1:1 mixture of ethylene carbonate/dimethyl carbonate as the electrolyte (Tomiyama Pure Chemical Industries).

In Situ XRD

In situ XRD experiments were performed at the powder diffraction beamline, 11-BM, at the Advanced Photon Source at Argonne National Laboratory. High angular resolution X-ray diffraction data were collected using a 12 channel analyzer detector array (λ = 0.413609 Å, beam size 1.5 × 0.5 mm).⁴⁷ Data spanning a 0–26° 2θ range were collected using a step size of 0.002°. Each measurement took 7 min 40 s. Rietveld refinements were undertaken within the Topas Academic software.⁴⁵

Ex Situ NMR

Hahn echo and MATPASS spectra were collected on a Bruker 200 Avance III spectrometer (4.7 T field strength) at a Larmor frequency of 81 and 78 MHz for the ³¹P and ⁷Li experiments, respectively, using a 1.8 mm MAS Samoson probe. For the ³¹P MATPASS experiments a series of five 90° pulses with a pulse width of 1.6 μs were employed, rotor synchronized at a MAS frequency of 38–39 kHz.⁴⁰ The recycle delay was 0.015 s. The decay time constant of the Hahn echo/MATPASS sequence, T₂′, was obtained at 4.7 T for Li_xCoPO₄ using a series of Hahn echoes where τ, the delay separating the centers of the 90° and 180° pulses, was varied between 250 μs and 16 ms in 8 increments. The signal decay was then fitted with an exponential function. The rotors were packed by mixing KBr and the partially cycled C-LiCoPO₄ composite electrode in a 2:1 ratio, in order to reduce paramagnetic interactions with the field that prevented the rotors from spinning. The ³¹P and ⁷Li data were referenced to an 85 wt % H₃PO₄ and 1 M LiCl aqueous solution, respectively, at 0 ppm.

DFT Calculations

Configurations with different spin states and spin alignments were generated for LiCoPO₄, CoPO₄, and for the intermediate phase (assumed to be Li_2/3CoPO₄ as discussed below), and their energetics were computed in a series of solid-state DFT simulations. The Vienna Ab Initio Simulation Package (VASP5.2)⁴⁸⁻⁵¹ was implemented within spin-polarized DFT,^52,53 and the projector-augmented wave (PAW) approach^54,55 was used to describe the electron–ion core interaction. Full relaxation of the atomic positions and cell parameters, and total energy calculations, were carried out in the absence of symmetry constraints. The Perdew–Burke–Ernzerhof (PBE) exchange-correlation functional^56,57 was used throughout, applying the Hubbard U model^58,59 within the rotationally invariant formalism proposed by Liechstenstein et al.⁶⁰ to correct for the known deficiencies of pure functionals for highly localized 3d states, as explained in more detail below.⁴ After testing for convergence of the total energy of the LiCoPO₄ and CoPO₄ end members with respect to the plane wave cutoff energy and k-point mesh density, a cutoff energy of 500 eV and a 24 k-point grid were selected for calculations within the 4 formula unit cells of the end member compounds. A smaller k-point grid (16 k-points) was used for the (a × 3b × c) Li_2/3CoPO₄ supercells comprising 12 formula units. The threshold difference for self-consistent field (SCF) convergence in the total free energy was set to 1 × 10^–5 eV, and a Gaussian-type smearing of the Fermi level, equivalent to a temperature of 1.2 K, was applied. Starting structures for the end member phases were taken from a previous study by Ehrenberg et al.,¹⁶ whereas the optimization of the intermediate phase proceeded from the LiCoPO₄ structure in which a third of the Li⁺ ions were removed.

The effect of spin polarization on the total energy of the different Li_xCoPO₄ phases (x = 0, 2/3, 1) was investigated by initializing each Co spin in a particular spin configuration (low spin t_2g⁶e_g¹ or high spin t_2g⁵e_g² for d⁷ Co²⁺ ions; and low spin t_2g⁶e_g⁰, high spin t_2g⁴e_g², or intermediate spin t_2g⁵e_g¹ for Co³⁺ ions) in the SCF process. The intermediate spin configuration was explored since it has been found in other Co³⁺ systems.^30,31 The total magnetization of the cell was fixed to the value corresponding to the initial magnetic spin configuration (equal to the sum of all individual Co spins in ferromagnetic cells, or to zero in antiferromagnetic cells) in the first structural optimization run, but the total cell magnetization constraint was released in a subsequent structural optimization run. The charge density was recalculated at the start of each new optimization and single point energy run, from the wave function obtained at the end of the previous run. The final energy, and spin and charge distributions of the different configurations were obtained from a single point energy run in the absence of magnetic constraints.

Values of 5.05 and 6.34 eV were chosen for the effective Hubbard interaction parameter U_eff = U – J for Co²⁺ (in LiCoPO₄) and Co³⁺ (in CoPO₄), respectively, where U is the intraband Coulomb term and J is the intraatomic exchange term. The U_eff values were obtained self-consistently and used successfully in a previous study on the LiMPO₄ compounds (M = Mn, Co, Ni, Fe).²⁹ To compare the total energies obtained for the various Li configurations with stoichiometry Li_2/3CoPO₄ to the total energies obtained for the LiCoPO₄, and CoPO₄ end members, a single U_eff value of 5.48 eV was assumed for all phases. This value is the weighted average of the U_eff values optimized for Co²⁺ in LiCoPO₄ and Co³⁺ in CoPO₄, assuming Co²⁺ and Co³⁺ are present in a 2:1 ratio. The effect of using a single U_eff value to calculate the energies of the end member LiCoPO₄ and CoPO₄ compounds is further discussed in the Supporting Information (SI). Moreover, the effect of electronic localization, through the use of a U Hubbard correction term, on the energies of the different spin and magnetic states of the end member LiCoPO₄ and CoPO₄ phases, and on the formation energies of the different intermediate configurations, was further explored by repeating all calculations in the ferromagnetic state within the pure GGA approach (U = 0 eV). Table S2 in the Supporting Information summarizes the outcome of all the calculations carried out in this study.

Results and Discussion

Synthesis and Characterization of LiCoPO₄

Carbon coated LiCoPO₄ (C-LiCoPO₄), Pnma, was synthesized via the solid-state method.⁴⁴ Additional heating steps beyond that used in the LiFePO₄ synthesis⁴⁴ were required to decrease the amount of impurities present in the product (including Li₃PO₄ and Co₂P; see the Supporting Information). XRD and solid-state ³¹P and ⁷Li NMR experiments were carried out on C-LiCoPO₄ and there were no detectable impurities (see the Supporting Information). The unit-cell parameters evaluated from a Rietveld refinement on the XRD pattern agree well with literature values (a = 10.202(48) Å, b = 5.922(28) Å, c = 4.700(23) Å and volume =283.9(24) ų).¹⁶ A single isotropic resonance is observed in both the ³¹P and ⁷Li NMR spectra (δ_iso of 2985 ppm and −104 ppm, respectively) as expected from single distinct P and Li environments in LiCoPO₄.

Diffraction and Electrochemical Studies

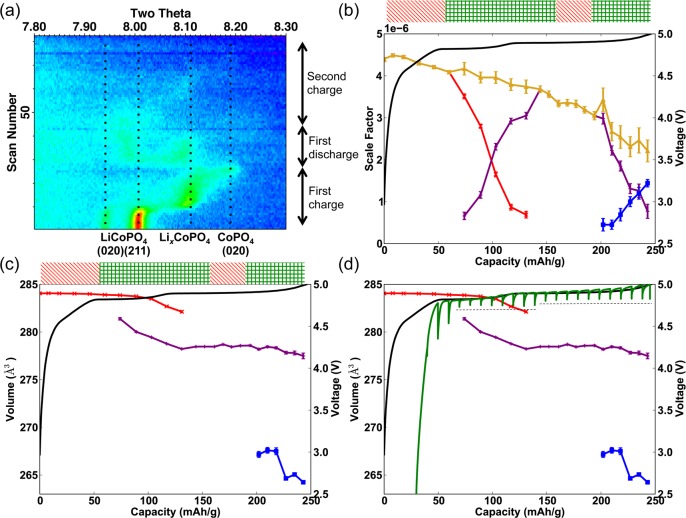
In situ XRD was carried out on the C-LiCoPO₄-composite film in the AMPIX cell⁴⁶ for 1.5 galvanostatic cycles at a charge rate of C/20 (see the Supporting Information). A two-dimensional representation of the XRD patterns is shown in Figure 1a. The region 2θ = 7.8–8.3° (at λ = 0.413609 Å) shows the (211) and the (020) reflections for LiCoPO₄ and CoPO₄, and most clearly reveals the changes in the unit cell parameters upon cycling. Upon charging, the characteristic two-phase behavior between LiCoPO₄ => Li_xCoPO₄ (at 4.82 V) and Li_xCoPO₄ => CoPO₄ (at 4.89 V) is observed via the simultaneous disappearance and appearance of the reflections of the starting material and product, respectively. After the first charge, the Bragg reflections are broadened to the point where they are difficult to distinguish from the background. However, a small peak at 2θ ≈ 8.1°, corresponding to the Li_xCoPO₄ phase, appears on discharge after the disappearance of the CoPO₄ (020) reflection, suggesting that both two-phase reactions involving the intermediate are reversible. Our results agree well with the diffraction results reported by Bramnik et al.,^15,17 as we see both a significant loss of long-range order after the first charge (shown by the decrease in intensity of the Bragg reflections) and the formation of an intermediate, Li_xCoPO₄. So-called “amorphization” has also been observed in ex situ XRD after chemical delithiation, which indicates that this behavior is intrinsic to the material and is not a consequence of interaction with the X-ray beam.^17,18 More recently, a slight loss of long-range order has also been seen for LiFePO₄, but the phenomenon is less pronounced than for LiCoPO₄.⁶¹

Figure 1.

XRD data for the first 1.5 galvanostatic cycles of LiCoPO₄ cycled at a rate of C/20. (a) Two-dimensional image of the patterns at a 2θ range of 7.8–8.3°, shows the transformation of the (211) and (020) reflections in LiCoPO₄ and CoPO₄. The y-axis is scan number (time) and x-axis is 2θ. The results from the Rietveld refinements using the Topas Academic software³⁵ show changes in (b) the scale factor (the sum of the scale factors is plotted in yellow) and (c) the unit cell volume in the three phases (LiCoPO₄, Li_xCoPO₄ and CoPO₄ shown in red, purple and blue, respectively). (d) GITT experiment (in green) for LiCoPO₄ (4th charge) is overlaid onto the unit-cell volume data obtained for the 1st charge; the OCV is indicated with a black dotted line.

Rietveld refinements were carried out using the diffraction patterns acquired during the first charge; the scale factor of the refined phases and the unit-cell volume are shown in panels b and c in Figure 1, respectively. The analyses confirm the qualitative observation of two distinct two-phase reaction processes (indicated by a block of green crosses above the figure). However, it is surprising that there are regions, denoted by diagonal red lines above the figure, within which there is very little evidence of any reaction, i.e., there is neither the formation of a new phase, nor a significant change in the lattice parameters (a solid solution mechanism would manifest itself in the XRD patterns as a gradual change in the unit-cell parameters). Very small changes do, however, occur with respect to the peak position, which are difficult to observe owing to the accompanying broadening of the peaks; these changes are more clearly seen in Figure S3c in the Supporting Information. This suggests that small structural changes (including some partial delithiation) are required to trigger the onset of the next process. The electrochemical activity in these regions is likely dominated by side reactions, i.e. oxidation of the electrolyte,^13,14 formation of the solid electrolyte interface, and/or metal dissolution.⁶² We tentatively suggest that the growth of the CoPO₄ phase from the intermediate phase is associated with a large activation energy, and the side-reactions compete with this structural transformation. The areas indicated with green crosses in panels b and c in Figure 1 sum to ∼160 mAh/g, suggesting that the main electrochemical reaction occurs within these regions (the theoretical capacity of LiCoPO₄ is 167 mAh/g). The crystalline phase fraction continues to diminish, even in regions where side reactions dominate, suggesting that the reduction in long-range order is not directly correlated with the delithiation reaction, but instead depends on the time that the cell remains at high potentials.

Overall, a very large capacity of ∼250 mAh/g is measured on the first charge. However, the discharge capacity for the first cycle is 149 mAh/g (89% of the theoretical capacity), suggesting that, while side reactions are significant (with 40% of the charge capacity being irreversible on the first cycle), Li intercalation and deintercalation in LiCoPO₄ is largely unaffected by them. This is the highest reversible capacity documented in the literature for this material, and is evidence that the loss of long-range order does not impact the reversibility of the reaction, at least for the first few cycles. The additional capacity associated with the side reactions at the beginning of charge (i.e., below 4.75 V) drops noticeably in subsequent cycles, while the additional capacity at higher voltages is still observed (see the Supporting Information). No attempt was made here to minimize the side reactions through the introduction of additives or by surface coating of electrode particles, since our focus here is on the structural transformations that occur in this system. We note that a recent XRD and NMR study of this system has shown these side reactions can be partially reduced by the use of electrolyte additives like HFiP.^43,63

Interestingly, the volume of the LiCoPO₄ primitive olivine cell decreases slightly from 284.1 to 282.1 ų (decrease of 0.7%) as its phase fraction decreases to zero, approaching that of the Li_xCoPO₄ phase when it first appears, at 281.4 ų. Similarly, the cell volume of Li_xCoPO₄ varies noticeably from 281.4 to 278.2 ų (decrease of 1.1%) across its two-phase coexistence with LiCoPO₄, and appears to sustain a larger solid solution range than the two end members. Of particular note, the phase that forms during each of the two-phase reactions (Li_xCoPO₄ followed by CoPO₄) has a larger solid solution regime (i.e., a larger range in cell volume) than the phase being consumed (LiCoPO₄ and Li_xCoPO₄, respectively). One explanation for this is that the new phase, which nucleates and grows within the parent phase, is distorted to compensate for the difference in cell parameters and to reduce the coherency strain at the grain boundary. The greater deviation in Li composition in the nucleating phase is consistent with the work carried out by Ravnsbæk et al. on the LiFe_xMn_1–xPO₄ materials, which they attribute to a small amount of a coherently nucleating phase.⁶⁴

There appears to be a lag between the two major plateaus observed in the galvanostatic cycling and the two-phase reaction regions emerging from the refinements, a voltage increase from 4.82 to 4.89 V being observed before the LiCoPO₄ phase has fully converted to Li_xCoPO₄. However, the agreement is significantly better if we compare the electrochemically active regions determined by XRD with the plateaus obtained from the open circuit voltage (OCV) within galvanostatic intermittent titration technique (GITT) experiments, as shown by black dashed lines in Figure 1d. Note that the GITT data was taken from the fourth cycle, where the “latent” (side reaction) period observed at the beginning of the charge is significantly shorter. Thus, the GITT data has been offset by 25 mAh/g in order to align the electrochemically active regions with the XRD volume changes. The overpotential increases noticeably before the end of the first plateau (with an OCV of 4.75 V), resulting in an increase in the potential measured under galvanostatic conditions from 4.82 to 4.89 V. The overpotential appears to correlate with the concentration and cell volume of the minority phase within the two-phase reaction. During the 4.75 V plateau, the overpotential is at a minimum when Li_xCoPO₄ nucleates and is the minority phase within the LiCoPO₄ particle. As Li_xCoPO₄ grows and LiCoPO₄ becomes the minority phase, the overpotential increases. The overpotential increases at the same point in the electrochemistry as the decrease in the volume of LiCoPO₄ from its initial value of 284.1 ų, the volume presumably contracting so that it can be accommodated within the Li_xCoPO₄ majority particle. The voltage associated with Li extraction will be increased by the overpotential required to drive the energetically unfavorable decrease in cell volume in LiCoPO₄.

To estimate the Li content in the intermediate phase, we compared the lattice parameters of the intermediate structure with those of the end members, and the Li content was obtained using Vegard’s Law. On the basis of the volume of Li_xCoPO₄, a value of x = 0.72 is obtained. However, the a, b, and c lattice parameters considered separately would indicate a Li stoichiometry of x = 0.80, 0.47 and 0.66, respectively (the end member cell parameters are shown in the Supporting Information). Therefore, due to the anisotropic changes in the lattice parameters of Li_xCoPO₄, compared to those of CoPO₄ and LiCoPO₄, we are only able to provide, based on the XRD results, a range (0.47 ≤ x ≤ 0.80) within which we expect to find the Li composition of the intermediate.

NMR Spectroscopy

Ex situ ³¹P and ⁷Li NMR spectroscopy was carried out on LiCoPO₄ at different states of charge and discharge, obtained by galvanostatically cycling the battery at a rate of C/20 (Figure 2). The Li_xCoPO₄ intermediate is observed in the spectra of both nuclei, and is therefore deemed stable in the absence of a current.

Figure 2.

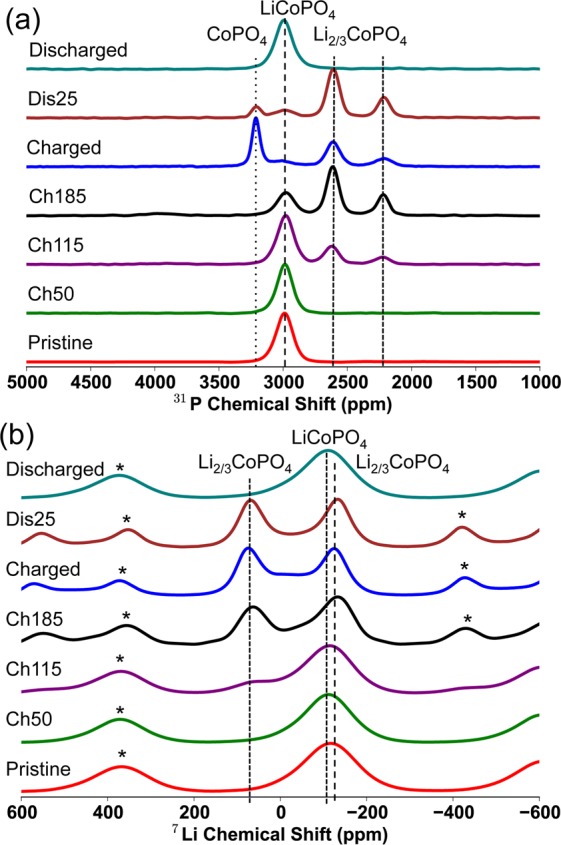
Ex situ (a) ³¹P MATPASS and (b) ⁷Li Hahn echo MAS NMR spectra recorded at a magnetic field strength of 4.7 T and at a spinning speed, ν_r, between 38 and 39 kHz, at different points in the first galvanostatic cycle of LiCoPO₄, cycled at a rate of C/20. The labels ‘Ch50′, “Ch115” and “Ch185” refer to the spectra of the LiCoPO₄-composite electrode, which has been charged up to 50, 115, and 185 mAh/g, respectively. The spectra labeled “discharged” and “Dis25”, were both fully charged and subsequently either fully discharged or discharged for 3 h, respectively. All of the spectra have been normalized so that the maximum intensity is equal to 1. Spinning sidebands are marked with an asterisk.

There is again a significant delay between the start of the electrochemistry and the onset of delithiation in LiCoPO₄, which agrees with the XRD data and strongly indicates the existence of side reactions in this region, the peaks from Li_xCoPO₄ only being observed after Li extraction corresponding to a capacity of 50 mAh/g. However, once commenced, the reaction apparently occurs steadily. After 185 mAh/g, the Li_xCoPO₄ peaks decrease with the growth of the CoPO₄ peak (this is only observable in the MATPASS ³¹P NMR spectra, as there is a negligible contribution from Li in a “Co³⁺” environment in CoPO₄). Both two-phase mechanisms are reversible on discharge: the ³¹P CoPO₄ peak (δ_iso = 3201 ppm) decreases with the growth of the Li_xCoPO₄ peaks, which then decrease with the growth of the LiCoPO₄ peak. The shift and line width of the LiCoPO₄³¹P resonance (at δ_iso = 2989 ppm) after one cycle is similar to that observed initially, indicating that the “amorphization” observed with in situ XRD corresponds only to a loss of long-range structure, the short-range structure being unchanged; this is consistent with the reversible electrochemistry of the LiCoPO₄ phase. The NMR results do not imply much compositional variation, as observed in the XRD data, specifically for the intermediate Li_xCoPO₄ phase. This must in part be due to the limited number of samples examined by using NMR spectroscopy, but may also be a result of the absence of a current in the ex situ NMR experiments, permitting solid solutions to relax into more structurally homogeneous end member phases of the reactions, so that only resonances associated with the LiCoPO₄, Li_xCoPO₄ and CoPO₄ phases are observed. Hahn-echo ³¹P NMR spectra were also acquired for the same samples (see the Supporting Information); yielding similar shifts and intensities for the various resonances across the electrochemical range. We chose to analyze the MATPASS spectra in greater detail since these spectra do not suffer the additional complications of the overlap between the isotropic resonance of one environment and the sidebands of another. Our ⁷Li and ³¹P NMR spectra are essentially identical to those obtained recently in an NMR and XRD study of this material.⁴³

From the NMR spectra, we are able to extract information about the local structure of the intermediate phase: two ³¹P resonances are observed at δ_iso = 2610 and 2210 ppm, and two ⁷Li resonances at δ_iso = 69 and −125 ppm. The ⁷Li resonance at −125 ppm in the intermediate overlaps with the isotropic shift observed for the fully lithiated phase, suggesting that it arises from a Li nucleus predominantly surrounded by Co²⁺ ions. From the “Charged” ⁷Li spectrum (i.e., the LiCoPO₄ electrode that has been fully charged to 5.0 V), where the features of the intermediate phase are most prevalent, the integrated intensity indicates that the two environments are present in an approximately 1:1 ratio (the measured ratio is 1:1.23, the higher intensity of the −125 ppm resonance being ascribed to minor contributions from the overlapping LiCoPO₄ resonance). The ³¹P MATPASS “Ch185” spectrum (i.e., the point at which the LiCoPO₄ electrode has been charged to a capacity of 185 mAh/g) shows the clearest resolution of the ³¹P intermediate peaks and suggests that the two P environments are present in an approximately 2:1 ratio (a value of 2:0.87 was calculated for resonances δ_iso = 2610 and 2210 ppm, respectively). Note that the different spin–spin (T₂) relaxation times for the two ³¹P and two ⁷Li environments have been accounted for in the intensity analysis (see the Supporting Information).

Although it is possible to have two ³¹P environments that have similar isotropic shifts and that give rise to overlapping peaks in the NMR spectrum, our former studies of the LiFe_xMn_1–xPO₄ and LiFe_xCo_1–xPO₄ materials^41,65 have shown that the hyperfine shift is highly sensitive to the geometry of the transition metals around P and to the oxidation state. It is therefore unlikely for two ³¹P environments to have the exact same shift, and, as there is no significant additional peak broadening or distortion of the more intense resonance, this suggests that the observed resonances correspond to two distinct environments occurring in a 2:1 ratio. It would be helpful to perform ⁷Li or ³¹P 2D homonuclear correlation experiments on the intermediate phase to obtain insight into the spatial proximities of the environments giving rise to the resonances. However, NMR simulations (see the Supporting Information) show that such experiments are extremely challenging because of the large hyperfine dipolar interactions which are much larger than the dipolar coupling between the nuclei, and the short spin–lattice (T₁) relaxation times relative to the time required to establish significant correlations between the different nuclei using a dipolar recoupling scheme.

Although it is surprising at first sight to observe ³¹P NMR resonances associated with Li_xCoPO₄ lying beyond the range demarked by the end member LiCoPO₄ and CoPO₄ shifts, a similar phenomenon was observed for the P environments in LiFe_xCo_1–xPO₄, where many of the observed resonances did not fall between those of pure LiFePO₄ and LiCoPO₄.⁶⁶ This is attributed to the high degree of sensitivity of the ³¹P hyperfine shift to the individual geometries and d-orbital occupancies of the M–O-P (M = Fe²⁺, Co²⁺, and Co³⁺) bond pathways.

Intermediate Structure, Li_xCoPO₄

We now use the constraints set by the NMR spectra (in particular, the number of different P and Li local environments and their spectral weights), in combination with the lattice parameters extracted from the XRD refinements, to propose a composition and structure for the intermediate phase. The anisotropic changes of the lattice parameters of the intermediate with respect to the unit-cell parameters of the end members led us to consider a range of intermediate phase compositions, i.e., Li_0.47–0.80CoPO₄. It is not possible to devise a Li and Co²⁺/Co³⁺ ordering scheme within the original olivine unit-cell that gives rise to two different ³¹P resonances with a 2:1 intensity ratio, since this cell contains four P atoms. Therefore, a reasonable first assumption is that the intermediate structure is represented by an expansion of the original olivine primitive cell. In order to analyze the different possible structures in a systematic way, we proceed by considering the following supercell expansions: (2a × b × c), (a × 2b × c), (a × b × 2c), (3a × b × c), (a × 3b × c), and (a × b × 3c) (i.e., three cells are doubled and three cells are tripled along either the a, b, and c axes) to create six supercells. We also consider a seventh expansion, the Na_2/3FePO₄ superstructure,^23,28 which formally involves cell tripling in two directions, (either (3a × 3b × c)²³ or (a−b × 3b × c)²⁸).

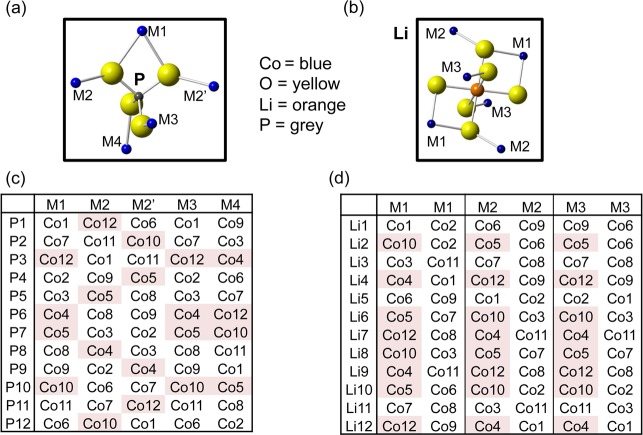
Because the ³¹P Fermi contact shifts are much more sensitive to the nature and/or oxidation state of the transition metals in the first coordination shell than the ⁷Li NMR spectra,^41,65 we first analyze the ³¹P spectra before proceeding to examine the Li environments. There are five Co positions (labeled M1, M2, M2′, M3, and M4 in Figure 3a) in the first cation coordination shell of P in the olivine structure, of which two are equivalent (M2 and M2′) because of the presence of a mirror plane passing through the P atoms in the pure LiMPO₄ and MPO₄ phases.⁶⁵ Seven tables were created (see the Supporting Information) with the 8, 12, and 12 P local sites (from cell doubling, tripling, and the (a−b × 3b × c) supercell, respectively) and the five different (labeled) Co atoms in the first coordination shell around the P sites. In these supercells, the periodicity imposes further limits on the possible range of P environments; e.g., in the (2a × b × c) supercell, P1 is surrounded by two Co1 atoms from two different cells on the M1 and M3 positions, two Co5 atoms from two cells on M2 and M2′ and a Co6 atom on M4.

Figure 3.

First coordination shell of Co atoms around (a) P and (b) Li in the olivine structure. Tables showing (c) the 12 P and (d) 12 Li sites generated in the (a × 3b × c) supercell of the olivine structure, and their nearest Co atoms. The Co atoms shaded in red and white represent Co³⁺ and Co²⁺, respectively, generating three P and two Li local environments in the Co²⁺/Co³⁺ arrangement shown here.

All configurations obtained when the cell is doubled were immediately dismissed because there are 8 P atoms in the supercell, so it is never possible to obtain two ³¹P sites in a 2:1 ratio. We then considered the different cells (and different P local environments) generated by assuming that the different Co sites were either Co²⁺ or Co³⁺, in the appropriate ratios to form Li compositions falling within the range Li_0.47–0.80CoPO₄.

When the unit cell is tripled along either the a, b, or c axis, every arrangement of Co²⁺ and Co³⁺ ions generates more than two ³¹P sites, in disagreement with the ³¹P NMR experimental data (illustrated in Figure S7d–i in the Supporting Information). After a thorough analysis in which all possible combinations were explored, the closest agreement with the NMR data was achieved with a Co²⁺ to Co³⁺ ratio of 2:1, resulting in three different P environments in a 1:1:1 ratio (Figure S7d, f in the Supporting Information). When the cell is tripled along the b-direction, however, two of these three P environments consist of one Co³⁺ on either the M2 or the M2′ site, and four Co²⁺ on the remaining sites (P1, P2, P4, P5, P8, P9, P11, and P12 in Figure 3c). Because the mirror plane on P is retained in the cosubstituted materials, LiFe_xMn_1–xPO₄ and LiFe_xCo_1–xPO₄, it strongly suggests that in Li_xCoPO₄, M2 and M2′ are also equivalent. The bond lengths and bond angles generated by our calculations support this assumption, as discussed in the DFT study. Therefore, even though three P environments arise, two of them are expected to give rise to identical shifts in the presence of the mirror plane, resulting in two peaks occurring in a 2:1 ratio.

There are three symmetrically equivalent possible combinations of Co²⁺/Co³⁺ ordering for the (a × 3b × c) superstructure. They can be superimposed onto each other by a translation in the direction perpendicular to the Co chains (see the Supporting Information), which, as observed in Figure 3d, results in a total of two distinct Li environments: four Li sites surrounded by six Co²⁺ (denoted Liα, Figure 4d) and eight Li sites surrounded by three Co²⁺ and three Co³⁺ (denoted Liβ, Figure 4e). Liα is assigned to the ⁷Li resonance at −125 ppm, as it overlaps with the pristine ⁷Li resonance (i.e., Li surrounded by 6 Co²⁺ ions). The composition Li_2/3CoPO₄ implies that four Li ions must be removed from the supercell. Given the experimentally observed intensities, the Li ions must be removed from the Liβ sublattice, yielding two Li environments in a 1:1 ratio, in agreement with the ⁷Li NMR results. The proposed Li environments are shown in Figure 4f. Note that this differs from the ordering scheme proposed in the recent ⁷Li and ³¹P NMR study.⁴³

Figure 4.

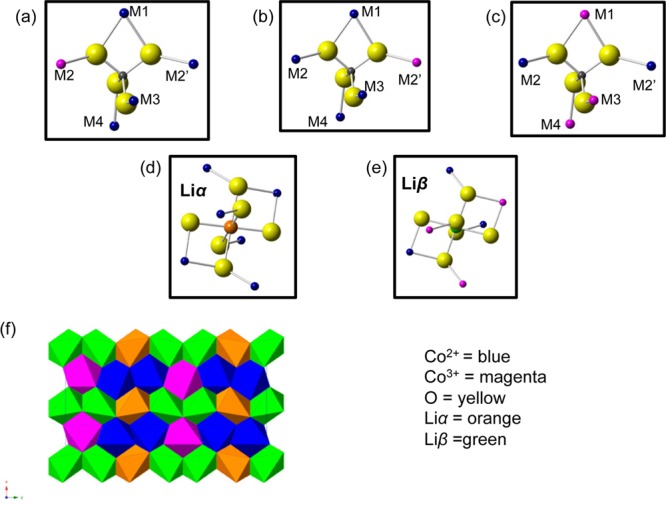
(a–c) Three P environments (present in a 1:1:1 ratio) and (d, e) two Li environments (which are present in a 1:1 ratio) in the Li_2/3CoPO₄ structure. Because M2 = M2′, a and b are equivalent. (f) There are 8 Liβ sites (shown in green), 4 of which must be removed for charge balancing (Co²⁺, Co³⁺ and Liα are shown in blue, magenta, and orange, respectively).

The (a−b × 3b × c) supercell present in the Na_2/3FePO₄^23,28 intermediate structure was explored, and the same Fe²⁺/Fe³⁺ ordering observed in both these studies was implemented for Co²⁺/Co³⁺ (Figure S8 in the Supporting Information). However, this ordering results in five different P sites. When M2 and M2′ are assumed to be equivalent, three distinct ³¹P environments are predicted in a 1:1:1 ratio, which still disagrees with the ³¹P NMR data. The (a × b × 3c) supercell, which was recently suggested by Kaus et al.⁴³ for the Li_2/3CoPO₄ intermediate, is presented in Figure S7d in the Supporting Information and results in the presence of five inequivalent ³¹P environments in a 2:1:1:1:1 ratio, so it is not considered further.

First-Principles Calculations

First-principles DFT calculations were performed on the end member phases and on the proposed Li_2/3CoPO₄ intermediate structure to determine the lowest-energy spin state and magnetic alignment at all three stages of charge of the LiCoPO₄ electrode. The calculations considered both structures with fixed experimental cell parameters and atomic positions, as obtained from Rietveld refinement of neutron and XRD data,¹⁶ and fully optimized structures. The relative stability of different Li⁺/vacancy ordering schemes in the intermediate was also explored.

Ab Initio Investigation of the Relative Stability of Different Spin States and Magnetic Alignments in the End Member Compounds

The calculations on LiCoPO₄ and CoPO₄ were performed using an average U_eff value of 5.48 eV, as derived for the mixed valence Li_2/3CoPO₄ system. A high spin ground state was predicted for both end member phases, in agreement with previous experimental¹⁶ and theoretical studies.²⁹ The previous DFT study reported that different magnetic ordering schemes of the transition metal ions lead to energy differences of 10–60 meV per formula unit.²⁹ Our results on the LiCoPO₄ and CoPO₄ end member phases, presented in the two diagrams in panels a and b in Figure 5, show that these energy differences can be orders of magnitude larger when the different spin states of the Co²⁺ and Co³⁺ atoms are also considered, a result in line with the fact that intraatomic exchange interactions are typically a few electron volts, whereas interatomic exchange interactions are in the millielectron volt range.

Figure 5.

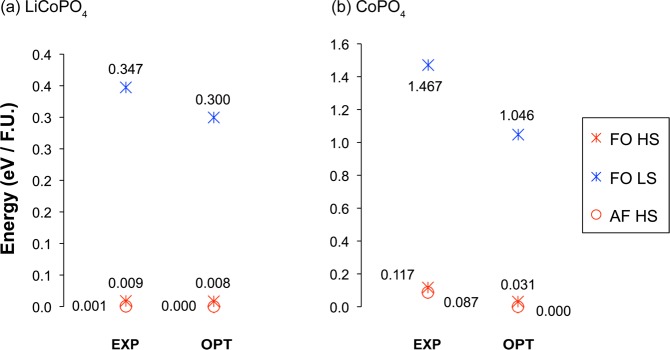
Energy diagrams of (a) LiCoPO₄ and (b) CoPO₄ in their experimental (EXP)¹⁶ and DFT optimized (OPT) structures, within the GGA+U (U_eff = 5.48 eV) approach. Total energies were calculated for cells in which all Co spins were ferromagnetically (FO) aligned (in either their low (LS) or high (HS) spin state), and on cells in which the HS Co spins were antiferromagnetically (AF) aligned, as reported in a previous magnetic study on these phases.¹⁶

Only one antiferromagnetic state is reported here for LiCoPO₄, as the antiferromagnetic low-spin cells converged to the high-spin state upon release of magnetic constraints. The total energies of the high spin ferromagnetic and antiferromagnetic LiCoPO₄ states differ by 8 meV per formula unit in both the experimental and optimized structures. As expected, the low-spin state is highly unfavorable and lies more than 300 meV per formula unit above the high-spin ground state.

In the DFT calculations performed on the CoPO₄ structure, all cells with the Co³⁺ spins initialized in the intermediate-spin state converged to high-spin states and are therefore not represented in Figure 5b. The high-spin antiferromagnetic ground state lies at ca. 30 meV per formula unit below the high spin ferromagnetic state. Again, the low-spin state is much higher in energy, by more than 1 eV per formula unit.

In summary, our calculations confirm the antiferromagnetic ground state and spin alignment deduced experimentally, for both LiCoPO₄ and CoPO₄ structures, by Ehrenberg et al.¹⁶ This study on the end member compounds yields results in good agreement with previous experimental^16,32 and theoretical²⁹ studies, and can now be used to determine the relative stabilities of the different (Li and magnetic) configurations considered here as potential Li_2/3CoPO₄ intermediate phases.

DFT Investigation of the Relative Stability of Different Spin States and Magnetic Alignments in the Li_2/3CoPO₄ Intermediate Structures

As previously described, the ³¹P NMR data for the intermediate phase Li_2/3CoPO₄ suggest a tripling of the LiCoPO₄ unit cell along the b-direction. The site occupation disorder (SOD) code,⁶⁷ devised to determine a minimal set of symmetry-unique configurations for site-disorder problems in solids, was used with the Pnma LiCoPO₄ unit cell as the input structure. The (a × 3b × c) supercell (Figure 4f) was created. It contains 12 Li atoms, four of which were systematically removed by the SOD code in order to generate all possible structures with a Li_2/3 stoichiometry. The code generated thirty-two symmetry inequivalent supercells, in which all the Co sites were assumed to be equivalent. Co³⁺/Co²⁺ ordering along the b-direction, identified on the basis of the ³¹P experimental NMR data, was implemented for each of the thirty-two possible Li configurations. Nineteen of these structures were discarded, as they did not agree with the ⁷Li NMR data (i.e., they involved the removal of one or more Li⁺ ion(s) from the Liα sublattice). Close examination of the 13 remaining structures lead us to reject a further seven of them that had either triple or higher aggregates of Li vacancies close to each other, and/or a highly anisotropic charge distribution. The final six configurations (a–f) are shown in Figure 6.

Figure 6.

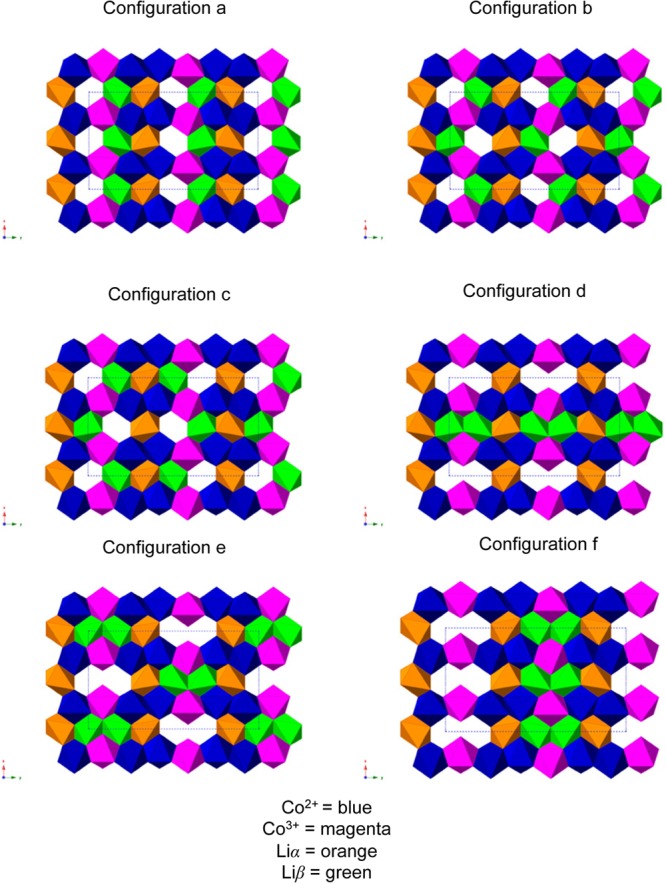
Six different Li⁺/vacancy ordering schemes on which DFT calculations were performed, which are all consistent with the experimental ⁷Li and ³¹P NMR and XRD data. Co²⁺ and Co³⁺ are shown in blue and magenta, respectively, and Liα and Liβ are shown in orange and green, respectively.

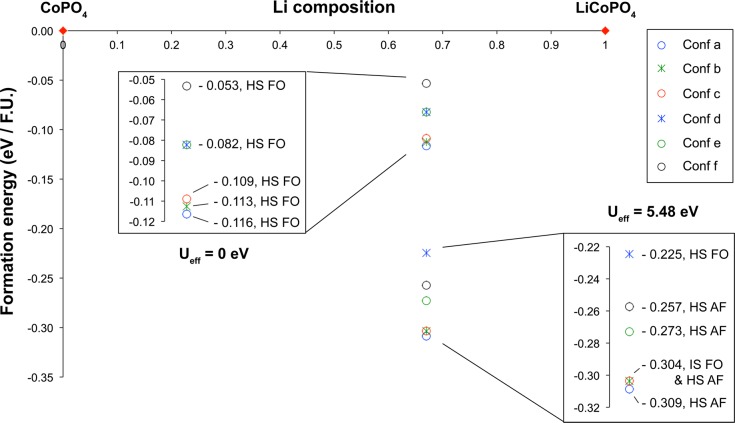
The energies of the most stable (antiferromagnetic high spin) configurations for the end member structures optimized ab initio were used to calculate the formation energies of the six different Li⁺/vacancy configurations. A Li_xCoPO₄ convex hull was generated (presented in Figure S10 in the Supporting Information), which includes the energy of all the (intermediate and high) spin states, and magnetic configurations (ferromagnetic, antiferromagnetic) which reached electronic convergence without spin constraints in the last single-point energy DFT calculation. Additionally, the formation energies of all of the LiCoPO₄, Li_2/3CoPO₄, and CoPO₄ spin and magnetic configurations investigated in this study are summarized in Table S2 in the Supporting Information. The Li_xCoPO₄ convex hull presented in Figure 7 only shows the lowest energy spin and magnetic state, for each of the six different Li configurations considered within the pure GGA and GGA+U (U_eff = 5.48 eV) approaches. We will analyze the GGA+U results in this section, then comment on the insight into the mechanisms stabilizing the Li_2/3CoPO₄ intermediate obtained from the GGA results in the Discussion section. Within GGA+U, apart from configuration b, none of the Li arrangements considered for the Li_2/3CoPO₄ structure are stable in the intermediate-spin state. The (ferromagnetically and antiferromagnetically coupled) intermediate-spin state either does not reach electronic convergence in the absence of magnetic constraints, or converges to the high-spin state when the magnetic constraints are released. Configuration b is the only exception to the rule: its ferromagnetic high-spin state is not stable and converges to the ferromagnetic intermediate-spin state in the absence of constraints on the Co spins. Moreover, this ferromagnetic intermediate-spin state is found to be the lowest-energy spin state for this configuration, and the second lowest energy configuration out of all the Li configurations investigated in this study.

Figure 7.

Convex hull for Li_xCoPO₄, calculated within the GGA (U_eff = 0 eV) and GGA+U (U_eff = 5.48 eV) approaches. The formation energies of the different Li_xCoPO₄ (x = 0, 2/3, 1) phases are plotted against Li composition, in eV per formula unit (eV/F.U.). The insets show the −0.32 to −0.22 eV/F.U. and the −0.12 to −0.05 eV/F.U. regions of the convex hull, corresponding to the range of formation energies of the Li_2/3CoPO₄ intermediate structures in GGA+U and in GGA, respectively. Although GGA calculations were only performed in the ferromagnetically aligned state, GGA+U calculations were performed in the ferromagnetically and antiferromagnetically aligned states. Only the lowest energy spin and magnetic state, for each of the different Li_2/3CoPO₄ Li arrangements investigated, is plotted. Table S2 in the Supporting Information summarizes the outcome of all calculations performed on the Li_2/3CoPO₄ cells, in GGA and in GGA+U. IS, HS, FO and AF denote the intermediate spin state, the high spin state and the ferromagnetically and the antiferromagnetically aligned phases, respectively.

Figure 7 and Figure S10 and Table S2 in the Supporting Information clearly demonstrate that all of the Li_2/3CoPO₄ configurations tested in this study are thermodynamically stable with respect to the two end member phases. The lowest energy configuration observed in Figure 7 (configuration a in the antiferromagnetic high spin state) has a negative formation energy of 309 meV per formula unit. A map of the spin density of this configuration is presented in Table S2 in the Supporting Information. All Li configurations considered in Figure 7 lie within an energy range of ca. 84 meV per formula unit. The formation energies of the three most stable configurations (Figure 6a–c) differ by less than 5 meV per formula unit, and we may expect more than one structure to be present at room temperature. These three low energy configurations (a, b and c) have minimal differences in the arrangement of the Li vacancies, and can be interconverted by Li ion hops to adjacent Liβ sites. It is likely that the intermediate structure contains a disordered Li sublattice comprising all of these different Li local environments. Configurations d–f contain vacancies arranged in pairs, which were shown in calculations on Li_0.6FePO₄ materials to be the most energetically favorable configurations.²¹

As previously discussed, the experimental observation of only two ³¹P resonances implies an equivalence of the M2 and M2′ metal positions in the first P coordination shell. To determine whether this equivalence is observed computationally, we compared the Co^3+/2+ (M2)–O–P and Co^3+/2+(M2′)–O–P bond pathway geometries, in the lowest-energy Li_2/3CoPO₄ supercell optimized ab initio (configuration a in the high-spin antiferromagnetic state). No differences are observed between the Co–O and O–P bond lengths and the Co–O–P bond angles involving either M2 or M2′ (i.e., the mirror plane is preserved), helping to validate our assertion that only two ³¹P local environments are present.

Discussion

The excellent agreement between the number of distinct Li and P local environments and their relative populations, predicted using the model outlined above and the experimental ⁷Li and ³¹P NMR data obtained for the intermediate structure, led us to propose an intermediate phase with stoichiometry Li_2/3(Co²⁺)_2/3(Co³⁺)_1/3PO₄, and with a superstructure obtained by tripling the unit cell in the b-direction. This result should be contrasted to previous structural reports for other A_2/3 polyanionic intermediates (A = Li, Na), Li_2/3VPO₄F and A_2/3FePO₄.^27,68 Although a Li_2/3VPO₄F intermediate has been identified when LiVPO₄F is electrochemically charged, the crystal structure is still unknown. The A_2/3FePO₄ and Li_2/3CoPO₄ intermediates adopt different superstructures with the former consisting of a tripling in both the b- and a-directions (Figure S8). Three inequivalent sites are generated from this superstructure, in disagreement with the experimental observations for Li_2/3CoPO₄. Interestingly, we observed two ³¹P resonances in our previous studies of Li_2/3FePO₄ obtained by cooling micron-sized particles of chemically delithiated LiFePO₄, suggesting that more than one superstructure may exist for Li_2/3FePO₄.⁶⁹ The absence of superlattice reflections in the in situ XRD data shown here was accounted for by performing simulations of the Li_2/3CoPO₄ diffraction pattern. The simulations show that the intensity of the superlattice reflections are 1/100th of that of the main Bragg peaks (see the Supporting Information), and are not observable because of the significant broadening of the peaks; further TEM analyses are ongoing.

Our calculations predict that all six Li_2/3CoPO₄ intermediate configurations investigated here lie below the LiCoPO₄–CoPO₄ convex hull, conversely to the Li_2/3FePO₄ case, for which the intermediate is only metastable and lies above the LiFePO₄–FePO₄ convex hull.^28,70 Therefore, in the Co system, the thermodynamics will drive the formation of the intermediate phase. The activation energy barrier associated with the structural transformations will also be lowered over that involving the direct delithiation of LiCoPO₄ to form CoPO₄, since the intermediate phase is able to buffer the volume changes associated with delithiation. The relative changes in the sizes of the a, b, and c unit-cell parameters, and subsequent changes in the areas of the ab, ac and bc faces of the unit cell (Table 1), allow us to speculate on a possible orientation of any interface between LiCoPO₄ and Li_2/3CoPO₄ and between Li_2/3CoPO₄ and CoPO₄ within a reacting particle. For the LiCoPO₄ => Li_2/3CoPO₄ and Li_2/3CoPO₄ => CoPO₄ reactions, the changes in the area of the bc cell faces are 0.7% and 0.1%, respectively. These changes are minor in comparison to the changes of 2.4% and 6.1% in the area of the ac cell faces for the LiCoPO₄ => Li_2/3CoPO₄ and Li_2/3CoPO₄ => CoPO₄ reactions, respectively. The latter being largely a result of the large change in the a-parameter during this reaction. These results strongly suggest that any interface between LiCoPO₄ and Li_2/3CoPO₄, and between Li_2/3CoPO₄ and CoPO₄, that forms during the electrochemical reaction, is in the bc-plane, in agreement with the work by Ravnsbæk et al. on LiFe_xMn_1–xPO₄.⁶⁴ Although coherency strain energy calculations have been carried out by Van der Ven⁷¹ and Cogswell⁷² on the LiFePO₄ system, it is not trivial to rationalize the additional stabilization of the intermediate phase in the LiCoPO₄ and CoPO₄ particles.

Table 1. Percentage Changes in the Unit-Cell Parameters, in the Areas of the ab, ac, and bc Faces of the Unit Cell, and in the Cell Volumes for the Two Reactions LiCoPO₄ => Li_2/3CoPO₄ and Li_2/3CoPO₄ => CoPO₄^a.

	%
	Δa	Δb	Δc	Δab	Δac	Δbc	Δvolume
LiCoPO4 - Li2/3CoPO4	1.2	1.2	–0.4	2.4	0.8	0.7	2.0
Li2/3CoPO4 – CoPO4	5.1	1.1	–0.9	6.1	4.2	0.2	5.3

^aThe changes are calculated relative to the LiCoPO₄ and Li_2/3CoPO₄ structures, respectively.

Ab initio calculations on the Li_2/3CoPO₄ intermediate predict its thermodynamic stability with respect to the disproportionation reaction leading to the formation of LiCoPO₄ and CoPO₄, in good agreement with experimental observations of a stable Li_2/3CoPO₄ intermediate phase in the absence of a current. These observations should be contrasted with mechanisms proposed for LiFePO₄ nanoparticles, where the LiFePO₄–FePO₄ interface was suggested to be unstable and the delithiation reaction to occur particle-by-particle, as proposed by the domino-cascade model.⁷³ Our recent results⁷⁴ and those of Zhang et al.⁷⁵ have suggested, in agreement with prior theoretical predictions,⁷⁰ that nanoparticles of LiFePO₄ react via a solid-solution mechanism rather than by forming an abrupt interface between the two end-member phases, at least at very high rates.

LiCoPO₄, Li_2/3CoPO₄, and CoPO₄ also show considerable variations in cell parameters from their equilibrium values during the in situ XRD measurement. This phenomenon is most pronounced when the phases exist as minority phases within the electrode (see Figure S13 in the Supporting Information). For example, the b-parameter of Li_2/3CoPO₄ approaches that of LiCoPO₄ in the initial stages of delithiation. This indicates that a substantial fraction of the particles within the electrode undergo electrochemical reaction simultaneously, in contrast to results obtained at low cycling rates for LiFePO₄. Thus, this system does not react particle-by-particle (the domino-cascade model). The mechanism observed here for LiCoPO₄ is related to the solid-solution mechanism, but is subtly different. Both mechanisms originate from the coherency strain between end-member phases. Here, the Li_2/3CoPO₄ phase must be able to accommodate a wide range of nonstoichiometry during the reaction (resulting in structural flexibility/elasticity) so that when it first forms within the LiCoPO₄ phase it contains excess lithium (i.e., Li_2/3+δCoPO₄). Because little evidence for nonstoichiometry is observed in the ex situ ³¹P NMR experiments, we suggest that these are also metastable solid solutions, but further calculations to determine the energetics of different compositions within this system are required to investigate this phenomenon in greater depth.

Nevertheless, the DFT calculations performed in this study provide insight into the mechanisms stabilizing the Li_2/3CoPO₄ phase. The U Hubbard term in GGA+U allows charges to be localized onto particular ions of mixed-valence systems, while pure GGA results in delocalization of charge over all metal atoms. The ab initio study by Zhou et al.⁷⁶ on the Li_xFePO₄ system showed that the electronic configurational entropy needed to be taken into account to produce an accurate model for the LiFePO₄-FePO₄ phase diagram and to reproduce the eutectic point at approximately x = 0.5. This electronic entropy, arising due to the tendency to form distinct Fe²⁺ and Fe³⁺ oxidation states in the GGA+U calculations and their subsequent arrangements, was found to be larger than the configurational entropy associated with the distribution of Li⁺ ions and vacancies in the lattice. In our work, the Li_2/3CoPO₄ formation energies obtained within the GGA approach are not as large as those calculated in the GGA+U case, the additional stability of the intermediate configurations observed in GGA+U arising from an electronic term related to localizing the charges in the structure. However, we note that the failure of pure DFT is not as severe in the case of Li_2/3CoPO₄, where the method still predicts the intermediate configurations to be below the convex hull. In contrast, in Li_xFePO₄, LDA and GGA do not predict the experimentally observed phase separation at low T.⁷⁷ This result is in agreement with previous GGA studies on the LiCoPO₄/CoPO₄ system.^78,79 Finally, the formation energies obtained within the pure GGA approach on the different Li_2/3CoPO₄ structures reveal that configurations a, b, and c, are lower in energy than configurations d, e and f, whether or not a U correction is applied. This suggests that the greater stabilization of configurations with single Li vacancies (a, b, and c), compared to configurations containing pairs of Li vacancies (d, e, and f), is due to more favorable electrostatics, in contrast to what has been observed for Li_0.6FePO₄.²¹

Conclusions

Both XRD and NMR studies show that the electrochemical delithiation reaction of LiCoPO₄ involves two distinct two-phase mechanisms, namely LiCoPO₄ => Li_2/3CoPO₄ and Li_2/3CoPO₄ => CoPO₄, both of which are reversible upon discharge. Li_2/3CoPO₄ is stable in the absence of a current, a result confirmed by DFT calculations of the energetics of this phase. The ex situ NMR spectra of a range of delithiated samples provide direct insight into the P and Li local environments occurring in the intermediate phase: two Li environments are present in a 1:1 ratio (one environment containing a first coordination shell of only Co²⁺ cations), along with two P environments in a 2:1 ratio. A thorough analysis of these NMR spectra led to the conclusion that the intermediate has the composition Li_2/3CoPO₄, with Co³⁺/Co²⁺ ordering along the b-axis. The DFT calculations indicate that the lowest energy Li⁺/vacancy ordering also occurs along the b-axis, with the vacancies residing next to the Co³⁺ ions. Three low energy Li⁺/vacancy ordering schemes, all at ca. 300 meV below the LiCoPO₄–CoPO₄ convex hull, are identified. Their total energies lie within a range of 5 meV per formula unit, and the three configurations only differ by single Li⁺ displacements between neighboring Liβ sites in the b-direction, in keeping with the fact that there is only a 50% occupancy of the sites neighboring both Co³⁺ and Co²⁺ ions. Thus, it is very likely that the intermediate phase contains a degree of disorder on the Li sublattice. A comparison of the formation energies obtained in GGA+U and GGA on the different Li_2/3CoPO₄ intermediate configurations reveals that an electronic term contributes to the stability of the intermediate phase.

Supporting Information Available

Additional information on computational methods, LiCoPO₄ impurity analysis during the solid-state synthesis, XRD, ³¹P NMR and ⁷Li NMR of LiCoPO₄, electrochemistry for the in situ XRD, the first two electrochemical cycles of LiCoPO₄, overlaid to demonstrate the reduction in the side reactions at the start, the unit-cell parameters of the end member phases (LiCoPO₄, Li_xCoPO₄ and CoPO₄), ex situ ³¹P and ⁷Li Hahn echo NMR spectra of Li_xCoPO₄ during the first electrochemical cycle and the points on the electrochemical curve at which ex situ NMR data was obtained, NMR homonuclear recoupling spin dynamics simulations, P environments in Li_xCoPO₄ when the primitive olivine unit cell has the following expansions: (2a × b × c), (a × 2b × c), (a × b × 2c), (3a × b × c), (a × 3b × c), (a × b × 3c), and (a−b × 3b × c), the three possible Co²⁺/Co³⁺ ordering schemes giving rise to the observed NMR data, the convex hull for Li_xCoPO₄, GITT of LiFePO₄ and LiCoPO₄, the superlattice reflections predicted for Li_2/3CoPO₄, the changes in the a, b, and c lattice parameters during the first charge of LiCoPO₄, a table summarizing the outcome of all DFT calculations performed on the Li_xCoPO₄ (x = 0, 2/3, 1) phases and a spin density map of the lowest energy Li_2/3CoPO₄ configuration obtained in GGA+U. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^§ D.S.M. is currently at Department of Chemistry, University of Warwick, Gibbet Hill, Coventry CV4 7AL, United Kingdom

Author Contributions

^† F.C.S. and R.J.C contributed equally. The manuscript was written through contributions of all authors.

The authors declare no competing financial interest.