Predicting Discharge Mortality after Acute Ischemic Stroke Using Balanced Data

Abstract

Several models have been developed to predict stroke outcomes (e.g., stroke mortality, patient dependence, etc.) in recent decades. However, there is little discussion regarding the problem of between-class imbalance in stroke datasets, which leads to prediction bias and decreased performance. In this paper, we demonstrate the use of the Synthetic Minority Over-sampling Technique to overcome such problems. We also compare state of the art machine learning methods and construct a six-variable support vector machine (SVM) model to predict stroke mortality at discharge. Finally, we discuss how the identification of a reduced feature set allowed us to identify additional cases in our research database for validation testing. Our classifier achieved a c-statistic of 0.865 on the cross-validated dataset, demonstrating good classification performance using a reduced set of variables.

1. Introduction

Stroke is a major cause of mortality and disability in the United States, with over 20% of affected individuals succumbing to the condition, and only one-fourth of surviving adults returning to normal health status [1–3]. There exist a variety of treatments for stroke, including intravenous and intra-arterial tissue plasminogen activator (tPA), as well as clot retrieval using mechanical devices (i.e. mechanical thrombectomy). However, the relationship among a patient's stroke presentation, treatment options, and functional outcomes is not well defined. To inform treatment, work in the literature has focused on building models to predict a patient’s functional status given initial presentation, in hopes of detecting cases that need to be treated more or less aggressively.

To build a predictive model that may be used in practice and which generalizes to multiple institutions, it is important to determine an informative feature set that is collected in the course of normal clinical care. More importantly, the distribution of data and associated class labels is also important. Recently, the problem of imbalanced data has received increased attention as it has been shown to decrease model performance and lead to biased prediction [4–6]. While previous work has been focused on using logistic regression models to predict stroke outcomes [7–10], alternative machine learning techniques are less studied, but potentially useful.

In this work, we present a comparison between six models for predicting stroke mortality at discharge that includes methods for data balancing. We calculated the c-statistic for each classifier, following a systematic approach to identify the optimal set for each classifier by sequentially adding informative features until performance no longer increased.

2. Previous Work

There are many models for predicting acute stroke outcomes, which in general apply multivariate logistic regression techniques. Counsell et.al. [7] developed a six simple variable (SSV) multivariate logistic regression model to predict survival rate 30 days and 6 months after stroke using a 530 patient dataset. The six variables used were age, living alone, independence in activities of daily living before the stroke, the verbal component of Glasgow Coma Scale, arm power, and the ability to walk. The model was validated using two external independent cohorts of stroke patients with c-statistics from 0.84 to 0.88. Teale et. al. [8] reviewed different literature databases (e.g., MEDLINE) and concluded that the SSV model demonstrated statistical robustness, good discriminatory function in external validation, and comprised clinically feasible variables that were easily collected; it performed well among all prognostic models for predicting outcome after acute stroke.

Konig et. al. [9, 10] developed a multivariate logistic regression model to predict three month survival rate after acute ischemic stroke using age and the National Institutes of Health Stroke Scale (Pre-NIHSS) [11]. They showed that Pre-NIHSS is a strong predictor variable that has significant impact on model accuracy. Further analyses [12, 13] have supported the effectiveness of Pre-NIHSS in 30-Day mortality prediction after acute ischemic stroke.

Saposnik et. al. [14–16] considered the utility of a predictive model in a clinical setting and developed an algorithm to predict mortality risk in ischemic stroke patients after hospitalization based on information routinely available in hospital, such as demographics, clinical presentation (diplopia, dysarthria, and aphasia, etc.), and patient comorbidities. The model, called iScore, was developed from multivariate logistic regression models by using a regression coefficient-based scoring method based on β coefficients. The iScore model is now available online [17].

In contrast to more general models, which attempt to predict an outcome based on a patient’s presentation, additional algorithms are under development that attempt to predict response to a specific therapy. Examples include the DRAGON score for intravenous thrombolysis therapy [18], and HIAT2 score for outcomes after intra-arterial thrombolysis [19].

While significant work has been done in predicting outcomes after acute stroke, there is little work regarding the problem of between-class imbalance, which is common in binary prediction tasks when one class (the majority) is more common than the other class (the minority). We address this problem by using a sampling method, called the Synthetic Minority Over-sampling Technique (SMOTE) [20]. We compare the performance of various models (logistic regression, support vector machines, naïve bayes, decision tree, and random forest) for balanced and imbalanced datasets and determine the best model for predicting discharge mortality. We then identify the best six features that appear to be critical for good model performance.

3. Methods

This section describes the stroke dataset used, the imbalanced dataset problem, and the modeling methods compared for mortality prediction.

3.1. Dataset

UCLA maintains a REDCap [21] database that stores acute stroke patients who have been treated with one or more of the following treatments from 1992 to 2013: intra-arterial tissue plasminogen activator (IA tPA), intravenous tissue plasminogen activator (IV tPA), or mechanical thrombectomy. There are 778 patients in this study cohort, each with more than 500 features, including demographic information, laboratory results, and medications. Our goal is to predict patient mortality at hospital discharge, which is indicated by the discharge modified Rankin Scale (discharge mRS) [22, 23]. Discharge mRS is a commonly used scale for measuring the degree of disability or dependence in the daily activities of patients who have suffered stroke. The scale runs from 0–6, with 0 indicating perfect health and 6 indicating death. Our binary prediction model collapses this scale to two groups: alive (0–5) and dead (6).

Using this dataset, we defined a cohort subset for analysis in this study using inclusion criteria (Table 1). The features are summarized in Table 2. The continuous features are patients’ demographics information and time-related information while the binary features are patients’ presentation, and medication. This subset was used to build the model.

Table 1.

Inclusion criteria for cohort subset.

Original dataset	778 patients; >500 features
Patients’ inclusion criteria	• Only patients with discharge mRS recorded. • Only patients with ischemic stroke (excluding patients with subarachnoid hemorrhage). • Only patients who received treatment solely at UCLA. • Only patients who with hospital stays less than 20 days (patients who stay longer are more likely to have other conditions in addition to stroke). • Only patients without missing any features’ values after using features inclusion criteria
Features inclusion criteria	• Only features that were available in over 90% of patient cases after the first four patients’ inclusion criteria.
Cohort subset	190 patients (156 alive, 34 dead); 26 features

Table 2.

Feature distribution of alive and dead patients in dataset before and after SMOTE.

		Alive	Dead (Before SMOTE)	Dead (After SMOTE)
Size		156	34	156
Continuous features		Average(SD)	Average(SD)	Average(SD)
	Age	67.91(17.05)	81.29(9.45)	81.41(8.06)
	Pre-NIHSS	12.16(7.20)	18.24(5.93)	18.16(4.84)
	Systolic blood pressure	151.03(28.20)	147.32(30.96)	145.54(27.54)
	Diastolic blood pressure	82.42(17.71)	79.12(19.12)	77.88(16.30)
	Blood glucose	131.72(48.14)	164.82(74.66)	160.81(61.98)
	Blood platelet count	224.99(75.63)	181.47(54.86)	179.43(50.50)
	Hematocrit	39.60(5.33)	38.66(5.37)	38.38(4.77)
	Time difference between first MRI image and time of symptoms (minute)	178.77(152.89)	166.15(109.27)	171.39(96.26)
	Time difference between first MRI image and admission (minute)	44.67(27.66)	49.35(34.73)	48.89(30.66)
Binary features		Percentage of true(%)	Percentage of true(%)	Percentage of true(%)
	Gender (Male)	44.87	52.94	37.82
	Hypertension	66.67	82.35	84.62
	Diabetes	16.67	20.59	6.41
	Hyperlipidemia	27.56	35.29	17.95
	Atrial fib	30.13	55.88	41.67
	Myocardial infarction	12.18	38.24	25.00
	Coronary artery bypass surgery	7.69	11.76	2.56
	Congestive heart failure	3.21	26.47	8.33
	Peripheral vascular disease	0.00	2.94	0.64
	Carotid endarterectomy angioplasty/stent	1.92	5.88	1.28
	Brain aneurysm	0.00	2.94	0.64
	Active internal bleeding	0.00	0.00	0.00
	Low platelet count	0.00	0.00	0.00
	Abnormal glucose	0.00	0.00	0.00
	Diabetes medication	14.74	32.35	10.90
	Hypertension medication	53.21	82.35	86.54
	Hyperlipidemia medication	16.67	23.53	7.69

3.2. Imbalanced Learning Problem

The cohort subset is imbalanced (156 alive vs. 34 dead). Previous research has shown that imbalanced learning can cause prediction bias, leading to inaccurate and unreliable results [4, 6]. In our case, models would predict all patients as alive to achieve high accuracy, but with low precision and recall. The imbalanced learning problem has received attention in both theoretical and practical application [5]. Most machine learning algorithms do not deal with imbalanced datasets during the training process [4]. In some cases, the minority are scattered in the feature space and the decision boundary is too specific. We addressed this issue by using Synthetic Minority Over-sampling Technique (SMOTE) [20], a sampling technique combining under-sampling of the majority class with oversampling of the minority class.

There are two parts to the SMOTE algorithm. In the first part, the minority class is over-sampled by taking each minority class sample and introducing new synthetic samples joining any or all of the k minority class nearest neighbors (by Euclidean distance). Neighbors from the k nearest neighbors are randomly chosen depending upon the amount of over-sampling required. Synthetic samples are generated in the following way:

1. Find the difference between the normalized feature vector (sample), F_orig, and a randomly selected normalized nearest neighbor, F_near.

2. Multiply the difference by a random number between 0 and 1.

3. Add the product to the feature vector to generate a new feature vector.

This approach essentially creates a random point along the line segment between two specific features and effectively forces the decision region of the minority class to become more general. The new feature vector, F_new, is defined as follows:

$${\mathrm{F}}_{\mathrm{new}}={\mathrm{F}}_{\mathrm{orig}}+\mathrm{rand}(0,1)*({\mathrm{F}}_{\mathrm{near}}-{\mathrm{F}}_{\mathrm{orig}})$$ (1)

The above step is used for continuous features. For binary features, the new value is obtained by the majority vote (0 or 1) of all the neighbors. In our training process, the second part of the SMOTE algorithm, under-sampling, was not performed because the dataset was small and all data should be considered. We applied the SMOTE algorithm using MATLAB, denoting this new dataset as SMOTE-dataset. Five neighbors (k) were used and one of them was randomly selected to generate a synthetic sample. The synthetic step was repeated until the number of minority is equivalent to the number of majority.

3.3. Model comparison and feature selection

Early research has emphasized using logistic regression models [24] to predict stroke outcome [7–10]. To the best of our knowledge, none have compared the performance of different machine learning methods in stroke outcome prediction, particularly with a balanced dataset. Therefore, we compared the performance of five common machine learning methods: Naïve Bayes (NB), Support Vector Machine (SVM), Decision Tree (DT), Random Forests (RF), and Logistic Regression (LR). In addition, we compared the performance of a combined method: principal component analysis followed by support vector machine (PCA+SVM).

Briefly, NB is a probabilistic classifier algorithm based on Bayes’ Rule that makes a conditional independence assumption between the predictor variables, given the outcome [25]. SVM is a supervised learning classification algorithm that constructs a hyperplane (or set of hyperplanes) in a higher dimensional space for classification [26]. DT is a tree-like prediction model in which each internal (non-leaf) node tests an input feature and each leaf is labeled with a class [27]. RF is an ensemble learning method in which a multitude of decision trees are constructed and the classification is based on the mode of the classes output by individual trees [28]. LR is a probabilistic classification model in which label probabilities are found by fitting a logistic function of feature values [29]. Principal component analysis is a statistical procedure that uses orthogonal transformation to reduce the dimensionality of the feature space containing only principal components (principal features) [30]. Yang et. al. [31] and Gumus et. al. [32] have shown the effectiveness of using PCA to extract principal components for SVM classification. We also used this combination of methods and determine whether PCA is beneficial before SVM on stroke patient mortality classification.

It is time-consuming to collect a comprehensive set of features for every patient, and not all the features are relevant. In addition, using all the features to construct a classifier may lead to decreased performance due to over-fitting, especially on small, imbalanced datasets, which are not uncommon in stroke. Thus, we sought a minimum feature set to mitigate these clinical and modeling challenges, and that could also be externally validated more easily.

Different machine learning methods may not perform equally on the same feature set. Therefore, optimal feature sets for each machine learning method were defined systematically, with the top performing method determined using the c-statistic. First, chi-square tests were used to weight the association between features (categorical variables/binned continuous variables) and discharge mRS in the original dataset. Then, the feature with the highest weight was used to construct a single-variable classifier and the c-statistic was calculated. The feature with the second highest weight was then added, and c-statistic was re-calculated. This process of adding features was repeated until an optimal feature set for a machine learning method was obtained. The optimal feature set (the first optimum) was defined as the point at which adding any additional features did not increase the performance of the classifier. All methods were compared and the best one was chosen for stroke patient mortality at discharge. A summary of steps is shown in Figure 1. Models were fitted and compared using RapidMiner (RM) [33], an open-source software platform which provides an integrated environment for machine learning, data mining, and predictive analytics [34, 35].

Figure 1.

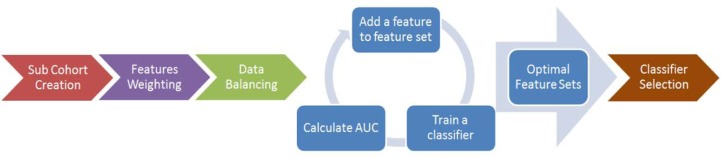
Summary of building classifier for predicting stroke patient mortality at discharge. A sub-cohort based on clinical and missing data factors was first created. Then, the relevance between features and the classes were weighted by chi-square statistics, and then the dataset is balanced by SMOTE. The fourth step was an iterative process in which the highest weighted feature was first used to build classifiers and AUC was calculated. Features were added to the training feature set sequentially in the order of weighting and classifiers were trained. After several iterations, optimal feature sets for all classifiers were obtained. Finally, performances were compared (SVM, PCA&SVM, DT, RF, NB, and LR) and the best classifier was selected.

4. Result and Discussion

4.1. SMOTE over-sampling

There were 190 patients in the training cohort with 156 class-1 patients (alive) and 34 class-2 patients (dead). The final SMOTE-dataset had 156 class-1 patients and 156 class-2 patients. Age and Pre-NIHSS have been shown to be two important features for stroke outcome prediction [9, 10, 12, 13]. Figure 2A shows the data distribution (x-axis: Pre-NIHSS; y-axis: age) between two the classes before SMOTE sampling and Figure 2B showed the distribution after SMOTE sampling. The original class-2 distribution was scattered, and it was hard to determine where the decision boundary should be. After oversampling by SMOTE, it was easy to observe that class-2 patients clustered in the region of high age and high Pre-NIHSS.

Figure 2.

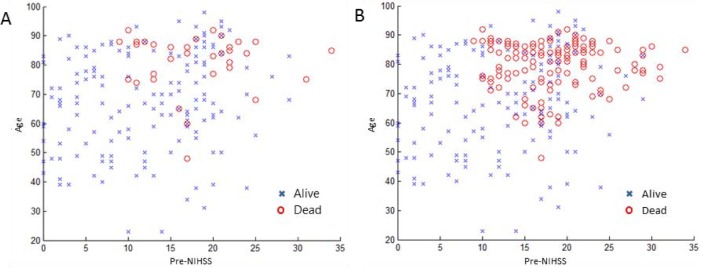
Two classes distribution before and after SMOTE sampling. (A) Before SMOTE, (B) After SMOTE. Two datasets for classifications: (A) original dataset with 156 class-1 patients and 34 class-2 patients), (B) SMOTE-dataset with 156 class-1 patients and 156 class-2 patients.

4.2. Feature Selection

Chi-square tests were used to weight the relevance between a feature and the classes in the original dataset. As our goal was to obtain a ranking of features (rather than finding statically significant features), we calculated the chi-squared statistics (weight) and normalized them for comparison. Continuous variables were discretized into ten bins. The top ten normalized weights are shown in Table 3.

Table 3.

Top ten normalized weights by chi-squared statistic.

Feature	Weight
Pre-NIHSS	1.000
Age	0.631
Patient history of congestive heart failure	0.565
Platelet count	0.450
Patient history of myocardial Infarction	0.346
Serum glucose	0.325
Patient on hypertension medication	0.249
Time difference between the first MRI image and admission	0.243
Systolic blood pressure	0.223
Patient history of atrial fibrillation	0.209

4.3. Model Comparison

Ten-fold cross-validation was used to compare different models on the datasets, measuring the model performance via c-statistic and model bias via F1-score [36]. In each validation, nine groups of original data were used to train the classifier and one group of data was classified. For the SMOTE-dataset, nine folds of data were balanced using SMOTE and then used to train the classifier. The held-out unbalanced dataset was then classified.

Features were added sequentially to train a classifier in order of largest weight to smallest weight. The c-statistic of each classifier is shown in Figure 3, with its distribution shown in Figure 4. The enlarged markers represent the size of the optimal feature set for each classifier. With only one feature (Pre-NIHSS), all classifiers performed poorly. The performance gradually increased as more features were added. Each classifier reached to the first maximum c-statistic at a different number of features, with performance for each leveling off with additional features. This validated our hypothesis that more features might not necessarily improve the performance. The size of each optimal feature set is summarized in Table 4.

Figure 3.

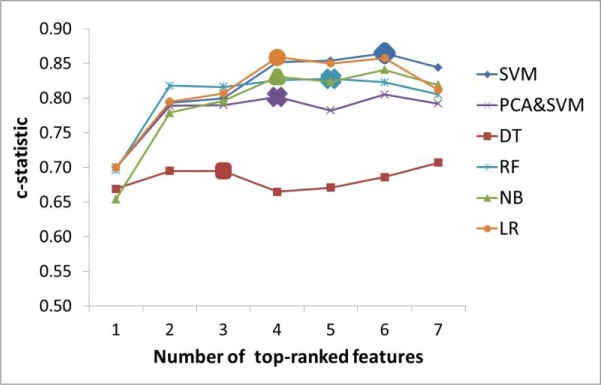
The c-statistics of classifiers with different number of top-ranked features based on Table 3. The size of the optimal feature set for each classifier was indicated by the enlarged marker. Each classifier has different size of optimal feature set. Among all classifiers, SVM has the highest c-statistic with 6 features being used.

Figure 4.

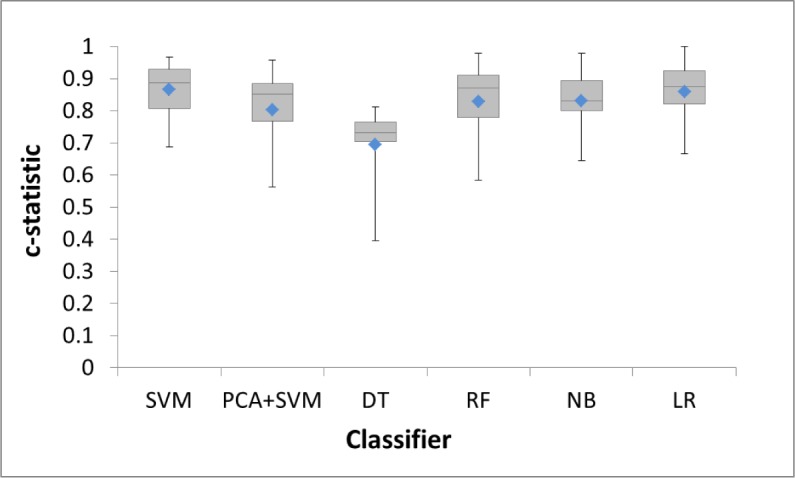
c-statistic distributions for classifiers with optimal feature set (means are represented by blue diamonds).

Table 4.

The size of the optimal feature set for each classifier and the cross-validation result.

		SMOTE-dataset		Original dataset
Classifier	Optimal feature set size	c-statistic	F1-score	c-statistic	F1-score
SVM	6	0.865	0.594	0.868	0.336
PCA&SVM	4	0.802	0.488	0.856	0.368
DT	2	0.695	0.441	0.709	0.061
RF	5	0.828	0.401	0.789	0.249
NB	4	0.831	0.560	0.839	0.354
LR	4	0.859	0.582	0.867	0.226

Among all the classifiers for the SMOTE generated dataset, SVM performed the best with a c-statistic of 0.865 and an F1-score of 0.594. PCA+SVM did not perform well, which could be due to a scenario where two classes overlapped more after projection [37]. RF and NB both generally performed more poorly than SVM in all feature sizes. DT had the worst performance with the first optimal c-statistic at 0.695. This is mostly because more features were required to build a good classifier based on the nature of DT. LR had the closest performance to SVM. However, previous research has shown that SVM performs better than LR in the case of multivariate and mixture of distributions with a better (or equivalent) misclassification rate [38, 39]. Therefore, SVM was determined to be the most suitable classifier.

The size of the optimal feature set for SVM was six: Pre-NIHSS, age, platelet count, serum glucose, congestive heart failure, and myocardial infarction. These features are routinely collected in acute stroke patients. Pre-NIHSS is a standard measure of impairment caused by a stroke, with most patients receiving Pre-NIHSS assessment immediately after hospital admission. Pre-NIHSS, age, platelet count, and serum glucose level have also been shown to be relevant to stroke outcomes [9, 40, 41]. Therefore, it is reasonable to expect other institutions may maintain these variables and could validate our model. Moreover, the c-statistic was nearly optimal (0.854) with only four features (Pre-NIHSS, age, congestive heart failure, and platelet count), suggesting the possibility of using even less information.

After identifying the top six features for the SVM model, we revisited the database and obtained an additional 39 patients that were not included in the initial filtering due to missing data, but had all six important features. These data were then used as an independent testing dataset to test the classifier. We compared the performance of six-variable SVM classifier trained with balanced and imbalanced testing dataset, and both c-statistic and F1-score were higher when the training dataset was balanced (Table 5). We also performed Mann-Whitney U tests to verify that both SVM1 and SVM2 are statistically better than random (p=0.020 and p=0.011, respectively), and used a weighted Wilcoxon signed-rank test to verify that the performance difference between SVM1 and SVM2 is statistically significant (p=0.039). These results suggest that balancing data (i.e., SMOTE) yields an improved classifier for predicting mortality at discharge in acute stroke patients.

Table 5.

Performance comparison of six-variable SVMs.

	SVM 1	SVM 2
Number of testing data	32 alive, 7 dead
Number of features	6
Applied SMOTE?	No	Yes
Number of training data	156 alive, 34 dead	156 alive,156 dead
c-statistic	0.750	0.781
F1-score	0.400	0.500

5. Conclusion and Future work

In this paper, we compared the performance of SVM, PCA-SVM, DT, RF, NB, and LR models for predicting stroke patient mortality at discharge and determined SVM was the best based on relative c-statistic and F1-score. We then developed an SVM predictive model with six common variables (Pre-NIHSS, age, platelet count, serum glucose level, congestive heart failure, and myocardial infarction) and predicted mortality on the testing data, achieving a 0.781 c-statistic. In addition, we demonstrated the importance of balancing the stroke dataset before training and illustrated the use of the SMOTE algorithm as a solution. We also discussed the benefits of identifying an optimal feature set for building the classifier.

There are a few limitations in our work. First, there are roughly 800 patients available in our dataset, but nearly half of them were missing discharge mRS or other feature values, reducing the size of available data. Our next step will be collecting this information via chart review. Also, we plan to seek independent external datasets on which to validate the proposed models. Second, the distributions of binary features became more imbalanced after SMOTE (Table 2). A possible solution to this problem would be to assign values to binary features by sampling the probability distribution of nearest neighbors, rather than a majority vote.

Lastly, mortality is a standard measure that most existing stroke models aim to predict. However, patients have different degrees of disability even though they are still alive. One clear difference is whether a patient can live independently or dependently [42]. We plan to investigate and improve existing methods in multi-class prediction [43–45] and extend our prediction ability to more classes (independent, dependent, and death), rather than just survival/non-survival.