A Novel Method to Assess Incompleteness of Mammography Reports

Abstract

Mammography has been shown to improve outcomes of women with breast cancer, but it is subject to inter-reader variability. One well-documented source of such variability is in the content of mammography reports. The mammography report is of crucial importance, since it documents the radiologist’s imaging observations, interpretation of those observations in terms of likelihood of malignancy, and suggested patient management. In this paper, we define an incompleteness score to measure how incomplete the information content is in the mammography report and provide an algorithm to calculate this metric. We then show that the incompleteness score can be used to predict errors in interpretation. This method has 82.6% accuracy at predicting errors in interpretation and can possibly reduce total diagnostic errors by up to 21.7%. Such a method can easily be modified to suit other domains that depend on quality reporting.

Introduction

Breast cancer affects 1 in 8 women in the United States. It is the second leading cause of cancer deaths amongst women. Mammography has shown to be beneficial for early detection of breast cancer¹. Currently, the American Cancer Society recommends that women over 40 with no specific risk for breast cancer get yearly screening mammograms to detect malignant findings early². However, a major issue with mammography for breast cancer detection and management is the inconsistency and variability in practice, particularly in terms of variations in sensitivity and specificity of diagnosing malignancy^1,3–7. Such variability is not limited to diagnosis. It has been shown that variability extends to report findings^2,8–10. Variability in diagnosis and reporting hamper the utility of mammography: false negatives result in delayed treatment at the expense of patient health while false positives cause excessive additional invasive testing (e.g., biopsy), rising healthcare costs, and long-term psychosocial harm for women ^11,12.

Decision-support systems have been developed to improve upon mammography interpretation and diagnosis^13–16, however most of these systems follow the Greek Oracle model of decision-support: they simply give an answer to the diagnostic task rather then assisting the radiologist to improve their own decision^17,18. Additionally, such systems interrupt the traditional radiological workflow¹⁹. We posit that improving the radiologist’s report during reporting time mitigates both of these issues and is the ideal time to deliver effective decision-support.

The mammography report is of crucial importance since it documents the radiologist’s imaging observations, interpretation of those observations in terms of likelihood of malignancy, and suggested patient management, such as follow-up imaging or biopsy. Studies have shown the importance of good reporting practices and identified several key traits of good reports: correctness of findings, completeness of the description of significant clinical findings, consistency of report language and findings, and timeliness of the report’s completion^20–22. There are numerous efforts to improve the mammography report with respect to these traits. The Breast Imaging-Reporting and Data System (BI-RADS) provides a standard lexicon of descriptors and interpretation guidelines to improve consistency in language and correctness of findings³. Furthermore, structured reporting systems have been designed to improve clarity of presentation and reduce variability of reports between readers²³. Despite these benefits, structured reporting is generally more time-intensive and can impair the traditional radiological workflow, directly interfering with timeliness²⁰. Moreover, current approaches aim mainly to improve upon reporting language and clarity rather than report content and decision-making.

In this study, we propose a system that evaluates the content of the report and links it to errors in diagnosis. We do this by quantifying and measuring the incompleteness of the report findings with respect to abnormalities seen in images. We define incompleteness to be the sensitivity of the radiologist’s decision to new information. Should gathering more data about a mammographic abnormality potentially change the radiologist’s decision about clinical management, a report is considered incomplete, and the radiologist can be alerted to provide more information to disambiguate report elements found to be inconsistent.

Mammography Diagnosis Problem

Radiologists presented with mammograms are tasked with two problems: detection and interpretation. Detection is the task of visually inspecting the mammogram and identifying abnormalities. Interpretation is evaluating whether detected abnormalities are suspicious for breast cancer. We will focus on the interpretation problem in this paper.

Formally, the interpretation problem is defined as follows: A radiologist is presented with a lesion in a mammogram, patient history and demographics, and possibly prior mammograms. The radiologist must decide whether this lesion warrants no action or follow-up (either imaging or biopsy) based on their suspicion of malignancy. This suspicion of malignancy is quantified as the BI-RADS assessment category, which is an ordinal value ranging from 1 to 6. An additional assessment category of 0 is used to indicate there is not enough information in the mammogram to make a decision. These assessment categories were designed to have probabilistic interpretations, where each value has a range of posterior probabilities of malignancy as shown in Table 1. A BI-RADS assessment of 1, 2, or 3 indicates the recommendation is no immediate follow-up (a negative assessment). A BI-RADS assessment of 4 or 5 indicates a recommendation for follow-up imaging or biopsy should be considered (a positive assessment). An assessment of 0 should not count as either positive or negative, but the fact that it necessitates immediate follow-up imaging means that it is treated as a positive finding ²⁴. BI-RADS 6 is a non-diagnositc category used to indicate that the images reflect a known cancer diagnosis being evaluated for treatment planning. These assessment categories implicitly mean that any lesion with a posterior probability of greater than 2% should be considered as a positive finding. Recent work has shown that this 2% threshold rule is justified via epidemiological risk analysis²⁵. In addition to providing an assessment, radiologists must provide a report that justifies their decision. This report has a set of categorical descriptors standardized by BI-RADS, which can be interpreted as evidence for their decision.

Table 1:

The BI-RADS assessment categories and their probabilistic interpretations.

BI-RADS Assessment	Probability of Malignancy	Description
0	N/A	Additional Imaging Needed
1	0%	No Abnormality
2	0%	Benign Finding
3	< 2%	Probably Benign Finding
4	2-95%	Suspicious Abnormality
5	> 95%	Highly Suggestive of Malignancy
6	100%	Biopsy Proven

Though BI-RADS assessments have objective probabilistic underpinnings, mammography interpretation is inherently subjective. Modern practice traditionally does not include quantitative estimates of these probabilities. Rather, radiologists provide the assessment categories based on training and experience. The use of BI-RADS assessment categories allows us to evaluate radiological performance as if radiologists are binary classifiers. We can measure their true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN) as well as all associated statistics (e.g. positive predictive value, sensitivity, specificity). Moreover, the use of categorical descriptors allows us to build joint models of their decision given evidence.

Measuring Incompleteness

Missing descriptors in mammography reports do not necessarily mean that the report does not have all the information to make a correct and justified diagnosis. Conversely, there are cases when most of the descriptors are reported, but the report still reaches an ambiguous diagnosis. Incompleteness of reports needs to be sensitive to the context of the information already given as well as the effect of missing information on the diagnosis.

Given that the final result of a mammogram is a decision whether to follow-up on patients with mammographic lesions, this decision should be the primary driver of determining whether enough information has been provided in the report. Early approaches to measuring whether medical diagnostic tests were necessary involved calculating thresholds for posterior probabilities that would warrant more testing or treatment ²⁶. Such methods required that the practicing physician provide the posterior probability. The Pathfinder system used a value of information calculation to repeatedly request more information for diagnosis until there was only one possible diagnosis left ²⁷. This did not provide a flexible framework for stopping if there was more than one possible diagnosis outside of physician judgment. The STOP criteria provide a quantitative algorithm for when to stop requesting information and make a decision, but this is formulated only to measure whether the probability of an event exceeds a certain threshold ²⁸.

In response to these shortcomings for decision support systems, the same-decision probability (SDP) has been proposed ²⁹. This is defined to be the probability that a diagnostician will make the same decision they are currently considering given the unobserved information in a system. This metric has a nice intuitive meaning; only collect more information if it will change a decision. The SDP is defined for systems that make binary decisions based upon a posterior probability of an event being above a threshold. Formally, given a system with a decision function D, observed variables O, unobserved variables U, and a decision threshold T the SDP is defined as:

$$\mathit{SDP}={\displaystyle \sum _{u\in U}\mathbb{I}[D(\mathrm{O};T)=D(\mathrm{u},\mathrm{O};T)]\mathit{Pr}(\text{u|O})}$$

Where I[•] is an indicator function that outputs 1 if true and 0 if false.

In the context of mammography, D(•) = diagnosis, O= report data, U = Unobserved descriptors, and T = BI-RADS 2% threshold.

Though this is a well-defined metric, it is intractable to compute ³⁰. The summation requires iterating over all possible combinations of missing data which is an exponentially large search space. Despite this challenge, there are algorithms to approximate it based on statistical bounds on its value ²⁹. The drawback here is that such bounds can be weak under a variety of non-trivial cases. There is also an exact algorithm that can take advantage of certain Bayesian network structures to compute it in tractable time ³⁰, but this method may break down for extreme value thresholds and Bayesian networks that do not have highly independent sets of unobserved nodes.

Here we propose a new method to compute an approximation of the SDP based on monte-carlo simulations. The difference between our approximation method and previous ones²⁹ is that they compute and exact value for an approximate bound on the SDP whereas we compute an approximation to the exact value of the SDP. This follows the advice of John Tukey, “It is far better an approximate answer to the right question, which is often vague, than the exact anwer to the wrong questions, which can always be made precise.” ³¹ Moreover, our approximation can be made arbitrarily accurate given more monte-carlo sampling steps.

For sake of convenience, we compute the complement of the SDP which is simply 1-SDP. This is the probability that our decision will change given new information. We will refer to this value as the incompleteness score. In this context, a lower value of the incompleteness score means the report is more complete.

Algorithm 1.

Compute incompleteness score in Bayesian network

Where join_tree_sample is the standard algorithm for sampling from a Bayesian network that has been compiled into a join-tree.

Experimental Methods

Study Design

Data used for this project were de-identified prior to analysis, and our work was thus not considered human subjects research. We acquired mammography report data from two teaching hospitals. Both of these institutions captured mammography findings using a structured reporting system (Mammography Information System, versions 3.4.99–4.1.22; PenRad, Buffalo, MN). Five attending radiologists read the mammograms at Institution 1. They reviewed 52,943 findings, of which 421 were malignant. These data were collected between April 5, 1999 and February 9, 2004. Eight attending radiologists read the mammograms at Institution 2. They reviewed 59,490 findings, of which 793 were malignant. These data were collected between October 3, 2005 and July 30, 2010. These datasets only contain 1 radiologist in common (though no interpreting radiologists were identifiable due to anonymization), the remainder of the radiologists in the two practices were distinct.

Analysis was done at the “finding” level, where a finding is defined as a set of observations about an abnormality in a mammogram, or the record for a mammogram with no abnormalities. Each finding can include patient demographic risk factors, BI-RADS descriptors characterizing an abnormality, BI-RADS assessment category, and pathologic findings from biopsy. Pathological ground truth was determined via matching patients with state cancer registries. By comparing the radiologist assessment to the pathological ground truth, we assessed whether a finding was a false positive (FP), false negative (FN), true positive (TP), or true negative (TN).

The structured reporting system separates masses, calcifications, and general findings. There is ambiguity in assessing when these three types of findings are associated with each other. In general, model builders can ignore the possible correlations since they do not seem to hamper performance of computer-aided diagnostic systems 14,15,32. Unfortunately, we cannot make such relaxations of the model since we require that all descriptors provide meaningful information. As an example, descriptors specific to calcifications would spuriously affect incompleteness scores on mass findings. We chose to focus on analyzing mass findings to mitigate this issue. The resulting data set had 24,645 mass findings, 672 of which were malignant.

Masses were randomly split into two sets, 85% training and 15% testing. Training and testing groups were stratified by malignancy and care was taken to ensure patients with multiple masses were not represented in both groups. The training set was used to learn a tree-augmented naïve bayes (TAN) model for mammography diagnosis as described by Burnside^32,33. The incompleteness score was calculated for all masses in the test set using 5,000 monte-carlo samples with a decision threshold of 2% in concordance with BI-RADS recommendations. All model learning and classification was done in Norsys Netica 5.14.

Statistical Analysis

We stratified resultant incompleteness scores by radiological predictive categories (FP, FN, TP, and TN) to assess how the incompleteness scores differentiated between correct and incorrect evaluations. We quantified this difference by comparing the scores for errors (FP, FN) to the scores for correctly diagnosed findings (TP, TN) with a one-tailed Mann-Whitney U Test (aka Wilcoxon rank-sum test) ³⁴. The test was performed using the wilcox.test function in R version 3.0.2 (2013-09-25) – “Frisbee Sailing.”

Results

We trained a Tree-Augmented Naïve Bayes network on 20,950 training cases and measured the incompleteness score on 3,695 test cases. The resulting incompleteness scores were heavily right-skewed distributions. 83% of the incompleteness scores were equal to zero, meaning no new information would have changed the follow-up decision. Hence, both the median and mode incompleteness scores were zero. The mean incompleteness score was 0.021, but this is not a good indicator of group tendency since the large tail distribution has a disproportionate effect on the mean.

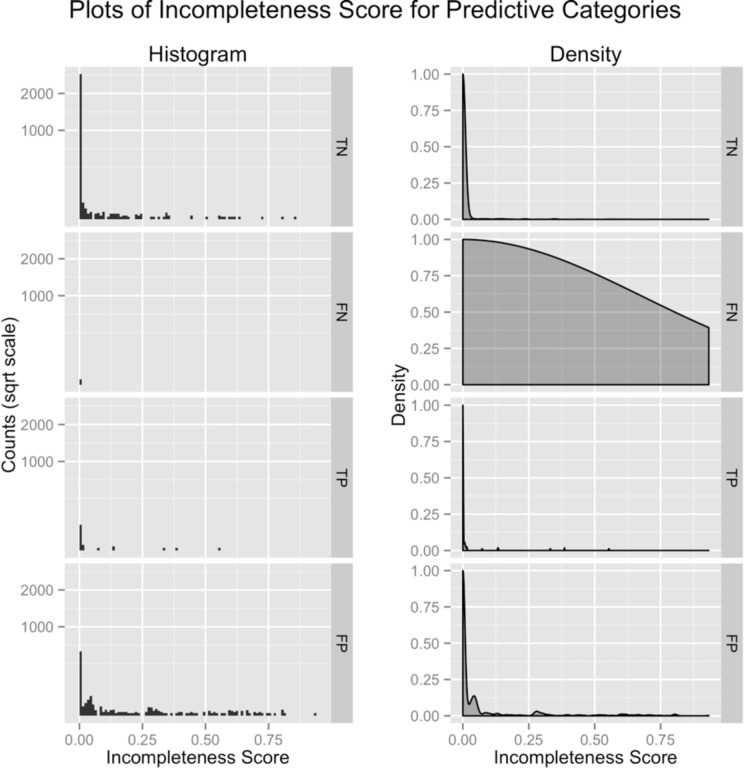
In order to verify that the incompleteness score can be used to predict mammographic error, we plotted its histogram and density estimate stratified by radiological predictive categories: true negative (TN), false negative (FN), true positive (TP), and false positive (FP) [Figure 1]. The graphs show that there are a large number of false positive and false negative cases that have non-zero incompleteness scores. Intuitively, this shows that incomplete reports have a higher likelihood of containing errors. The difference between error (FP,FN) and non-error (TP,TN) incompleteness scores was statistically significant (p < 2.2*10⁻¹⁶).

Figure 1:

Plots of the histogram and density of incompleteness scores, stratified by radiologist performance on their respective cases. True Negative (TN) findings have the lowest incompleteness scores (indicating they are most complete) while false positive (FP) findings have higher incompleteness scores (indicating less completely reported findings). Joining (TN,TP) and (FP,FN), we can compare cases that were correctly assessed to cases with errors. Note that the false negative density graph has a nearly uniform distribution. This is an artifact due to the small amount of false negatives in the data set that skew density estimation.

An issue with this data is that there are a small number of false negative findings compared to false positive findings. This could skew results since positive findings may contain descriptors more prone to noise in the model. To account for this, we compared false positive to true positive results since both groups would have similar descriptors. The analysis showed that they were still statistically significantly different (p<0.0026).

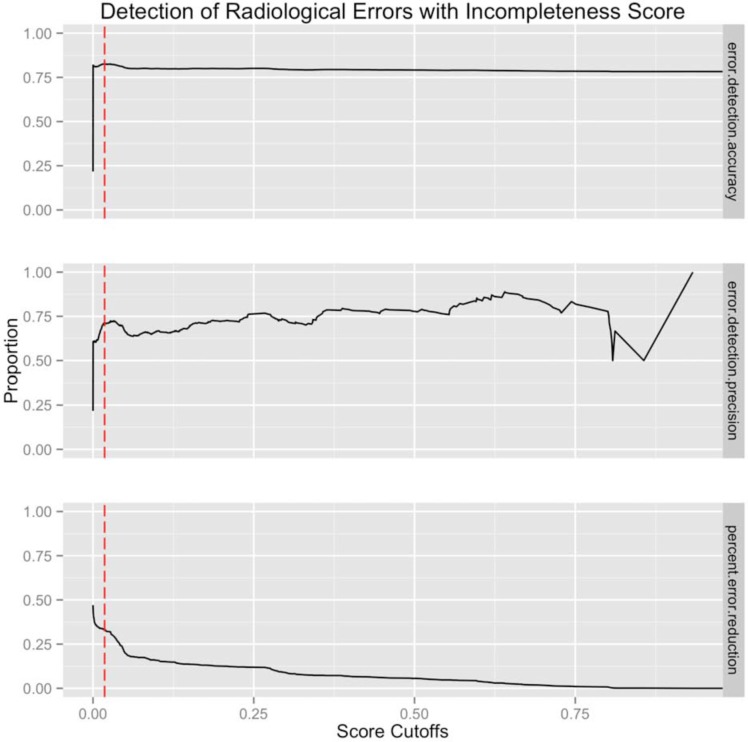
We then tested how well the incompleteness score could predict error in mammography reading. Figure 2 shows several performance metrics for different cutoffs of the incompleteness score. The maximal accuracy with respect to cutoffs was 0.826 at a cutoff of 0.018. This means that > 1.8% probability of changing decisions when given new information should warrant describing more observations. The precision associated with this cutoff was 0.713 meaning 71.3% of cases classified as errors via the incompleteness score with cutoff 0.018 will actually be errors. Finally, we measured the percentage reduction in total mammography error if each error marked for revision was corrected. Using the given cutoff, we saw a potential 21.7% decrease in total errors.

Figure 2:

Improvement in radiological performance for difference incompleteness cutoffs. First row shows the incompleteness score accuracy in predicting radiological errors. Second row shows incompleteness score positive predictive value in predicting error. Third row shows the percent reduction in error if identifying error at the specified cutoff. The red-dotted line shows the cutoff point that maximizes error classification accuracy (first panel).

Discussion

We described a method to quantify how incomplete the content is in a mammographic report. We then presented an algorithm to measure this value in a computationally tractable manner. Finally, we showed that this incompleteness score is a strong indicator of errors in mammography interpretation. Implementation of this metric during mammography reporting time could provide a useful real-time feedback to radiologists to indicate possible errors.

Reporting in mammography is a labor intensive but critically important task for results communication. Though there is pressure for radiologists to expend their efforts efficiently, we show that poor report quality (measured by our incompleteness score) is a marker for interpretation errors. This result might stem from a few different causes. The causal explanation is that poor interpretation leads to poor reports. In this case, a radiologist might have not seen a relevant descriptor in the image or neglected to highlight its importance. Another possibility is that incomplete reporting is a function of available time. When required to read large volumes of images, speed may decrease accuracy. In this case, a practitioner producing brief or incomplete reports may also be spending less time interpreting the image. A third possibility is that the process of reporting improves diagnosis by requiring radiologists to reason about their diagnosis. Thus, individuals who do not spend as much time on their reports do not go through the same formal thinking process. For future work, we will consult breast imaging radiologists on cases that were correctly classified as erroneous to see if humans can also identify when poor reporting leads to misdiagnosis. If this is the case, we can begin to discover reporting practices that reduce error rates.

Though the system we present shows promising results with regards to predicting radiological errors, it does have some shortcomings. The use of an approximate algorithm to estimate the incompleteness score allows for some degree of error. We correct for this by using a large number of samples with respect to the number of hidden variables, but unfortunately, it is difficult to empirically evaluate our system as calculating the exact incompleteness score is prohibitively expensive with regards to computational time. For future work, we will evaluate alternative approaches for measuring incompleteness. Another issue with our system is that it does not actually correct the errors in interpretation or give any constructive feedback. So although the system can potentially reduce the amount of errors by ~20%, we have not shown which of these reports would actually be corrected. We plan to incorporate this into a clinical setting to measure the true impact of this decision-support system. Finally, this study was designed to be descriptive rather than predictive, so we did not measure classification results with an optimal cutoff in a third held-out test set. Thus, the results will be overly-optimistic in terms of error-prediction. In the future, we plan to implement our algorithm on faster cluster computers, which will allow us to perform a thorough cross-validation analysis to obtain better accuracy measurements.

Though we developed this system for mammography reporting, this methodology could be extend to any domain that uses expensive information to make threshold-based decisions. All this system requires is a generative model linking descriptors to diagnosis and a method to sample from this model. It is straightforward to implement this in any medical domain where testing can be a costly and/or risky task. Not only can this method improve diagnostic accuracy, but it inherently rewards good, thorough reporting practices. This is beneficial for patients and researchers alike.