Exploring Joint Disease Risk Prediction

Abstract

Disease risk prediction has been a central topic of medical informatics. Although various risk prediction models have been studied in the literature, the vast majority were designed to be single-task, i.e. they only consider one target disease at a time. This becomes a limitation when in practice we are dealing with two or more diseases that are related to each other in terms of sharing common comorbidities, symptoms, risk factors, etc., because single-task prediction models are not equipped to identify these associations across different tasks. In this paper we address this limitation by exploring the application of multi-task learning framework to joint disease risk prediction. Specifically, we characterize the disease relatedness by assuming that the risk predictors underlying these diseases have overlap. We develop an optimization-based formulation that can simultaneously predict the risk for all diseases and learn the shared predictors. Our model is applied to a real Electronic Health Record (EHR) database with 7,839 patients, among which 1,127 developed Congestive Heart Failure (CHF) and 477 developed Chronic Obstructive Pulmonary Disease (COPD). We demonstrate that a properly designed multi-task learning algorithm is viable for joint disease risk prediction and it can discover clinical insights that single-task models would overlook.

1. Introduction

Disease risk prediction [1] has been extensively studied in the literature. The latest trends include building risk prediction models based on a large amount of features from Electronic Health Record (EHR) databases and adopting state-of-the-art machine learning algorithms, such as Generalized Linear Regression, Support Vector Machine, Bayesian Networks, etc. [2, 3, 4]. What many existing risk prediction models have in common is that they are designed to be single-task, i.e. they only predict the risk of a single disease at a time. With a given target disease, a single-task risk model would select features that are most informative for this particular target, and then train the model using the training data set.

However, in practice we often have training data for multiple different yet related target diseases at the same time, e.g. hypertension and heart diseases, diabetes and cataract, depression and obesity, etc. In these application scenarios, single-task risk models have two significant limitations. First, by treating different target diseases separately, they fail to identify the underlying correlation between these diseases such as their common causes, similar symptoms, comorbid conditions, and distinguishing factors. These information are sometimes more important to clinical practitioners than risk prediction itself because they lead to insights on the underlying mechanisms of diseases. Second, applying a single-task model limits us to the training data that have been labeled for that particular disease, even though the training data from other related diseases can also be helpful. For instance, a single-task model will not be able to augment a small training data set labeled for heart failure with another large training data set labeled for hypertension, even though it is common knowledge that hypertension is closely related to heart failure and share many important risk predicators.

In the machine learning literature multi-task learning has been extensively studied [5, 6, 7]. However, existing multitask learning techniques cannot be directly applied to the problem of EHR-based risk prediction because the validity of each algorithm relies on the specific assumption it makes about task relatedness and these assumptions often fail to hold for many clinical applications. For example, some models assume different tasks are close to each other as if they are derived from the same underlying distribution [7, 8], or alternatively, assume the tasks have group structure and are similar within each group [9, 10, 11]. Other models formalize task relatedness by assuming all tasks share a latent feature space [6, 5, 12]. Our proposed framework falls into this category.

In this paper we explore the viability of designing a multi-task framework for EHR-based risk prediction. In order to do this, we first need to define the relatedness between multiple diseases. In particular, we make the assumption that if two (or more) diseases are related then they must share some common risk predictors and these risk predictors can be characterized by groups of the clinical evidence from the EHR database.

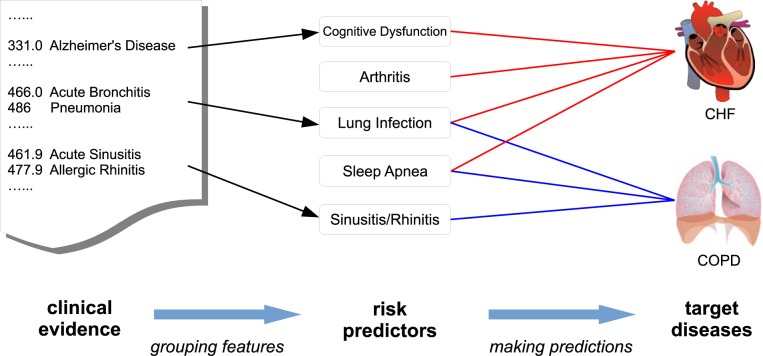
To intuitively understand what our assumption implies in practice, consider a group of individuals who are at risk of two diseases: Congestive Heart Failure (CHF) and Chronic Obstructive Pulmonary Disease (COPD). Traditional risk models attribute the risks directly to the raw medical features from the EHR database, such as individual diagnosis codes, lab results, vitals, etc., which are often noisy and sparse [13]. Under our framework, we attribute the risks to some higher-level latent risk predictors, which are modeled as groups of the raw medical features. As show in Figure 1, our two target diseases, CHF and COPD, share some common risk predictors such as sleep apnea, hypertension, respiratory system infection [14, 15, 16, 17]. Therefore, studying them jointly will help us more accurately pinpoint these underlying predictors and consequently facilitate the risk prediction. In addition, these two diseases also have their own risk predictors, such as Rhinitis for COPD and Arthritis for CHF. It will be beneficial to identify such predictors because they can help us better distinguish these two diseases with very similar symptoms and comorbidities [18].

Figure 1:

An intuitive example to demonstrate the problem setting for multi-task risk prediction. The lines between target diseases and risk predictors indicate strong connection. The arrows show the mapping from the raw clinical evidence (diagnosis code in this case) to the high-level risk predictors. We want to learn both the lines and the arrows.

Given our mild assumption, which will hold for a wide range of diseases and EHR data, our goal becomes how to jointly identify these common predictors across different diseases. To do so, we develop an optimization based formulation that simultaneously learns the feature groups and predicts the risk for all diseases based on the identified predictors. We show how to solve our objective function efficiently using an alternating minimization algorithm. To validate our proposed framework, we apply it to a real EHR database with 7,839 patients, among which 1,127 developed Congestive Heart Failure and 477 developed Chronic Obstructive Pulmonary Disease. By using diagnosis codes as underlying features, we demonstrate that our model is able to identify a meaningful set of shared risk predictors for CHF and COPD and good prediction accuracy ensues.

2. Study Design

We chose two tasks for joint prediction: CHF onset and COPD onset. CHF and COPD are well known to have significant overlap in terms of common comorbidities, risk factors, and symptoms [14, 15, 16]. In fact they are so similar that in practice they are often misdiagnosed for each other [18]. Thus it is highly desirable if we could risk stratify them jointly and identify not only the common predictors that they share but also the unique predictors that distinguish them.

Our study is on a real-world EHR data warehouse including the records of 319,650 patients over 4 years. We identified 1,127 CHF case patients with 3,850 control match, and 477 COPD case patients with 2,385 control match. We extracted the same features for both cohorts, namely ICD-9 diagnosis codes.

2.1. CHF Cohort Construction

We defined CHF diagnosis using the following criteria (which are similar to the criteria used in [3]): (1) ICD-9 diagnosis of heart failure appeared in the EHR for two outpatient encounters, indicating consistency in clinical assessment; (2) at least one medication were prescribed with an associated ICD-9 diagnosis of heart failure. The diagnosis date was defined as the first appearance in the EHR of the heart failure diagnosis. These criteria have also been previously validated as part of Geisinger Clinical involvement in a Centers for Medicare & Medicaid Services (CMS) pay-for-performance pilot [19]. With this criteria, we extracted from the database 1,127 CHF case patients. Following the case-control match strategy in [3], a primary care patient was eligible as a control patient if they are not in the case list, and had the same PCP as the case patient. Approximately 10 eligible clinic-, sex-, and age-matched (in five-year age intervals) controls were selected for each heart failure case. In situations where 10 matches were not available, all available matches were selected. Following this strategy, we got CHF 3,850 control patients, so on average each case patient was matched with approximately 3 controls.

2.2. COPD Cohort Construction

We defined COPD diagnosis also using two criteria: (1) the occurrence of at least one COPD-related ICD-9 diagnosis code; (2) the prescription of at least one COPD-related medication. The diagnosis date was defined as the date when both criteria were met. In the end we identified 477 COPD case patients. We matched these case patients by identifying control patients were similar in age, sex, and PCP. An eligible control patient should also have a valid ICD-9 outpatient diagnosis which is not (a) a symptom code (b) a screening diagnosis, or (c) a COPD-related diagnosis. In the end we identified 2,385 control patients, which gave us a 1:5 case-control match.

2.3. Feature Extraction

For all patients we extracted their ICD-9 codes from the EHR database. We only considered the medical records that occurred from 540 days prior to the diagnosis date till 180 days prior to the diagnosis date. In other words, we used about a year worth of data to make prediction at least half a year before the disease onset. Patients who had insufficient amount of records were not included. For control patients, we set the last day of their available records as the diagnosis date and followed the same rule. In total there were 4,784 unique ICD-9 codes from all patients. After removing infrequent features, i.e. ICD-9 codes that occurred to fewer than 100 different patients (case and control combined), we had 267 distinct features left. In total 80,472 medical records were considered, which indicates our input data was extremely sparse. After features were extracted, we discarded the temporal order within the observation window and used binary encoding to record wether or not a certain feature was assigned to a certain patient during that time.

3. Model Derivation

Objective

Suppose we have T target diseases (tasks), D features from the EHR database, and N_t patients for the t-th task. For each task we have an observation matrix $X_t\in {ℝ}^{D\times N_t}$. The (j, i)-th entry of X_t denotes the occurrence of feature j to patient i. ${\mathrm{x}}_{t_i}$ is the i-th column of X_t. ${\mathrm{y}}_t\in {\{-1,1\}}^{N_t}$ is the response vector for task t: ${\mathrm{y}}_{t_i}=1$ means patient i is diagnosed disease t, -1 otherwise. $U_t\in {\{0,1\}}^{D\times K}$ is a mapping from the D medical features to K groups. The rows of U sum up to one, which means each feature belongs to one group. ${\mathrm{w}}_t\in {ℝ}^K$ is the regression coefficients over the K feature groups for the t-th disease. A positive entry in w_t means that feature group contributes positively to the risk of disease t and vice versa. Figure 2 is an illustration of our framework.

Figure 2:

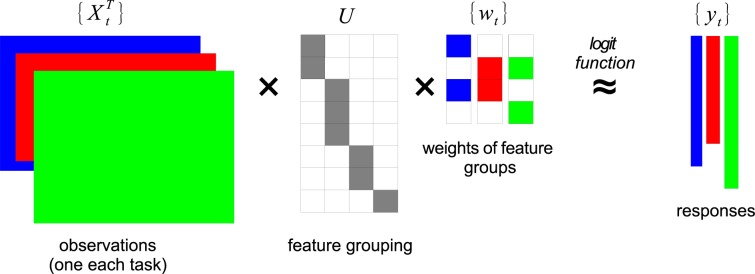
An illustration of our multi-task learning framework. The clinical features from the EHR database are assigned into feature groups, as defined by the assignment matrix U that is shared across all diseases. {X_t, yt} are input and we want to learn U and {w_t}. In this illustration, D = 8, K = 4, T = 3.

Our objective is to learn the feature grouping U and the regression coefficients {w_t} simultaneously and jointly over T diseases. Formally it can be written as:

$$\underset{\{{\mathrm{w}}_t\in {ℝ}^K\},U\in {\{0,1\}}^{D\times K}}{\arg \min }{\displaystyle \sum _{t=1}^T\left(\frac{1}{N_t}{{\displaystyle \sum _{i=1}^{N_t}\log (1+\mathrm{e}{-}^{{\mathrm{y}}_{t_i}{\mathrm{x}}_{t_i}^{T}U{\mathrm{w}}_t})+\lambda \Vert {\mathrm{w}}_t\Vert }}_1\right)}\mathrm{s}.\mathrm{t}.{\displaystyle \sum _{k=1}^K{U}_{dk}=1,\forall d=1,\dots ,D}$$ (1)

where $\Vert ·\Vert$ is element-wise ℓ1 norm ${\Vert A\Vert }_1={\displaystyle {\sum }_{i,j}\left|A_{ij}\right|},\lambda >0$ is a user-specified parameter.

Interpretation

The first term inside the summation of Eq.(1) is the empirical loss. Here we choose the logistic loss, one that is mostly commonly used for clinical risk models. The second term is a regularizer that enforces sparsity on the regression coefficients w_t. Intuitively this term wants each disease to be explained by a smaller number of groups (thus a simpler explanation). Additional regularizers can be added according to the practical needs. The constraint term in Eq.(1) says the rows of U should sum up to 1, which implies the K feature groups are a disjoint partition of the D medical features. This is to make the feature groups semantically distinct.

Eq.(1) is intractable due to the combinatorial nature of U. To overcome this, we relax the constraint on U by allowing the entries in U to take real values. After the relaxation, our objective becomes:

$$\underset{\{{\mathrm{w}}_t\in {ℝ}^K\},U\in {\{0,1\}}^{D\times K}}{\arg \min }{\displaystyle \sum _{t=1}^T\left(\frac{1}{N_t}{{\displaystyle \sum _{i=1}^{N_t}\log (1+\mathrm{e}{-}^{{\mathrm{y}}_{t_i}{\mathrm{x}}_{t_i}^{T}U{\mathrm{w}}_t})+\lambda \Vert {\mathrm{w}}_t\Vert }}_1\right)}\mathrm{s}.\mathrm{t}.U^{T}U=I_K$$ (2)

Note that the orthogonality constraint now replaces the original constraint in Eq.(1) to enforce distinction among different groups. Eq.(2) now allows an efficient solution.

Optimization

To solve the objective function in Eq.(2), we alternate between U and {w_t} by fixing one and updating the other to minimize Eq.(2) until a local optimum is reached. When U is fixed, Eq.(2)

$$\underset{\{{\mathrm{w}}_t\in {ℝ}^K\}}{\arg \min }{\displaystyle \sum _{t=1}^T\left(\frac{1}{N_t}{{\displaystyle \sum _{i=1}^{N_t}\log (1+\mathrm{e}{-}^{{\mathrm{y}}_{t_i}{\tilde{x}}_{t_i}^T{\mathrm{w}}_t})+\lambda \Vert {\mathrm{w}}_t\Vert }}_1\right)}$$ (3)

where ${\tilde{x}}_{t_i}^T=x_{t_i}^{T}U$. This is a set of T standard ℓ1-regularized logistic regression problems [20] and can be solved independently using a variety of ready-to-use solvers.

When {w_t} is fixed, Eq.(2) becomes

$$\underset{\{{\mathrm{w}}_t\in {ℝ}^K\}}{\arg \min }{\displaystyle \sum }_{t=1}^T\frac{1}{N_t}{\displaystyle \sum }_{i=1}^{N_t}\log (1+\mathrm{e}{-}^{{\mathrm{y}}_{t_i}{\tilde{x}}_{t_i}^T{\mathrm{w}}_t}),\mathrm{s}.\mathrm{t}.U^{T}U=I_K$$ (4)

We solve this subproblem by using the Augmented Lagrange Multipliers method, which minimizes the following Lagrangian of Eq.(4):

$$F(U,\Lambda )={\displaystyle \sum _{t=1}^T\frac{1}{N_t}}{\displaystyle \sum _{i=1}^T\log (1+{\mathrm{e}}^{-}{}^{{\mathrm{y}}_{t_i}{\mathrm{x}}_{t_i}^{T}U{\mathrm{w}}_t})}+\mathrm{tr}(\Lambda (U^{T}U-I_K))+\frac{\rho }{2}{\Vert U^{T}U-I_K\Vert }_F^2$$ (5)

where Λ ∈ ℝ^K×K is the Lagrange multipliers and ρ > 0 is a given constant.

4. Results

4.1. Identified Feature Groups

The key difference between our multi-task model and the single-task models is that our model uses feature groups instead of individual raw features as predictors. Therefore we first examine the feature groups identified from the real patient cohort for their clinical validity. An important parameter of our model is K, the number of the feature groups we want to project the raw features into. Generally speaking, K should increase with the number of tasks T to ensure enough descriptive power. Here since we only have two tasks, we set K = 3 for the clarity of presentation. Also for the sake of clarity, we pre-grouped ICD-9 codes into ICD-9 group codes, i.e. the first 3 digits. For each feature group we display in Table 1 the top ICD-9 group codes according to their weights, U_ki. A larger weight indicates this ICD-9 group code is associated more strongly with the feature group. For each feature group we also display its regression coefficients w_t for both tasks, from which we can tell how much this feature group as a predictor contributes to the risk of respective diseases.

Table 1:

Feature groups identified by our model with top-5 features with highest weights (K = 3).

Weights	ICD-9	Description
Feature Group 1: Predictors shared by CHF and COPD (wCHF = 2.176, wCOPD = 1.390)
0.329	715	Osteoarthrosis and Allied Disorders
0.257	729	Disorders of Soft Tissues
0.246	724	Disorders of Back
0.229	V72	Special Investigations and Examinations
0.227	719	Cardiac Dysrhythmias
Feature Group 2: Predictors mainly associated with CHF (wCHF = 1.739, wCOPD = 0.767)
0.248	427	Cardiac Dysrhythmias
0.224	250	Diabetes Mellitus
0.196	414	Chronic Ischemic Heart Disease
0.120	429	Ill-Defined Descriptions of Heart Disease
0.109	411	Acute Ischemic Heart Disease
Feature Group 3: Predictors mainly associated with COPD (wCHF = 0.082, wCOPD = 5.084)
0.318	493	Asthma
0.171	592	Kidney Stones
0.162	388	Disorders of Ear
0.148	461	Acute Sinusitis
0.144	305	Tobacco Use Disorder

The first group in Table 1 consists of ICD-9 codes that are associated with both CHF and COPD. We can see that they are mainly musculoskeletal disorders. These are common problems that can be caused either by CHF or COPD. The second group consists of diagnosis that are mainly associated with CHF, such as heart arrhythmia, diabetes, ischemic heart diseases, and so on. These are all known risk factors for CHF. As a contrast, the third feature group shows diagnosis that are mainly associated with COPD, where we can find tobacco use, a leading risk factor for COPD, as well as asthma, a major comorbid condition for COPD.

Table 1 suggests that our model is indeed able to identify significant risk predictors across different tasks and group them based on whether they are shared by different tasks or only belongs to a specific task. However, we observe that there are still overlapping between the feature groups (e.g. 427 Cardiac Dysrhythmias in Group 1 and 2). This calls for more detailed investigation by physicians because the same ICD-9 (group) code can have different implications in different medical contexts. Therefore there is no simple “ground truth” on whether a specific feature should be associated with a specific target disease.

Note that after our relaxation from exclusive grouping to orthogonality constraint, every feature will appear not only in one feature group but in all feature groups with different weights (and the weights can be either positive or negative). Therefore, for each feature we need to consider the sum of its weights across all groups before we can interpret its overall contribution to the risk of task t.

4.2. Prediction Accuracy

Next we evaluate the performance of our approach in terms of prediction accuracy. The measurement we used was Area Under Receiver Operating Characteristic Curve (AUC) [21], which is a commonly used evaluation metric for risk prediction models. An AUC score of 1 means the prediction perfectly matches the ground truth whereas 0.5 means the prediction is no better than a random guess. We used 10-fold cross validation and report the median, the 25th, and the 75th percentiles as boxplot in Figure 3. For each fold we sampled 60% of the entire dataset for training and used the rest for validation.

Figure 3:

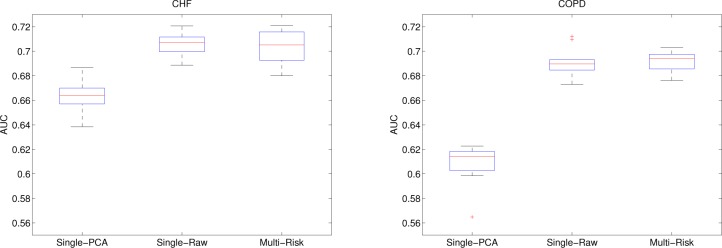
Accuracy of our model (Multi-Risk) for both tasks with comparison to two baseline methods. Showing the median, 25th, and 75th percentiles over 10-fold cross validation.

We compare our approach (Multi-Risk) to two baseline methods. The first one is denoted Single-PCA. Instead of learning U jointly from all diseases, Single-PCA used a fixed U derived from the top-K principal components of all observed. Single-PCA represents the result we get in the single-task setting where the feature groupings are learned without supervision. The second baseline is denoted Single-Raw, which means U is set to be an identity matrix I_D. This is an extreme case of our framework where K = D and all the raw features are used directly for logistic regression (without grouping). For all methods we used the same parameter settings for logistic regression. For Single-PCA and our model (Multi-Risk) we set K = 3.

From Figure 3 we observe that our model significantly outperformed Single-PCA after joint feature grouping. This is expected because the groupings are learned with supervision to maximize the discriminative power. On the other hand, the AUCs of our model and Single-Raw were comparable (no significant difference). However, we would like to point out that Single-Raw is designed to achieve the highest prediction accuracy possible without considering the potential association between different diseases, whereas our model can capture common predictors across different diseases without sacrificing prediction accuracy.

5. Discussion

This work is a first step towards multi-task clinical risk prediction. Our main purpose is to demonstrate that a properly designed multi-task learning objective can indeed capture the latent relatedness between different target diseases. It provides a principled way of identifying the common predictors and the discriminative predictors, both of which are clinically interesting. We also show that the identified feature groups can achieve the state-of-the-art prediction accuracy.

In our experiment, the two tasks shared a same training set. Namely, we have only one patient cohort and each patient was labeled for both tasks. This setting does not fully demonstrate the advantage of a multi-task risk model, which can combine disjoint patient cohorts from different tasks. For example, the CHF task can have one patient cohort labeled only for CHF from one database and the COPD task can have a different patient cohort (with different patients) labeled only for COPD. The only requirement is that these two cohorts must share the same feature space. Such augmentation of the training data can potential further improve the risk prediction accuracy of our multi-task model and gives it advantage over the state-of-the-art single-task models. We leave this to future investigation.

Our multi-task learning framework can be extended in many aspects. For instance, it will be very interesting to jointly study multiple tasks from different problem domains. In our experiments, we used two similar tasks (disease onset prediction) that share the same feature set (ICD-9 codes). However, our framework can be extended to incorporate tasks from different domains, e.g. disease onset vs. hospitalization vs. need for social assistance, by grouping heterogeneous features together (diagnosis codes, medications, social behaviors, and so on). This will be a big step forward because we will be able introduce predictors from different domains for more comprehensive risk analysis.

A second direction to extend our model is to incorporate prior knowledge from domain experts. Currently our model only groups features based on how they contribute to the respective outcomes. It is not aware the clinical meaning of each feature, therefore the groups are not coherent in terms of clinical interpretation. This can be overcome if we incorporate prior knowledge into the model, which specifies the semantics of each group. For instance, domain experts can assign a few ICD-9 codes related to cardiovascular diseases to a certain group and let our model automatically identify the remaining ICD-9 codes that should also belong to the same group. Such integration can be achieved by carefully initializing U and/or introducing an additional term to regularize key entries in U.

In order to make our objective function tractable, we used the orthogonality constraint as a surrogate for exclusive group partition. The side effect of this relaxation was that U will have negative weights, which are not clinically interpretable. To overcome this, we can replace the orthogonality constraint with non-negativity constraint, i.e. U ≥ 0. This change calls for a different optimization algorithm but produces more interpretable results.

6. Conclusion

In this work we explore a multi-task framework for joint disease risk prediction. Our framework exploits the assumption that related diseases share some common risk predictors that can be represented by groups of clinical evidence. We use the proposed model to simultaneously predict the onset risk of a CHF cohort and a COPD cohort. Preliminary results suggest that our model can identify both common and discriminative risk predictors for both diseases while pertaining good prediction accuracy. We discussed the potential of using our model to integrate patient cohorts from multiple sources and problem domains. We also discussed future improvements that can be made to enhance the interpretability of our model.