Divisive Hierarchical Clustering towards Identifying Clinically Significant Pre-Diabetes Subpopulations

Abstract

Type 2 Diabetes Mellitus is a progressive disease with increased risk of developing serious complications. Identifying subpopulations and their relevant risk factors can contribute to the prevention and effective management of diabetes. We use a novel divisive hierarchical clustering technique to identify clinically interesting subpopulations in a large cohort of Olmsted County, MN residents. Our results show that our clustering algorithm successfully identified clinically interesting clusters consisting of patients with higher or lower risk of diabetes than the general population. The proposed algorithm offers fine control over the granularity of the clustering, has the ability to seamlessly discover and incorporate interactions among the risk factors, and can handle non-proportional hazards, as well. It has the potential to significantly impact clinical practice by recognizing patients with specific risk factors who may benefit from an alternative management approach potentially leading to the prevention of diabetes and its complications.

Introduction

Type 2 Diabetes Mellitus is one of the fastest growing chronic diseases in the United States, with a profound influence on public health quality and cost^1,2. It is a progressive disease, associated with an increased risk of developing serious cardiac, vascular, renal and ophthalmological complications, and it is one of leading causes of death². With no cure per se, prevention and management are of paramount importance. As effective preventive measures such as lifestyle change and drug therapy exist^3,4, early identification and management of patients at high risk is an important healthcare need.

Numerous diabetes risk indices aimed at early identification of patients at high risk have been developed⁵. Arguably, the most popular such index is the Framingham score⁶, which has gained wide acceptance in clinical practice. The Framingham model assigns a risk to a patient based on the risk factors the patient presents with and the resulting score can be used to stratify patients into low, moderate, or high-risk groups. Almost all indices, the Framingham score included, estimate the risk of diabetes in an additive fashion, assuming that the risk factors act independently.

Interactions among risk factors are known to exist^7–11. Recent work^7–10 aimed to address interactions, most prominently through the application of association rule mining (ARM)^12–15. ARM was specifically designed to discover sets of associated risk factors, along with the affected subpopulations. While association does not always translate into (non-additive) interaction, it often does. Given its ability to seamlessly incorporate interactions, ARM has successfully identified patient subpopulations that face significantly increased or decreased risk of diabetes^7,11. Another beneficial characteristic of the ARM model lies in the straightforward interpretability of the individual rules. Thus the ARM model does not just provide a risk estimate, but it also offers a “justification” in the form of the associated risk factors in the rule.

ARM has its own shortcomings. While interpretability is one of the hallmarks of the ARM modeling approach, ARM algorithms tend to extract combinatorially large sets of redundant rules, which quickly erodes interpretability. Under these conditions, it is necessary to offer fine control of the amount of details the ARM model extracts; however, this is precisely where ARM falls flat. When ARM discovers a manageable number of rules, they tend to be too general to be useful; when the model is sufficiently detailed to give the user new insights, the sheer number of rules impedes interpretation. There is a reason for this phenomenon. The ARM rule set is highly redundant: the same subpopulation is described by an exponential number of rules, each rule associating the subpopulation in question with a different set of risk factors. This unfortunate property obfuscates the disease mechanism.

In this work, we propose the use of a novel divisive hierarchical clustering¹⁶ technique, which retains most of the advantages of ARM, while it alleviates the interpretability issues. From a hierarchical clustering, depending on the desired amount of detail, many clusterings can be extracted. Each clustering consists of a varying number of clusters, is complete (they include all patients) and non-overlapping (each patient belongs to exactly one cluster).

Our proposed approach retains all advantageous properties of ARM and alleviates its primary shortcoming: interpretability is enhanced through the elimination of redundancy and through lending the user fine control over the amount of details the clustering should incorporate.

Methods

Data

In this study we utilized a large cohort of Olmsted County, Minnesota, residents identified by using Rochester Epidemiology Project resources. The Rochester Epidemiology Project (REP)¹⁷ is a unique research infrastructure that follows residents of Olmsted Co., MN over time. The baseline of our study was set at Jan. 1, 2005. We included all adult Mayo Clinic patients with research consent, who are part of the REP, resulting in a study cohort of 69,747 patients. From this cohort, we excluded all patients with a diagnosis of diabetes before the baseline (478 patients), missing fasting plasma glucose measurements (14,559 patients), patients whose lipid health could not be determined (1,023 patients) and patients with unknown hypertension status (498 patients). Our final study cohort consists of 52,139 patients (overlaps between the groups exist) who were followed until the summer of 2013.

We collected demographic information (age, gender, body mass index BMI), laboratory information (primarily fasting plasma glucose and lipid panel), vital signs (blood pressure and pulse), relevant diagnosis diagnoses (obesity, hyperlipidemia, hypertension, renal failure and various cardiac and vascular conditions), aspirin use, and medications used to treat hypertension and hypercholesterolemia. Additional known risk factors for diabetes (such as tobacco usage) were also included.

Features

To enhance the interpretability of our results, the variables were transformed into binary variables to indicate the presence and severity of risk factors. These variables are typically constructed as a meaningful combination of diagnoses, abnormal vital signs, abnormal laboratory results, and use of medications by drug class. Laboratory results were considered abnormal when they exceeded the cutoffs published in the American Diabetes Association (ADA)18 guidelines. Table 1 shows the definitions of the variables used henceforth.

Table 1.

Predictors and their definitions

Predictors	Definitions
Demographics
age.18+	Age > 18 and < 45
age.45+	Age ≥ 45 and < 65
age.65+	Age ≥ 65
genderM	Male
Comorbidities
obese	Obesity (BMI ≥ 30 or diagnosis)
tobacco	Current smoker
renal	Renal disease
chf	Congestive Heart Failure
ihd	Ischemic Heart Disease
Major risk factors and their severities
ifg.no	Normo – glycemic patients: fasting plasma glucose (FPG) ≤ 100
ifg.pre1	Impaired Fasting Glucose level 1: FPG > 100 and ≤ 110
ifg.pre2	Impaired Fasting Glucose level 2: FPG > 110 and ≤ 125
htn.no	No indication of Hypertension: no diagnosis of HTN, no hypertensive drugs are described and blood pressure results (if present) are normal.
htn.any	Indication of Hypertension exists in the form of either a HTN diagnosis or abnormal blood pressure measurement
htn.tx	Hypertension required therapeutic intervention; however, at most 3 HTN drugs were prescribed.
htn.pers	Persistent Hypertension. Patien ts present with abnormal blood pressure measurements despite having been prescribed 3 or more drugs; or they are prescribed 4 or more drugs (regardless of blood pressure results).
hyperlip.no	No indication of Hyperlipidemia: no diagnosis of hyperlipidemia drugs and no abnormal lipid panel results are present. no cholesterol
hyperlip.any	Indication of Hyperlipidemia exists in the form of diagnosis or abnormal laboratory results.
hyperlip.tx	Hyperlipidemia with therapeutic intervention: a diagnosis code or abnormal laboratory result indicates hyperlipidemia and a single cholesterol drug is prescribed.
hyperlip.multi	Hyperlipidemia requiring multi prescribed. – are drug intervention: multiple cholesterol drugs

Patient Clustering

The purpose of clustering is to partition patients into groups (clusters), such that patients within the same cluster are more similar to each other than to patients in a different cluster. Formally, in our application, a cluster is a set of patients, who share risk factors relevant to diabetes progression and have similar diabetes risk. A clustering is a non-overlapping complete set of clusters. A clustering is complete in the sense that all patients in the population are assigned to a cluster, and it is non-overlapping, as each patient is assigned to a single cluster in a clustering. Our goal is to create a patient clustering, where the clusters correspond to clinically meaningful patient subpopulations.

To identify such subpopulations, we applied bisecting divisive hierarchical clustering. The algorithm iteratively constructs a hierarchy of clusters in a top-down (divisive) fashion, in each iteration bisecting a cluster into two new (child) clusters. A cluster is bisected using a splitting variable. One of the two child clusters contains all patients from the parent cluster for whom the splitting variable is true, and the other child contains all patients for whom the splitting variable evaluates to false. For example, if the parent cluster (cluster to split) consists of patients with hypertension (htn is true) and the splitting variable is ifg.pre2 (fasting plasma glucose FPG > 110), one of the child clusters is comprised of hypertensive patients having high FPG (ifg.pre2=true) and the other cluster is comprised of hypertensive patients with lower FPG (ifg.pre2 is false).

The algorithm proceeds by recursively bisecting each cluster into two child clusters starting with a cluster that represents the entire population. The algorithm terminates when no cluster can be bisected without having insufficient number of patients in the resultant child clusters; or when the patients in the cluster are sufficiently similar to each other.

The splitting variable is selected on the basis of how much variability in the diabetes outcome it can explain; bisections that explain a large amount of variability are preferred. Let t_j denote the follow-up time (in days) and the diabetes status at the end of follow-up for patient j. This patient is censored when the diabetes outcome is negative (δ_j = false) at the end of follow-up. The martingale residual M_j(t) for a patient j at time t_j is computed as the difference between the observed number δ_j(t) of event (1 if a patient j had developed diabetes before (or exactly at) time t_j, 0 if censored) and the estimated number H_j(t) of events (cumulative hazard)

$$M_j(t)={\delta }_j(t)-H_j(t).$$

To calculate the cumulative hazard, we use the Nelson-Aalen estimator,

$$H_j(t)={\sum }_{t_i\le t}{h}_j(t_i)={\sum }_{t_i\le t}{\sum }_k\frac{d{N}_k(t_i)}{Y_k(t_i)},$$

where the h_j(t_i) denotes (non-cumulative) hazard of patient j at time t_i, k iterates over all patients, dN_k(t_i) denotes the number of diabetes incidents that patient k suffers exactly at time t_i (0 or 1) and Y_k (t_i) indicates whether patient k is at risk at time t_i. The formula for the non-cumulative hazard can be thought of as the number of events occurring exactly at time t_i divided by the number of patient at risk at that time. When multiple patients suffer events at exactly the same time, these events are arbitrarily serialized.

Suppose we have a cluster C₁, which we need to bisect into clusters C₁₁ and C₁₂ using a particular splitting variable. Further, let SSR(C) denote the sum of squared martingale residuals for any cluster C. Bisecting C₁ will decrease the total SSR by

$$\mathrm{G}=\text{SSR}(C_1)–[\text{SSR}(C_{11})+\text{SSR}(C_{12})].$$

Each splitting variable produces a different G value. Among the possible splitting variables, we select the one that reduces the SSR the most, or equivalently, maximizes G. This is the splitting variable that explains the diabetes outcome in C₁ the best, thus it can be thought of as ‘most relevant’ to diabetes in the subpopulation corresponding to cluster C₁.

Once the cluster hierarchy has been constructed, the final clustering can be extracted. A leaf cluster is a cluster that is not bisected. Our hierarchical clustering algorithm ensures that each patient falls into exactly one leaf cluster, thus the collection of leaf clusters form a non-overlapping complete clustering of the patient population.

We wish to make two notes. First, our clustering algorithm is similar to the survival tree construction algorithm¹⁹; in fact, one can think about it as an adaptation of the recursive partitioning algorithm²⁰ for censored outcomes to a clustering application. Indeed, we follow Therneau et al.²¹ in broad strokes and adapt their ANOVA criterion for censored outcome: we use sum squared martingale residuals instead of sum squared error. Second, the analogy between recursive partitioning and our algorithm goes deeper. The martingale residual can be rescaled into a deviance residual. Just as the sum squared error relates to the “deviance” of two nested Gaussian models, the sum squared deviance residuals relate to the deviance of two nested survival models, enabling the use of likelihood ratio tests for significance testing. Since our purpose is to construct the full hierarchy of clusters, we do not perform significance testing and use the martingale residuals instead of the deviance residuals.

Clustering and statistical analysis were conducted with the use of R version 3.0.1.

Results

In what follows, we demonstrate that our clustering algorithm successfully identified potentially interesting clusters that consist of patients with substantially higher or lower risk of diabetes than the general patient population. The clustering (the collection of leaf clusters) assigns each patient to exactly one leaf cluster and each leaf cluster possesses a cumulative hazard curve (specific to the subpopulation that the leaf consists of). Thus the clustering can be used to estimate a patient’s risk of diabetes and can hence serve as a diabetes index. We will also demonstrate that our clustering used in this fashion outperforms the popular Framingham score. Thirdly, we will also show by constructing the entire hierarchy of clusters, that we can extract clusterings that encompass varying amounts of detail. Finally, we will demonstrate that our clustering can model non-proportional hazards as well as interactions among the risk factors.

Identifying high and low risk subpopulations

We performed hierarchical clustering of our patient population under the user-defined constraint that clusters with less than 50 patients are not bisected further. We identified 275 leaf clusters. From these leaves, we selected two: one indicative of very high risk and one indicative of very low risk. We then compared these leaves with the general population.

In Figure 1, we display the Kaplan-Meier survival curve and the cumulative hazard curve for the entire population (blue dotted line) and for the above two clusters: red solid line is used for the high-risk cluster and green dotdash line for the low-risk one. The patients (n = 61) in the high-risk cluster have fasting plasma glucose greater than 110 mg/dL (ifg.pre2), hyperlipidemia that requires therapeutic interventions (hyperlip.tx), and are current smokers (tobacco). The low-risk cluster consists of the patients (n = 498) characterized by fasting plasma glucose level equal to or lower than 100 mg/dL, no indication of hypertension, no indication of hyperlipidemia, no obesity, no renal disease, no congestive heart failure, no ischemic heart disease, no aspirin use, male non-smokers being between 45 and 65 years of age.

Figure 1.

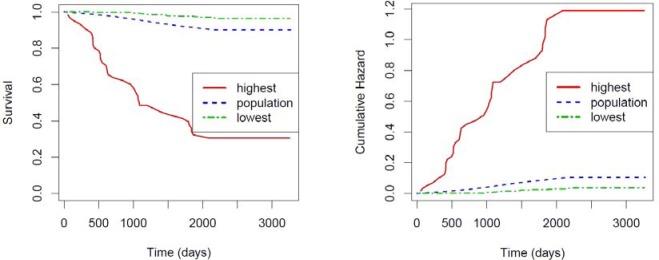
Kaplan-Meier survival curve (Left) and Cumulative incidence of diabetes (Right) for two pre-diabetic subpopulations (red sold and green dotdash) and the entire population (blue dotted)

From Figure 1, the difference in diabetes progression among these three subpopulations is obvious and the risk factors for these patients are consistent with our clinical expectation.

Clustering as a diabetes index

As we described earlier, the leaf clusters form a non-overlapping clustering, where each patient belongs to exactly one leaf cluster. Since each leaf cluster contains a survival function of the corresponding subpopulation, it is possible to use the clustering as a diabetes index, providing a risk estimate for each patient. In this section, we compare the clustering as a diabetes index against the popular Framingham score, an actual diabetes index in clinical use. Specifically, we use concordance as our evaluation measure. Concordance is the probability that for any two patients where one progressed to diabetes earlier than the other, the one that progressed earlier has a higher predicted risk. The clustering achieved a concordance of 0.78, while the Framingham score achieved a lower concordance of 0.70, signifying the clustering has imporved discriminatory power.

Controlling the amount of detail

An important advantage of the proposed clustering technique over alternative methods, such as association rules, is that it offers fine control over the amount of detail it presents to the user. This control can be achieved by cutting the hierarchy at a particular level. To illustrate this point, we depict the entire cluster hierarchy in Figure 2. The leaf clusters are listed along the horizontal axis and the vertical axis indicates the SSR of the cluster. The hierarchy is represented by a dendrogram, which can be interpreted as follows. The root of the dendrogram is at the top (SSR=4645) and it represents a cluster that includes all patients. The root is split into two clusters (on ifg.pre2; not shown) one with SSR 730 (ifg.pre2=true) and one with SSR 3914 (ifg.pre2=false). The subpopulation having ifg.pre2=true is split on htn.pers into two clusters, one with SSR 41 (persistent hypertension present) and one with SSR 688 (htn.pers=false). In short, the dendrogram allows us to trace the bisections our algorithm performed and it also depicts the SSR of the resultant clusters.

Figure 2.

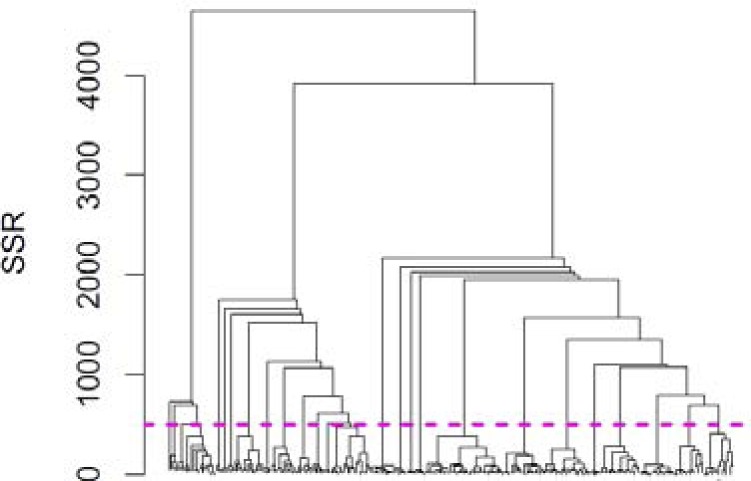
Dendrogram of the entire hierarchy of clusterings

We can cut the dendrogram at any SSR of our choice. Cutting the hierarchy produces a new set of leaf clusters, which in turn forms a non-overlapping complete clustering of the patient population. For example, if we cut the dendrogram at SSR of 4000 (which is very close to the top), we obtain only two leaf clusters: ifg.pre2=true with SSR of 730 and ifg.pre2=false with SSR of 3914. If we cut the dendrogram at a lower SSR, say at 500, we will obtain a larger set of leaf clusters (26 in this example) each having lower SSR. This particular cut is shown in Figure 2 as a magenta line. Larger number of leaf clusters offers a larger amount of detail. Selecting an SSR for cutting the dendrogram is what allows us to control the amount of detail (number of leaf clusters) in a predictable fashion. The SSR of the resulting leafs also shows the within-cluster similarity of the patients.

Naturally, a tradeoff exists between the amount of detail and the predictive capability of a clustering. In Figure 3, we visualize this tradeoff. The horizontal axis represents the SSR at which the dendrogram was cut and the vertical axis represents the resultant clustering with the number of clusters depicted in left pane and the predictive capability (as measured by concordance) in the right pane. The figure shows that as we increase the SSR (move right on the horizontal axis), we decrease the amount of detail (number of clusters) and along with the decreased amount of detail, the predictive capability of the clustering decreases, as well.

Figure 3.

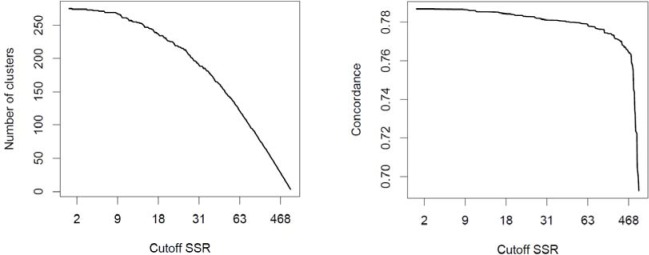
Tradeoff between the amount of detail (number of clusters) and the predictive capability (concordance)

Non-proportional hazard

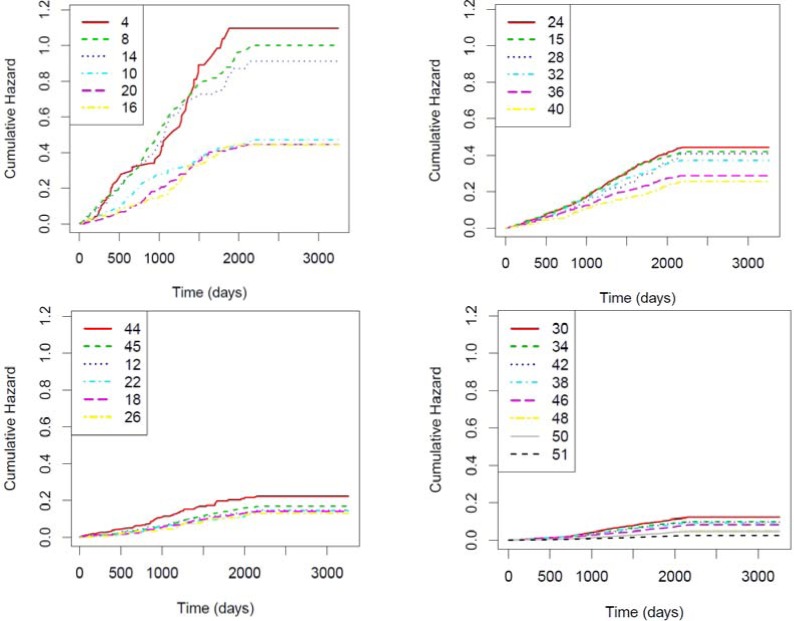
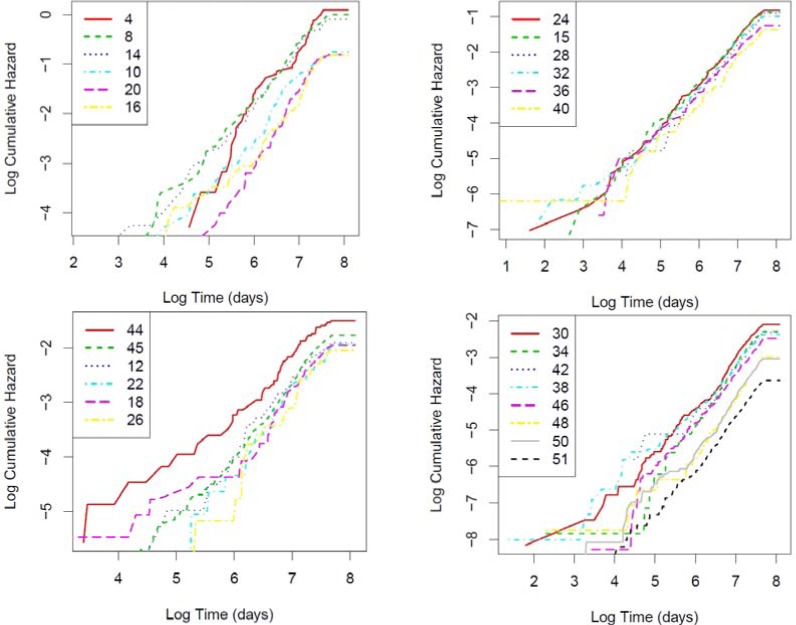
We plot the cumulative hazard functions for the 26 clusters we extracted earlier (by cutting the hierarchy at SSR 500) in Figure 4. To avoid overcrowding the image and preserve good visibility of the lines, we separated the 26 clusters into four panes essentially at random. The IDs in the legend refer to their original IDs (IDs before cutting), thus they can exceed 26. Cumulative hazards across the clusters are not proportional because the LOGLOGS plots of the 26 clusters (shown in Figure 5) do not appear as parallel lines, indicating interactions between time and subpopulations. This non-proportionality was correctly captured by our approach. To show these clusters are clinically relevant, we selected the 12 highest risk clusters out of the 26 and described in Table 2.

Figure 4.

Identified pre-diabetic subpopulations based on cumulative hazard after infinite follow up time

Figure 5.

LOGLOGS plot of cummulative hazard

Table 2.

Subpopulation summarization in terms of cumulative hazard at the end of the study.

Cluster ID	Patient Count	SSR	Cumulative hazard	Risk factors
4	74	40	1.02	ifg.pre2=true, htn.pers=true
8	297	180	1.00	ifg.pre2=true, htn.pers=false, obese=true
14	212	121	0.91	ifg.pre2=true, htn.pers=false, obese=false, hyperlip.tx=true
10	227	81	0.47	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=true
20	280	88	0.45	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=true
12	736	88	0.15	ifg.pre2=false, ifg.pre1=false, htn.pers=true
24	1130	380	0.44	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=false, hyperlip.tx=true
15	1276	384	0.42	ifg.pre2=true, htn.pers=false, obese=false, hyperlip.tx=false
28	241	68	0.41	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=false, hyperlip.tx=false, ihd=true
32	949	277	0.37	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=false, hyperlip.tx=false, ihd=false, obese=true
36	735	166	0.28	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=false, hyperlip.tx=false, ihd=false, obese=false, htn.tx=true
40	493	102	0.25	ifg.pre2=false, ifg.pre1=true, hyperlip.multi=false, renal=false, htn.pers=false, hyperlip.tx=false, ihd=false, obese=false, htn.tx=false, aspirin=true

Interactions among risk factors

Cluster 4 consists of patients who have ifg2.pre2 and htn.pers, and the estimate of the cumulative hazard at the end of the study is 1.02. To estimate the hazard under the assumption that the two risk factors are additive (act independently), we fit a Cox regression model to the entire population using only the above two variables as predictors. We used this Cox model to make a prediction for the subpopulation represented by cluster 4 and their cumulative hazard is 1.44. The difference between this prediction (of 1.44) and the prediction of 1.02 by the clustering strongly suggests that an interaction between these two risk factors (FPG and HTN) exists. While we do not know the exact risk of diabetes (true value for the cumulative hazard) in this subpopulation, it is between the observed prevalence of diabetes in this subpopulation, which is 0.57, and 1.0 (each patient can only experience at most one event of diabetes). 1.02 is closer to this range than 1.44, thus the additive Cox regression model overestimated the risk

Discussion

In this paper, we presented a novel bisecting divisive hierarchical clustering algorithm to identify clinically relevant patient subpopulations using type 2 diabetes as the endpoint. In a good clustering, patients within the same cluster are more similar to each other than to patients in a different cluster. Patients in our clusters are similar to each other because they share the same risk factors that are most relevant to diabetes and also have similar risk of developing diabetes. We have shown that our clustering can be used as a diabetes index: when the clustering is sufficiently detailed, it outperformed the Framingham score in terms of concordance (ability to distinguish high-risk patients from low-risk patients). While ARM models have also shown excellent predictive performance, their high level of redundancy leads to unnecessary computational cost. In the following discussion, we examine the beneficial properties of the clustering particularly compared to ARM models and the potential of overfitting.

Comparison to Association Rule Mining

Recent developments of ARM²², including survival association rule mining⁹ have demonstrated its applicability in the EHR mining domain and its appropriateness to serve as a diabetes index. The key advantage of the ARM methodology lies in its interpretability: individual rules are straightforward to interpret and the interpretation provides a context around the risk estimate (e.g. the high risk is due to persistent hypertension and severe hyperlipidemia). As previously discussed, the disadvantage of ARM is that it generates an exponentially large, redundant rule set. With many rules applying to the same patient, making prediction for an individual becomes nontrivial^7,9, making a direct comparison between ARM and clustering leave room for arguments. Just to show that the predictive performance of ARM and clustering are similar, we performed a simple, albeit admitted imperfect, comparison. We largely followed the methodology outlined in the studies using ARM to assess the risk of type 2 diabetes^7,14: we built a Cox model with age and gender as the predictors, and extracted distributional association rules^7,15 indicating an association between the martingale residual and the major risk factors (IHD, hypertension and hyperlipidemia as defined in Table 1 that covered at least 50 patients (same coverage as used for clustering). For each patient, we made a prediction using the most specific rule. The concordance of the resultant model was .7601 with a standard error of 004. This is comparable to the performance of the clustering model. Additionally, both the ARM-based models and our clustering have the ability to automatically discover interactions among risk factors and seamlessly incorporate them into the model or clustering.

Our proposed method goes beyond the state of the art by allowing the user to control the amount of details the clustering should incorporate. This is particularly beneficial, because the amount of detail can be adjusted to the needs of the consumer of the model. For example, when the user of the clustering is an automated clinical decision support system, a highly detailed clustering may be desirable. Computational systems can handle complex models, even as complex as the ARM models, and thus a clustering that incorporates a large amount of details (without overfitting) can be most appropriate.

Another potential use of the clustering produced by our method concerns clinical investigation, where clinicians, rather than computers, view the clustering results. Presenting excessively detailed complex models to investigators can be more distracting than useful, thus a moderately complex clustering may be most desirable. Our method constructs the entire cluster hierarchy upfront allowing investigators to drill down for further details. This can be achieved through further clustering a specific subpopulation (leaf), as needed.

Overfitting

Models as flexible as the clustering-based model or the association rule set are susceptible to overfitting the data. In this application, we were not particularly concerned with the predictive performance of the model as it is secondary to its interpretability. To avoid overfitting, we required the presence of at least 50 patients in each node (or association rule), which is sufficient to reliably estimate their risk. Also, Figure 3 shows no sign of overfitting: increased number of nodes have consistently led to improved performance on a validation set. Nonetheless, when the clustering is used as a predictive modeling tool, the number 50 needs to be tuned more carefully and attention must be paid to the potential overfitting.

In summary, we have demonstrated that our clustering method retains the benefits of existing diabetes risk models and adds its own advantage through allowing for fine control of detail that is presented to the user. This promises great potential of contributing to clinical practice.