Motivating the Additional Use of External Validity: Examining Transportability in a Model of Glioblastoma Multiforme

Abstract

Despite the growing ubiquity of data in the medical domain, it remains difficult to apply results from experimental and observational studies to additional populations suffering from the same disease. Many methods are employed for testing internal validity; yet limited effort is made in testing generalizability, or external validity. The development of disease models often suffers from this lack of validity testing and trained models frequently have worse performance on different populations, rendering them ineffective. In this work, we discuss the use of transportability theory, a causal graphical model examination, as a mechanism for determining what elements of a data resource can be shared or moved between a source and target population. A simplified Bayesian model of glioblastoma multiforme serves as the example for discussion and preliminary analysis. Examination over data collection hospitals from the TCGA dataset demonstrated improvement of prediction in a transported model over a baseline model.

Introduction

Substantial amounts of time, money, and effort are exerted to run scientifically sound experiments in the form of randomized controlled trials (RCTs) to determine the efficacy of medical therapies. In addition, systematic reviews and meta-analysis of the findings in RCTs and other research has been made paramount to demonstrating the validity of findings across the large body of medical research. The major focus to date has been in support of calculating the statistics of these experimental endeavors. Utilizing the combined findings from experimental studies and collected observational data, researchers attempt to develop prognostic disease models to aid in clinical decision-making. However, these models often show decreased performance when used to predict results for new data that were not a part of the original modeling dataset.

RCTs, systematic reviews, and meta-analyses investigate the internal validity of data obtained from one or more trials. Despite the rigors employed to ensure statistical accuracy and understanding, the derived knowledge still only represents a level of certainty in regards to the population examined during experimentation. Previous work has demonstrated that the internal validation of results is not suggestive of applicability to future patients¹. The ability to apply obtained knowledge to new cases is still somewhat nebulous and rarely applies despite expectations². This issue is related to the complexity of disease and treatment, the issues involved in working with populations without incorporating bias, and the difficulty in completely observing any population. The ability to apply data between populations by determining the external validity of findings is a growing area of study. The primary function of validated data is the ability to apply, or transport, experimental or observational results to future domains. Transportability theory is a recently developed method suggested for evaluating when the findings for a population meet the proper constraints to be considered externally valid and therefore are applicable to another population³.

In this work we: 1) develop a limited Bayesian belief network (BBN) disease model for prediction of glioblastoma multiforme (GBM) survival; 2) examine the ability of transportability theory to provide information concerning the external validity of data collected for the model; and 3) test the transport of data between different contributing hospitals in our dataset. Publicly available data from The Cancer Genome Atlas (TCGA)⁴ initiative of the National Cancer Institute (NCI) were obtained to form our training and test set populations. This work is meant to demonstrate the use of transportability and some of the complexities involved in moving data (and the resultant models) between populations for predictive purposes. The model used in this paper is simplified to provide an opportunity to examine the characteristics of a disease model and transportability without the complications a large set of predictive variables may add.

Background

Internal and external validity

Prognostic modeling research is largely driven by evidence-based medicine (EBM) tasks: RCTs, subsequent systematic reviews of RCTs, and meta-analysis derived from completed systematic reviews play a critical role in establishing accepted clinical practice. Physicians update their understanding of disease, as well as new treatments or changes to existing treatment options, by reviewing these studies. These efforts establish important variables and design parameters for collecting data from a controlled population of patients and healthy controls. Despite attempts to use a standard design, it is often difficult to compare across RCTs, even when both studies examine the same drug’s effect on a given condition; (confounding) differences can exist in the sampling size, collection constraints, patients lost to follow-up, etc. Moreover, randomized trials are designed to maximize internal validity (i.e. consistency within a cohort by controlling for potentially confounding variables). These studies validate the efficacy of an intervention under ideal conditions but do not necessarily address its clinical effectiveness across a real-world population (i.e., the external validity/generalizability of the intervention to routine practice)⁵. Though more “practical” or “pragmatic” clinical trials are now promoted to relax subject eligibility requirements (thereby broadening the test population), a given investigation may still encompass assumptions about the underlying study group and environment that are difficult to overcome.

The concept of internal validity allows claims about the treatment methods tested. With robust clinical trial design one can determine if true statistical differences exist between intervention and control groups. However, these statistical claims are only valid for the population observed in the RCT. Systematic reviews gather related RCTs, standardizing the differences between trials and providing documentation of the trends of findings for a particular disease or target therapy. Efforts such as the Cochrane Collaboration recognized the need for maintaining unbiased systematic review and meta-analysis for all of medical research. Contributions by members of the community to collaborations ensure that more medical treatments are reviewed than in the past.

Meta-analyses generate a further statistical evaluation of the internal validity of a set of RCTs linked through the systematic review process. In essence, meta-analysis aggregates the statistical findings of a group of RCTs into the semblance of a single, larger study. This analysis is not a combination of all the raw data from the individual populations of each trial, but an examination of the outcome statistics calculated in the results of each trial by performing a weighted average. This revised statistical evaluation of the individual findings is used to make claims about the consensus of medical research on the given topic examined. The conflicting information from RCTs can lead to inconclusive findings concerning a treatment with the suggestion of further research. Significant findings from a meta-analysis are suggestive of strong associations of the experimental findings; however, these conclusions are still decidedly internal as the analysis steps examine the consensus of medical research and do not directly evaluate the external applicability by applying findings from the RCTs to different populations. Thus, it remains difficult to apply the knowledge to future cases where not all circumstances of the RCT-defined environment will hold.

For this reason, a new set of research efforts are examining the concept of external validity, and the direct application of past studies’ results to future analysis and prediction. Unlike the significant body of work for evaluating internal validity, few techniques have been developed to test external validity; and internal validity methods are not directly applicable to understanding how findings generalize. External validity is a growing concern in epidemiological research^1,6,7, and is encouraging a move towards testing all data findings with methods relevant to both internal and external validity so that evidence and study conclusions are fully contextualized and applied appropriately⁸.

Causal models and transportability

Graphical notation is an increasingly prevalent technique for modeling probabilistic and causal relationships across observation and outcome variables of a disease in order to represent disease’s etiology, presentation, interventions, and ultimate course. Graphical notation provides a visual interpretation using well-defined sets of vertices and edges: vertices are representative of the variables chosen for a domain of interest, and edges describe relationships that exist between a pair of variables. The relationships are descriptive of the inferences derived from experiments, the belief the model developer has about the variables from past experience or observations, and other sources of knowledge such as domain experts. For example, disease model graphs can make use of RCT and meta-analytical findings, as they provide a set of presumed belief in the relationships between disease variables.

When graphs contain only directional edges and do not provide any cyclical pathway between vertices they are termed directed acyclic graphs (DAGs). The special constraints of a DAG, in addition to only representing causal relationships between variables, form the basis for a causal model or causal network. Representation using DAGs has proven effective for working within a Bayesian framework as graph notation is able to provide an efficient means for describing the environment of variables and the associated probabilities of their states in the environment. Figure 1 contains an example of a graphical causal model for treatment effect on lung tumor progression.

Figure 1.

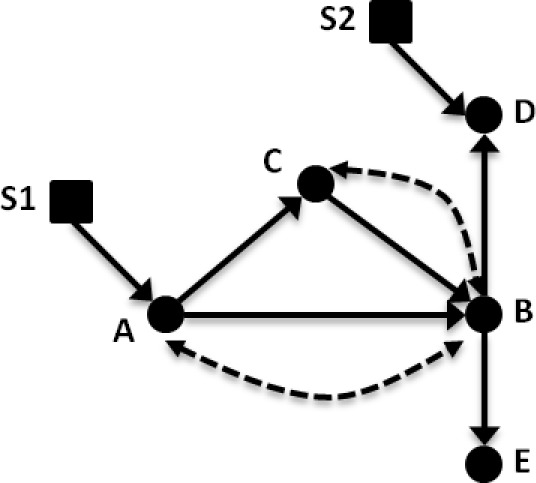
Example causal diagram for lung cancer treatment. Variables: (A) treatment; (B) tumor progression; (C) tumor biopsy gene expression; (D) clinical history; and (E) CT imaging findings. In this causal diagram, solid circles represent standard variables (such as in a Bayesian belief network), and solid arrows between these nodes represent causal relationships. Dashed arrows/arcs indicate confounding influences between two variables that may exist when considering other populations. Selection nodes, shown as squares, provide a means to sub-select or filter a given variable so that the evidence is comparable between two groups.

Pearl and Barenboim introduced transportability theory as a basis for using relations expressed through a causal model to describe which variables’ probability distributions “transport”, or move, between populations⁹. For example, a physician in a rural setting might wish to apply the results of an RCT conducted at a large research hospital to decision making for patients locally under his/her care. The RCT findings can be understood in the context of a causal graph, per Figure 1, as a treatment (A) with effect on a patient outcome (B), with additional measured factors such as clinical history, imaging, or genetics (C, D, E). Transportability allows a researcher to identify potential confounding evidence between variables (represented by dotted lines) and population differences (indicated by square nodes, S1 and S2) that are known or believed to exist between two cohorts. The influence of these constraints can be used to determine what data from the RCT can be applied to the rural patients in a principled way. For instance, the physician may not have enough genetic information for his population to build a model; applying transportability can help ascertain whether the genetic information collected in the RCT can be reused (i.e., transported) to the local group (and if not, under what different graphical circumstances such data transport would be valid). Similarly, differences between the hospital and local populations (e.g., demographics) can be accommodated via transportability. In general, if all existing differences can be accounted for, then the external validity of the findings makes the model variables transportable to the new population.

A distinction should be made concerning the differences between causal and probabilistic models (e.g., BBNs). Application of transportability theory is performed on a causal model where an arrow from node X to node Y denotes that X is used in the function that determines Y. Connections are representative of the process “X causes Y” seen in nature, conveying an inherent ordering of events and representing direct functional relationships. Within the probabilistic (Bayesian) context, edges between nodes are often interpreted in a similar fashion as causal connections, but relationships between variables are encoded only by conditional probability tables and statistical relationships. However, arrows in a causal model are meant not only to represent probabilistic dependence but also direct causation. Therefore a causal graphical model is a robust description of the assumptions made by the modeler.

To properly describe the full set of causal connections in the graph, additional information not commonly captured in a Bayesian belief network must be explicitly represented. First, unmeasured confounding information expected to exist between any two nodes needs to be marked accordingly. These confounders are represented by bi-directional dashed edges and cover the counterfactual circumstances of variables that may be impossible to observe or measure. An example of this situation could be the potential interaction of a non-prescription pain-killer and treatments prescribed by the physician (Figure 1, the dashed arc between A and B). Patients may not report their non-prescription drug use or there may be unmeasurable interactions even if the physician knows both drugs are being taken. Second, when population differences are suspected or known to exist for a particular variable, a selection node is added that embeds a method to control for this variation. A selection node serves this purpose by explicitly identifying population differences in the mechanism (e.g., disparities in demographics, socioeconomic status) that are responsible for assigning a value to that variable. By way of illustration, if age differences were significant between two populations, a selection node could be used to indicate the need to select patients who are age-matched. We discuss these points further in our methods and describe them in the context of the simplistic Bayesian model of GBM shown in Figure 2.

Figure 2:

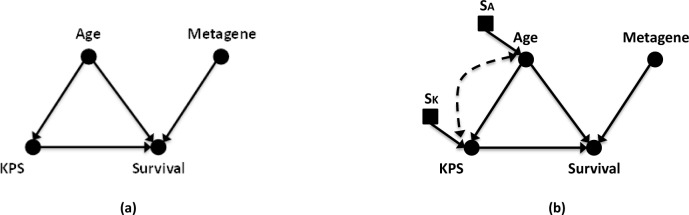
Example causal diagram for (a) GBM survival prediction and (b) the same causal diagram of GBM with links and nodes representing expected confounding information and population differences for variables. In the diagram, solid circular nodes represent observed variables; while square nodes indicate selection nodes controlling for population differences. Causal links are represented with solid lines with directional arrows. Bi-directional dashed lines indicate a variables linked by confounders. The selected observational variables are Patient Age (Age); Karnofsky Performance Score (KPS); 9-gene metagene score (Metagene); and Patient Survival at Population Median (Survival). Unique selection nodes for Age and KPS are shown as S_A and S_K.

Motivating disease and data resources

Nearly half of the 45,000 newly diagnosed cases of adult brain tumor seen annually in the United States are cases of glioblastoma multiforme, an aggressive malignant primary brain tumor. When receiving targeted care at large research hospitals, GBM patients have an average survival time of 12–24 months. In addition, NCI SEER (Surveillance, Epidemiology, and End Results) data over the last 20 years show little effective change in the survival of GBM patients¹⁰. A combination of surgical resection, radiation treatment, and chemotherapy are the current standard of care in modern brain cancer treatment. The attempt to improve patient survival time increases the need to study new chemotherapeutic agents and other potential interventions. A growing body of genetic research on the many types of cancer demonstrates the intricate variations that exist between cancer cells, both across tissue types and within individual cancer groups^11,12. To aid future decision making tasks, statistical examination of cancer findings strive to provide predictive models of treatment and outcomes. However, statistical analysis of cancer studies have been unable to reach a consensus on the most effective predictive variables for GBM patients^13–16. As our present understanding of cancer and effective treatments are limited, the field continues to work towards integrative models of disease to better employ the influx of experimental data towards improving clinical decision making tasks.

A number of multi-institutional efforts now exist to establish observational databases, supplementing experimental datasets. Two efforts focused on building databases for GBM research are The Cancer Genome Atlas (TCGA) and the Repository for Molecular Brain Neoplasia Data (REMBRANDT). TCGA is a public database of clinical and genetic information for 20 different types of cancer. Containing primarily clinical and genomic (copy number, DNA methylation, gene expression, single nucleotide polymorphisms) data, the TCGA dataset has ongoing efforts to also make radiological and pathological images available. The REMBRANDT database is focused specifically on data obtained for all types of brain glioma (astrocytoma, GBM, mixed, oligodendroglioma) with a limited number of unmatched non-tumor controls.

Methods

Many potential modeling variables from the clinical, treatment, imaging, and genetic domains have been explored in GBM research. A brief list of example variables from existing public GBM datasets are shown in Table 1. A subset of the available data related to a chosen clinical question is selected to facilitate discussion of transportability in the network. In this work, the number of variables considered is substantially limited in order to build a simple BBN. In this way, focus is given to introducing core concepts involved with the theory without discussing advanced causal situations prematurely.

Table 1:

Partial list of potential predictive variables from among two multi-institutional data sources, TCGA and REMBRANDT.

Variable
Demographics	Total radiation dosage
Presenting age	Other drug name
Family & social history	Other drug Frequency
Environmental exposure	Other drug Dosage
Tumor location	Steroid drug name
Tumor size	Steroid frequency
Tumor grade	Steroid dosage
VEGF	Karnofsky score
EGFR VIII	Other performance score
PTEN	Tumor volume (on imaging)
TP53	Necrosis imaging finding
MGMT	Contrast enhancement imaging finding
DNA methylation	Non-contrast enhancing region
Chemotherapy drug name	Tumor multi-focality
Chemotherapy frequency/dosage	Edema volume (on imaging)
Number of chemotherapy cycles	Mass effect
Type of surgical resection procedure	Satellites
Extent of resection	ADC map (imaging)
Type of radiation therapy	Time to progression (TTP)
Radiation therapy fractionation	Time to survival (TTS; death)

Predictive Model

Our example model (Figure 2) contains four variables; 1) a demographic variable, age 2) a cognitive assessment variable, Karnofsky performance score (KPS) 3) a genetic variable, a 9-gene metagene score derived from Colman, et al.¹⁷, and 4) an outcome variable, overall survival (survival past median of 12 months). Age and KPS were chosen due to their predictive significance in previous GBM models^18–20. Overall survival is the most common outcome variable used for prediction in previous GBM models and is most commonly predicted using median survival time cutoff^18–20.

The incorporation of a genetic variable relates to the growing interest in genetic prediction variables for cancer. For example, a number of papers in GBM treatment discuss O6-methylguanine-DNA-methyltransferase (MGMT) methylation and tumor protein 53 (TP53) gene expression as potential predictive markers for GBM patient survival. Previous work has found a significant up-regulation of MGMT expression in the tumor tissue when treated with O6-alkylating agents such as temozolomide (Temodar), indicating a potential benefit for patient’s survival^21–26. Similarly, up/down regulation of TP53 factors into cell apoptosis; reduced rates of apoptosis are characteristic of many types of cancer and can contribute to large growth rates of cancerous cells²⁷

Genetic testing is not available to most clinical locations and smaller locations will not have a large enough sample of cases to estimate the rates of expression for their population. Therefore, a genetic variable is a suitable example of an item from a model that would benefit from transportation from a source to target location.

As previously mentioned, our genetic variable is a metagene score derived from nine gene expression values measured in the TCGA dataset. The selection of these significant genes and the metagene scoring technique were derived from Colman, et al.¹⁷. Briefly, the metagene score is calculated by summation of the weighted expression levels of the genes for each patient and then discretized into high and low score classes. Discretized ranges for all variables in the model are shown in Table 2.

Table 2.

Selected model variables.

Variable	Range/Categorical values
Age	0 (<40); 1 (40<65); 2 (65<80);3 (>80)
Karnofsky Performance Score	20,40,60,70,80,90,100 – 7 Category Assignment
Metagene Score	0 (Low, Score <= 0), 1 (High, Score > 0)
Survival past median	0 (No); 1 (Yes)

Data selection

Data was obtained from the TCGA public data repository. In total, 579 cases exist in the TCGA database with clinical information. Variable selection and preprocessing steps were performed on the full set of available TCGA cases with available clinical and genomic data. Cases were first selected for no evidence of prior glioma to match our analysis with the methods of Colman et al. and provide similar metagene analysis, reducing the number of available cases to 544. Because of the small number of variables in our Bayesian network we further sought to avoid missing data and the need for any imputation. A portion of the desired KPS variables were blank or unavailable for 143 cases. Finally, only cases observed until death or past the median survival cutoff are appropriate for the analysis in a Bayesian framework, so censored patients were removed. This reduced the final count of available cases for analysis to 346.

The final selected population for TCGA was then discretized based on the categories in Table 2. The dataset was divided into three source and target subsets based on contributing hospital location. Source cohorts serve as our “previous location” used for the majority of model construction and the Target cohorts are “new patients” for prediction at another location. Three target splits were made into a large, medium, and small set of cases to examine the effects of prediction when varying amounts of target data is available. The final TCGA hospitals chosen to serve as targets for analysis were Hospitals 2, 6, and 19 with contributed subjects of 84, 65, and 18 respectively. All remaining hospital locations supplied data to the complementary source cohort (262, 281, and 328 cases respectively).

Applying transportability

In the example GBM model in Figure 2a, we have a set of four variables and their causal connections. The example network comprises no connective links other than the direct causal connections derived from literature. Causal assumptions have been made in constructing this graph, and we must consider the differences that may exist between source nodes and nodes of a target population. Confounders and selection nodes are likely involved in most graphical networks and must be considered and dealt with when problematic. An example graph with a number of these issues, such as in Figure 2b, is a case where data may not be transportable unless certain constraints can be met either by transportability rules (do-calculus/d-separation mentioned below) or a valid belief that removal of the connections can be made without affecting the outcomes. The goal is to map between the messy real-world graph in Figure 2b and the ideal causal graph in Figure 2a to enable the transport of information. We review two issues below:

1. Unobserved and confounding variables. Let us consider the dotted connections in the example GBM network. Bidirectional dotted lines represent latent confounding variables in the causal graph. For this discussion, let us say that a connection represents interactions between age and Karnofsky performance score mediated by unmeasured variables (i.e., data that could not be observed). The addition of this link denotes that there is belief that complex biology explains the interaction between KPS and age and could mask our causal assumption. For example, KPS is derived from an examination of a patient’s current mental and physical status. This status derives from a combination of the current symptomatic state of disease in the patient and some mix of other past disease. The patient’s symptoms might be tied to a damaged hip from osteoporosis, causing a decreased score due to lost mobility, or be tied to a past stroke, causing a decreased score due to aphasia. These kinds of effects would mask our attempt to measure age’s effect on KPS values caused exclusively by GBM. If proof exists in the literature that such an interaction is common, it might be required that additional variables be added to the model to correct the confounding before a proper transportability assessment can be made. This particular confounding example seems farfetched and we would remove the confounding link as we have a reasonable belief that clinicians are considering past injury when quantifying the KPS value.

2. Population differences. In addition to confounders, consideration must be given to the population differences that exist in the collected data. For example, the number of patients treated with given chemotherapies may vary between two locations depending on physician treatment preferences/experience, hospital practices, and availability of the potential drugs. Selection nodes in Figure 2b represent potential cohort differences in age and KPS scoring. Age often varies depending on the type and location of hospital where data is collected. KPS scoring can vary depending on factors such as amount of clinician training in performance scoring, the overall experience with patients in the domain, and the standard variability seen between different examiners. Adding new selection nodes changes how we consider these variables as we evaluate the ability to transport the network findings. Unless a belief or measurement can be made about invariance between the populations, selection nodes may indicate that stratification or re-estimation of variables may be warranted.

Having described the links assigned to the graph, the application of Pearl’s work with transportability is possible for a given graph²⁸. A set of algebraic rules called do-calculus^9,28 enables a formal mathematical statement to be derived that determines what elements of information are transportable with the given variables, relationships, confounders, and selection nodes. The do-calculus allows for links in the graph to be broken based upon forced experimental constraints. Further graphical analysis via d-separation, and front- and back-door criteria, can help determine which variables of the model are identifiable. Identification entails the evaluation of the graph edges that remain when observational data is used to set a variable to a specific state and then determining when the network is not directly affecting the transportation of findings. Thus, when a causal graph is not identifiable, its findings are not transportable. For example, KPS, a scoring of the neurological performance of a patient based on symptoms, can serve as a surrogate measure for imaging findings of brain tumor growth, which is influenced by population differences. When KPS can be determined as conditionally independent of population differences, it can serve as a replacement for the imaging information using the front door criterion of d-separation and unblock a situation where imaging findings may not be available. A full description of the do-calculus and d-separation can be found in Pearl’s work^9,28. Further individual examples can be drawn for situations involving back door paths and bidirectional counterfactual edges; many are reviewed in more detail in the available work from Pearl and Barenboim^9,29.

Network evaluation

Our Bayesian belief network predictive model for GBM was tested using custom code in MATLAB (version 7.10.0, Math-Works, Inc, Natick, MA). Source and target cohorts were built by splitting the TCGA dataset by contributing location; one TCGA participating location was held out as the Target set while all remaining data formed the Source set. For example, Hospital 2 contributed 84 cases to the 346 total TCGA dataset. A target dataset for the Hospital 2 split contains these 84 cases. Then, a source dataset was made from all remaining TCGA sites (6, 8, 12, 14, 15, 19, etc) containing 262 cases. In this way, the Source cohort acts as a previous location used for model construction and the Target cohort is a location with new patients in need of prediction. For this analysis, three splits were performed targeting locations with a large (Hospital 2, n=84), medium (Hospital 6, n=65), and small (Hospital 19, n=18) number of cases in the TCGA set. Four model considerations were used while varying the training and test cohorts from the three source-target splits. The four model considerations are: Source versus Source (SS), Target versus Target (TT), Source versus Target (ST), and Transported Source versus Target (TrST). Each consideration describes the Training-Test setup used for modeling. Leave-one-out validation was performed on test cases to determine the prediction rate of the models. Mann Whitney U-tests were used to test for significant difference between prediction classes of the model.

The SS and TT examinations represent the gold standard evaluation of a model built using data from source and target locations respectively. This emulates the current state of practice where each research location builds a model rather than pooling data or using a past model. The ST examination tests the external validity of the Source model at predicting new cases from the Target cohort. The ST examination represents the special case where all variables are assumed to be trivially transportable (i.e., there are no differences affecting the Source variables, a very rare circumstance). All model probabilities are obtained from the original Source cohort with no training input from Target patients. Finally, the TrST split examines a more realistic transport where the KPS variable is trained by the Target data under the assumption that the Source KPS data is too different from the Target patients. In this model, all other variables are trained using transported values from the Source cohort. The expectation is that the joint use of information from the Target and Source datasets will outperform the ST method where differences of target information are not taken into account. Table 3 provides a full breakdown of the training and test data used in each of the four model considerations.

Table 3:

Description of training and test data used in the model considerations. Test data is cross validated using the leave-one-out cross validation method.

Model	Training Data	Test Data
SS	All Source	Source
TT	All Target	Target
ST	All Source	Target
TrST	Age: Source, KPS: Target, Metagene: Source, Survival: Source	Target

Results

After variable selection and application of selection criteria, 346 TCGA cases were available for analysis and were split into three source-target cohorts of Hospital 2 (262 source, 84 target), Hospital 6 (281 source, 65 target) Hospital 19 (328 source, 18 target). Each source-target cohort was then used for model training, followed by testing using leave-one-out cross validation (LOOCV) across the four described training variations (SS, TT, ST, TrST). LOOCV was chosen in order to maximize the number of cases available for the training steps, as the available hospital sample sizes are small. Complete results of the Bayesian analysis are shown in Table 4 and are discussed in more detail below.

Table 4:

Leave-one-out validation results of transportability analysis. Values represented are Area under the curve (AUC) and Mann-Whitney U p-value for significant difference between survival prediction classes. Three hospitals in the TCGA dataset are compared to demonstrate the effects of target cohort size. Karnofsky performance score (KPS) was held out as missing/unmeasured data in this model.

	Model
	SS		TT		ST		TrST
Hospital 2 (262,84)	0.69	(2.7E-08)	0.76	(1.5E-05)	0.74	(1.1E-04)	0.76	(1.7E-05)
Hospital 6 (281,65)	0.72	(1.6E-11)	0.68	(0.007)	0.63	(0.056)	0.63	(0.059)
Hospital 19 (328,18)	0.71	(4.7E-12)	0.94	(0.004)	0.68	(0.248)	0.94	(0.004)

Prediction using source training data (SS and TT)

Results from the analysis of standard methods of source and target modeling demonstrate moderate rates for LOOCV. Area under the curve (AUC) values ranged from 0.69–0.72 (LOOCV) for SS models. TT models ranged from 0.68–0.94 (LOOCV). TT models outperformed SS models in most considerations. However, the sample sizes of each TT model are smaller, reducing confidence in AUC values holding steady under all circumstances as seen by the weaker p-values in Mann-Whitney testing. We refer to the TT model AUC values as the standard accuracy target for the subsequent model applications, ST and TrST.

Prediction using outside training data (ST)

When the source model is applied as training data for a target location in the ST model, a decrease in performance is seen for all hospital combinations when compared to the TT score. In LOOCV, AUC values drop by 2.7%, 5.3%, and 26% respectively for the three hospital splits. These lower AUC values indicate that the training data from the source model is not able to predict cases in the target set as accurately as a target trained model. Results are most externally valid when populations are the same and variations between variables are minimal. Only in the large target cohort split, Hospital 2, do we see a significant differentiation (p = 1.1E-04) between prediction classes and therefore see potential external validity. For the other splits, external validity does not hold for the source model on outside data as p-values do not reach significance (0.056 and 0.248).

Prediction using transported probabilities (TrST)

By transporting appropriate information from the source location and using information for appropriate variables from the target location, the intention is to improve the model by making it more accurate against the differing variables and distributions at the target location. In our TrST model, the KPS value is assumed to vary between Source and Target populations. Therefore, KPS probabilities are trained using Target patient data while other variables use transported data from the Source.

In two applications of the TrST model, we see an improvement of AUC over the application of the source trained model, ST. Performance for Hospital 2 and Hospital 19 improved to match the original prediction accuracy seen in the TT model for this validation. In the case of Hospital 19, the smallest target cohort, the Mann-Whitney U test statistic also changed from being insignificant (ST p=0.248) to significant (TrST p=0.004). These improvements suggest that data from the KPS variable in the Target was able to better model local cases. Hospital 6, however, showed no improvement in accuracy between ST and TrST attempts, suggesting no significant difference between the Source and Target KPS data for this split. When these values are similar, little new information is added to improve predictions and the external validity of a source must be high to match prediction accuracies reached using target data. Detecting these cases is important to using transportability for improving model accuracies.

Discussion

The transport of probabilities for prediction from a source model to a target cohort imparted an increase in the predictive power of the model over an original source model for two of the three sites in our evaluation. These results demonstrate at a basic level the potential power of transportability theory to assess a model and determine appropriate variables for transport. Consideration of confounding and population difference that are possible in new cases is important when determining whether external validity applies to a model.

Transport of data for Hospital 2 and Hospital 19 demonstrated improvements over source models. This result indicates that the recovered target information works in concert with the transported source information to bring model predictions back to a rate similar to training a full model from scratch. Transporting data in this way can lead to more accurate models when data is unmeasurable or unavailable. In addition, it can be beneficial to future studies by reducing the number of variables that must be measured at the new location, saving time and money. Recall, in our simplified model for this work (Figure 2) we transported age, metagene, and survival information from the source. In doing so, the target was not required to provide information to estimate probabilities for these variables: only KPS data was collected from the target.

Overall, the predictive power of the models in this work is moderate, a common issue for current GBM models. While the highest AUC for a gold standard model in our analysis is 0.94, this score is for a very small dataset. Nevertheless, our results demonstrate the effect transportability can have in making an outside model useful to a target location. In two of the three splits of TCGA data, performance was improved over directly applying the source model.

One limitation within this work is the overall simplification of the problem. A probabilistic model of GBM should include a number of variables covering clinical, treatment, imaging, and genetic factors. The presented model only examines two such facets (clinical and genetic) and minimized the feature set to four specific nodes for the prediction task. This simplification was necessary for an introductory discussion of transportability, but is unrealistic as we consider the proper model options for testing external validity in the future. More realistic models with 10–20 features will complicate the ability to analyze the transportability of findings. Future analysis must examine the computational sophistication of larger disease models in order to find tractable solutions to transportability questions.

Also, low prediction rates for the current model are likely tied to the simplistic model representation chosen in order to facilitate discussion. Other statistical models have reported higher levels of time to survival prediction in GBM (AUC 0.81)²⁰. In addition, we only explore a limited number of contributions from confounding information and population differences related to this model. Additional examination of location differences in the TCGA dataset might elicit the variable(s) that cause poor improvement in a situation such as Hospital 6 and indicate problems assumed away incorrectly. Providing a robust examination of factors that can disturb the external validity of data is necessary to support the claims made when completing evaluations with transportability rules. Such factors may lead to inaccurate decisions that findings are applicable externally. Overlooked or ignored confounders may destroy this capability in practice.

Another limitation of the current model is the use of a 9-gene metagene score that summarizes a set of gene expression values. The 9-gene metagene was used in this work based upon a previous assessment against TCGA data by Colman et al.¹⁷. An examination that treats each gene as a variable of the model rather than a summary statistic might yield improved results. In addition, many other gene expression rates are measured for these populations and more statistical examination of the predictive involvement of these genes is warranted.

Application of transportability theory to increasingly complex model designs will be important to expand the utility of this approach. For instance, adding a new variable to the model can cause a number of complications in the causal network not fully discussed here. A few considerations that might be made when adding items to the network include: how the variable was measured, what other variables it is causally connected to, how the addition affects the previous assumptions of the links in the model (changes to independence), and if measurement of the variable introduces difference into the population. As model complexity rises, it appears that the number of considerations may become difficult to appreciate.

While this work has a simplified model and assumptions, the potential utility of transportability theory is clearly demonstrated. In our working example, the step of adding confounding arcs and selection nodes in the simplified GBM model imparts that there are additional factors to consider. Honestly evaluating where these links and nodes can exist enables a discussion that faithfully considers the causal nature of the relationships described in a graph. In this way, a researcher can use transportability theory to demonstrate that issues have been considered and the assumptions made when attempting to claim findings are externally valid. With the proper examination, a mathematical description of this fact is derivable via the do-calculus.

Another potential area for future investigation is the addition of better descriptions for model design, parameters, and causal graph assumptions. One mechanism for providing this information is through the Predictive Model Markup Language (PMML), an XML-based language for describing models to improve interoperability³⁰. However, PMML currently lacks descriptions for Bayesian networks, so extensions will be necessary for application. By including model information and graphs designs to experiments and RCTs, investigators can explicate the study’s experimental target and the specific assumptions and decisions involved with the chosen design. The provided graph might then act as a template for outside researchers to test the model transportability against their own datasets. With the time and cost investment involved with running RCTs and cleaning observational data, these explicit descriptions could aid in the discovery process and also influence future investigations if transportable findings from a previous study mean that time and resources can be spent targeting previously unexamined variables in the domain.

Despite the strengths of transportability, there is difficulty in describing the method using more than basic examples with a minimized set of considerations such as those used above. Pearl and Bareinboim have incorporated more complex graph models in their work^9,28,29, but those models are not always contextualized in a way that is clear to the layman. In this work we have attempted to begin bridging this gap and make an attempt at introducing the core concepts of transportability. However, future work must address the best means to introduce the complex methods involved in determining external validity in this fashion. Further efforts must be made to provide descriptions of the theory that are accessible to a broader audience with an interest in testing external validity. This will require communication between computer scientists, statisticians, and informaticians to balance the descriptive language used and ensure that papers related to transportability and external validity can be published more widely.

Conclusions

Testing the external validity of scientific findings is important for the application of knowledge across populations. Transportability theory provides a robust method for describing the causal relationships of experimental variables and the circumstances that allow findings to be transported to additional populations. We have described core concepts of transportability in the context of a GBM model that describes transportability of a metagene biomarker for gene expression between two cohorts. The increase in AUC in testing for two of the three examined test cases is indicative of the utility of transporting information. The need to perform robust analysis of the potential confounders and population differences using a technique like transportability is important and future work will focus more heavily on these restrictions. The simplified model provides an understandable introduction to transportability and the examination of how poor assumptions and population differences may encourage use of models prematurely. Additional work in the area of transportability can provide a useful tool set for examining the causal relationships of experimental work and calculating the circumstances where the findings are externally valid with another population.