Disease progression subtype discovery from longitudinal EMR data with a majority of missing values and unknown initial time points

Abstract

Electronic medical records (EMR) contain a longitudinal collection of laboratory data that contains valuable phenotypic information on disease progression of a large collection of patients. These data can be potentially used in medical research or patient care; finding disease progression subtypes is a particularly important application. There are, however, two significant difficulties in utilizing this data for statistical analysis: (a) a large proportion of data is missing and (b) patients are in very different stages of disease progression and there are no well-defined start points of the time series. We present a Bayesian machine learning model that overcomes these difficulties. The method can use highly incomplete time-series measurement of varying lengths, it aligns together similar trajectories in different phases and is capable of finding consistent disease progression subtypes. We demonstrate the method on finding chronic kidney disease progression subtypes.

Introduction

Electronic medical records (EMR) increasingly provide comprehensive clinical data collected during routine clinical care encounters. EMR has a collection of longitudinal phenotypic data that potentially offer valuable information for discovering clinical population subtypes and using them further in association studies in medical research and even in prediction of outcomes in patient care. A number of clinical parameters and laboratory tests are collected as part of routine clinical care and their results are stored in the EMR or in data warehouses. The data warehouse represents a general patient population and the data can be used for statistical analyses. The common examples of routinely collected variables are systolic blood pressure (SBP), low-density lipoproteins (LDL), high-density lipoproteins (HDL), triglycerides, hemoglobin A1C (marker for diabetes and diabetes (blood glucose) control), and estimated glomerular filtration rate (eGFR; a marker of kidney function).

There is obvious interest towards discovering groups of similar patients with similar disease progression patterns in metabolic syndrome that involves varying accumulation of obesity, hypertension, hyperlipidemia, Type 2 diabetes, coronary artery disease and chronic kidney disease (CKD). Previous research has suggested¹ that using population subtypes in association studies instead of broad disease definitions can lead to superior results. Separating differential progression patters in the phenotypic variables can potentially discover these subpopulations. Especially with chronic and progressive diseases, the crucial difference between subtypes of a disease is often differential rates of progression, and any model attempting to find subtypes in progressive diseases must be able to account for this.

We use CKD as a case study in this paper. The prevalence of CKD ranges from 10% to 15% in the United States, Europe and Asia². CKD is associated with increased mortality, decreased quality of life, and increased health care expenditure. CKD is defined in most cases clinically by loss of kidney function as estimated by a glomerular filtration rate (eGFR) below a threshold of 60 ml/min/1.72kg² (normal eGFR range 90 to 120 ml/min/1.73kg²) and/or persistent increased urinary albumin excretion lasting more than 90 days³. Untreated CKD can result in end-stage renal disease (ESRD) and necessitate dialysis or kidney transplantation in 2% of cases. CKD is also a major independent risk factor for cardiovascular disease, all-cause mortality including cardiovascular mortality^6,7. Approximately two thirds of CKD are attributable to diabetes (40% of CKD cases) and hypertension (28% of cases)³. However, CKD is also characterized by variable rates of progression with a significant proportion of patients having stable kidney function over time while some patients have rapid progression. These differential rates of progression⁹ lead to clinically relevant, interesting subtypes among patient populations.

We aim to develop an unsupervised machine learning approach that takes longitudinal data of one variable from all patients and clusters them to population subtypes of which some are healthy and some turn out to be disease subtypes. The aim is to be able to include as many of the samples as possible in the analysis. Using the population subtypes as disease labels in association studies may be superior to the standard approaches of assigning disease labels from EMR data. We also hypothesize that using population subtypes and their temporal progression patterns may lead to improved performance in risk prediction. Most existing disease risk prediction models are coarse case/control models (do not account for subtypes) and use only snapshots of data without considering the temporal patterns. Examples are Framingham risk score or the kidney disease progression model⁴. Even most of the advanced time-series models remain case/control models and do not attempt to discover population subtypes.

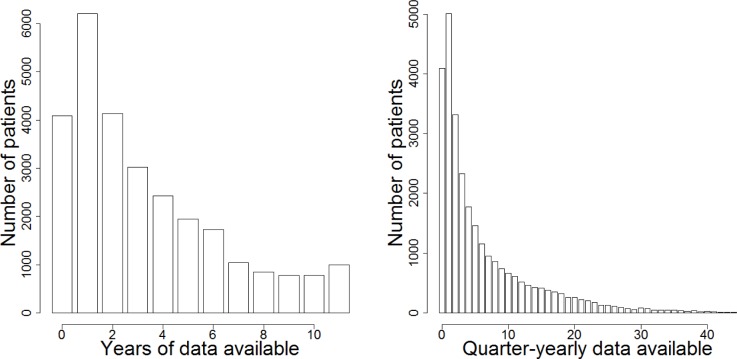
Electronic medical records are a messy, observational data source, as opposed to randomized controlled trials used in designed disease or drug studies. In the latter, data is collected at regular intervals under tight control of the investigators and disease onset times (first time points) are clearly recorded. In statistical analysis of EMR data, however, there are two major challenges: (a) Sparse data (large proportion of missing data) and (b) Unaligned nature of the longitudinal data. For instance, the Mount Sinai BioMe Biobank program has a longitudinal data collection from a period of 11 years and our aim is to use quarterly (every three months) median values of the laboratory measurements to reach a clinically relevant resolution. However, the number of years from which there are data from an individual patient varies greatly and only a minority of patients have a full coverage of data from 11 years; extremely few when quarterly values are sought (see Figure 1). When a large portion of the data is missing, imputation or removing samples or rows with missing data are not sensible options since we would end with a very small number of samples available. An even more difficult problem in modeling longitudinal EMR data is that there is no clear initial time point (t=0). Since patients have their first visit to a certain hospital at highly varying phases of progression of a disease, the first hospital visit with recorded data cannot be used as the initial time point. We have also concluded that using diagnostic criteria (such as the first eGFR<60 measurement in CKD) to fix the initial time point does not give adequate results in subtype modelling [data not shown]. Furthermore, many patients do not yet even have any major disease but it is desirable to include all patients in the analysis. Without the start point, standard clustering algorithms cannot be used since time points do not match between patients. Consequently, most studies in EMR are restricted to using only a single snapshot from the longitudinal data: usually the first or last time point.

Figure 1.

(Left) Most of the 27985 patients enrolled in Mount Sinai BioMe biobank have eGFR data available only from a small number of years out of a total of 11 years. The histogram shows from how many years patients have eGFR data available. (Right) Very few patients have a full coverage of 44 quarterly measurement of eGFR available. The histogram shows from how many quarterly time-points patients have eGFR data available. Multiple measurements from the same quarter-year have been converted into one median value.

In this paper, we present a Bayesian clustering and alignment model that is capable of identifying subpopulations of patients from a longitudinal dataset and overcoming the main challenges of sparse and unaligned data. The method aligns together time-series profiles in different phases of their disease progression in order to find clusters of similar progression patterns. Our generative latent variable formulation enables constructing a model that can use also samples with a large proportion of their time points missing. As a result, we can use a large proportion of the patients in the database in our modelling. A latent variable model is also a good approach for clustering short time-series, since different rates of progression can be separated easily.

One obvious purpose of clustering the longitudinal data collection in an EMR database is to visualize the progression patterns present in the entire patient population. Another application is using the cluster labels as traits in association studies with e.g. ICD9 codes, laboratory, medication or genomic data. We demonstrate that our method finds meaningful CKD progression subtypes and validate our model by showing that certain CKD-related ICD9 codes are much more common in certain disease clusters than in the rest of the patient population.

Data

The Mount Sinai BioMe Biobank Program has a collection of DNA and blood plasma from over 28000 patients linked to their full medical histories in the Mount Sinai electronic medical records database. In this paper, we use a collection of sparse longitudinal eGFR measurements from 2003–2013 from 27985 patients. We simplify the longitudinal dataset by binning each variable to quarter-yearly median values, which results in 44 time points. The eGFR has been estimated from measured serum creatinine. Though proteinuria is included in the KDIGO definition of CKD; in real-world practice, it is rarely collected and there is significant variability in the measurement tools. Also there are recent data indicating that neither microalbuminuria nor proteinuria is a significant predictor of decline in kidney function⁵.

We have transformed the collection of all ICD9 diagnosis codes into a binary matrix that indicates whether patient has had a certain diagnosis code observed. Furthermore, an ICD9 is also considered observed if any more specific ICD9 code in the hierarchy has been observed (For example, 250 is considered observed if 250.1 or 250.03 has been observed. 250.1 is considered observed if 250.11 has been observed).

Methods

Clustering and alignment model

We have constructed a Bayesian generative model for the task of clustering and alignment of a longitudinal dataset. In this paper, we concentrate on one variable only. The combination of clustering and alignment of longitudinal data is an active machine learning research topic with many application areas⁸; here we consider the case of a large proportion of missing values and apply it to EMR disease progression data.

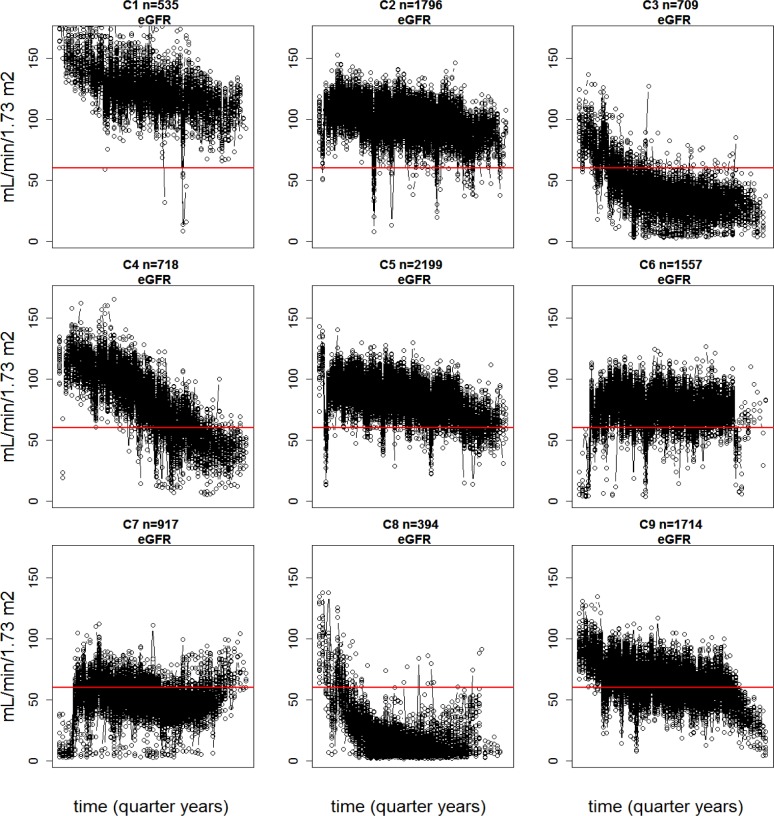
Clustering is a standard statistical method that partitions observations (patients) to sets of similar observations (clusters). This is accomplished by iterating between assigning the observations to clusters and updating the cluster centers. The number of clusters to be sought is defined a priori as a model parameter, but there are procedures for determining the optimal number of clusters. Clustering time-series data is a well-studied problem in the case where clear start points are known. As there are no well-defined start points in EMR data (first visit to the hospital is not a valid start point), we have to learn the start points (iteratively) from the data as well. Aligning the start point of each patient’s trajectory in the cluster trajectory (cluster center) is an extra step in the iterative model. The start point parameter does not have an exact interpretation (such as disease onset), but it enables the alignment of the unaligned time-series so that coherent progression patterns can be found (Figure 2).

Figure 2.

Many distinct coherent eGFR progression patterns can be found from the 10539 patients that represent the entire hospital cohort. The figure shows clustering and alignment results for eGFR using 9 clusters; each cluster in the figure consists of eGFR trajectories of all the patients in that cluster that have been aligned together. These trajectories have highly varying lengths (see Figure 1 and Table 2) and varying numbers of missing values. The time span corresponds to 16 years; each patient has data from 4–11 years (up to 44 quarter-yearly time points) and 20 possible start points are allowed. The n indicates the number of patients in each cluster; C indicates the cluster index.

Each patient i (i = 1:I) comes with a data vector x_i of T time points so that the first element is the first visit to the clinic, and in general most elements are missing (Figure 1). In this paper, T = 44, I = 10539. The clustering model is essentially a multivariate mixture of Gaussians with two modifications. Firstly, as the data have missing values, cluster assignments of the samples (patients) are sampled such that the likelihood of the sparse time-series with respect to the corresponding cluster center trajectory is evaluated using only the time points with non-missing data. Secondly, the longitudinal data vectors need to be temporally aligned and we allow M different starting points in each cluster; as a result, each cluster center is of length (T + M − 1), using M = 20. The alignment is done jointly with clustering by additionally evaluating the likelihood of the time-series in each possible start point in each cluster. The reason why we use a Bayesian generative model to tackle our problem is that when sampling the cluster assignments and alignments of time-series of varying lengths and with many missing time points, some of the time points of the cluster trajectories may not have any data currently assigned to them. In that case, priors determine the values of those cluster trajectory points.

By following the Bayesian formalism, we assume a generative model that has generated the observed data. The model can then be used to learn the model parameters from the data; the relevant model parameters here are cluster assignments k and learned start points m for each patients and the cluster trajectories (centers) θ_kt that can be viewed as average progression patterns.

The generative model is

$$\begin{array}{c}{x}_{it}=N({\theta }_{k(t+m-1)},\sigma ),\\ k~multinomial(\pi ),\\ m~multinomial(\beta ),\\ \pi \sim Dirichlet(\alpha ),\\ {\theta }_{kt}~N(H,{\sigma }_2).\end{array}$$

We thus assume that the observed data has been generated by the following mechanism: patient i comes from cluster k that is randomly chosen from a multinomial distribution of cluster weights π and the patient has the first visit to a hospital at phase m in the cluster trajectory, randomly chosen from a multinomial distribution of prior weights β. The data points in the time-series x_it are generated from a Gaussian distribution, where the cluster trajectory point θ_k(t+m−1) is the mean and σ is the standard deviation. Cluster weights π are determined by a Dirichlet distribution with a base measure α. The cluster centers θ_kt come from a Gaussian distribution with hyperpriors H and σ₂.

The σ is here a fixed parameter set to a tight value σ = 1 to get coherent clusters. We set H as the average of all eGFR measurements in the dataset. The σ₂ = 30 is set as a loose value to enable the modelling of a wide range of cluster trajectories, α = 1. We set the first five and last five values of the prior weights of the alignments β to a low value and all the middle values to a uniform high value in order to improve the mixing in the sampling of the model (that trajectories would not get stuck in the beginning or end).

When a clustering configuration has been reached, the cluster assignments can be used for making inference of the data. The progression patterns can be visualized by plotting the data divided into clusters together with the alignments (Figure 2). Gibbs sampling was used for approximate inference (iteratively). It is straightforward to derive the Gibbs sampling equations from the generative model (see¹⁹). The method was implemented using the R statistical software. The analysis took 20 hours using a single Intel Core i7-2600 3.40GHz processor, but the computation can be made significantly faster by parallelization.

Validation of clusters by association studies

The population subtypes (cluster labels) are used in an association study where we ask whether a certain ICD9 disease diagnosis code is more common in a certain population subtype compared to the rest of the patients. We use Fisher’s exact test and we run the association test between all disease subtype - ICD9 code pairs. When the association tests are run over 10000 ICD9 codes and 9 clusters, the Bonferroni multiple correction rate is p = 10⁻⁷. Ordering the obtained p-value matrix by rows and columns gives information on what are the most distinctive subtypes and what are the most interesting disease diagnoses enriched in these subtypes. The maximum enrichment of selected relevant ICD9 codes can be used as a criterion for determining the optimal number of clusters. With K = 9, a 100% enrichment of ICD9 code 585 (Chronic kidney disease) was found in one cluster. The same statistical testing procedure is used to study the enrichment of males and self-reported ethnicities in the clusters.

Patient selection criterion

As patients have different numbers of data points available (Figure 1), we need a criterion for deciding which patients to include in the clustering analysis. It is clear that patients with zero or one eGFR measurements are not useful in finding longitudinal trajectories; patients with two or three measurements contain some information on the progression, but the measurements may be noisy and a large number of very short time-series may result in less coherent progression patterns. On the other hand, we aim to include as large a proportion of the available patients as possible in the analysis and the more stringent the selection criterion, the fewer patients fulfill it. We will compare the progression trajectories obtained by different selection criteria. The quantity to compare is the number of years from which patients have at least one data point available. The years do not need to be consecutive.

We construct a metric to evaluate the goodness of the learned trajectories. As differentiating disease progression rates between clusters is an important aspect of our modeling, we evaluate the difference of the eGFR slopes of individual trajectories compared to the slope of the cluster trajectory they have been assigned to. The slopes are calculated simply by fitting a regression line. Furthermore, as it turns out that some trajectories are non-linear (see Results section) and patients may have their available data from different parts of the non-linear trajectory, fitting a linear curve to a non-linear trajectory is not an optimal solution. We alleviate this problem by fitting a “local slope”, i.e. fitting the curve only to the part of the cluster trajectory from which the patient has data available and has been aligned to, and compare the individual slope to the local slope.

Results

We demonstrate our method on finding CKD progression subtypes from eGFR measurements. As can be seen in (Figure 1), only a small fraction of the total 27985 Biobank patients have eGFR data from the full period of 11 years and very few have a full coverage of 44 quarter-yearly measurements that would correspond to fully observed dataset (no missing values). As explained in the Introduction, even such full coverage data would not be readily usable since patients are in highly different phases of their disease progression and there are no clear start points. By using our Bayesian clustering and alignment approach, we can, however, use a significant portion of this heavily incomplete dataset.

Patient data criteria and evaluation

We now evaluate how many eGFR measurements are required for patients to be included in the clustering as a tradeoff between patient attrition and model accuracy. In (Table 1) we compare the criteria from how many years the patients need to have at least one measurement available (each year has been divided into four quarters). The number of available patients decreases with tighter criterion, with the benefit of better model accuracy. The slope error is the difference of the slope of an individual trajectory compared to the slope of the cluster trajectory. Please refer to the methods section for the definition of the accuracy of the model.

Table 1.

Sample size and median error for different number of years

Selection criterion (Years)	2	3	4	5
Number of patients with data available	17672	13558	10539	8117
Median slope error	1.66	1.35	1.24	1.18

As can be seen from (Table 1), the number of patients with a sufficient amount of data available to meet the inclusion criterion drops rapidly when tightening the criterion. In the same time, the accuracy of the model increases, as there are a smaller number of short, potentially inaccurate time-series worsening the clustering result. We choose to include patients with eGFR measurement from at least 4 different years. Using this selection, we get very coherent progression subtypes yet have a large number of patients (10539) available.

We show in (Figure 2) the eGFR progression patterns for 9 clusters, representing the entire BioMe Biobank subcohort with at least 4 years of eGFR data. We have chosen 9 as the number of clusters as we have empirically observed it to be the minimum number that finds all the clinically meaningful main progression patterns and at least one cluster (C8, lowest eGFR values) with 100% enrichment of the ICD9 code 585 (Chronic kidney disease). As can be seen from the images, there is considerable noise in the data since eGFR measurements are inherently noisy and the trajectories from 10539 patients have been forced to 9 clusters. This noise could be reduced by using yearly medians instead of quarterly medians (with the cost of clinically important time resolution); even more coherent clusters could be sought by increasing the number of clusters.

In (Table 2) we demonstrate the median and interquartile range of the first and last time points of the eGFR of patients in each cluster, the mean duration (years) of data available, and the average slope of progression. Columns 4–7 show the values of the first and last points of the cluster trajectories (cluster centers) and the slope that has been fitted to the cluster trajectories. The values are in accordance with one another and with (Figure 2). Note that the median of the first values of the individual trajectories is different from the first point of the cluster trajectory since the patients in a cluster have their first time point (first visit to the clinic) at varying stages of the cluster trajectory (this also applies to the last time points). The accordance of the slopes of individual trajectories in a cluster with cluster trajectories is further visualized in (Figure 3).

Table 2.

Summary of the eGFR progression patterns

	Mean (S.d.) years eGFR data	Median first eGFR [IQR]	Median last eGFR [IQR]	Average ΔeGFR per year	Cluster center first eGFR	Cluster center last eGFR	Cluster center ΔeGFR per year
C1	7.5(2.3)	127.6[18.1]	120.3[17.1]	−1.6	142.9	86.9	−2.9
C2	7.6(2.4)	105.7[13.4]	98.7[14.8]	−0.9	105.9	91.2	−1.7
C3	6.9 (2.5)	50.3[28.1]	33.2[15.7]	−3.4	78.1	31.4	−3.4
C4	6.4(2.6)	108.0[18.0]	76.9[38.3]	−5.2	118.2	43.2	−7
C5	6.9(2.6)	93.8[12.4]	83.9[15.6]	−1.5	94.5	63.7	−2
C6	6.5(2.6)	80.9[14.4]	77.5[12.6]	−0.6	79.6	73.4	−0.7
C7	6.9(2.7)	58.2[15.8]	50.3[12.4]	−0.8	50.5	47.8	−1.4
C8	6.5(2.4)	26.9[31.9]	9.9[8.6]	−3.6	51.8	13.7	−2.5
C9	6.9(2.64)	74.2[16.4]	62.4[13.4]	−2.1	89.2	41.2	−1.6

Figure 3.

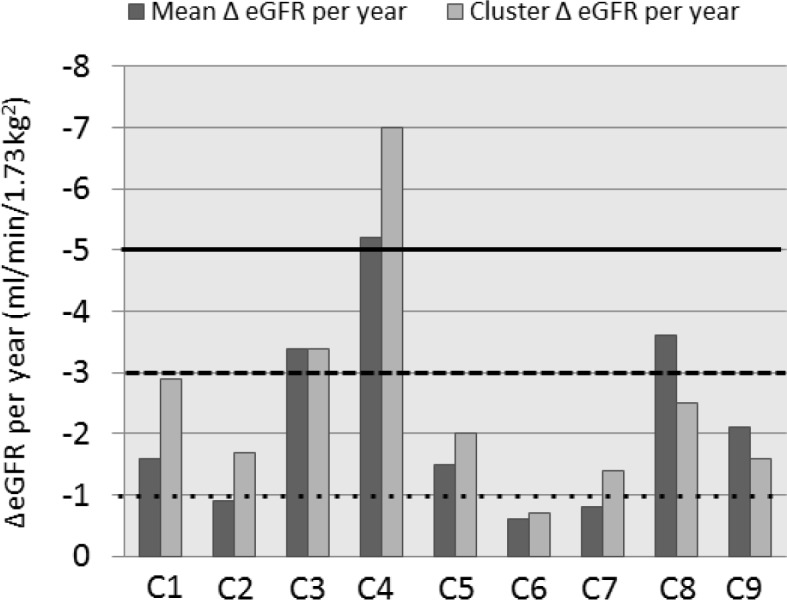
Bar graph of mean of eGFR change (ΔeGFR) per year (dark grey) and cluster center ΔeGFR (light grey) for patients in clusters C1 to C9. Lines indicate usual thresholds for nonprogression (dotted line), moderate progression (dashed line), and rapid progression (solid line).

In order to assess the clinical applicability and relevance of this clustering method, we hypothesized that demographic and disease patterns that were seen in longitudinal studies with similar patterns of eGFR progression would replicate independently in these clusters. In (Table 3) we show the mean and standard deviation of age, percentage of males and self-reported ethnicities (European ancestry (EA), African ancestry (AA), Hispanic/Latino (HL), Others) in each cluster. The star denotes clusters were the enrichment of a certain ancestry or gender was statistically significantly higher than for all the other patients using Fisher’s exact test (Bonferroni rate p = 10⁻⁷).

Table 3.

Demographic characteristics of clusters, of all the patients in the analysis and all the patients in the biobank

	Age [Sd]	Males (%)	EA (%)	AA (%)	HL (%)	Other (%)
C1	36.9[10.7]*	32	5.5	59.3*	32.1	3.1
C2	50.1[10.6]*	36	13.1	34.3*	46	6.6
C3	71.7[12.2]*	40	24.4	28	42	5.6
C4	49.7[13.3]*	32	14.1	44.3*	34.1	7.5
C5	57.8[11.0]*	37	22	26.1	44.9	7
C6	62.5[11.6]*	40	28.6*	22.4	42.2	6.9
C7	70.3[11.7]*	40	26.3*	25.3	41.6	6.8
C8	62.9[13.9]*	52*	14.9	40.7*	36.4	8
C9	66.1[11.1]*	37	25.3*	25	42.8	6.9
All	59.1[14.4]	38	21	30.2	42.1	6.7
ALL in Biobank	53.7[17.2]	41	30.8	24.3	35.3	9.6

Each cluster had a statistically significantly different mean age compared to the patients in the other clusters using t-tests.

Table 4 shows the percentage of patients in each cluster with a diagnosis of selected ICD9 codes (or a more specific ICD9 code in the same hierarchy). The star denotes clusters were the enrichment of ICD9 codes is statistically significantly high compared to all patients in the other clusters (pooled). The Bonferroni multiple correction rate is p = 10⁻⁷.

Table 4.

Distribution of ICD9 codes among clusters, of all the patients in the analysis and all the patients in the biobank

		C1	C2	C3	C4	C5	C6	C7	C8	C9	All	Biobank
585.xx	CHRONIC KIDNEY DISEASE (CKD) (%)	1	2	89*	21	4	6	55*	100*	21	21	12
585.6	END STAGE RENAL DISEASE (%)	0	0	14*	2	0	1	7	77*	1	5	2
v45.1x	RENAL DIALYSIS STATUS (%)	0	0	6	1	0	0	3	64*	0	3	1
403.xx	HYPERTENSIVE CHRONIC KIDNEY DISEASE (%)	0	1	67*	14	2	3	35*	93*	13	15	8
401.xx	ESSENTIAL HYPERTENSION (%)	43	62	95*	63	70	72	88*	97*	81*	73	52
250.xx	DIABETES MELLITUS (%)	31	36	65*	45	39	38	55*	65*	44	43	28
410.xx	ACUTE MYOCARDIAL INFARCTION (%)	1	2	12*	4	3	4	8	19*	6	5	3
414.xx	CHRONIC ISCHEMIC HEART DISEASE (%)	5	12	53*	20	18	22	41*	68*	31	25	20
428.xx	HEART FAILURE (%)	8	9	41*	18	10	10	28*	60*	18	17	10
584.xx	ACUTE KIDNEY FAILURE (%)	3	5	58*	22	5	8	30*	67*	17	16	8
285.xx	OTHER AND UNSPECIFIED ANEMIAS (%)	43	38	73*	42	31	30	50	92*	41	42	24

These demographics and ICD9 codes present an independent clinical validation of the relevance and applicability for the clustering patterns. For example; cluster 1 represents a group of patients that start at a high eGFR with the median eGFR being more than 120 ml/min/1.73m². Clinically, this represents a group of patients who have glomerular hyperfiltration (a precursor to developing kidney injury with elevated eGFR above 120 ml/min/1.73m²) which usually happens in younger patients who are usually African-American and occurs in the very early stages of diabetes mellitus and hypertension and thus might not have a confirmed diagnosis of them^10,11,12. As demonstrated in (Table 3 and 4); patients in cluster 1 are significantly younger than those in other clusters with a mean age of 36.9 years and have a lower prevalence of diabetes mellitus and hypertension as compared to the other clusters.

Clusters 3 and 8 provide more evidence for this validation. As shown in (Figure 2), these are clusters where patients starting from a CKD stage 3/4 with a mean eGFR of 50 and 27 ml/min/1.73m² progress rapidly to a low eGFR (mean eGFR of 33 and 10 ml/min/1.73m² respectively). These clusters have the highest prevalence of an ICD9 code for acute kidney injury (AKI), heart failure and anemia amongst the clusters. As shown in multiple studies, AKI^13,14, heart failure and anemia¹⁵ are very significant risk factors for both CKD progression and end stage renal disease (ESRD) development. This is further validated within these clusters since cluster 8 that has a higher prevalence of acute kidney injury, heart failure and anemia compared to cluster 3, also has a higher proportion of ESRD and dialysis and a lower final eGFR. Cluster 2 is an example of healthy patients with normal eGFR and they do not have many CKD diagnoses.

Thus we demonstrate that this automated machine learning approach organizes sparse and non-aligned data into coherent and clinically meaningful subtypes based on disease progression and this finds further independent validation after comparing demographics and ICD9 code enrichment.

Conclusions

We have demonstrated the use of clustering and alignment modelling for finding disease progression subtypes from highly incomplete EMR laboratory data. We have shown that using this type of modelling, we can use a large portion of a longitudinal dataset that has irregular time series of varying lengths and a high proportion of missing data. In particular, we have shown how to deal with the fact that there are no clear initial time points in the time-series; the solution is to align similar trajectories together. Our method was successful in finding from the data meaningful CKD progression patterns that correspond to known disease subtypes and stages.

The generative Bayesian modelling formalism is a flexible approach that allows for the construction of models that take into account all the necessary aspects of the modelling problem. In our case, clustering longitudinal data, alignment and dealing with missing data could all be done within a single unified model. We also successfully validated our clusters by association studies between the clusters, demographics and ICD9 diagnosis codes.

There are many potential applications for this approach. For instance, although novel genetic associations with eGFR have been reported, there are other potential genetic associations that explain the differential rates of CKD in different ethnic populations^16,17. However most genetic association studies are cross-sectional in nature and longitudinal studies require the resources of clinical cohorts. This clustering approach could be applied to evaluating genetic associations with longitudinal disease progression especially in institutions which have EMR linked biobanks. This is of special importance with national consortia such as the Electronic Medical Records and Genomics (eMERGE) Network, a NHGRI funded consortium tasked with developing methods and best-practices for the utilization of the Electronic Medical Record (EMR) as a tool for genomic research¹⁸. Also, since this approach can be deployed at multiple sites with EMR, a large number of patients can be used for modeling purposes that would not be possible in conventional longitudinal cohort studies.

In this paper, we considered the clustering of only one longitudinal variable, however, our model can be directly used for multiple variables. One can, for instance, cluster and align longitudinal eGFR, SBP and hemoglobin AIC data together in order to find clusters with similar progression in multiple variables. Adding more variables and increasing the number of clusters in the analysis can lead to discovering ever more specific clinical subtypes, critical in the future direction of personalized treatment decision support. Finally, though we used CKD as an example the opportunities for examining distinct disease progression subtypes and making innovative discoveries are endless in any disease area depending on available data in the EMR