Clinical Risk Prediction by Exploring High-Order Feature Correlations

Abstract

Clinical risk prediction is one important problem in medical informatics, and logistic regression is one of the most widely used approaches for clinical risk prediction. In many cases, the number of potential risk factors is fairly large and the actual set of factors that contribute to the risk is small. Therefore sparse logistic regression is proposed, which can not only predict the clinical risk but also identify the set of relevant risk factors. The inputs of logistic regression and sparse logistic regression are required to be in vector form. This limits the applicability of these models in the problems when the data cannot be naturally represented vectors (e.g., medical images are two-dimensional matrices). To handle the cases when the data are in the form of multi-dimensional arrays, we propose HOSLR: High-Order Sparse Logistic Regression, which can be viewed as a high order extension of sparse logistic regression. Instead of solving one classification vector as in conventional logistic regression, we solve for K classification vectors in HOSLR (K is the number of modes in the data). A block proximal descent approach is proposed to solve the problem and its convergence is guaranteed. Finally we validate the effectiveness of HOSLR on predicting the onset risk of patients with Alzheimer’s disease and heart failure.

1. Introduction

Predictive modeling of clinical risk, such as disease onset [1] or hospitalization [2], is an important problem in medical informatics. Effective risk prediction can be very helpful for the physician to make proper decision and provide the right service at point-of-care.

Typically we need three steps to perform patient clinical risk prediction:

1. Collecting all potential risk factors from patient historical data and utilizing them to properly represent each patient (e.g., as a vector [1][3]).

2. Identifying important risk factors from the risk factor pool collected in the first step, such that the value change of the selected risk factors could generate big impact on the predicted risk.

3. Training a proper predictive model based on the patients represented with the selected risk factors from the second step. Such model will be used to score the clinical risk of new testing patients.

One representative clinical risk prediction work that follows those three steps is the work by Sun et al. [1], where the goal is to predict the onset risk for potential heart failure patients. The authors first collect all potential risk factors from the two year patient electronic health records, and then designed an scalable orthogonal regression method to identify important risk factors, which will be used to train a logistic regression model for risk prediction at last. The authors showed that they can achieve the state-of-the-art performance as well as identify clinically meaningful risk factors for heart failure.

Note that in practice, depending on the concrete risk factor identification method and predictive model, step 2 and 3 could be combined into one step, i.e., a unified model can be constructed for both prediction and risk factor identification (e.g., LASSO [4]). This will make the constructed model more integrative and interpretable. Sparse Logistic Regression [5] is one such model. As is known to all that logistic regression is a popular model for clinical risk prediction [6] [1][3]. However, the pool of potential risk factors is usually very large and noisy, which would affect the efficiency and performance of predictive modeling. The main difference between sparse and convectional logistic regression is it adds an one norm regularizer on the model coefficients to encourage the model sparsity, so that only those important risk factors will contribute to the final predictions. In recent years people have also been doing research on constructing different regularization terms to enforce different sparsity structures on the model coefficients, such as the l_p norm [7], group sparsity [8] and elastic net regularization [9].

One limitation of the existing sparse logistic regression type of approaches is that they assume vector based inputs, which means that we need to have a vector based representation for each patient before we can use those methods to evaluate the patient’s clinical risk. However, we are in the era of big data with variety as one representative characteristic, so does medical data, i.e., there are many medical data are not naturally in vector form. For example, typical medical images (e.g., X-Ray and MRI) are two dimensional matrices, with some more advanced medical imaging technologies can even generate three-dimensional image sequences (e.g., functional Magnetic Resonance Imaging (fMRI)). In a recent paper, Ho et al. [10] proposed a tensor (which can be viewed as high order generalization of matrix) based representation of patient Electronic Health Records (EHRs) to capture the interactions between different modes in patient EHRs. For example, medication order information for every patient could be captured by a 2nd order tensor with 2 modes, where each mode is an aspect of a tensor: a) medication and b) diagnosis. With such a representation we can take into consideration the correlation between diagnosis and drugs when predicting the patient risk. If there are more inter-correlated modes in the data then we will need to represent the patient in higher order tensors. In these cases, if we still want to apply logistic regression one straightforward way is to stretch those matrices and tensors into vectors as people did in image processing, but this will lose the correlation information among different dimensions. Moreover, after stretching the dimensionality of the data objects will become very high, which will make traditional sparse logistic regression inefficient.

In recent years, there has been a lot of research on extending traditional vector based approaches to 2nd (matrix based) or higher order (tensor based) settings. Two representative examples are two-dimensional Principal Component Analysis (PCA) [11] and Linear Discriminant Analysis [12], which have been found to be more effective on computer vision tasks compared to traditional vector based PCA and LDA. Recently, Huang and Wang [13] developed a matrix variate logistic regression model and applied it in electroencephalography data analysis. Tan et al. [14] further extended logistic regression to tensor inputs and achieved good performance in a video classification task.

In this paper, we propose HOSLR, a High-Order Sparse Logistic Regression method that can perform prediction based on matrix or tensor inputs. Our model learns a linear decision vector on every mode of the input, and we added an ℓ₁ regularization term on each decision vector to encourage sparsity. We developed a Block Proximal Gradient (BPG) [15] method to solve the problem iteratively. The convergence of the proposed algorithm can be guaranteed by the Kurdyka–Lojasiewicz inequality [16] (for proof details please see a more technical version of this paper [17]). Finally we validate the effectiveness of our algorithm on two real world medical scenarios on the risk prediction of patients with Alzheimer’s Disease and Heart Failure.

The rest of this paper is organized as follows. Section 2 reviews some related works. The details along with the convergence analysis of HOSLR is introduced in Section 3. Section 4 presents the experimental results, followed by the conclusions in Section 5.

2. Related Work

Logistic regression [18] is a statistical prediction method that has widely been used in medical informatics [1][6][19]. Suppose we have a training data matrix X = [x₁, x₂, ⋯, x_n] ∈ ℝ^d×n, where x_i ∈ ℝ^d (1 ≤ i ≤ n) is the i-th training data vector with dimensionality d, and associated with each x_i we also have its corresponding label y_i ∈ {+1, −1}. The goal of logistic regression is to train a linear decision function f(x) = w^⊤x + b to discriminate the data in class +1 from the data in class −1 by minimizing the following logistic loss

$${\mathrm{\ell }}_{org}\left(\mathrm{w},b\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\log \left[1+\exp \left(-y_i\left({\mathrm{w}}^{\top }{\mathrm{x}}_i+b\right)\right)\right]}$$ (1)

where w ∈ ℝ^d is the decision vector and b is the bias. They can be learned with gradient descent type of approaches.

In many medical informatics applications, the data vectors ${\left\{{\mathrm{x}}_i\right\}}_{i=1}^n$ are sparse and high-dimensional (e.g., each patient could be a tens of thousands dimensional vector with bag-of-feature representation [1]). To enhance the interpretability of the model in these scenarios, we can minimize the following ℓ₁-regularized logistic loss

$${\mathrm{\ell }}_{sp}\left(\mathrm{w},b\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\log }\left[1+\exp \left(-y_i\left({\mathrm{w}}^{\top }{\mathrm{x}}_i+b\right)\right)\right]+\lambda {\Vert \mathrm{w}\Vert }_1$$ (2)

where ||·||₁ is the vector ℓ1 norm and λ > 0 is a factor trading off the prediction accuracy and model sparsity. The resultant model is usually referred to as sparse logistic regression model [5][20]. Compared with the conventional logistic regression model obtained by minimizing J_org, the w obtained by minimizing J_sp is sparse thanks to the ℓ₁ norm regularization. In this way, we can not only get a predictor, but also know what are the feature dimensions that are important to the prediction (which are the features with nonzero classification coefficients).

Sparse logistic regression has widely been used in health informatics because it can achieve a good balance between model accuracy and model interpretability. For example, sparse logistic regression has been used in the prediction of Leukemia [21], Alzheimer’s disease [22] and cancers [23]. In recent years people also designed different regularization terms [7][8][9] to enforce more complex sparsity patterns on the learned model. However, all these works require a vector based data representations. Under this framework, if the data naturally come as tensors (like medical imaging), we need to first stretch them into vectors before we can apply sparse logistic regression. This may lose the correlation structure among different modes in the original data, while for the HOSLR method proposed in this paper, we directly work with data in tensor representations. Fig. 1 provides a graphical illustration on the difference of traditional vector based logistic regression and high order logistic regression when working on multi-dimensional data.

Figure 1:

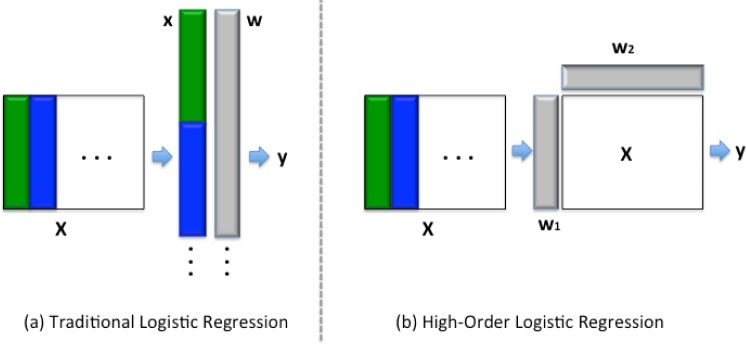
Traditional vector based logistic regression and high-order logistic regression work on multi-dimensional data.

3. Methodology

We introduce the details of HOSLR in this section. First we will formally define the problem.

3.1. Problem Statement

Without the loss of generality, we assume each observation is a tensor ${\mathcal{X}}^i\in {\mathcal{R}}^{d_1}{}^{\times d_2\times \cdots d_k}$, suppose its corresponding response is yⁱ ∈ {0, 1}, then HOSLR assumes

$$y^i\leftarrow {\mathcal{X}}^i{\times }_1{\mathrm{w}}^1{\times }_2{\mathrm{w}}^2\cdots {\times }_K{\mathrm{w}}^K+b$$ (3)

where ×_k is the mode-k product, and ${\mathrm{w}}^k\in {\mathrm{R}}^{d_k\times 1}$ is the prediction coefficients on the k-th dimension. Then

$${\mathcal{X}}^i{\times }_1{\mathrm{w}}^1{\times }_2{\mathrm{w}}^2\times \cdots {\times }_K{\mathrm{w}}^K={\displaystyle \sum _{i_1=1}^{d_1}{\displaystyle \sum _{i_2=1}^{d_2}\cdots {\displaystyle \sum _{i_K=1}^{d_k}{w}_{i_1}^1{w}_{i_2}^2\cdots w_{i_K}^K{\mathcal{X}}_{i_1{i}_2\cdots i_K}^i}}}$$ (4)

Let W = {w₁, w₂, ⋯, w_K} be the set of prediction coefficient vectors. The loss we want to minimize is

$$\begin{array}{l}\mathrm{\ell }\left(\mathcal{W},b\right)=\frac{1}{n}{\displaystyle \sum _{i=1}^n\mathrm{\ell }\left({\mathcal{X}}_i,y_i,\mathcal{W}\right)=\frac{1}{n}}{\displaystyle \sum _{i=1}^n\mathrm{\ell }\left(y_i,{\mathcal{X}}^i{\times }_1{\mathrm{w}}^1{\times }_2{\mathrm{w}}^2\cdots {\times }_K{\mathrm{w}}^K+b\right)}\\ =\frac{1}{n}{\displaystyle \sum _{i=1}^n\mathrm{\ell }\left(y_i,f_{\left(\mathcal{W},b\right)}\left({\mathcal{X}}^i\right)\right)}\end{array}$$

where for notational convince, we denote

$$f_{\left(\mathcal{W},b\right)}\left({\mathcal{X}}^i\right)={\mathcal{X}}^i{\times }_1{\mathrm{w}}^1{\times }_2{\mathrm{w}}^2\times \cdots {\times }_K{\mathrm{w}}^K+b$$ (5)

The loss function we considered in this paper is Logistic Loss:

$${\mathrm{\ell }}_1\left(\mathcal{W},b\right)=\log \left[1+\exp \left(-y_i{f}_{\left(\mathcal{W},b\right)}\left({\mathcal{X}}_i\right)\right)\right]$$ (6)

We also introduce the regularization term

$$\mathcal{R}\left(\mathcal{W}\right)={\mathcal{R}}_1\left(\mathcal{W}\right)+{\mathcal{R}}_2\left(\mathcal{W}\right)={\displaystyle \sum _{k=1}^K{\lambda }_k{\Vert {\mathrm{w}}^k\Vert }_1}+\frac{1}{2}{\displaystyle \sum _{k=1}^K{\mu }_k{\Vert {\mathrm{w}}^k\Vert }_2^2}$$ (7)

which is usually referred to as elastic net regularization [24]. This regularizer is a combination of ℓ₁ and ℓ₂ norm regularizations, thus it can achieve better numerical stability and reliability [24]. Then the optimization problem we want to solve is

$$\underset{\mathcal{W}}{\min }\mathcal{J}\left(\mathcal{W},b\right)=\mathrm{\ell }\left(\mathcal{W},b\right)+\mathcal{R}\left(\mathcal{W}\right)$$ (8)

We adopt a Block Coordinate Descent (BCD) procedure to solve the problem. Starting from some initialization (W₍₀₎, b₍₀₎), at the i-th step of the t-th round of updates, we update $({\mathrm{w}}_{\left(t\right)}^k,b_{\left(t\right)})$ by

$$\left({\mathrm{w}}_{\left(t\right)}^k,b_{\left(t\right)}\right)=\underset{\left(\mathrm{w},b\right)}{\arg \min }\left[\mathrm{\ell }\left({\mathcal{W}}_{\left(t\right)}^{1\sim \left(k-1\right)},\mathrm{w},{\mathcal{W}}_{\left(t-1\right)}^{\left(k+1\right)\sim K},b\right)+{\lambda }_k{\Vert \mathrm{w}\Vert }_1+\frac{{\mu }_k}{2}{\Vert \mathrm{w}\Vert }_2^2\right]$$

where ${\mathcal{W}}_{\left(t\right)}^{1\sim \left(k-1\right)}=\left\{{\mathrm{w}}_{\left(t\right)}^1,{\mathrm{w}}_{\left(t\right)}^2,\cdots ,{\mathrm{w}}_{\left(t\right)}^{k-1}\right\}$ and ${\mathcal{W}}_{\left(t-1\right)}^{\left(k+1\right)\sim K}=\left\{{\mathrm{w}}_{\left(t-1\right)}^{k+1},{\mathrm{w}}_{\left(t-1\right)}^{k+2},\cdots ,{\mathrm{w}}_{\left(t-1\right)}^K\right\}$.

Algorithm 1.

Block Coordinate Descent Procedure

3.2. Proximal Gradient Descent

Algorithm 2 summarized the whole algorithmic flow of our algorithm, where ${\alpha }_{\left(t\right)}^k={\lambda }_k/({\tau }_{\left(t\right)}^k+{\mu }_k)$ and $S_{{\alpha }_{\left(t\right)}^k}$ is the component-wise shrinkage operator defined as

$$\left(S_{{\alpha }_{\left(t\right)}^k}\left(\mathrm{v}\right)\right)=\{\begin{array}{ll}{v}_i-{\alpha }_{\left(t\right)}^k,& \text{if}{v}_i>{\alpha }_{\left(t\right)}^k\\ v_i+{\alpha }_{\left(t\right)}^k,& \text{if}{v}_i>-{\alpha }_{\left(t\right)}^k\\ 0,& \text{if}\left|v_i\right|\le |{\alpha }_{\left(t\right)}^k|\end{array}$$ (9)

At each iteration the most time consuming part is evaluating the gradient, which takes $O(n{\displaystyle {\prod }_{i=1}^K{d}_i})$ time, that is linear with respect to data set size and data dimension. The detailed algorithm derivation can be referred to [17].

Algorithm 2.

Block Proximal Gradient Descent for Multilinear Sparse Logistic Regression

4. Experiments

In this section we will present the experimental results on applying HOSLR to predict the onset risk of potential Alzheimer’s Disease patients from their fMRI images, and the onset risk of potential heart failure patients from their EHR data.

4.1. Experiments on Predicting the Onset Risk of Alzheimer’s Disease

Alzheimer’s disease (AD) is the most common form of dementia. It worsens as it progresses and eventually leads to death. There is no cure for the disease. AD is usually diagnosed in elder people (typically over 65 years of age), although the less-prevalent early-onset Alzheimer’s can occur much earlier. There are currently more than 5 million Americans living with Alzheimer’s disease and that number is poised to grow to as many as 16 million by 2050. The care for has been the country’s most expensive condition, which costs the nation $203 billion annually with projections to reach $1.2 trillion by 2050 [25].

Early detection of AD is of key importance for its effective intervention and treatment, where functional magnetic resonance imaging or functional MRI (fMRI) [26] is an effective approach to investigate alterations in brain function related to the earliest symptoms of Alzheimer’s disease, possibly before development of significant irreversible structural damage.

In this set of experiment, we adopted a set of fMRI scans collected from real clinic cases of 1,005 patients [27], whose cognitive function scores (semantic, episodic, executive and spatial - ranges between −2.8258 and 2.5123) were also acquired at the same time using a cognitive function test. There are three types of MRI scans that were collected from the subjects: (1) FA, the fractional anisotropy MRI gives information about the shape of the diffusion tensor at each voxel, which reflects the differences between an isotropic diffusion and a linear diffusion; (2) FLAIR, Fluid attenuated inversion recovery is a pulse sequence used in MRI, which uncovers the white matter hyperintensity of the brain; (3)

GRAY, gray MRI images revealing the gray matter of the brain. In the raw scans, each voxel has a value from 0 to 1, where 1 indicates that the structural integrity of the axon tracts at that location is perfect, while 0 implies either there are no axon tracts or they are shot (not working). The raw scans are preprocessed (including normalization, denoising and alignment) and then restructured to 3D tensors with a size of 134 × 102 × 134. Associated with each sample we have a label, which could be either normal, Mild Cognitive Impairment (MCI) or demented.

We constructed three binary classification problems to test the effectiveness of our HOSLR method, i.e., Normal vs. Rest (MCI and Demented), MCI vs. Rest (Normal and Demented), Demented vs. Rest (Normal and MCI). For HOSLR, because the input fMRI images are three dimensional tensors, we set the ℓ₁ term regularization parameters on all three dimensions equal, i.e., λ₁ = λ₂ = λ₃ and tune it from the grid {10⁻³, 10⁻², 10⁻¹, 1, 10, 10², 10³} with five fold cross validation. The ℓ₂ term regularization parameters are set to μ₁ = μ₂ = μ₃ = 10⁻⁴. For comparison purpose, we also implemented the following baseline algorithms:

• Nearest Neighbor (NN). This is the one nearest neighbor classifier with standard Euclidean distance.

• Support Vector Machine (SVM). This is the regular vector based SVM method.

• Logistic Regression (LR). This is the traditional vector based logistic regression method.

• Sparse Logistic Regression (SLR). This is the vector based sparse logistic regression.

• Multilinear Logistic Regression (MLR). This is equivalent to HOSLR with all ℓ1 regularization parameters setting to 0.

We use LIBLINEAR [28] for the implementation of LR and SLR, and LIBSVM [29] for the implementation of SVM. Note that in order to test those vector based approaches, we need to stretch those fMRI tensors into very long vectors (with dimensionality 1,831,512). Fig. 2 summarized the average performance over 5-fold cross validation in terms of Areas Under the receiver operating characteristics Curve (AUC) values. The data we used are the FLAIR images. From the figure we can observe that HOSLR beats all other competitors in all three tasks. This is because HOSLR can not only take into consideration the spatial correlation between three different dimensions in those fMRI images, but also exploring their joint sparsity structures (the FLAIR images are sparse in nature).

Figure 2:

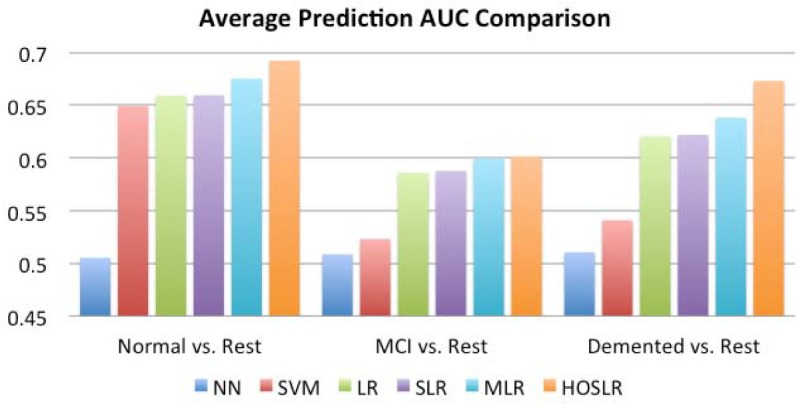
Average prediction AUC over 5-fold cross validation comparison for different methods.

4.2. Experiments on Predicting the Onset Risk of Congestive Heart Failure Patients

Congestive heart failure (CHF), occurs when the heart is unable to pump sufficiently to maintain blood flow to meet the needs of the body, is a major chronic illness in the U.S. affecting more than five million patients. It is estimated CHF costs the nation an estimated $32 billion each year [30]. Effective prediction of the onset risk of potential CHF patients would help identify the patient at risk in time, and thus the decision makers can provide the proper treatment. This can also help save huge amount of unnecessary costs.

The data set we use in this set of experiments is from a real world Electronic Health Record (EHR) data warehouse including the longitudinal EHR of 319,650 patients over 4 years. On this data set, we identified 1,000 CHF case patients according to the diagnostic criteria in [3]. Then we obtained 2,000 group matched controls according to patient demographics, comorbidities and primary care physicians similar as in [3]. We use the medication orders of those patients within two years from their operational criteria date (for case patients, their operational criteria dates are just their CHF confirmation date; for control patients that date is just the date of their last records in the database). On each medication order we use the corresponding pharmacy class according to the United States Pharmacopeial (USP) convention¹ and the primary diagnosis in terms of Hierarchical Condition Category (HCC) codes [31] for the medication prescription. In total there are 92 unique pharmacy classes and 195 distinct HCC codes appeared in those medication orders. Therefore each patient can be represented as a 92 × 195 matrix, where the (i, j)-th entry indicates the frequency that the i-th drug was prescribed during the two years with the j-th diagnosis code as primary diagnosis.

The parameters for HOSLR are set in the same manner as the experiments in last subsection. For comparison purpose, we also implemented NN, SVM, LR, SLR, MLR and reported the averaged AUC value over 5-fold cross validation along with their standard deviations on Fig. 3. From the figure we can get similar observations as we saw in Fig. 2.

Figure 3:

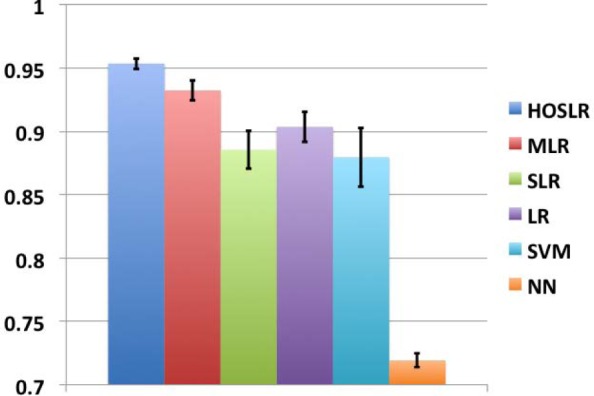
Prediction performance for different methods on the CHF onset prediction task in terms of averaged AUC value with 5-fold cross validation along with their standard deviations.

Another interesting thing to check is which medications and diagnosis play key roles during the decision. Because in this set of experiments we have two feature modes: medications and diagnosis, we will get two decision vectors w_med and w_diag, one on each mode. The bilinear decision function in this case can be written as

$$f\left(\mathrm{X}\right)={\mathrm{w}}_{\text{med}}^{\top }\mathrm{X}{\mathrm{w}}_{\text{diag}}=1^{\top }\left(\left({\mathrm{w}}_{\text{med}}{\mathrm{w}}_{\text{diag}}^{\top }\right)\odot \mathrm{X}\right)1$$ (10)

where 1 denotes all-one vector of appropriate dimension, ⊙ is element-wise matrix product. The importance of the (i, j)-th feature X_ij to the decision can be evaluated as w_med(i)w_diag(j). Therefore if both the magnitudes of w_med(i) and w_diag(j) are large, then the feature pair (medication i, diagnosis j) will definitely be important. We list in Table 1 the top diagnoses and medications according to their coefficient magnitudes in w_diag and w_med. From the table we can see that the diagnoses are mainly hypertension, heart disease and some common comorbidities of heart failure including chronic lung disease (e.g., Chronic Obstructive Pulmonary Disease (COPD) [32]) and chronic kidney disease [33]. The top medications include drugs for treating heart disease such as Beta blockers and calcium blockers, and medicine for treating lung disease such as Corticosteroids. There are also medicine for treating heart failure related symptom, such as Gout, which is a well-known Framingham symptom [34]. Vaccine is also an important treatment for reducing the stress on heart [35].

Table 1:

Top diagnosis and medications according to the magnitude of their corresponding decision coefficient

Diagnosis
Heart Disease	Congestive Heart Failure
	Acute Myocardial Infarction
	Specified Heart Arrhythmias
	Ischemic or Unspecified Stroke
Hypertension	Hypertension
	Hypertensive Heart Disease
Lung Disease	Fibrosis of Lung and Other Chronic Lung Disorders
	Asthma
	Chronic Obstructive Pulmonary Disease (COPD)
Kidney Disease	Chronic Kidney Disease, Very Severe (Stage 5)
	Chronic Kidney Disease, Mild or Unspecified (Stage 1–2 or Unspecified)

Medication
Antihyperlipidemic
Antihypertensive
Beta Blockers
Calcium Blockers
Cardiotonics
Cardiovascular
Corticosteriods
Diuretics
General Anesthetics
Gout
Vaccines

5. Conclusions

We propose a high order sparse logistic regression method called HOSLR in this paper, which can directly take data matrices or tensors as inputs and do prediction on that. HOSLR is formulated as an optimization problem and we propose an effective BCD strategy to solve it. We validate the effectiveness of HOSLR on two real world medical scenarios on predicting the onset risk of Alzheimer’s disease and heart failure. We demonstrate that HOSLR can not only achieve good performance, but also discover interesting predictive patterns.