Agreement of single- and multi-frequency Bioimpedance Measurements in hemodialysis patients: An Ancillary Study of the Frequent Hemodialysis Network (FHN) Daily Trial

Abstract

Background

Bioimpedance analysis (BIA) is well established to assess body composition. Agreements between single- and multi-frequency bioimpedance (SF-BIA, MF-BIS) assessments in subjects undergoing 6 or 3 times per week hemodialysis (HD) were analyzed.

Methods

Total body water (TBW), intra- and extracellular fluid (ICF, ECF) of subjects enrolled in the Frequent Hemodialysis Network (FHN) Daily Trial (www.clinicaltrials.gov # NCT00264758) were measured with a Hydra 4200 at baseline (BL) and at 5 months (M5). Volumes were computed using SF (at 50 kHz) and MF approaches. Agreement was assessed by means of Linear Regression and Bland-Altman analysis and treatment effects by T-Test.

Results

35 subjects (17 on the more frequent regimen, 26 male, 20 blacks, 48±9 years, pre-HD weight 84±19 kg) were studied. Assessments with SF-BIA and MF-BIS correlated significantly at BL and M5 in both arms. No proportional errors, but systematic biases over the entire range of values were found at BL and M5. Agreement did not differ between subjects randomized to either HD treatment arm at both time points. MF-BIS appears to have better precision than SF-BIA allowing the observation of a significant treatment effect by the intervention [−1.5 (95% CI −2.5 to −0.5) L] on ECF, not found for ECF SF-BIA. Precision also affected the statistical power of the SF-BIA data in the current analysis.

Conclusion

Both methods showed agreement without significant proportional errors regardless of HD frequency and can be used for longitudinal analyses. SF-BIA has lower precision which needs thorough consideration in the design of future trials with similar outcomes.

Introduction

Bioimpedance analysis (BIA) is a portable and relatively inexpensive tool for the assessment of body composition. A high level of reliability and good agreement to “gold-standard methods” has been reported for single-frequency BIA (SF-BIA) and multi-frequency bioimpedance spectroscopy (MF-BIS) [1–5].

Regression models, developed based on data from validation studies using “gold standard” methods such as magnetic resonance imaging, DEXA or isotope dilution, are used for the estimation of body composition of the body segment of interest using the collected bioimpedance data. The aforementioned good agreement to “gold standard” is only true for the method the regression model has been developed with, but may very well differ from other approaches based on other methods. Recent evidence suggests that at the current state-of-the-art no absolute correct measure [particularly for the assessment of extracellular fluid volume (ECF)] may exist since different dilution markers provide different volumes of distribution [5,6].

Most commonly used is the whole body bioimpedance technique, which measures whole body resistance and reactance and thus allows the estimation of total body water (TBW), ECF and intracellular fluid (ICF). From the technical point of view bioimpedance can be separated into two main categories: Methods using one frequency only (most commonly 5, 50 or 100 kHz) and those using multiple frequencies (mostly in the range from 5 to 1000 kHz).

The frequency determines whether the current penetrates the cells or remains in the extracellular compartment. Low frequencies pass through the extracellular compartment, whereas higher frequencies penetrate the cells. This allows the assessment of the resistance of both extra- and intracellular compartments [3]. By using the well-established Cole-model it is possible to distinguish extra- and intracellular resistance in the spectrum of frequencies [7]. Kotler and Wang have published models designed for SF-BIA and DeLorenzo for MF-BIS, however both studied patient populations did not include dialysis patients [3]. Evidence shows MF-BIS to be more accurate when compared to SF-BIA in determining fluid volumes [8,9].

Differences in body composition have also been reported to affect the accuracy and precision of bioimpedance methods for fluid volume estimation [10]. Accordingly, interventions which alter fluid overload and body hydration may potentially affect the accuracy and precision of used measurement techniques by introducing bias in the measurement. This may also affect the ability of a method to detect changes of either fluid volume over a defined period of time, as was for example reported for the comparison between whole body and segmental MF-BIS [11].

More frequent hemodialysis has been reported to affect interdialytic weight gains [12] and extracellular volume assessed by single-frequency bioimpedance [13]. To the best of the authors’ knowledge the potential bias introduced by a change in frequency of hemodialysis has not yet been investigated in detail.

The primary aim of this study was to investigate whether more frequent hemodialysis affects the agreement between the assessment of intra- and extracellular volume and total body water (TBW) during two different regimens of dialysis frequency using two technically and conceptually distinguished bioimpedance approaches: SF-BIA and MF-BIS. As the secondary aim both bioimpedance methods where used for the assessment of the treatment effect of increased HD frequency on all measured fluid volumes, ultrafiltration volume and pre HD weights. The tertiary aim was the determination of the statistical power of the treatment effect analysis with either method.

Methods

All patients enrolled in the FHN Daily Trial (www.clinicaltrials.gov #NCT00264758) from 07/2006 to 03/2010 at nine of the participating centers were approached for participation in this ancillary study to the main trial. Patients were enrolled at University of California, Davis, part of the California Consortium, and dialysis clinics of the Renal Research Institute (RRI) in the urban area of New York City, part of the RRI consortium (see Appendix and [14]). A detailed overview of the in- and exclusion criteria of the main trial has been published [15]. The study was approved by the Institutional Review Board of Beth Israel Medical Center and University of California Davis, and was conducted according to the Declaration of Helsinki. All patients signed informed consent.

Study design

This ancillary study followed enrolled subjects during the entire active study period in the prospective, randomized, controlled FHN Daily Trial. Patients enrolled in the main trial were randomized on a facility level to receive either more frequent (6 times per week) or a conventional (3 times per week) HD regimen. Due to the randomization on a facility base and the approach of all patients enrolled in the main trial, the study population of this ancillary study can be considered as being randomized to treatment arm allocation.

Measurements

Bioimpedance spectroscopy measurements were performed before dialysis treatment prior to randomization at Baseline and after 5 months into the trial by trained personnel. Measurements were conducted after patients were in a supine position for a minimum of 10 minutes. Electrodes attached at wrist and ankle measured intra- and extracellular resistance serving the computation of extra- and intracellular volume. All measurements were performed using the Hydra 4200 Bioimpedance Analyzer (San Diego, CA, USA) at the same time and the data were saved electronically for analyses.

Bioimpedance

Multi-frequency Bioimpedance Spectroscopy

Measurements of resistance, reactance and impedance at frequencies in the range from 5 to 1000 kHz were used for the calculation of extra-and intracellular resistance using the Cole Model [7] with software provided by the manufacturer. Extra- and intracellular resistances were used for the computation of ECF and ICF using the model developed by DeLorenzo et al. [3] (see Appendix). TBW was calculated as the sum of ECF and ICF.

Single-frequency Bioimpedance Analysis

Resistance and reactance data at 50 kHz was extracted for the computation of total body water and intracellular water employing the models developed by Kotler et al. [16] and Wang et al. [17] (see Appendix). ECF was calculated as the difference between TBW and ICF.

Statistical analyses

Data is reported as mean and standard deviation or 95% confidence intervals, as appropriate. P-values less than 0.05 were considered significant. All analyses were conducted with R version 3.0.3 (“Warm Puppy”; R Foundation for Statistical Computing; Vienna, Austria) [18] and the packages pwr and hydroGOF were used to perform the power calculation and the computation of the root mean square error (RMSE), respectively.

Agreement between methods

As the primary aim, the assessment of agreement between methods for this analysis follows the approach by Altman and Bland [18] and the assessment of the methods’ precisions: 1) Regression plot and visual inspection of data, 2) assessment of relative bias (difference between the methods) and the associated error (standard deviation of this difference), and 3) the assessment of measurement errors proportional to the mean [19].

Treatment effect

The secondary aim, the treatment effect on body fluid volumes, ultrafiltration volume and pre HD weight, between the study arms, was assessed following a two-step approach: First, the mean difference for each treatment arm between the volume estimation at Month 5 and at baseline was calculated, and then, in a second step, the difference between the differences in the treatment arm was used to compare the effectiveness of the intervention of increasing the dialysis frequency. Comparisons are reported as means and 95% confidence intervals (CI) and were formally tested using paired and Welch’s unpaired T-Test.

Power calculation

Based on the precision obtained from the data presented in this manuscript we estimated the statistical power at which we are able to draw conclusions in regard of our results. The effect size was estimated based on the treatment effect and the error of each respective method. Based on this effect size power and sample size, which would have been required in order to reach a power of 80%, were estimated.

Results

Data on recruitment efficiency [14], baseline characteristics [20,21] and on primary [12] and secondary outcomes [13,22] of the FHN Daily Trial have been published previously. Forty-eight patients were enrolled in the study. Of these 9 subjects were withdrawn from the main trial and measurements of 4 subjects could not be analyzed due to technical problems with the measurement data. Thus 35 subjects (see Table 1 for Demographics at Baseline) completed measurements at Baseline and Month 5 of the study and were included in this comparative analysis.

Table 1.

Demographics of a) all enrolled study subjects who completed all measurements and b) a subset of subjects who were randomized to the more frequent arm (6 times per week hemodialysis) and c) and those who were randomized to the conventional group (3 times per week hemodialysis). Continuous variables are displayed as mean±SD, categorical variables as count in the respective category.

	All Patients	Conventional subjects	Daily subjects	P-value
N	35	18	17	n/a
Age [years]	47.8±8.7	48.5±10.8	47.1±6.1	n.s.
Gender (male / female)	26/9	12/6	14/3	n.s.
Race (black / non-black)	15/20	8/10	7/10	n.s.
Pre-dialysis body weight [kg]	84.2±18.8	85.8±18.7	82.6±19.3	n.s.
BMI [kg/m2]	29.4±6.7	30.9±7.0	27.9±6.3	n.s.

Agreement between Methods

Total Body Water (TBW)

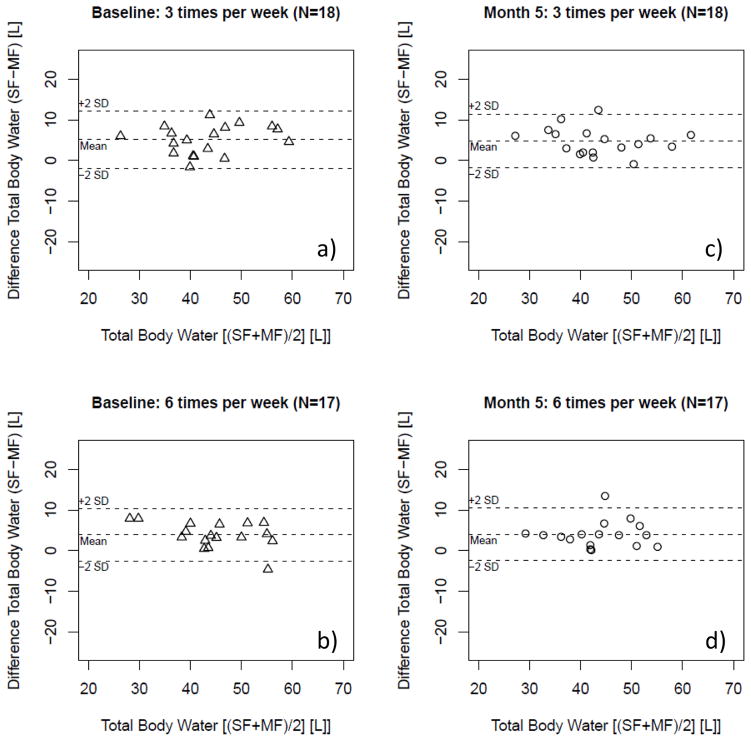
Measurement of TBW by both MF-BIS and SF-BIA values were correlated [in those randomized to the more frequent arm (6 times a week dialysis): R² of 0.88 (P<0.01); and in those randomized to the conventional arm (3 times a week dialysis): R² of 0.83 (P<0.01)]. Figure 1 shows the corresponding Regression plots. The data showed on average a significant systematic bias with SF yielding higher values than MF-BIS (see Table 3, Figure 2), but no proportional error was evident (see Figure 2).

Figure 1.

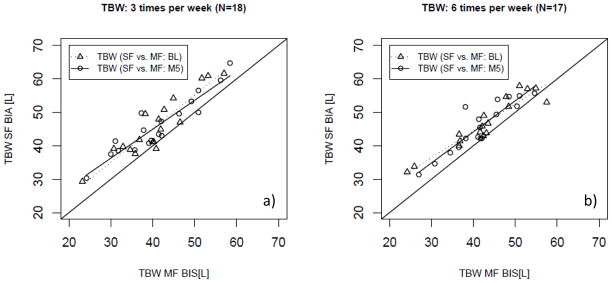
Regression Analysis of total body water (TBW) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in a) the conventional (3 times per week hemodialysis; N=18) and b) the interventional (more frequent hemodialysis 6 times per week hemodialysis; N=17) arm at baseline and 5 months after randomization.

Table 3.

Systematic biases between assessments of total body water (TBW), intra- and extracellular water (ICF, ECF) by single- and multi-frequency bioimpedance (SF-BIA, MF-BIS) at Baseline and at Month 5 of the study, and the treatment effect of more frequent hemodialysis [6 times per week hemodialysis (HD)]. Data on systematic bias and treatment effects reported as mean differences and 95% confidence intervals.

Parameter	Baseline		Month 5		Treatment effect of 6 times per week hemodialysis.
	Conventional HD (SF-BIA -MF- BIS)	More frequent HD (SF-BIA - MF-BIS)	Conventional HD (SF-BIA - MF- BIS)	More frequent HD (SF-BIA - MF-BIS)
TBW [L]	5.1 (3.5 to 6.7)	3.9 (2.4 to 5.4)	4.8 (3.3 to 6.3)	4 (2.5 to 5.6)	0.4 (−1.8 to 2.7)
ICF [L]	1 (−1.1 to 3)	0.3 (−1.2 to 1.8)	0.2 (−0.8 to 1.2)	0.2 (−0.7 to 1.2)	0.7 (−1.5 to 2.8)
ECF [L]	4.1 (2.7 to 6.2)	3.6 (2.6 to 4.5)	4.6 (3.5 to 5.6)	3.8 (2.5 to 5.1)	−0.2 (−1.8 to 1.3)

Figure 2.

Bland-Altman plot of total body water (TBW) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in the conventional (3 times per week hemodialysis; N=18) and the interventional (more frequent hemodialysis 6 times per week hemodialysis; N=17) arm at baseline [a) and b)] and 5 months [c) and d)] after randomization.

Among subjects who had been randomized to more frequent HD for 5 months, both MF-BIS and SF-BIA assessment of TBW correlated [more frequent: R² of 0.80 (P<0.01); conventional: R² of 0.86 (P<0.01)] (Figure 1). As observed at baseline, SF-values were significantly greater (Table 3, Figure 2), but without proportional error (Figure 2). The analysis of the agreement of TBW between both arms did not significantly differ from baseline or between the treatment arms following randomization (Table 3) as shown by the treatment comparison (Table 3).

Intracellular Fluid (ICF)

In regression analysis ICF assessments using MF-BIS and SF-BIA correlated significantly [more frequent: R² of 0.72 (P<0.01); conventional: R² of 0.60 (P<0.01)] (Figure 3). The values obtained with the SF method and MF method did not show a significant bias (Table 3). No proportional error was observed in the data (Figure 4). ICF MF-BIS and SF-BIA assessments after 5 months in those patients randomized to receive HD 6 times per week showed a significant correlation [more frequent: R² of 0.85 (P<0.01); conventional: R² of 0.87 (P<0.01)] (Figure 3). Consistent with the baseline assessment the SF values did not show a significant bias and did not show a proportional error (see Table 3, Figure 4). The treatment comparison showed that treatment allocation did not significantly affect the systematic bias between SF-BIA and MF-BIS (see Table 3).

Figure 3.

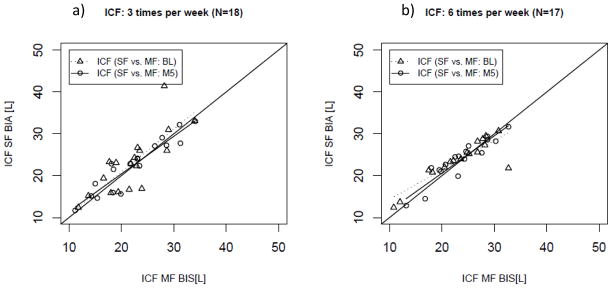
Regression Analysis of intracellular fluid volume (ICF) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in a) the conventional (3 times per week hemodialysis; N=18) and b) the interventional (more frequent hemodialysis 6 times per week; N=17) arm at baseline and 5 months after randomization.

Figure 4.

Bland-Altman plot of intracellular water (ICF) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in the conventional (3 times per week hemodialysis; N=18) and the interventional (more frequent hemodialysis 6 times per week hemodialysis; N=17) arm at baseline [a) and b)] and 5 months [c) and d)] after randomization.

Extracellular Fluid (ECF)

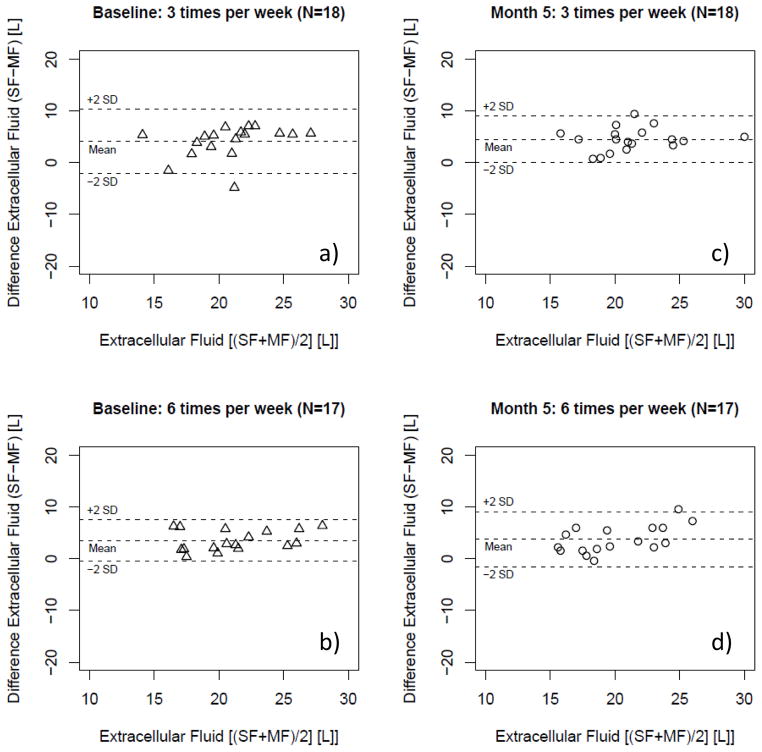
ECF assessment with MF-BIS and SF-BIA correlated significantly [more frequent: R² of 0.74 (P<0.01); conventional: R² of 0.37 (P<0.01)] (Figure 5). The values obtained with the SF method were systematically greater than those assessed with MF (Table 3, Figure 6). No proportional error was observed in the data (Figure 6).

Figure 5.

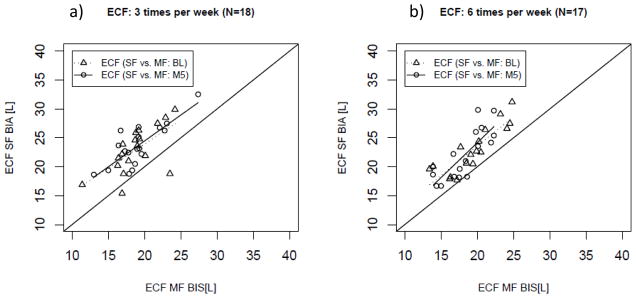
Regression Analysis of extracellular fluid volume (ECF) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in a) the conventional (3 times per week hemodialysis; N=18) and b) the interventional (more frequent hemodialysis 6 times per week hemodialysis; N=17) arm at baseline and 5 months after randomization.

Figure 6.

Bland-Altman plot of extracellular fluid volume (ECF) as estimated per single- and multi-frequency (SF; MF) bioimpedance in patients randomized in the conventional (3 times per week hemodialysis; N=18) and the interventional (more frequent hemodialysis 6 times per week hemodialysis; N=17) arm at baseline [a) and b)] and 5 months [c) and d)] after randomization.

Five months into the study SF-BIA values also correlated significantly [more frequent: R² 0.61 (P<0.01); conventional: R² 0.61 (P<0.01)] (Figure 5). Values estimated with SF-BIA were again higher than MF-BIS values regardless of treatment allocation (see Table 3, Figure 6). The data showed no proportional error in Bland-Altman analysis (Figure 3). Treatment comparison showed that treatment allocation did not significantly affect the systematic bias between SF-BIA and MF-BIS (Table 3). At both baseline and at month 5, the bias observed in TBW was similar to that observed in measurement of ECF.

Treatment effect of more frequent hemodialysis (HD)

The comparison of the precision at each time point showed no treatment effects on the precision of all volume estimations (reflected by the confidence intervals at each time point in the Table 2 and Table 3) using either measurement method (see Table 2 for univariable treatment effects of more frequent dialysis).

Table 2.

Treatment effect of the more frequent hemodialysis (6 times per week as compared to 3 times per week) on total body water, extra- and intracellular volume as measured by single- and multi-frequency bioimpedance (SF, MF), ultrafiltration volume and pre HD body weight of enrolled study subjects, who completed all measurements until Month 5 (18 conventional subject, 17 daily subjects). Data are presented as mean ± SD or mean and 95% CI as indicated.

Outcome	Method	Treatment	Baseline	Month 5	Change (Month 5 – Baseline)	Treatment effect of 6 times per week hemodialysis.
TBW [L]	MF BIS	conventional	40.7+/−8.2	41.3+/−9.3	0.6 (−5.3 to 6.6)	−1.8 (−4.2 to 0.6)
		more frequent	42.8+/−9.1	41.7+/−7.3	−1.1 (−6.9 to 4.6)
	SF BIA	conventional	45.8+/−9	46.1+/−8.6	0.3 (−5.7 to 6.3)	−1.3 (−3.1 to 0.5)
		more frequent	46.7+/−7.8	45.7+/−7.5	−1 (−6.3 to 4.3)
ICF [L]	MF BIS	conventional	22+/−5.6	22.3+/−6.5	0.3 (−3.8 to 4.5)	−0.3 (−2.4 to 1.8)
		more frequent	23.4+/−6.1	23.5+/−5.2	0.1 (−3.9 to 4)
	SF BIA	conventional	22.9+/−7.3	22.5+/−6.3	−0.4 (−5 to 4.2)	0.4 (−1.6 to 2.3)
		more frequent	23.7+/−5	23.7+/−5	−0.1 (−3.5 to 3.4)
ECF [L]	MF BIS	conventional	18.7+/−3.1	19+/−3.3	0.3 (−1.8 to 2.5)	−1.5 (−2.5 to −0.5)
		more frequent	19.4+/−3.5	18.2+/−2.8	−1.2 (−3.4 to 1)
	SF BIA	conventional	22.9+/−4	23.6+/−3.7	0.7 (−1.9 to 3.3)	−1.7 (−3.5 to 0.1)
		more frequent	23+/−4	22+/−4.3	−0.9 (−3.9 to 2)
UFV (per session [L])**	flowmeter	conventional	3.3±0.8	3.2±1.0	−0.1 (−0.9 to 0.6)	−1.0 (−1.6 to −0.4)*
		more frequent	3.2±0.9	2.0±0.6	−1.2 (−1.7 to −0.5)
Pre HD weight [kg]	weighing scale	conventional	85.8±18.7	85.6±17.3	−0.2 (−12.4 to 12.0)	0.9 (−3.8 to.5.6)
		more frequent	82.6±19.3	83.3±18.3	0.7 (−12.4 to 13.9)

^*and bold letters indicates P<0.05.

^**data only available from 14 daily and 13 conventional subjects.

Measured by MF-BIS and SF-BIA, TBW showed a non-significant trend to decrease from Baseline to Month 5 of the study. It is of note that the treatment effect estimated by MF-BIS is larger in magnitude compared to SF-BIA (Table 2).

ICF measured at Month 5 by both methods was not significantly different from Baseline. (Table 2) and no significant treatment effect by the intervention was found.

A significant treatment effect was detected when change was quantified using MF-BIS, which, while similar in magnitude, was not significant when measured with SF-BIA (Table 2). Paired analysis of changes in ECF measured by MF-BIA showed a significant treatment effect while SF-BIA did not achieve significance (Table 2). Pre HD weight did not show any significant changes and no treatment effect. Ultrafiltration volume was significantly lower in those randomized to the more frequent arm due to the shorter interdialytic period.

Power calculation

The treatment effect on ECF estimated with MF-BIS was significant [−1.5 (95% CI −2.5 to −0.5 with an estimated power of 83%) L] but not significant with SF-BIA [−1.5 (95% CI −3.5 to 0.1) L] with a probability of 58% to accept the null-hypothesis despite a significant difference being present (Type II error); (Table 2)]. Based on these data of ECF it would have required 86 subjects to be measured with SF-BIA to achieve a statistical power of 80% (as commonly targeted for clinical trials).

Discussion

Statement of principal findings

The primary analysis showed that changes in frequency of dialysis treatment, which have been shown to be associated with significant changes in interdialytic weight gain [12] and a decrease in both TBW and ECF as measured by SF-BIA [13], did not affect the agreement (evaluated by Bland Altman Analysis) between TBW, ICF and ECF values estimated by SF-BIA and MF-BIS. Correlations between the assessments using both methods were significant at all time points. Regardless of the limitations of correlational analysis (mainly that the actual coefficient is dependent on the broadness of the range of values) in the context of an analysis testing the agreement between two methods [18,23], the good correlation in concert with a constant systematic error which is independent of the actual value, this analysis suggested that the precision between SF-BIA and MF-BIS is not affected by HD frequency, and subsequent change in the relative hydration of either the extracellular or intracellular compartment. No conclusion on the actual accuracy can be made based on these data, but the treatment comparison clearly shows that treatment allocation did not affect the systematic bias or the precision (reflected by the standard deviations of the measurements) between SF-BIA and MF-BIS.

As a secondary aim the changes from baseline to Month 5 were estimated, the treatment effects were calculated from these changes and compared between the methods. Only MF-BIS was able to capture a borderline significant treatment effect on ECF, while SF-BIA showed only a non-significant trend. Treatment effects on the other fluid volumes were not significant with either method. The lack of statistical power and sufficient precision is likely to be the reason for not finding the results reported by Kaysen et al. with all methods [13]. We can conclude from our data that the significant treatment effect on ECF by the intervention seen with the use of MF-BIS but not with the SF-BIA, was a consequence of the higher precision found for MF-BIS as compared to SF-BIA in the estimation of ECF. This suggests that the higher level of precision has enabled MF-BIS to detect the treatment effect. Thus for the design of future studies the use of MF-BIS may be beneficial and require a lower recruitment target.

Comparison to other studies

It was reported, in a randomized cross-over study inducing deviations from euvolemia by either administering Ringer’s Lactate infusion or a potent loop diuretic, a more accurate assessment (in relation to bromide space assessments) after 2 hours of treatment of volume changes using MF-BIS compared to SF-BIA in 27 healthy subjects [4]. The accuracy of MF-BIS and SF-BIA in detecting intradialytic volume changes compared to ultrafiltration volume as the reference method was recently studied in a non-randomized cohort of Chinese dialysis patients [8]. The precision reported in the results of this study was comparable to our data and the comparison to weight change suggested MF-BIS to be more accurate in detecting short term changes in body volumes. [8]. A comparable precision of the measurements at all time points and in both treatment arms suggests that, despite the reportedly slightly better accuracy of MF-BIS, SF-BIA appears to be an equally valid and useful tool for longitudinal analyses. Of note, both methods provide non biased values in measurements of ICF. The difference in the estimation of ECF accounts for the difference observed in the values reported for TBW, whereas ICF shows comparable results. It may also be added that a more recently developed model designed for the use with MF-BIS also incorporating the body mass index as an additional input parameter may show improved accuracy and precision and be subject of future studies [24,25].

One of the major strengths of this analysis is the prospective study design and the randomization of patients after the baseline assessments. There had not been any significant differences between the subject groups suggesting a successful randomization of the studied subjects in the main trial (Table 1 and Table 2) [21]. Subjects enrolled in the FHN Daily Trial were reportedly generalizable to the hemodialysis population in the United States as per data of the United States Renal Data System [21], which suggests that also our data may be considered generalizable. Furthermore, measurements were done at the same time, location and condition in each of the study sites and also that all repeat measures carried out in the same patients were done with the same device, which excludes the possibility of differences between used devices, electrodes and similar potentially confounding factors.

The main weakness is an inability to draw conclusions on the accuracy of the measurements due to the lack of comparison against dilution methods such as total body potassium and deuterium-oxide or an extracellular space marker such as bromide, inulin or iothalamate. The small sample size is an additional weakness.

Our data suggest that body fluid volume and distribution are both affected by increases in hemodialysis frequency without altering the agreement between SF-BIA and MF-BIS. In the absence of data from dilution methods it is difficult to judge the accuracy of either method. However, in terms of precision, MF-BIS appears to perform better. This appears to be particularly true for ECF estimation where this technique detected a significant treatment effect which was not detected in the SF-BIA data (despite similar overall changes in volume). The trends found in this analysis are consistent with the data reported by Kaysen et al. [13] showing significant changes in TBW and ECF. The differences in precision of both methods however, do affect the power of the analysis. Kaysen et al. reported a treatment effect (Month 5 – BL) on ECF of −1.3 [95% CI −1.9 to −0.7 with an estimated power of 98% (n=134)] [13]. The comparably lower power which was evident in our data (power of 83% with MF-BIS and 42% only with SF-BIA) strongly suggests that the lack of significance for SF-BIA can entirely be explained by the small sample size. The effects on the power of our analysis were substantial and for SF-BIA the number of patients required to find a treatment effect at a power of 80% would have been substantially larger for SF-BIA (N=86). These findings may be of particular importance when trials are designed and recruitment aims are set. Methods with higher precision and sensitivity for treatment effects of studied interventions may be considered to need less enrolled subjects to successfully show effects of the studied intervention. However the level of precision unaffected by factors resulting from change in frequency such as fluid overload and interdialytic weight gain, confirms the usefulness of either technique in drawing conclusions about changes in TBW and its distribution in prospective longitudinal settings.

The main question of the accuracy of the techniques could not be adequately addressed in this analysis and remains a field for future research. However, this study aimed to assess the usefulness of both techniques for the use in longitudinal settings, which is supported by a good degree of precision unaffected by change in treatment frequency.

Appendix

Dialysis Clinics of Enrollment

Renal Research Institute Consortium

Irving Place Dialysis Center, Queens Artificial Kidney Center, South Queens Dialysis Center, Southern Manhattan Hemodialysis Center, St. Alban’s Dialysis, Upper Manhattan Dialysis Center, Yorkville Dialysis Center. California Consortium: University of California Davis, DCI University Dialysis Clinic, Sacramento, Calif., USA

Multi-Frequency Bioelectrical Impedance Spectroscopy

According to the Model developed by De Lorenzo et al., based on the Cole-Cole Model and the Hanai Theory, calculation of intracellular fluid volume (V_ICF) [L] and Total Body Fluid (TBW) [L] requires the calculation of extracellular volume (V_ECF) [L] as

$$V_{\mathit{ECF}}={\left(\frac{40.5K_B{\mathit{height}}^2\sqrt{\mathit{weight}}}{1,025R_e}\right)}^{\frac{2}{3}}$$ (1a)

or men and,

$$V_{\mathit{ECF}}={\left(\frac{39.0K_B{\mathit{height}}^2\sqrt{\mathit{weight}}}{1,025R_e}\right)}^{\frac{2}{3}}$$ (1b)

for women,

where R_E is the extracellular resistance [Ω] deriving from Model Fitting using the Cole-Cole Model, height the height of the subject [cm], weight the body mass [kg] and KB the geometry constant (assumed to be 4.3) [3, 26].

Intracellular volume is then calculated as

$$V_{\mathit{ICF}}=V_{\mathit{ECF}}\left({\left[\frac{{\rho }_{\mathit{MIX}}\left(R_i+R_e\right)}{40.5R_i}\right]}^{\frac{2}{3}}-1\right)$$ (2a)

for men and,

$$V_{\mathit{ICF}}=V_{\mathit{ECF}}\left({\left[\frac{{\rho }_{\mathit{MIX}}\left(R_i+R_e\right)}{39.0R_i}\right]}^{\frac{2}{3}}-1\right)$$ (2b)

for women,

where

$${\rho }_{\mathit{MIX}}=273.9-(273.9-40.5){\left(\frac{R_i}{R_i+R_e}\right)}^{\frac{2}{3}}$$ (3a)

for men and,

$${\rho }_{\mathit{MIX}}=264.9-(264.9-39.0){\left(\frac{R_i}{R_i+R_e}\right)}^{\frac{2}{3}}$$ (3b)

for women,

where R_e and R_i are intra- and extracellular resistance deriving from Model Fitting using the Cole-Cole Model, respectively [3, 26].

In a final step TBW is then calculated as

$$\text{TBW}={\mathrm{V}}_{\text{ECF}}+{\mathrm{V}}_{\text{ICF}}$$ (4)

Single-Frequency Bioelectrical Impedance Analysis

According to the model by Kotler et al.[16] Total Body Water (TBW) can be calculated as

$$\mathit{TWB}=0.58\left[\frac{L^{1.62}}{Z^{0.70}}\frac{1.0}{1.35}\right]+0.32\mathit{weight}-3.66$$ (5a)

for men, and

$$\mathit{TWB}=0.76\left[\frac{L^{1.99}}{Z^{0.58}}\frac{1.0}{18.91}\right]+0.14\mathit{weight}-0.86$$ (5b)

for women,

where L is the height [cm], Z the electrical impedance and weight the body mass [kg] [16].

Total body potassium (TBK) [mmol] can be calculated as

$$\mathit{TBK}=0.76\left[\frac{L^{1.60}}{X_{cp}^{0.50}}(59.06)\right]+18.52\mathit{weight}-386.66$$ (6a)

for men, and

$$\mathit{TBK}=0.96\left[\frac{L^{2.07}}{X_{cp}^{0.36}}(1.30)\right]+5.79\mathit{weight}-230.51$$ (6b)

for women,

where L is the height [cm], X_cp the reactance [Ω] and weight the body mass [kg] [16].

The ICV estimation based on the TBK [mmol] is conducted under the assumption that intracellular K⁺ concentration is considerably stable at around 152 mEq/l and allows, in the knowledge of TBW, the estimation of the intracellular K⁺ distribution volume [17].