Abstract
Purpose
Head motion is a significant problem in diffusion-weighted imaging as it may cause signal attenuation due to residual dephasing during strong diffusion encoding gradients even in single-shot acquisitions. Here, we present a new real-time method to prevent motion-induced signal loss in DWI of the brain.
Methods
The method requires a fast motion tracking system (optical in the current implementation). Two alterations were made to a standard diffusion-weighted echo-planar imaging sequence: first, real-time motion correction ensures that slices are correctly aligned relative to the moving brain. Second, the tracking data are used to calculate the motion-induced gradient moment imbalance which occurs during the diffusion encoding periods, and a brief gradient blip is inserted immediately prior to the signal readout to restore the gradient moment balance.
Results
Phantom experiments show that the direction as well as magnitude of the gradient moment imbalance affects the characteristics of unwanted signal attenuation. In human subjects, the addition of a moment-restoring blip prevented signal loss and improved the reproducibility and reliability of diffusion tensor measures even in the presence of substantial head movements.
Conclusion
The method presented can improve robustness for clinical routine scanning in populations that are prone to head movements, such as children and uncooperative adult patients.
Keywords: diffusion weighted imaging, signal loss, real-time motion tracking, gradient moment restoration
INTRODUCTION
Head motion during diffusion-weighted imaging (DWI) remains a problem both in the research and clinical settings. The strong diffusion gradients that sensitize DWI to incoherent microscopic water motion also cause phase changes and signal loss in the presence of bulk head motion (1,2). While subject motion during structural imaging typically results in motion artifacts, such as blurring, motion during DWI can lead to partial or complete signal loss due to signal dephasing within the voxels. DWI uses large amplitude and long duration diffusion gradients, making DWI more sensitive to the detrimental effects of motion than most other MRI techniques. Additionally, advanced applications of DWI, such as HARDI, q-ball (3,4), and diffusion spectrum imaging (5), use a large number of gradient directions, resulting in longer scan times and increased likelihood of involuntary subject motion. Such applications also routinely use high b-values (>1000 s/mm2), which exacerbate motion-related signal losses even further. Considering the clinical importance of DWI in evaluating neurological diseases, notably acute ischemic stroke (6) and multiple sclerosis (7), the need for robust motion- tolerant DWI is great.
Several prior studies have addressed the effects of motion in DWI scans. Retrospective corrections can eliminate in-plane spatial misalignment by volume-to-volume (8) or slice-to-volume (9) realignment, but fail to correct effects of through-plane motion that cause inconsistent slice excitation. Prospective techniques (10), relying on navigators (11–19) or external tracking devices (20–22), adjust scan geometry in real-time and thus reduce the effects of both in-plane and through-plane motion. Aksoy et al. (22) used an optical tracking device to track head motion during DWI and updated the position and orientation of the imaging volume before acquisition of each slice. Although these methods can improve the quality and reproducibility of DWI measures, none can correct the most severe artifact commonly seen in DWI—signal loss caused by uncorrected motion during the diffusion encoding gradients (23).
For subject motion-induced signal loss, one possible solution is to discard DWI volumes displaying obvious artifacts during postprocessing, or alternately reacquire corrupted volumes in real time (18,24). These methods attempt to reduce the effect of the signal loss, but discarding of volumes decreases the robustness of tensor measures, and reacquisition increases the scan time. Additionally, such methods do not truly prevent or restore the signal loss, and it may be difficult to determine which volumes are affected by more subtle artifacts. Therefore, restoration of motion-induced signal loss should ideally be performed using a real-time approach. Only one paper has demonstrated elimination of motion-induced signal loss (25), using continuous real- time updates of diffusion gradients. However, the technique requires complex programming of gradient pulses including continuous direction updates, which may not be easily implemented on all scanner platforms, and is sensitive to delays in pose information provided by the tracking system.
Herein, we present a novel method to eliminate movement-induced signal loss in diffusion-weighted MRI. In brief, the technique uses a fast optical tracking system (26) that provides accurate head motion data in real-time. A DW echo-planar imaging (EPI) pulse sequence (27) was modified to dynamically update all slice positions (excitation and refocusing pulses), and calculate motion-induced gradient imbalances. The correct gradient moment was restored by inserting a brief gradient blip immediately prior to the signal acquisition, thereby reducing or eliminating signal attenuation. While the approach is demonstrated using an EPI-based DWI sequence, it is equally applicable to any other readout trajectory including multi spin-echo, Periodically Rotated Overlapping Parallel Lines with Enhanced Reconstruction (PROPELLER) or spiral acquisitions.
THEORY
In this section, it is shown that, in the presence of a field gradient, head translations result in a global phase shift and head rotations induce a spurious gradient moment (1). The excess gradient moment causes signal loss and location-dependent phase shifts.
Modeling the head as a rigid body, we can completely specify its orientation at time t by a translation vector and a rotation matrix . The phase accumulated by a spin with initial position during an arbitrary gradient waveform is given by:
| [1] |
The first term in Eq. [1] represents the effects of pure translation on the spin phase. Importantly, this term is independent of , and hence leads to a global phase shift. Given an accurate estimate of , this phase shift can be calculated and corrected by adjusting the receive phase of subsequent analog-to-digital-converter events or by adjusting the image phase during reconstruction. In this work, we consider single-shot magnitude images only and, therefore, ignore this term. However, the correction of this global phase shift is easily possible with the proposed method.
The second term in Eq. [1] can be rearranged to give
| [2] |
where we have defined an effective gradient moment as:
| [3] |
Note that, for the purpose of computing , refocusing radiofrequency pulses are equivalent to reversing the sign of . If there is no motion, the rotation matrix is unity and the integral in Eq. [3] yields zero at the echo time, since the pulse sequence, including the diffusion encoding gradients, is usually balanced. However, in case of rotational motion during the (diffusion) gradients, there will be an excess (non-zero) gradient moment after the diffusion preparation as per Eq. [3], i.e. the gradients appear unbalanced in object coordinates. Thus, the effect of rotational motion between excitation and readout is mathematically equivalent to an additional gradient moment (23).
The gradient moment will result in position- dependent phase accumulation according to Eq. [1], and its effect on the signal will be different for the in-plane and through-plane directions of the gradient moment. If the signal immediately after excitation is denoted by S0, then the effect of an excess through-plane (z) gradient moment (Mz) on the signal of a slice of thickness Δz (rectangular slice profile) can be obtained by integrating the signal along the slice direction:
| [4] |
The signal will be reduced by 1/2 when
| [5] |
Conversely, an in-plane gradient moment () acts as an unwanted frequency or phase-encoding gradient and shifts samples in k-space. When the k-space shift is larger than the k-space extent, a sudden, dramatic signal loss occurs. Therefore, the signal loss as a function of is almost a step function (23). In-plane motioninduced signal loss occurs when
| [6] |
where Δxi is the voxel size for any given coordinate direction xi (23). Note that for typical voxel sizes and slice thickness, signal loss due to in-plane gradient moments (Eq. [6]) occurs for smaller moments than for through-plane moments (Eq. [5]).
METHODS
DWI Sequence and Motion Correction
Experiments were performed on a Siemens 3 T TIM Trio scanner with a 12-channel phase-array receiver head coil (Siemens Healthcare, Erlangen, Germany), using an EPI- based twice-refocused DWI sequence. Both phantom and in vivo experiments were performed with the following parameters: 20 axial slices, pulse repetition time = 4000 ms, echo time = 100 ms, field of view = 220 mm, slice thickness 4 mm, acquisition matrix 64 × 64, bandwidth = 1396 Hz/pixel, b = [0, 1000] s/mm2, diffusion encoding period ~90 ms, 12 diffusion directions for in vivo, and 6 diffusion directions for phantom studies.
A prototype Moir,e Phase Tracking (MPT) (26) system was used to track head motion in real-time (Metria Inc, Milwaukee, WI). The MPT system uses an MR- compatible camera that operates at 80 frames per second and is mounted inside the scanner bore to track a 15 × 15 mm target, which is attached to a phantom or subject’s forehead. The MPT target has a bi-layer structure, which generates moir,e patterns to allow accurate estimation of through-plane orientation with a single camera. From the acquired image frames of the target, the tracking system estimates the head pose with 6 degrees of freedom (3 translations and 3 rotations). Head pose data are transmitted to the scanner control unit for prospective motion correction with a lag time of approximately 30 ms. Additional information about the tracking system has been reported previously (26).
At a frame rate of 80 Hz, the MPT system provided 7 or 8 pose updates during the diffusion encoding period (~90 ms). Position and rotation updates were applied immediately before each of the 3 radiofrequency pulses and the EPI readout train (Fig. 1) by recalculating and adjusting the gradient rotation matrix and the frequency offset of the radiofrequency pulses. The rotation data () from all available poses between excitation and readout were stored and used to calculate the residual gradient moment by numerical integration of Eq. [3]. The final two packets (P6 and P7 in Figure 1) are unavailable during the calculation of the blip amplitude due to the ~30 ms latency in the MPT system. Therefore, the rotational motion at the end of the diffusion preparation period was approximated by linear extrapolation. A gradient blip of moment (variable amplitude, 1.2 ms duration) was inserted immediately prior to the EPI readout to dynamically restore the gradient balance.
FIG. 1.
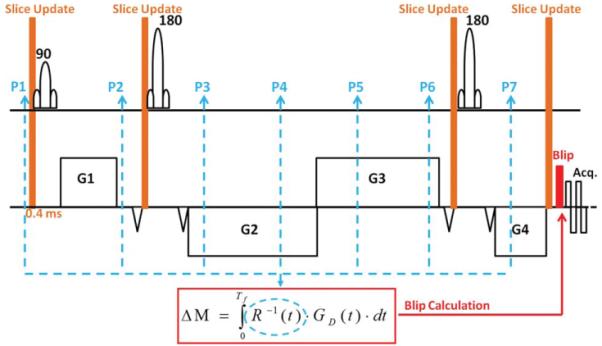
Pulse diagram for the twice- refocused diffusion weighted sequence. Blue dashed lines indicate feedback from the MPT system (P1 through P7). The residual gradient moment due to movement is calculated according to Eq. [3], and a short blip (duration 1.2 ms) is inserted prior to the readout to restore gradient balance.
Phantom Experiments
An experiment was performed to evaluate the dependence of signal loss on the amplitude and direction of the gradient moment imbalance using a stationary spherical phantom. The phantom was imaged with the DWI sequence. A variable blip gradient was inserted before the EPI readout to generate an intentional gradient imbalance. The blip moment varied from 0 to 10 mT ms/m in 64 steps. The experiment was repeated with the blip gradient applied along the readout and slice axes.
In Vivo Experiments and Data Analysis
Five healthy volunteers provided verbal and written consent, using a protocol approved by the local Institutional Review Board at the University of Hawaii. Prior to scanning, subjects were examined by a physician to screen for safety, and were instructed to perform two types of head movements: a slow speed, low amplitude (approximately ±2° , 0.2 Hz) right-left “head shake,” resulting in primarily in-plane motion, and a faster speed, large amplitude motion (approximately ±5°, 0.2 Hz) where the tip of the nose traces a “figure eight” to generate both through-plane and in-plane motion. DTI data were acquired under six different conditions: (1) no intentional head movement, no corrections (“baseline” scan), (2) no intentional head movement but blip correction “ON,” (3) two slow head shake scans with and without blip correction and (4) two faster figure eight motion scans with and without blip correction. The goal of the slow motion scans was to evaluate the utility of signal loss correction for slower rotations that may cause relatively subtle signal loss. For all scans with head motion, correction of slice position was performed; therefore, only the effects of blip correction were investigated.
DTI measures were calculated in DTI Studio (28). First, uncorrected and corrected images were aligned to the b = 0 s/mm2 volume of the baseline image for each subject to eliminate scan-to-scan misalignments. During the scan, slice orientation was updated using MPT feedback while diffusion gradients were kept stationary in the scanner frame to avoid eddy current artifacts. Thus, the b-matrix was adjusted for each slice offline before being used in the tensor calculation, using the rotational data received immediately before the excitation pulse. Fractional anisotropy (FA) and trace measures were calculated for baseline, uncorrected and gradient moment- corrected images using DTI Studio. For a representative slice above the ventricles (to avoid the cerebrospinal fluid [CSF]), FA and trace maps for uncorrected and corrected scans were subtracted from the corresponding baseline maps, and the residuals were displayed as histograms and characterized in terms of mean and standard deviation. The FA and trace residuals were tested for statistical difference from zero using one-sample t-tests.
Additionally, the principal eigenvector orientation of the tensor data was investigated. First, a white matter mask for each subject was created after normalizing the International Consortium for Brain Mapping (ICBM) FA atlas (JHU-ICBM-FA-1 mm) to the baseline FA map (no motion, no correction case), using voxels with FA > 0.25. The absolute angular deviation between the principal eigenvectors of baseline data and those of uncorrected and corrected data were calculated and averaged in masked regions, using the dot product of principal eigenvectors. A one-sample t-test was used to compare the difference in angular deviations between uncorrected and corrected data across subjects.
RESULTS
Figure 2 shows the phantom experiment results for b = 1000 s/mm2 data with diffusion direction [1, 1, 0]. A blip inserted in the X-direction (in-plane) caused minimal signal loss until the moment reached a value of ~3.4 mT ms/m; above this value, a sudden and almost complete signal loss was observed (Fig. 2, top). The threshold value agrees with the theoretical value from Eq. [6] (Mi ≥ = 3.4 mT·ms/m). A gradient blip inserted in Z-direction (through-plane) resulted in smoother, sincshaped signal attenuation (Fig. 2, bottom), in good agreement with the analytic prediction in Eq. [4]. The full width at half maximum was measured to be 3.97 mT·ms/m. Figure 2 also shows that a gradient moment of 3 mT·ms/ m along the in-plane direction caused almost no signal loss, whereas the same gradient moment applied in the slice direction caused ~30% signal loss. In contrast, a 4 mT·ms/m imbalance caused 50% signal attenuation when applied in the slice direction, but almost complete signal loss (about 90%) when applied along the in-plane direction.
FIG. 2.
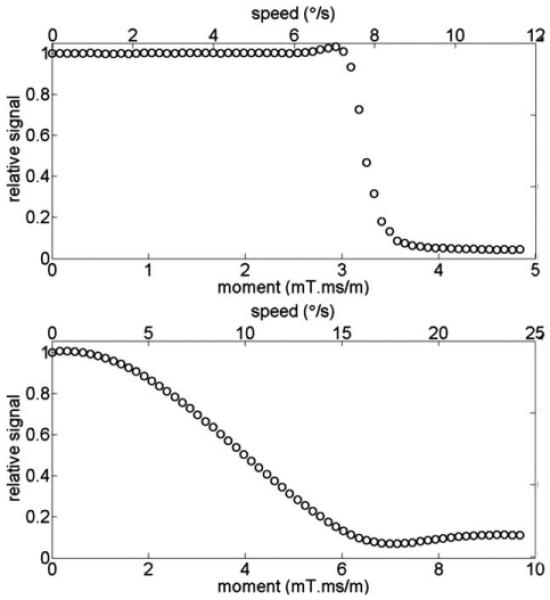
Phantom experiment results that show the dependence of signal loss on the magnitude and the direction of the imbalance in gradient moment: in-plane direction (top) and through-plane direction (bottom). Secondary x-axes (top) show the angular speed of subject motion in ° /s that corresponds to each gradient moment (assuming constant velocities).
The top row of Figure 3 displays the slices from one volume together with the motion trajectory for uncorrected (left) and corrected (right) fast motion scans. The amplitude of the extra gradient moment is displayed beneath each slice; in the uncorrected case (left), the moments were calculated but the blip gradient was not played out. The motion trajectories for both scans are similar in amplitude and frequency. The images demonstrate that signal loss occurred in case of unbalanced gradients, but was prevented if the gradient moment was restored by the compensating blip.
FIG. 3.
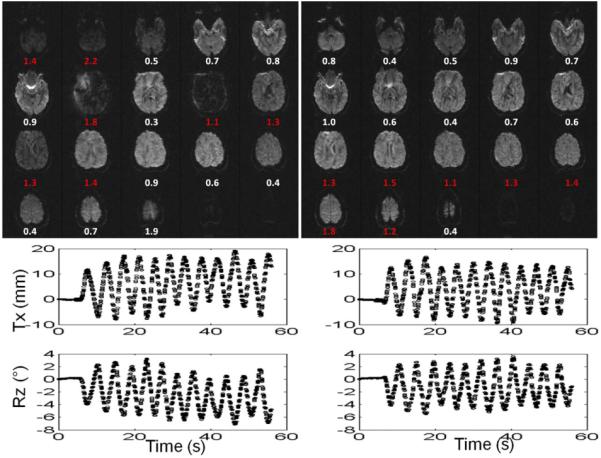
Uncorrected (left) and corrected (right) images for a subject performing fast motion and the calculated gradient imbalances (mT·ms/m) for each slice. For the scan with correction on, the numbers reflect actual blip values applied in real-time (right). Corresponding motion trajectories for Tx and Rz are shown below the diffusion images. Data points in groups of 6–8 indicate the feedbacks received during each diffusion encoding period. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Figure 4 displays representative (a) baseline, (b) uncorrected, and (c) corrected FA maps for one slice of a subject performing fast motion. The baseline FA histogram (d) displays a bimodal distribution (red arrows in Figure 4), with a low FA peak populated by gray matter pixels and a high FA peak populated by white matter pixels. In the uncorrected scan with fast motion (e), gray matter pixels show increased FA, resulting in a single broad peak. In the corrected scan (f), the correct (lower) FA values are mostly restored for gray matter pixels. The third row displays the residuals of uncorrected (g) and corrected (h) maps after subtracting the baseline map. The corresponding histograms (i and j) indicate that signal loss in DW images increases the mean and standard deviation of the FA maps. The correction largely restores the maps back to normal values. The residual differences between the baseline and corrected maps may be due to the inaccuracies and latency of the tracking system, and issues with fixation of the marker to the skin.
FIG. 4.

Representative FA maps from a single slice for a baseline (a), uncorrected (b), and corrected (c) scan, their corresponding histograms (d, e, and f), the residuals of uncorrected and corrected maps after subtracting the baseline map (g, h), and their corresponding histograms (i and j). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Table 1 presents the mean and standard deviation of FA and trace residuals (calculated by subtracting the baseline maps from the uncorrected and corrected maps with motion) across subjects, and associated P-values from one-sample t-tests, for both fast and slow motion. For both FA and trace, the residuals of uncorrected maps overall had higher mean and standard deviations than those of corrected maps for both fast and slow motions, highlighting the effect of signal loss on DTI measures and efficacy of the proposed correction. While motion without correction resulted in trace residuals significantly greater than zero (P < 0.05), the correction restored the trace residuals back to almost zero for both fast and slow motions (non-significant P-values). Similarly, motion without correction caused FA residuals to significantly differ from zero for fast motions. Gradient moment correction somewhat normalized FA values. In the slow motion case, P-values were non-significant for FA. Table 1 also demonstrates that motion correction reduces errors in principal eigenvector orientation across subjects (corrected versus uncorrected deviations from baseline) for the fast motion case (7° reduction in average absolute angular error, P < 0.02). However, no significant change in orientation errors was observed for slow movements.
Table 1.
Mean and STD of FA, Trace, and Fiber Orientation Residuals, and Statistical Significance from One Sample t-Tests
| Mean | STD | P-value | |||
|---|---|---|---|---|---|
| Trace (×10−3) (mm2/s) | Fast motion | Uncorr-BL | 0.35 | 0.24 | 0.03 |
| Corr-BL | 0.17 | 0.18 | 0.10 | ||
| Corr-Uncorr | −0.17 | 0.12 | 0.03 | ||
| Slow motion | Uncorr-BL | 0.12 | 0.10 | 0.03 | |
| Corr-BL | 0.05 | 0.10 | 0.24 | ||
| Corr-Uncorr | −0.07 | 0.11 | 0.20 | ||
| FA | Fast motion | Uncorr-BL | 0.098 | 0.060 | 0.02 |
| Corr-BL | 0.043 | 0.009 | <0.001 | ||
| Corr-Uncorr | −0.055 | 0.052 | 0.08 | ||
| Slow motion | Uncorr-BL | 0.014 | 0.024 | 0.21 | |
| Corr-BL | 0.013 | 0.020 | 0.17 | ||
| Corr-Uncorr | −0.001 | 0.013 | 0.85 | ||
| Eigenvector orientation (degree) |
Fast motion | Uncorr-BL | 38.15 | 0.67 | - |
| Corr-BL | 31.19 | 0.74 | - | ||
| Uncorr-Corr | 6.96 | 0.60 | 0.012 | ||
| Slow motion | Uncorr-BL | 21.78 | 0.80 | - | |
| Corr-BL | 22.90 | 0.89 | - | ||
| Corr-Uncorr | −1.12 | 0.85 | 0.12 |
DISCUSSION
Effects of Motion on DTI
Head motion during the diffusion-encoding period of DWI scans can cause subtle or severe signal losses that render diffusion measures unreliable. These signal losses may occur even when slice-selective radiofrequency pulses are properly aligned, and are due to a rotation- induced excess gradient moment (23). We demonstrate that if head rotation can be measured sufficiently rapidly, this signal loss can be prevented by insertion of a blipped gradient to restore the gradient balance and reverse the detrimental phase accrual.
The effect of motion-induced gradient imbalances is different for in-plane versus through-plane gradient moments. An in-plane moment causes negligible signal loss unless it shifts the echo center out of the sampling window, at which point almost all of the signal is suddenly lost (23). This all-or-nothing behavior has also been observed as a result of mechanical scanner vibrations (29). Sensitivity to this effect may generally be reduced by increasing the width of the sampled region of k-space, i.e., by increasing spatial resolution and avoiding partial Fourier encoding. Since this type of signal loss is almost complete, postprocessing algorithms may detect its occurrence relatively reliably, and suppress select diffusion weighted images from tensor calculations.
Conversely, gradient imbalances in through-plane direction cause signal losses that show an approximate sinc dependence on the rotational speed, making signal attenuation gradual and, therefore, more difficult or impossible to detect. For typical slice thicknesses, rotational velocities as small as 5–10° per second may cause noticeable signal attenuation. The sensitivity to this kind of signal loss can be reduced by using thinner slices. However, thinner slices may cause an entirely different type of signal loss: in case of through-plane motion (e.g., head nodding in an axial scan), imperfectly aligned refocusing pulses may fail to properly refocus the excited slice due to the altered orientation of the head. This kind of artifact is also avoided in the proposed method by updating slice orientations prior to each refocusing pulse.
Head motion interacts with the gradient sequence in a rather complex manner to create gradient imbalances. In general, due to the specific form of Eq. [3], the orientation of the induced gradient moment is approximately mutually orthogonal to the axis of head rotation and that of the diffusion gradient. For instance, for an axial DWI scan, head nodding (X-rotations) during a Z-diffusion gradient leads to a Y-gradient imbalance (in-plane), whereas the same motion results in a Z-gradient imbalance (through-plane) if it occurs during a Y-diffusion gradient. Therefore, for axial slices, head nodding can cause signal loss that shows a sinc or step function dependence on velocity and diffusion gradient direction and amplitude. In contrast, head shaking (left-right, or Z- rotation) only causes in-plane gradient imbalances (X- or Y-direction) for axial scans, leading to step function type (all-or-none) signal losses. Head rotations or diffusion gradients involving all three axes will generally lead to both in-plane and through-plane gradient imbalances. The motion trajectory performed during the fast motion scans (figure eight) was selected to produce both inplane and through-plane motion. The lower threshold for signal loss in the in vivo case (Fig. 3) as compared to the phantom experiments (Fig. 2) is presumably due to the combined effects of both in-plane and through-plane motion, and due to motion during the EPI readout train.
We evaluated how FA, trace and fiber orientation measures are affected by motion-induced signal losses that are difficult to detect visually. First, since the trace reflects the average apparent signal attenuation due to diffusion along the three orthogonal directions, we expect any motion-induced signal loss to increase trace values throughout the brain. In contrast, motion- corruption of FA maps is more location-dependent. In gray matter, where diffusion is essentially isotropic, (random) motion-induced signal loss will likely increase the apparent FA, whereas in white matter head motion can falsely increase or decrease FA measures depending on which diffusion directions are affected by motion artifacts. These considerations are supported by the results shown in Figure 4. While trace values generally show an increase due to motion-induced signal losses, FA values increase predominantly for gray matter voxels.
Finally, head motion can also cause inaccuracies in fiber orientation calculations. We specifically evaluated the principal eigenvector of the diffusion tensor, which reflects the orientation of the fibers in a voxel. The proposed correction reduced angular deviations in eigenvector orientation for fast, but not slow, movements, and, therefore, most likely results in more accurate fiber tracking for severe motions (Table 1). The relatively substantial variance in residual orientation for the slow motion case (over 20° with and without correction) may be due to the relatively low angular resolution of the DTI scans performed (12 directions only), noise and latency in the tracking system, as well as errors in the normalization of brain atlas to the subject space.
Alternative Approaches
Currently, the most common solution for motion- induced signal loss in DWI is to exclude volumes with obvious signal losses and/or to reacquire them (22). Since both motion and diffusion lead to signal attenuation, such techniques are most effective when the motion-induced signal loss is sufficiently large to be identified unambiguously, such as when an in-plane gradient imbalance pushes the echo outside of the acquisition window. However, our experiments demonstrate that even the subtle signal loss that accompanies slow movements may result in errors in trace values. This is most likely due to phase accumulation in the through- plane direction where signal attenuation follows a sinc function, causing the effect to be too subtle to be identified as an artifact, but large enough to yield inaccurate tensor estimates.
One alternative solution was recently proposed by Herbst et al. (25), who demonstrated that motion- induced signal losses in DWI can be prevented by continuously updating (every 2 ms) the orientation of diffusion gradients using the rotation data from a fast optical tracking system. Such an approach involves several challenges. First, it is unclear whether all scanner platforms would allow quasi-continuous updates of gradient pulses. Second, the method necessitates tedious pulse programming since diffusion gradients have to be updated approximately 50 times per slice. Third, the method may suffer from latencies in the tracking system if not accounted for. Fourth, rapid modification of diffusion gradients may induce eddy current artifacts. In contrast, the correction method proposed here achieves the same goal of balancing the diffusion gradients with a single low-amplitude blip. In that sense, the blipped correction presented here is simple, easy to program, and has been implemented to explicitly account for the system latency. Furthermore, due to the lower frequency of sequence updates, more scanner platforms should be able to accommodate the technique.
Limitations
In this proof-of-concept study, we used a relatively small acquisition matrix (64 × 64), a moderate number of diffusion directions (12), and a common b-value (1000 s/mm2); we also avoided methods that accelerate the acquisition (partial-Fourier, parallel imaging, and multishot techniques) to simplify the acquisition as much as possible. However, the proposed method is likely to be valid for other settings as well. The theory and results demonstrate an inverse linear dependence between signal drop-off point and in-plane voxel size. Accordingly, a larger acquisition matrix (higher resolution) reduces the likelihood of in-plane signal losses, since it increases the k-space field-of-view. Conversely, partial Fourier encoding reduces the sampling window and renders the sequence more vulnerable to this artifact, for instance, in the case of mechanical vibrations (29). Acquisitions using parallel imaging generally maintain the k-space field of view compared to fully sampled acquisitions, and may be expected to show the same motion sensitivity as non-accelerated EPI. An additional problem may occur with multi-shot acquisitions, where one has to ensure that the phase is matched across shots. Finally, for a given motion, the degree or likelihood of signal attenuation generally increases with the b-value used for diffusion encoding (Eq. [3]). Therefore, dynamic correction of signal loss becomes particularly important for high b-value techniques, such as HARDI or q-ball (3,4), and diffusion spectrum acquisitions (5). The validation of our method with the aforementioned features will be the topic of future studies.
It can be advantageous to rotate the b-matrix when correcting for subject motion during DTI scans (30). In this work, since the diffusion gradients were kept stationary, the b-matrix was rotated separately for each slice during postprocessing. While this is somewhat tedious using current DTI analysis packages, automated slice-by-slice b-matrix realignments would not be particularly difficult to implement. However, one distinct advantage of keeping diffusion gradients stationary is that the eddy current nulling property of the twice-refocused DWI sequence remains intact (27). Also, since the blip correction gradient is of similar duration and amplitude as typical phase encoding gradients, we expect that eddy currents are not substantially different from those present during a conventional DTI acquisition.
A related issue is what exact diffusion direction to use for DTI analyses, since the head rotation is not constant within the diffusion encoding period. However, changes in head rotation within diffusion encoding were within 1° in our studies, which is likely to be negligible in terms of tensor calculation. First, only 12 diffusion directions were used in the current implementation, i.e., the step size amongst diffusion directions exceeded 15° . However, the issue of inaccuracies in diffusion direction may need to be revisited in the context of acquisitions with substantially higher angular resolution, such as HARDI or q-ball (3,4).
Another limitation of the current method is that it ignores the effect of motion during the EPI readout train. Given typical peak rotational speeds of 5° /s, and an EPI readout length of 50 ms, residual motion during readout was typically less than 1° ; therefore, the generally accepted assumption of minimal residual motion holds fairly well. However, for faster movements, correction during the EPI readout may become necessary.
CONCLUSIONS
We present a novel method to prevent signal loss in DWI scans. Our approach uses head pose information from a fast tracking system to calculate the apparent motion- induced imbalance in gradients, and restores the gradient balance in real-time by inserting a blip gradient prior to the readout. The correction method results in accurate calculation of DTI measures even in the presence of relatively fast head movements. We expect improved robustness for clinical routine scanning in populations that are prone to head movements, such as children and uncooperative adult patients.
ACKNOWLEDGMENTS
This project was supported by NIH grants to TE (R01- DA021146) and LC (1U54-NS056883 and 2K24-DA016170). BAP is partly funded by DFG grant. The authors thank Dr. Benjamin Zahneisen for helpful discussions and the subjects for volunteering.
Grant sponsor: NIH; Grant number: 1R01-DA021146 (BRP), U54-NS56883 (SNRP), K02-DA16991 (to TE), K24-DA61427 (to LC), and G12-RR00306121 (RCMI); Grant sponsor: DFG grant; Grant number: Po1576/1-1 (to BAP).
REFERENCES
- 1.Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med. 1994;32:379–387. doi: 10.1002/mrm.1910320313. [DOI] [PubMed] [Google Scholar]
- 2.Trouard TP, Sabharwal Y, Altbach MI, Gmitro AF. Analysis and comparison of motion-correction techniques in diffusion-weighted imaging. J Magn Reson Imaging. 1996;6:925–935. doi: 10.1002/jmri.1880060614. [DOI] [PubMed] [Google Scholar]
- 3.Tuch DS, Reese TG, Wiegell MR, Makris N, Belliveau JW, Wedeen VJ. High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn Reson Med. 2002;48:577–582. doi: 10.1002/mrm.10268. [DOI] [PubMed] [Google Scholar]
- 4.Tuch DS. Q-ball imaging. Magn Reson Med. 2004;52:1358–1372. doi: 10.1002/mrm.20279. [DOI] [PubMed] [Google Scholar]
- 5.Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54:1377–1386. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- 6.Kloska SP, Wintermark M, Engelhorn T, Fiebach JB. Acute stroke magnetic resonance imaging: current status and future perspective. Neuroradiology. 2010;52:189–201. doi: 10.1007/s00234-009-0637-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Filippi M, Agosta F. Imaging biomarkers in multiple sclerosis. J Magn Reson Imaging. 2010;31:770–788. doi: 10.1002/jmri.22102. [DOI] [PubMed] [Google Scholar]
- 8.Rohde GK, Barnett AS, Basser PJ, Marenco S, Pierpaoli C. Comprehensive approach for correction of motion and distortion in diffusion-weighted MRI. Magn Reson Med. 2004;51:103–114. doi: 10.1002/mrm.10677. [DOI] [PubMed] [Google Scholar]
- 9.Jiang S, Xue H, Counsell S, Anjari M, Allsop J, Rutherford M, Rueckert D, Hajnal JV. Diffusion tensor imaging (DTI) of the brain in moving subjects: application to in-utero fetal and ex-utero studies. Magn Reson Med. 2009;62:645–655. doi: 10.1002/mrm.22032. [DOI] [PubMed] [Google Scholar]
- 10.Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: a review. Magn Reson Med. 2013;69:621–636. doi: 10.1002/mrm.24314. [DOI] [PubMed] [Google Scholar]
- 11.Ordidge RJ, Helpern JA, Qing ZX, Knight RA, Nagesh V. Correction of motional artifacts in diffusion-weighted MR images using navigator echoes. Magn Reson Imaging. 1994;12:455–460. doi: 10.1016/0730-725x(94)92539-9. [DOI] [PubMed] [Google Scholar]
- 12.Butts K, de Crespigny A, Pauly JM, Moseley M. Diffusion-weighted interleaved echo-planar imaging with a pair of orthogonal navigator echoes. Magn Reson Med. 1996;35:763–770. doi: 10.1002/mrm.1910350518. [DOI] [PubMed] [Google Scholar]
- 13.Bammer R, Augustin M, Prokesch RW, Stollberger R, Fazekas F. Diffusion-weighted imaging of the spinal cord: interleaved echo-planar imaging is superior to fast spin-echo. J Magn Reson Imaging. 2002;15:364–373. doi: 10.1002/jmri.10075. [DOI] [PubMed] [Google Scholar]
- 14.Nunes RG, Jezzard P, Behrens TE, Clare S. Self-navigated multishot echo-planar pulse sequence for high-resolution diffusion-weighted imaging. Magn Reson Med. 2005;53:1474–1478. doi: 10.1002/mrm.20499. [DOI] [PubMed] [Google Scholar]
- 15.Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn Reson Med. 2009;62:468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
- 16.Weih KS, Driesel W, von Mengershausen M, Norris DG. Online motion correction for diffusion-weighted segmented-EPI and FLASH imaging. MAGMA. 2004;16:277–283. doi: 10.1007/s10334-004-0036-x. [DOI] [PubMed] [Google Scholar]
- 17.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52:1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 18.Alhamud A, Tisdall MD, Hess AT, Hasan KM, Meintjes EM, van der Kouwe AJ. Volumetric navigators for real-time motion correction in diffusion tensor imaging. Magn Reson Med. 2012;68:1097–1108. doi: 10.1002/mrm.23314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kober T, Gruetter R, Krueger G. Prospective and retrospective motion correction in diffusion magnetic resonance imaging of the human brain. Neuroimage. 2012;59:389–398. doi: 10.1016/j.neuroimage.2011.07.004. [DOI] [PubMed] [Google Scholar]
- 20.Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic resonance imaging of freely moving objects: prospective real-time motion correction using an external optical motion tracking system. Neuroimage. 2006;31:1038–1050. doi: 10.1016/j.neuroimage.2006.01.039. [DOI] [PubMed] [Google Scholar]
- 21.Qin L, van Gelderen P, Derbyshire JA, Jin F, Lee J, de Zwart JA, Tao Y, Duyn JH. Prospective head-movement correction for high- resolution MRI using an in-bore optical tracking system. Magn Reson Med. 2009;62:924–934. doi: 10.1002/mrm.22076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Aksoy M, Forman C, Straka M, Skare S, Holdsworth S, Hornegger J, Bammer R. Real-time optical motion correction for diffusion tensor imaging. Magn Reson Med. 2011;66:366–378. doi: 10.1002/mrm.22787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wedeen VJ, Weisskoff RM, Poncelet BP. MRI signal void due to inplane motion is all-or-none. Magn Reson Med. 1994;32:116–120. doi: 10.1002/mrm.1910320116. [DOI] [PubMed] [Google Scholar]
- 24.Benner T, van der Kouwe AJ, Sorensen AG. Diffusion imaging with prospective motion correction and reacquisition. Magn Reson Med. 2011;66:154–167. doi: 10.1002/mrm.22837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Herbst M, Maclaren J, Weigel M, Korvink J, Hennig J, Zaitsev M. Prospective motion correction with continuous gradient updates in diffusion weighted imaging. Magn Reson Med. 2012;67:326–338. doi: 10.1002/mrm.23230. [DOI] [PubMed] [Google Scholar]
- 26.Maclaren J, Armstrong B, Barrows RT, et al. Measurement of microscopic head motion during in vivo brain imaging. PloS ONE. 2012;7:1–9. doi: 10.1371/journal.pone.0048088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy- current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–182. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- 28.Jiang H, van Zijl PC, Kim J, Pearlson GD, Mori S. DtiStudio: resource program for diffusion tensor computation and fiber bundle tracking. Comput Methods Programs Biomed. 2006;81:106–116. doi: 10.1016/j.cmpb.2005.08.004. [DOI] [PubMed] [Google Scholar]
- 29.Gallichan D, Scholz J, Bartsch A, Behrens TE, Robson MD, Miller KL. Addressing a systematic vibration artifact in diffusion-weighted MRI. Hum Brain Mapp. 2010;31:193–202. doi: 10.1002/hbm.20856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Leemans A, Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. Magn Reson Med. 2009;61:1336–1349. doi: 10.1002/mrm.21890. [DOI] [PubMed] [Google Scholar]


