Detecting treatment-covariate interactions using permutation methods

Abstract

The primary objective of a Randomized Clinical Trial usually is to investigate whether one treatment is better than its alternatives on average. However, treatment effects may vary across different patient subpopulations. In contrast to demonstrating one treatment is superior to another on the average sense, one is often more concerned with the question that, for a particular patient, or a group of patients with similar characteristics, which treatment strategy is most appropriate to achieve a desired outcome. Various interaction tests have been proposed to detect treatment effect heterogeneity; however, they typically examine covariates one at a time, do not offer an integrated approach that incorporates all available information and can greatly increase the chance of a false positive finding when the number of covariates is large. We propose a new permutation test for the null hypothesis of no interaction effects for any covariate. The proposed test allows us to consider the interaction effects of many covariates simultaneously without having to group subjects into subsets based on pre-specified criteria and applies generally to randomized clinical trials of multiple treatments. The test provides an attractive alternative to the standard likelihood ratio test, especially when the number of covariates is large. We illustrate the proposed methods using a dataset from the Treatment of Adolescents with Depression Study.

1. Introduction

The primary objective of a Randomized Clinical Trial (RCT) usually is to investigate whether one treatment is better than its alternatives on average. However, treatment effects may vary across different patient subpopulations. How to detect treatment effect heterogeneity poses serious analytical challenges. Attempts to address this issue have been focused on use of subgroup analysis. Various interaction tests have been proposed to detect treatment effect heterogeneity [1-9]. Several graphical methods have been proposed. Song and Pepe [10] propose the selection impact curve, which can be used to choose a treatment strategy based on whether a single biomarker value is higher than a threshold or not. Bonetti and Gelber [11,12] propose the subpopulation treatment effect pattern plot (STEPP) method, which provides a display of treatment effect estimates for different but potentially overlapping subsets of patients defined by a continuous covariate. However, one limitation of these and related methods is that they typically examine covariates one at a time, hence they do not offer an integrated approach that incorporates all available information and can greatly increase the chance of a false positive finding when the number of covariates is large. Poorly planned and conducted analyses often lead to spurious results [4,13,14].

Attempts have been made to address these concerns. For example, Kent and Hayward [15] consider a specific subgroup analysis where patients are grouped into subgroups based on their risks, which are calculated using multiple baseline characteristics simultaneously. Another method which makes use of multiple baseline characteristics for estimating the subject-level treatment differences for guiding future patients’ management and treatment selection is proposed in Cai et al. [16]. This method involves first using estimated individual-level treatment differences between two treatment strategies to create an index for clustering subjects, and then calibrating the average treatment differences for each cluster of subjects using a non-parametric approach. Extending this approach to more than 2 treatment options is not straightforward because the index becomes multi-dimensional which makes difficult the comparisons among treatment options and the use of the non-parametric approach. Also, the baseline characteristics under consideration are limited to a few and are considered given a priori as the index is created using parametric models fitted to each treatment group and standard inference methods require that the number of parameters in the model is not too large compared to the number of observations. This limitation has been overcome in Zhao et al. [17]. Similarly to Cai et al. [16], their methods first create a scoring system as a function of multiple baseline covariates in order to estimate subject-specific treatment differences, however, their method allows for model selection through cross-validation and can be applied to the setting where the number of covariates is large. In addition, Zhao et al. [17] show how to identify a group of future subjects who would have a desired treatment benefit.

Data mining techniques have also been considered. Ruberg et al. [18] illustrate how classification tree built through recursive partitioning can be used to identify a small set of variables defining a subgroup of subjects who may have an enhanced treatment response as exploratory analysis. However, the authors caution that such approaches can be prone to over-fitting. Subsequently, Foster et al. [19] propose the ‘Virtual Twins’ method, which involves predicting response probabilities for treatment and control for each subject, and then use the differences in these probabilities as the outcome in a classification or regression tree, to identify a subgroup of patients who may have an enhanced treatment effect. They also investigate the use of resampling strategies to obtain an honest estimate of the magnitude of the treatment effect in the identified subgroup and find that a bias-corrected bootstrap procedure can reduce but not eliminate the bias resulting from the over-fitting.

It would be useful to have an overall test for the null hypothesis of no treatment-covariate interaction effects for any covariate as an initial step for searching for subgroup effects. If this overall test is statistically significant, it provides evidence that there exists treatment-covariate interaction and warrants further search for these covariates; otherwise, it suggests that the evidence for treatment-covariate interaction is low and it may not be necessary to continue searching for specific covariates that interact with treatment. When the number of covariates is small relative to the number of observations, a likelihood ratio test comparing the model with all the treatment-covariate interaction terms and the model without is a valid and asymptotically optimal test under mild regularity conditions. However, in many settings, especially in clinical trials with modest sample size, when the number of covariates is large, the number of parameters quickly increases and can be greater than the number of observations; the likelihood ratio test will no longer be applicable because the parameters in the model may not be identifiable.

In this paper we propose a simple permutation test for the null hypothesis of no treatment-covariate interaction effects for any covariate. The proposed test allows us to consider the interaction effects of many covariates simultaneously without having to group subjects into subsets based on pre-specified criteria and applies generally to randomized clinical trials of K (≥2) treatment arms. Although various permutation tests have been proposed to make inference about different parameters in regression models representing fixed effects or random effects through creating and permuting residuals that are exchangeable under the null hypothesis [20-22], permutation test for interaction terms is challenging due to the difficulty in creating exchangeable residuals under the null. It has been noted that in general there is no exact permutation method for testing the interaction term even for models with one or two main effects and an interaction [23,24]. Either restricted permutations or approximate solutions are needed to make separate inferences on the main effects and the interaction effects [25]. This issue becomes more complicated when the number of covariates is large and a variable selection procedure is applied. Wang and Lagakos [26] propose permutation methods to determine the distribution of the regression coefficients conditional on its selection by an automatic variable selection technique. However, their methods cannot be used to make inference about the treatment-covariate interaction terms as the interaction terms involve both treatment and covariates that are also present in the model and the key independence assumptions between the covariates that we are interested in make inference about and other variables present in the model are violated, i.e., the interaction term is not independent of the treatment indicator. Furthermore, the permutation tests in Wang and Lagakos [26] are restricted permutation tests and only those reverse-transformed datasets that give arise to the same selected covariates will be included to generate the null distribution, which is not the case here.

This research was motivated through our collaboration with clinical researchers in the Department of Psychiatry at the Massachusetts General Hospital. For treatment of depression, both Fluoxetine and cognitive-behavioral therapy (CBT) are effective. However, Fluoxetine may be associated with undesirable side effects (e.g., increased risk for serotonin syndrome and cardiovascular complications), and thus it would be important to identify patient subpopulations who many benefit from CBT alone. When treatments have different mechanisms of action, whether patient would respond well for a particular treatment is likely to depend on their individual characteristics.

In Section 2 we describe notation and the permutation test for the null hypothesis of no treatment-covariate interaction effects for any covariate. The proposed test involves three steps. In step 1 we transform the original data matrix to one that can be partitioned into two parts that are independent of each other under the null hypothesis. In step 2 we permute the rows of one part to obtain data matrices that are equally likely as the transformed dataset. In Step 3 we reverse transform the permuted transformed dataset to obtain datasets that are equally likely as the observed dataset. These three steps allow us to create datasets that are equally likely as the observed datasets under the null hypothesis, so that we can evaluate a particular test statistic on the observed dataset as well as these generated datasets to generate a null distribution for making inference. In Section 3 we illustrate the proposed method using data from the Treatment for Adolescents with Depression Study (TADS) [27], which was conducted with 439 participants over 4 years and collected over 4000 variables at baseline, reflecting depression symptoms, psychopathology and cognitive functions. In Section 4 we present simulation results. We discuss areas for future research in Section 5.

2. A global permutation test for treatment covariate interaction

Suppose there are K treatments in a randomized clinical trial. Let X = X = {X₁, X₂, . . . , X_p} denote the collection of p measured baseline covariates of interest. Let Y denote some continuous response variable and T denote the treatment arm. Let n denote the total sample size and n_k, k = 1, . . . , K denote the number of subjects on treatment k. Suppose that the observations consist of n i.i.d. copies of the random vector (Y, T, X₁, X₂, . . . , X_p). Let W_k = I(T = k), where k = 1, 2, ..., K − 1 and I (·) is an indicator function so that W_k equals to 1 if T = k, and 0 otherwise. Let W = (W₁, W₂, ..., W_K−1) and X = (X₁, X₂, ..., X_p).

We consider the following linear model

$$Y={\alpha }^{T}W+{\beta }^{T}X+{\gamma }^{T}W\otimes X+{∊}_0,{∊}_0\perp (W^T,X^T),$$ (1)

where α, β, and γ are vectors of length K − 1, p, and (K − 1) × p, respectively, whose components may be zero; and we use ⊗ to denote the Kronecker product between K − 1 treatment indicator variables and p covariates so that W ⊗ X represents the resulting (K − 1)p interaction terms. We are interested in testing the null hypothesis of γ = 0_(K−1)p×1, here we use 0_(K−1)p×1 to denote a vector of 0's with length (K − 1)p. If we consider a linear model for each treatment k,

$$Y={\beta }^{{\left(k\right)}^T}X+{∊}_k,{∊}_k\perp X,$$

then the null hypothesis of no interaction effects for any covariates can also be expressed as

$$H_0:{\beta }^{\left(1\right)}={\beta }^{\left(2\right)}=\cdots ={\beta }^{\left(K\right)}.$$

This can be verified by first writing γ^T = (γ^(1)T, γ^(2)T , . . . , γ^(K−1)T), where each γ^(k), k = 1, 2, . . . ,K − 1, is a vector of length p, and observing that

$$\begin{array}{cc}\hfill {\beta }^{\left(k\right)}=& \beta +{\gamma }^{\left(k\right)},\text{for}k=1,2,\cdots ,K-1,\hfill \\ \hfill {\beta }^{\left(K\right)}=& \beta .\hfill \end{array}$$

If the number of covariates p is relatively small compared to the number of observations, to test H₀ : γ = 0_(K−1)p×1, we can fit model (1) and the model without the terms W ⊗ X, and apply a likelihood ratio test. However, if p is large compared to the number of observations and the number of parameters in model (1) can be larger than the number of observations, the standard least squares estimation method and the likelihood ratio test will no longer be applicable.

Let D = (Y, W, X) denote the observed n = (K + p) data matrix. In Appendix we show that we can obtain a valid permutation test by comparing a test statistic calculated from the observed dataset T (D) to the permutation distribution formed by test statistics calculated from datasets created by first subtracting the overall treatment effect from the outcome, permuting the treatment indicator, then adding back the overall treatment effect. Under the null hypothesis, the generated datasets are equally likely as the observed datasets. The test statistic evaluated on the observed dataset can be viewed as a random sample of 1 from the generated permutation distribution, which forms the basis for inference. An extreme value of T (D) provides evidence against the null hypothesis.

The proposed test would be an exact test α if were known. However, in practice, α is not known and is replaced with a consistent estimate $\widehat{\alpha }$ that remains constant across all permutations of the data. The effects of replacing nuisance parameters with their estimates on the validity and power of permutation tests have been studies in other settings. In deriving optimal permutation tests for the analysis of group randomized trials, Braun and Feng [28] argue that using the same estimates for all permutations maintains the invariance of the null distribution of the data with respect to the permutation space and does not affect the validity of the test. Furthermore, they show that the permutation test will suffer no loss of power asymptotically if $\widehat{\alpha }$ is consistent. Weinberg and Lagakos [29] show that the test statistic has the same limiting distribution when the scores are replaced by their consistent estimates. In our setting, replacing α with its estimate will affect the validity of the test through its effect on the independence of treatment indicators and residuals after subtracting the treatment effect conditional on covariates. Therefore, the proposed test is approximately valid. In Section 3, we show through extensive simulations that the actual type I errors using a consistent estimate of α are very close to those using the true unknown α, even with small sample sizes. A similar situation is provided in Wang and Lagakos [25]: When using permutation tests to make inference about an individual coefficient in a linear model in the presence of other covariates, the effects of other covariates are estimated. Simulations show that the actual type I errors associated with using estimates are close to those obtained from using the true values.

Note that when the null hypothesis is true and W ⊥ X,

$$E(Y\mid W)=E_X\left\{E(Y\mid W,X)\right\}=E_X({\alpha }^{T}W+{\beta }^{T}X+{∊}_0)={\alpha }^{T}W+{\beta }^T{E}_X\left(X\right)+{∊}_0,$$

The overall treatment effect α is the same parameter in the model relating outcome Y and treatment indicators W as in the model relating outcome Y, W and covariates X. Therefore, we can estimate α using the marginal model relating Y and W alone in the absence of covariates.

In what follows, we will consider a test statistic that can incorporate variable selection. The test statistic is the difference between the mean predictor error from the model with treatment-covariate interactions and that from the model without treatment-covariate interactions. More specifically, the test statistic is calculated in the following way:

• Step 1 For each treatment arm, fit a model relating outcome and all the covariates, with variable selection when appropriate (e.g., the number of candidate covariates is large and there is no prior knowledge to limit the covariates to a few selected ones);

• Step 2 For each individual i on treatment k, calculate a prediction ${\widehat{Y}}_i^k$ based on the fitted model from Step 1, the overall prediction error is calculated as $Er{r}_1=n^{-1}{\sum }_{k=1}^K{\sum }_{i=1}^{n_k}{(Y_i-{\widehat{Y}}_i^k)}^2$.

• Step 3 Fit a model relating outcome, treatment indicators, and all the covariates. Treatment indicators are always included in the model, with variable selection applied to all the covariates when appropriate.

• Step 4 For each individual i, calculate a prediction Ŷ based on the overall fitted model from Step 3, the overall prediction error is calculated as $Er{r}_2=n^{-1}{\sum }_{i=1}^n{(Y_i-{\widehat{Y}}_i)}^2$.

• Step 5 The test statistic Δ = Err₁ − Err₂.

Let m denote the number of permutations and for each permutation, we calculate a test statistics Δ_i, i = 1, ... , m. The p-value for the proposed permutation test is given by

$$\frac{1+{\sum }_{i=1}^{m}I(\mid {\Delta }_i\mid \ge \mid {\Delta }_{obs}\mid )}{1+m}.$$

where Δ_obs is the test statistic corresponding to the observed dataset and I(·) is an indicator function.

3. The treatment for adolescents with depression study

In the Treatment for Adolescents with Depression Study (TADS), patients with diagnosis of major depressive disorder were randomized to receive twelve weeks of Fluoxetine alone, cognitive-behavioral therapy (CBT) alone, their combination, or placebo. The main outcome measures are Children's Depression Rating Scale-Revised (CDRS-R) total score and a Clinical Global Impressions improvement score. Overall the combination treatment was found to be superior to each treatment alone and to placebo. The outcome we considered here was the value of CDRS-R total score at 12 weeks.

We first considered the setting with all four treatment groups and 116 candidate covariates that are either demographical or having the words Total, Scale or Score in their description. The initial data reduction was made in part because the 4617 variables were collected from various questionnaire that contained overlapping information. The overall sample size was 378. In this setting, the full model including the main effects of treatment, all covariates, and all possible two-way interactions between treatment and covariates had 468 parameters (3 for the treatment effects, 116 for the main effects of covariates, 348 for all two-way treatment and covariate interactions and 1 for error variance) to estimate. We were not able to use the standard likelihood ratio test because the number of parameters in the full model was larger than the overall sample size. We applied the proposed permutation test with difference in prediction error as the test statistics, using the lasso [30], implemented in a R package “glmnet” [31], to obtain the predicted outcomes. The lasso procedure minimized the residual sum of squares subject to the sum of the absolute value of the coefficients being less than a constant. This constant, the tuning parameter, was selected through 10-fold cross-validation.

The p-value for the proposed permutation test was based on 2000 permutations. The number of permutation controls the discreteness of the permutation null space and determines the accuracy of the estimated p-values. With 2000 permutations, we can distinguish estimated p-values about 5 × 10⁻⁴ apart. The error in estimating the p-value is given by $\sqrt{p\times (1-p)∕m}$, where p is the true p-value and m is the number of permutations. We chose 2000 permutations here and thereafter to achieve a balance between reasonable accuracy and computing time. With 2000 permutations, the error in the estimation of the p-value is smaller than 0.011 for a true p in interval (0, 1). For a p around 0.05, this error is about 0.005. In practice when analyzing a particular dataset, it may be ideal to use an even larger number of permutations to get more accurate p-value estimates. We can choose the number of permutations so that the upper bound of the confidence interval of the estimated p-value falls below the decision threshold for a fixed level of precision. For example, if the desired precision is 0.01, and the decision threshold is 0.05, we would need 7600 permutations so that the upper bound of the 95% confidence interval of the estimating p-values would be below 0.05.

To account for dependency of variable selection and permutation tests on random seeds, we repeated the tests 100 times to assess the robustness of the p-value. The median (inter-quartile range) for p-values from 100 tests were 0.004 (0.002-0.005), suggesting presence of treatment-covariate interactions. Table 1 lists the selected variables and their frequency of being selected among 100 runs using the lasso procedure by each treatment group. Among the selected variables, CDRS-R Summary Score (Best Description) was always selected in the CBT group, occasionally selected (3% of the times) in the combination group, but never in other treatment groups, suggesting that CDRS-R Summary Score (Best Description) was predictive of the outcome for subjects in the CBT group, but not for those randomized to other treatment groups and was potentially a treatment effect modifier.

Table 1.

Selected variables and their frequency of selection among 100 runs

Variable Name	Fluoxetine	CBT	Combination	Control
Symptom Dimension: Psychoticism score	0	0	11%	0
T score for Problems with Self-Concept	0	0	2%	0
T score DSM-IV* Inattentive Symptoms	0	3%	0	0
Cognitive Problems/Inattention Score	0	0	11%	0
Anger Control Problems Score	0	0	3%	0
CDRS-R Summary Score (Best Description)	0	100%	3%	0
CDRS 14 Question Summary Score (Best)	0	59%	0	0
Scale 9: Problems with emotional symptoms	0	5%	0	0
T score for Performance Fears Subscale	0	0	3%	0
Total number of questions answered Yes	0	0	9%	0
Quality of Life Questionnaire Total Score	0	17%	0	0
Suicidal Ideation Questionnaire Total Raw Score	0	0	11%	0

^*DSM-IV: Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition.

It is particularly of interest to identify patient subpopulations who may benefit from CBT alone, because it would be sensible not to treat them with Fluoxetine because of the potential side effects. Likewise, CBT requires substantial time investment on the part of the patient and a therapist with relevant expertise, so it is of interest to identify patient subpopulations who may benefit from medication and who may not benefit as much from CBT. Therefore we first restricted our attention to comparisons of the Fluoxetine arm (n = 97) and the CBT arm (n = 90). Among 4617 variables that were recorded at baseline, we obtained a list of 36 variables as potential effect modifiers from experts in psychiatry. The standard likelihood ratio test yielded a p-value of 0.096. We used the same variable selection procedure as described in the previous paragraph, the median (inter-quartile range) for 100 p-values were 0.026 (0.020-0.031), again suggesting presence of treatment-covariate interaction. Based on 100 runs, no variables were selected to predict the outcomes for those randomized to the Fluoxetine group; CDRS-R Summary Score (Best Description) was again always selected for the CBT group. The only other variable that was selected (13% of the times) for the CBT was Quality of Life Questionnaire Total Score. Increasing further the number of permutations led to very similar results. Based on 5000 permutations, the median (inter-quartile range) for 100 p-values were 0.023 (0.018-0.028).

4. Simulation Results

In our simulation studies, we first examined a general clinical trial case (setting 1) with two or three randomized treatment arms, and 5 covariates, among which, one was dichotomized and the remaining ones were continuous. The continuous outcome Y was generated from a linear model, under varying assumptions about main treatment effects, covariate effects and treatment-covariate interactions. We then generated datasets similar to that from the TADS study with 36 covariates (setting 2). We assessed the performance of the permutation test (“Perm”) and compared it to the standard likelihood ratio test (“LRT”), both in the absence and presence of variable selection. The likelihood ratio test we considered here is one based on comparing the likelihood between the null model (without any treatment-covariate interaction) to the alternative model (with all two-way treatment-covariate interactions).

4.1. Setting 1

4.1.1. Two treatment groups; in the absence of variable selection

Suppose $X_1^0$ is Bernoulli with success probability p, X₁ is centered $X_1^0$, and (X₂, X₃, X₄, X₅) follows a multivariate normal distribution with mean 0 and covariance matrix having (i, j)th element ρ^|i−j|, and that conditional on (X₁, X₂, X₃, X₄, X₅),

$$Y=0.5+{\alpha }_1{W}_1+{\beta }_1{X}_1+{\beta }_2{X}_2+{\gamma }_{11}{W}_1{X}_1+{\gamma }_{12}{W}_1{X}_2+\epsilon ,$$

where W₁ = I(treatment group = 1), ε ⊥ (X₁, X₂, X₃, X₄, X₅).

We first considered situations where the total number of covariates was small and no variable selection was applied in building prediction equations for each treatment group and calculating the test statistic. The settings examined corresponded to various magnitudes of main treatment effects, covariate effects and error distributions, for total sample size n = 60, 100, 200, equally allocated to two treatments. Throughout we fixed p = 0.4 and ρ = 0.3. Table 2 presents the empirical type I error estimates for 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for varying magnitudes of overall treatment effect α₁, covariate effects β₁ and β₂, error distributions, and total sample size n = 60, 100, 200. Four error distributions were considered: 1) Normal Distribution: ε ~ N(0, 1); 2) Cauchy Distribution with location parameter 0 and scale parameter 1, i.e., $∊\sim \frac{1}{\pi {(1+∊)}^2}$; 3) Lognormal distribution where the mean and standard deviation of the logarithm were 0 and 1; 4)Pareto distribution with location parameter 1 and shape parameter 3, i.e., ε ~ 3/ε⁴, for ε > 1. Each p-value was based on 2000 permutations. Both results for the case where the overall treatment effect was estimated (in practice) and was assumed to be known (unachievable scenario) are presented. In general, the empirical type I errors for the permutation test, using true or estimated α₁, were close to the nominal level of 0.05 regardless of the form of error distribution, even when the sample size was small (n = 60). In contrast, the empirical type I errors for the LRT can be slightly inflated (around 0.07 − 0.08) for small sample sizes, even when the error was normally distributed.

Table 2.

Empirical Type I error estimates {P̂(rej. H₀)} for 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for varying magnitudes of overall treatment effect, covariate effects and error distributions. Perm and Perm* represent the case where the overall treatment effect α₁ is estimated and the unachievable case where α₁ is known respectively. Results were based on 1000 experiments.

α 1	β 1	β 2	n = 60			n = 100			n = 200
			Perm	Perm*	LRT	Perm	Perm*	LRT	Perm	Perm*	LRT
Normal Distribution
0	0.1	0.2	0.059	0.055	0.052	0.051	0.049	0.049	0.053	0.053	0.058
0.2	0.1	0.2	0.051	0.047	0.080	0.059	0.058	0.060	0.057	0.058	0.058
0.5	0.1	0.2	0.045	0.039	0.081	0.060	0.057	0.061	0.052	0.052	0.059
0	0.1	0	0.060	0.058	0.076	0.049	0.047	0.057	0.052	0.052	0.056
0.2	0.1	0	0.061	0.055	0.063	0.039	0.035	0.069	0.051	0.049	0.052
0	0	0.2	0.046	0.043	0.070	0.058	0.054	0.055	0.042	0.042	0.068
0.5	0	0.2	0.059	0.055	0.070	0.051	0.049	0.061	0.053	0.053	0.066
Cauchy Distribution
0	0.1	0.2	0.044	0.032	0.071	0.056	0.064	0.057	0.048	0.048	0.056
0.2	0.1	0.2	0.044	0.038	0.069	0.056	0.032	0.058	0.058	0.064	0.067
0.5	0.1	0.2	0.054	0.050	0.073	0.038	0.052	0.042	0.058	0.050	0.049
0	0.1	0	0.044	0.038	0.079	0.038	0.036	0.061	0.050	0.050	0.046
0.2	0.1	0	0.050	0.050	0.069	0.032	0.032	0.068	0.046	0.050	0.057
0	0	0.2	0.046	0.038	0.067	0.057	0.060	0.068	0.058	0.058	0.052
0.5	0	0.2	0.060	0.054	0.083	0.050	0.052	0.060	0.050	0.050	0.056
Lognormal Distribution
0	0.1	0.2	0.062	0.032	0.054	0.040	0.046	0.051	0.048	0.046	0.062
0.2	0.1	0.2	0.064	0.070	0.068	0.044	0.036	0.066	0.034	0.044	0.057
0.5	0.1	0.2	0.064	0.054	0.081	0.054	0.084	0.058	0.038	0.066	0.054
0	0.1	0	0.064	0.050	0.071	0.052	0.056	0.046	0.044	0.060	0.047
0.2	0.1	0	0.062	0.058	0.069	0.042	0.054	0.069	0.044	0.044	0.045
0	0	0.2	0.043	0.058	0.081	0.045	0.048	0.056	0.052	0.038	0.064
0.5	0	0.2	0.052	0.052	0.065	0.047	0.038	0.058	0.053	0.060	0.060
Pareto Distribution
0	0.1	0.2	0.062	0.056	0.077	0.048	0.048	0.068	0.060	0.058	0.049
0.2	0.1	0.2	0.060	0.044	0.077	0.054	0.054	0.048	0.032	0.048	0.056
0.5	0.1	0.2	0.054	0.038	0.060	0.050	0.046	0.061	0.066	0.058	0.060
0	0.1	0	0.036	0.054	0.087	0.060	0.036	0.063	0.056	0.046	0.056
0.2	0.1	0	0.038	0.036	0.088	0.058	0.058	0.058	0.062	0.052	0.057
0	0	0.2	0.072	0.048	0.071	0.072	0.051	0.056	0.056	0.060	0.055
0.5	0	0.2	0.052	0.046	0.059	0.052	0.048	0.063	0.052	0.054	0.048

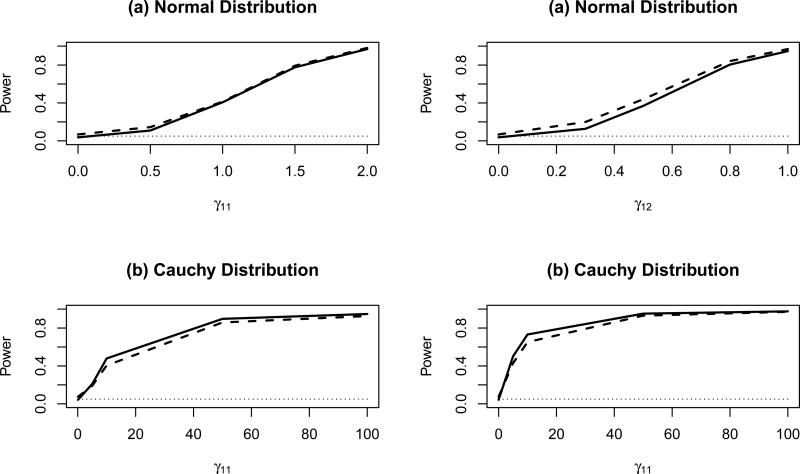
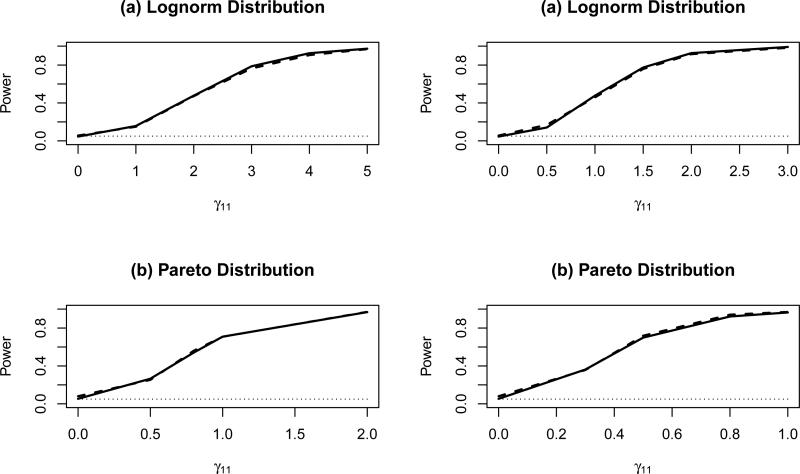
Figures 1-2 present empirical size and power estimates for a 0.05 level test comparing the proposed permutation test and the LRT for varying magnitude of treatment-covariate interaction effects and error distributions. The power of the permutation test (solid lines) was in general very similar to that of the likelihood ratio test (dashed lines). When the data were normally distributed, the power of the permutation tests was slightly lower than that of the LRT [see Figure 1(a)]; while when the data followed a cauchy distribution, permutation tests were associated with a slightly greater power [Figure 1(b)].

Figure 1.

Empirical size/power estimates of the permutation tests (solid lines) and the LRT (dashed lines) for a 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for varying magnitude of treatment-covariate interaction effect γ ₁₁ and γ₁₂ and error distributions [(a) Normal or (b) Cauchy], and fixed overall treatment effect α = 0.2 and covariate effects β₁ = 0.2, β₂ = 0.4, based on a total sample size n = 100 (50 subjects in each treatment group)

Figure 2.

Empirical size/power estimates of the permutation tests (solid lines) and the LRT (dashed lines) for a 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for varying magnitude of treatment-covariate interaction effect γ₁₁ and γ₁₂ and error distributions [(a) Lognorm or (b) Pareto], and fixed overall treatment effect α = 0.2 and covariate effects β₁ = 0.2, β₂ = 0.4, based on a total sample size n = 100 (50 subjects in each treatment group)

4.1.2. Three treatment groups; in the presence of variable selection

We then considered the case where there are three treatment groups and a stepwise variable selection procedure was used in building prediction equations for calculating the test statistic. Here we used the same covariate setting as in section 4.1.1, but included another treatment indicator W₂ = I(treatment group = 2) to represent the case where there were three treatment groups involved in a randomized clinical trial. Similarly as before, conditional on (X₁, X₂, X₃, X₄, X₅),

$$Y=0.5+{\alpha }_1{W}_1+{\alpha }_2{W}_2+{\beta }_1{X}_1+{\beta }_2{X}_2+{\gamma }_{11}{W}_1{X}_1+{\gamma }_{12}{W}_1{X}_2+{\gamma }_{21}{W}_2{X}_1+{\gamma }_{22}{W}_2{X}_2+∊,$$

where W₁ = I(treatment group = 1), W₂ = I(treatment group = 2), ε ⊥ (X₁, X₂, X₃, X₄, X₅).

Table 3 provides empirical Type I error estimates of the permutation tests and the likelihood ratio test for varying magnitudes of overall treatment effect, covariate effects and error distributions. We again found that the actual Type I error estimates of the permutation tests were very close to the nominal level in all settings, even when the sample size was as small as 30 subjects per treatment arm. The accuracy of the proposed test was minimally affected by the fact that the overall treatment effects had to be estimated in practice. In contrast, the LRT could lead to inflated type I errors, for non-normally distributed data and/or small sample sizes. For example, when data followed a Cauchy distribution, in some settings, the actual type I errors for a 0.05 level test increased to above 0.1 when n = 90 and to around 0.09 when n = 150.

Table 3.

Empirical Type I error estimates {P̂(rej. H₀)} for 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for varying magnitudes of overall treatment effect and covariate effects. Perm and Perm* represent the case where the overall treatment effects α₁ ad α₂ are estimated and the unachievable case where α₁ and α₂ are known respectively. Results were based on 1000 experiments.

α 1	α 2	β 1	β 2	n = 90			n = 150			n = 300
				Perm	Perm*	LRT	Perm	Perm*	LRT	Perm	Perm*	LRT
Normal Distribution
0	0	0.1	0.2	0.048	0.044	0.073	0.047	0.045	0.062	0.057	0.055	0.052
0.2	0.4	0.1	0	0.044	0.045	0.081	0.050	0.046	0.050	0.056	0.056	0.056
0.2	0.4	0	0.5	0.043	0.040	0.078	0.053	0.052	0.069	0.055	0.054	0.057
0.2	0.4	0.2	0.4	0.046	0.047	0.075	0.056	0.053	0.068	0.056	0.056	0.061
Cauchy Distribution
0	0	0.1	0.2	0.064	0.061	0.112	0.048	0.049	0.090	0.042	0.041	0.077
0.2	0.4	0.1	0	0.053	0.059	0.112	0.051	0.051	0.081	0.042	0.042	0.068
0.2	0.4	0	0.5	0.068	0.060	0.108	0.050	0.050	0.076	0.042	0.034	0.072
0.2	0.4	0.2	0.4	0.066	0.059	0.113	0.049	0.049	0.091	0.041	0.039	0.085
Lognorm Distribution
0	0	0.1	0.2	0.047	0.045	0.066	0.051	0.054	0.070	0.046	0.046	0.081
0.2	0.4	0.1	0	0.052	0.046	0.090	0.054	0.048	0.059	0.048	0.042	0.065
0.2	0.4	0	0.5	0.050	0.048	0.090	0.059	0.057	0.059	0.051	0.051	0.072
0.2	0.4	0.2	0.4	0.048	0.046	0.082	0.058	0.050	0.075	0.048	0.047	0.056
Pareto Distribution
0	0	0.1	0.2	0.061	0.051	0.080	0.051	0.050	0.077	0.057	0.057	0.073
0.2	0.4	0.1	0	0.064	0.054	0.082	0.055	0.047	0.097	0.052	0.049	0.071
0.2	0.4	0	0.5	0.060	0.050	0.081	0.058	0.057	0.076	0.061	0.051	0.065
0.2	0.4	0.2	0.4	0.054	0.049	0.084	0.051	0.049	0.063	0.055	0.050	0.076

We then compared the power of the permutation test and the LRT when data were normally distributed(see Table 4). The power of the proposed permutation test increases as the magnitudes of the interaction effects increase and slightly lower than the likelihood ratio test. We did not present results for other error distributions in this case because the size of LRT could be inflated.

Table 4.

Empirical power estimates for 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction, for overall treatment effect α₁ = 0.2 and α₂ = 0.4, and varying treatment-covariate interaction effect, based on a total sample size n = 150 (50 subjects in each treatment group)

γ 11	γ 12	γ 21	γ 22	Perm	LRT
0.1	0	0.1	0	0.055	0.072
0.1	0	−0.1	0	0.052	0.063
0.5	0	0.5	0	0.104	0.121
0.5	0	−0.5	0	0.273	0.304
1.0	0	−1.0	0	0.914	0.925
0	0.1	0	0.1	0.062	0.073
0	0.1	0	−0.1	0.066	0.084
0	0.5	0	0.5	0.370	0.442
0	0.5	0	−0.5	0.902	0.922
0	1.0	0	−1.0	1.000	1.000
0.1	0.1	0.1	0.1	0.065	0.073
0.1	0.1	−0.1	−0.1	0.071	0.091
0.5	0.5	0.5	0.5	0.476	0.535
0.5	0.5	−0.5	−0.5	0.963	0.963
1.0	1.0	−1.0	−1.0	1.000	1.000

4.2. Setting 2

We generated datasets similar to TADS and restricted our attention to 36 covariates and 2 treatment (tx = 0 or 1 represents CBT or Fluoxetine respectively) as before. The total number of subjects was 187, among which 97 were in the Fluoxetine group and 90 in the CBT group. For each experiment, we took a sample of observed covariate values with replacement. The outcome was generated based on the following model:

$$Y=41.0-4.2tx+0.9cdrs\_s\_b+\alpha tx\ast cdrs\_r\_b+∊,∊\sim N(0,12),$$

where ‘tx’ referred to the treatment indicator and ‘cdrs r b’ referred to the baseline Children's Depression Rating Scale -Revised (CDRS-R) Best Description of Child summary score.

The parameters in this model except the coefficient of the interaction term, α, which was allowed to vary, were estimated from TADS data with treatment indicator, cdrs_r_b, and their interaction term as independent variables. cdrs_r_b was centered at 0 so that E(cdrs_r_b) = 0 and E{E(Y | tx = 1, cdrs_r_b) − E(Y | tx = 0, cdrs_r_b)} = −4.2, where the expectation was taken first with respect to Y then cdrs_r_b, Fluoxetine (tx = 1) was the better treatment on average. min(cdrs_r_b) = −14.2 and max(cdrs_r_b) = 24.8.

$$E(Y\mid tx=1,cdrs\_r\_b)-E(Y\mid tx=0,cdrs\_r\_b)=-4.2+\alpha cdrs\_r\_b$$

When α = 0, there is no treatment and covariate interaction. When α> 0, if max(cdrs_r_b) $<\frac{4.2}{\alpha }$, then E(Y | tx = 1) < E(Y | tx = 0) for all cdrs_r_b, no qualitative interaction; otherwise, qualitative interaction exists since for those subjects with cdrs_r_b $>\frac{4.2}{\alpha }$, CBT is expected to yield better outcome. When α< 0, if min(cdrs_r_b) $>\frac{4.2}{\alpha }$, then E(Y | tx = 1) < E(Y | tx = 0) for all cdrs_r_b, no qualitative interaction; otherwise, qualitative interaction exists: for subjects with cdrs_r_b $<\frac{4.2}{\alpha }$, CBT is expected to yield better outcome.

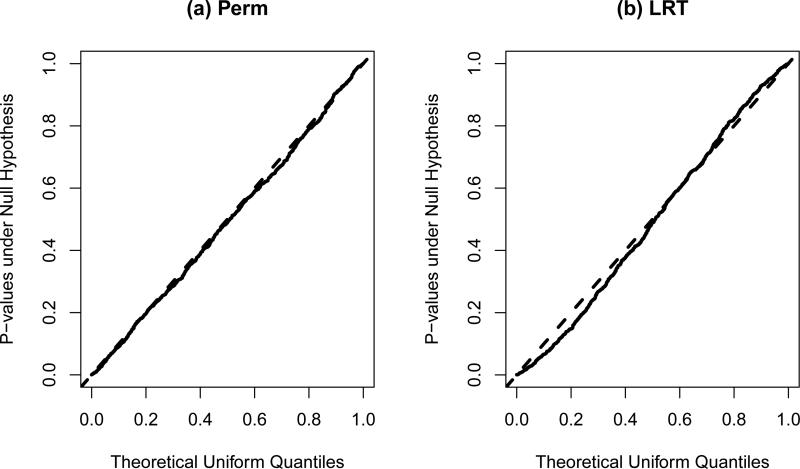
We used the same variable selection procedure, the lasso, as in analyzing the TADS dataset in section 3. To assess the validity of the test, we used the quantile-quantile plot to compare the distribution of the empirical p-values to the uniform distribution (Figure 3) and found that the quantiles were lined up on the 45 degree straight line, demonstrating the validity of the proposed test in the presence of variable selection and when the overall treatment effect was estimated. Figure 3 (b) showed the corresponding quantile-quantile plot for the ‘LRT’. In this case where the number of covariates was modestly large, the size of ‘LRT’ was slightly inflated. For a nominal 5% level test, the empirical type I errors for ‘Perm’ and ‘LRT’ were 0.056 and 0.078 respectively.

Figure 3.

Quantile-quantile plot for p-values under the null hypothesis H₀: no treatment-covariate interaction.

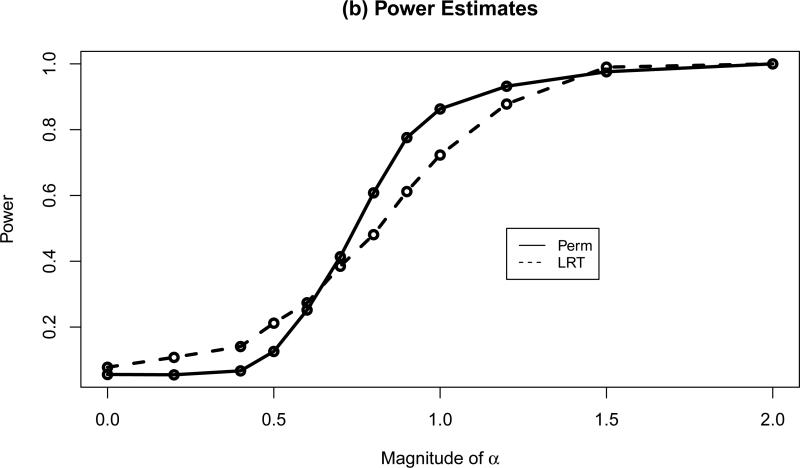
Figure 4 compares the power of ‘Perm’ and ‘LRT’. As the magnitude of interaction effect increases, the power of both tests increases. ‘Perm’ yielded higher power than ‘LRT’ when the interaction effect was larger than 0.7. While ‘LRT’ appeared to have higher power than ‘Perm’ with small interaction effect, the fact that ‘LRT’ was associated with slightly inflated type I error makes ‘LRT’ a less desirable test in this setting.

Figure 4.

Empirical size/power estimates for 0.05 level test of the null hypothesis H₀: no treatment-covariate interaction.

5. Discussion

In this paper we propose a permutation test for the null hypothesis of no treatment-covariate interactions for any covariate, for the setting where there are multiple randomized treatment options and many candidate covariates. The proposed test maintains type I error in the absence or presence of variable selection. The validity of the test relies on an important feature of randomized clinical trials; that is, successful randomization ensures that the treatment assignment is independent of all covariates. One future research direction is to extend the proposed method to observational studies, possibly using inverse probability weighting.

The proposed test provides an attractive alternative to the standard likelihood ratio test, especially when the number of covariates is large or when the error distribution is skewed. In the settings with normal error distribution and small number of covariates, the proposed test yields slightly lower power than the likelihood ratio test. When the number of covariates is substantially large compare to the sample size, such as in the TADS example, there was 36 covariates and 187 subjects, the size of likelihood ratio test may be slightly inflated and the proposed test may have greater power to detect the treatment-covariate interactions for certain alternatives. When the number of covariates is even larger so that the number of parameters in the full model with all the 2-way treatment-covariate interaction terms is larger than the sample size, the likelihood ratio test can no longer be applied since the parameters in this model will not be identifiable; while the proposed test still apply. The likelihood ratio test could also lead to inflated type I error when the error distribution is non-normal while the proposed test remains valid regardless of the specific error distribution. Furthermore, in calculating the test statistic for the proposed permutation test, one can apply a variable selection procedure for each treatment arm which can provide a list of potential treatment effect modifiers for future investigation. When there are many candidate covariates and only a small number of variables interacts with treatment, the proposed test is expected to perform better than the likelihood ratio test in terms of power as indicated in the setting 2 of the simulation section (section 4.2). The test statistic for the proposed test is constructed using prediction errors calculated from a model relating outcome and selected covariates, rather than models relating outcome and all the covariates as in the likelihood ratio test. The model selection process can help eliminate the random noises associated with irrelevant covariates and therefore improve power.

The outcome in TADS is continuous and we used linear regression models for prediction. It would be useful to extend the permutation test to the cases where the outcome is dichotomous or time-to-event outcome and a corresponding logistic regression model or Cox proportional hazards model is assumed. In addition, the prediction models do not need to be linear in covariates. Although a linear model is assumed to relate outcome with treatment indicators, covariates and their interaction terms, the validity of the test only relies on the independence of treatment indicators (W) with the residuals after removing treatment effect (ε) conditional on covariates. This coupled with the fact that treatment indicators are independent of all covariates(X), resulting in the independence of treatment indicators W and (ε,X), which provides the basis for permuting the treatment indicators and subsequently generating the permutation null space for inference.

The proposed test provides an overall test to detect the presence of any treatment-covariate interaction. The natural next step is to identify the source of interaction. When we analyzed the TADS dataset in Section 3, the results of the proposed permutation test suggested the existence of treatment-covariate interaction. Although the proposed test does not directly yield a list of covariates that interact with treatment, in calculating the test statistic, we can obtain a set of selected covariates that predicts outcome for each treatment group. Comparing the coefficients of covariates in the model for each treatment can provide some indications for covariates that warrant further investigation. For a specific covariate, statistically significantly different coefficients from different treatment-specific models would provide evidence for existence of a treatment-covariate interaction. In the TADS example, CDRS-R Summary Score (Best Description) was associated with a zero coefficient for the Fluoxetine group and a non-zero coefficient for the CBT group, suggesting that it might be a potential treatment effect modifier. A formal comparison would be very useful. However, analytical challenges in a formal comparison lie in the difficulty of obtaining accurate standard error estimates for the coefficients that can properly take into account the uncertainty in variable selection [32].

APPENDIX

Under the null hypothesis of no interaction effects, model (1) can be written as:

$$Y={\alpha }^{T}W+∊,\text{where}∊={\beta }^{T}X+{∊}_0.$$

It follows that ε = Y − α^TW = β^TX + ε₀ ⊥ W | X. This, combined with W ⊥ X by randomization, we have

$$W\perp (Y-{\alpha }^{T}W,X).$$

Apply the one-to-one transformation g: g(y, w, x) = (y − α^T w, w, x) to each row of D, we obtain a transformed data matrix D̃ = (Y − α^T W, W, X), which can be partitioned into two parts D̃_P = W and D̃_F = (Y − α^T W, X). The independent relation in (2) allows us to permute the rows of the matrix D̃_P and keep D̃_F fixed, resulting in permuted transformed data matrices D̃^l = (Y − α^T W, W^l, X) that are equally likely as the transformed observed data matrix D̃. Here we use W^l to denote a row permutation of W. Let g⁻¹ denote the inverse of g, that is, g⁻¹(v, w, x) = (v + α^T w, w, x). Apply g⁻¹ to each row of ${\tilde{D}}^{\ell }$ and let ${\tilde{D}}_{(-1)}^{\ell }$ denote the resulting reverse-transformed matrix. Note that D̃₍₋₁₎ = D, the observed data matrix. Because g⁽⁻¹⁾ is a one-to-one transformation, it follows that ${\tilde{D}}_{(-1)}^{\ell }$ and D are equally likely. Let T be any test statistic, T(D) is a random sample of size 1 from the permutation distribution formed by $T\left({\tilde{D}}_{(-1)}^{\ell }\right)$ under the null hypothesis.