Analysis of Repeated Low-Dose Challenge Studies

Abstract

Preclinical evaluation of candidate human immunodeficiency virus (HIV) vaccines entails challenge studies whereby non-human primates such as macaques are vaccinated with either an active or control vaccine and then challenged (exposed) with a simian-version of HIV. Repeated low-dose challenge (RLC) studies in which each macaque is challenged multiple times (either until infection or some maximum number of challenges is reached) are becoming more common in an effort to mimic natural exposure to HIV in humans. Statistical methods typically employed for the testing for a vaccine effect in RLC studies include a modified version of Fisher’s exact test as well as large sample approaches such as the usual log-rank test. Unfortunately, these methods are not guaranteed to provide a valid test for the effect of vaccination. On the other hand, valid tests for vaccine effect, such as the exact log-rank test, may not be easy to implement using software available to many researchers. This paper details which statistical approaches are appropriate for the analysis of RLC studies, and how to implement these methods easily in SAS or R.

1 Introduction

Preclinical proof-of-concept vaccine trials using animal models limit the risk, time and cost of clinical trials involving human subjects by providing preliminary evidence of potential safety and efficacy of an investigational vaccine [1, 2]. A large portion of the preclinical studies of human immunodeficiency virus (HIV) vaccines have been conducted using macaques because the disease progression of simian immunodeficiency viruses in macaques is similar to that of HIV in humans [2]. The virus challenge in these preclinical trials has historically been administered via a single high-dose intravenous or mucosal inoculation, often resulting in a high probability of infection for all unvaccinated macaques [3, 4]. Such high infection rates do not mirror the low probability of heterosexual HIV transmission per sexual act or low per month probability of late postnatal HIV transmission via breastfeeding [5, 6, 7]. Moreover, vaccines may not be equally efficacious against high-dose and low-dose challenges, such that vaccines efficacious against low-dose challenges (and hence of possible utility) may be discarded due to not demonstrating efficacy in high-dose challenge studies [8].

As an alternative, repeated low-dose challenge (RLC) studies have been employed more recently; see e.g. [3, 9, 10]. In these studies, each macaque is challenged and infection status assessed. If the animal is uninfected, another challenge is administered and infection status assessed again. This process continues until infection or a pre-specified maximum number of challenges is reached. Simulation studies examining the power of RLC studies to detect vaccine effects have demonstrated that these trials are viable alternatives to traditional single high-dose challenge studies [8, 11].

A standard analysis used for the single-dose challenge study entails performing Fisher’s exact test on a 2 × 2 contingency table of infection status by treatment assignment where cell counts are the number of the macaques in each category (i.e., vaccinated and infected, vaccinated and not infected, control and infected, control and not infected). For the RLC setting, Regoes et al. [8] proposed Fisher’s exact test be conducted on a 2 × 2 contingency table of infection status by treatment assignment, where the cell counts are the number of challenges across all macaques within each category. Alternative analytic approaches implemented in this setting include the exact log-rank test as well as non-exact (i.e., large sample) approaches including the log-rank test and Cox proportional hazard modeling [9, 12, 13, 14]. Unfortunately, some of these analytic approaches are not appropriate in the RLC setting because the assumptions required for these methods to provide a valid test for a vaccine effect are not met. On the other hand, other analysis methods which are valid may not be easy to implement using software available to clinical researchers.

This paper describes appropriate analytic approaches for RLC studies. The methods presented are motivated by two important aspects of the data generated in RLC studies: (i) the number of challenges until infection can be viewed as a discrete failure time subject to right censoring, and (ii) sample sizes are often very small such that large sample frequentist-based analytic approaches may yield incorrect inference. The outline of this paper is as follows. Section 2 introduces notation and Section 3 reviews randomization-based inference, a mode of inference appropriate for randomized studies with small sample sizes. Section 4 provides details regarding why Fisher’s exact test as described above does not provide a valid test of RLC studies. Valid analytic approaches for RLC studies are discussed in Section 5 and compared in a simulation study in Section 6. In Section 7 some of the different methods are illustrated using data from a recent RLC study. Section 8 concludes with a discussion. Sample SAS and R code as well as select simulation results are provided in the Supplemental Information document.

2 Notation

Suppose there are n macaques in a study. In the single challenge study, let d_i(z) denote the potential infection outcome when macaque i is assigned z, where z = 0 denotes control and z = 1 denotes vaccine. Let d_i(z) = 1 if the macaque becomes infected after the single challenge and d_i(z) = 0 otherwise. Prior to the study each macaque has two potential outcomes, only one of which is observed during the trial. Let Z_i denote the treatment randomly assigned to macaque i and let $D_i^{\mathit{\text{obs}}}=d_i(0)(1-Z_i)+d_i(1)Z_i=d_i(Z_i)$ denote the observed outcome.

For RLC studies, let t̃_i(z) denote the number of challenges until infection were macaque i assigned z and challenged indefinitely. In practice, a maximum number of challenges is typically pre-specified, which we denote by $c_i^{\mathit{\text{max}}}$ for macaque i. Often $c_i^{\mathit{\text{max}}}$ will be the same for all macaques, but to maintain generality we allow for $c_i^{\mathit{\text{max}}}$ to depend on i. We do however assume that $c_i^{\mathit{\text{max}}}$ is the same regardless of randomization assignment Z_i. Let $t_i(z)=\text{min}\{{\tilde{t}}_i(z),c_i^{\mathit{\text{max}}}\}$, i.e., the number of challenges macaque i would receive if assigned z. Let $d_i(z)=I\{{\tilde{t}}_i(z)\le c_i^{\mathit{\text{max}}}\}$ denote the potential infection indicator, where d_i(z) = 1 if macaque i would become infected during the study when assigned z and d_i(z) = 0 otherwise. Denote the observed number of challenges and infection indicator by $T_i^{\mathit{\text{obs}}}=t_i(Z_i)$ and $D_i^{\mathit{\text{obs}}}=d_i(Z_i)$.

3 Randomization-Based Inference

Because pre-clinical challenge studies typically randomize a small number of macaques, randomization-based statistical methods are ideal for inference about the effect of vaccination. Randomization-based inference is based on distributions created from the randomization process rather than assuming random sampling from an infinite population or that particular parametric distributions hold [15, 16, 17]. Under randomization-based inference the potential outcomes (i.e., (d_i(1), d_i(0)) for a single challenge experiment or (t_i(1), t_i(0), d_i(1), d_i(0)) for a RLC experiment) are considered fixed, discrete features of the finite population of n macaques and Z_i is considered a random variable. As observed outcomes are functions of treatment assignment, they are also considered random.

Consider the null hypotheses that vaccine has no effect on any of the n macaques for a single challenge study:

$$H_0:d_i(0)=d_i(1)\text{for}i=1,\dots ,n.$$ (1)

Likewise, the null hypothesis in a RLC study is:

$$H_0:d_i(0)=d_i(1)\text{and}{t}_i(0)=t_i(1)\text{for}i=1,\dots ,n.$$ (2)

These types of null hypotheses are sometimes referred to as sharp null hypotheses of no effect [18]. Under a sharp null the potential outcomes for each macaque are the same under either treatment assignment.

Under either null (1) or (2) the observed outcomes become fixed regardless of treatment assignment. Moreover, all potential outcomes are observed for each macaque, which allows exact characterization of the sampling distribution of any chosen test statistic by computing the statistic for each possible re-randomization of the macaques. The resulting p-values are considered exact in that they are based on calculating the exact distribution of the test statistic as opposed to relying on asymptotic approximations. Such tests are often referred to as permutation tests. See §2 of [17] for additional details.

4 Fisher’s Exact Test

Fisher’s exact test is commonly employed for the analysis of 2 × 2 tables to assess the sharp null hypothesis that treatment has no effect on any individuals. In this section, we explain why Fisher’s exact test provides a valid test for a single challenge study, but does not provide a valid test in the RLC setting.

4.1 Single Challenge Study: Valid Use of Fisher’s Exact Test

Suppose a single challenge study is conducted where four macaques are randomized such that two receive vaccine and two receive control. Assume without loss of generality the observed treatment assignments are Z₁ = Z₂ = 1 and Z₃ = Z₄ = 0. Further suppose only one macaque, i = 1, escapes infection from the single challenge $(D_1^{\mathit{\text{obs}}}=0\text{and}{D}_2^{\mathit{\text{obs}}}=D_3^{\mathit{\text{obs}}}=D_4^{\mathit{\text{obs}}}=1)$. The observed data can be summarized in the 2 × 2 table

(3).

	Infected	Non-infected
Vaccine	1	1	2
Control	2	0	2
	3	1	4

which in general can be written

(4).

	Infected	Non-infected
Vaccine	${\sum }_i{Z}_i{D}_i^{\mathit{\text{obs}}}$	${\sum }_i{Z}_i(1-D_i^{\mathit{\text{obs}}})$	∑iZi
Control	${\sum }_i(1-Z_i)D_i^{\mathit{\text{obs}}}$	${\sum }_i(1-Z_i)(1-D_i^{\mathit{\text{obs}}})$	∑i(1-Zi)
	${\sum }_i{D}_i^{\mathit{\text{obs}}}$	${\sum }_i(1-D_i^{\mathit{\text{obs}}})$	n

where here and in the sequel ∑_i denotes ${\sum }_{i=1}^n$.

Conducting Fisher’s exact test relies on the assumption the row and column margin totals are fixed. In single challenge studies, the fixed row margin assumption follows from the number of macaques assigned each treatment being fixed by design, and the fixed column assumption follows from the number of infected and non-infected macaques being the same regardless of treatment assignment under the sharp null (1). For the example given in (3), only one other table is possible under the assumption the margins are fixed. This other table can be constructed by switching the rows of (3) such that there is one non-infected control macaque and zero non-infected vaccine macaques. The probability of each of these two possible tables under the null (1) is obtained by recognizing that any cell in the table has a hypergeometric distribution when the margins are fixed. Given the 4 margins from table (3), the probability of each of the two possible 2 × 2 tables is 0.5, and therefore the one-sided p-value for this example is 0.5.

To see that Fisher’s exact test can be viewed as a randomization-based or permutation test as described in Section 3, note there are $\left(\begin{array}{c}\hfill 4\hfill \\ \hfill 2\hfill \end{array}\right)=6$ possible treatment assignment combinations which are all equally likely, each occurring with probability 1/6. Under the sharp null (1), the potential treatment assignments and corresponding observed outcomes are:

(5).

	Vaccine		Control
Z1Z2Z3Z4	#Infected	#Not infected	#Infected	#Not infected
1100	1	1	2	0
1010	1	1	2	0
1001	1	1	2	0
0110	2	0	1	1
0101	2	0	1	1
0011	2	0	1	1

where the randomization assignment given in the first row is observed. The Fisher’s exact test p-value of the null hypothesis (1) versus a one-sided alternative that the vaccine has a protective effect is calculated as the proportion of assignments that result in an outcome at least as extreme as the observed data (in the direction of the alternative). This proportion includes assignments where the number of infected vaccine macaques is ≤ 1, i.e., the first three rows of (5). Therefore the one-sided p-value is 3/6 = 0.5.

4.2 RLC Studies: Invalid Use of Fisher’s Exact Test

Now suppose for the example in Section 4.1 that the macaque that was not infected after a single exposure was subsequently exposed a second time (i.e., $c_1^{\mathit{\text{max}}}=2$). Suppose after the second exposure the macaque remained uninfected. Thus now the observed data are $(T_1^{\mathit{\text{obs}}},D_1^{\mathit{\text{obs}}})=(2,0)$ and $(T_i^{\mathit{\text{obs}}},D_i^{\mathit{\text{obs}}})=(1,1)$ for i = 2, 3, 4. Regoes et al. [8] proposed applying Fisher’s exact test to the following table:

(6).

	Infected	Non-infected
Vaccine	${\sum }_i{Z}_i{D}_i^{\mathit{\text{obs}}}$	${\sum }_i{Z}_i(T_i^{\mathit{\text{obs}}}-D_i^{\mathit{\text{obs}}})$	${\sum }_i{Z}_i{T}_i^{\mathit{\text{obs}}}$
Control	${\sum }_i(1-Z_i)D_i^{\mathit{\text{obs}}}$	${\sum }_i(1-Z_i)(T_i^{\mathit{\text{obs}}}-D_i^{\mathit{\text{obs}}})$	${\sum }_i(1-Z_i)T_i^{\mathit{\text{obs}}}$
	${\sum }_i{D}_i^{\mathit{\text{obs}}}$	${\sum }_i(T_i^{\mathit{\text{obs}}}-D_i^{\mathit{\text{obs}}})$	${\sum }_i{T}_i^{\mathit{\text{obs}}}$

Note here the table entries correspond to the number of challenges that resulted in infection or not. This is a modification of the usual fashion in which Fisher’s exact test is applied. Ordinarily Fisher’s exact test is applied to a table where each individual (macaque) contributes only once to a table entry. In contrast, in table (6) a macaque that is challenged more than once contributes multiple times to the table entries. For our example this table equals

(7).

	Infected	Non-infected
Vaccine	1	2	3
Control	2	0	2
	3	2	5

Applying Fisher’s exact test to (7) entails enumerating all other possible 2 × 2 tables with the same margins as (7); there are two such other tables. Then the probabilities of observing the table given in (7) and two other tables are calculated. One of these other tables is

(8).

	Infected	Non-infected
Vaccine	2	1	3
Control	1	1	2
	3	2	5

However, if the sharp null (2) is true, it is not possible to ever observe table (8). Under the sharp null, only one macaque ever escapes infection from a challenge (namely macaque 1). To the contrary, according to table (8), there exists a scenario where a macaque in the vaccine arm is not infected after a challenge and also a macaque in the control arm that is not infected after a challenge. Thus the sampling distribution of Fisher’s exact test under the null includes a table that cannot be observed. In general, under this set-up Fisher’s exact test p-values are computed utilizing the incorrect set of potential tables, such that non-zero probabilities of observation are assigned to tables that are not actually observable under any possible treatment assignment and conversely zero probabilities may be assigned to tables that are observable. The problem is that for table (6) the fixed margins assumption does not hold under the sharp null (2) because the numbers of challenges per treatment group (row margins) are not necessarily fixed. For example, if macaque 1 were assigned to the control arm, then the second row total of (6) would be 3, not 2 as in (7); and so the row totals are not fixed, but rather are randomly 3 or 2 according to the group to which macaque 1 is randomly assigned. Because the sampling distribution of the test under the null is being computed incorrectly, there is no assurance that the type I error rate will be correct. Indeed Hudgens et al. [10] showed empirically that using Fisher’s exact test in this fashion can lead to type I error rates greater than the nominal significance level.

To illustrate further, consider the example above but suppose that the uninfected vaccine macaque in (3) was subsequently challenged multiple times and ultimately remained uninfected after 20 challenges such that (6) equals

(9).

	Infected	Non-infected
Vaccine	1	20	21
Control	2	0	2
	3	20	23

Applying a one-sided Fisher’s exact test to this table in order to test for vaccine benefit yields a p-value of 0.012, leading to rejection of the null at significance level α = 0.05. There are $\left(\begin{array}{c}\hfill 4\hfill \\ \hfill 2\hfill \end{array}\right)=6$ possible randomizations (as in (5)). Under the sharp null, three of these randomizations will yield table (9) and one-sided p = 0.012 for Fisher’s exact test; the other three randomizations will yield a table with the macaque remaining uninfected after 20 challenges allocated to the control group and one-sided p = 1. Thus a one-sided Fisher’s exact test applied in this fashion will reject at the α = 0.05 significance level with probability 3/6 = 0.5 under the null, i.e., the actual type I error rate is an order of magnitude greater than the nominal significance level!

A reviewer suggested additional intuition why Fisher’s exact test as formulated in this fashion is not valid. In particular, table (9) is the same table that would have been observed had there been 20 different vaccinated macaques which each escaped infection from a challenge. However, it is impossible for us to have observed 20 infections among these 20 hypothetical macaques; rather, at most one infection could have in fact been observed.

5 Analytic Approaches

If the maximum number of challenges $c_i^{\mathit{\text{max}}}$ is the same for all macaques, i.e., $c_i^{\mathit{\text{max}}}=c$ for all i and some constant c > 1, then data from the RLC setting can be represented by the following 2 × (c + 1) table:

(10).

	Infected at t = 1	Infected at t = 2	…	Infected at c	Not infected after c
Vaccine	$\sum Z_{i}I[T_i^{\mathit{\text{obs}}}=1]$	$\sum Z_{i}I[T_i^{\mathit{\text{obs}}}=2]$	…	$\sum Z_i{D}_i^{\mathit{\text{obs}}}I[T_i^{\mathit{\text{obs}}}=c]$	$\sum Z_i(1-D_i^{\mathit{\text{obs}}})$
Control	$\sum (1-Z_i)I[T_i^{\mathit{\text{obs}}}=1]$	$\sum (1-Z_i)I[T_i^{\mathit{\text{obs}}}=2]$	…	$\sum (1-Z_i)D_i^{\mathit{\text{obs}}}I[T_i^{\mathit{\text{obs}}}=c]$	$\sum (1-Z_i)(1-D_i^{\mathit{\text{obs}}})$

In this case, exact methods for a 2 × (c + 1) table can be employed (e.g., see Agresti [19] Chapter 3.5). For example, the null (2) can be tested using Fisher’s exact test for 2 × (c + 1) tables, although this approach may often have unacceptably low power. In order to test for vaccine benefit, an exact trend test with rank based scores (Wilcoxon or logrank), such as the Cochran-Armitage exact trend test in SAS PROC FREQ [20, 21], may be employed and generally will be more powerful than Fisher’s exact test.

However, in many RLC studies $c_i^{\mathit{\text{max}}}$ is not the same for all macaques; e.g., see [22]. If $c_i^{\mathit{\text{max}}}$ varies across macaques, then table (10) cannot be used to summarize the data. In this case, survival analysis methods for analyzing right-censored discrete time to event data can be employed to test for a vaccine effect. Methods frequently employed include the logrank test as well as model-based approaches that typically use large-sample approximations based on the asymptotic distribution of the likelihood ratio test (LRT), score test, or Wald test statistics. These statistics and the corresponding large sample p-values can be obtained via a variety of statistical packages. Randomization-based p-values for these test statistics can be obtained using standard packages as well, but options are more limited. The remainder of this section details these tests, including asymptotic distributions used for large-sample p-values and methods for obtaining randomization-based (i.e., exact) p-values.

5.1 Log-Rank Test

The Mantel-Cox log-rank test is a popular test employed in survival analysis to assess whether there is a difference in the failure time distributions between two groups when there is right censoring. For the RLC setting, the log-rank test can be derived by constructing a series of 2 × 2 tables after each challenge. For challenge t, let $N_t(z)=\sum I(T_i^{\mathit{\text{obs}}}\ge t,Z_i=z)$ denote the number of macaques at risk and $D_t(z)=\sum I(T_i^{\mathit{\text{obs}}}=t,D_i^{\mathit{\text{obs}}}=1,Z_i=z)$ denote the number infected in study arm z = 0, 1. Let N_t = N_t(0) + N_t(1) denote the total number at risk and D_t = D_t(0) + D_t(1) be the total number of infections due to challenge t. At each time t (i.e., challenge) construct the following table

(11).

	Infected	Non-infected
Vaccine	Dt(1)	Nt(1) − Dt(1)	Nt(1)
Control	Dt(0)	Nt(0) − Dt(0)	Nt(0)
	Dt	Nt − Dt	Nt

Conditional on the row and column totals, under the null hypothesis (2) that the vaccine has no effect D_t(1) has a hypergeometric distribution with expectation E{D_t(1)} = N_t(1)D_t/N_t and variance $V\{D_t(1)\}=N_t(1)N_t(0)D_t(N_t-D_t)/\{N_t^2(N_t-1)\}$. The log-rank test statistic is then defined as $LR={\sum }_{t=1}^{c^{\mathit{\text{max}}}}[D_t(1)-E\{D_t(1)\}]$ where $c^{\mathit{\text{max}}}=\text{max}\{c_i^{\mathit{\text{max}}}:i=1,\dots ,n\}$. Dividing LR squared by the sum of the conditional variances, the statistic $L{R}_{CMH}=L{R}^2/{\sum }_{t=1}^{c^{\mathit{\text{max}}}}V\{D_t(1)\}$ is identical to the stratified Cochran-Mantel-Haenszel statistic where the strata are defined by time (i.e., challenge).

5.2 Model-based Tests

Suppose the n macaques are envisaged to be a random sample from an infinite (super) population of macaques such that ($T_i^{\mathit{\text{obs}}}$, $D_i^{\mathit{\text{obs}}}$, Z_i) for i = 1, …, n are considered iid copies of the random variables (T^obs, D^obs, Z). Denote the probability a macaque becomes infected at challenge t when assigned z by f_t(z) = Pr(T^obs = t|Z = z). Define the corresponding survival and hazard functions by $S_t(z)=\text{Pr}(T^{\mathit{\text{obs}}}\ge t|Z=z)=1-{\sum }_{j=1}^{t-1}{f}_j(z)$ and p_t(z) = Pr(T^obs = t|T^obs ≥ t,Z = z) = f_t(z)/S_t(z). Consider the following model

$$\frac{p_t(z)}{1-p_t(z)}=\frac{p_t(0)}{1-p_t(0)}\text{exp}(z\beta )$$ (12)

or equivalently logit{p_t(z)} = α_t + zβ where α_t = logit{p_t(0)} and logit(x) = log{x/(1 − x)}. Model (12) is often referred to as the Cox discrete logistic model [23]. Under this model, for − ∞ < β < 0 the vaccine is said to have a “leaky effect” because vaccination affords some but not complete protection from infection. Note the formulation of model (12) relies on the potentially strong assumption that all macaques within a treatment group have the same probability of being infected at each challenge; relaxing this assumption is discussed in Section 5.4 below.

Typically interest is primarily focused on the treatment effect β and not the baseline log odds α_t. Considering α₁, α₂, … to be unknown nuisance parameters, inference for β alone can be based on the partial likelihood function

$$\prod _{t=1}^{c^{\mathit{\text{max}}}}\frac{\text{exp}(\beta {\sum }_{i\in {𝒟}_t}{Z}_i)}{{\sum }_{q\in {𝒵}_t}\text{exp}(\beta {\sum }_{l\in q}{Z}_l)}$$ (13)

where 𝒟_t is the set of D_t macaques infected at challenge t and 𝒵_t is the set of all possible subsets of macaques of size D_t chosen without replacement from the set of N_t macaques at risk at t. Inference about β then proceeds by applying the usual large sample maximum likelihood methods based on (13). Moreover, it is straightforward to show that the score test for the partial likelihood (13) equals LR_CMH given in the previous section.

Alternatively, estimates of the parameters in model (12) can be obtained using a standard (i.e., full) likelihood approach by fitting a logistic regression model with treatment and challenge number as covariates [24, 25, 26]. This full likelihood approach provides estimates of both β and α₁, …, α_c^max. Estimates of β obtained by maximizing the full likelihood will tend to be similar but not identical to the maximum partial likelihood estimates. The full likelihood function can be expressed as

$$\prod _{i=1}^n\prod _{t=1}^{T_i^{\mathit{\text{obs}}}-1}\{1-p_t(Z_i)\}{\{1-p_{T_i^{\mathit{\text{obs}}}}(Z_i)\}}^{1-D_i^{\mathit{\text{obs}}}}{p}_{T_i^{\mathit{\text{obs}}}}{(Z_i)}^{D_i^{\mathit{\text{obs}}}}$$ (14)

which can be expressed as a function of (α₁, …, α_c^max, β) by replacing p_t(Z_i) with logit⁻¹(α_t + Z_iβ) and $p_{T_i^{\mathit{\text{obs}}}}(Z_i)$. with ${\text{logit}}^{-1}({\alpha }_{T_i^{\mathit{\text{obs}}}}+Z_i\beta )$ Maximum likelihood based inference may not be valid in small sample settings such as RLC challenge experiments. The usual maximum likelihood approaches are particularly suspect if the number of parameters, in this case c_max + 1, is large relative to the sample size n. Likelihood-based inference may be more reliable if additional assumptions are made which limit the number of parameters, provided such assumptions are reasonable. For instance, a special case of model (12) entails the additional assumption that, conditional on treatment assignment Z_i, the probability of infection does not vary across challenges. In this case α₁ = α₂ = ⋯ = α_c^max, which we denote by α. Similarly, denoting the per contact infection probability by p(z), i.e., p_t(z) = p(z) for all t, the (full) likelihood reduces to

$$\prod _{i=1}^n{\{1-p(Z_i)\}}^{T_i^{\mathit{\text{obs}}}-1}{\{1-p(Z_i)\}}^{1-D_i^{\mathit{\text{obs}}}}p{(Z_i)}^{D_i^{\mathit{\text{obs}}}}$$ (15)

which can be expressed as a function of (α, β) by replacing p(Z_i) with logit⁻¹(α + βZ_i).

The partial likelihood (13) or full likelihoods (14) or (15) can be used to test the null hypothesis β = 0 that the vaccine effect has no effect using either the LRT, score, or Wald statistics. These test statistics are all asymptotically ${\chi }_1^2$ under the null. Note that the null hypothesis here β = 0 of no vaccine effect is implied by (but does not imply) the sharp null that (2) holds in the infinite (super) population. The null β = 0 can be interpreted as the vaccine having no effect per challenge on average, where the average is being taken over the infinite population of macaques; a special case of the vaccine having no average effect is when the sharp null (2) holds in the population.

5.3 Implementation

Large sample p-values for the LRT, score (log-rank) test, or Wald test described in the previous section can be obtained via a variety of statistical software packages. For example, p-values for the LR_CMH log-rank test statistic can be obtained in SAS [21] using PROC FREQ, LIFETEST or PHREG, or in R [27] using mantelhaen.test or the functions survdiff or coxph from the survival package [28]. Full likelihood based approaches can be implemented using a myriad of SAS procedures or R functions, e.g., using PROC LOGISTIC in SAS or glm in R.

Exact randomization-based p-values using the LRT, score (log-rank), and Wald statistics can be obtained in the same fashion as described in Section 3 and illustrated with Fisher’s exact test in Section 4.1. Unlike large sample p-values which rely on asymptotic approximations that may be dubious in small sample studies, exact p-values are valid for any sample size and thus are attractive for use in RLC experiments which usually entail a limited number of macaques. Unfortunately, however, built-in procedures for calculating such randomization-based p-values are somewhat limited.

StatXact [29] includes a procedure for obtaining randomization-based p-values for the log- rank test statistic. While the exact log-rank test employed in StatXact is a valid randomization- based test, the test statistic is not exactly equivalent to LR or LR_CMH in the discrete time setting [30]. Rather, the exact ‘log-rank test’ in StatXact is based on Savage scores and therefore is only equivalent to the LR when there is no censoring and there are no tied failure times (the latter of which will be unlikely in many RLC studies). An exact p-value based on LR can be obtained in StatXact by manually calculating log-rank scores for each individual and then conducting a general permutation test [30]. Both approaches are valid and the difference in the resulting p-values are typically minimal.

Because StatXact is a specialized commercial software package for performing exact infer- ence, it is less frequently available to analysts and investigators as compared to SAS or R. Accordingly, alternative approaches that may be more readily employed might be preferred. For example, the surv_test function from the R coin package [31] produces randomization-based p-values for a log-rank test statistic that is similar, but not exactly equivalent, to LR_CMH [31, 32]. Alternatively, exact conditional logistic regression models using the SAS LOGISTIC procedure with an EXACT statement provide a randomization-type p-value based on the score statistic. These exact p-values can also be obtained in R using mantelhaen.test or cmh_test from the coin package. Exact conditional logistic regression comprises generating the permutation or exact distribution for the parameter of interest based on the likelihood conditional on sufficient statistics for all other parameters in the model which are considered nuisance parameters [33]. In the simplest case where time is the only covariate in the model besides treatment, conditioning on sufficient statistics for time is equivalent to conditioning on the margins of the per-challenge 2 × 2 tables (11). Thus the conditional logistic regression score statistic is equivalent to LR_CMH and the partial likelihood score statistic. Note, however, that the margins of the 2 × 2 tables (11) are not necessarily fixed (except at the first infection time t) under the sharp null (2). Thus while the exact conditional logistic regression approach relies on permutation type arguments for inference, the actual sampling distribution utilized is not equivalent to the re-randomization distribution described in Section 3 above. In practice, the exact conditional logistic regression score test and the exact logrank test tend to yield similar results. Besides being easily implemented in SAS, exact conditional logistic regression also allows for covariate adjustment and treatment effect estimation.

To our knowledge no built-in procedures in SAS or R provide randomization-based p-values based on Wald or LRT statistics. However, such p-values can be obtained via user-developed code that calls the SAS PHREG or LOGISTIC procedures or the R coxph or glm functions for all possible treatment assignment permutations. In SAS possible re-randomizations can be generated using simple data manipulations or by utilizing the MULTTEST procedure. In general computations can quickly become infeasible as the sample size, and hence the number of possible re-randomizations $\left(\begin{array}{c}\hfill n\hfill \\ \hfill m\hfill \end{array}\right)$ increases. In cases where enumerating all possible re-randomizations is not computationally feasible, the exact p-value can be approximated using a Monte Carlo sampling approach.

Illustrative SAS and R code implementing the approaches described above is provided in the Supplemental Information document.

5.4 Heterogeneity

The leaky vaccine effect model (12) assumes all macaques within a treatment group have the same probability of being infected at each challenge. This assumption can be relaxed to allow for heterogeneity in the per-exposure probability of infection [10, 34, 8, 11]. An extreme form of such heterogeneity might entail allowing for a subset of the population to be immune from infection. For example, the likelihood (15) can be modified to allow for an immune subset as follows

$$\prod _{i=1}^n{[(1-\theta ){\{1-p(Z_i)\}}^{T_i^{\mathit{\text{obs}}}-1}p(Z_i)]}^{D_i^{\mathit{\text{obs}}}}{[\theta +(1-\theta ){\{1-p(Z_i)\}}^{T_i^{\mathit{\text{obs}}}}]}^{(1-D_i^{\mathit{\text{obs}}})}$$

where θ is the probability that a macaque is immune (i.e., not susceptible to infection). Likelihoods can also be constructed allowing for an all-or-none vaccine effect such that a macaque susceptible to disease when receiving control is no longer susceptible (i.e., immune) when receiving vaccine, as well as a mixture vaccine effect where the vaccine may provide both all-or-none and leaky effects. There is currently no default SAS or R procedure that assume these likelihoods; however, user-developed code that manually defines (and optimizes) the likelihood function can be constructed to obtain the corresponding LRT, score, and Wald statistics. Large sample and exact p-values can then be computed accordingly.

6 Simulations

Simulations were conducted to compare the operating characteristics of the exact and large sample tests described above. RLC studies were simulated with macaques (i) randomized 1:1 to either vaccine or a placebo control and then (ii) challenged repeatedly until infected or $c_i^{\mathit{\text{max}}}$ challenges were administered. Simulations were conducted under three different sets of assumptions (“Scenarios”) about the rates of infection in the vaccine and placebo arms. In Scenario 1 a leaky vaccine effect was simulated where the probability of infection at each challenge for macaques receiving placebo was p₀ = 0.5 and the probability of infection at each challenge for macaques receiving vaccine was p₁ = ϕp₀ for various fixed values of ϕ (described below). In Scenario 2 a leaky vaccine effect was also simulated but with animal heterogeneity in the per- exposure probability of infection, where the mean (over all macaques) probability of infection per challenge was p₀ when receiving placebo and p₁ = ϕp₀ when vaccine. Individual macaque probabilities of infection per challenge were obtained from a beta distribution as in Regoes et al. [8] with mean μ = p₀ for the placebo group, mean μ = p₁ for the vaccine group, and coefficient of variation (standard derivation/mean) 0.5 for both groups. In Scenario 3 a leaky vaccine effect was simulated as in Scenario 1 but with θ × 100 = 20% of the population immune to infection. For Scenarios 1 – 3, RLC trials were simulated for a range of values of n and $c_i^{\mathit{\text{max}}}$. For each simulated RLC experiment, whether each test rejected the null hypothesis of no vaccine effect at the α = 0.05 significance level was recorded in order to compute the empirical type I error rate and power. For all tests two-sided p-values were used to determine whether to reject the null.

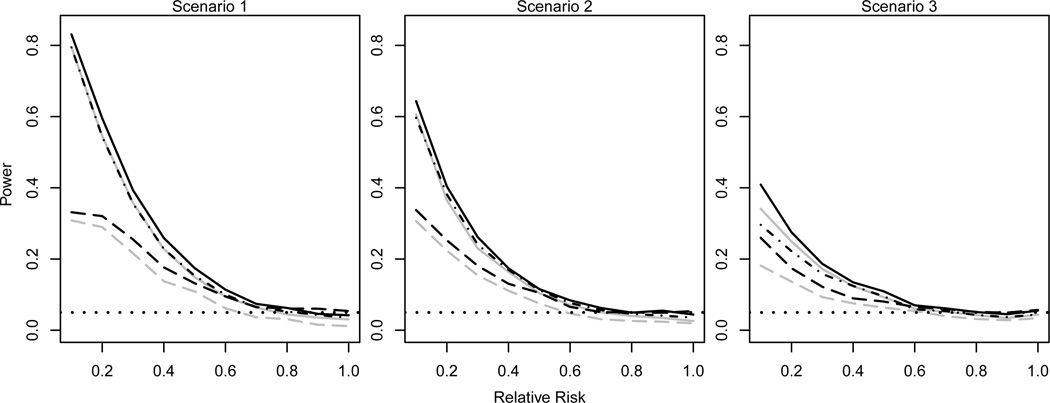
Figure 1 displays the empirical type I error rate and power of the randomization-based tests for various values of ϕ = 0.1, 0.2, …, 1 (ϕ = 1 under the null) based on 2,000 simulated RLC studies with n = 10 and $c_i^{\mathit{\text{max}}}=12$ for all i. In all settings, likelihood-based test statistics were computed assuming the leaky effect model with no heterogeneity or immunity. P-values for the exact LRT and Wald tests were approximated using Monte Carlo methods with 4,000 samples per test. As expected, all exact tests preserved the nominal type I error rate, even when the assumed likelihood was mis-specified (i.e., the likelihood for the simulated data did not correspond to the likelihood used as the basis for the test statistic). The full LRT was the most powerful test in all scenarios, although power for this test was lower when the leaky effect model was not the true underlying likelihood of the simulated data. The exact logrank test (not shown in Figure 1) yielded results very similar to the exact conditional logistic regression score test (shown in Figure 1). The Wald tests (both full and partial) consistently had the lowest power. Larger values of $c_i^{\mathit{\text{max}}}$ did not substantially alter the relative power between the different tests. On the other hand, for larger n (i.e., n ≥ 20) empirical power was approximately equal among the exact tests (results not shown). Power of the exact logrank test for n = 10, 20, and 30 is displayed in the Supplemental Information document (Figure S1); power increased with n as expected in all three scenarios. The Supplemental Information document Figure S2 provides a comparison of the power of the exact Cochran-Armitage trend test (using Wilcoxon rank scores) with the conditional logistic regression score test; the results are very similar, suggesting the exact trend test is a suitable alternative to the exact conditional logistic regression score or logrank tests when the maximum number of challenges is the same across macaques.

Figure 1.

Empirical type 1 error rate and power for the exact LRT {solid line (full=black, partial=gray)}, score test (dot/dashed line), and Wald test {dashed line (full=black, partial=gray)} as a function of relative risk (ϕ) for p₀ = 0.5 probability of infection per challenge when not vaccinated, n = 10 macaques (five per arm), and $c_i^{\mathit{\text{max}}}=12$ maximum challenges per macaque. Scenario 1 includes no heterogeneity or immunity, Scenario 2 includes heterogeneity, and Scenario 3 includes immunity. The dotted horizontal line corresponds to the nominal significance level α = 0.05.

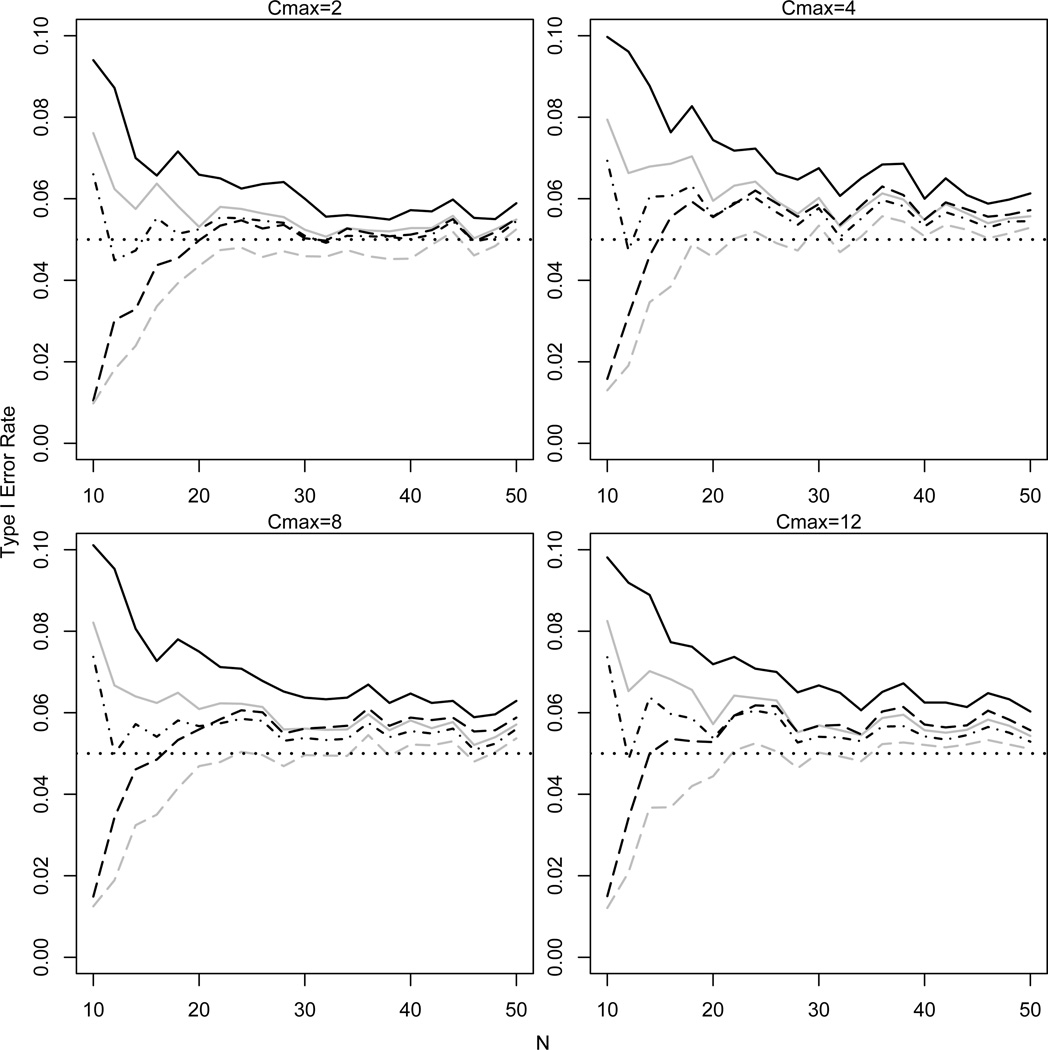
Figure 2 displays the empirical type I error rate of the large sample tests for various values of $c_i^{\mathit{\text{max}}}$ and n based on 10,000 simulated RLC studies. The type I error rate varied by test but in general tended to be inflated for most values of $c_i^{\mathit{\text{max}}}$ and n, with the one exception being the partial Wald test. The inflation of the type I error rate tended to increase with $c_i^{\mathit{\text{max}}}$ but decreased with n, suggesting the large sample tests might be employed provided the total sample size is at least 30.

Figure 2.

Empirical type 1 error rate for large sample LRT {solid line (full=black, partial= gray)}, score/log-rank test (dot/dashed line), and Wald test {dashed line (full=black, partial=gray)} as a function of sample size n = N (i.e., N/2 per arm) for p₀ = p₁ = 0.5 probability of infection per challenge under Scenario 1 (no heterogeneity or immunity) and various values of c^max = Cmax. The dotted horizontal line corresponds to the nominal significance level α = 0.05.

Additional simulations were conducted to examine the empirical bias and coverage probabilities for point estimates and confidence intervals from fitting either a Cox discrete logistic model or an exact conditional logistic regression model to RLC study data generated under Scenario 1. Table S1 of the Supplemental Information document shows the two approaches give similar results in terms of bias. Confidence intervals from exact conditional logistic regression preserve the nominal coverage probability, whereas Cox model confidence intervals tend to undercover when the sample size is small (n = 10) or the vaccine is highly effective (odds ratio of infection per challenge near zero).

7 Application

Hessell et al. [9] presented analyses of a RLC study with four macaques in a control group and five macaques in each of two vaccine groups (b12 and LALA). All groups were initially challenged with a very low-dose challenge 3TCID₅₀. After only one macaque (from the b12 group) was infected after 11 challenges (infected at the sixth challenge), the challenge dose was escalated to 10TCID₅₀. In the published analysis of the study, the macaque that was infected while being challenged with 3TCID₅₀ was analyzed as though infected at the first 10TCID₅₀ challenge; otherwise the 3TCID₅₀ challenges were ignored in the analysis. Of the four control macaques, three macaques were infected after two 10TCID₅₀ challenges and one macaque was infected after four 10TCID₅₀ challenges. Of the five b12 macaques, four macaques were infected after one (described above), six, 23, and 38 challenges and one macaque remained uninfected after 40 challenges.

Hessell et al. reported a significant difference between the b12 and control groups based on the version of Fisher’s exact test suggested by Regoes et al.; in this case the one-sided and two-sided Fisher’s exact test p-values both equal p = 0.002. However, as shown in Section 4.2 above, this version of Fisher’s exact test is not guaranteed to control the type I error rate. In contrast, the two-sided exact log-rank test (using surv_test from the R coin package) yields a two-sided p-value p = 0.14, implying the null (2) would not be rejected at the 0.05 significance level. Similarly the score test from exact conditional logistic regression (using PROC LOGISTIC in SAS or cmh_test or mantelhaen.test in R) yields p = 0.11 and the Cochran-Armitage exact trend test with Wilcoxon rank scores (using SAS PROC FREQ) yields p = 0.17.

Inferences based on point estimates and exact confidence intervals (CIs) instead of hypothesis test p-values lead to similar conclusions. In particular, based on the 2 × 2 table (6) for the Hessell et al. RLC study data, the estimated odds ratio is $\widehat{OR}=0.06$ with exact 95% CI (0.01, 0.41). Just as Fisher’s exact test may overstate significance, such exact CIs based on (6) are not in general guaranteed to provide nominal coverage. Alternatively, applying exact conditional logistic regression to these data yields $\widehat{OR}=0.13$ (95% CI 0.00, 1.69), with the CI clearly including the null value of OR = 1.

Finally, we note that as an alternative to the published analysis, the 3TCID₅₀ challenges could be included with $T_i^{\mathit{\text{obs}}}=6$ for the b12 macaque infected prior to dose escalation, $T_i^{\mathit{\text{obs}}}=17,34,49,51$ for the other four b12 macaques, and $T_i^{\mathit{\text{obs}}}=13,13,13,15$ for the four control macaques. In this case, the exact logrank, score, and trend tests yield identical results to those given above.

8 Discussion

In RLC studies with small sample sizes, randomization-based inference should be employed to ensure the type I error rate is appropriately controlled. On the other hand, asymptotic-based methods should not be used in this setting in order to avoid misleading inferences. While randomization-based tests constructed using the LRT statistic tend to be the most powerful if the assumed likelihood is correct, such tests may require user-defined programming and also may require Monte-Carlo sampling for even moderate sample sizes. In contrast, randomization- based tests constructed using the log-rank statistic are easy to obtain in StatXact or using the surv_test function from the coin package in R. Alternatively, the score test from exact conditional logistic regression can be obtained in SAS using the LOGISTIC procedure with an EXACT option or in R using mantelhaen.test or the coin package function cmh_test. In simulations the empirical power of these tests is approximately comparable to the power of the randomization-based test LRT when there is no heterogeneity or immune fraction. An added benefit of the exact conditional logistic regression approach in comparison to the exact log-rank test is that estimates of the vaccine effect can be obtained from the fitted model. Additionally, covariates of potential interest can easily be incorporated using this approach. Using either approach, the analyst should be mindful that the exact logrank test and the exact conditional logistic regression approach will both have reductions in their power to detect a vaccine effect in accordance with the extent to which the assumption of model (12) does not hold, in which case other tests and/or models may enable better power.

There are many possible future areas of study regarding the design, conduct, and analysis of RLC studies. For instance, time and resources might be saved if formal interim analyses were employed in RLC experiments as in clinical trials. Such interim analyses might be performed at one or more time points during the conduct of an RLC study to assess whether the experiment can be stopped early for futility or efficacy. Of course adjustments would be required for any repeated significance testing in order to preserve the overall type I error rate of the experiment. Another possible area of future study entails development of statistical methods for principled approaches to extrapolating findings from RLC studies to humans.