Development of an online, publicly accessible naive Bayesian decision support tool for mammographic mass lesions based on the American College of Radiology (ACR) BI-RADS lexicon

Abstract

Purpose

To develop and validate a decision support tool for mammographic mass lesions based on a standardized descriptor terminology (BI-RADS lexicon) to reduce variability of practice.

Materials and Methods

We used separate training data (1276 lesions, 138 malignant) and validation data (1177 lesions, 175 malignant). We created naïve Bayes (NB) classifiers from the training data with 10-fold cross validation. Our “inclusive model” comprised BI-RADS categories, BI-RADS descriptors and age as predictive variables, our “descriptor model” comprised BI-RADS descriptors and age. The resulting NB classifiers were applied to the validation data. We evaluated and compared classifier performance with ROC-analysis.

Results

In the training data, the inclusive model yields an AUC of 0.959, the descriptor model yields an AUC of 0.910 (P<0.001). The inclusive model is superior to the clinical performance (BI-RADS categories alone, P<0.001), the descriptor model performs similarly. When applied to the validation data, the inclusive model yields an AUC of 0.935, the descriptor model yields an AUC of 0.876 (P<0.001). Again, the inclusive model is superior to the clinical performance (P<0.001), the descriptor model performs similarly.

Conclusion

We consider our classifier a step towards a more uniform interpretation of combinations of BI-RADS descriptors. We provide our classifier at www.ebm-radiology.com/nbmm/index.html.

Introduction

To date, no guidelines exist to link the full morphological description of a mass lesion detected on x-ray mammography to a definitive risk of malignancy. Standardized description of mass lesions is based on the BI-RADS (breast imaging: reporting and data system) lexicon provided by the American College of Radiology [1]. The BI-RADS lexicon requires the interpreting radiologist to assign a final assessment category to a described lesion, which reflects the level of suspicion the radiologist has that this particular lesion is malignant.

Most likely due to the missing links of descriptor combinations to assessment categories, there is a substantial variability among radiologists for the assignment of BI-RADS assessment categories [2–4]. Variability is found on the level of practicing site [5] and on the level of single readers [2–4]. A possible way to reduce the variability of assignment of BI-RADS assessment categories has been found to be training of radiologists in usage of the lexicon [3; 6]. Additionally, the development of computer assisted diagnostic systems for mammographic lesions based on the BI-RADS lexicon has gained substantial attention in the past. Classification algorithms have been developed that feature neural networks, Bayesian networks, logistic regression and decision trees; these approaches resulted in impressive diagnostic accuracy [7–12]. However, none of these diagnostic systems has been provided as an actually usable research tool to the scientific community.

In the long run, such a diagnostic system could help to reduce the variability of practice in BI-RADS assessment category assignment. Unambiguous communication between radiologists (even at different practicing sites) and clinicians could be enhanced, and so could be uniform patient management. The purpose of this study is therefore to develop a naïve Bayes classifier based on combinations of BI-RADS descriptors for mammographic mass lesions, validate its performance and provide this tool to the research community.

Materials and Methods

Study population

We considered all mammography examinations rated BI-RADS 0, 2, 3, 4 or 5 [1] performed between October 2005 and December 2011 in our university hospital as potentially eligible for this retrospective, institutional ethical review board approved investigation. This resulted in 28857 (23093 screening, 5443 diagnostic, 321 unknown reason) patients examined during the data collection period. In our practice all lesions detected on x-ray mammography are prospectively assigned BI-RADS descriptors by the interpreting radiologist; these descriptors are stored in an electronic database. In case of mass lesions, the shape (round, oval, lobulated or irregular), margin (circumscribed, microlobulated, obscured, ill-defined or spiculated) and density (fat-dense, low, isodense, high) of the lesion can be assessed. Our system does not require the radiologist to assign a value to all of these variables: for example, it is possible to enter a descriptor for shape but to leave the margin and density fields blank. Additional information about the location of the single lesion is stored (required are side and clockwise location).

During the data collection period, 11769 mass lesions were described in 5894 patients. We included all lesions in our analysis for which a match with our institutional (United States Comprehensive Cancer Center) cancer registry could be established based on histopathology. We considered a report of in-situ or invasive cancer within 365 days after the mammography as malignant. The cancer registry provides information about the side and clockwise location of the lesion, so that matching on a per lesion basis is feasible. The cancer registry thus provided us with information for 1719 mass lesions (989 benign, 730 malignant). We secondly included mass lesions with available follow-up examination >365 days (n=7910). We regarded lesions rated as benign with a sufficient follow-up that established the lesion’s stability as benign. We then selected lesions with complete information for shape (missing in 1654 lesions), margin (missing in 3103 lesions) and density (missing in 5297 lesions); the rationale for this approach is detailed in the discussion. This selection resulted in 2453 lesions for our analysis (2140 benign, 313 malignant), the pretest probability in our study population therefore was 313/2453=12.8%.

Naïve Bayes classifiers

Bayesian network classifiers calculate the posttest probability (of malignancy) for a case (herein mass lesion in mammography) given the values of various predictive variables. In our work, predictive variables denote BI-RADS descriptors, BI-RADS assessment categories and patient age. Information regarding the side and clockwise location of the lesions was not used as predictive variable. Table 1 lists the BI-RADS mass lesion descriptors assessed in the first column. For pictorial examples of the descriptors, refer to [13].

Table 1.

Distribution of BI-RADS mass lesion descriptors, age and BI-RADS assessment categories in the training data (n=1276 lesions, thereof 138 malignant). Percentages denote the proportion of lesions with the specific descriptor in the respective descriptor subgroup.

descriptor	n malignant (%)	n benign (%)
mass shape
round	22 (15.9%)	293 (25.7%)
oval	26 (18.8%)	569 (50.0%)
lobulated (4th edition)	16 (11.6%)	152 (13.3%)
irregular	74 (53.6%)	124 (10.9%)
mass margin
circumscribed	15 (10.9%)	733 (64.4%)
microlobulated	7 (5.1%)	13 (1.1%)
obscured	12 (8.7%)	169 (14.9%)
ill-defined	51 (37.0%)	205 (18.0%)
spiculated	53 (38.4%)	18 (1.6%)
mass density
fat-like	1 (0.7%)	64 (5.6%)
low	1 (0.7%)	57 (5.0%)
isodense	35 (25.4%)	690 (60.6%)
high	101 (73.2%)	327 (28.7%)
age
< 50 years	18 (13.0%)	465 (40.9%)
50 – 64 years	57 (41.3%)	476 (41.8%)
>= 65 years	63 (45.6%)	197 (17.3%)
BI-RADS category
0	37 (26.8%)	566 (49.7%)
2	0 (0%)	431 (37.9%)
3	0 (0%)	77 (6.8%)
4	40 (29.0%)	60 (5.3%)
5	61 (44.2%)	4 (0.4%)

The structure of a Bayesian network classifier can be visualized with a directed acyclic graph, where nodes represent variables and edges between the nodes represent dependencies among the variables. Within a node a variable can take several distinctive values, each with a certain probability. A special case of Bayesian network classifiers is the naïve Bayes classifier. The ground truth is considered the root node of the network, it has a connection to all predictive variables and does not itself depend on any other variable (compare for figure 1). In mathematical terms, for each predictive variable P(variable value|ground truth) is estimated – i.e. the sensitivity and false-positive rate are estimated for the BI-RADS descriptors.

Figure 1.

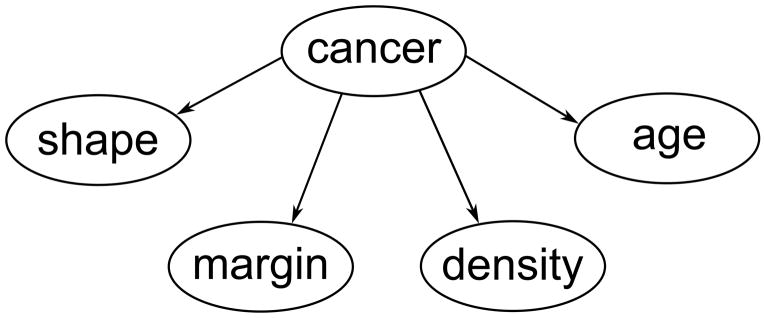
Representation of our naïve Bayes classifier as a directed acyclic graph. “cancer” represents disease status, i.e. “malignant” or “benign”. Note that the predictive variables BI-RADS descriptors and age depend solely on the ground truth.

The calculation of the posttest probability is achieved by using Bayes’ theorem with the estimated probabilities for the imaging features observed. For a more detailed and accessible review of Bayesian network classifiers refer to [14], for a discussion of the naïve Bayes to [15]. We perform all analyses using R 2.15.3 [16] and use the e1071 package [17] to generate naïve Bayes classifiers. We perform ROC (receiver operating characteristic) curve analysis with the ROCR package [18] and compare ROC curves with the DeLong test [19; 20]. We employ the AUC (area under the curve) of an ROC curve as measure for diagnostic accuracy [21]. We consider a P-value <0.05 to denote statistical significance.

Classifier construction

We split our dataset into training data (n=1276 lesions, thereof 138 malignant) and external validation data (n=1177 lesions, thereof 175 malignant). The split was performed on a temporal basis: all lesions detected earlier than 01/01/2009 were sorted into the training data, lesions detected later were sorted into the validation data. This approach is considered, contrary to a random split of the data, as a particular type of external validation [22].

From the training data we generate our naïve Bayes classifier, internal validation is secured by 10-fold cross validation. Table 1 lists the diagnostic variables employed and their distribution in the training data. This data allows the reader to completely rebuild our classifier. We split the numerical variable patient age into three subgroups comparable to those used in the literature [23]: <50 years, 50 – 64 years and ≥ 65 years. We included patient age as a predictive variable since it is proven to be one of the major risk factors for breast cancer [24]. To assess the influence of the final BI-RADS assessment category, we build the classifier a) with age, BI-RADS descriptors and BI-RADS assessment categories (referred to as “inclusive model”) and b) with age and BI-RADS descriptors, but without BI-RADS assessment categories (referred to as “descriptor model”). We compare classification performance of BI-RADS assessment categories alone (“clinical performance”) with the inclusive model and descriptor model. A classification aid would only be meaningful if the performance of the tool is better than or equal to the clinical performance.

Classifier validation

We apply the inclusive model and descriptor model to the separated validation data (n=1177 lesions, thereof 175 malignant). We compare validated ROC curves between the inclusive and descriptor model, and compare both with the clinical performance in the validation data.

Calibration of the classifier

Measurement of performance of classification algorithms commonly focuses on discriminative performance (as summarized by ROC curves). The naïve Bayes classifier achieves generally a high discriminative performance [15; 25], but at the same time is not well calibrated [26]. That is, the probabilities are not accurate in estimating the actual risk of malignancy. To overcome this problem we calibrate our classifier according to the method proposed by Zadrozny and Elkan [27]:

During cross validation, each lesion in the training data is assigned a probability of malignancy. We sort the lesions according to these probabilities, and then divide the lesions into ten equally sized subsets (called bins). Each bin consequently has a lower and upper probability threshold. For each bin we calculate how many lesions actually are malignant; bins that comprise low values of the calculated probability have a low cancer yield, bins that comprise higher probabilities have a high cancer yield. The cancer yield in the respective bin is considered the “true” classifier score. This method reduces the degree of detail of the classifier, but also decreases the variance of classifier scores [27]. When new lesions are classified, they are sorted into the bins depending on the probability of malignancy the classifier assigns them. A well calibrated classifier, when applied to new data, will have for each bin an equal predicted probability of malignancy and actual probability of malignancy.

We then continue to analyze the cancer yield in the bins created with our calibration step and define diagnostic groups that allow risk stratification in a fashion analogously to the BI-RADS assessment categories. In the BI-RADS lexicon, category 2 denotes a definitely benign lesion (0% risk for malignancy), category 3 denotes a probably benign lesion (<2% risk of malignancy), category 4 denotes lesions with a risk of 2% – 95%, category 5 denotes lesions with a risk >95% of being malignant. To address the central point of our paper, we compare the performance of the validated descriptor model based on these diagnostic groups with the clinical performance.

Results

Classifier performance in the training data

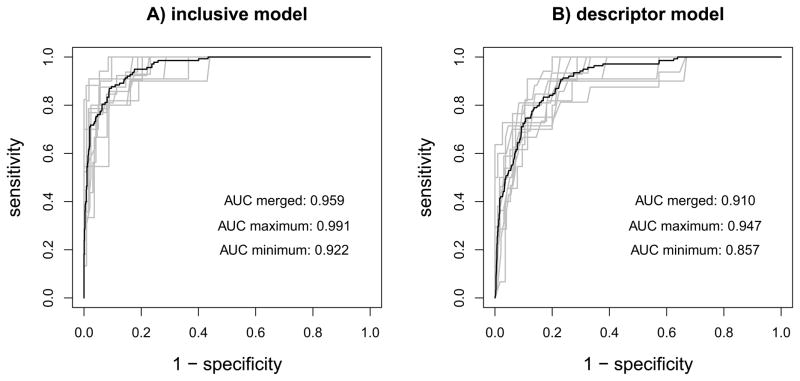
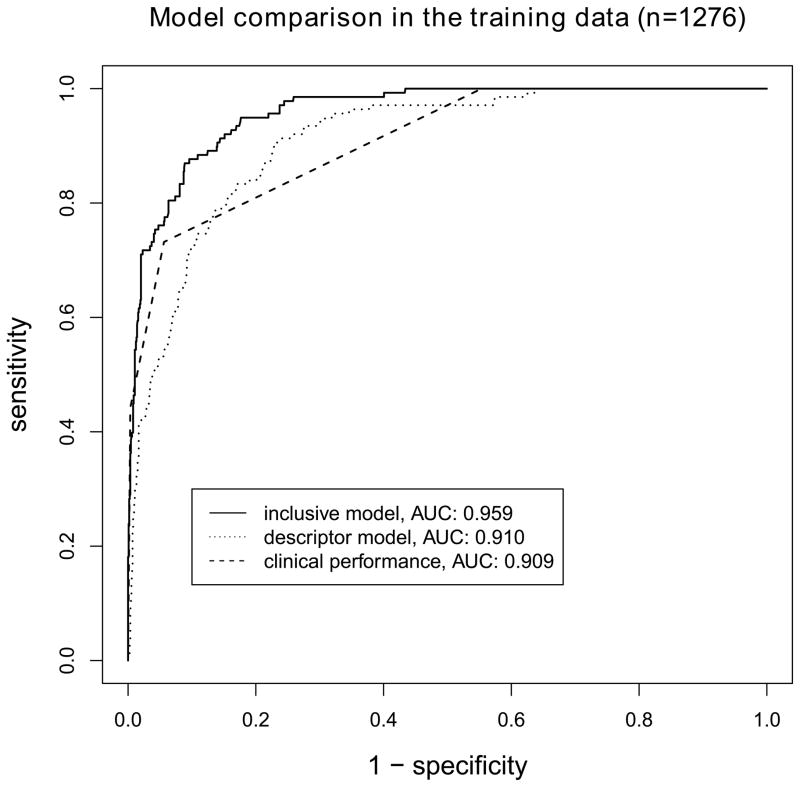
The clinical performance (BI-RADS assessment categories alone) in the training data yields an AUC of 0.909. The 10-fold cross validated descriptor model yields an AUC of 0.910, the 10-fold cross validated inclusive model yields an AUC of 0.959, compare for figure 2. The descriptor model performs similar to the clinical performance (P=0.953), the inclusive model performs superior to the clinical performance (P<0.001) and the descriptor model (P<0.001), compare for figure 3.

Figure 2.

Results from 10-fold cross validation of the naïve Bayes classifiers in the training data (n=1276). A) inclusive model, with age, BI-RADS descriptors and BI-RADS assessment categories as predictive variables B) descriptor model, with age and BI-RADS descriptors as predictive variables. Gray lines: cross validation runs, black lines: overall performance. ROC curves from A) and B) differ with P<0.001.

Figure 3.

Comparison of ROC curves for models developed in the training data (n=1276). The inclusive model significantly outperforms the descriptor model and the clinical performance (P<0.001 for both comparisons). No difference is found between the descriptor model and the clinical performance.

Classifier performance in the validation data

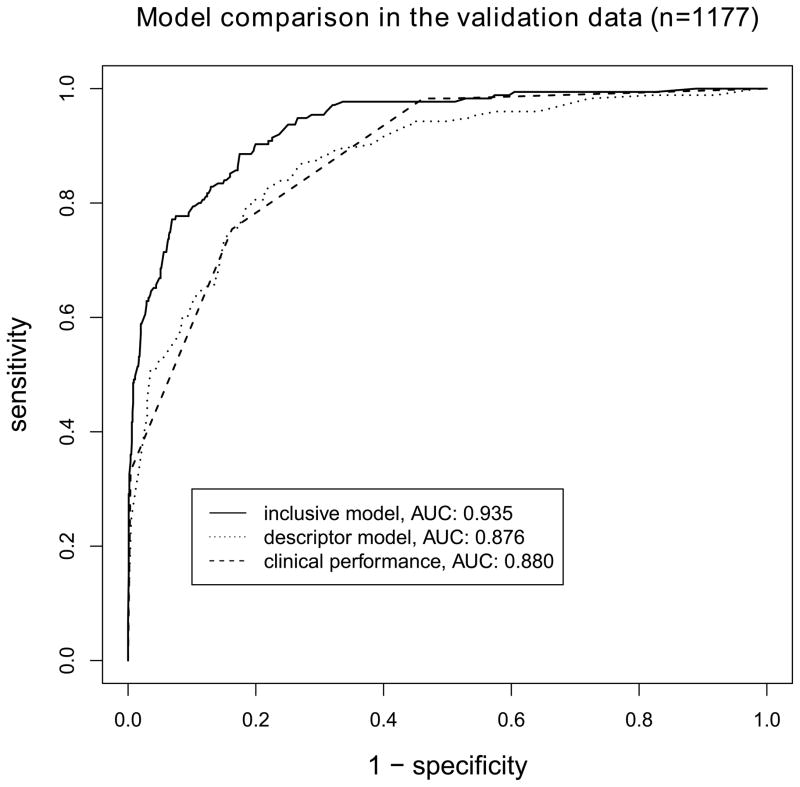
The clinical performance in the validation data yields an AUC of 0.880. The descriptor model yields an AUC of 0.876, the inclusive model yields an AUC of 0.935, compare for figure 4. The descriptor model performs similar to the clinical performance (P=0.799), the inclusive model performs superior to the clinical performance (P<0.001) and the descriptor model (P<0.001). The inclusive model performs marginally worse when compared to the training scenario (P=0.04), the descriptor model performs similar when compared to the training scenario (P=0.07).

Figure 4.

Comparison of ROC curves for models applied to the validation data (n=1177). The inclusive model significantly outperforms the descriptor model and the clinical performance (P<0.001 for both comparisons). No difference is found between the descriptor model and the clinical performance.

Calibration of the classifier

Table 2 gives the results for the calibrated inclusive model. The cancer yield in the single bins for the validated inclusive model is comparable to the cancer yield in the bins estimated from the training data. Table 3 gives the results for the calibrated descriptor model. As expected, given the lower AUC value of the model compared to the inclusive model, cancer yield in the bins 1 – 5 is higher than in the inclusive model. For both models, tables 2 and 3 show that higher bin rankings correlate with higher cancer yield.

Table 2. Inclusive model.

Calibrated classifier performance in the training data (10-fold cross validated), the calculated probabilities are sorted into 10 equally sized bins. Additionally, the results from applying the calibrated inclusive model to the validation data are given.

bin	training data			validation data
	n benign	n malignant	cancer yield	n benign	n malignant	cancer yield
1	128	0	0	174	1	0.005714
2	128	0	0	152	0	0
3	128	0	0	115	2	0.017094
4	128	0	0	68	1	0.014493
5	128	0	0	89	0	0
6	126	2	0.015625	83	1	0.011905
7	123	5	0.039063	53	4	0.070175
8	119	9	0.070313	122	20	0.140845
9	104	24	0.1875	125	43	0.255952
10	26	98	0.790323	21	103	0.830645

Table 3. Descriptor model.

Calibrated classifier performance in the training data (10-fold cross validated), the calculated probabilities are sorted into 10 equally sized bins. Additionally, the results from applying the calibrated descriptor model to the validation data are given.

bin	training data			validation data
	n benign	n malignant	cancer yield	n benign	n malignant	cancer yield
1	128	0	0	80	2	0.02439
2	128	0	0	95	0	0
3	128	0	0	191	5	0.02551
4	124	4	0.03125	102	2	0.019231
5	128	0	0	137	6	0.041958
6	126	2	0.015625	101	7	0.064815
7	119	9	0.070313	82	12	0.12766
8	110	18	0.140625	79	26	0.247619
9	94	34	0.265625	100	27	0.212598
10	53	71	0.572581	35	88	0.715447

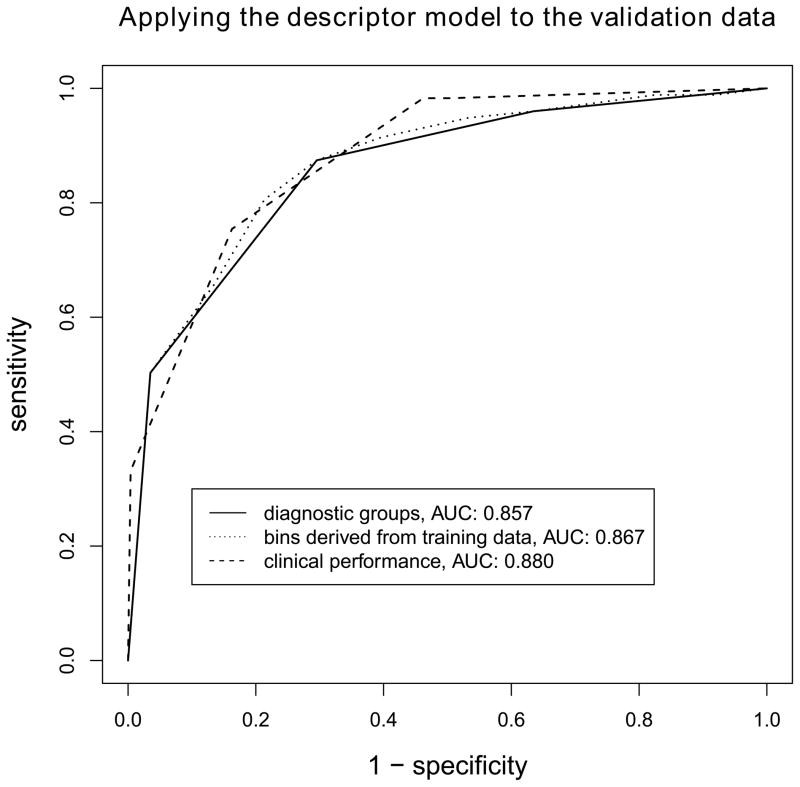
From the cancer yield in the bins (tables 1 and 2, training data column) we define diagnostic groups analogously to the BI-RADS assessment categories. For the inclusive model, bins 1 to 5 denote benign lesions (0% risk of malignancy), bin 6 denotes a probably benign lesions (<2% risk of malignancy), bins 7 to 9 denote lesions indicative for malignancy, and bin 10 denotes lesions highly indicative for malignancy. For the descriptor model, bins 1 to 3 denote benign lesions (0% risk of malignancy), bins 4 to 6 denote probably benign lesions (<2% risk of malignancy), bins 7 to 9 denote lesions indicative for malignancy, and bin 10 denotes lesions highly indicative for malignancy. Our classifier reports the diagnostic group a described lesion is sorted into. Thus a direct link between combinations of BI-RADS descriptors and risk categories is established. Figure 5 gives the ROC curves for the calibrated descriptor model with “bin” as predictive variable, and secondly with the derived “diagnostic group” as predictive variable. Both curves do not differ from the clinical performance (P=0.444 and P=0.197, respectively).

Figure 5.

Diagnostic performance of the descriptor model in the validation data, a) when posttest probabilities are binned according to the results from the training data and b) when these bins are used to form diagnostic groups comparable to the assessment categories used by the BI-RADS lexicon. The two resulting classifiers do not differ significantly from the clinical performance (BI-RADS assessment categories alone, P=0.444 and P=0.197, respectively). Our online classifier reports the diagnostic group for a given descriptor combination.

The accessible classifier

We provide our classifier as a research tool at www.ebm-radiology.com/nbmm/index.html. We require the user to choose from the BI-RADS descriptors for shape, margin and density of the observed mass lesion as well as age. We do not require the user to set a specific BI-RADS assessment category. If the “not sure” option is chosen here, the descriptor model is employed as detailed above. The online classifier reports the calculated posttest probability. More important however, the classifier automatically bins this calculated probability into one of the 10 bins generated with our calibration approach. Based on this result, the classifier sorts the posttest probability into one of the derived diagnostic groups. The classifier finally reports this diagnostic group.

Discussion

The main result of our study is the establishment of a functional linking of arbitrary combinations of BI-RADS descriptors to a risk assessment category. We demonstrate that our descriptor model achieves a similar diagnostic performance as the clinical performance (BI-RADS assessment categories alone). Second, our inclusive model demonstrates that the clinical performance can be significantly enhanced when a formal analysis of morphological BI-RADS descriptors and patient age is taken into account for mammographic mass lesions.

We consider our descriptor model to be a step towards a more uniform interpretation of mammographic findings. Inter-observer agreement about the assignment of a specific BI-RADS assessment category tends to be low: kappa values (as measure for agreement) between 0.28 and 0.37 have been reported [2–4]. A more uniform interpretation of mammographic findings leads ultimately to a more uniform communication between radiologist and referring physicians, and thus to a more uniform patient management. Second, the superior performance of our inclusive model compared to the clinical performance suggests that BI-RADS assessment categories do at the moment not capture the full information that can be derived from a mammogram. This point has been made before [8], and it underlines the importance to become more consistent in the interpretation of combinations of morphological descriptors. The inclusive model is significantly better in separating clearly benign findings from other findings when compared to the descriptor model (compare for tables 2 and 3). We regard this as evidence that radiologists evaluate additional diagnostic information different from pure morphological BI-RADS descriptors and the risk factor patient age.

Computer assisted diagnostic (CADx) systems for mammographic lesions have received substantial attention in the past [28]. In an early work Baker and colleagues employed artificial neural networks to diagnose mammographic lesions based on BI-RADS descriptors, their work resulted in an AUC of 0.89 [7]. Fischer and colleagues reported an AUC for Bayesian networks based on BI-RADS descriptors applied to mammographic mass lesions of 0.88 [10]. Burnside and colleagues reported an AUC of 0.96 for mammographic lesions with a Bayesian network taking into account BI-RADS descriptors, assessment categories and various patient characteristics [8]. Elter and colleagues proposed a case-based learning approach and a decision tree model, with corresponding AUCs of 0.89 and 0.87 respectively [9]. Although all of these approaches demonstrate good diagnostic performance in terms of AUC, none of them has been implemented as an interactive interface to allow its actual application (the decision tree proposed by Elter and colleagues [9] could be used as an offline aid, though). Our classifier, with a validated AUC of 0.935 for the inclusive model and 0.876 for the descriptor model, is in accordance with these past studies in terms of classification performance.

However, deriving AUC values of predictive models is only a first step towards the development of a working classification aid. First, it is impossible for the reader to infer from a given AUC meaningful decision thresholds (or rules) at which to call lesions malignant or benign, given a set of predictive variables. Second, even if a classifier performs well in terms of discrimination, it does not follow that it is well calibrated [22; 29]. In the case of mammographic lesions, a well calibrated classifier is clinically desired, since patient management depends on the risk category the patient is placed into after the test [1]. Contrary to past studies, we provide an actually usable, calibrated decision aid as a tool for further research.

A prerequisite for an actually usable decision aid is the existence of a standardized terminology to describe findings. The BI-RADS lexicon lends itself to such an analysis. Having been established in 1992, it currently is in its 5^th edition [1]. Through the years the lexicon has undergone a process of refinement, with misleading terms being eliminated or replaced [30]. We collected our data when the fourth edition of the BI-RADS lexicon was in place; so the mass shape “lobulated” is included in the classifier. We highlighted it as a term from the 4^th edition in the interface, since in 5^th edition the term was eliminated to avoid confusion with the descriptor “microlobulated margin” [1].

The problem with the usage of manually extracted features in CADx approaches, even if the features are highly standardized as in the case of the BI-RADS lexicon, is a potential inter-observer variance of the evaluation. For mass lesion descriptors, Baker and colleagues report substantial agreement between readers, with kappa values >0.6 [31], somewhat lower values were reported by Berg and colleagues [2] and Lazarus and colleagues [4]. Generally, agreement about the assignment of mass lesion descriptors is higher than agreement about the final BI-RADS assessment category [2–4]. However, we cannot exclude bias introduced by inter-observer variance in feature assignment. To address this issue, future external validation of the classifier is required, as detailed in the next paragraph.

External validation is the empirical evaluation of a prediction model with data that was not used to generate the model [22]. In our work, we use a temporal split to generate training data and validation data, and thus provide a true external validation with cases from the same practice [22]. However, it does not plainly follow that our model is applicable to different practices [22; 32]. Differences in the patient population considered may affect the diagnostic performance of the classifier. This phenomenon is known as spectrum effect [32]. On the other hand, the above described inter-observer variance (possibly being practice dependant) may cause differences in classifier performance. We will expand our research project into this direction and plan to investigate the performance of our classifier among a variety of different practices, featuring populations with different pretest probability.

A further limitation of the present study concerns the lesions included in the analysis. Since we excluded a large proportion of lesions that had missing values for mass lesion descriptors, we cannot guarantee that the sample considered was representative for our practice. Maybe fully described lesions were especially easy to evaluate, or on the other hand, especially hard to read and the radiologist spent more than the usual amount of time contemplating the case. This possible selection bias [33] is another reason to perform a future external validation study to establish stability of our results. The restriction to lesions with complete information for descriptors, however, was not an arbitrary decision. The posttest probability calculated by the naïve Bayes classifier depends on the number of features considered and their corresponding predictive potential [15]. Since we are interested in the interpretation of combinations of descriptors, we want the calculated posttest probabilities to be as comparable as possible. E.g. the comparison of a mass lesion labelled “round” with a mass lesion labelled “round, obscured and isodense” is not the focus of this study, but may be addressed in future research. We did not employ the split of BI-RADS category 4 into categories 4A, 4B and 4C [1]. This step could in principle result in a more differentiated ROC curve in future versions of our decision support tool.

Our decision support tool focuses on mass lesion morphology and patient age as predictive variables. Of course, other factors like a family history of breast cancer [34] or breast parenchyma density [35] affect the posttest probability for breast cancer. The framework of the naïve Bayes classifier allows us (or other researchers) to incorporate these variables in future work without having to alter our probabilities as provided in table 1 and thus the diagnostic accuracy of the descriptors already used. Ultimately, the aim for a highly standardized mammography interpretation aid should be an augmented descriptor model that performs as good as the inclusive model.

In conclusion, in our work we present a probabilistic classifier to link combinations of BI-RADS descriptors and patient age to risk categories analogously to those used by the BI-RADS lexicon. Our classifier performs well when validated with an external dataset from the same practice, and shows a similar diagnostic performance when compared to the clinical performance (BI-RADS assessment categories alone). We consider this as a step towards a more uniform interpretation of combinations of BI-RADS descriptors for mammographic mass lesions, and thus as a step towards a more uniform patient management. We furthermore demonstrate that a formal analysis of descriptors and patient age may significantly enhance diagnostic performance of the BI-RADS assessment categories. Our classifier is at a research stage; the logical next step is the conduction of an external validation study to establish stability of the classification algorithm, taking into consideration multiple datasets from a range of different practices [22]. We provide our classifier online at http://www.ebm-radiology.com/nbmm/index.html, and the scientific and clinical communities are invited to test it on their own databases.

Key points.

1. We provide a decision support tool for mammographic masses at www.ebm-radiology.com/nbmm/index.html.

2. Our tool may reduce variability of practice in BI-RADS category assignment.

3. A formal analysis of BI-RADS descriptors may enhance radiologists’ diagnostic performance.