Spatial working memory interferes with explicit, but not probabilistic cuing of spatial attention

Abstract

Recent empirical and theoretical work has depicted a close relationship between visual attention and visual working memory. For example, rehearsal in spatial working memory depends on spatial attention, whereas adding a secondary spatial working memory task impairs attentional deployment in visual search. These findings have led to the proposal that working memory is attention directed toward internal representations. Here we show that the close relationship between these two constructs is limited to some but not all forms of spatial attention. In five experiments, participants held color arrays, dot locations, or a sequence of dots in working memory. During the memory retention interval they performed a T-among-L visual search task. Crucially, the probable target location was cued either implicitly through location probability learning, or explicitly with a central arrow or verbal instruction. Our results showed that whereas imposing a visual working memory load diminished the effectiveness of explicit cuing, it did not interfere with probability cuing. We conclude that spatial working memory shares similar mechanisms with explicit, goal-driven attention but is dissociated from implicitly learned attention.

Introduction

In a seminal study, Awh and colleagues demonstrated that spatial attention is an integral component of spatial working memory: when people rehearse locations in their spatial working memory they also actively attend to those locations (Awh, Jonides, & Reuter-Lorenz, 1998; Awh & Jonides, 2001). Since then, extensive research has revealed a close relationship between visual attention and visual working memory (for recent reviews, see Franconeri, Alvarez, & Cavanagh, 2013; Olivers, Peters, Houtkamp, & Roelfsema, 2011; Woodman, Carlisle, & Reinhart, 2013). Prominent new theories of attention consider visual working memory as attention directed to an internal representation (Chun, 2011; Kiyonaga & Egner, 2013). Although there is no doubt that attention and working memory are closely related, this relationship may not be as ubiquitous as existing data suggest. Most studies on the relationship between attention and working memory have examined one form of attention: explicit, goal-driven attention. However, decades of research have shown that visual attention may be driven by multiple sources (Awh, Belopolsky, & Theeuwes, 2012; Egeth & Yantis, 1997; Pashler, 1999; Wolfe, 2007). Here we demonstrate that when other sources of attention are considered, spatial working memory is closely related to some but not all sources of spatial attention.

Our study examined the impact of a concurrent visual working memory load on spatial attention. For these experiments, participants first encoded an array of visual stimuli into working memory. During the retention interval they performed a visual search task. We employed a spatial cue to guide attention to regions that were likely to contain the search target. If spatial working memory and spatial attention rely on the same mechanisms, then a concurrent working memory load should interfere with spatial cuing in the search task. On the other hand, if spatial attention is dissociated from working memory, then spatial cuing should not depend on the availability of working memory resources.

Multiple sources guide spatial attention. These include bottom-up (i.e., stimulus-driven, “exogenous” attention) and top-down sources (i.e., goal-driven, “endogenous” attention) (for a review, see Egeth & Yantis, 1997; Wolfe, 2007). This article focuses on top-down attention. In the laboratory top-down attention is often directed based on task instructions, such as a verbal cue or a central arrow (Posner, 1980). In the real world one's previous experience is also a major source of top-down attention. Locations that were important previously may be prioritized again, even though people are unaware of using previous experience (Chun & Jiang, 1998). However, influential theories of attention have not distinguished explicit, goal-driven attention from implicitly learned attention (Desimone & Duncan, 1995; Wolfe, 2007; for a review of attention, see, Nobre & Kastner, 2014). The main goal of the present study is to provide evidence for their dissociation. We do so by demonstrating differences in how the two sources of top-down attention interact with visual working memory.

We examined two forms of top-down attentional guidance: spatial cuing based on implicit learning of the target's location probability (Druker & Anderson, 2010; Geng & Behrmann, 2002; Miller, 1988; Walthew & Gilchrist, 2006) and spatial cuing based on an explicit goal such as a central arrow or a verbal instruction (Jonides, 1980; Posner 1980). For simplicity of description we will refer to the first type of spatial cuing as “probability cuing” and the second type as “explicit cuing”. To induce probability cuing, across multiple trials we placed the visual search target in one visual quadrant more often than in any one of the other quadrants. Previous research has shown that participants rapidly develop a spatial bias toward the high-probability “rich” quadrant, and they do so without having explicit knowledge about the target's location probability (Geng & Behrmann, 2005; Jiang, Swallow, & Rosenbaum, 2013). To induce explicit cuing, we explicitly asked participants to prioritize one visual quadrant over other quadrants. Previous studies have shown that explicit instructions and location probability learning are both effective at driving attention to the probable locations (Jiang, Swallow, & Rosenbaum, 2013). If these two forms of spatial cuing are qualitatively similar, then imposing a concurrent visual working memory load should reduce the effectiveness of both. But if these two forms of spatial cuing are dissociated, then they should show different patterns of interaction with a concurrent visual working memory load.

Section I focused on probability cuing. We imposed three types of visual working memory load in different experiments: working memory for the locations of colored squares (Experiment 1: color working memory), for an array of simultaneously presented locations (Experiment 2: spatial working memory), and for the spatial-temporal sequence of successively presented locations (Experiment 3: spatiotemporal working memory). Section II examined explicit cuing. Here we tested two types of visual working memory: color working memory (Experiments 4A and 5) and spatial working memory (Experiment 4B). In addition, we employed two types of explicit cuing. The cue changed from trial-to-trial in Experiment 4 but was stable within a run of 12 trials in Experiment 5. In both sections we examined whether spatial cuing significantly diminished under a concurrent visual working memory load. Our study builds a rich empirical foundation for understanding the relationship between spatial attention and spatial working memory. In addition, they have theoretical implications for ways in which different sources of spatial attention may be fractionated.

Section I. Visual working memory and probability cuing

Does implicitly learned attention depend on the availability of visual working memory? Several studies have addressed this question using a paradigm known as “contextual cuing.” In this paradigm, participants conduct visual search among displays that occasionally repeat. Attentional cuing by the repeated spatial context leads to a faster response to repeated displays than unrepeated ones, even when participants are unaware of the display repetition (Chun & Jiang, 1998; Chun & Jiang, 2003). Several studies have tested whether contextual cuing is impaired when participants hold a concurrent visual working memory load. Whereas some studies found that contextual cuing is preserved (Vickery, Sussman, & Jiang, 2010), others found diminished cuing under working memory load (Travis, Mattingley, & Dux, 2013), and still others found mixed results (Annac, Manginelli, Pollmann, Shi, Müller, & Geyer, 2013; Manginelli, Langer, Klose, & Pollmann, 2013). These contradictory findings may be attributed to the complex nature of contextual cuing. Contextual cuing depends on participants’ ability to (implicitly) distinguish repeated from nonrepeated displays and then use the repeated context to guide attention. Visual working memory could interfere with learning of repeated spatial context, attentional cuing by repeated context, or both. To understand the specific role of visual working memory in implicit attentional cuing, it is important to use simpler experimental paradigms that tap into just attentional cuing. Fortunately, probability cuing provides such a paradigm. Unlike contextual cuing, the probability cuing paradigm does not employ repeated spatial contexts. Instead, it reflects changes of spatial attention following location probability learning (Geng & Behrmann, 2002, 2005; Jiang, Swallow, & Rosenbaum, 2013). It is an ideal paradigm for examining the interaction between visual working memory and implicitly learned attention.

Experiment 1

Experiment 1 examined the impact of a color working memory load on probability cuing. To enhance comparability with previous studies, we adopted the same working memory task as used in a previous study (Vickery et al., 2010). For the visual working memory task, participants performed change detection on two sequentially presented visual arrays. The two arrays were identical except for the change of one color. Participants reported the location of the color change. This task required color memory as well as memory for the spatial locations of the colors.

During the memory retention interval, we presented participants with a visual search task. Participants searched for a T among Ls and reported the orientation of the T. Several previous studies have examined the impact of working memory load on visual search (for a review, see Woodman et al., 2013). Although the results were somewhat mixed, most studies observed impaired search performance when a visual working memory load was imposed (Oh & Kim, 2004; Woodman & Luck, 2004). We expect that much like previous studies, a concurrent working memory load should slow down visual search in our study. Our focus, however, was on whether the visual working memory load impaired probability cuing.

To examine probability cuing, we presented the search target in one visual quadrant on 50% of the trials and in each of the other three quadrants on 16.7% of the trials. The high-probability, “rich” quadrant was randomly selected for each participant but remained the same throughout the experiment. Participants were not informed of this experimental manipulation. As will be described in the results, they also exhibited little awareness of the target's location probability. Probability cuing was measured as the difference in visual search RT between the rich and sparse conditions. If implicit spatial cuing depends on the availability of visual working memory, then probability cuing should be smaller when participants held a concurrent working memory load than when they did not.

Method

Participants

Participants in this study were students at the University of Minnesota between the age of 18 and 35 years old. A pre-specified sample size of 18 was used in all experiments. The sample size was chosen to be comparable to previous studies on spatial working memory and attention (e.g., Vickery et al., 2010). All participants had normal or corrected-to-normal visual acuity and normal color vision. Participants signed an informed consent before the experiment and were compensated for their time.

Equipment

Participants were tested individually in a room with normal interior lighting. The experiment was programmed with Psychtoolbox (Brainard, 1997; Pelli, 1997) implemented in MATLAB (www.mathworks.com). All stimuli were projected on a 17” CRT monitor (75 Hz vertical refresh rate, 1024 × 768 pixels). Viewing distance was unrestrained but was estimated to be about 40 cm.

Material

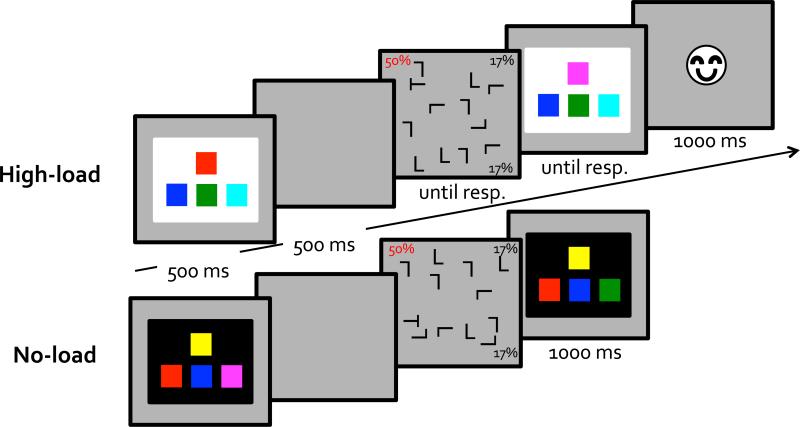
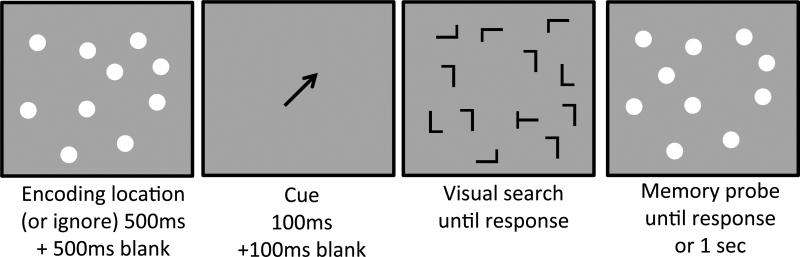
In the working memory task, two arrays were presented sequentially, each containing four colored squares (each square subtended 3.9°×3.9°). The colors were arranged in the same spatial configuration as the arrow keys on standard US keyboards, with three colors aligned horizontally and a fourth color above the middle of the three (Figure 1). This alignment was used because participants used the arrow keys to report the location of the color change. The gap between the colored squares was 0.50°. The colors were randomly drawn from six distinctive colors (red, green, blue, yellow, magenta, and cyan). All colors on a given array were different, and the two arrays differed in one color. The location of the color that changed was randomly chosen on each trial. The arrays were presented against either a black or a white background (15.8°×15.8°).

Figure 1.

A schematic illustration of stimuli and trial sequences used in Experiment 1's high-load and no-load conditions. Items are not drawn to scale.

Visual search was presented during the retention interval of the working memory task. The search display contained one target (a white T rotated to the left or right) and several distractors (white Ls rotated 0°, 90°, 180°, or 270°) presented against a neutral gray background. Each search item subtended 1.9°×1.9°. The locations of the items were chosen randomly from a 10x10 invisible matrix (29°×29°), with the constraint that an equal number of items appeared in every visual quadrant. The orientation of the target was randomly chosen on each trial, so the target identity and motor response did not correlate with any experimental variables.

Procedure

Participants initiated each trial by clicking on a small white square (1.0°×1.0°) which occupied a random location within the central 2.5° of the monitor. The mouse click required eye-hand coordination and enforced fixation before each trial. After the click and a 300ms delay, an array of 4 colored squares was displayed for 500ms and then erased. Participants were asked to remember the colors and their locations if the array was presented against a white background, or to ignore the array if it was presented against a black background (see also Vickery et al., 2010). We used the no-load condition as the baseline to maximize the difference in working memory load. A previous study found similar results whether the high-load condition was compared with a reduced load (low-load) or a no load condition (Vickery et al., 2010). Following a 500ms neutral-gray blank interval the visual search display was presented. Participants searched for a T among Ls and pressed a button (the left or right arrow) to indicate whether the T was rotated to the left or to the right. The response erased the visual search display. This was followed by a sound feedback (three chirps lasting a total of 300ms for a correct response, or a 200ms buzz and a 2s timeout for an incorrect response. Footnote¹). The working memory probe array appeared after the feedback. The probe display was identical to the encoding display except for the color of one square. On trials when the background was black (participants ignored the color task) the probe display required no response. It disappeared after 1s. On trials when the background was white (participants attended to the color task), the probe display appeared until participants pressed one of the arrow keys to report the corresponding location of the color change. A smiley face icon followed each correct change-detection response whereas a sad face icon followed each incorrect response. Figure 1 illustrates the procedure.

After about 10 practice trials (more if the participants had difficulty coordinating the two tasks), participants completed 432 experimental trials. They were asked to perform the working memory task as accurately as they could. Both accuracy and speed were emphasized for visual search. Trials were self-paced and participants could take a break whenever they wanted.

Design

We manipulated working memory load (no-load or high-load), probability cue type (target in the rich or sparse quadrants), and set size (8, 12, or 16 items). On half of the trials (i.e., when the color array was displayed against a black background) participants ignored the working memory task, whereas on the other half of the trials (i.e., when the color array was displayed against a white background) they encoded the array in memory. In orthogonal to the working memory manipulation, we varied the target's location probability. On 50% of the trials the target appeared in one (the high-probability “rich” quadrant), whereas on the other trials the target appeared in one of the other three quadrants (the low-probability “sparse” quadrants; 16.7% probability in each quadrant). Which quadrant was rich was randomly selected for each participant but remained the same for a given participant. Although there were an equal number of rich and sparse trials, owing to the presence of four quadrants the target's location probability was biased toward the rich quadrant. We did not inform participants about the target's location probability, so any attentional prioritization of the rich quadrant would have to be acquired incidentally. Finally, the number of items on the search display could 8, 12, or 16, allowing us to measure the slope of visual search RT as a function of set size. All trial types were randomly intermixed in presentation order.

Location probability awareness

At the end of the experiment we tested explicit awareness of the probability manipulation. Participants were first asked to report whether they thought the location of the search target was random or whether it was more often found in some parts of the screen than others. Regardless of their answer they were told that the target's location was not random and they were asked to choose the quadrant where the search target was most often found.

Results

(1) Visual working memory accuracy

Because the memory delay was longer when search was incorrect (see footnote 1), our analysis on visual working memory focused on trials in which a correct visual search response was made. This criterion eliminated 1.2% of the trials.

Participants correctly identified the color that had changed on 91.8% of the trials. Working memory accuracy was comparable whether the search target appeared in the rich quadrant (92.6%) or the sparse quadrants (91.1%), t(17) = 1.66, p > .10.

(2) Visual search

Visual search accuracy was uniformly high across all conditions (mean 98.8%). It was not significantly affected by probability cue condition, working memory load, set size, or their interactions, all ps > .23. Because search accuracy was at ceiling (over 98.3%) in all subsequent experiments and showed little systematic variation across conditions, we will no longer report accuracy data. Appendix Table A lists mean accuracy in all experiments.

In this and all subsequent experiments we excluded trials with an incorrect search response. We also removed outliers, defined as trials with an RT exceeding 10s. The percentage of outlier data was less than 0.5% in all experiments. Figure 2 shows mean RTs across different conditions of Experiment 1.

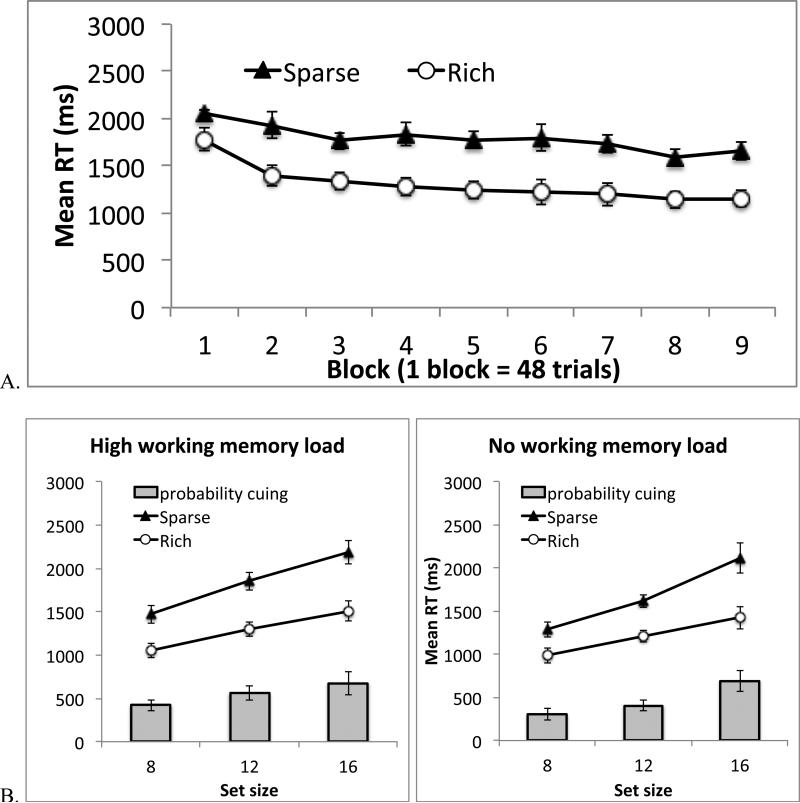
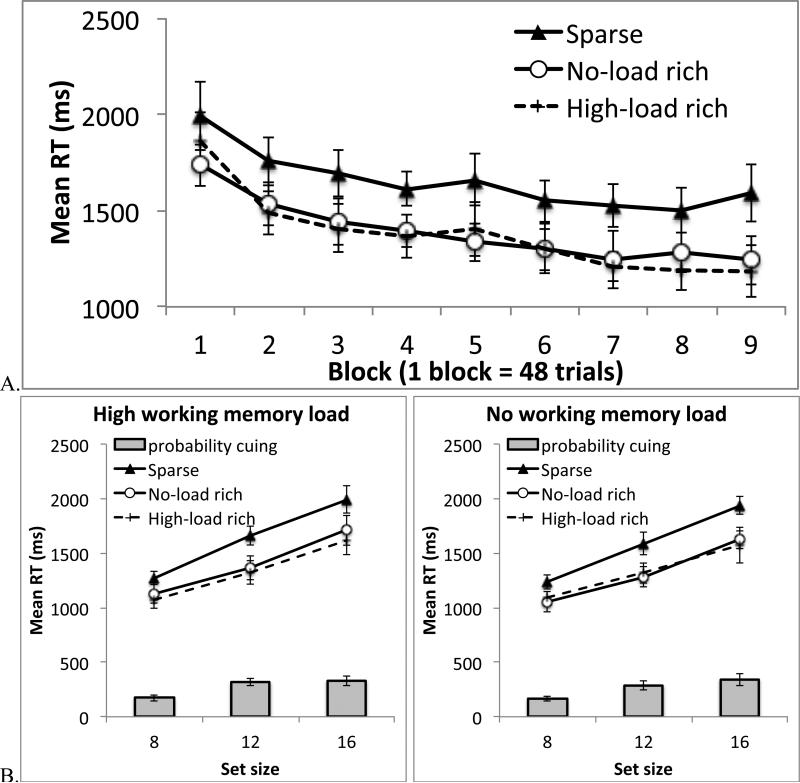
Figure 2.

Results from Experiment 1. A. Search RT across 9 blocks of trials (each block has 48 trials). B. Search RT in Blocks 2-9, separately for different working memory conditions and different set sizes. The gray bars the difference between the rich and sparse conditions. Error bars show 95% confidence interval based on the within-subject S.E.M. (See Cousineau, D. (2005). Confidence intervals in within-subject designs: A simpler solution to Loftus and Masson's method. Tutorial in Quantitative Methods for Psychology, 1: 42-45).

We first examined location probability learning over time, pooling data across all set sizes and both working memory conditions (Figure 2A). The data were binned into 9 blocks. An ANOVA on probability cue condition (rich or sparse) and block (1-9) revealed a significant main effect of probability cue, F(1, 17) = 101.38, p < .001, η_p² = .86; RT was faster when the target was in the rich quadrant rather than the sparse quadrants. RT also became faster as the experiment progressed, producing a significant main effect of block, F(8, 136) = 14.86, p < .001, η_p² = .47. The two factors showed a marginally significant interaction, F(8, 136) = 1.83, p =.076, η_p² = .10. In the trend analysis, the linear trend in the interaction term was not significant, F(1, 17) = 1.71, p = .20, but the quadratic trend was, F(1, 17) = 6.63, p = .02, η_p² = .28. Probability cuing increased from the first to the second block and then stabilized. The early learning was also shown in previous studies (Jiang, Swallow, Rosenbaum, & Herzig, 2013; Umemoto, Scolari, Vogel, & Awh, 2010). For subsequent analyses, we examined probability cuing in Blocks 2-9 because attentional cuing had been established in those blocks.

Figure 2B shows search RT in Blocks 2-9, separately for different working memory load, target quadrants, and set sizes. An ANOVA including working memory load, probability cue condition, and set size revealed a significant main effect of working memory load, F(1, 17) = 4.87, p < .05 η_p² = .22. Search RT was slower when participants had to perform the working memory task than when they could ignore it. The main effect of probability cue was significant, F(1, 17) = 108.69, p < .001, η_p² = .87, as was the main effect of set size, F(2, 34) = 159.67, p < .001, η_p² = .90. In addition, probability cuing manifested not only as faster overall RT in the rich quadrant, but also as a reduction in the slope of the linear function relating RT to set size. This resulted in a significant interaction between probability cue condition and set size, F(2, 34) = 18.89, p < .001, η_p² = .53. Visual search slope declined from 98 ms/item when the target was in the sparse quadrants to 57 ms/item when it was in the rich quadrant, t(17) = 5.27, p < .001.

Importantly, adding a working memory load did not reduce probability cuing. In fact, the data went in the opposite direction: the difference between the rich and sparse conditions was greater when participants performed the working memory task than when they did not, leading to a significant interaction between working memory load and probability cue condition, F(1, 17) = 5.27, p < .04, η_p² = .24. Follow-up tests showed a significant probability cuing effect in both the high-load condition, F(1, 17) = 89.98, p < .001, η_p² = .84, and the no-load condition, F(1, 17) = 105.06, p < .001, η_p² = .86. The 3-way interaction was not significant, F(2, 34) = 1.30, p > .25, nor was the interaction between working memory load and set size, F(2, 34) = 1.17, p > .30.

The results reported above were replicated when we excluded the 9.2% of trials in which participants made an incorrect working memory response. Similarly, in all subsequent experiments we obtained the same pattern of results whether or not incorrect working memory trials were included. Appendix Table B shows the search RT results after incorrect working memory trials were excluded, separately for each experiment.

(4) Recognition

When asked whether they thought the target was randomly placed or more often located in some regions than others, 12 of the 18 participants said that the target's location was random. Among them, 3 correctly identified the target-rich quadrant in the forced-choice response. This percentage (3 out of 12) was at chance. Among the 6 participants who said that the target's location was not random, only 2 correctly identified the target-rich quadrant. The total number of participants (5 out of 18) who correctly identified the target-rich quadrant did not differ from chance, χ(1) = 0.074, p > .50.

To examine whether recognition performance correlated with the size of probability cuing, we performed an additional analysis on search RT that separated participants based on their recognition accuracy in the forced-choice task. People who failed to identify the target-rich quadrant were in one group, and those who correctly identified the target-rich quadrant were in the other. Table 1 shows visual search RT for these two groups of participants. Group did not interact with probability cue condition (rich or sparse), or with any higher-order effects involving cue condition, all ps > .25. Thus, consistent with previous findings (Geng & Behrmann, 2002; Jiang, Swallow, & Rosenbaum, 2013), probability cuing occurred largely independently of an intention to learn or an awareness of what was learned.

Table 1.

Visual search RT (ms) in Experiment 1, separately for participants who correctly identified the rich quadrant (“aware” group) and those who did not (“unaware” group).

	High working memory load						No working memory load
T location	Sparse quadrant			Rich quadrant			Sparse quadrant			Rich quadrant
Set size	8	12	16	8	12	16	8	12	16	8	12	16
Aware	1336	1776	2322	1028	1286	1541	1224	1533	2017	924	1122	1283
S.E.	69	204	229	141	241	195	31	83	134	90	131	106
Unaware	1521	1880	2135	1057	1296	1498	1313	1651	2154	1009	1247	1480
S.E.	136	136	159	96	93	115	71	98	114	53	68	108

Discussion

Experiment 1 showed that the target's location probability could cue spatial attention to high-probable locations. However, probability cuing was unabated when a concurrent visual working memory load was added. This finding cannot be dismissed by claiming that the working memory load was trivial. First, participants were significantly slower in visual search when they had to perform a concurrent working memory task than when they could ignore it. Thus the working memory load did impact visual search performance. In addition, probability cuing was statistically greater under high-load than under no-load. The increased cuing under working memory load may seem surprising, but it has been observed in previous research. For example, in a subset of Vickery et al. (2010)'s experiments contextual cuing was greater under increased working memory load. The increase is likely due to a scaling effect: the longer RT in the high-load condition leaves more room for performance to improve. Nonetheless, because the increase was not consistently observed in this study (see Experiments 2 and 3) or in Vickery et al. (2010)'s study, it is likely attributable to a combination of statistical noise and the scaling effect. What is clear, however, is that working memory load did not diminish probability cuing. Recognition test revealed no evidence that explicit awareness of the target's location probability had influenced performance. As we will see in Section II, these results differed sharply from those of explicit cuing. Thus, Experiment 1 provided the first evidence that probability cuing did not depend on visual working memory.

Experiment 2

The findings of Experiment 1 challenge the idea that attention and working memory are always closely related. The novelty of this finding warrants a replication and extension to other types of visual working memory. Some models of working memory distinguish visual and spatial working memory (Logie, 1995). The former holds visual properties of objects such as their colors, whereas the latter retains spatial properties such as locations. Several previous studies have shown that spatial working memory load is more detrimental to visual search than visual working memory load is (Travis et al., 2013; Woodman & Luck, 2004). It is therefore important to examine whether probability cuing also survives the interference from a spatial working memory task.

Experiment 2 replaced the color working memory task of Experiment 1 with a standard spatial working memory task. This task required participants to remember the locations of an array of 10 dots (Jiang, Olson, & Chun, 2000; Vickery et al., 2010). Because the number of locations exceeds the capacity of spatial working memory (typically 4-6, see Jiang et al., 2000; Simons, 1996), the 10-dot spatial working memory task is highly demanding and may interfere with probability cuing.

In addition to replicating and extending Experiment 1's findings, Experiment 2 aimed to introduce a new design to examine the impact of working memory on probability cuing. This design evaluated the specificity of location probability learning to concurrent spatial working memory load. To this end, we trained participants to develop an attentional bias toward two regions of the display. On no-load trials the target was frequently found in one visual quadrant (the “no-load rich” quadrant). On high-load trials the target was frequently found in another visual quadrant (the “high-load rich” quadrant). If probability cuing is sensitive to spatial working memory load, then the sensitivity may manifest in two ways. First, exerting a working memory load may diminish learning on high-load trials. Second, participants may acquire load-specific learning. That is, they would prioritize search in the high-load rich quadrant on high-load trials but in the no-load rich quadrant on no-load trials. Sensitivity to the contingency between load and the search target's location would suggest that working memory load can be an integral component of location probability learning. Conversely, a lack of load-specific learning would provide strong evidence for the independence between probability cuing and spatial working memory.

Method

Participants

Eighteen new participants completed Experiment 2.

Materials

The visual search task used the same materials as those of Experiment 1. However, the nature of the working memory task differed.

In the 10-dot spatial memory task, the encoding and probe displays each contained an array of 10 dots presented in randomly selected locations from an invisible 10x10 matrix (matrix size: 29°×29°; dot diameter: 1°). The background was gray. On half of the trials the dots were black, in which case participants ignored them. On the other half of the trials the dots were white and participants were asked to report whether the two arrays were the same or different. Regardless of the color of the dots, on half of the trials the encoding and probe arrays used identical locations. On the other half of the trials the two arrays differed in the location of one dot. Participants pressed a key (up or down arrows) to report whether the encoding and probe arrays were the same or different.

Procedure

The procedure was the same as Experiment 1, except for the change in the working memory task. Participants first saw a memory array. They encoded it to memory if the dots in the array were white (high-load), or ignored it if the dots were black (no-load). Then they performed the visual search task. Following the search response and sound feedback, the memory test probe was presented. Participants ignored the probe on no-load trials, or judged whether the probe was the same as the encoding array on high-load trials.

Design

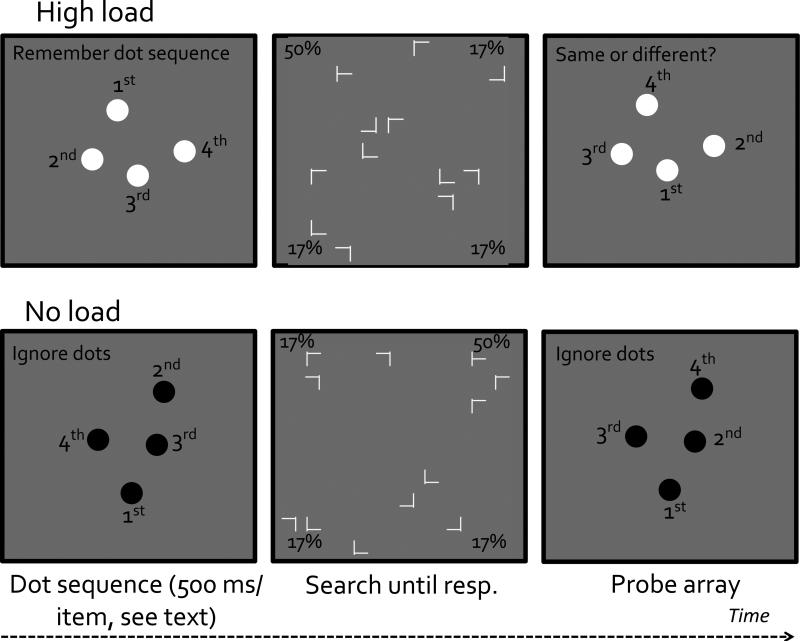
Similar to Experiment 1, we manipulated working memory load (high-load or no-load), probability cue condition, and set size (8, 12, or 16). The probability cue condition differed from the simpler design used in Experiment 1. Specifically, for each participant we randomly selected two visual quadrants and assigned them to be the high-load rich quadrant and the no-load rich quadrant. On trials when participants had to hold dot locations in working memory, the visual search target was more often located in the high-load rich quadrant (50% of the time) than in either the no-load rich quadrant or the sparse quadrants (16.7% of the time in each). On trials when participants ignored the dot locations, the visual search target was more often located in a different, no-load rich quadrant (50% of the time) than in either the high-load rich quadrant or the sparse quadrants (16.7% of the time in each). Participants were not informed of the probability manipulation. Figure 3 illustrates the design and the procedure used in Experiment 2. All conditions were presented in a randomly intermixed order.

Figure 3.

A schematic illustration of stimuli and trial sequences used in Experiment 2. Items are not drawn to scale.

Location probability awareness

The recognition test was the same as that used in Experiment 2. After answering whether they thought the target was more often in some locations than others, participants selected the quadrant where the target was most often found. To enhance the statistical power to detect explicit awareness, we combined the recognition data from Experiments 2 and 3 (these two experiments used similar designs). The recognition data from both experiments will be presented in Experiment 3.

Results

(1) Visual working memory accuracy

Similar to Experiment 1, we excluded trials in which participants made an incorrect visual search response. This removed 1.1% of the trials. Table 2 shows mean accuracy in the spatial working memory task, separately for trials in which the visual search target fell in the sparse quadrants, the no-load rich quadrant, and the high-load rich quadrant.

Table 2.

Working memory performance in Experiments 2 and 3. S.E. of the mean is shown in parenthesis.

Target quadrant in the search task	Sparse	No-load rich	High-load rich
Experiment 2	64.2% (2.1%)	64.6% (2.8%)	65.4% (2.2%)
Experiment 3	81.7% (2.9%)	82.2% (3.4%)	83.2% (3.3%)

As seen in Table 2, the 10-dot spatial working memory task was challenging. Accuracy in this task was significantly lower than accuracy in Experiment 1's color working memory task, t(34) = 10.29, p < .001. Nonetheless, similar to Experiment 1, working memory performance was unaffected by probability cue conditions, F < 1.

(2) Visual search RT

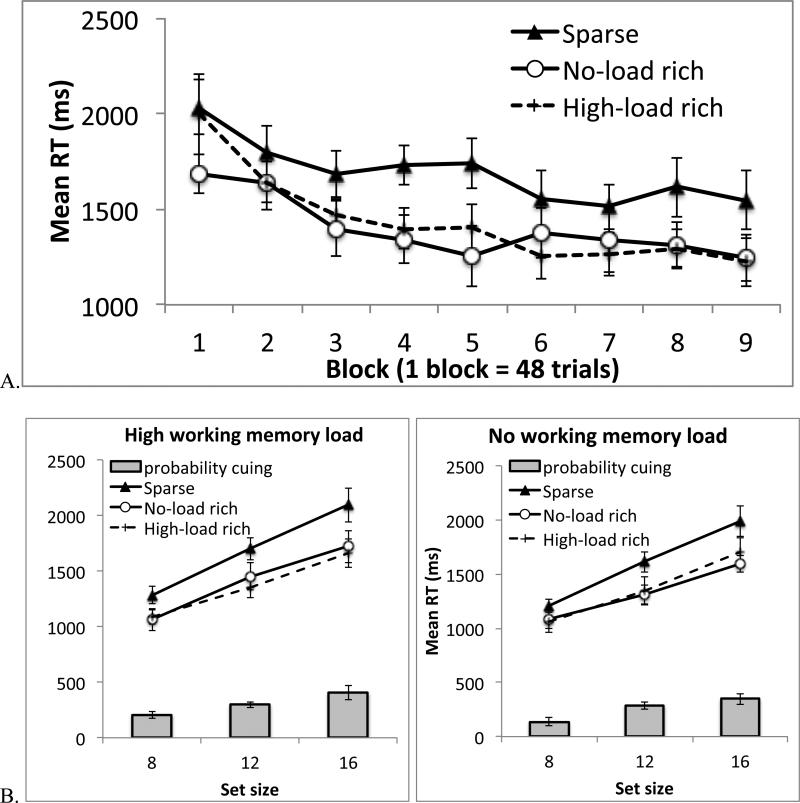
In the visual search RT analysis, we first examined location probability learning over time by binning the 432 trials into 9 experimental blocks. This analysis combined data across all set sizes and both working memory conditions (Figure 5A). An ANOVA on probability cue condition and block revealed a significant main effect of cue condition, F(2, 34) = 12.30, p < .001, η_p² = .42, a significant main effect of block, F(8, 136) = 23.33, p < .001, η_p² = .58, and a significant interaction, F(16, 272) = 1.94, p < .02, η_p² = .10. The linear trend in the interaction term was significant, p < .05. Follow-up tests showed that RT was significantly slower when the target was in the sparse quadrant relative to both the no-load rich quadrant, F(1, 17) = 18.78, p < .001, η_p² = .53, and the high-load rich quadrant, F(1, 17) = 17.68, p = .001, η_p² = .51. RT was comparable between the no-load rich quadrant and the high-load rich quadrant, F < 1. These data showed that probability cuing gradually emerged in the experiment and that it manifested as an attentional preference for both the no-load rich and the high-load rich quadrants.

Figure 5.

A schematic illustration of stimuli and trial sequences used in Experiment 3. Items are not drawn to scale.

To examine how working memory load impacted probability cuing, we included data from Blocks 2-9 during which probability cuing had developed, this time separating trials from different experimental conditions (Figure 5B). These data were entered into an ANOVA using working memory load (no-load or high-load), probability cue condition (sparse, no-load rich, or high-load rich), and set size (8, 12, or 16) as factors. This analysis produced three main effects: slower RT when participants held a concurrent working memory load than when they did not, F(1, 17) = 6.95, p < .02, η_p² = .29, slower RT at higher set sizes, F(2, 34) = 179.82, p < .001, η_p² = .91, and slower RT in the sparse quadrants than the rich quadrants, F(2, 34) = 11.57, p < .001, η_p² = .41. In addition, a significant interaction between probability cue condition and set size was observed, F(4, 68) = 3.72, p < .01, η_p² = .18, showing shallower search slope in the rich quadrants than the sparse quadrants. None of the other effects were significant, all ps > .16. It is important to note that search RT was slowed down by the addition of a spatial working memory task. However, working memory load did not affect probability cuing, yielding no interaction effects between load and probability cue conditions, all ps > .16.

The above analyses revealed that participants had developed probability cuing under both the high-load and no-load conditions. Thus, probability cuing did not diminish when spatial working memory was heavily occupied. In addition, our design allowed us to assess whether participants were sensitive to the contingency between working memory load and the target's location probability. Recall that on high-load trials, the target was more often found in the high-load rich quadrant, but not in the no-load rich quadrant; the opposite was true on no-load trials. It would seem logical for participants to develop an attentional preference only toward the high-load rich quadrant on high-load trials, and only toward the no-load rich quadrant on no-load trials. Such load-specific learning should yield a significant interaction between the type of trials (high-load or no-load) and the target's location (the high-load rich quadrant or no-load rich quadrant). An ANOVA on these two factors, along with set size, revealed no interaction, F(1, 17) = 1.66, p > .20 (Figure 4). Follow-up tests confirmed that learning was independent of load. On high-load trials, as expected participants were faster when the target was in the high-load rich quadrant (mean = 1367ms) than the sparse quadrants (mean = 1693ms), F(1, 17) = 25.78, p < .001, η_p² = .60. However, they were also faster when the target was in the no-load rich quadrant (mean = 1414ms) than the sparse quadrants, F(1, 17) = 10.77, p < .005, η_p² = .39, even though the target was equally improbable in these quadrants. RT was comparable between the two rich quadrants, F < 1. Similarly, on no-load trials, participants were faster when the target was in the no-load rich quadrant (mean = 1329 ms) than the sparse quadrants (mean = 1605ms), F(1, 17) = 15.80, p = .001, η_p² = .48. In addition, they were faster when the target was in the high-load rich quadrant (mean = 1369ms) than the sparse quadrants, F(1, 17) = 10.96, p < .005, η_p² = .39. RT did not differ between the two rich quadrants, F < 1. Even though we had introduced dependency between working memory load and location probability in the experimental design, participants showed no evidence that they were sensitive this dependency. The lack of load-specific learning provides additional evidence for the independence between probability cuing and spatial working memory.

Figure 4.

Results from Experiment 2. A. Search RT across 9 blocks of trials. B. Search RT in Blocks 2-9, separately for different working memory conditions and different set sizes. The gray bars show the difference between the rich conditions (the mean of high-load rich and low-load rich) and the sparse condition. Error bars show 95% confidence interval based on the within-subject S.E.M.

Discussion

Using a spatial working memory task, Experiment 2 extended findings of Experiment 1 by showing that probability cuing was dissociated from spatial working memory. The 10-dot memory task required encoding a large number of locations in spatial working memory, exerting strong demands on spatial working memory (Jiang et al., 2000; Travis et al., 2013; Vickery et al., 2010). In addition, imposing a spatial working memory load slowed down visual search. Nonetheless, a concurrent spatial working memory load had virtually no effects on probability cuing itself. Probability cuing toward the high-load rich quadrant was significant when participants were under high working memory load. In addition, cuing toward the high-load rich quadrant transferred to no-load trials (and vice versa), even though on those trials the target was rarely located in the high-load quadrant. Working memory load did not influence the overall size of probability cuing. It also failed to induce load-specific learning. These data provided some of the strongest evidence, to date, for the dissociation between spatial working memory and one form of spatial attention: implicitly learned attention.

Experiment 3

Spatial working memory has traditionally been assessed in two different ways. The spatial working memory task used in Experiment 2 represents one such test, in which participants remember an array of simultaneously presented locations (Jiang et al., 2000; Phillips, 1974). On the other hand, the neuropsychological literature has typically assessed spatiotemporal sequence memory. In the Corsi Block task, participants must repeat the same sequence of locations that an examiner had just touched (Kessels, van Zandvoort, Postma, Kappelle, & de Haan, 2000). In the Cambridge Neuropsychological Tests Automated Battery (CANTAB; Sahakian et al., 1988), participants must discover a hidden token by touching boxes at several locations and avoid revisiting a box in which a token had already been found. Several studies have argued that these two types of spatial working memory tasks necessitate different computations (Travis et al., 2013; Vickery et al., 2010; Woodman & Luck, 2004). Travis et al. (2013) showed that whereas contextual cuing survived a concurrent spatial working memory load, it diminished under a concurrent spatiotemporal working memory load. Therefore, we deemed it necessary to test effects of spatiotemporal memory on probability cuing. Any interference can potentially falsify the claim that implicitly learned attention is independent of visual working memory.

Experiment 3 used the same design as that of Experiment 2, except that we replaced the 10-dot spatial working memory task with a 4-dot spatiotemporal working memory task. This task was modeled closely after Travis et al. (2013)'s study. It required participants to remember the temporal order of four sequentially presented locations and to judge whether another sequence had identical spatiotemporal sequence as the memorized one.

Method

Participants

Eighteen new participants completed Experiment 3.

Design and Procedure

This experiment was identical to Experiment 2 except that we replaced the 10-dot spatial working memory task with a 4-dot spatiotemporal working memory task (Travis et al., 2013). For this task, the encoding and probe sequences were both composed of a sequence of four dots (dot diameter = 1.4°), presented one at a time against a gray background. Dots in the sequence were presented at a pace of 500 ms/item, including a 100ms presentation and a 400ms blank period. The locations of the four dots were chosen randomly from 16 possible locations: there were 8 equidistant locations on an imaginary outer concentric circle (eccentricity = 10°) and 8 other equidistant locations on an imaginary inner concentric circle (eccentricity = 5°). The dots were either black or white. Participants were asked to ignore the dots when they were black (the no-load condition) or to memorize the locations of the dots and their temporal sequence when they were white (the high-load condition). On half of the trials the order of the dots was identical for the encoding and probe sequences. On the other half of the trials the temporal order of the dots was randomly reshuffled. Although the same spatial locations were occupied, the temporal order differed between the encoding and the probe sequences half of the time (see Figure 5). On high-load trials participants reported whether the two sequences were the same or different. Other aspects of the experiment were the same as those of Experiment 2.

Results

(1) Visual working memory accuracy

We excluded 0.9% of the trials in which participants made an incorrect visual search response. As shown in Table 2, accuracy in the 4-dot spatiotemporal working memory task was moderately high, and was unaffected by probability cue conditions, F < 1. The overall level of performance in this task was lower than that of the color working memory task, t(34) = 2.62, p < .02, and higher than that of the 10-dot spatial working memory task, t(34) = 4.88, p < .001.

(2) Visual search RT

In the first visual search RT analysis we binned the 432 trials into 9 experimental blocks, but combined data across all set sizes and both working memory conditions (Figure 6A). An ANOVA on probability cue condition and block revealed significant main effects of cue condition, F(2, 34) = 15.61, p < .001, η_p² = .48, and block, F(8, 136) = 19.47, p < .001, η_p² = .53, The interaction between cue condition and block was not significant, F < .1. Like Experiment 1, probability cuing emerged early.

Figure 6.

Results from Experiment 3. A. Search RT across 9 blocks of trials. B. Search RT in Blocks 2-9, separately for different working memory conditions and different set sizes. The gray bars show the difference between the rich conditions (the mean of high-load rich and low-load rich) and the sparse condition. Error bars show 95% confidence interval based on the within-subject S.E.M.

To further examine probability cuing and its interaction with working memory load, in a second analysis we included data from Blocks 2-9, but separated trials from different working memory load, cue condition, and set size (Figure 6B). An ANOVA using these three factors showed significant main effects of all factors. RT was slower when people held a concurrent working memory load than when they ignored it, F(1, 17) = 5.24, p < .05, η_p² = .24, slower at higher set sizes, F(2, 34) = 167.19, p < .001, η_p² = .91, and slower when the target as in the sparse quadrants rather than the rich quadrants, F(2, 34) = 15.67, p < .001, η_p² = .48. Search slope was shallower in the rich quadrants than the sparse quadrants, yielding a significant interaction between probability cue condition and set size, F(4, 68) = 4.47, p < .005, η_p² = .21. Similar to the first two experiments, working memory load did not interact with probability cue condition, F < 1, and none of the other interaction effects were significant, smallest p >. 5.

The size of probability cuing, defined as the RT difference between sparse and rich conditions, was unaffected by working memory load. Probability cuing toward the high-load rich quadrant on high-load trials was comparable in size to probability cuing toward the no-load rich quadrant on no-load trials, t(17) = .53, p > .50. This suggests that participants had developed probability cuing under both the high-load and no-load conditions. In addition, participants failed to develop load-specific cuing (Figure 5). On high-load trials, participants were not significantly faster when the target was in the high-load rich quadrant (mean = 1336ms) than when it was in the no-load rich quadrant (mean = 1402ms), F < 1, and conversely, on no-load trials, participants were not significantly faster when the target was in the no-load rich quadrant (mean = 1321ms) than when it was in the high-load rich quadrant (mean = 1328ms), F < 1. The pattern of statistical results observed in Experiment 2 was fully replicated in Experiment 3. Thus, participants were insensitive to the contingency between working memory load and the target's location probability.

(3) Recognition

Because Experiments 2 and 3 used the same probability cuing design, we combined data from all 36 participants to increase the power to detect explicit awareness (Table 3).

Table 3.

Number of participants who made different recognition responses in Experiments 2 and 3. The total number of participants was 36.

	Thought the target's location was random (N=15)			Thought the target was more often in some places (N=21)
Quadrant identified as the high-probability locations	No-load rich quad	High-load rich quad	Sparse quadrants	No-load rich quad	High-load rich quad	Sparse quadrants
	8	3	4	12	2	7

The total number of participants who selected the no-load rich, high-load rich, or a sparse quadrant as where the target was most often found was 20, 5, and 11, respectively. If participants had guessed at random, the expected number of participants who chose these quadrants should have been 9, 9, and 18, respectively. The observed frequency deviated from chance, χ(2) = 17.94, p < .001. Specifically, the number of participants who chose the no-load rich quadrant was higher than chance, but the number of participants who chose the high-load rich quadrant was at chance. These data showed that participants had some explicit awareness of the target's location probability, particularly for the no-load rich quadrant. However, they had little insight that the target was just as frequently biased toward the high-load rich quadrant.

Thus, the secondary working memory load appeared to have influenced participants’ explicit knowledge about where the target was likely to be. However, explicit awareness did not correspond to visual search performance. This is because although participants had recoverable awareness of the no-load rich quadrant but not the high-load rich quadrant, probability cuing was equal in strength toward these quadrants. In addition, we conducted a further analysis on search RT using participant group as an additional factor, separating participants based on the forced-choice recognition results. This factor did not interact with probability cue condition, working memory, or their interactions, all ps > .10. Thus, explicit awareness did not correspond to the pattern of probability cuing and did not contribute to visual search.

Discussion

Experiment 3 supported the findings from Experiments 1 and 2 using a new working memory task. The 4-dot spatiotemporal working memory task had previously been shown to interfere with contextual cuing (Travis et al., 2013). Here we showed that it did not interfere with probability cuing. This difference suggests that the spatiotemporal working memory load interferes primarily with the learning of repeated configurations (a unique component of contextual cuing), but not with attentional cuing per se.

Together, the first three experiments have tested the three most often employed visual working memory tasks in the literature. As shown previously, these tasks place significant demand on both the central executive and the visuospatial storage system (Baddeley, 2012; Makovski, Shim, & Jiang, 2006; Vogel, McCollough, & Machizawa, 2005). Because probability cuing was preserved under a concurrent working memory load, it was insensitive to the reduction in central executive function, visual storage capacity, or spatial storage capacity.

Section II

Experiments in this section examined the role of visual working memory on explicit, goal-driven attention. Several previous studies have shown that when performing a difficult, conjunction search task, participants are slower when they had to hold a concurrent visual working memory load (for a review, see Woodman et al., 2013). Because conjunction search involves serial shift of attention (Wolfe, 1998), it is possible that it shares similar mechanisms as visual working memory. However, direct evidence for this hypothesis is lacking. The main novelty of experiments in Section II, compared with previous studies (e.g., Oh & Kim, 2004; Woodman & Luck, 2004), is that we focused on spatial cuing rather than visual search. Whereas spatial cuing measures the orienting of spatial attention to cued locations (Posner, 1980), visual search measures the serial shift of spatial attention among multiple stimuli (Wolfe, 1998). It is possible that a concurrent working memory load may slow down visual search without affecting the effectiveness of spatial cuing. In fact, data from Section I supported this possibility. Here we test whether the same is true with explicit cuing.

Experiment 4

Experiment 4 examined Posner type explicit cuing. During the working memory retention interval, participants performed a cued visual search task. A central arrow at the center was predictive of the target's quadrant. The cued quadrant contained the target on 50% of the trials, whereas each of the three uncued quadrants contained the target on just 17% of the trials. Participants were encouraged to prioritize the cued quadrant. The central arrow changed its direction from trial to trial, necessitating rapid readjustment of spatial attention. To examine spatial cuing, we compared search performance on valid trials in which the target fell in the cued quadrant, with that on invalid trials in which the target fell in the uncued quadrants. To increase comparability between explicit cuing and probability cuing, we used the same working memory tasks as before. Experiment 4A used the color working memory task and Experiment 4B the 10-dot spatial working memory task. In addition, the central arrow cue yielded the same information as the location probability cue: much like the rich quadrant in Experiment 1, the cued quadrant in Experiment 4 contained the target on 50% of the trials. If explicit cuing relies on the same mechanism as visual working memory, then contrary to our earlier finding on probability cuing, imposing a memory load should reduce the size of explicit cuing.

Method

Participants

Thirty-six new participants completed Experiment 4. There were 18 participants in each of Experiments 4A and 4B.

Design and Procedure

The experimental design was similar to that of Experiment 1. In Experiment 4A, participants first viewed an array of 4 colors and had to either remember their locations or ignore them, depending on the background color. During the memory retention interval they performed a cued visual search task. They then reported the location of the square that had changed its color. In Experiment 4B, we substituted the color working memory task with the 10-dot spatial working memory task (see Experiment 2). Experiments 4A and 4B were otherwise identical.

For the visual search task we provided a spatial cue using a black arrow (size 1.9°×1.9°) directed toward one of the four visual quadrants. The arrow was presented after the 500ms memory retention interval. The arrow lasted 100ms, followed by a 100ms blank interval and then the visual search display. The direction of the arrow was 45°, 135°, 225°, or 315°, determined randomly on each trial. On 50% of the trials the quadrant cued by the central arrow contained the target (valid cue trials), whereas on the other trials the target appeared in one of the three uncued quadrants (invalid cue trials; 16.7% probability in each quadrant). Participants were encouraged to prioritize the cued quadrant. Because the direction of the arrow was random, across all trials the target was equally likely to appear in any visual quadrant. Therefore, participants could not accumulate location probability learning in Experiment 4. Cuing depended entirely on their ability to use the arrow cue on a trial-by-trial basis.

The trial sequence was similar to that used in Experiment 1, except for the inclusion of the arrow cue. Figure 7 shows a schematic illustration of the trial sequence.

Figure 7.

A schematic illustration of stimuli and trial sequences used in Experiment 4's spatial working memory task. Items are not drawn to scale.

Results

(1) Visual working memory accuracy

In this analysis we removed trials in which an incorrect search response was made. This eliminated 1.7% of the trials in Experiment 4A and 0.9% of the trials in Experiment 4B.

In the color working memory task of Experiment 4A, memory accuracy was significantly higher when the spatial cue used in the search task validly predicted the target's quadrant (mean = 87.1%) than when the cue was invalid (mean = 83.9%), t(17) = 2.99, p = .008, Cohen's d = 1.45. The interference could come from the need to re-orient spatial attention to uncued quadrants. Alternatively, it may be attributed to greater memory decay owing to the longer RT on invalid trials than valid trials. Such interference effects were not robust, however, as they were not observed in the spatial working memory task of Experiment 4B. Here, memory accuracy was similar whether or not the spatial cue used in the search task validly predicted the target's quadrant (mean = 71.6% in the valid condition, 74.8% in the invalid condition), t(17) = 0.96, p > .30.

(2) Visual search RT

Figure 8 plots visual search results from Experiment 4, separately for the color working memory (Experiment 4A) and the spatial working memory (Experiment 4B) tasks.

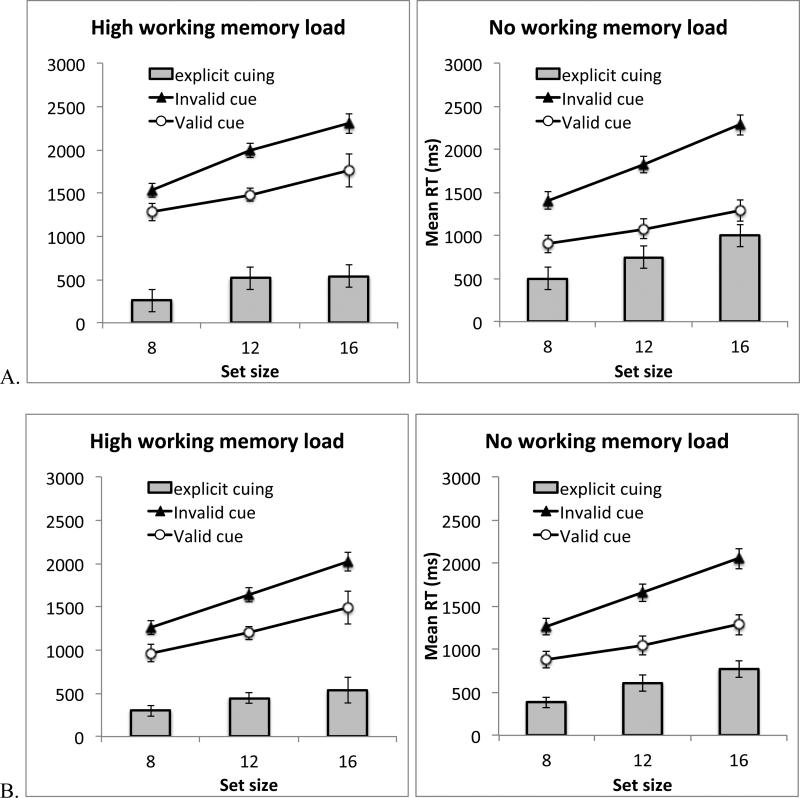
Figure 8.

Results from Experiment 4. A. Search RT in Experiment 4A. B. Search RT in Experiment 4B. The gray bars show the difference between the invalid cue condition and the valid cue condition. Error bars show 95% confidence interval based on the within-subject S.E.M.

We conducted an ANOVA using experiment as a between-subject factors, working memory load, cue validity, and set size as within-subject factors. First, we observed a significant explicit cuing effect: RT was faster in the validly cued quadrant than the other quadrants, F(1, 34) = 158.76, p < .001, η_p² = .82. In addition, the explicit cue made the visual search slope shallower, resulting in a significant interaction between cue validity and set size, F(2, 68) = 41.83, p < .001, η_p² = .55. The main effect of set size was also significant, F(2, 68) = 377.85, p < .001, η_p² = .92. These effects were observed in both Experiments 4A and 4B: the interaction between experiment and the effects described above were not significant, all ps > .10.

Adding a concurrent working memory load significantly affected visual search. First, participants were slower in the high-load than the no-load condition, resulting in a significant main effect of load, F(1, 34) = 40.98, p < .001, η_p² = .55. Second, adding a working memory load interfered with explicit cuing, resulting in a significant interaction between cue validity and working memory load, F(1, 34) = 26.09, p < .001, η_p² = .43. Follow-up tests showed that explicit cuing was significant both in the no-load condition, F(1, 34) = 169.00, p < .001, η_p² = .83, and in the high-load condition, F(1, 34) = 83.18, p < .001, η_p² = .71, but the former (validity effect: 668 ms) was nearly twice as large as the latter (validity effect: 432 ms). Third, without a working memory load, explicit cuing reduced search slope from 105 ms/item in the uncued quadrants to 49 ms/item in the cued quadrant. Under a working memory load, the reduction in search slope was smaller (slope was 96 ms/item in the uncued quadrants and 63 ms/item in the cued quadrant). This yielded a significant three-way interaction between working memory load, cue validity, and set size, F(2, 68) = 3.41, p = .039, η_p² = .09. The pattern of results described here were similar for Experiment 4A and 4B. The only difference between the two experiments was that the color working memory load slowed down RT by a larger degree (260 ms) than the spatial working memory load did (66 ms). This led to a significant interaction between load and experiment, F(1, 34) = 14.58, p < .001, η_p² = .30. This difference could be partly attributed to a scaling effect, as participants in Experiment 4A were slower than those in Experiment 4B, leading to a significant main effect of experiment, F(1, 34) = 4.12, p = .05, η_p² = .11. Importantly, in both experiments, adding a working memory load reduced the validity effect (the interaction between load, validity, and experiment was not significant, F(1, 34) = 2.68, p > .10), and adding a working memory load reduced the cue benefit on search slope (the interaction between load, validity, set size, and experiment was not significant, F < 1). None of the other interaction effects were significant.

(4) Explicit cuing versus probability cuing

Experiment 4 showed that explicit cuing became less effective when participants held a concurrent working memory load. These results contrasted sharply with those from probability cuing. To directly compare explicit cuing with probability cuing, we conducted an analysis comparing Experiment 4A and Experiment 1. These two experiments used the same working memory task but differed in the type of spatial cuing. This analysis was restricted to data from Blocks 2-9 to allow for adequate establishment of probability cuing. We conducted an ANOVA using cue type (explicit cue or probability cue) as a between-subject factor, working memory load, cue validity, and set size as within-subject factors. This analysis revealed one significant interaction that involved cue type: the interaction between working memory load, cue validity, and cue type, F(1, 34) = 19.58, p < .001, η_p² = .37. Whereas adding a visual working memory load impaired explicit cuing, it did not diminish probability cuing. Notably, cue type did not interact with any other factors. It did not interact with cue validity or set size, for instance, suggesting that explicit cuing and probability cuing were equally effective in facilitating RT and in reducing search slope. Their difference lies in their sensitivity to concurrent working memory load.

Discussion

Experiment 4 showed that the effectiveness of explicit cuing was reduced when participants held a concurrent working memory load of colors or spatial locations. This finding replicated and extended previous research on the relationship between visual working memory and visual attention. Consistent with these previous studies, adding a visual working memory load slowed down search RT (Oh & Kim, 2004; Woodman & Luck, 2004). More importantly, we showed that loading up visual working memory interfered with people's ability to orient spatial attention based on a central arrow cue. These data showed that explicit, goal-driven spatial orienting draws on the same processing resource as visual working memory. Experiment 4 therefore supports the idea that visual attention and visual working memory are closely related (Awh & Jonides, 2001; Chun, 2011; Franconeri et al., 2013; Gazzaley & Nobre, 2012; Kiyonaga & Egner, 2013). However, these results differed from those observed in Section I. Together, our study showed that not all sources of top-down attention depend on visual working memory. Whereas explicit, goal-driven attention draws from the same resource as visual working memory, implicitly learned attention is dissociated from visual working memory.

Our experiments leave open the question of the exact source of interference between explicit cuing and visual working memory. For example, we do not know whether it is the visuospatial component or the central executive component of working memory that had interfered with explicit cuing. This question needs to be tested in future studies by using verbal or auditory working memory tasks. We also do not know which component of explicit cuing depend on visual working memory. For example, did the working memory load impair the perception of the arrow cue, or did it interfere with people's ability to prioritize the cued locations? To address this question, in a control experiment (N=18) we examined whether adding a color working memory load impaired people's ability to perceive a briefly presented central arrow. Participants reported the direction of a central arrow under either high-load or no-load conditions similar to those used in Experiment 4A. Their accuracy in identifying the central arrow was comparable in the high-load (100%) and the no-load (99%) conditions. RT was slower in the high-load condition (351 ms) than the no-load condition (306 ms), p < .001, but this difference was nearly 10 times smaller than the large reduction in explicit cuing under high load (Experiment 4A). Thus the reduction in explicit cuing cannot be adequately accounted for by impaired perception of the arrow cue under high load. The next experiment provided additional evidence that explicit cuing depended on visual working memory, even when people did not have to process a central arrow.

Experiment 5

Experiment 5 aims to provide converging evidence for the idea that visual working memory is involved in explicit cuing. Specifically, we would like to substitute the central arrow cue with a verbal instruction. At the beginning of a block of 12 trials participants were asked to prioritize a specific quadrant for all subsequent trials within the block. Because the task goal was stable for all trials within the block, there was no need to change the attentional priority on a trial-to-trial basis. To prevent the build-up of probability cuing we changed the verbal instruction every 12 trials. This design had two advantages. First, because explicit cuing originated from relatively stable verbal instructions, visual working memory load could not have interfered with trial-by-trial perception of the cue. Second, because the central arrow was not presented in this experiment, trial sequence was identical between Experiment 5 and Experiment 1, increasing the comparability between these experiments. If visual working memory interfered primarily with the perception of the central arrow cue in Experiment 4, then its impact on explicit cuing should be much reduced in Experiment 5.

Method

Participants

Eighteen new participants completed Experiment 5.

Procedure

This experiment was divided into 24 blocks, each comprised of 12 trials. The experiment used the color working memory task of Experiments 1 and 4A. During the retention interval participants performed the T/L search task. Trial timing was identical to that of Experiment 1.

Design

At the beginning of each mini-block participants saw a blue outline square that framed one of the four visual quadrants. Participants were told that the target would be found in that quadrant on 50% of the trials, and therefore they should prioritize visual search in that quadrant. To ensure that participants had encoded this instruction, before each trial a computer voice reinforced the location of the cued quadrant (e.g., “upper left”). Only after the computer had finished speaking this phrase could participants click on the fixation point to initiate the trial. At the end of the 12 trials participants were asked to recall the quadrant that they had been asked to prioritize. All participants successfully recalled it with 100% accuracy. Consistent with the instruction given to participants, the target was in the cued quadrant 50% of the time, and in each of the three uncued quadrants 16.7% of the time. To prevent the build-up of location probability learning, we changed the instruction every 12 trials. Across the 24 blocks each quadrant was assigned to be the cued quadrant 6 times, presented in a random order. The 12 trials of each block were randomly and evenly divided into the two working memory load conditions (high-load or no-load) and three set sizes (8, 12, and 16). The experiment was otherwise identical to Experiment 1.

Results

(1) Visual working memory accuracy

We removed the 1.6% of the trials in which participants made an incorrect visual search response. For the remaining trials, accuracy in the color working memory task was unaffected by the location of the visual search target: 85% when the target was in the cued quadrant and 83.4% when it was in an uncued quadrant, F < 1.

(2) Visual search RT

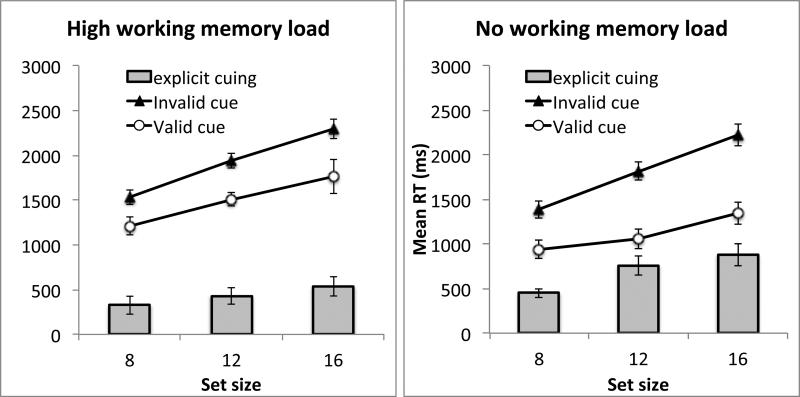
Visual search results from Experiment 5 (Figure 9) replicated those of Experiment 4. An ANOVA on memory load, cue validity and set size showed a significant main effect of cue validity, F(1, 17) = 92.01, p < .001, η_p² = .84. Participants were successful at using the blocked verbal cue to prioritize search in the instructed quadrant. Such prioritization reduced visual search slope, resulting in a significant interaction between cue validity and set size, F(1, 17) = 23.59, p < .001, η_p² = .58. The main effect of set size was also significant, F(2, 34) = 111.55, p < .001, η_p² = .87. Much like Experiment 4, working memory load slowed down overall RT, resulting in a significant main effect of load, F(1, 17) = 19.63, p < .001, η_p² = .54. Importantly, it significantly reduced the validity effect, producing an interaction between load and cue validity, F(1, 17) = 23.59, p < .001, η_p² = .58. The validity effect was significant in both the high-load (mean 429 ms; F(1, 17) = 53.89, p < .001, η_p² = .76) and the no-load (mean 697 ms, F(1, 17) = 97.44, p < .001, η_p² = .85) conditions, but declined by nearly half when a working memory load was imposed. Finally, the cue effect on search slope also became smaller when participants held a concurrent working memory load. In the no-load condition, search slope was 51 ms/item in the cued quadrant and 104 ms/item in the uncued quadrants. In the high-load condition, search slope was 69 ms/item in the cued quadrant and 95 ms/item. These results were highly similar to those found in Experiment 4. Although the three-way interaction between load, cue validity, and set size was only marginally significant, F(2, 34) = 2.40, p < .10, η_p² = .12, the effect size was comparable to that reported in Experiment 4. In fact, given the directionality of the effect was predicted a priori, a one-tailed test is justifiable. The reduction in search slope in the high load condition (27 ms/item) was significantly smaller than that in the no-load condition (53.5 ms/item) on a one-tailed test, t(17) = 1.93, p < .035.

Figure 9.

Results from Experiment 5. The gray bars show the difference between the invalid cue condition and the valid cue condition. Error bars show 95% confidence interval based on the within-subject S.E.M.

(3) Experiment 1 versus Experiment 5

Experiments 1 and 5 used identical trial timing, but differed in the nature of spatial cuing. A direct comparison between these two experiments revealed a significant interaction between experiment, working memory load, and cue validity, F(1, 34) = 28.20, p < .001, η_p² = .45. A concurrent working memory load weakened explicit cuing (Experiment 5) but did not weaken probability cuing (Experiment 1).

Discussion

Experiment 5 provided additional evidence that explicit, goal-driven attention depends on the availability of visual working memory resources. The utility of a verbal cue on search RT and slope diminished when participants held a concurrent color working memory load than when they ignored the colors. These results replicated the findings from Experiment 4. Unlike Experiment 4, the verbal instructions were delivered at the beginning of a 12-trial block. Participants therefore did not have to rapidly perceive the explicit cue on each trial. Any concerns about working memory interfering with cue perception were removed. Under this condition, concurrent working memory load must have interfered with participants’ ability to use the verbal cue to prioritize the cued quadrant.

Together, experiments reported in Section II provide strong evidence for the reliance of explicit, goal-driven attention on working memory resources. This was found with two types of working memory load – color and spatial working memory, and with two types of explicit cuing – a central arrow cue that changed from trial to trial and a verbal cue that was stable for a block of 12 trials. These findings strengthen the theoretical connection between working memory and explicit cuing. They also contrast sharply with results from Section I, demonstrating that visual working memory interferes with some, but not all, sources of top-down attention.

General Discussion

Working memory and attention exert major capacity limitations to human performance. Although studied separately for many years, recent empirical and theoretical approaches have related these two constructs because they tap into similar cognitive and brain mechanisms (Cowan, 2001). Rehearsal of information in spatial working memory depends on attending to those locations (Awh & Jonides, 2001), and conversely, exerting a concurrent visual working memory load interferes with the deployment of spatial attention in visual search (Olivers et al., 2011; Woodman et al., 2013). In fact, recent theoretical accounts consider working memory as attention deployed to an internal representation (Chun, Golomb, & Turk-Browne, 2011; Chun, 2011; Kiyonaga & Egner, 2013). The current study both confirms these important theoretical considerations and extends them in new ways.

First, using a spatial cuing paradigm that required participants to adjust their spatial attentional priority according to task instructions, we showed that the utility of goal-driven attention declined when participants performed a secondary visual working memory task. The need to remember the locations of 4 colored squares or 10 simultaneously presented locations interfered with one's ability to flexibly orient spatial attention to cued locations in another part of the display. These findings extend previous research from visual search (Oh & Kim, 2004; Woodman et al., 2013; Woodman & Luck, 2004) to spatial cuing. Whereas visual search influences rapid shift of attention among multiple search elements (Wolfe, 1998), spatial cuing reflects the orienting of spatial attention to a cued location (Posner, 1980). Results were similar whether attention was driven trial-by-trial with the use of a central arrow cue or by a verbal instruction that stayed the same for a block of 12 trials. This similarity narrowed down the interference effect to participants’ ability to use the cue to prioritize attention. Our study therefore demonstrates that spatial orienting, a major component of spatial attention, depends on visual working memory.

The second important contribution of the current study is the finding that not all forms of spatial cuing depend on visual working memory. When cued by the target's location probability rather than by an explicit cue, attentional orienting was largely immune to concurrent visual working memory load. Participants were able to prioritize high-probability, target-rich regions even when they held several colors, dot locations, or the spatiotemporal sequence of dots in working memory. Not only was there no evidence for a reduction in the size of probability cuing, but also was cuing fully transferred across memory load. These results were found even though overall search RT was slower under working memory load, and even though the working memory load modulated participants’ explicit awareness. The contrast between probability cuing and explicit cuing was striking, so was the discrepancy between explicit awareness and the implicit manifestation of probability cuing. These data refine our understanding of the relationship between spatial attention and spatial working memory. Spatial working memory interferes with some, but not all, forms of spatial orienting.

The claim that spatial working memory is dissociated from some forms of spatial attention depends on the qualification of probability cuing as a form of spatial attention. What is the evidence that probability cuing affects spatial attention, rather than post-search decisional processes or oculomotor routines? Several studies have shown that probability cuing indeed qualifies as a form of spatial attention. First, like goal-driven attention, probability cuing not only facilitates visual search RT but also enhances visual search efficiency. The slope of the linear function that relates RT to the number of search items becomes shallower when the target is in the high-probability region rather than the low-probability region (Jiang, Swallow, & Rosenbaum, 2013; the current study). Enhanced search efficiency is a hallmark of attentional guidance (Wolfe, 2007), suggesting that probability cuing affects spatial attention. Second, the first saccadic eye movement, an index of spatial attention during a relatively early stage of processing, is more often directed toward the rich quadrant rather than the sparse quadrants (Jiang, Won, & Swallow, in press). Third, frequently saccading to the target-rich region is neither necessary nor sufficient to produce probability cuing. Probability cuing was observed even when participants viewed briefly presented displays under strict fixation conditions (Geng & Behrmann, 2005). In addition, frequently saccading to one region of the display did not yield probability cuing if a central arrow had already cued the target's location (Jiang, Swallow, & Rosenbaum, 2013). Thus, probability cuing affects attentional allocation rather than, or in addition to, other stages of processing.

If explicit cuing and probability cuing both affect spatial orienting, then why does the former depend on spatial working memory but the latter does not? To understand these data, it is important to reconsider the nature and heterogeneity of spatial attention. Influential models of spatial attention consider it as a sort of “priority map” (Bisley & Goldberg, 2010; Fecteau & Munoz, 2006; Itti & Koch, 2001). Locations that are behaviorally relevant and contain salient features are prioritized and are more likely to be attended first. These models do not explicitly distinguish between explicit, goal-driven attention and implicitly learned attention. In fact, influential theories of attention have used a single term to describe them: “top-down attention” (Desimone & Duncan, 1995; Wolfe, 2007). In addition, contextual cuing, a form of implicitly learned attention, has been theorized to affect the “context map,” much like the priority map of attention (Brady & Chun, 2007; Chun & Jiang, 1998). Because these theories and models do not distinguish between goal-driven and implicitly learned attention, in their current form they do not produce an account for the dissociation seen in this study.

A refined, dual-system view of attention distinguishes two components of spatial attention: a declarative component and a procedural component(Jiang, Swallow, & Capistrano, 2013). Goal-driven attention taps into the declarative component of attention, which can be used to set different priority weights offline. The priority setting can happen before the onset of visual stimuli, affecting baseline activities of neurons that code different regions of space (Luck, Chelazzi, Hillyard, & Desimone, 1997). The declarative component of attention is under direct control by the participants’ behavioral goals. The explicit cues used in Experiments 4 and 5 influenced declarative attention. The procedural component of attention, on the other hand, refers to the online shift of spatial attention. For any visual tasks such as visual search, the task involves not only planning but also actual execution. The shift of spatial attention is often implemented in saccadic eye movements, but it is not limited to the oculomotor response itself. Several theories, such as the premotor theory of attention (Rizzolatti, Riggio, Dascola, & Umiltá, 1987) and the attention-for-action theory (Allport, 1989), consider covert attention as an integral component of eye movements or other actions. Much like eye movement which is procedural, premotor attention has a strong procedural component. It is involved in the actual shift of attention in space. In our view, implicit learning modulates primarily the procedural component of spatial attention. It influences the deployment of spatial attention during the visual search task, modulating the direction and size of the next attentional shift. Empirical studies have provided evidence for this view, showing that contextual cuing, a form of implicit learning, occurs during but not before visual search (Jiang, Sigstad, & Swallow, 2013). In addition, implicitly learned attention codes space in a viewer-centered reference frame, consistent with its close relationship to visuomotor action (Goodale & Haffenden, 1998; Jiang, Swallow, & Sun, 2014; Y. V. Jiang & Swallow, 2013). Declarative and procedural attention may be supported by different neural substrates, such as the frontoparietal network for declarative attention and the basal ganglia and/or superior colliculus for procedural attention.

The reliance of some but not all forms of spatial cuing on spatial working memory provides additional evidence for the idea that top-down attention may be guided by qualitatively different sources, namely an explicit goal and implicit learning. To retain the colors or dot locations in working memory, it is necessary to prioritize the spatial locations occupied by these items. This prioritization occurs potentially interferes with one's ability to setup a different attentional priority for the cued quadrant. On this account, working memory load interferes with both the initial determination of the priority map (where should I attend first?), as well as the ability to deploy attention to the high priority locations (implementing the task goal; see Duncan et al., 2008). Both components are integral to the priority map theory (Bisley & Goldberg, 2009). The lack of interference from spatial working memory on probability cuing, on the other hand, supports the idea that probability cuing is a different source of top-down attention than explicit, goal-driven attention. Because probability cuing is acquired implicitly, participants never have to explicitly setup a priority map or to explicitly implement the task goal. However, as participants perform the visual search task, each successive attentional shift is biased toward the previously reinforced direction. This procedural aspect of attentional shift is largely immune to interference from a concurrent visual working memory task.

Using a different implicit learning paradigm – contextual cuing, several previous studies have found conflicting results about whether implicit learning is impaired by a secondary visual working memory task (Annac et al., 2013; Manginelli et al., 2013; Travis et al., 2013; Vickery et al., 2010). In these studies, participants searched for a target among distractors during the retention interval of various visual working memory tasks. Unbeknownst to participants, some visual search displays were repeatedly presented. In the absence of a working memory load, participants were faster on repeated displays than unrepeated ones, showing contextual cuing (Chun & Jiang, 1998). When a visual working memory load was added, some studies found that contextual cuing was reduced (Travis et al., 2013) whereas others found that contextual cuing was intact (Vickery et al., 2010) or the results were mixed (Annac et al., 2013; Manginelli et al., 2013). It is important to note that contextual cuing is a more complex paradigm than probability cuing. Contextual cuing involves at least two processes: implicitly distinguishing repeated from unrepeated configurations, and directing attention to the target on repeated configurations. Any interference from a secondary visual working memory task could reflect either impaired configuration learning or impaired attention. In contrast, probability cuing does not involve configuration learning, so it is a simpler and more direct measure of implicitly learned attention. Whereas sequential memory of dot locations interfered with contextual cuing (Travis et al., 2013), it did not affect probability cuing (current study). Thus, our study provides some of the clearest evidence that implicitly learned attention is robust in the presence of a secondary spatial working memory task. It is consistent with the larger literature on the relationship between implicit learning and working memory load (for a review, see Stadler & Frensch, 1998).

In sum, this study presents strong evidence for the idea that spatial working memory is related to some but not all sources of top-down attention. Whereas explicit cuing is reduced under a secondary visual working memory load, implicitly learned probability cuing is robust to interference from various visual working memory tasks. These findings indicate that top-down attention have qualitatively different sources. Our study affirms the close relationship between goal-driven attention and spatial working memory, but also reveals a dissociation between implicitly learned attention and spatial working memory. These findings show that the relationship between attention and working memory is more nuanced than previously thought (see also Fougnie & Marois, 2006; Olivers et al., 2011). Future studies should examine exactly how a concurrent working memory load interferes with explicit, goal-driven attention. More generally, determining when attention and working memory are related and when they are dissociated is an important future research topic.

Appendix

Appendix Table A.

Percent correct in the visual search task.

A.1. Experiments 1, 4, and 5.
	High-load						No-load
Cue condition	Valid/Rich			Invalid/Sparse			Valid/Rich			Invalid/Sparse
Set size	8	12	16	8	12	16	8	12	16	8	12	16
Exp1	98.3	99.2	99.1	98.8	98.9	98.6	98.8	98.9	98.5	98.5	99.2	98.6
Exp4A	97.8	99.2	99.4	98.5	98.1	98.6	97.7	98.6	99.1	97.4	98.0	97.5
Exp4B	99.4	99.2	99.2	98.9	98.9	99.5	99.1	99.4	99.2	98.8	99.2	98.1
Exp5	99.5	99.1	97.9	97.7	98.8	97.9	98.4	97.2	98.8	97.7	98.6	98.8

A.2. Experiments 2 and 3.
Cue condition	High-load rich			No-load rich			Sparse
Set size	8	12	16	8	12	16	8	12	16
Exp2 High-load	99.4	99.1	98.5	99.1	99.5	99.5	99.1	98.6	98.8
Exp2 No-load	98.1	99.5	98.6	98.8	99.4	98.6	97.7	99.5	98.6
Exp3 High-load	99.5	98.5	99.1	99.5	99.5	98.1	99.5	98.8	99.8
Exp3 No-load	100	99.1	99.1	99.4	98.6	99.2	99.5	98.8	98.6

Appendix Table B.

Mean visual search RT (ms) after the exclusion of trials in which an incorrect response was made to the concurrent working memory task.

B.1. Experiments 1, 4, and 5.
	High-load						No-load
Cue condition	Valid/Rich			Invalid/Sparse			Valid/Rich			Invalid/Sparse
Set size	8	12	16	8	12	16	8	12	16	8	12	16
Exp1	1036	1276	1489	1451	1862	2177	985	1213	1425	1289	1618	2126
Exp4A	1217	1471	1718	1500	1965	2263	903	1077	1288	1405	1827	2287
Exp4B	953	1155	1437	1253	1594	1972	880	1047	1284	1263	1655	2053
Exp5	1170	1501	1745	1478	1934	2215	938	1060	1342	1388	1818	2221

B.2. Experiments 2 and 3.
Cue condition	High-load rich			No-load rich			Sparse
Set size	8	12	16	8	12	16	8	12	16
Exp2 High-load	1067	1316	1660	990	1430	1755	1252	1693	2043
Exp2 No-load	1056	1351	1700	1085	1307	1593	1208	1614	1993
Exp3 High-load	1072	1305	1562	1154	1338	1616	1285	1601	1993
Exp3 No-load	1089	1320	1575	1054	1283	1625	1238	1590	1940