Dynamic Encoding of Speech Sequence Probability in Human Temporal Cortex

Abstract

Sensory processing involves identification of stimulus features, but also integration with the surrounding sensory and cognitive context. Previous work in animals and humans has shown fine-scale sensitivity to context in the form of learned knowledge about the statistics of the sensory environment, including relative probabilities of discrete units in a stream of sequential auditory input. These statistics are a defining characteristic of one of the most important sequential signals humans encounter: speech. For speech, extensive exposure to a language tunes listeners to the statistics of sound sequences. To address how speech sequence statistics are neurally encoded, we used high-resolution direct cortical recordings from human lateral superior temporal cortex as subjects listened to words and nonwords with varying transition probabilities between sound segments. In addition to their sensitivity to acoustic features (including contextual features, such as coarticulation), we found that neural responses dynamically encoded the language-level probability of both preceding and upcoming speech sounds. Transition probability first negatively modulated neural responses, followed by positive modulation of neural responses, consistent with coordinated predictive and retrospective recognition processes, respectively. Furthermore, transition probability encoding was different for real English words compared with nonwords, providing evidence for online interactions with high-order linguistic knowledge. These results demonstrate that sensory processing of deeply learned stimuli involves integrating physical stimulus features with their contextual sequential structure. Despite not being consciously aware of phoneme sequence statistics, listeners use this information to process spoken input and to link low-level acoustic representations with linguistic information about word identity and meaning.

Introduction

In auditory perception, listeners are tuned to the statistical properties of the sensory environment (Winkler et al., 2009), including learned knowledge about the structure of acoustic sequences (Furl et al., 2011; Yaron et al., 2012; Tremblay et al., 2013). On both short (Ulanovsky et al., 2003) and long (Kiebel et al., 2009) time scales, neurons and neural populations throughout the auditory system process sequential information (Margoliash and Fortune, 1992; Brosch and Schreiner, 2000; Gelfand and Bookheimer, 2003; Gentner and Margoliash, 2003; Bouchard and Brainard, 2013), in addition to discrete elements of sequences. Speech is an important sequential auditory input for human communication, yet it is presently unknown how discrete speech features (Chang et al., 2010; Mesgarani et al., 2014) are processed as sequences that comprise words.

Languages are defined not only by the physical characteristics of individual speech sounds (the acoustics of phonemes), but also by the sequential arrangements of these phonemes (phonotactics) (Vitevitch and Luce, 1999). For example, hearing the sound /k/ followed by /uw/ (“koo”) is more common than hearing /k/ followed by /iy/ (“kee”). Thus, in English, /k/ predicts /uw/ more strongly than /iy/, which is less likely to be the next sound (see Fig. 1A). In both cases, the two phonemes in the sequence are conditionally predictable from each other, assuming the listener has learned the statistics of English phoneme sequences (although listeners may not be consciously aware of these distributions). While there is an ongoing debate regarding the behavioral role of phonotactics in speech perception (Lipinski and Gupta, 2005; Vitevitch and Luce, 2005), there is currently a lack of neurobiological data examining how language-level statistical structure is encoded in the brain at fine temporal and spatial scales. Specifically, it is unknown how the encoding of phonotactic statistics relates to the encoding of both lower-level acoustic and higher-level lexical features.

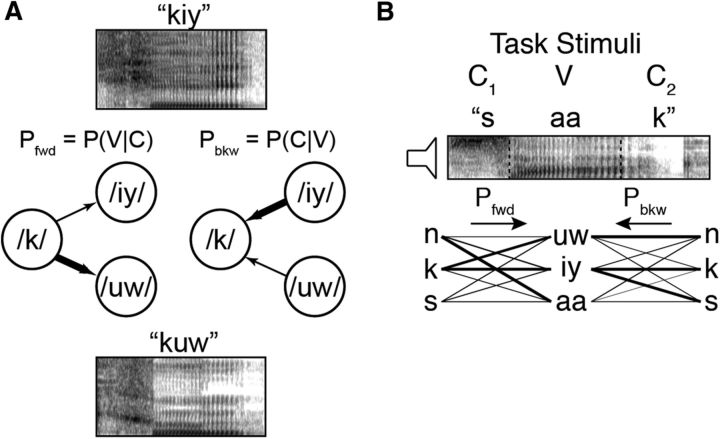
Figure 1.

Phonotactic transition probabilities. A, Based on co-occurrence statistics in English, the probability of hearing a given phoneme can be deduced from its neighboring phonemes. Two sequences, /k/-/iy/ (top spectrogram) and /k/-/uw/ (bottom spectrogram), have different transition probabilities between the consonant and the vowel. The probability that /k/ is followed by /iy/ or /uw/ in English (P_fwd) is indicated by the thickness of the arrows in the left diagram. Likewise, the probability that /iy/ or /uw/ is preceded by /k/ in English (P_bkw) is indicated by the thickness of the arrows in the right diagram. P_fwd (prediction of future phonemes) and P_bkw (analysis of preceding phonemes) can be different from each other even for the same sequences, and thus reflect different statistics of the language. In both cases, conditional probabilities are normalized by the marginal probabilities of individual phonemes. B, In the present study, participants heard CVC words and pseudowords (e.g., /s-aa-k/) that had varying P_fwd and P_bkw transition probabilities. All CVC combinations are shown in the schematic diagram, with lines reflecting P_fwd for the C₁V transition and P_bkw for the VC₂ transition (C₁V P_bkw and VC₂ P_fwd not shown).

Here we used high-density electrocorticography (ECoG) to examine how sequences of phonemes are encoded in real time. Participants listened to a set of 26 consonant-vowel-consonant (CVC) words and pseudowords that allowed us to compare responses with the same sounds in different phonotactic contexts (see Fig. 1B). We hypothesized that, as the speech signal unfolds, neural populations track spectrotemporal, phonetic, and phonotactic information. We specifically examined how modulation of neural responses by various phonotactic measures (having controlled for acoustic tuning as measured by various spectrotemporal and phonetic models) indicates different real-time neural processing strategies, which contribute to the capability for rapidly understanding speech.

Materials and Methods

Participants.

Four human subjects (2 female) were implanted with a high-density 256-electrode array (4 mm pitch) subdurally over the left (language-dominant) hemisphere as part of clinical treatment for epilepsy. All subjects reported normal hearing and were within normal range on a battery of neuropsychological language tests. They gave written informed consent before surgery.

Stimuli and tasks.

Subjects were told to listen to each CVC stimulus (Fig. 1B) and wait for a visual cue (2 s after the onset of the stimulus) before repeating what they heard aloud. The purpose of the behavioral response was to ensure that participants were awake and paying attention to the sounds. Each block of the task consisted of 43 stimuli (26 of which make up the balanced set used in the ECoG analyses; the remainder were distractor stimuli made up of other phonemes to preserve some natural distribution of speech statistics). Subjects 1, 2, and 4 heard each CVC (randomized order) 8 times, whereas Subject 3 heard them 10 times. The stimuli were generated using the built-in speech synthesizer in Mac OS X (“Alex” voice), were highly intelligible, and had a mean length of 491 ± 28 ms. To calculate the English transition probabilities, we used a large speech corpus (Vaden et al., 2009) to generate the conditional probability of one phoneme given another based on individual and co-occurrence counts (Perruchet and Desaulty, 2008) (e.g., P_fwd for the C₁V transition) as follows:

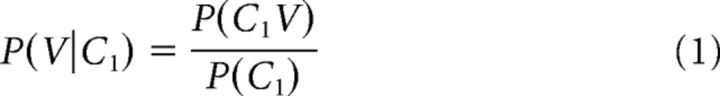Similar logic was used to calculate the P_bkw transition probabilities (e.g., for the VC₂ transitions) as follows:

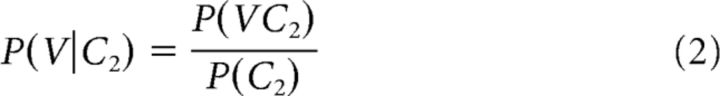P_fwd and P_bkw were obtained for both the C₁V and VC₂ transitions; however, we chose to focus on the effects of P_fwd in the C₁V transition, and P_bkw in the VC₂ transition because those comparisons captured the most interesting dynamics (for a description of position-dependent and position-independent phonotactic effects, see Results).

It is well established that the brain is sensitive to higher-order regularities, such as the frequency of whole words in the language (Dahan et al., 2001; Prabhakaran et al., 2006). To obtain a probability measure that was not influenced by higher-order statistics, we controlled for lexical frequency by dividing the right sides of Equations 1 and 2 by the sum of the log lexical frequencies of words (W) containing each biphone (C₁V or VC₂), for example:

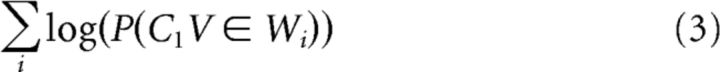This procedure is equivalent to including a term for lexical frequency in the linear models described below. It provides an estimate of phoneme-level transition probabilities that are not biased by the fact that more frequent words inherently contain more frequent transitions, and vice versa. We hypothesized that such a control would enhance the ability to detect pure phonotactic effects, given previous work showing that phoneme-level segmentation is influenced by higher-order statistics at the lexical level (Kurumada et al., 2013).

In a separate task, subjects listened passively to 484 unique naturally spoken sentences (2 repetitions of each sentence) from the TIMIT database (Garofolo et al., 1993), which were used to estimate spectrotemporal receptive fields for each electrode. As an additional control analysis to verify the generality of any observed phonotactic effects, forward and backward transition probabilities were calculated on all phoneme transitions in TIMIT, and the same linear regression analyses described below were performed.

Data acquisition and preprocessing.

Electrocorticographic data were recorded from 256 electrodes simultaneously as broadband local field potentials with a multichannel amplifier optically connected to a digital signal processor sampled at 3052 Hz (TuckerDavis Technologies). Offline, each electrode was inspected for artifacts or excessive noise, which was not included in the final analyses. High-gamma band (HG) signals were extracted by averaging the analytic amplitude of 8 logarithmically spaced bands from 70 to 150 Hz (Crone et al., 1998; Bouchard et al., 2013). The data were downsampled to 400 Hz (and then to 100 Hz to generate STRF residuals) and segmented into epochs with 500 ms prestimulus and 1000 ms poststimulus periods. The HG analytic amplitude was converted to z-scores relative to the prestimulus baseline for each electrode individually. Preliminary analyses in other frequency bands (δ, θ, α, and β) did not reveal significant effects, possibly due to spatial averaging and lower signal-to-noise (Jerbi et al., 2009). Future analyses specifically designed to examine phonotactic encoding in these frequencies may elucidate the relationships between low- and high-frequency activity for these types of sublexical features.

Cortical surface and electrode visualization.

Electrodes were localized on each individual brain by aligning the preoperative MRI volume with the postoperative CT scan. Using FreeSurfer (Dale et al., 1999), each subject's cortical surface was reconstructed from the anatomical T1-weighted MRI volume. Electrode locations were projected onto the individual cortical surface and verified by comparison with intraoperative photographs. Using a nonlinear transformation that matches individual cortical folding patterns to a spherical atlas, the 3D coordinates of each electrode were projected onto a common brain in the MNI coordinate space (cvs_avg35_inMNI152) (Fischl et al., 1999). Finally, each electrode was projected out onto a convex hull that approximates the interior of the dural surface (Dykstra et al., 2012), preserving each individual grid's conformity to the pial surface. This method allows electrodes from multiple patients to be visualized on a single brain, with relative locations (e.g., anterior-lateral superior temporal gyrus [STG]) conserved from the original subject's anatomy.

Acoustic controls.

Human STG neural populations are acutely sensitive to the acoustic and phonetic properties of spoken input (Chang et al., 2010; Mesgarani et al., 2014). Given that phonotactic information is hypothesized to reflect the relationships between individual speech sounds, it is important to attempt to understand how acoustic and phonotactic encoding contribute separately to neural activity. This is particularly important given that speech is not simply the concatenation of individual phonemes but is produced through an overlapping sequence of multiple articulatory gestures and related acoustic features. This phenomenon, known as coarticulation (Hardcastle and Hewlett, 1999), provides extemporaneous cues to the identity of the phonemes being heard, in some cases to a greater extent than the transition probabilities between those phonemes (McQueen, 1998; Johnson and Jusczyk, 2001; Newman et al., 2011). To be able to examine phonotactic encoding separately from both general acoustic tuning properties of electrodes and these finer-scale nonlinear acoustic properties, we performed several control analyses using a series of acoustic models (Fig. 2).

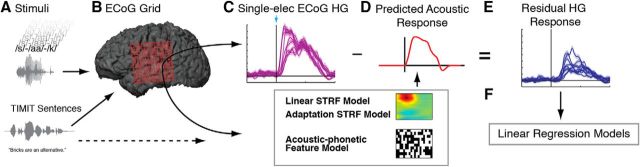
Figure 2.

Procedure for obtaining residual portion of HG cortical response after acoustic controls. A, CVC stimuli varying on phonotactic probability measures are presented aurally to each subject. In a separate experiment, the same subjects hear sentences from the TIMIT database, used to estimate single-electrode spectrotemporal receptive fields (STRFs). B, ECoG is recorded from left hemisphere frontal, temporal, and parietal areas with a 256 electrode grid with 4 mm spacing. C, For each electrode, time-varying HG activity is calculated relative to stimulus onset (blue arrow) and is converted to z-scores relative to prestimulus baseline. D, Acoustic response (red line) is predicted for both the linear and adaptation spectrotemporal models by convolving the stimulus spectrogram with the STRF for each electrode. The acoustic–phonetic feature model controls for fine-scale acoustics by representing each stimulus as a binary matrix of phonetic features. E, Acoustic model predicted responses are subtracted from recorded HG signal on each electrode to isolate the portion of the signal not explained by the spectrotemporal model. F, These residuals are submitted to linear regression models to determine the effects of phonotactic probability independent of acoustic effects explained by each control.

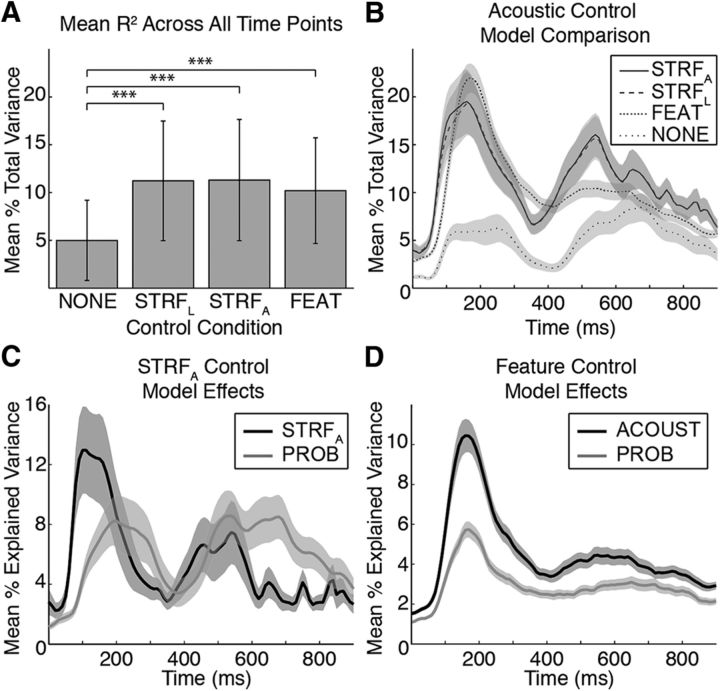
Figure 3 compares the amount of variance explained by each of these models. First, we examined phonotactic encoding with no acoustic control (NONE). Across all time points, this model accounted for a mean of ∼5% of the variance (Fig. 3A) and showed a similar time course as the other models, albeit with overall lower R² values (Fig. 3B, sparse dotted line). Although still showing significant phonotactic effects (p < 0.05, corrected), the model with no acoustic control accounted for less variance than each of the other three models (p < 10⁻⁵), and critically, accounted for less explained variance than phonotactic features when they were controlled for acoustics (p < 0.009). This suggests that phonotactic and acoustic features described by these controls contribute nonoverlapping information.

Figure 3.

Controls for acoustic selectivity and dynamic coarticulation. To examine the encoding of phonotactic statistics having controlled for a given electrode's spectrotemporal tuning or phonetic feature preferences, we used a variety of acoustic models. We compared the encoding of P_fwd and P_bkw transition probabilities with no acoustic control (NONE), after removing STRF_L, after removing the effects of an STRF that accounts for neuronal adaptation through synaptic depression (David and Shamma, 2013) (STRF_A), and through a phonetic feature encoding model (FEAT) that explains acoustic selectivity as a linear combination of phonetic features, such as fricatives, plosives, high-back vowels, etc. A, Across all time points and significant electrodes in each model, the STRF_L, STRF_A, and FEAT models explained more of the total variance in the neural signal than the NONE model (p < 10⁻⁵) but did not differ significantly from each other (p > 0.3). B, At each time point, the percentage of total variance in the neural signal explained by each acoustic model plus P_fwd and P_bkw transition probabilities showed similar time courses for all four controls. The NONE model (sparse dotted line) had lower R² values compared with the other three models, except well after acoustic offset (∼650 ms). The two STRF models had nearly identical time courses (solid and dashed lines), with the STRF_A model performing slightly better on average early in the word. The FEAT model (dense dotted line) showed a similar time course, but with a less pronounced peak around word offset (∼500 ms). C, For the STRF_A model, we compared the percentage of explained variance for the acoustic versus phonotactic probability (PROB) features and found nearly identical dynamics as in the STRF_L model (Fig. 8B). D, Acoustic and probability encoding in the FEAT model showed similar dynamics as the two STRF models, although with a less pronounced lag between acoustic and phonotactic features. In all four models, P_fwd and P_bkw explain a significant amount of the neural data, suggesting that, when both gross and fine-scale acoustics (e.g., coarticulation) are controlled, phonotactic probability still shows significant modulatory effects on the neural response.

The second control analysis used the linear STRF (STRF_L), calculated for each electrode based on responses to the TIMIT stimuli according to previously described procedures (Theunissen et al., 2001; Mesgarani and Chang, 2012). Electrodes with relatively strong STRF_L correlations (r > 0.1) were selected to generate residual responses on the phonotactic task by subtracting the linear STRF prediction from the HG response to each CVC stimulus (Fig. 2). Varying this threshold did not qualitatively change the results, except for very weak or negative correlations, which introduced artifacts into the residual responses. For the analyses comparing the time courses of STRF_L and phonotactic effects, we calculated the moment-by-moment correlation between the predicted and actual responses on the phonotactic task, having removed the phonotactic effects from the STRF_L model, and the STRF_L effects from the phonotactic model. This control (STRF R² + phonotactic R²) accounted for a mean of ∼11% of the variance across all time points (Fig. 3A), with peaks at ∼200 and 550 ms (Fig. 3B, dashed line).

It is possible that the linear STRF does not fully capture the spectrotemporally dependent context effects (Machens et al., 2004; Ahrens et al., 2008; Sadagopan and Wang, 2009; David and Shamma, 2013) in acoustic responses that might confound analyses of phonotactic transition probabilities. To test this, we applied an input nonlinearity to the STRF calculation, which models the neural response taking into account a time delay, τ, and magnitude, v, of synaptic depression (Ahrens et al., 2008; David and Shamma, 2013). Each Mel-frequency spectral band in the stimulus was filtered through a series of functions that varied τ and v, and then the linear STRF was estimated for the reverse correlation between each depression spectrogram and the neural response. Values of τ and v that provided the strongest correlation between the predicted and actual responses were selected for each electrode, and the optimal adaptation STRF (STRF_A) was removed from the neural response to examine the residual effects of phonotactics, as in the linear model. The STRF_A models the effects of synaptic depression to understand how the cumulative spectrotemporal input influences activity over time (David and Shamma, 2013). Phonological perception may be heavily influenced by neural adaptation mechanisms (Steinschneider and Fishman, 2011), and the fine-scale dynamics of coarticulatory acoustics may be encoded in such a manner. This is because coarticulation is the outcome of a dynamic and overlapping process of phonetic feature sequencing, where the acoustics of a given speech sound are directly influenced by neighboring speech sounds.

For individual electrodes, the optimal combination of adaptation parameters resulted in higher R² values for predicting neural activity from stimulus acoustics compared with the STRF_L model (∼1%-5% increase). However, across electrodes and time points, the STRF_A model (STRF_A R² + phonotactic R²) did not perform differently compared with other acoustic controls (mean = ∼11%, p > 0.3; Fig. 3A). The time course of the total variance explained by the STRF_A model (Fig. 3B, solid line) was nearly identical to the STRF_L model, and the individual contributions of acoustic and probability effects had the same dynamics as in the linear model (compare Fig. 3C with Fig. 8B).

Figure 8.

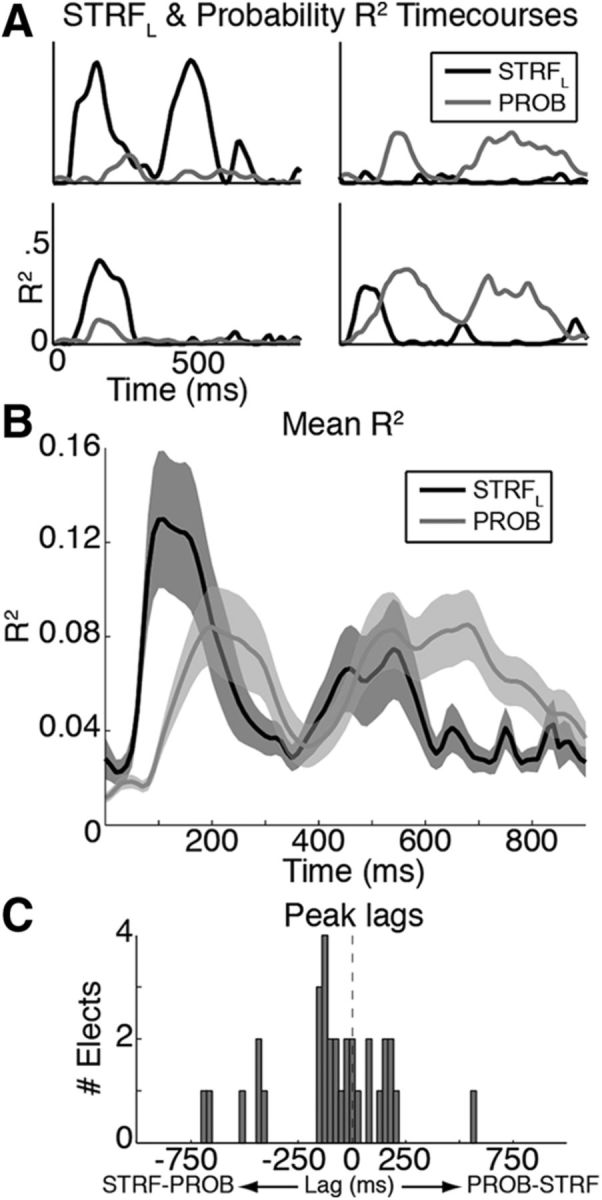
Relative timing of acoustic (STRF_L) and phonotactic (PROB) selectivity in superior temporal cortex. A, Time courses of percentage variance explained (R²) in neural responses by STRF_L (black lines) and PROB (gray lines) effects in four representative electrodes. Effects vary from responses predominantly driven by acoustics (top left) to those predominantly driven by phonotactics (top right). Some sites show near-simultaneous effects (bottom left), whereas others show lagged effects (bottom right). B, Mean (± SEM) R² time courses across all significant electrodes show that STRF_L effects generally precede PROB effects and persist beyond acoustic offset (∼491 ms). C, Histogram of temporal lags to peak cross-correlation between STRF_L and PROB R² time courses, showing modal peak lag of ∼120 ms, with STRF_L generally preceding PROB effects.

Because no model perfectly captures the acoustic sensitivities of individual electrodes, we used a fourth control that examines acoustic encoding in a different and complementary manner. Rather than modeling acoustics based on spectrotemporal features derived from a large spoken corpus, this control models acoustic sensitivity using a linear model based on acoustic–phonetic features (Mesgarani et al., 2014). Each CVC stimulus was parameterized as a binary vector of consonant features (“plosive,” “fricative,” “nasal,” “velar,” “alveolar,” and “voiced”) and vowel features (“tongue frontness,” and “tongue height”). Because of linear dependence between features, the matrix of n stimuli × p features was reduced in dimensionality using principal components analysis. The first k PCs, accounting for ∼96% of the variance, were used to describe the set of acoustic features. The two phonotactic features, P_fwd and P_bkw, were appended to the reduced feature matrix, and thus fit simultaneously with the acoustics. To obtain the percentage of the explained variance attributed to each feature set (acoustics vs phonotactics), the strength of the linear weights was used as a relative measure across features as follows:

Where k is either the number of acoustic or phonotactic features, β_i is the linear weight associated with each feature, and R² is the total variance explained by the full model. This model provides a means for capturing the coarticulatory dynamics of the sounds through the encoding of combinations of phonetic features of the sounds in the triphone (e.g., fricative consonant → high-front vowel → plosive consonant; /s-iy-k/). For example, whereas the steady-state portion of the vowel can be accounted for primarily through the encoding of vocalic place features, its transition from the first consonant is a dynamic combination of those features with the consonantal place of articulation features.

The FEAT model (phonetic features R² + phonotactic features R²) accounted for a mean of ∼10% of the variance in the neural response over all time points, which was not significantly different from the two STRF models (p > 0.3; Fig. 3A). Additionally, the time course of the total variance explained by the FEAT model was similar to the STRF models, with slightly higher R² values early in the word, and lower R² values around word offset (Fig. 3B, dense dotted line). The relative explained variance of acoustic and phonotactic features was similar to the STRF models; however, the lag between the two feature sets was less clear, particularly for the early peak (Fig. 3D).

We did not find evidence from any of these control analyses that the phonotactic effects we observed in lateral temporal lobe electrodes could be explained by acoustic sensitivity. Furthermore, despite controlling for acoustics in different ways, the residual phonotactic effects did not differ across acoustic control models. Therefore, because of its widespread use and relative simplicity, we used the linear STRF as the primary acoustic control in all subsequent analyses.

Linear phonotactic model.

Preliminary analyses revealed that phonotactic effects were apparent only in the temporal lobe, and not on electrodes over frontal or parietal cortex. To reduce the number of statistically dependent comparisons, we restricted the electrodes to those on the temporal lobe, below the Sylvian fissure (125–142 electrodes per subject). The residual nonacoustic HG response to all CVC stimuli was regressed against the transition probability measures at each time point, generating time courses of the linear weights (β-coefficients) for each condition (e.g., P_fwd and P_bkw):

where HG on the ith electrode at the jth time point is equal to the best least-squares estimate of the sum of the forward (P_fwd) and backward (P_bkw) probabilities. We also calculated model statistics, including R² and p values (significance was determined based on a Bonferroni corrected α < 0.05, unless described otherwise; the correction was done across electrodes and time points for an effective p < 10⁻⁶). The transition probabilities were either the lexical frequency controlled or uncontrolled values described above.

k-means clustering analysis.

To determine whether the different types of transition probability correlation effects (e.g., negative, positive, early, late) indicated distinct categories of responses, we submitted the P_fwd and P_bkw β-coefficient time courses for each electrode to k-means clustering analysis. Because we were interested in the separability of full time courses, rather than individual data points, we minimized distance-to-centroid values using the point-by-point sample correlation in MATLAB's kmeans function. Visual examination of peak correlation effects indicated that k = 3 clusters were appropriate for this analysis.

Effects of lexicality.

To examine lexical effects at the single-electrode level, we constructed a linear model that included lexicality (real vs pseudoword) and its interactions with frequency-controlled P_fwd and P_bkw as follows:

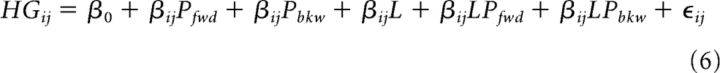where L is a binary indication of lexical status.

For the across-electrode population decoding analysis, we first used principal component analysis on the n = 38 electrodes × k = 26 × 91 data points (all time points for each token concatenated) to find optimal weighted combinations of the 38 significant electrodes, and then used the top 25 PCs, which accounted for ∼94% of the variance. To further reduce the dimensionality of the predictors, we took a random subsampling approach, which was necessary to make the regression matrices well formed. It is possible that the effect of lexicality is present in the data but is a relatively small modulator of STG responses compared with acoustics and phonotactics. Because PCs are ordered according to decreasing explained variance, random subsets of 15 of the top 25 PCs were drawn (with replacement). This random subset of PCs was entered into a ridge regression (L2-regularized linear regression) model for each time point. The model separately estimated P_fwd and P_bkw probabilities for real and pseudowords as optimal linear combinations of the randomly selected PCs. We used leave-one-out cross-validation on each of the 26 tokens to measure model performance. The whole procedure was repeated 200 times with different random subsets of 15 PCs, and the optimal subset was defined as minimizing the model R² during a baseline (−200 to 100 ms) and maximizing the peak R² for the rest of the trial (100–900 ms). The optimal time courses were averaged into 100 ms bins for plotting clarity. R² values for this optimal set were calculated 15 times with a resampling (with replacement) procedure, and two-sample t tests (with Bonferroni correction) were performed on each time bin between real and pseudowords for P_fwd and P_bkw conditions.

Results

We examined the encoding of two distinct types of phonotactic information. Figure 1A shows two examples of CV sequences in English, /k/-/uw/ and /k/-/iy/. In English, both sequences are possible; however, the probability of each vowel following the consonant is different, as indicated by the thickness of the arrows connecting the phonemes. Figure 1A (left) shows the forward probability of the consonant transitioning to the vowel (P_fwd). P_fwd quantifies the probability of upcoming phonemes given the present phoneme [e.g., P(/uw/|/k/) > P(/iy/|/k/)]. Figure 1A (right) shows the same sequence, but with the transitions reflecting the backward probability of the vowel transitioning from the consonant (P_bkw). P_bkw quantifies the probability of preceding phonemes given the present phoneme [e.g., P(/k/|/iy/) > P(/k/|/uw/)]. Both transition probability measures represent the English-specific statistics of how often certain sounds co-occur, and in which order (see Materials and Methods). As this example illustrates, P_fwd and P_bkw can have different values even for the same phoneme sequence, which allows us to disambiguate encoding of one from the other. Indeed, for 931 biphones that occur in a naturally spoken English corpus (Garofolo et al., 1993), while P_fwd and P_bkw are significantly correlated (r = 0.42, p < 10⁻¹⁰), only ∼16% of the variability in one can be predicted from the other. Although most previous investigations of phonotactics have focused on P_fwd transition probabilities, it has been suggested in multiple domains that P_bkw is also a useful statistical cue for processing sequences and that it provides information not contained in the P_fwd distributions (Perruchet and Desaulty, 2008; Pelucchi et al., 2009; Bouchard and Brainard, 2013). Therefore, finding sensitivity to either one or both probability measures would imply encoding of fundamentally different aspects of the phonotactic structure of the language (Grossberg, 1987).

In the present study, we used a set of CVC words and pseudowords that had varying P_fwd and P_bkw transition probabilities, calculated from a large English corpus (Vaden et al., 2009). We calculated both P_fwd and P_bkw transition probabilities on both the C₁V and VC₂ transitions for all CVC stimuli in the task. Figure 1B illustrates an example of these values, showing the P_fwd and P_bkw transition probabilities for the C₁V and VC₂ transitions (thicker lines indicate higher probabilities), respectively, of all CVC combinations.

Temporal lobe neural responses are modulated by both the acoustics and sequence statistics of speech

We examined neural responses in the lateral superior temporal lobe, a well-characterized region that is known to be sensitive to the acoustics of speech. Population neural responses in STG represent aspects of the stimulus spectrogram that are important for understanding spoken input (Pasley et al., 2012), and single electrodes show sensitivity to acoustic features that give rise to phonetic contrasts (Chang et al., 2010; Mesgarani et al., 2014). We focused our analyses on stimulus-evoked neural activity in the HG frequency range (70–150 Hz; see Materials and Methods), which are known to be strongly associated with the fine-scale dynamics of speech (Crone et al., 1998; Steinschneider et al., 2011).

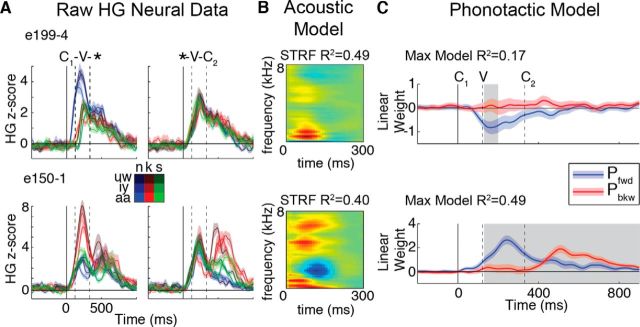
We found that responses in STG electrodes were sensitive to the specific sounds in this stimulus set. Figure 4A shows responses from two electrodes to all C₁-V-* (left plots) and *-V-C₂ (right plots) combinations. Electrode e199-4 showed a stronger response to the nasal phoneme /n/ (blue lines in left plot) when in position C₁ compared with all other phonemes (100–300 ms: Welch's t test: p < 0.0001). Similarly, electrode e150-1 showed stronger responses to the plosive /k/ than to either the nasal or fricative sounds in position C₁. To measure the auditory tuning of HG responses, we calculated the linear STRF (STRF_L) for each electrode, which reflects the combination of frequencies over time that are most strongly correlated with the activity on that electrode (Theunissen et al., 2001). The STRF for e199-4 showed strong sensitivity to lower frequencies that are typically associated with nasal phonemes, whereas electrode e150-1 showed a pattern that was consistent with the short burst associated with unvoiced plosive phonemes (brief low- and high-frequency increases in power, followed by a mid-range decrease), including the /k/ phoneme in the present task (Fig. 4B).

Figure 4.

Phoneme selectivity and modulatory effects of phonotactics on cortical responses. A, Mean (± SEM) HG cortical responses to all CVC combinations in two example STG electrodes. Each electrode shows preferential responses to specific speech sounds (see color grid); however, contextual effects are apparent (e.g., e199-4 is most active when /n/ is the first phoneme). Dashed vertical lines indicate average V and C₂ phoneme onsets. B, Linear STRFs, modeling each electrode's preferred acoustic frequencies, demonstrate that selectivity is driven by phoneme acoustics. C, P_fwd and P_bkw transition probabilities modulate neural activity not explained by the linear STRF in electrodes from A, B. Time courses of linear weights (red and blue lines ±95% CI) show significant effects during CV transition, vowel, and word offset time periods (p < 0.05; gray shading).

This sensitivity to specific phonemes does not fully describe the way in which speech is produced or heard. In particular, speech is not simply the concatenation of invariant acoustic units, but rather the acoustics of adjacent phonemes blended with each other in both the forward and backward directions, resulting in smooth trajectories through the speech sequence (coarticulation) (Hardcastle and Hewlett, 1999). We observed that the neural responses to these sounds differed depending on the phoneme sequence in which they occurred. The preference for /n/ on e199-4 was not apparent when the nasal occurred in position C₂, regardless of the sound that preceded it (400–600 ms: Welch's t test: p = 0.80) (Fig. 4A, right plot), and the response to /k/ at e150-1 was influenced by either the upcoming or preceding vowel (gradient from dark to light red). As described in Materials and Methods, we performed several control analyses to account for coarticulatory and other linear and nonlinear acoustic differences between stimuli. We found that, with and without these controls, we obtained robust and consistent sequence statistics effects that could not be explained by acoustic or coarticulatory features. Given a lack of differences between acoustic controls, we used the most straightforward and widely used model (the linear STRF) as our primary control in subsequent analyses.

To examine the encoding of transition probabilities, we removed the portion of the HG signal explained by the linear STRF, leaving the residual activity that was not explained by the control model (i.e., responses in Fig. 4A minus predicted responses from STRFs in Fig. 4B; see Fig. 2 and Materials and Methods). For each electrode and moment in time (10 ms), we used regression to fit a linear model to predict the residual activity as an optimal weighted combination of forward (P_fwd) and backward (P_bkw) probabilities. Figure 4C shows that both probability measures modulated HG activity in a dynamic fashion. For example, from ∼100 to 200 ms, higher P_fwd values evoked smaller responses in e199-4 (linear weights < 0, negative modulation). In contrast, e150-1 showed positive modulation (linear weights > 0) with P_fwd from ∼200 to 400 ms and with P_bkw from ∼400 to 600 ms. These results suggest that STG neural responses are modulated by the phonotactics of speech beyond auditory sensitivities captured by the acoustic controls.

Temporal lobe encoding of forward and backward transition probabilities

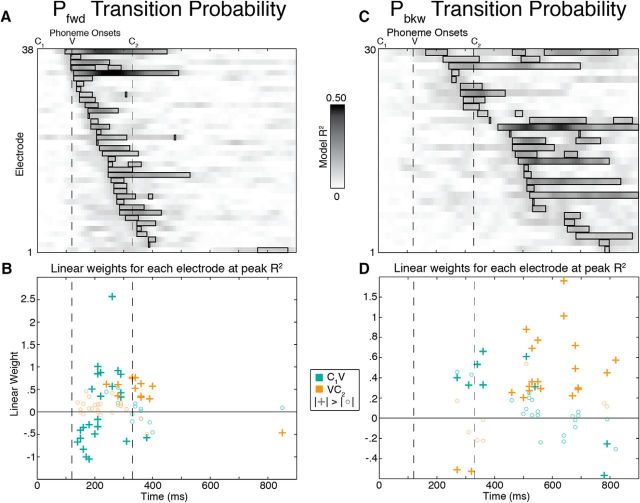
Across all four participants, HG activity at 32 of 531 electrodes showed significant probability effects (p < 0.05, corrected for multiple comparisons; actual threshold of p < 10⁻⁶), and the optimal linear combination of P_fwd and P_bkw explained up to 49% of the residual response variability after accounting for the linear effects of stimulus acoustics as modeled by the STRF. All significant electrodes in these analyses were confined to middle and posterior lateral STG, and posterior middle temporal gyrus; however, there was no apparent spatial organization for P_fwd vs P_bkw in that region (Fig. 5A). Therefore, the encoding of speech sequence statistics takes place in a spatially distributed network.

Figure 5.

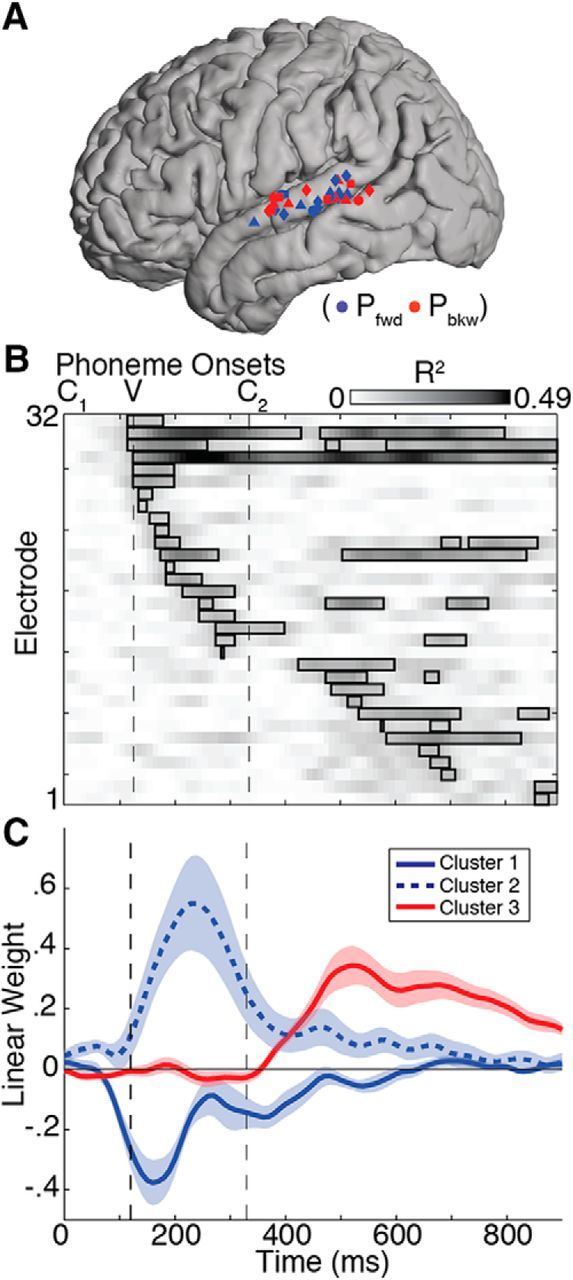
Phonotactic effects for all temporal lobe electrodes. A, Significant electrodes in these analyses were primarily on STG with no apparent spatial organization along either the posterior–anterior or dorsal–ventral axes. Electrodes are colored based on whether P_fwd (blue) or P_bkw (red) showed the greatest contribution to the linear regression model. Shapes represent the four different subjects. B, Percentage explained variance (R²) over time for each of the 32 significant electrodes across all subjects. Black boxes represent significant time points at corrected p < 0.05, and electrodes are sorted according to significance onset time. C, P_fwd and P_bkw linear regression weight time courses (± SEM) for each electrode were classified using k-means clustering with k = 3. The first cluster shows a negative peak at ∼170 ms, followed by cluster 2 with a positive peak at ∼240 ms. Cluster 3 shows a positive peak around stimulus offset (∼530 ms). For main effects of P_fwd and P_bkw across both phoneme transitions, see Figure 6.

The effect of probability on temporal lobe responses was also distributed throughout the stimulus duration and differed across electrodes, with some sites showing modulation around the C₁V transition, some during the vowel, some around and beyond word offset, and some both early and late in the word (Fig. 5B). At time points of maximal explained variance (R²), visual inspection of peak R² time points revealed that these electrodes could be categorized into three distinct effects: a negative modulation of neural responses by P_fwd, a positive modulation by P_fwd, and a positive modulation by P_bkw. To examine the distinctiveness of these patterns, we used k-means clustering on the time courses of regression weights associated with P_fwd and P_bkw (e.g., Fig. 4C) for all 32 electrodes and found that they were indeed separable (Fig. 5C). These effects were temporally distinct, with the negative P_fwd peak occurring on average 75 ms earlier than the positive P_fwd peak (independent-samples t test: p < 0.005), which in turn occurred earlier than the positive modulation by P_bkw. Therefore, negative effects precede positive effects.

The analyses above focused on position-specific effects of P_fwd and P_bkw transition probabilities; however, it is likely the case that both values are encoded for both phoneme transitions. We further examined the effects of P_fwd and P_bkw transition probabilities independent of their positions in the word. We constructed separate linear models for each probability measure calculated on both the C₁V and VC₂ transitions (Fig. 6). Across both phoneme transitions, P_fwd peak effects (Fig. 6A,B) occurred significantly earlier than P_bkw effects (Fig. 6C,D) (independent-samples t test: p < 10⁻¹⁰), illustrating that these two probability measures exert different influences on neural processing. Furthermore, we observed that negative modulations based on P_fwd were unique to the C₁V transition (Fig. 6B), confirming that negative effects precede positive effects.

Figure 6.

Linear regression for P_fwd and P_bkw separately on both C₁V and VC₂ transitions. Separate linear models were constructed for each probability measure calculated on both transitions. A, R² time courses for the P_fwd model show effects that begin around the C₁V transition and mostly end by the VC₂ transition. B, In the P_fwd model, peak effects from the C₁V transition are negative at the earliest time points, followed by a positive effect (green crosses). The VC₂ transition effects are positive (orange crosses) and occur significantly later than both the negative and positive C₁V effects (independent-samples t test: p < 10⁻⁴). C, R² time courses for the P_bkw model show effects that begin toward the end of the vowel and persist beyond word offset. D, In the P_bkw model, the majority of effects are positive, and there is a slight trend for C₁V effects to precede C₂V effects (independent-samples t test: p = 0.1). Across both phoneme transitions, P_fwd peak effects occur significantly earlier than P_bkw effects (independent-samples t test: p < 10⁻¹⁰). Because P_fwd effects precede P_bkw effects and because negative modulation is unique to the first transition, we chose to focus most of our other analyses on P_fwd in the C₁V transition and P_bkw in the VC₂ transition.

To examine the generality of the main findings, we performed the same linear regression analysis on data obtained while the participants listened passively to naturally spoken sentences from the TIMIT database. Like with the controlled CVC stimuli, we observed robust phonotactic effects confined mostly to STG in 118 electrodes (corrected p < 0.05; Fig. 7A). The time course of P_fwd and P_bkw modulation was similar to that in the CVC task, with negative P_fwd modulation peaking around the phoneme transition, followed by positive P_fwd modulation (Fig. 7B). P_bkw modulation showed smaller, but simultaneous, effects with P_fwd. The sentential context of these data may contribute to the fact that the effects begin well before the acoustic phoneme transition (t = 0), although similar effects were observed in the CVC task, where higher-level linguistic information was not available. These results demonstrate that, even in the presence of a richer and much more variable set of acoustic and linguistic cues (McQueen, 1998; Johnson and Jusczyk, 2001; Newman et al., 2011), sublexical transition probabilities significantly modulate neural responses to speech.

Figure 7.

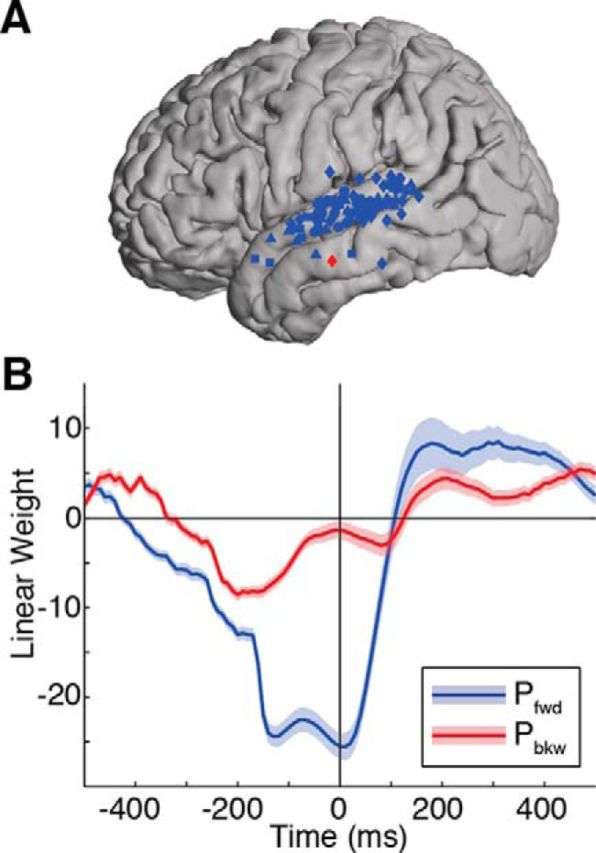
Phonotactic effects during passive listening to sentences. A, A total of 118 electrodes showed significant (corrected p < 0.05) effects, mostly confined to STG. Most electrodes showed peak effects for P_fwd (blue dots) while also showing smaller P_bkw effects (red dots). Shapes represent the four different subjects. B, The time course of linear weights from the regression model shows a strong correspondence with the same analysis in the CVC task. Around the time of the phoneme transition (t = 0), there is a negative peak for P_fwd, followed by a positive peak for P_fwd. P_bkw effects were also present in continuous speech, although they were weaker and largely simultaneous with P_fwd effects.

Together, these results suggest that lateral temporal lobe responses to speech sequences are modulated by the local transition probabilities of the language. The temporally specific pattern of P_fwd and P_bkw effects suggests that learned phoneme sequence statistics play a role in real-time speech processing, possibly providing a link between lower-level acoustic and higher-order linguistic representations.

Dynamics of acoustic and transition probability encoding

As shown in Figure 4, the responses of many of the STG electrodes were sensitive to both the acoustics of phonemes and the transition probabilities between phonemes. To understand the relationship between acoustic and phonotactic encoding in STG, we compared the amount of explained variability (R²) in the STRF_L model (after removing the effects of phonotactics; Fig. 8A, black lines) versus the phonotactic model (PROB, after removing the effects of acoustics explained by the linear STRF; Fig. 8A, gray lines) (see Materials and Methods). The four representative electrodes in Figure 8A show that effects of acoustics and phonotactics could occur sequentially or near-simultaneously and that some electrodes were more sensitive to one or the other effect. For example, the top left electrode shows greater STRF_L than PROB effects, whereas the bottom right electrode shows the opposite pattern.

We found that STG dynamically encodes both the acoustics and transition probabilities of the speech stimuli. Across all electrodes, average R² values tended to be slightly higher for the STRF_L model than for the PROB model only during early times, from ∼100 to 200 ms. Then, at intermediate times during the words (∼200–500 ms), the R² values were nearly identical. Finally, probability effects persisted after the offset of the stimulus (∼500–800 ms), whereas the effects of acoustics subsided by ∼600 ms (Fig. 8B). This further suggests a separation between transition probabilities and acoustic sensitivity, as we observed phonotactic effects well after the acoustic input ceased, and after the acoustic models no longer had significant predictive power. The time course of significant R² values for the STRF_L model appeared to precede the effects for phonotactics, suggesting that phonotactic encoding lags acoustic encoding. Indeed, cross-correlation analysis between these R² time courses on each electrode revealed a modal peak lag of ∼120 ms, with acoustic encoding preceding phonotactic encoding (Fig. 8C). While the majority of electrodes (∼63%) showed peak acoustic effects earlier, the rest were either nearly simultaneous or showed probability effects first. Simultaneous effects in single electrodes may reflect modulation of acoustic responses based on context (Mesgarani and Chang, 2012), whereas lagged effects suggest that probabilities are processed at an intermediate stage between acoustics and lexical recognition (Vitevitch et al., 1999).

Lexical encoding and transition probabilities

It has been suggested that, because of their intermediacy between acoustic and word-level representations, phonotactics may be ideal for constraining the lexical possibilities consistent with incoming acoustic input (Pitt and McQueen, 1998). Indeed, the fact that phonotactic encoding tended to be lagged relative to acoustic encoding suggests that sensitivity to language-level phoneme statistics may mediate low-level acoustic and higher-level lexical representations. Therefore, we next examined how transition probability encoding relates to the transformation from local acoustic representations into abstract lexical representations of words in the superior temporal lobe.

To explore the potential for phoneme transition probabilities to mediate this transformation, we examined how transition probability modulations were affected by lexical features. Approximately half the stimuli were real words (e.g., /s-aa-k/), whereas the rest were pseudowords (e.g., /s-aa-n/), which have the same acoustic, phonetic, and syllabic structure as real English words but lack any association with lexical or semantic features. This comparison allowed us to examine whether transition probability effects differ depending on whether a word is part of the listener's lexicon. Across all temporal lobe electrodes (n = 531), we observed only two instances where average HG amplitude was different between real and pseudowords (false discovery rate-corrected p < 0.05). Thus, no general magnitude differences were found between words and pseudowords in single temporal lobe electrodes with our stimulus set, even at more anteroventral sites that models of word processing predict should show such differences (Obleser et al., 2007; Davis and Gaskell, 2009; Leaver and Rauschecker, 2010; DeWitt and Rauschecker, 2012). This may be due to the relatively short CVC stimuli used in the present task, the fact that the pseudowords (e.g., /s-aa-n/) are relatively word-like, and the spatial resolution afforded by ECoG, which may be finer than the broader patterns of differential activity elicited by these two stimulus types.

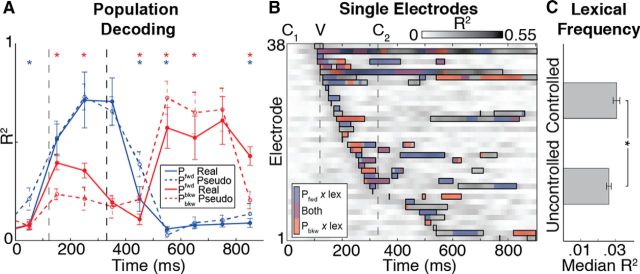
We next examined whether transition probability encoding differed depending on lexical status at the neural population level. Figure 9A shows that P_fwd (blue lines) and P_bkw (red lines) transition probabilities can be decoded from optimal linear combinations of activity across electrodes that showed significant effects of transition probability and lexicality (Fig. 9B; see Materials and Methods), demonstrating that the patterns observed in individual electrodes (e.g., Fig. 5) are also reflected in population responses. The fact that transition probability distributions can be decoded from neural activity also further supports the claim that these distributions are robustly encoded in temporal lobe neural networks. When population activity is examined separately for words (solid lines) and pseudowords (dashed lines), P_fwd and P_bkw are decoded with different accuracies throughout the word (p < 0.05, corrected), with more pronounced differences in lexical status for P_bkw during the vowel and around word offset (red lines).

Figure 9.

Transition probability and lexicality. A, Linear regression was used to predict P_fwd (blue) and P_bkw (red) from the population of recorded activity for real (solid) and pseudowords (dashed). Decoding performance was significantly different for real and pseudowords for both P_fwd and P_bkw throughout the trial. *p < 0.05 (corrected for multiple comparisons). Error bars indicate SD. B, Percentage of explained variance (R²) time courses for a linear model, including lexicality (real vs pseudowords) and its interactions with P_fwd and P_bkw. Black boxes represent full model significance at corrected p < 0.05. Colored shading represents time windows where interactions have non-0 contributions to the model (β ≠ 0, p < 0.05). C, Median R² values (±95% CI) are significantly greater for transition probabilities when lexical frequency is controlled, indicating neural population sensitivity to the frequency of whole words occurring in English.

Although we observed no general magnitude differences between real words and pseudowords for individual electrodes, the neural population results suggest that there are direct interactions between transition probabilities and lexical status. Therefore, we analyzed single-electrode HG with a linear model that included lexicality (real vs pseudo) and its interactions with P_fwd and P_bkw transition probabilities. This analysis showed significant interaction effects in multiple electrodes throughout the word (p < 0.05, corrected; Fig. 9B); however, there was no clear temporal structure. Overall, these results show that lexicality is not a feature of the stimulus that is determined in the lateral superior temporal cortex at a single time point or neural population but rather is heterogeneously distributed across both time and cortical sites as a function of phoneme transition probabilities.

We also examined another lexical variable that is known to be a major modulator of neural activity: lexical frequency (Prabhakaran et al., 2006). In the above analyses, phoneme transition probability values were controlled for the effect of lexical frequency; however, we also examined the amount of explained variance when P_fwd and P_bkw were not controlled for how often words occur in English (raw transition probabilities, as calculated in, e.g., Saffran et al., 1996). In the single-electrode phonotactic regression models (e.g., Fig. 5), controlling for lexical frequency resulted in a distribution of R² values that was significantly higher compared with when P_fwd and P_bkw were not controlled for lexical frequency (Wilcoxon rank-sum test: p < 10⁻¹⁰; Fig. 9C). This demonstrates that, in addition to sublexical phonotactic statistics and lexical status, single electrodes are also sensitive to the frequency of a whole word occurring in English.

Discussion

Speech is a complex sensory stimulus that unfolds extremely rapidly, making it remarkable that listeners understand words in real-time. For speech perception, neural populations must encode the spectrotemporal features of the acoustic signal that correspond to different categories of sounds (Mesgarani et al., 2014). However, understanding discrete sounds as sequences in words requires significant temporal integration of surrounding contextual information.

We found that the lateral superior temporal lobe not only encodes the spectrotemporal and phonetic feature characteristics of speech sounds, but also dynamically encodes multiple statistics of English phoneme sequences. Remarkably, the pattern of P_fwd and P_bkw modulation was temporally specific, corresponding to relevant landmarks, such as phoneme onsets and transitions. Given that the most illustrative effects were for P_fwd and P_bkw in the C₁V and VC₂ transitions, respectively, we focused our main analyses on these combinations. Early in the word, responses were negatively modulated by P_fwd, consistent with predictive coding frameworks (Friston, 2005; Kiebel et al., 2009; Yildiz et al., 2013) that explain neural activity in terms of minimizing the difference between bottom-up sensory input and top-down predictions of that input (prediction error). In this specific context, when neural circuits encounter a phoneme that is not likely given the forward transition probability from the previous phoneme, they generate a response that is inversely proportional in magnitude to the phonotactic prediction. This negative modulation based on prediction was not observed during the VC₂ transition, suggesting that predictive strategies are most useful early in the word, when there is less information about the word's identity.

Encoding prediction error early in the word facilitates the recognition of subsequent segments in the sequence. According to precision encoding accounts, larger prediction errors increase the uncertainty of predictions, which are updated as more information arrives (Bastos et al., 2012). For example, in an oddball paradigm where a sequence of frequent stimuli is interspersed with rare deviants, large mismatch negativity responses are generated when deviants are presented. The fact that repetition of deviant stimuli extinguishes the mismatch negativity suggests that predictability is directly dependent on the local statistics of the stimulus context (Garrido et al., 2009) and that the recognition and encoding of stimuli in a sequence are closely related to the encoding of both prediction error and precision. The negative P_fwd modulation, followed by positive P_fwd modulation for the C₁V transition, is consistent with this framework of the recognition process through predictive coding. Unlike the oddball paradigm, however, which is designed to elicit responses to stimulus sequences that reflect relatively short time scale learning (on the order of minutes), natural languages contain statistical regularities in the sequencing of phonemes that require long-term exposure to those sequence statistics (on the order of years). The present results demonstrate that prediction error and precision encoding are used to process sensory input in the context of deeply learned implicit knowledge.

We also observed responses that suggest that the current element in a sequence is recognized in the context of the elements that preceded it (P_bkw). Enhanced responses for sequences with more likely backward transition probabilities are consistent with such a retrospective process. It has been suggested that responses that scale positively with the degree to which observations match expectations may reflect the physical structure of the underlying neural network, and may be outcomes of a Hebbian associative learning process (Hebb, 1949; Dan and Poo, 2004; Bouchard and Brainard, 2013). In the context of speech, the massive experience that humans have with the sound sequences of their own language may allow this type of mechanism to engrain phonotactics in speech processing circuits over the course of years of learning. This results in stronger associations between co-occurring phonemes, where recognition of current input based on the probability of preceding input is therefore expected to generate neural responses that increase in proportion to the degree to which sensory inputs match expectations. Here, we demonstrate that this recognition process is facilitated not only by sequential bottom-up input, but also by the learned local dependencies represented by phonotactic distributions.

These results contribute to an active debate over the role of STG in speech perception. Whereas existing models suggest that the primary role of dorsal STG is spectrotemporal analysis (Hickok and Poeppel, 2007; Obleser et al., 2007; Turkeltaub and Coslett, 2010), recent work using multivariate analyses and high-resolution recording methods have indicated a broader set of functions (Leonard and Chang, 2014). In other auditory tasks, both posterior and anterior STG population activity has been shown to encode a relatively fine-scale representation of the spectrotemporal profile of speech sounds (Pasley et al., 2012; Steinschneider, 2013; Mesgarani et al., 2014), while at the same time showing sensitivity to contextual processes, such as attention (Mesgarani and Chang, 2012), phonetic category (Formisano et al., 2008; Chang et al., 2010; Steinschneider et al., 2011), and lexical–semantic content (Travis et al., 2013). These findings suggest that cortical sensory responses at single electrodes throughout the STG (particularly in anterior–lateral regions) are strongly and dynamically context-dependent, and phonotactic modulation may represent a linguistic instantiation of this principle.

There are additional outstanding questions related to how phonotactic encoding fits into the speech perception hierarchy. Numerous studies have demonstrated a hemispheric asymmetry for higher-order speech processing, with the strongest activity evoked in the left hemisphere (Poeppel et al., 2008). Given that phonotactic encoding occurs between acoustic and lexical processing, it will be critical for future studies to examine the role of the right hemisphere, and in particular right posterior STG, in the encoding of speech sequence statistics.

It is important to note that, in the context of the current experiments, coarticulation and other nonlinear acoustic effects cannot be ruled out definitively. Other studies in both auditory (Yaron et al., 2012; Bouchard and Brainard, 2013; Tremblay et al., 2013) and visual (Yang and Shadlen, 2007) modalities have demonstrated sequence probability effects with discrete stimuli, suggesting that neural populations are sensitive to statistical structure independent of other acoustic cues. In the present study, we were specifically interested in how these effects manifest in a natural stimulus, such as speech (as opposed to pure tones, for example). Even when spoken stimuli have been used in previous studies, they have been presented as concatenated syllables, which does not allow for a direct examination of the neural processes that interpret continuous acoustic input as auditory objects, such as words. Any examination of phonotactics with speech stimuli necessarily involves coarticulation, as it is impossible to produce truly noncoarticulated stimuli at the level of single phonemes. We used a set of complementary controls to account for these acoustic cues; however, additional studies will be required to more fully characterize the nonlinearities of acoustic representations in STG. For example, auditory cortex is sensitive to the acoustic similarity of adjacent sounds, which cause both facilitation and inhibition through forward and backward masking (Brosch and Schreiner, 1997). These complex temporal dependencies may play an additional role in acoustic processing beyond the spectrotemporal tuning and phonotactic encoding demonstrated here. Ultimately, it is likely that both bottom-up coarticulatory and recurrent or top-down phonotactic information is involved in speech comprehension in complex and interactive ways. The present results are an initial description of the STG representation of fine-scale dynamics of multiple sources of information that can only be examined with spoken stimuli, providing testable hypotheses for future work.

Finally, our results provide unique insight into a fundamental problem for neural encoding: How are sensory signals abstracted into entities that have behaviorally relevant meaning? The anatomical pathways that carry signals from the peripheral sensory organs to the cortex show characteristics of hierarchical processing (Chechik et al., 2006; Kikuchi et al., 2010; Chechik and Nelken, 2012), where upstream representations are less sensitive to variability in the input. Abstraction is presumably critical for speech, where variability across speakers, accents, and environments must be overcome to access representations of words. It has been suggested previously that sublexical statistics (e.g., phonotactics) play a key role in word identification (Pitt and Samuel, 1995; Saffran et al., 1996; Vitevitch et al., 1999). Here, we showed that phonotactics and lexical status have interactive effects on STG activity throughout the course of neural processing. These results argue that lexical access is not a binary process, that it can begin well before the uniqueness point of a word (Marslen-Wilson, 1987; Pitt and Samuel, 1995), and that transition probabilities (themselves abstract features of the stimulus, as they are not physically encoded in the input) mediate acoustic and word-level representations. This is consistent with the view that distributed lexical representations (Gaskell and Marslen-Wilson, 1997) are an emergent phenomenon from multiple bottom-up and contextual sources of information (Elman, 2009). Generally speaking, neural representations of temporally specific probabilistic quantities are ideally situated to link incoming sensory signals and their intended abstract representations. Therefore, our results suggest that encoding of local contextual statistics via the coordinated effects of predictive, precision, and retrospective recognition processes may be a general principle of neural processing in high-level sensory areas.