Characterization of blood flow in the mouse dorsal spinal venous system before and after dorsal spinal vein occlusion

Abstract

The availability of transgenic strains has made the laboratory mouse a popular model for the study of healthy and diseased state spinal cord (SC). Essential to identifying physiologic and pathologic events is an understanding of the microvascular network and flow patterns of the SC. Using 2-photon excited fluorescence (2PEF) microscopy we performed in vivo measurements of blood flow in the lower thoracic portion of the mouse dorsal spinal vein (dSV) and in the first upstream branches supplying it, denoted as dorsal ascending venules (dAVs). We found that the dSV had large radiculomedullary veins (RMVs) exiting the SC, and that flow in the dSV between pairs of RMVs was bidirectional. Volumetric flow increased in each direction away from the point of bifurcation. Flow in the upstream dAVs varied with diameter in a manner consistent with a constant distal pressure source. By performing ex vivo 2PEF microscopy of fluorescent-gel perfused tissue, we created a 3-D map of the dorsal spinal vasculature. From these data, we constructed a simple model that predicted changes in the flow of upstream branches after occlusion of the dSV in different locations. Using an atraumatic model of dSV occlusion, we confirmed the predictions of this model in vivo.

Introduction

Spinal cord injury (SCI) remains one of the most debilitating neurologic diseases known, affecting an estimated 265,000 persons in the USA alone.¹ In addition to the immediate tissue disruption caused by trauma, considerable secondary injury results from vascular disruptions, including hemorrhage, ischemia, and edema.^{2, 3, 4} Besides traumatic SCI, spontaneous spinal cord (SC) infarction^{5, 6, 7, 8, 9, 10} is a clinically observed ischemic condition leading to paralysis. While the majority of these thromboses occur in arteries, venous obstructions have also been observed.^{11, 12} A complete understanding of the ischemic susceptibility of the SC to SCI and thrombosis requires a detailed understanding of the SC microvascular anatomy and physiology.

To this end, previous studies have used the corrosion cast techniques to study the anatomy of the SC vasculature in humans,^{13, 14} rabbits,¹⁵ cats,¹⁶ pigs,^{17, 18} and rats.^{19, 20, 21} The increasing availability of transgenic mouse strains makes the mouse spinal vasculature of particular interest for preclinical SC studies, yet the vascular architecture of the mouse SC remains much less explored.

In addition to vascular architecture, spinal cord blood flow (SCBF) has been measured directly^{22, 23, 24, 25, 26, 27} in healthy and diseased states. In all but one case,²⁵ these studies determined blood flow as an average over some region and did not consider flow at the level of individual vessels. Exceptionally, Miyazaki et al²⁵ have measured blood flow and diameters of individual capillaries in the anterior horn of the lumbar SC in wild-type mouse and a transgenic mouse model of familial amyotrophic lateral sclerosis. Nevertheless, SCBF at the microvascular scale remains largely unexplored.

The dorsal spinal vein (dSV) is the largest and most superficial vein in the mouse dorsal SC. Unlike the deeper-lying arterial counterparts that are obscured by intensely scattering myelin, the dSV is particularly well suited to in vivo studies utilizing optical microscopy. Its location also results in the dSV being injured in nearly every preclinical model of SCI, making an understanding of its blood flow patterns and their alterations after occlusion essential to understanding the secondary injury phase of SCI. Moreover, the human ortholog of this vein—the median posterior spinal vein—is similarly the most prominent vein in the human posterior SC²⁸ and its disruption is nearly certain in any SCI cases resulting in posterior compression of the SC. The pathologic consequence of such disruption will depend greatly on whether there exists redundancy in this flow network as there does in the surface arterioles²⁹ or collaterally-joined surface venules³⁰ of the cortex.

In this paper, we quantitatively analyzed the mouse dorsal spinal venous geometry and topology using intraluminal vessel fills. The focus of our study was the dSV and its primary upstream vessels that we have termed dorsal ascending venules (dAVs). Using 2-photon excited fluorescence (2PEF) microscopy, we performed in vivo SCBF measurements in both the dSV and the dAVs. We characterized SCBF in these vessels in relation to pairs of large radiculomedullary veins (RMVs) that drain blood from the dSV and out of the SC. On the basis of topological analysis and blood flow measurements, we constructed a simple SCBF model that both accounted for our flow observations and predicted the redistribution of blood flow after dSV occlusion for clots at different locations relative to the RMVs. Finally, we evaluated these predictions experimentally using chemically-induced clotting of the dSV.

Materials and methods

Ex Vivo Intraluminal Blood Vessel Fills

The care and experimental manipulation of all mice in this paper followed the ‘Guide for the Care and Use of Laboratory Animals' provided by the National Research Council of the National Academies and was approved by the Cornell University Institutional Animal Care and Use Committee. Mice were deeply anesthetized using sodium pentobarbital. After the absence of reflex in response to foot or tail pinch stimulus, animals were perfused transcardially with phosphate-buffered saline solution (PBS; pH=7.4; Sigma-Aldrich, St Louis, MO, USA) before perfusion with 4% W/V paraformaldehyde (Thermo-Fischer Scientific, Waltham, MA, USA) in PBS. In mice where ex vivo fluorescence imaging of blood vessels was performed, these solutions were warmed to at least 37.5°C before perfusion and followed by perfusion with 1% low-melting point agarose (Sigma-Aldrich) mixed with 5% W/V lysine fixable Texas Red dextran (MW=70,000; Invitrogen, Carlsbad, CA, USA). Mice were then rapidly cooled using crushed ice until the agarose had set. In experiments to determine gross dSV architecture, we injected 2 mL India ink after paraformaldehyde perfusion and SCs were imaged in situ immediately using white light reflection.

Tissue Clearing

We followed the clearing procedure described by Dodt et al³¹ closely. All SCs perfused with lysine-fixable-Texas-Red-dextran-labeled agarose were extracted on ice and immediately placed in 4% paraformaldehyde fixative for 1 day at 4°C. We then dissected away the SCs from vertebrae T9 through T13 and placed them in fixative again for 1 h at room temperature (20°C to 25°C). We rinsed all tissues two times in PBS, and stored them in PBS for 1 day at 4°C. Spinal cords were dehydrated by successive incubation in ethanol (30%, 50%, 70%, 80%, 96%, and twice in 100% for 1 day each) at room temperature. The tissues were then rinsed and left in 95% hexane (Sigma-Aldrich) for 1 hour. Tissues were finally transferred to a solution of 1:2 benzyl alcohol/benzlbenzoate, which was the final clearing solution in which the tissue was stored and imaged. We observed that a 4-day incubation in this final solution allowed for imaging depths over 700 μm below the dorsal surface of the SC using 2PEF microscopy while maintaining robust vessel labeling. Shorter incubation periods did not result in sufficient clearing and longer periods led to dye leaching from the vessel lumens. During imaging, samples were housed in an imaging chamber filled with the 1:2 benzylalcohol/benzybenzoate clearing solution. Since the clearing solution dissolved polystyrene petri-dishes, we constructed a custom-made imaging chamber. The imaging chamber consisted of a glass-bottom petri dish edged with Kwik-Sil Elastomer (World Precision Instruments, Sarasota, FL, USA) and topped with a coverslide. This construction also prevented the spinal cord from moving during imaging. In one animal, we used Imaris (Bitplane, Zurich, Switzerland) software to create a 3D reconstruction of the major blood vessels in a section of tissue, ~2 mm × 2 mm × 0.85 mm, where depth is measured from the dorsal aspect of the SC. We mapped the dorsolateral arteries (dLAs) bilaterally and the dSV, as well as their primary and major secondary downstream and upstream connections, respectively.

Surgical Procedure for In Vivo Imaging

Mice of a C57B6/J background were anesthetized using a 5% isofluorane in 100% oxygen mixture, which was reduced to 1% to 2% after induction of anesthesia. Mice received 50 μg glycopyrrolate per 100-g mouse intramuscularly at the start of surgery and 0.1 mL of 5% W/V glucose hourly throughout both surgery and imaging. Surgery was performed on a custom table, and core temperature was maintained at 37.5°C using a feedback-controlled heating pad. Skin and muscles were retracted and a double dorsal laminectomy was performed between T10 and T13 using spring scissors. In clotting experiments, a small section of the dura was removed to facilitate chemically-induced clot formation. Warm 1% agarose (Sigma-Aldrich) solution was applied to the spinal cord and a #0 coverslip (Electron Microscopy Sciences, Hatfield, PA, USA) was laid on top. For animals in which clots were induced, the coverslip was removed and a wedge of the flat-profile agarose over the target clot site was removed using a scalpel blade to facilitate access to the dSV. Gel foam (Pharmacia & Upjohn, Kalamazoo, MA, USA) and 0.9% W/V saline were applied over the exposed spinal cord to maintain irrigation, and the coverslip was replaced before imaging.

Two-Photon Excited Fluorescence Microscopy

After surgery, mice were transported to the microscopy laboratory where we performed 2PEF imaging on a custom microscope. The microscope was sourced by a 1,043-nm wavelength, 300-fs pulse duration, 1-MHz repetition rate fiber laser source (FCPA μJewel D-400; IMRA America, Ann Arbor, MI, USA). Mice were injected retroorbitally with 50 μL of 2.5% W/V Texas Red dextran in saline (MW=70,000 kDa; Invitrogen) to label the blood plasma. A 645/65 nm (center wavelength/bandwidth) emission filter (Chroma Technology, Bellows Falls, VT, USA) was used to isolate fluorescence from the plasma. A low numerical aperture (NA) objective (NA=0.28; Olympus America, Center Valley, PA, USA) was used to take a large (~3 mm) field of view image of the vasculature. To measure blood vessel diameters and flow speeds, we used a large NA objective (NA=1.0; Carl Zeiss Microscopy, Thornwood, NY, USA). After focusing on the vessel of interest in the xy plane, the animal was translated axially in the z direction in increments of 1 to 2 μm while simultaneously recording images. Average vessel diameter was determined using custom Matlab (Mathworks, Inc., Natick, MA, USA) software, in which vessel boundaries were manually traced from the maximum intensity projection of the image sequences. To measure flow speeds, we used the 2PEF line-scan method described previously.³² The center of the vessel was estimated visually, and after centering the vessel in the xy plane, along the z axis, and rotating the scan pattern such that the vessel was oriented along the x axis, a single line was repeatedly raster-scanned over time. Since red blood cells (RBCs) exclude the fluorescently labeled plasma, they appear as dark regions against a bright background on the scan. Scans are repeated at constant intervals, generating a 2-D image with time as the y axis. The slope of these lines was then calculated using a radon-transform algorithm,³³ giving the average speed in the vessel center. The volumetric flow, Q, was determined according to Poiseuille flow as:

where r is the vessel radius and v_max is the RBC speed at the center of the vessel. This flow profile was assumed on the basis that venules in the mouse neocortex of comparable size to those we measured follow this trend.³³

The RBC speed at the center of the dSV was too fast to be accurately measured at the center of the vessel. We therefore measured blood flow 30 μm from the edge of the dSV lumen, and calculated v_max assuming laminar flow:

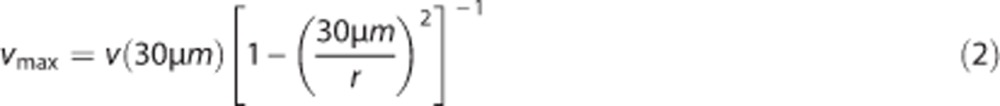Ex vivo imaging was performed using the same objectives. We found that we could obtain imaging depths between 550 and 700 μm from the posterior surface of the intact spinal cord using the clearing procedure described.

Clot Formation

Due to the large diameter of the dSV, complete occlusion of the dSV was not possible using the technique of nonlinear laser ablation of the vascular endothelium that we have previously employed for vessel occlusion studies.³⁴ As such, we adapted a ferric chloride (FeCl₃)-mediated thrombosis technique³⁵ to produce a complete point occlusion of the dSV. In experiments where a clot was induced, animals were transferred from the imaging facility to the operating room after initial imaging of vascular structure and blood flow speed measurements. Briefly, the coverslip was removed and dry gel foam and cotton swabs were used to reduce fluid over the dSV locally. A glass micropipette filled with 5% W/V FeCl₃ (Sigma-Aldrich) was touched to the exposed dSV, depositing a small droplet by capillary action. A clot was seen to form within 10 to 20 minutes of exposure by cessation of blood flow at the point of application (i.e., a ‘white clot'). The area was subsequently flooded with saline to remove and dilute the FeCl₃ to avoid undesired clotting of other vessels. Control animals received saline treatment in place of FeCl₃ and 20 minutes was allowed to elapse before proceeding. Excess fluid was removed before reimaging.

After clot formation, animals were returned to the imaging facility. Once repositioned under the 2PEF microscope, the clot site was imaged. If the clot was observed to be incomplete, especially by the observation of flow at the edges of the dSV, then the animal was discarded from further analysis. If the clot was complete, then we remeasured blood flow speeds in the same vessels measured before clot formation.

Mathematical Modeling

All mathematical analysis was performed in Matlab. Briefly, our model consisted of 100 dAVs of uniform resistance, R₀, with a constant distal pressure of P₀. Each segment of the dSV between dAVs was taken to have a resistance of 10⁻³ R₀, based on Poiseuille's law and measurements of dAV and dSV vessel diameters. Poiseuille's Law relates the volumetric flow, Q, in a cylinder due to the pressure drop, ΔP, across it according to:

where resistance, R, is given by

for viscosity, η, and length, L. Since our model only depends on pressure drops, the ends of the dSV– where RMVs drained blood away from the SC– were taken to be the reference point for all other pressures and thus have zero pressure. It should be noted that this value was used for mathematical convenience but does not correspond to the physiologic pressure, which is nonzero. Conservation of flow of an incompressible liquid and summation of pressure drops between points was used to generate a system of equations. The system was solved, giving the flow in each dAV and segment of the dSV. Clots were simulated by setting the resistance of the target dSV segment equal to 10⁴ R₀. This value was heuristically chosen as it approximated the infinite resistance limit while avoiding numerical round-off errors associated with large numbers. Post-clot flows were calculated by solving the system with the new resistance taken into account (See Supplementary Materials for details).

For calculations in which dAV resistance was allowed to vary (see Supplementary Materials), dAVs were assigned radii, r_j, from a normal distribution with mean of 12.5 μm and standard deviation of 5 μm, congruent with measured data. A resistance of R₀ was taken to correspond to 12.5 μm, with subsequent resistances, R_j, calculated according to Equation (4) as:

Results

Intraluminal Blood Vessel Fills Revealed Key Aspects of Venous Microvasculature in the Mouse Spinal Cord

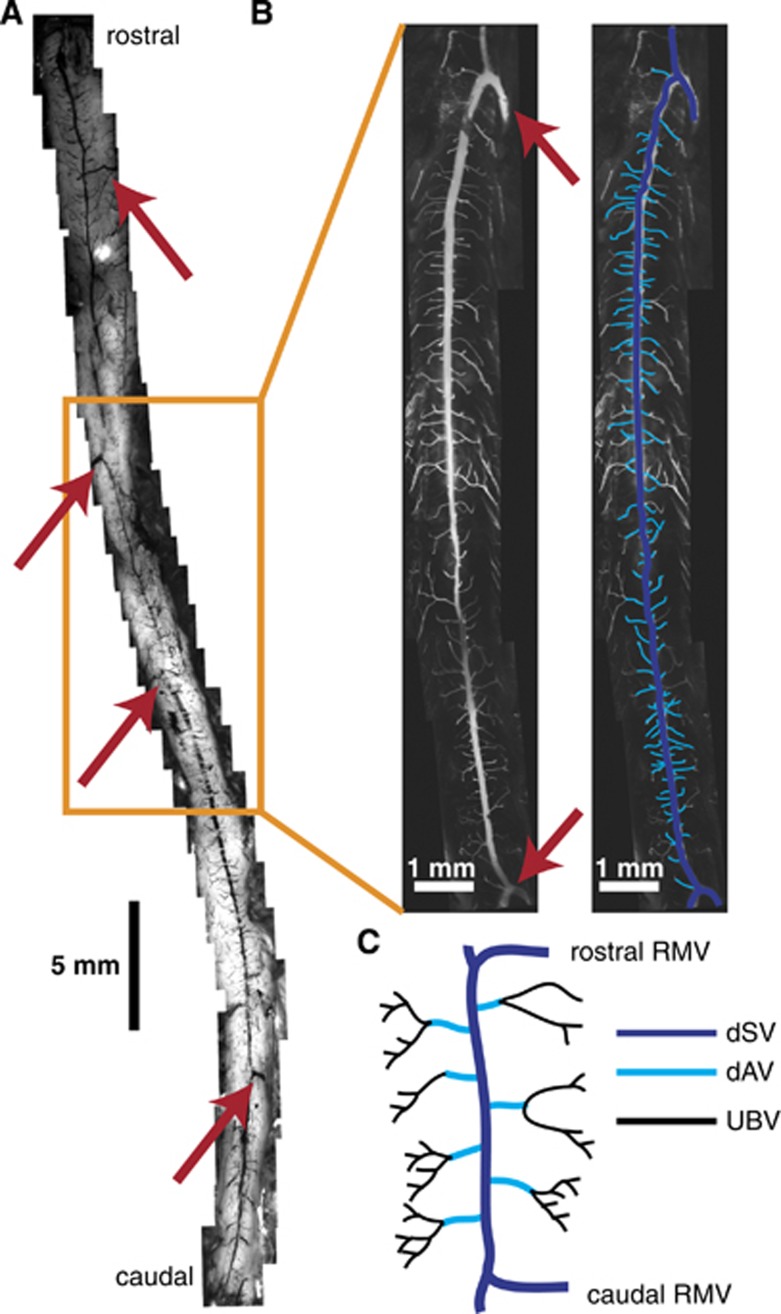
Mice were deeply anesthetized with pentobarbital before intracardiac perfusion with paraformaldehyde. Mice were subsequently perfused with India ink (Figure 1A) or a fluorescently-labeled agarose gel (Figure 1B). White light images were taken along the whole length of the SC, from the medulla oblongata to the beginning of the cauda equina (Figure 1A). We observed at least four large vessels branching off the dSV and exiting the SC at nearly orthogonal angles to the axis of the SC (Figure 1A, arrows), which we identified as RMVs. While size and specific location varied across animals, the overall distribution of these RMVs was stereotyped (see Supplementary Figure 1).

Figure 1.

The dorsal spinal vein (dSV) is fed by dorsal ascending venules (dAVs) and drained by radiculomedullary vessels (RMVs) along its length. The spinal cord (SC) of a mouse perfused with an India ink/agarose gel (A) revealed large radiculomedullary branches exiting the SC along its length (A and B, red arrows). Two-photon excited fluorescence (2PEF) microscopy of fluorescent dextran/agarose perfused spinal cords (B) showed the dSV morphology (navy) and its tributary dAVs (cyan). Subsequent analysis focused on the dSV and dAV vasculature of the thoracic SC (A, orange box) in the region spanning two RMVs (C). Blood flow from upstream branching venules (UBVs; C) was not considered in detail.

The most prominent of these RMVs occurred in the thoracic and thoracolumbar regions of the SC (Figure 1A, box; Figure 1B) and showed a ‘coathook' morphology described elsewhere.³⁶ Between this pair of RMVs, we observed 110±30 dAVs (n=5 mice;±s.d.) uniformly distributed over a length of 10.8±3 mm (n=20 mice;±s.d.). For the rest of our study, we focused on the dSV and dAVs spanning this pair of RMVs, designating all vessels upstream of the dAVs to be upstream branching vessels (UBVs; Figure 1C).

In Vivo Blood Flow Measurements Showed Bidirectional Flow in the Dorsal Spinal Vein and Characteristic Size-Flow Relationship in the Dorsal Ascending Venules

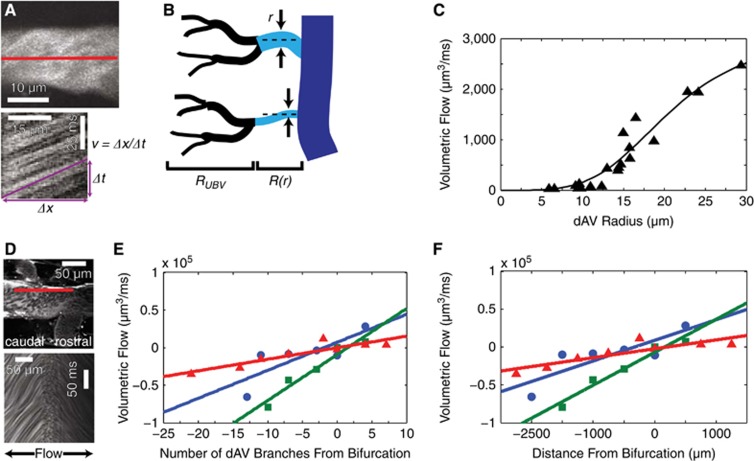
After a dorsal laminectomy in anesthetized mice, we injected a high-molecular weight fluorescent dextran retro-orbitally and imaged the mice using 2PEF microscopy. We calculated volumetric flow in each dAV using Equation 1. Vessel radius was measured directly from maximum-intensity projections of small stacks (Figure 2A, top). We determined the mean dAV diameter to be 24.8±9 μm (187 dAVs in n=9 mice;±s.d.) and the mean thoracic dSV diameter at the locations considered to be 146±40 μm (n=9 mice;±s.d.). The RBC speed was measured using a line-scan method (Figure 2A, bottom) at the center of the dAV, which corresponded to v_max.

Figure 2.

In vivo blood flow measurements confirm an anatomy-driven flow model and reveal a bifurcation in flow direction along the dorsal spinal vein (dSV). Maximum intensity projections of small image stacks (A, top) and one-dimensional linescans at the center of the vessel (A, bottom) allow for volumetric flow measurements in dorsal ascending venules (dAVs). A simple flow model (B) considered dAVs (cyan) to have a composite resistance consisting of a radius-dependent resistance, R(r) and an average upstream branching venule (UBV) (black) resistance, R_UBV. Representative data (C; symbols) and least-squares fit (solid line) show the correspondence between the model and measurements. Linescans at the edge of the dSV (D; top) were used to extrapolate speeds at the dSV center. A change in the slope of the linescan from positive (caudal-flowing) to negative (rostral-flowing) over the length scale of single linescan (D; bottom) shows a blood flow bifurcation in the dSV. Measurements (symbols) of dSV blood flow along with accompanying trend lines (solid lines) show an increase in magnitude of flow in either direction away from the bifurcation point both as a function of dAV branches (E) and geometrical distance (F). Colors correspond to individual animals (n=3 mice).

Since the dAVs were uniformly distributed along the dSV, and since Equation (4) depends much more critically on radius than length, we approximated the dAVs to have equal length. We further hypothesized that the UBVs bridged a constant distal pressure source to the dAVs and constituted a constant upstream resistance, R_UBV. The total resistance for each dAV was therefore the composite resistance (Figure 2B) given by:

For closely spaced dAVs, we expected the pressure in the dSV to vary little. Under these assumptions, we measured 20 adjacent dAVs corresponding to ~20% of the length of the dSV. With these assumptions in place, we developed a model (see Supplementary Materials for details) that showed a quartic dependence of blood flow on radius for small dAV radii and was bounded above by an asymptote corresponding to R=R_UBV. Our fit used only two parameters that depended on the pressure drop across the dAVs and combined constants of resistance, and captured the trend well (Figure 2C).

Since the blood flow speed at the center of the dSV was too fast to measure reliably at the center of the vessel using the linescan technique, we measured the RBC speed at a constant distance of 30 μm from the lumen wall (Figure 2D, top). A bifurcation in the blood flow was observed approximately halfway in between the rostral and caudal RMVs (4.9±1 mm and 5.6±2 mm from the rostral and caudal RMVs, respectively; n=3 mice). We observed RBCs traveling in opposite directions on either side of this point. Linescans taken about the bifurcation showed a change in slope (Figure 2D, bottom) indicative of bidirectional flow. Blood flow increased in either direction away from the bifurcation both as a function of the number of tributary dAV branches (Figure 2E) and the geometric distance (Figure 2F). In each mouse (separate colors in Figures 2E and 2F; n=3 mice), a linear fit captured the trend. Anatomic demarcations of the flow bifurcation in these same mice varied from nonexistent to a sharp decrease in dSV diameter (see Supplementary Figure 2; results are color coded to match the same mice in Figures 2E and 2F).

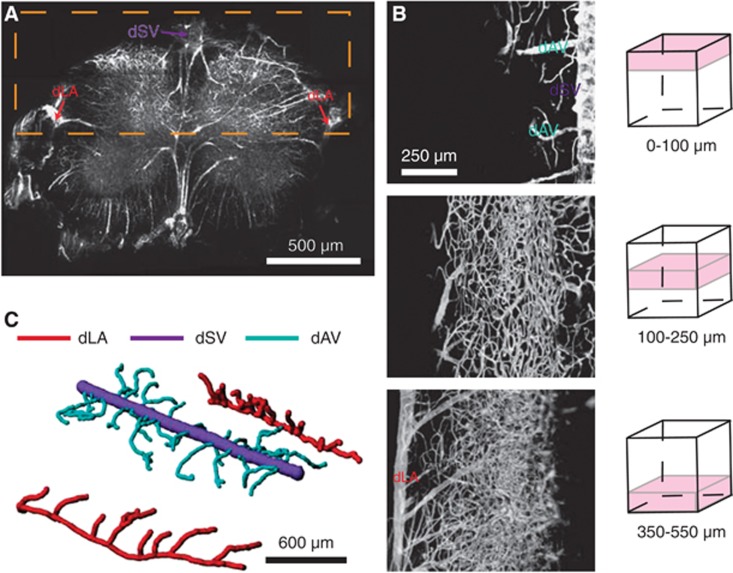
Three-Dimensional Vascular Reconstructions Show Effective Isolation of Adjacent Dorsal Ascending Venules

Due to the short scattering length of myelin, detailed vascular mapping in vivo was not possible. To circumvent this limitation, we adopted a clearing protocol described previously³¹ in combination with the fluorescent gel perfusion protocol described above. Using this approach, we were able to see hundreds of micrometers into the tissue, including the white matter. We performed imaging in both coronal (Figure 3A) and longitudinal (Figure 3B) orientations. We focused our attention on vasculature from the dLAs to the dorsal surface (Figure 3A, orange box; Figure 3B). We manually traced dAVs from the dSV to the first or second branch point of each dAV, after which only smaller venules or capillaries were connected. We observed no low-resistance collaterals connecting adjacent dAVs (Figure 3C). We performed similar analysis for the primary downstream branches off the dLAs, and found no noncapillary-containing routes from these branches to the dAVs.

Figure 3.

Dorsal ascending venules have no conjoining low-resistance collateral branches. Two-photon excited fluorescence (2PEF) images of index-matched, fluorescent dextran/agarose perfused spinal cords allowed for vascular mapping from either coronal (A) or dorsal orientations (B). When imaging from the dorsal aspect (B), the dorsal spinal vein (dSV), dorsal ascending venules (dAVs), and intermediate vessels were imaged out to the dorsolateral arteries (dLAs; A, orange box). A three-dimensional reconstruction (C) clarified the branching structure of dAVs and dLAs.

A Simple Model Accounts for Bidirectional Flow and Predicts Flow Changes After Point Occlusion

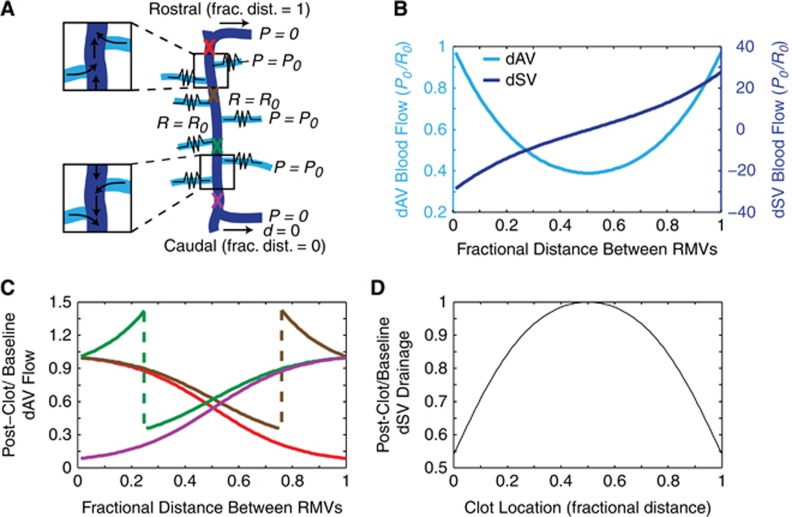
Using these observations, we constructed a mathematical model of blood flow in the dorsal SC vasculature. We modeled the segment of the dSV of interest to be sourced by 100 dAVs uniformly distributed along its length. The caudal exiting branch of the dSV was taken to be at zero distance and the rostral branch to be at unit distance. Each dAV was taken to have the same resistance, R₀, and had a distal pressure of P₀, with the connections of the dSV to RMVs taken to be the zero pressure points (Figure 4A). Since we observed no small-resistance paths between adjacent dAVs, they were approximated to interact only through the dSV. Under these conditions, we observed flow bifurcation in the dSV (Figure 4A, inset; Figure 4B, dark blue). We found that the predicted flow in dAVs varied along the rostral-caudal direction with a U-shaped distribution, with the highest flows observed in dAVs at the caudal and rostral ends (Figure 4B, light blue).

Figure 4.

A simple flow-resistance model accounts for the bifurcation in the dorsal spinal vein (dSV) and predicts changes in flow after dSV occlusion. A simple model (A) considered the dSV (navy) to be of negligible resistance and supplied by 100 dorsal ascending venule (dAV) tributaries (cyan) of uniform resistance, R₀, with a constant distal pressure source, P₀, while maintaining the radiculomedullary veins (RMVs) at the rostral and caudal end of the dSV segment at zero pressure. Baseline flows in normalized units as a function of the fractional distance between the RMVs (B) for both the dAVs (cyan, left axis) and dSV (navy, right axis) were computed. The ratio of postclot to baseline dAV flows (C) was computed by simulating clots at various locations along the dSV (A, colored ‘X' markings). Each color corresponds to a different clot location, with red indicating a clot near the rostral RMV, brown one quarter of the distance caudal to the rostral RMV, green three quarters of the distance caudal to the rostral RMV, and purple near the caudal RMV. By summing the flow out of the dSV at the rostral and caudal RMVs, the net drainage of the dSV was determined as a function of clot location (D).

We then simulated a ‘clot' by interrupting the blood flow in the dSV at different locations (Figure 4A, ‘X' markings) and computed the ratio of the postclot flow to the baseline flow for each dAV (Figure 4C). Clots occurring at the rostral (Figures 4A to 4C, purple) or caudal (Figures 4A to 4C, red) extremes of the dSV segment resulted in a reduction in all dAVs. Surprisingly, creating a clot midway between the bifurcation and the rostral or caudal extremes (Figures 4A to 4C, green and brown) resulted in both flow increases and decreases in the dAVs. For dAVs upstream of the clot, flow was reduced analogously to clots at the extremes. However, for dAVs downstream of the clot, dAV flow increased. It should be noted that since flow bifurcated about the midpoint, ‘upstream' refers to vessels rostral or caudal of the occlusion for clots rostral or caudal of the bifurcation, respectively. No flow changes occurred for clots occurring at the bifurcation point (data not shown).

Finally, we investigated computationally whether the increases in downstream dAV flow were able to compensate for the decreases in upstream dAV flow. We summed the outflow at both the rostral and caudal ends of the dSV and compared the overall postclot dSV drainage with baseline (Figure 4D). We observed a strong decrease in dSV drainage as the clot location moved away from the bifurcation point, indicating that no such passive compensation could restore drainage. Overall drainage was reduced to nearly 50% of baseline for clots located near the rostral or caudal connection between the dSV and the RMVs.

To assess the impact of nonuniform resistances, we performed analogous simulations using resistances that were based on the experimentally observed diameter distribution of dAVs (see Supplementary Materials for details). We found that the average result was qualitatively similar to the uniform resistance model (Supplementary Figure 3). The location of the bifurcation was strongly dependent on the resistance distribution (data not shown), resulting in more severe features in the median flow response as compared with the mean response (Supplementary Figure 3).

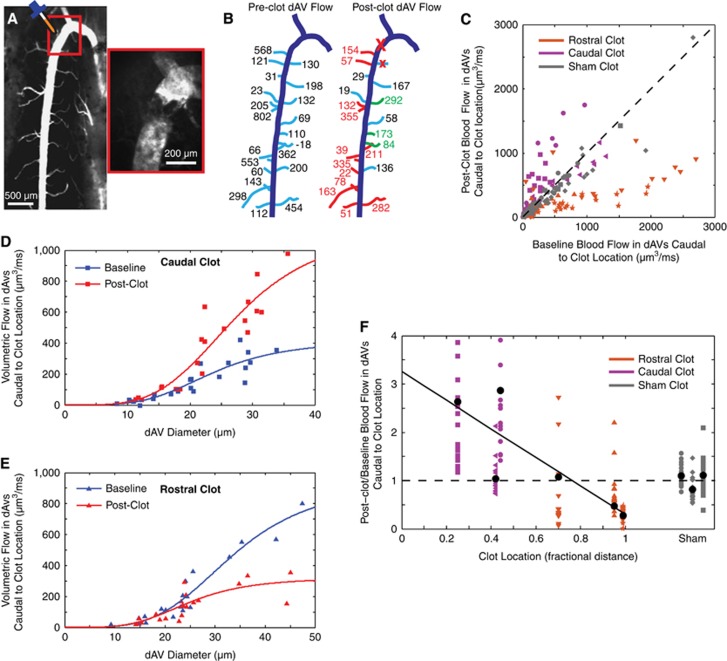
A Point-Occlusion Technique Results in Flow Changes Congruent with the Model Predictions

To test the predictions of our model concerning changes in upstream and downstream flow in the dAVs after point occlusion of the dSV, we adopted a FeCl₃-based clotting technique to occlude the dSV. By carefully confining the FeCl₃ solution to a small area of exposed tissue, we were able to produce a full-thickness clot in the dSV, without clotting other vessels (Figure 5A). For the rare cases where dAVs were occluded (four dAVs in three mice) by this technique, these dAVs were excluded from subsequent analysis. We measured RBC velocity and dAV diameter in approximately 20 vessels caudal to the clot site both before and after occlusion. These measurements were used to calculate preclot and postclot volumetric flows in each of the 20 dAVs (Figure 5B). We performed clots at various locations between the rostral and caudal RMVs. It is important to note that since we always measured caudal to the site of occlusion, our measurements of dAV blood flow for clots proximal to the rostral and caudal exiting branches corresponded to measurements of dAV flow upstream and downstream from the clot, respectively. We compared the postclot blood flow with the preclot blood flow (Figure 5C) for each condition, grouping animals by clot location. Flow reversals (two vessels in two mice) and vessels exceeding 3,000 μm³/ms (four vessels in two mice) were not shown for graphical clarity. As the bifurcation was not usually visible during the course of imaging, the geometrical distance between RMVs was used to classify the clot location rather than the distance from flow bifurcation. Rostral and caudal clots were identified as being beyond and less than the half-way point, respectively. Using our two-parameter fit, we considered the relationship between blood flow and dAV diameter for the caudal-most (Figure 5D) and rostral-most (Figure 5E) clots both before (blue lines) and after (red lines) occlusion. For the caudal (rostral) clot, the change in fit parameters amounts to an increase (decrease) in the pressure drop across the measured dAVs. Finally, we considered the average change in dAV blood flow as a function of clot location, and found that these were negatively correlated (Pearson's, P=0.04). Flow reversals and flow ratios larger than four (six vessels in two mice) are not shown in the plot but were included in all analysis. Controls receiving saline treatment showed no change in blood flow. These findings agreed qualitatively with our model predictions.

Figure 5.

Measurements of dorsal ascending venule (dAV) blood flow after point occlusion of the dorsal spinal vein (dSV) confirmed the flow model. FeCl₃ was applied (A) to a point along the dSV, resulting in the formation of a thrombus and blockage of flow (A; inset). Baseline (B; left) and postclot (B; right) flow measurements were performed in ~20 vessels caudal to the clot site (B; large red ‘X'). Vessels in green (red) denote an increase (reduction) in flow greater than the error in measurement. In a few cases, 1 to 2 dAVs proximal to the clot site were occluded (small red ‘X') and not considered in subsequent analysis. Blood flow in the dAVs before and after dSV occlusion was compared (C) with respect to the unity line (C, dashed line). Blood flow was also compared against dAV diameter for extreme caudal (D) and rostral (E) clots, and results were fit to the composite resistance model (solid lines). Mean postclot to baseline flow ratio for the ~20 vessels caudal to the clot location for each animal (black circles) was compared against clot location (F) and found to be correlated (Pearson's, P=0.04). A line of best fit (solid line) shows the trend. Symbols of the same shape correspond to dAVs within the same animal. The unity ratio (dashed line) is shown for reference.

Discussion

The Mouse Dorsal Spinal Cord Vasculature is Topologically Stereotyped but Geometrically Variable

We observed the mouse dorsal SC to be supplied by two dLAs and drained by the dSV. This architecture is analogous to the human SC,¹⁴ further supporting mice as a valuable model for studies of SC pathology. However, while we consistently observed large ‘shunting' branches (i.e., the RMVs) along the length of the dSV, the location of these shunts varied considerably, occurring even in different segments across animals. This observation is consistent with the high degree of variability in spinal vasculature more generally. In humans, the number of anterior and posterior radicular arteries was reported as varying between 2 to 17 and 11 to 25, respectively³⁷ and the variability of the venous system is reportedly higher than the arterial side.²⁸

The Dorsal Spinal Vein Serves as a Bidirectional Drain for the Mouse Spinal Cord and May Have a Role In Neurovascular Coupling

Unlike veins in the periphery, the CNS (central nervous system) venous system does not contain one-way valves. This absence raises the possibility of bidirectional SCBF, which has been described for the arterial supply by a partial flow theory.² However, to the best of our knowledge, simultaneous blood flow in opposite directions within the same vessel has not been observed in the venous system of the CNS previously. This observation raises the question as to what purpose might be served by such a feature.

In the brain, basal and stimulus-induced fluctuations in blood flow of individual vessels have been observed,³² owing to neurovascular coupling. Like the brain, the SC is auto-regulatory in blood pressure,³⁸ and functional MRI studies of the SC³⁹ have revealed similar changes in activity-dependent perfusion. With respect to network topology, recent modeling⁴⁰ has revealed that the optimal structure of a transport network depends not only on steady-state flow, but also on fluctuating sources. In particular, conservation of flow in a closed system requires that activity-driven fluctuations in blood flow in the arterial supply be compensated for in venous drainage. Our model predicts that the bifurcation point is metastable and will shift in location with varying upstream pressures, a feature that would be prevented by the directional valves found in peripheral vasculature. It is therefore possible that the allowance for bidirectional blood flow in the dSV is part of an evolutionary adaptation that results in passive redistribution of venous drainage during activity-dependent arteriole blood pressure changes without either the occupation of precious neurologic space by additional blood vessels or the introduction of active venous compensation mechanisms. However, it should be noted that our model considered only flow in the downstream dAVs and dSV, and is therefore not suited to considering the effects of upstream dilating arterioles or to fully capture the dynamics of flow through a complex capillary network.

The Mouse Spinal Cord is Susceptible to Ischemic Injury of Venous Origin

Our in vivo measurements showed that occlusion of the dSV near large RMV anastomoses can result in blood flow reductions of more than 50% in individual upstream dAVs. Unlike studies in the cortex where collateral connections between nearby surface venules could compensate for a point occlusion in an adjacent surface venule,³⁰ the dSV is the sole draining vein for the dorsal SC and its occlusion necessarily results in severe blood flow reduction. Furthermore, our topological analysis suggests that since dAVs have no low-resistance collateral connections between them, there is no way for dAV flows to bypass the clot. This observation is in accord with a detailed study of the rodent neocortex by Blinder et al,⁴¹ who determined that ascending venules are arranged such that they sink blood flow from neighboring penetrating arterioles but are not mutually compensatory. Finally, our model predicts that flow out of the dSV is always reduced in the event of an occlusion, with increased severity as the clot approaches either the rostral or the caudal RMV draining branches. All of these observations suggest that occlusion of the dSV will result in severe loss of tissue perfusion in the area between these shunting branches—which can span several vertebral segments—making the mouse SC susceptible to ischemic injury from venous occlusion. As the dSV is the most dorsal blood vessel in the mouse SC, it is almost certain to be occluded by most preclinical models of SCI, and this consideration is important for secondary injury disease mechanisms. Our data also suggest that the location at which blood flow in the dSV is disrupted will critically affect the extent of ischemic injury sustained.

In line with our predictions of ischemic injury, longitudinal studies^{42, 43} of dSV occlusion in rats have shown atrophy of the posterior columns, reactive gliosis, macrophage infiltration, and onset of paraplegia. Interestingly, in a study examining the results of dSV ligation,⁴³ variability in the extent of pathologic SC ‘softening' was attributed to unobserved venous anastomoses connecting to the dSV. This attribution fits well with both our model and measurements, which predict that the extent of ischemic injury will depend critically on occlusion location with respect to those draining anastomoses.

In contrast, a study in rhesus monkeys⁴⁴ showed that large-scale occlusion (as many as nine vertebral segments) of the dSV did not result in behavioral pathology, although demyelination was observed in posterior columns. Dilation of the anterior spinal vein was seen to compensate for dSV occlusion. Care must therefore be taken when applying murine models of venous SC ischemic injury to humans or other animal models, despite anatomic similarities.

Conclusion

Using topological observations and in vivo flow measurements, we have developed a simple model that can account for the observed blood flow patterns in both the dSV and its connecting upstream dAVs. In addition to providing a framework in which to understand dorsal SCBF in healthy states, we are also able to predict how this flow rearranges after occlusion in a clot location-dependent manner. These findings have important implications for clinical management of venous thrombosis and preclinical models of SCI.

The authors declare no conflict of interest.