Abstract
The goal of this study was to investigate the reciprocal interactions among oxygen (O2), nitric oxide (NO), and superoxide (O2−) and their effects on medullary oxygenation and urinary output. To accomplish that goal, we developed a detailed mathematical model of solute transport in the renal medulla of the rat kidney. The model represents the radial organization of the renal tubules and vessels, which centers around the vascular bundles in the outer medulla and around clusters of collecting ducts in the inner medulla. Model simulations yield significant radial gradients in interstitial fluid oxygen tension (Po2) and NO and O2− concentration in the OM and upper IM. In the deep inner medulla, interstitial fluid concentrations become much more homogeneous, as the radial organization of tubules and vessels is not distinguishable. The model further predicts that due to the nonlinear interactions among O2, NO, and O2−, the effects of NO and O2− on sodium transport, osmolality, and medullary oxygenation cannot be gleaned by considering each solute's effect in isolation. An additional simulation suggests that a sufficiently large reduction in tubular transport efficiency may be the key contributing factor, more so than oxidative stress alone, to hypertension-induced medullary hypoxia. Moreover, model predictions suggest that urine Po2 could serve as a biomarker for medullary hypoxia and a predictor of the risk for hospital-acquired acute kidney injury.
Keywords: mathematical model, hypoxia, oxygen, sodium transport
nitric oxide (no) and superoxide (O2−) exert opposite effects on renal vascular and tubular function, and the balance between the two significantly modulates the renal handling of Na+. NO promotes natriuresis and diuresis and thus favors reductions in blood pressure; O2− promotes salt and water retention, which raises blood pressure (8).
In vitro experiments on the rat (5) and bovine (66) kidney have shown a dependence of NO and O2− production on local oxygen tension (Po2), but the net effects of these three interacting solutes on medullary transport and function remain unclear. What is clear is that medullary tissue Po2 is low even though the kidney receives 25% of the cardiac output. The low medullary Po2 stems primarily from the high metabolic demands of the medullary thick ascending limbs (TALs) of the loops of Henle. As a result, the renal medulla is vulnerable to ischemic and hypoxic injury (8).
In vivo microdialysis studies in the rat have demonstrated that medullary NO production can protect the kidney from large reductions of medullary blood flow and ischemia, even in the face of significantly reduced cortical blood flow (9, 70, 72). The renal protective influence of NO may be attributed to its two key physiological effects: vasodilation, which increases medullary blood flow and O2 supply, and natriuresis, which reduces O2 consumption. In contrast, increases in O2− reduce medullary blood flow and result in antinatriuresis (71). Chronic elevation of medullary O2− levels can reduce NO bioavailability and raise medullary TAL sodium absorption, resulting in a decrease in sodium excretion, both of which may contribute to the development of hypertension (8, 21, 31, 32, 35).
In light of these issues, a principal goal of this study was to investigate how the interactions between NO and O2− affect medullary oxygenation and active sodium transport and vice versa. To do this, we developed a highly detailed mathematical model of NO and O2− steady-state transport in the renal medulla that takes into account its three-dimensional (3D) architecture and examined a range of physiological and pathophysiological conditions.
MODEL DESCRIPTION
Our model is based on previously applied models of the urine-concentrating mechanism and oxygen transport in the rat kidney (15, 25, 26), as well as a rat outer medulla (OM) model of NO and superoxide interactions (13). Our model representation accounts for the 3D architecture of the renal medulla using the “region-based” approach (described further below) developed by Layton and Layton (28) and simulates steady-state solute transport in the renal medulla.
The descending limbs, ascending limbs, and collecting ducts (CDs) are represented by rigid tubes that extend from the corticomedullary boundary at x = 0 to the papillary tip at x = L. Two-thirds of the model loops of Henle are assumed to turn at the OM-inner medulla (IM) boundary, whereas the other one-third turn at all depths of the IM. The model separates blood flow in the vasa recta into two compartments, plasma and red blood cells (RBCs), which are both also represented by rigid tubes along the corticomedullary axis. The vasa recta terminate or originate at all depths of the medulla and are assumed to peel off and supply the capillary plexus.
To represent the 3D architecture of the renal medulla and the resulting preferential interactions among vessels and tubules, the model interstitium is divided into four regions. Each region represents the combination of interstitial spaces, interstitial cells, and capillary plasma flow and is assumed well mixed at a particular medullary depth. Each region also contains an RBC compartment, representing RBCs within capillaries traversing the region. To determine the interactions among tubules and vessels, each tubule or vas rectum is assigned to a certain region (or, potentially, fractions of each tubule or vas rectum are assigned to 2 regions); in this way, vessels and tubules contained in different regions are influenced by different interstitial environments.
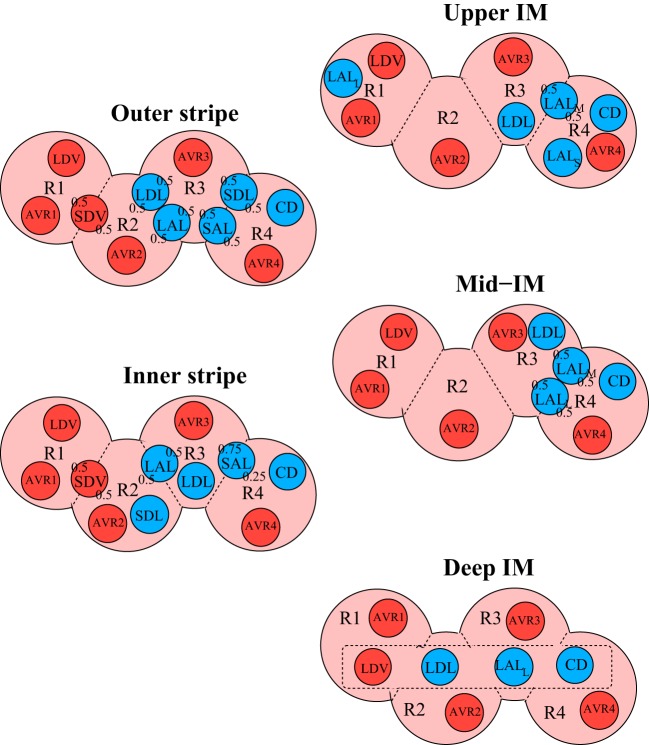
The positions of the tubules and vessels within the regions at different medullary depths are shown in Fig. 1. The organization of the OM regions is centered around an innermost region that represents a vascular bundle (R1), which contains long vasa recta that reach into the IM. Most of the TALs are contained in the interbundle regions (R3 and R4), far from the oxygen-supplying descending vasa recta (DVR) (30). Similarly, the organization in the IM is centered around the region (R4) that denotes a cluster of CDs. In the upper 3–3.5 mm of the IM, these CD clusters dominate the structural organization of the medulla, with DVR found distant from those clusters (R1) (46, 47, 48, 49). In the bottom 1.5–2 mm of the IM, CD clusters are no longer distinguishable, and the radial organization of the deep medulla is increasingly homogeneous.
Fig. 1.
Schematic diagram of a cross section through the outer stripe, inner stripe, upper inner medulla (IM), mid-IM, and deep IM, showing interstitial regions (R1, R2, R3, and R4) and relative positions of tubules and vessels. Decimal numbers indicate relative interaction weightings with regions [e.g., in the outer stripe, half of the short descending vasa recta (SDV) lie in R1, and half lie in R2]. CD, collecting duct; LDV, long descending vas rectum; AVRs, populations of ascending vasa recta; SDL/SAL, descending/ascending limbs of short loops of Henle; LDL/LAL, descending/ascending limbs of long loops of Henle. Subscript “S,” “M,” and “L” associated with a LAL denotes limbs that turn with the first mm of the IM (S), within the mid-IM (M), or reach into the deep IM (L). Dotted-line box in deep IM indicates that LDV, LDL, LAL, and CD are weighted evenly between the 4 regions. Tubules, vessels, and interstitium are denoted in blue, red, and pink, respectively.
The model predicts fluid flows in the tubules and vessels, as well as concentrations of NaCl, urea, O2, NO, O2−, deoxyhemoglobin (Hb), oxyhemoglobin (HbO2), and nitrosyl-heme (HbNO), in each tubule and vessel, as well as in the interstitium. Model equations are based on transmural transport and conservation of water and solutes. Below we summarize key components of the model that represent generation and consumption of oxygen, NO, and superoxide. Full model equations can be found in Refs. 4, 13, 27.
Generation and consumption of NO.
The rate of NO synthesis in the vascular endothelium and tubular epithelium is dependent on the local O2 concentration. This dependence of the NO generation rate (Gi,NO) on O2 is modeled by a Michaelis-Menten relationship:
| (1) |
where Ci,O2 is the O2 concentration in tubule or vessel i, Gi,NOmax is the maximal rate of NO synthesis, and KO2NO is the Michaelis constant, taken here to be 50.9 μM (66). The value of Gi,NOmax in the vasa recta is chosen to yield interstitial NO concentrations ∼100 nM, based on experimental findings in the rat (72). The ratios between maximal NO generation rates in the vasa recta and the descending limbs, ascending limbs, and CDs are derived from published measurements in microdissected rat renal segments (67).
As in our previous models of NO transport (12, 13, 69), we consider the following NO consumption reactions: the auto-oxidation of NO (rate V1), the scavenging of NO by O2− (rate V2), the irreversible reaction of NO with HbO2 to form methemoglobin (rate V3), and the reversible reaction of NO with Hb to form HbNO (rate V4). The reaction rates for these processes are
| (2) |
| (3) |
| (4) |
| (5) |
Reactions with rates Vi,1 and Vi,2 take place in all compartments, whereas reactions with rates Vi,3 and Vi,4 take place only in the RBCs. The total volumetric rate of NO consumption in tubule or vessel i is thus given by
| (6) |
The steady-state conservation equation for NO in tubule i is given by
| (7) |
where x is the position along the medulla; Fi,NO(x) is the flow rate of NO in tubule i; Ji,NO is the transmural flux of NO into tubule i; Ailum and Aiepi are the cross-sectional areas of the lumen of tubule i and that of the surrounding epithelium, respectively; Ri,NOlum and Ri,NOepi are the volumetric consumption rates of NO in the lumen of tubule i and that of the surrounding epithelium, respectively; Gi,NO is the epithelial volumetric generation rate of NO; and θ is the fraction of the amount of NO generated in epithelia that diffuses toward the lumen [with the remainder (1 − θ) diffusing toward the interstitium]. The present model does not explicitly take into account epithelial and endothelial cell barriers. As seen in Eq. 7, NO synthesis and consumption in these cell layers are accounted for by “source” or “sink” fluxes into the interstitium and into the lumens of the vessels and tubules. Because endothelial and epithelial solute concentrations are not explicitly determined, the fraction of NO consumption attributed to the interstitium is calculated based on interstitial region concentrations, while the fraction attributed to the tubular or vascular lumen is calculated based on tubular lumen or plasma concentrations (13).
Generation and consumption of superoxide.
Studies on kidney homogenates from normotensive and hypertensive rats have suggested that endothelial and epithelial superoxide synthesis is inhibited by low Po2 (5). Thus the O2− generation rate is modeled by the following Michaelis-Menten relationship:
| (8) |
where is fixed for vessel or tubule i, and the Michaelis constant is set to 20.6 μM (5).
As far as we know, measurements of absolute medullary O2− concentrations have not been reported. A previous modeling study (13) used measurements of H2O2 and its steady-state generation and consumption rates to estimate that interstitial superoxide concentrations are on the order of 1 nM. Thus the basal rate of O2− synthesis in the vasa recta is chosen to give predicted values of interstitial superoxide concentrations ∼1 nM. The ratios between basal O2− generation rates in the vasa recta and the descending limbs, ascending limbs, and CDs are based on experimental results from microdissected rat nephron segments (31).
Superoxide scavenges NO (rate V2, Eq. 3) and in turn is consumed by superoxide dismutase (SOD). The reaction rate for this process is
| (9) |
which takes place in all compartments (13). The total volumetric rate of O2− consumption in tubule or vessel i is thus given by
| (10) |
As was the case with NO, the fraction of O2− consumption attributed to the interstitium is calculated based on interstitial region concentrations, while the fraction attributed to the tubular or vascular lumen is calculated based on tubular lumen or plasma concentrations (13).
Sources of NO and O2− from capillary endothelium.
As little quantitative data are available on the capillary network in the medulla, we assume that the capillaries are well mixed with the local interstitium. To represent production of NO and O2− by the capillary endothelium, it is assumed that the endothelium releases NO and superoxide directly into the surrounding interstitial region. The maximum NO and O2− generation rates in the capillaries are taken to be the same as in the vasa recta (13).
O2 consumption.
In the model, basal O2 consumption (i.e., for processes other than sodium transport) is assumed to take place in the vascular endothelial cells, tubular epithelial cells, and interstitial cells, and O2 consumption due to active sodium transport occurs in the medullary proximal straight tubules (PSTs), thick ascending limbs, and CDs. The volumetric rate of basal O2 consumption in tubule or vas rectum i is given by
| (11) |
where Ci,O2 is the O2 concentration in tubule or vessel i, KM,iO2 is the Michaelis constant, and Rmax,O2basal is the maximal volumetric rate of O2 consumption. Here, Rmax,O2basal is taken to be 10 μM/s (4).
To account for the inhibition by NO of mitochondrial utilization, KM,iO2 is varied according to the local NO concentration as follows:
| (12) |
where KM,O2 is the Michaelis constant in the absence of NO and CNOinhib is the NO concentration that doubles KM,iO2. Here, they are taken to be 1 mmHg and 27 nM (3), respectively.
In the PSTs, TALs, and CDs, sodium is actively reabsorbed via basolateral Na+-K+- ATPase pumps; the stoichiometry of metabolic reactions suggests that under maximal efficiency, the number of Na+ moles actively reabsorbed per mole of O2 consumed is 18. That is, the TNa-to-QO2 (where TNa denotes the moles of Na+ transported and QO2 denotes the amount of O2 consumed, also abbreviated as TQ) ratio is 18 for active transport. Under favorable thermodynamic conditions, additional moles of Na+ may be reabsorbed paracellularly, which then raises the TQ ratio; on the other hand, unfavorable thermodynamic conditions lower the TQ ratio. In the model, TQ ratios are fixed at 18 for the TAL and PST and 12 for the CD, based on tubular epithelial transport simulations (37, 62). We further assume that below some critical Po2 (denoted Pi,c for tubule i), anaerobic metabolism maintains some fraction (denoted FAN) of the energy required to actively transport Na+. The rate of active O2 consumption in the epithelia of the PSTs, TALs, and CDs is then given by
| (13) |
where ri is the inner radius of tubule i, TQi is the TQ ratio, Ψi,Naactive is the Na+ active transport rate, and Θ(Pi,O2) is the fraction of that rate that is supported by aerobic respiration, given by
| (14) |
The values of parameters Pi,c and FAN are discussed in the subsequent section.
Active Na+ transport.
The volumetric active Na+ transport rate is characterized in the model assuming Michaelis-Menten kinetics
| (15) |
where Ci,Na is the Na+ concentration in tubule i, Vmax,i,Na [in nmol/(cm2·s)] is the maximal rate of Na+ transport, and KM,Na is the Michaelis constant (taken here to be 70 mM; Refs. 17, 29). When luminal Po2 drops below some critical level, the maximum rate of Na+ transport may become limited by O2 concentration.
In addition, Na+ transport is inhibited by NO and stimulated by O2− (16, 38, 39, 40, 45, 50, 51, 57, 61). The effects of O2, NO, and O2− availability on active Ψi,Naactive are individually taken into account as follows
| (16) |
where is the maximal rate of Na+ transport when O2 is not limiting and in the absence of NO and O2− (13). As described above, it is assumed that below some critical Po2 (Pi,c), anaerobic metabolism will supply some of the energy needed to actively transport Na+, so that, in the complete absence of O2, a fraction (FAN) of the active transport when O2 is abundant is maintained. This gives
| (17) |
We assume that Pi,c = 10 mmHg (15) in all tubules. The value of FAN is taken to be 0.5 in the outer medullary CD (OMCD) (60, 68), 0.4 in the inner medullary CD (IMCD) (56), 0.1 in the TALs (1), and 0.14 in the PSTs (11).
In vitro experiments have demonstrated that NO inhibits active solute transport across rat TALs (38, 40) and mouse cortical CDs (50), although studies on NO effects specifically on IM Na+ transport are lacking. In the present model, the inhibitory effects of NO on active Na+ transport are taken into account by assuming that the active transport rate decreases with increasing NO concentration as follows
| (18) |
where Ci,NO is the NO concentration in tubule or vessel i and βi is the Michaelis constant. In the TAL, Ortiz et al. (40) found that 10 μM spermine NONOate (SPM, an NO donor) inhibits chloride reabsorption by 46%. With a 10 μM SPM concentration, a bath NO concentration of 50–60 nM is expected (52). Thus βi is assumed to be 47 nM in the TALs. In the CD, Pech et al. (50) found that 10 μM MAHMA NONOate (another NO donor) reduces chloride flux by ∼50%. Assuming a physiological level of NO, βi is set to 232 nM in the CDs, so that an average baseline CD NO concentration results in a 50% reduction in active transport. In the PSTs, there is conflicting experimental evidence concerning stimulating/inhibiting effects of NO and O2− on active Na+ transport (38, 45, 51, 61); thus it is assumed in the model that NO and O2− neither inhibit nor stimulate active Na+ transport in the PST.
In vitro studies in the rat have shown that O2− stimulates Na+ transport in the TAL (39) and may do the same in the CD (16, 57), independently of NO. The model takes into account the stimulating effects of O2− on active Na+ transport in the TALs and CDs by assuming that the active transport rate increases with increasing O2− concentration as follows (13)
| (19) |
where is the O2− concentration in tubule or vessel i and i is a Michaelis constant. The values of i are chosen so that h ∼ 1 in the base case. Based on baseline simulations, i is set to 0.2 pM in the TALs and 0.06 pM in the CDs.
Full model equations and transport parameters not described above, as well as CD inflow boundary conditions, can be found in Refs. 4, 13, 15, 25. Inlet flow rates and solute concentrations for the descending vessels and tubules are listed in Table 1, and maximum NO and O2− generation rates are listed in Table 2.
Table 1.
Boundary conditions for descending tubules and vessels at x = 0
| DVR |
|||||
|---|---|---|---|---|---|
| SDL | LDL | CD | Plasma | RBC | |
| Fv,* nl/min | 10 | 12 | 6.5 | 6 | 2 |
| CNa, mM | 160 | 160 | 80.5 | 163.7 | 163.7 |
| Curea, mM | 15 | 15 | 152.7 | 8 | 8 |
| CO2, μM | 15.2 | 15.2 | 15.2 | 60.4 | 60.4 |
| CNO, nM | 100 | 100 | 100 | 100 | 0.1 |
| , pM | 20 | 20 | 20 | 100 | 100 |
| CHbNO, μM | 0 | 0 | 0 | 0 | 1 |
| CHbO2, mM | 0 | 0 | 0 | 0 | 17.3 |
| CHb, mM | 0 | 0 | 0 | 0 | 3.0 |
SDL/LDL, descending limb of short/long loop of Henle; CD, collecting ducts; DVR, descending vasa recta; RBC, red blood cells; C, concentration.
Fluid flows (Fv) are given for individual tubules or vessels.
Table 2.
Base case maximum and average generation rates and average consumption rates for NO and O2− in the tubules and vessels
| NO |
O2− |
|||||
|---|---|---|---|---|---|---|
| Max generation | Avg generation | Avg consumption | Max generation | Avg generation | Avg consumption | |
| CD | ||||||
| OM | 0.415 | 3.20 × 10−2 | 4.10 × 10−5 | 1.8 | 5.59 × 10−5 | 8.34 × 10−4 |
| IM | 3.59 × 10−2 | 8.67 × 10−5 | 6.05 × 10−5 | 2.52 × 10−4 | ||
| LAL | ||||||
| OM | 0.985 | 0.103 | 5.87 × 10−5 | 3.2 | 1.25 × 10−4 | 1.40 × 10−3 |
| IM | 0.143 | 4.40 × 10−5 | 1.58 × 10−4 | 5.31 × 10−4 | ||
| LDL | ||||||
| OM | 12.3 | 1.27 | 5.11 × 10−4 | 15.2 | 5.91 × 10−4 | 9.96 × 10−3 |
| IM | 1.60 | 2.05 × 10−4 | 7.04 × 10−4 | 2.19 × 10−3 | ||
| DVR | ||||||
| OM | 76.6 | 19.2 | 3.81 × 10−4 | 21.0 | 1.50 × 10−3 | 2.20 × 10−2 |
| IM | 15.5 | 1.01 × 10−4 | 1.30 × 10−3 | 5.73 × 10−3 | ||
Consumption rates are in μM/s. NO, nitric oxide; LAL, ascending limb of long loops of Henle, IM, inner medulla; OM, outer medulla.
RESULTS
Base case results.
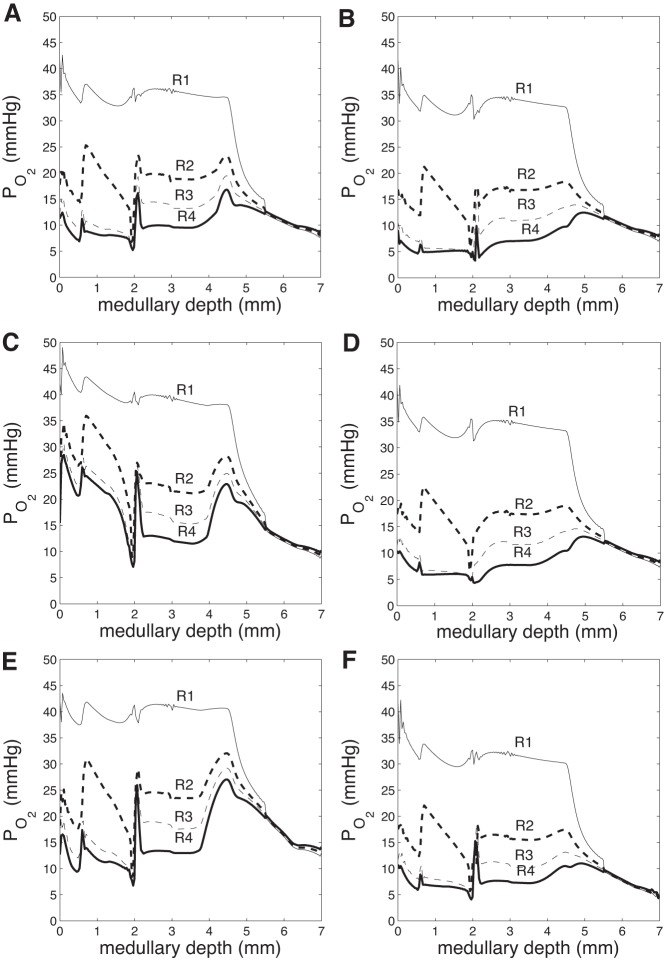
Figure 2A shows region Po2 profiles in the base case. As described in our previous model of oxygen transport in the rat medulla (15), the structure of the OM, in particular, the separation of the O2-supplying DVR from the active O2-consuming TALs, generates a substantial radial Po2 gradient across the regions. This gradient continues throughout the upper IM, where the CD clusters are separated from the DVR. This medullary structure preserves oxygen delivery to the deep IM but leaves the TALs in the OM vulnerable to hypoxic injury.
Fig. 2.
Region Po2 (mmHg) vs. depth (cm) in the 6 cases. A: base case. B: gactive,NO = 1. C: = 0.7. D: gactive,NO = 1 and = 0.7. E: DVR inflow 12 nl/min. F: DVR inflow 6 nl/min. Outer medullary (OM)/IM boundary at 0.2 cm.
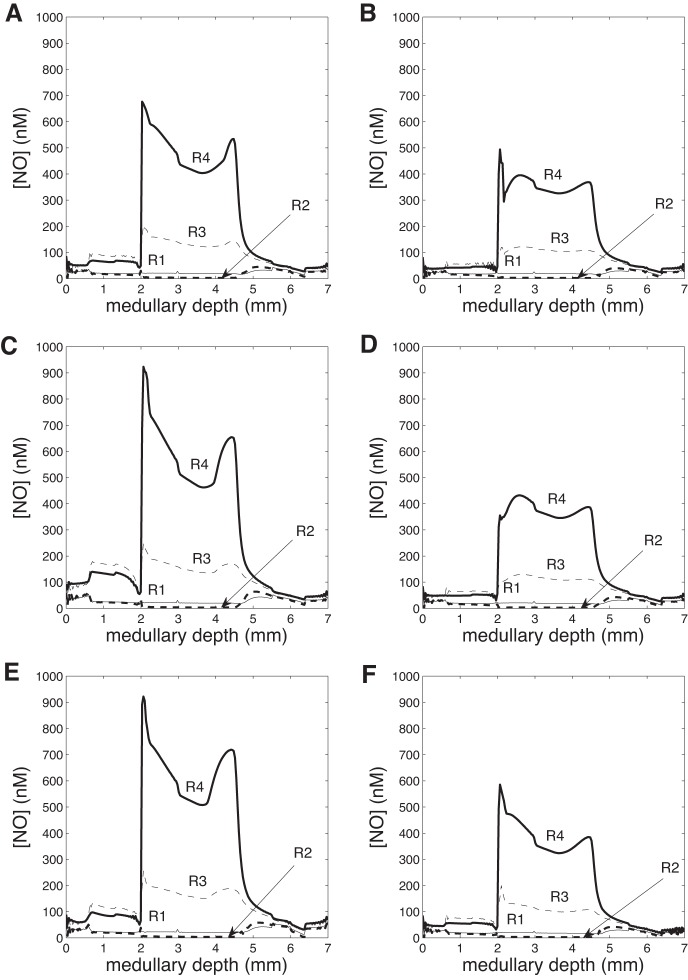
In Fig. 3A, NO concentrations are given in the four regions. Once again, a noticeable radial gradient exists, with NO levels higher in R3 and R4 than in R1 and R2 throughout the medulla. This occurs because NO consumption rates in the RBCs of the DVR (DRBCs, located in R1 and R2) are orders of magnitude larger than in other structures, as hemoglobin scavenges NO at a rate proportional to the Hb concentration. Between the OM and IM, there is a large increase in NO concentrations in R3 and R4, due to increases in net NO generation in the descending and ascending limbs (resulting from higher Po2 levels), as the latter move into R4 in the IM (Table 2).
Fig. 3.
Region NO concentration (nM) vs. depth (cm) in the 6 cases. A: base case. B: gactive,NO = 1. C: = 0.7. D: gactive,NO = 1 and = 0.7. E: DVR inflow 12 nl/min. F: DVR inflow 6 nl/min. OM/IM boundary at 0.2 cm.
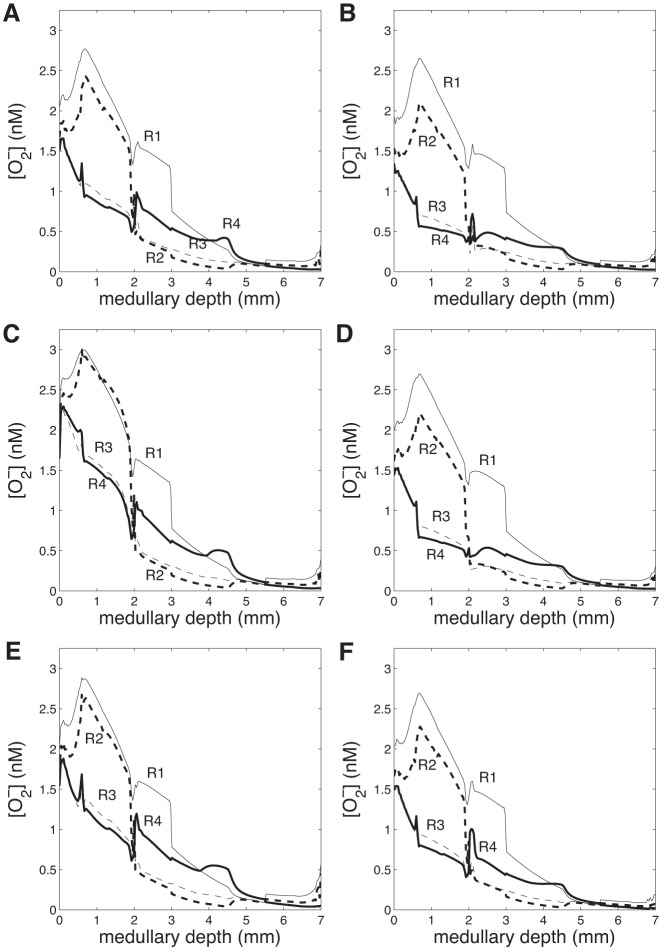
Region concentrations of superoxide are given in Fig. 4A. Whereas O2− concentrations are much lower than NO concentrations, there is still a substantial radial gradient in the interstitial regions. In the OM, superoxide concentrations are highest in R1 and R2, near the vascular bundles, as better oxygenation results in a higher rate of O2− synthesis. In the IM, O2− concentrations are consistently lower in R2 and R3 than in R1 and R4, as no O2-supplying DVR are left in R2 at this depth, and more capillary flow is directed to R4. Moreover, superoxide concentrations in all regions decline fairly steadily throughout the axial length of the medulla, as O2− consumption rates are larger than rates of O2− synthesis throughout (Table 2).
Fig. 4.
Region O2− concentration (nM) vs. depth (cm) in the 6 cases. A: base case. B: gactive,NO = 1. C: = 0.7. D: gactive,NO = 1 and = 0.7. E: DVR inflow 12 nl/min. F: DVR inflow 6 nl/min. OM/IM boundary at 0.2 cm.
Measurements of medullary NO concentrations generally range from 60 to 100 nM (23, 58, 72), with one study reporting an order-of-magnitude larger value, ∼800 nM (53). The predictions of the model generally lie within this range, with base-case region NO concentrations averaging 45 nM in the OM and 110 nM in the IM. Measurements of medullary O2− concentrations have not been made directly, to the best of our knowledge. Previous models of NO and O2− transport suggest that O2− concentrations are on the order of 0.1 to 1 nM (3, 13). The present model predicts base-case region O2− concentrations averaging 1.5 nM in the OM and 0.28 nM in the IM, which is consistent with previous modeling studies.
Effects of stimulation/inhibition of sodium transport by NO and O2−.
In the next set of simulations, we aimed to assess the impact NO and superoxide have on sodium transport in the medulla, beginning with NO. To that end, we conducted a simulation in which NO-mediated inhibition of active Na+ transport was abolished. That is, g(Ci,NO) was set to 1 in equation (16). [In the base case, g(Ci,NO) < 1.] Without NO affecting sodium transport, total TAL Na+ reabsorption increases by 38%. As a result, urine NaCl flow rate drops by 32% (from 0.198 to 0.134 nmol·min−1·nephron−1). The higher Na+ reabsorption rate raises interstitial fluid osmolality and water reabsorption from tubules and vessels. Thus urine flow decreases by 17% and urine osmolality increases from 1,215 to 1,223 mosmol/kgH2O (Table 3). In addition, Po2 decreases throughout the regions (Fig. 2B), as O2-consuming active NaCl transport increases in the OM and IM. There is a slight reduction in region superoxide concentrations (Fig. 4B) and a significant reduction in region NO concentrations (Fig. 3B), due to the decreasing rate of NO and O2− production with decreasing Po2. Overall, these results suggest that NO elicits a significant reduction in Na+ reabsorption and urine osmolality under basal conditions.
Table 3.
Urine water flow rates, solute concentrations, and osmolalities for the different cases
| Case | Water Flow | [Na], mM | [Urea], mM | Po2, mmHg | [NO], nM | [O2−], fM | Osmolality, mosmol/kgH2O |
|---|---|---|---|---|---|---|---|
| (1) Base | 0.706 | 281 | 598 | 3.31 | 83.9 | 3.82 | 1215 |
| (2) g(CNO) = 1 | 0.586 | 228 | 679 | 2.75 | 78.7 | 3.30 | 1223 |
| (3) h() = 0.7 | 0.769 | 312 | 539 | 4.13 | 94.6 | 4.54 | 1205 |
| (4) g(CNO) = 1, h() = 0.7 | 0.688 | 246 | 627 | 3.03 | 80.4 | 3.57 | 1184 |
| (5) × 10 | 0.693 | 263 | 609 | 2.66 | 72.6 | 31.3 | 1197 |
| (6) × 10, TQ × ½ | 0.737 | 309 | 551 | 1.46 | 47.8 | 18.7 | 1215 |
| (7) × 0.5 | 0.694 | 262 | 611 | 2.24 | 48.4 | 27.5 | 1195 |
| (8) × 0.5, TQ × ½ | 0.736 | 308 | 552 | 1.28 | 34.4 | 16.8 | 1214 |
| (9) DVR inflow = 12 nl/min | 0.909 | 210 | 520 | 6.81 | 122 | 6.44 | 987 |
| (10) DVR inflow = 9 nl/min | 0.740 | 262 | 578 | 4.21 | 96.5 | 4.59 | 1157 |
| (11) DVR inflow = 7 nl/min | 0.650 | 312 | 625 | 2.47 | 68.6 | 3.03 | 1307 |
| (12) DVR inflow = 6 nl/min | 0.630 | 329 | 635 | 1.31 | 31.7 | 1.84 | 1354 |
| (13) SNGFR = 42 nl/min | 3.59 | 137 | 381 | 5.60 | 71.3 | 5.82 | 662 |
| (14) SNGFR = 24 nl/min | 0.223 | 377 | 643 | 2.72 | 91.5 | 3.23 | 1572 |
Urine water flow rates are in nmol·min−1·nephron−1. Square brackets indicate concentration. SNGFR, single nephron glomerular filtration rate.
Next, we examined the extent to which superoxide affects active sodium transport by conducting a simulation in which O2−-mediated stimulation of active Na+ transport was abolished. That is, h() was set to 0.7 in Eq. 16. [In the base case, h() > 0.7.] In the absence of such stimulative effects, total TAL Na+ reabsorption decreases by 47%, and urine NaCl flow rate increases by 21% (from 0.198 to 0.240 nmol·min−1·nephron−1). The concentrating capacity of the model is slightly reduced, with an increase in urine flow from 0.706 to 0.769 nl/min and a decrease in urine osmolality from 1,215 to 1,205 mosmol/kgH2O (Table 3). In addition, Po2 increases throughout the regions (Fig. 2C), and the resulting higher rates of NO and O2− production are evident in the noticeably higher region NO and O2− concentrations (Figs. 3C and 4C). In other words, the model predicts that under basal conditions O2− substantially raises Na+ reabsorption to the detriment of medullary O2 levels.
To study these competing effects of NO and O2− on oxygenation and urine NaCl flow, we conducted a simulation in which both the NO and O2− effects on the maximum active transport rate were removed. That is, g(Ci,NO) was set to 1, and h(Ci,O2−) was set to 0.7 in Eq. 16. The net result is a 29% increase in TAL Na+ reabsorption and a 15% decrease in urine NaCl flow (from 0.198 to 0.169 nmol·min−1·nephron−1). Po2 decreases significantly throughout the regions (Fig. 2D), following more closely the NO-decoupled case than the O2−-decoupled case. The lower Po2 decreases NO production rate, resulting in significantly lower interstitial NO concentrations (similar to the NO-decoupled case, with minor differences). Region O2− concentrations also decrease slightly due to the lower O2− production rate with lower Po2.
It is somewhat surprising that removing the effects of both NO and O2− on Na+ transport yield a less concentrated urine than removing only the effect of O2−, given the diuretic effect of NO (see Table 3). This result can be attributed to the nonlinear interactions among O2, NO, and O2−, as concentrations of these solutes, used to determine Vmax,i,Na in Eq. 16, change significantly with g(Ci,NO) or h() set to constant values. In the inner stripe, where most of the active Na+ transport takes place, Vmax,i,Na is lowest in the case where the effects of both NO and O2− are removed. This is due to the nonlinear effects of O2, NO, and O2−, for even though Po2 is higher in this case than in the NO-decoupled case, the additional removal of O2− stimulation of active Na+ transport is enough to sufficiently lower Vmax,i,Na (see Fig. 6). This in turn causes osmolality to be lowest in this case.
Fig. 6.
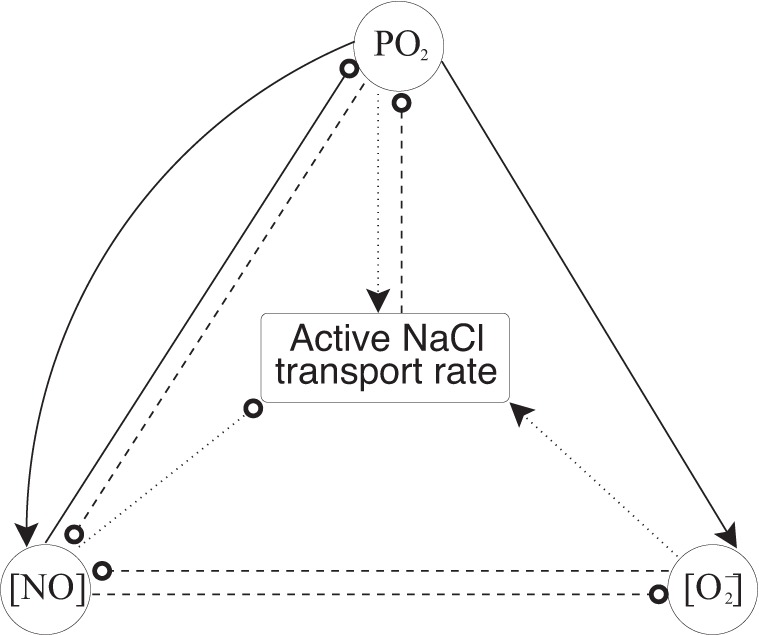
Feedback loop outlining the effects of O2, NO, and O2− on active NaCl transport rate. Solid lines indicate effects on production rate, dashed lines indicate effects on consumption rate, and dotted lines indicate effects on active NaCl transport rate (TNa). Arrows at the ends of lines indicate stimulation (or increase), whereas circles at the ends of lines indicate inhibition (or decrease).
Effects of sodium load on Po2 and NO and O2− concentrations.
Given the interdependence among the transport of Na+, O2, NO, and O2−, we then investigated the influence of Na+ delivery on Po2 and NO and O2− concentrations. To examine this, we varied the single nephron glomerular filtration rate (SNGFR) from 80 to 140% of its base-case value, that is, from 24 to 42 nl/min in the superficial nephrons and from 28.8 to 50.4 nl/min in the juxtamedullary nephrons (where base-case values are 30 and 36 nl/min, respectively).
Figure 5, A and B, shows values of effective ascending limb and CD Vmax vs. depth as SNGFR is varied, and Fig. 5C shows R4 Po2. In the OM, when SNGFR increases, Vmax increases overall and R4 Po2 decreases. Conversely, in the IM, when SNGFR increases, Vmax decreases and R4 Po2 increases. This difference in behavior comes from the dependence of Vmax on NO and O2−. Per se, the higher SNGFR enhances Na+ reabsorption and thus reduces Po2. This lowers NO and O2− production, which in turn affects Vmax. The net effect on Vmax is nonmonotonic, since NO inhibits and O2− stimulates Na+ reabsorption (i.e., lower NO and O2− concentrations does not necessarily imply higher or lower Vmax; it could be either, depending on the exact values of NO and O2− concentrations). As a consequence of this nonlinear behavior (Fig. 6), the predicted effects of an increase in SNGFR on Vmax (and thus Po2) are different in the OM and IM.
Fig. 5.
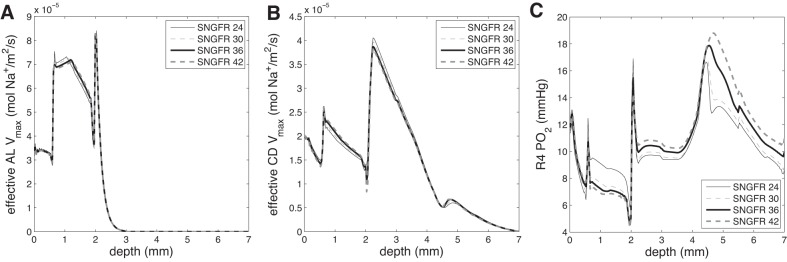
Effective ascending limb Vmax (A), effective CD Vmax (B), and R4 Po2 (C) vs. depth for superficial single nephron glomerular filtration rates (SNGFRs) of 24, 30 (base case), 36, and 42 nl/min.
Furthermore, urine Po2 is predicted to increase by 69% over base case when superficial nephron SNGFR is increased to 42 nl/min; conversely, there is an 18% decrease in urine Po2 when SNGFR decreases to 24 nl/min (Table 3). Table 3 also shows that when SNGFR increases, urine flow increases, and urine osmolality decreases; in addition, overall Na+ excretion increases with increasing SNGFR (as can be calculated from Table 3).
Effects of hypertension.
In hypertension, angiotensin II induces oxidative stress (32, 43), resulting in significantly lower renal tissue Po2 (42, 44, 64, 65). Reduced NO formation diminishes renal tissue Po2 further by decreasing medullary blood flow and therefore O2 supply. To simulate oxygenation in a hypertensive kidney, we raised the superoxide generation rate, by a factor of 10. As expected, the higher rate of superoxide production results in larger O2− concentrations in the regions and a significantly higher urine O2− concentration (Table 3). However, the increase in O2− concentration is severely damped by corresponding increases in superoxide consumption rates when O2− generation rates are increased. In addition, region Po2 and NO concentrations decrease, as higher superoxide levels stimulate NaCl reabsorption. As a result, urine NaCl flow rate decreases by 8.1% from 0.198 to 0.182 nmol·min−1·nephron−1.
Some evidence from in vivo rat micropuncture experiments exists suggesting that NO and/or reactive oxygen species limit the number of moles of Na+ that can be actively reabsorbed per mole of O2 consumed (63). Data from spontaneously hypertensive rats (64) suggest that the TQ ratio may be approximately halved when superoxide concentrations are significantly increased. Thus we simulated the situation where the superoxide generation rate was kept at 10 times the base-case value, while the TQ ratio for active sodium transport was halved. Lowering the TQ ratio significantly lowered Po2 and urine O2 flow rate (Table 3), as expected. In addition, urine NO flow rate (Table 3) and region NO concentrations were significantly decreased, due again to the fact that lower Po2 results in a lower NO generation rate. Furthermore, urine NaCl flow rate increased to 0.228 nmol·min−1·nephron−1 (calculated from Table 3), as NaCl active transport efficiency was reduced by half.
Some hypertensive rat models have indicated a decrease in NO production as well (33). Thus, we simulated a 50% decrease in the NO generation rate, along with a 10-fold increase in the O2− generation rate. Decreasing the NO generation rate by 50% decreased Po2 and NO and O2− region concentrations. In addition, with a 50% decrease in NO production, the urine osmolality fell to 1,195 mosmol/kgH2O. However, there was little effect on the urine NaCl flow rate, which remained at 0.182 nmol·min−1·nephron−1 (calculated from Table 3).
In addition, when the TQ ratio was halved, urine flow rates and osmolalities increased (Table 3); however, Po2 and NO and O2− concentrations were significantly decreased. The impact of the increase, Gi,NOmax decrease, and TQ ratio decrease on average R4 inner stripe Po2 is shown in Fig. 7. This interstitial region (R4), which contains the short ascending limb and CD (Fig. 1), was chosen as a proxy for a vulnerable part of the kidney to hypoxia, as it had a consistently lower Po2 than other regions and depths (see, for example, Fig. 2A). As can be seen in Fig. 7, all simulated hypertensive conditions resulted in lower Po2 levels than the base-case value of 7.9 mmHg. Increasing the O2− generation rate decreased the Po2 by 8.3%, with little change when Gi,NOmax was lowered by 50% in addition. However, lowering the TQ ratio by 50% further decreased Po2 by another 44%, suggesting that elevated oxidative stress (represented by a 10-fold increase in ) has much less of an impact on tissue oxygenation than metabolic dysfunction (represented by a halving of the TQ ratio) in hypertension.
Fig. 7.
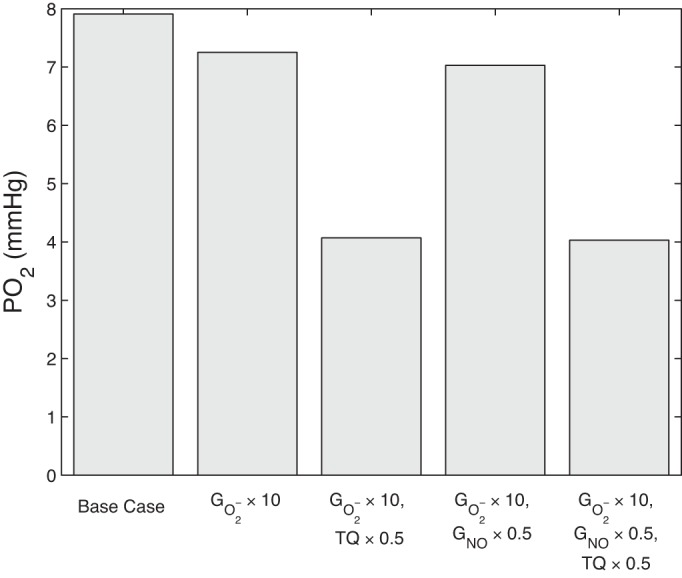
Average R4 inner stripe Po2 in the base case and under hypertensive conditions.
Effects of vascular inflow.
Blood flow in the medulla increases when renal hydrostatic pressure in the interstitium is elevated and is known to be modulated by the antidiuretic hormone (6, 7, 41, 59). To determine what effect medullary blood flow has on NO and superoxide, vascular inflow was varied between 6 and 12 nl/min at the cortico-medullary boundary (base-case inflow was 8 nl/min).
We first increased DVR inflow to 12 nl/min. Urine water flow increased by 29% (from 0.706 to 0.909 nl·min−1·nephron−1), and urine Po2 increased 2.1-fold (from 3.31 to 6.81 mmHg). Due to washout from high DVR flow rate, urine osmolality decreased by 19%, from 1,215 to 987 mosmol/kgH2O. Region Po2 increased significantly in both the OM and IM (Fig. 2E), with significant increases in region NO and O2− concentrations (Figs. 3E and 4E).
When the DVR flow rate was progressively lowered, Po2 and NO and O2− concentrations decreased concomitantly, accompanied by a steady increase in urine osmolality (Table 3). At the lower end, DVR inflow was decreased by 25% relative to base case, to 6 nl/min. Urine water flow decreased by 11% (from 0.706 to 0.630 nl·min−1·nephron−1), and urine Po2 decreased by 60% (from 3.31 to 1.31 mmHg). Due to less washout from DVR flow, urine osmolality increased by 11%, from 1,215 to 1,354 mosmol/kgH2O. Region Po2 decreased significantly in both the OM and IM (Fig. 2F), with significant decreases in region NO and O2− concentrations (Figs. 3F and 4F).
DISCUSSION
We extended a highly detailed mathematical model of NO and superoxide transport in the rat renal OM (13) to include the IM. The model yields predictions of NaCl, urea, O2, NO, and O2− concentrations in all represented structures (and of Hb, HbO2, and HbNO in the RBCs), as well as water and solute flow rates in all tubules and vessels. The model uses a region-based approach to represent the radial organization of medullary tubules and vessels, centered around vascular bundles in the OM and CD clusters in the IM. Model predictions suggest that the balance between NO and O2− affects medullary oxygenation and urine osmolality and that the nonlinear interactions between these solutes and oxygen lead to effects that cannot be determined by examining each in isolation. Furthermore, the results of the model shed some light on the mechanisms underlying the pathway to medullary hypoxia in hypertension and suggest that urine Po2 could serve as a biomarker for medullary hypoxia.
Comparison with experimental results.
NO concentration measurements in the rat renal IM range from 60 to 120 nM, generally measured in the upper half of the IM. In one study, NO concentration was measured as 79 nM at a depth of 1.5 mm below the OM-IM boundary (58). In another study at the same depth, NO concentration was measured as ∼120 nM (23). In a third study using the rat kidney, an NO concentration of ∼105 nM was measured at 1 mm below the OM-IM boundary (72). Model predictions from the present study generally lie within this range throughout the IM, with small discrepancies: NO concentration averages 24 nM in R1, 16 nM in R2, 100 nM in R3, and 293 nM in R4. Due to the highly structured organization of the renal medulla, the model predicts large radial and axial gradients in NO concentration; thus average predicted NO concentrations are on the same order of magnitude as experimental measurements but with a fairly large variation.
In the OM, one study measured NO concentration as ∼796 nM, using differential pulsed voltammetry (53), a different technique than the one used in the other studies. Model predictions in the OM are noticeably below this value, closer to the experimental range measured in the IM: NO concentration averages 23 nM in R1, 21 nM in R2, 74 nM in R3, and 61 nM in R4. Because these predictions are similar to measurements in other parts of the medulla, it is likely that the discrepancy is due to the difference in experimental technique, one that yields a measurement an order of magnitude larger than previous experiments.
As also noted in Base case results, we are unaware of direct measurements of O2− concentration in the renal medulla. Previous modeling work suggests that O2− concentrations lie in the range of 0.1 to 1 nM (3, 13), and model predictions from the present study are generally contained within this interval throughout the OM and IM. In the OM, predicted O2− concentrations average 2.2 nM in R1, 1.9 nM in R2, 1.0 nM in R3, and 0.97 nM in R4. In the IM, predicted O2− concentrations average 0.50 nM in R1, 0.14 nM in R2, 0.16 nM in R3, and 0.32 nM in R4. If experimental measurements of O2− concentration in the renal medulla are made in the future, we will be able to better validate these model predictions.
Comparison with previous models.
The main difference between the present model and our previous NO and O2− transport model (13) is that the current one includes the whole medulla, whereas the old one included only the OM. The most important consequence of this change is that the current model allows for explicit prediction of IM flow rates, concentrations, and papillary outflows, instead of making bulk assumptions about IM behavior based on the OM model. For instance, the previous NO-O2− model assumed that O2 consumption in the IM was a fixed 5% of O2 supply to the OM; however, simulations from the present model that explicitly include the IM architecture predict that IM O2 consumption is 11% of medullary O2 supply. Thus our current whole medulla model provides a richer set of predictions than the previous study.
In contrast with our previous whole medulla O2 transport model (15), the present model explicitly represents NO and O2− and thus takes into account the nonlinear interactions among O2, NO, and O2−. Specifically, the previous model did not take into account the impact of NO and O2− on Po2 via modulation of the active transport of NaCl and the concomitant modulation of O2 consumption. In particular, the previous O2 model predicted interstitial Po2 levels ∼2–3 mmHg lower than the current model; this discrepancy is largely due to NO inhibition of active sodium transport in the current model, which leads to higher Po2 levels. This reveals the mitigating effects of NO on medullary hypoxia that could not be gleaned from our previous study.
Feedback among O2, NO, and O2−.
Results of the model suggest that NO and O2− significantly modulate renal function. However, the effects of NO and superoxide on NaCl transport cannot be considered in isolation, due to the feedback loops among O2, NO, and O2− (Fig. 6).
The generation rates of both NO and O2− are oxygen dependent, with higher Po2 resulting in a higher production rate. In a previous model (13), we considered two possibilities for Po2 effects on O2− synthesis, both inhibition and stimulation. Results from Chen et al. (5) provided stronger evidence for the latter case, demonstrating a drop in O2− production during hypoxia; thus, we assumed stimulating effects in the present study.
The consumption rates of O2, NO, and O2− are all interdependent, as well. Both NO and superoxide are consumed at rates proportional to the product of the local NO and O2− concentrations; thus the two solutes are mutual scavengers. In addition, due to the dependence of the Michaelis constant in Eq. 12 on NO, the rate of basal O2 consumption decreases with increasing NO concentration.
All of these solutes then affect the rate of active NaCl transport, which itself modulates Po2. As seen in Eq. 16, the maximum NaCl transport rate increases with increases in oxygen and superoxide concentration and decreases with growing NO concentrations.
NO and O2− scavenge each other and have opposite effects on NaCl transport and therefore on O2 consumption. Given these complicated interactions among oxygen, NO, and superoxide, a somewhat unexpected result is that NO and O2− concentrations seem to always vary in tandem with Po2. This strong Po2 dependence of medullary NO and O2− concentrations suggests that medullary oxygenation may be a primary factor in the regulation of blood flow and blood pressure in the kidney.
Urine salt excretion.
An important aspect of medullary function that the present whole medulla model can predict, whereas previous models could not, is the impact of NO and superoxide on urine salt excretion. In the base case, which includes the effects of NO and O2− on NaCl active transport, urine sodium flow rate is predicted to be 0.198 nmol·min−1·nephron−1.
If NO did not have an inhibitory effect on active NaCl transport, urine sodium flow rate would drop by 32% (to 0.134 nmol·min−1·nephron−1); however, due to a concomitant decrease in urine water flow rate, urine osmolality would slightly increase. In other words, the net impact of NO is to lower urine osmolality. Conversely, if O2− did not have a stimulating effect on active NaCl transport, urine sodium flow rate would rise by 21% (to 0.240 nmol·min−1·nephron−1), but urine osmolality would slightly decrease due to an increase in urine water flow rate. Stated differently, the net impact of O2− is to raise urine osmolality. If neither NO nor O2− had an effect on NaCl active transport, urine water and sodium flow rates would both decrease compared with the base case, such as in the absence of NO effects only, but urine osmolality would also noticeably decrease. Due to the nonlinear feedback loops, the effect on osmolality of removing both NO- and O2−-mediated regulation is not merely an average of the effects of removing NO- and O2−-mediated regulation in isolation. That is, it is the combined effect of NO and O2− that helps to keep urine osmolality at a higher level. We should point out that the model does not assume that NO and O2− are from the same enzyme source. To the best of our knowledge, the principal enzymes that catalyze the production of NO and superoxide, NO synthases and NADPH oxidases, are different under most conditions. Under diabetic conditions, endothelial dysfunction can result in endothelial NO synthase (eNOS) “uncoupling,” which may lead to eNOS producing superoxide instead of (or in addition to) NO (18). The concentrations we are matching to infer the NO and O2− generation rates do not involve diabetes; thus we are implicitly assuming that the enzymes that catalyze their formation sources are different in this model.
Hypertension.
Renal tissue Po2 has been shown to be significantly lower in several models of experimental hypertension, including the spontaneously hypertensive rat; the two-kidney, one-clip model; and angiotensin II-induced hypertension (42, 44, 64, 65). One contributing factor for low renal tissue Po2 in hypertension is the increased oxidative stress induced by angiotensin II. Elevated oxidative stress reduces tubular transport efficiency, causes mitochondrial uncoupling, and leads to increased O2 consumption (43). Furthermore, reduced NO formation increases tubular transport but reduces O2 supply.
Model results suggest that a sufficiently large reduction in tubular transport efficiency may be the key contributing factor to hypertension-induced medullary hypoxia (Table 2). More specifically, under hypertensive conditions, and no change in the TQ ratio, urine sodium excretion and osmolality both decrease (by 8.1 and 1.6%, respectively). If it is assumed that hypertension further results in a 50% decrease in the TQ ratio, osmolality increases back to base-case levels, and urine sodium excretion increases above base-case levels. However (see Fig. 7), a reduction in the TQ ratio results in a significant decrease in Po2, potentially leaving the kidney vulnerable to hypoxic injury. This indicates that elevated oxidative stress on its own may have less impact than the subsequent metabolic dysfunction on the progression of medullary hypoxia due to hypertension.
Other factors, not considered in the present study, also contribute to the development of renal hypoxia in a hypertensive kidney. At the onset of hypertension, renal autoregulation effectively prevents the transmission of the elevated systolic blood pressure to the glomeruli or peritubular capillaries. Renal autoregulation is mediated by several mechanisms: the myogenic response, which is a property of the preglomerular vasculature wherein a rise in intravascular pressure elicits a reflex constriction that generates a compensatory increase in vascular resistance; and tubuloglomerular feedback, a negative feedback response that balances glomerular filtration rate with tubular reabsorptive capacity (10, 19, 22). However, as hypertension progresses, renal arteries, including the afferent arterioles, undergo pathological alterations, such that vasodilation becomes impaired. Autoregulation is compromised, and as a consequence a temporary reduction in blood pressure can impair renal perfusion (20, 24). In the absence of a compensatory increase in O2 delivery, these pathological changes may also explain renal tissue hypoxia and thus eventually, chronic kidney diseases.
Urine Po2 as a biomarker.
The present model allowed us to investigate whether urinary Po2 could be used as a biomarker for renal hypoxia, which is a pathway to acute kidney injury (AKI). As a motivation, we note that AKI is a prevalent complication of surgical procedures including cardiac surgeries that require cardiopulmonary bypass (24). Diagnosis of AKI is usually based on either an elevation of serum creatinine or the detection of oliguria (34). Serum creatinine is a poor marker of early renal dysfunction, because its serum concentration is greatly influenced by numerous nonrenal factors (e.g., body weight, race, age, gender, total body volume, drugs, muscle metabolism, and protein intake) (2). The utility of serum creatinine is worse in AKI, because the patients are not in steady state; hence, serum creatinine lags far behind renal injury. Thus substantial rises in serum creatinine are often not witnessed until 48–72 h after the initial insult to the kidney (34, 55).
Evans et al. (14) recently suggested that urine in the CDs should equilibrate with tissue Po2 in the IM. Accordingly, the Po2 of urine in the renal pelvis may change in response to stimuli that would be expected to alter oxygenation of the renal medulla. Thus they proposed that urinary Po2 may be a predictor of AKI risk in hospital settings. It is noteworthy that the renal structures that are most susceptible to hypoxic injuries are the TALs and proximal tubules in the OM; therefore, even if urinary Po2 equilibrates with the IM tissue Po2, what does it tell us about the OM, a much more vulnerable region?
We thus analyzed our simulation results to determine the relationship between OM tissue and urinary Po2. Note that these simulations do not represent the most common conditions that lead to hospital-acquired AKI, e.g., cardiac surgery performed under cardiopulmonary bypass. Rather, model parameters were adjusted to simulate hypertension and other conditions that affect medullary oxygenation. Nonetheless, we hoped to obtain new insights regarding the potential of urinary Po2 as a prognostic tool to guide the on-going management of renal health in patients. We compared urinary Po2 against the luminal Po2 of the most vulnerable segment, i.e., the short TAL in the inner stripe, for all the cases considered in Table 3. Model results, shown in Fig. 8, indicate a strong correlation between urinary and short TAL Po2. The lone outlier is case 3 (with hactive,SOX = 0.7), where the effect of O2− on TAL active transport is disabled, producing a substantially higher medullary Po2. This case bears little resemblance to the physiological conditions that lead to AKI. Thus our model simulations suggest that urinary Po2 may be used as a prognostic tool in monitoring the renal health in patients undergoing surgeries with AKI as a known complication, especially in patients with hypertension, diabetes, and chronic kidney diseases, who are believed to be at elevated risk for developing hospital-acquired AKI.
Fig. 8.
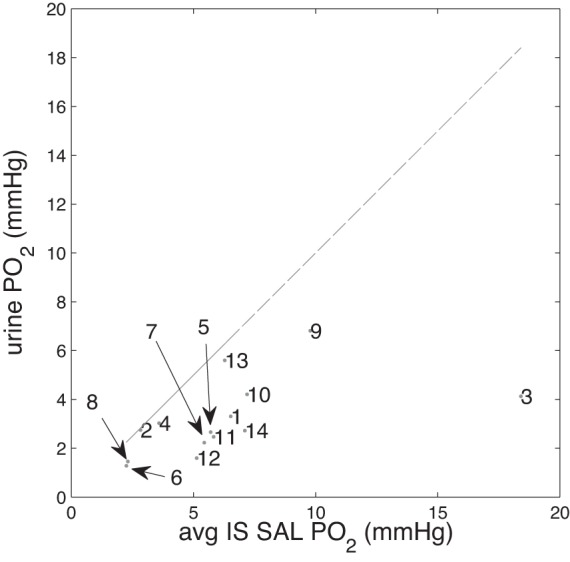
Urine Po2 vs. average inner stripe short ascending limb (IS SAL) Po2 (mmHg) for all cases in results. Numbers (1–14) correspond to those listed in Table 3 (e.g., marker “9” in figure corresponds to the urine Po2 and average inner stripe short ascending limb Po2 in the “DVR inflow = 12 nl/min” simulation).
Model limitations and future extensions.
The model in the present study is necessarily limited by the dearth of experimental data concerning medullary NO and superoxide. As noted above, measurements of NO in the medulla vary over an order of magnitude, and we are unaware of any absolute measurements of O2− in the medulla. Thus experiments measuring NO and superoxide levels at various depths of the renal medulla would help to validate model assumptions concerning baseline generation rates. In addition, model parameters related to the effects of NO and O2− on active Na+ transport are uncertain, due a lack of quantitative data. We estimated these processes and values based on the scarce available data, but measurements of transport rates or reabsorption in the presence of different amounts of NO and O2− would allow for better estimation of parameters in the model. That being said, it is precisely because experimental studies in this area are difficult and scarce that a modeling approach can be helpful. Predictions from the model provide suggestions for future experiments. In particular, the predicted relationships among NO, O2−, and Po2 suggest experiments involving alteration of renal Po2 and determining what effect (if any) this has on regulation of blood pressure and renal blood flow; the results of such experiments could either be used to validate our modeling approach or serve as a guide to improve the model.
Renal oxygenation is the result of a delicate balance between O2 supply and demand, and that relation changes in diseased states. The present model represents solute transport and reactions in the renal medulla; however, the renal autoregulatory mechanisms, which control renal and medullary blood flow and thus O2 supply, are not represented. Medullary blood flow is assumed to be known a priori, even though NO is known to cause vasodilation and to increase blood flow. Hence, the present model cannot be used to assess the extent to which impairment of renal autoregulation in diseases such as diabetes and hypertension (see above) gives rise to renal hypoxia. It is our goal to extend the present model to represent the whole kidney (similar to Ref. 36) and to incorporate tubuloglomerular feedback and the myogenic response. The autoregulatory mechanisms can be represented using our published model (54). The resulting model could then be used to study the development of renal hypoxia in diabetes and hypertension and the mechanisms underlying the pathways to chronic kidney diseases.
GRANTS
This research was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK-089066.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: B.C.F., A.E., and A.T.L. conception and design of research; B.C.F. performed experiments; B.C.F., A.E., and A.T.L. analyzed data; B.C.F., A.E., and A.T.L. interpreted results of experiments; B.C.F. prepared figures; B.C.F. and A.T.L. drafted manuscript; B.C.F., A.E., and A.T.L. edited and revised manuscript; B.C.F., A.E., and A.T.L. approved final version of manuscript.
REFERENCES
- 1.Bagnasco S, Good D, Balaban R, Burg M. Lactate production in isolated segments of the rat nephron. Am J Physiol Renal Fluid Electrolyte Physiol 248: F522–F526, 1985. [DOI] [PubMed] [Google Scholar]
- 2.Bjornsson TD. Use of serum creatinine concentrations to determine renal function. Clin Pharmacokinet 4: 200–222, 1979. [DOI] [PubMed] [Google Scholar]
- 3.Buerk D, Lamkin-Kennard K, Jaron D. Modeling the influence of superoxide dismutase on superoxide and nitric oxide interactions, including reversible inhibition of oxygen consumption. Free Radic Biol Med 34: 1488–1503, 2003. [DOI] [PubMed] [Google Scholar]
- 4.Chen J, Layton AT, Edwards A. A mathematical model of oxygen transport in the rat outer medulla: I. Model formulation and baseline results. Am J Physiol Renal Physiol 297: F517–F536, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen Y, Gill PS, Welch WJ. Oxygen availability limits renal NADPH-dependent superoxide production. Am J Physiol Renal Physiol 289: F749–F753, 2005. [DOI] [PubMed] [Google Scholar]
- 6.Correia AG, Denton KM, Evans RG. Effects of activation of vasopressin-V1-receptors on regional kidney blood flow and glomerular arteriole diameters. J Hypertens 19: 649–657, 2001. [DOI] [PubMed] [Google Scholar]
- 7.Cowley AW., Jr Control of the renal medullary circulation by vasopressin v1 and v2 receptors in the rat. Exp Physiol 85: 223s–231s, 2000. [DOI] [PubMed] [Google Scholar]
- 8.Cowley AW., Jr Renal medullary oxidative stress, pressure-natriuresis, and hypertension. Hypertension 52: 777–786, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cowley AW Jr, Mori T, Mattson D, Zou AP. Role of renal NO production in the regulation of medullary blood flow. Am J Physiol Regul Integr Comp Physiol 284: R1355–R1369, 2003. [DOI] [PubMed] [Google Scholar]
- 10.Cupples WA, Braam B. Assessment of renal autoregulation. Am J Physiol Renal Physiol 292: F1105–F1123, 2007. [DOI] [PubMed] [Google Scholar]
- 11.Dickman KG, Mandel LJ. Differential effects of respiratory inhibitors on glycolysis in proximal tubules. Am J Physiol Renal Fluid Electrolyte Physiol 258: F1608–F1615, 1990. [DOI] [PubMed] [Google Scholar]
- 12.Edwards A, Layton AT. Nitric oxide and superoxide transport in a cross section of the rat outer medulla. I. Effects of low medullary oxygen tension. Am J Physiol Renal Physiol 299: F616–F633, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Edwards A, Layton AT. Modulation of outer medullary NaCl transport and oxygenation by nitric oxide and superoxide. Am J Physiol Renal Physiol 301: F979–F996, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Evans RG, Smith JA, Wright C, Gardiner BS, Smith DW, Cochrane AD. Urinary oxygen tension: a clinical window on the health of the renal medulla? Am J Physiol Regul Integr Comp Physiol 306: R45–R50, 2014. [DOI] [PubMed] [Google Scholar]
- 15.Fry BC, Edwards A, Sgouralis I, Layton AT. Impact of renal medullary three-dimensional architecture on oxygen transport. Am J Physiol Renal Physiol 307: F263–F272, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Garvin JL, Ortiz PA. The role of reactive oxygen species in the regulation of tubular function. Acta Physiol Scand 179: 225–232, 2003. [DOI] [PubMed] [Google Scholar]
- 17.Greger R, Schlatter E, Lang F. Evidence for electroneutral sodium chloride cotransport in the cortical thick ascending limb of Henle's loop of rabbit kidney. Pflügers Arch 396: 308–314, 1983. [DOI] [PubMed] [Google Scholar]
- 18.Guzik TJ, Mussa S, Gastaldi D, Sadowski J, Ratnatunga C, Pillai R, Channon KM. Mechanisms of increased vascular superoxide production in human diabetes mellitus: role of NAD(P)H oxidase and endothelial nitric oxide synthase. Circulation 105: 1656–1662, 2002. [DOI] [PubMed] [Google Scholar]
- 19.Holstein-Rathlou NH, Marsh DJ. Renal blood flow regulation and arterial pressure fluctuations: a case study in nonlinear dynamics. Physiol Rev 74: 637–681, 1994. [DOI] [PubMed] [Google Scholar]
- 20.Iversen BM, Sekse I, Ofstad J. Resetting of renal blood flow autoregulation in spontaneously hypertensive rats. Am J Physiol Renal Fluid Electrolyte Physiol 252: F480–F486, 1987. [DOI] [PubMed] [Google Scholar]
- 21.Juncos NJ, Garvin JL. Differential effects of superoxide on luminal and basolateral Na+/H+ exchange in the thick ascending limb. Am J Physiol Regul Integr Comp Physiol 290: R79–R83, 2006. [DOI] [PubMed] [Google Scholar]
- 22.Just A. Mechanisms of renal blood flow autoregulation: dynamics and contributions. Am J Physiol Regul Integr Comp Physiol 292: R1–R17, 2007. [DOI] [PubMed] [Google Scholar]
- 23.Kakoki M, Kim HS, Arendshorst WJ, Mattson DL. l-Arginine uptake affects nitric oxide production and blood flow in the renal medulla. Am J Physiol Regul Integr Comp Physiol 287: R1478–R1485, 2004. [DOI] [PubMed] [Google Scholar]
- 24.Karkouti KE, Wijeysundera DN, Yau TM, Callum JL, Cheng DC, Crowther M, Dupuis JY, Fremes SE, Kent B, Laamme C, Lamy A, Legare JF, Mazer CD, Mc-Cluskey SA, Rubens FD, Sawchuk C, Beattie WS. Acute kidney injury after cardiac surgery: focus on modifiable risk factors. Circulation 119: 295–502, 2009. [DOI] [PubMed] [Google Scholar]
- 25.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla: I. Formulation and base-case results. Am J Physiol Renal Physiol 300: F356–F371, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla: II. Functional implications of three-dimensional architecture. Am J Physiol Renal Physiol 300: F372–F394, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Layton AT, Dantzler WH, Pannabecker TL. Urine concentrating mechanism: impact of vascular and tubular architecture and a proposed descending limb urea-Na+ cotransporter. Am J Physiol Renal Physiol 302: F591–F605, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Layton AT, Layton HE. A region-based mathematical model of the urine concentrating mechanism in the rat outer medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol 289: F1346–F1366, 2005. [DOI] [PubMed] [Google Scholar]
- 29.Layton HE, Pitman EB, Moore LC. Bifurcation analysis of TGF-mediated oscillations in SNGFR. Am J Physiol Renal Fluid Electrolyte Physiol 261: F904–F919, 1991. [DOI] [PubMed] [Google Scholar]
- 30.Lemley KV, Kriz W. Cycles and separations: the histotopography of the urinary concentrating process. Kidney Int 31: 538–548, 1987. [DOI] [PubMed] [Google Scholar]
- 31.Li N, Yi FX, Spurrier JL, Bobrowitz CA, Zou AP. Production of superoxide through NADPH oxidase in thick ascending limb of Henle's loop in rat kidney. Am J Physiol Renal Physiol 282: F1111–F1119, 2002. [DOI] [PubMed] [Google Scholar]
- 32.Makino A, Skelton MM, Zou AP, Roman RJ, Cowley AW Jr. Increased renal medullary oxidative stress produces hypertension. Hypertension 39: 667–672, 2002. [DOI] [PubMed] [Google Scholar]
- 33.Manning RD Jr, Hu L, Tan DY, Meng S. Role of abnormal nitric oxide systems in salt-sensitive hypertension. Am J Hypertens 14: 68S–73S, 2001. [DOI] [PubMed] [Google Scholar]
- 34.Mehta RL, Chertow GM. Acute renal failure definitions and classification: time for change? J Am Soc Nephrol 14: 2178–2187, 2003. [DOI] [PubMed] [Google Scholar]
- 35.Miyata N, Cowley AW Jr. Renal medullary interstitial infusion of l-arginine prevents reduction of medullary blood flow and hypertension in Dahl salt-sensitive rats. Hypertension 33: 446–450, 1999. [DOI] [PubMed] [Google Scholar]
- 36.Moss R, Layton AT. Dominant factors that govern pressure natriuresis in diuresis and antidiuresis: a mathematical model. Am J Physiol Renal Physiol 306: F952–F969, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nieves-Gonzalez A, Clausen C, Layton AT, Layton HE, Moore LC. Transport efficiency and workload distribution in a mathematical model of the thick ascending limb. Am J Physiol Renal Physiol 304: F653–F664, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ortiz PA, Garvin JL. Role of nitric oxide in the regulation of nephron transport. Am J Physiol Renal Physiol 282: F777–F784, 2002. [DOI] [PubMed] [Google Scholar]
- 39.Ortiz PA, Garvin JL. Superoxide stimulates NaCl absorption by the thick ascending limb. Am J Physiol Renal Physiol 283: F957–F962, 2002. [DOI] [PubMed] [Google Scholar]
- 40.Ortiz PA, Hong NJ, Garvin JL. NO decreases thick ascending limb chloride absorption by reducing Na+-K+-2Cl− cotransporter activity. Am J Physiol Renal Physiol 281: F819–F825, 2001. [DOI] [PubMed] [Google Scholar]
- 41.Pallone TL, Turner MR, Edwards A, Jamison RL. Countercurrent exchange in the renal medulla. Am J Physiol Regul Integr Comp Physiol 284: R1153–R1175, 2003. [DOI] [PubMed] [Google Scholar]
- 42.Palm F, Connors SG, Mendonca M, Welch WJ, Wilcox CS. Angiotensin II type 2 receptors and nitric oxide sustain oxygenation in the clipped kidney of early Goldblatt hypertensive rats. Hypertension 51: 345–351, 2008. [DOI] [PubMed] [Google Scholar]
- 43.Palm F, Nordquist L. Renal oxidative stress, oxygenation, and hypertension. Am J Physiol Regul Integr Comp Physiol 301: R1229–R1241, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Palm F, Onozato M, Welch WJ, Wilcox CS. Blood pressure, blood flow, and hypertension in the clipped kidney of chronic 2-kidney, 1-clip rats: effects of tempol and angiotensin blockade. Hypertension 55: 298–304, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Panico C, Luo Z, Damiano S, Artigiano F, Gill P, Welch WJ. Renal proximal tubular reabsorption is reduced in adult spontaneously hypertensive rats: roles of superoxide and Na+/H+ exchanger 3. Hypertension 54: 1291–1297, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Pannabecker TL, Abbott DE, Dantzler WH. Three-dimensional functional reconstruction of inner medullary thin limbs of Henle's loop. Am J Physiol Renal Physiol 286: F38–F45, 2004. [DOI] [PubMed] [Google Scholar]
- 47.Pannabecker TL, Dantzler WH. Three-dimensional lateral and vertical relationship of inner medullary loops of Henle and collecting duct. Am J Physiol Renal Physiol 287: F767–F774, 2004. [DOI] [PubMed] [Google Scholar]
- 48.Pannabecker TL, Dantzler WH. Three-dimensional architecture of inner medullary vasa recta. Am J Physiol Renal Physiol 290: F1355–F1366, 2006. [DOI] [PubMed] [Google Scholar]
- 49.Pannabecker TL, Dantzler WH. Three-dimensional architecture of collecting ducts, loops of Henle, and blood vessels in the renal papilla. Am J Physiol Renal Physiol 293: F696–F704, 2007. [DOI] [PubMed] [Google Scholar]
- 50.Pech V, Thumova M, Dikalov SI, Hummler E, Rossier BC, Harrison DG, Wall SM. Nitric oxide reduces Cl− absorption in the mouse cortical collecting duct through an ENaC-dependent mechanism. Am J Physiol Renal Physiol 304: F1390–F1397, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Persson P, Hansell P, Palm F. NADPH oxidase inhibition reduces tubular sodium transport and improves kidney oxygenaton in diabetes. Am J Physiol Regul Integr Comp Physiol 302: R1443–R1449, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Plato CF, Stoos BA, Wang D, Garvin JL. Endogenous nitric oxide inhibits chloride transport in the thick ascending limb. Am J Physiol Renal Physiol 276: F159–F163, 1999. [DOI] [PubMed] [Google Scholar]
- 53.Salom MG, Arregui B, Carbonell LF, Ruiz F, González-Mora JL, Fenoy FJ. Renal ischemia induces an increase in nitric oxide levels from tissue stores. Am J Physiol Regul Integr Comp Physiol 289: R1459–R1466, 2005. [DOI] [PubMed] [Google Scholar]
- 54.Sgouralis I, Layton AT. Theoretical assessment of renal autoregulatory mechanisms. Am J Physiol Renal Physiol 306: F1357–F1371, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Star RA. Treatment of acute renal failure. Kidney Int 54: 1817–1831, 1998. [DOI] [PubMed] [Google Scholar]
- 56.Stokes JB, Grupp C, Kinne RK. Purification of rat papillary collecting duct cells: functional and metabolic assessment. Am J Physiol Renal Fluid Electrolyte Physiol 253: F251–F262, 1987. [DOI] [PubMed] [Google Scholar]
- 57.Sun P, Yue P, Wang WH. Angiotensin II stimulates epithelial sodium channels in the cortical collecting duct of the rat kidney. Am J Physiol Renal Physiol 302: F679–F687, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Szentiványi M, Park F, Maeda CY, Cowley AW Jr. Nitric oxide in the renal medulla protects from vasopressin-induced hypertension. Hypertension 35: 740–745, 2000. [DOI] [PubMed] [Google Scholar]
- 59.Turner MR, Pallone TL. Vasopressin constricts outer medullary descending vasa recta isolated from rat kidneys. Am J Physiol Renal Physiol 272: F147–F151, 1997. [DOI] [PubMed] [Google Scholar]
- 60.Uchida S, Endou H. Substrate specificity to maintain cellular ATP along the mouse nephron. Am J Physiol Renal Fluid Electrolyte Physiol 255: F977–F983, 1988. [DOI] [PubMed] [Google Scholar]
- 61.Wang T. Nitric oxide regulates HCO3− and Na+ transport by a cGMP-mediated mechanism in the kidney proximal tubule. Am J Physiol Renal Physiol 272: F242–F248, 1997. [DOI] [PubMed] [Google Scholar]
- 62.Weinstein AM. A mathematical model of the inner medullary collecting duct of the rat: pathways for Na and K transport. Am J Physiol Renal Physiol 274: F841–F855, 1998. [DOI] [PubMed] [Google Scholar]
- 63.Welch WJ. Intrarenal oxygen and hypertension. Clin Exp Pharmacol Physiol 33: 1002- 1005, 2006. [DOI] [PubMed] [Google Scholar]
- 64.Welch WJ, Baumgartl H, Lubbers D, Wilcox CS. Nephron Po2 and renal oxygen usage in the hypertensive rat kidney. Kidney Int 59: 230–237, 2001. [DOI] [PubMed] [Google Scholar]
- 65.Welch WJ, Blau J, Xie H, Chabrashvili T, Wilcox CS. Angiotensin-induced defects in renal oxygenation: role of oxidative stress. Am J Physiol Heart Circ Physiol 288: H22–H28, 2005. [DOI] [PubMed] [Google Scholar]
- 66.Whorton AR, Simonds DB, Piantadosi CA. Regulation of nitric oxide synthesis by oxygen in vascular endothelial cells. Am J Physiol Lung Cell Mol Physiol 272: L1161–L1166, 1997. [DOI] [PubMed] [Google Scholar]
- 67.Wu F, Park F, Cowley AW Jr, Mattson DL. Quantification of nitric oxide synthase activity in microdissected segments of the rat kidney. Am J Physiol Renal Physiol 276: F874–F881, 1999. [DOI] [PubMed] [Google Scholar]
- 68.Zeidel ML, Silva P, Seifter JL. Intracellular pH regulation and proton transport by rabbit renal medullary collecting duct cells: role of plasma membrane proton adenosine triphosphatase. J Clin Invest 77: 113–120, 1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Zhang W, Pibulsonggram T, Edwards A. Determinants of basal nitric oxide concentration in the renal medullary microcirculation. Am J Physiol Renal Physiol 287: F1189–F1203, 2004. [DOI] [PubMed] [Google Scholar]
- 70.Zhou AP, Cowley AW Jr. α2-Adrenergic receptor-mediated increase in NO production buffers renal medullary microcirculation. Am J Physiol Regul Integr Comp Physiol 279: R769–R777, 2000. [DOI] [PubMed] [Google Scholar]
- 71.Zhou AP, Li N, Cowley AW Jr. Production and actions of superoxide in the renal medulla. Hypertension 37: 547–553, 2001. [DOI] [PubMed] [Google Scholar]
- 72.Zhou AP, Wu F, Cowley AW Jr. Protective effect of angiotensin II-induced increase in nitric oxide in the renal medullary circulation. Hypertension 31: 271–276, 1998. [DOI] [PubMed] [Google Scholar]